Epitaxial Graphene on SiC: A Review of Growth and Characterization
Abstract
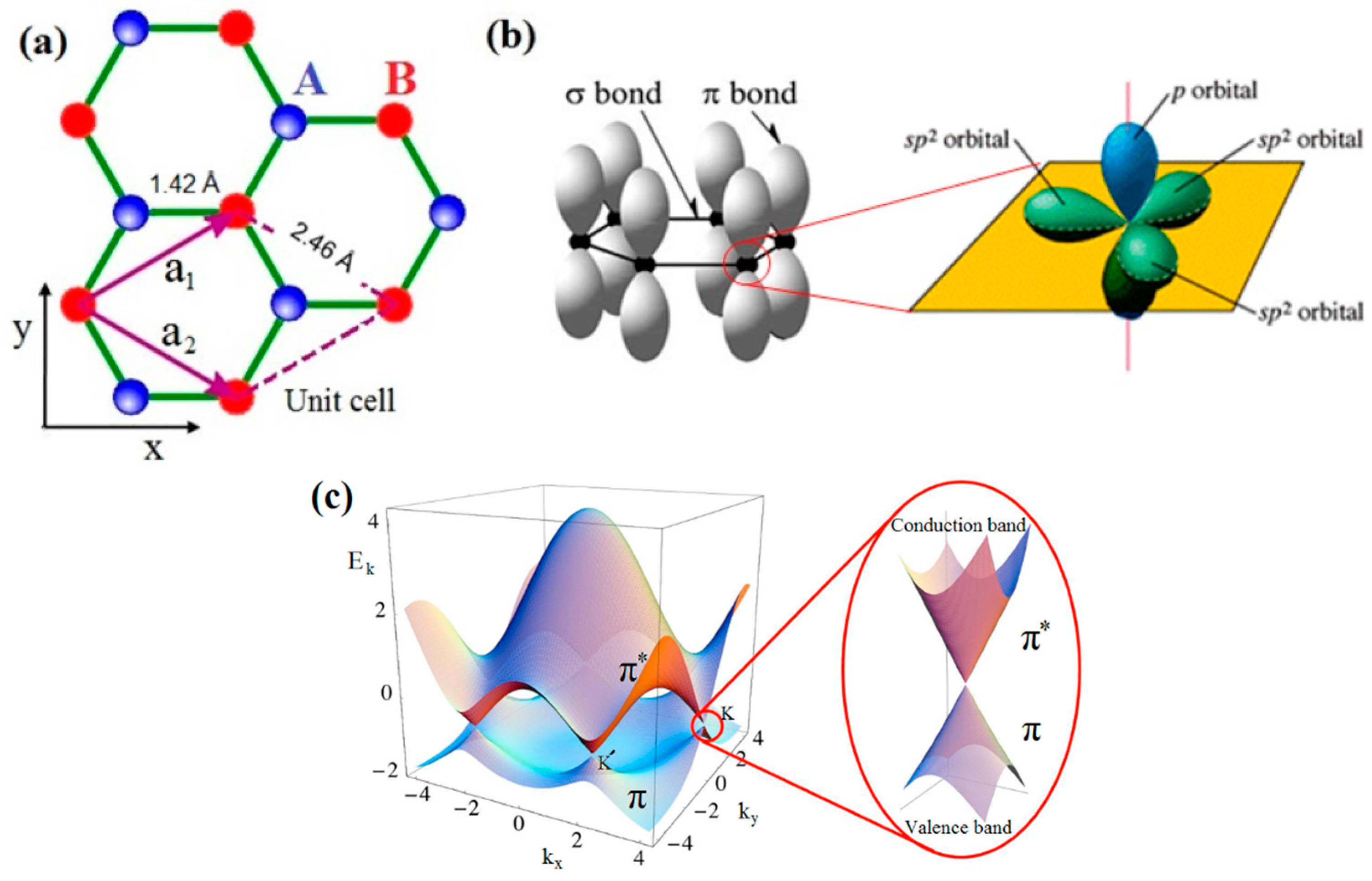
:1. Introduction
2. Main Methods for Graphene Characterization
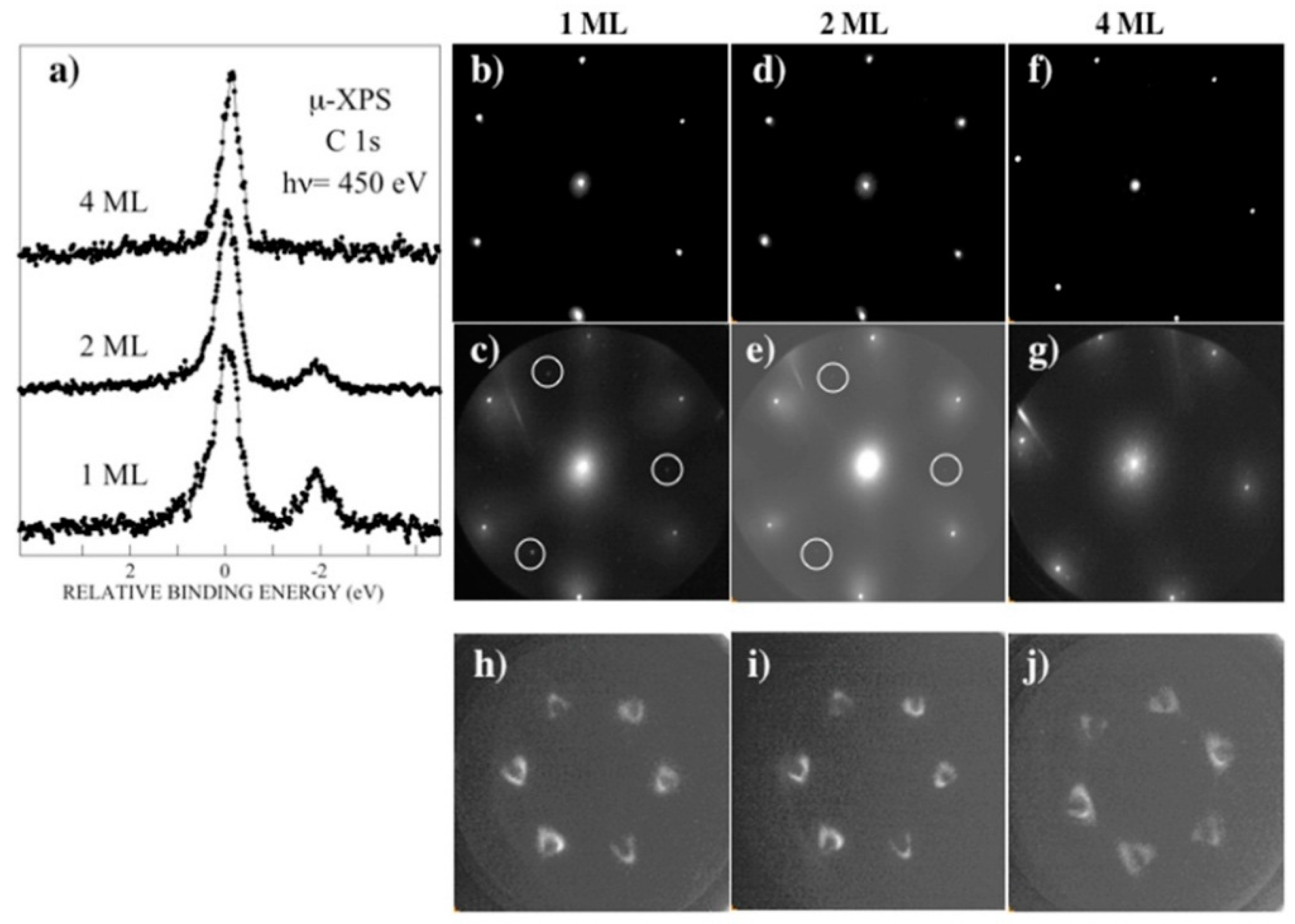
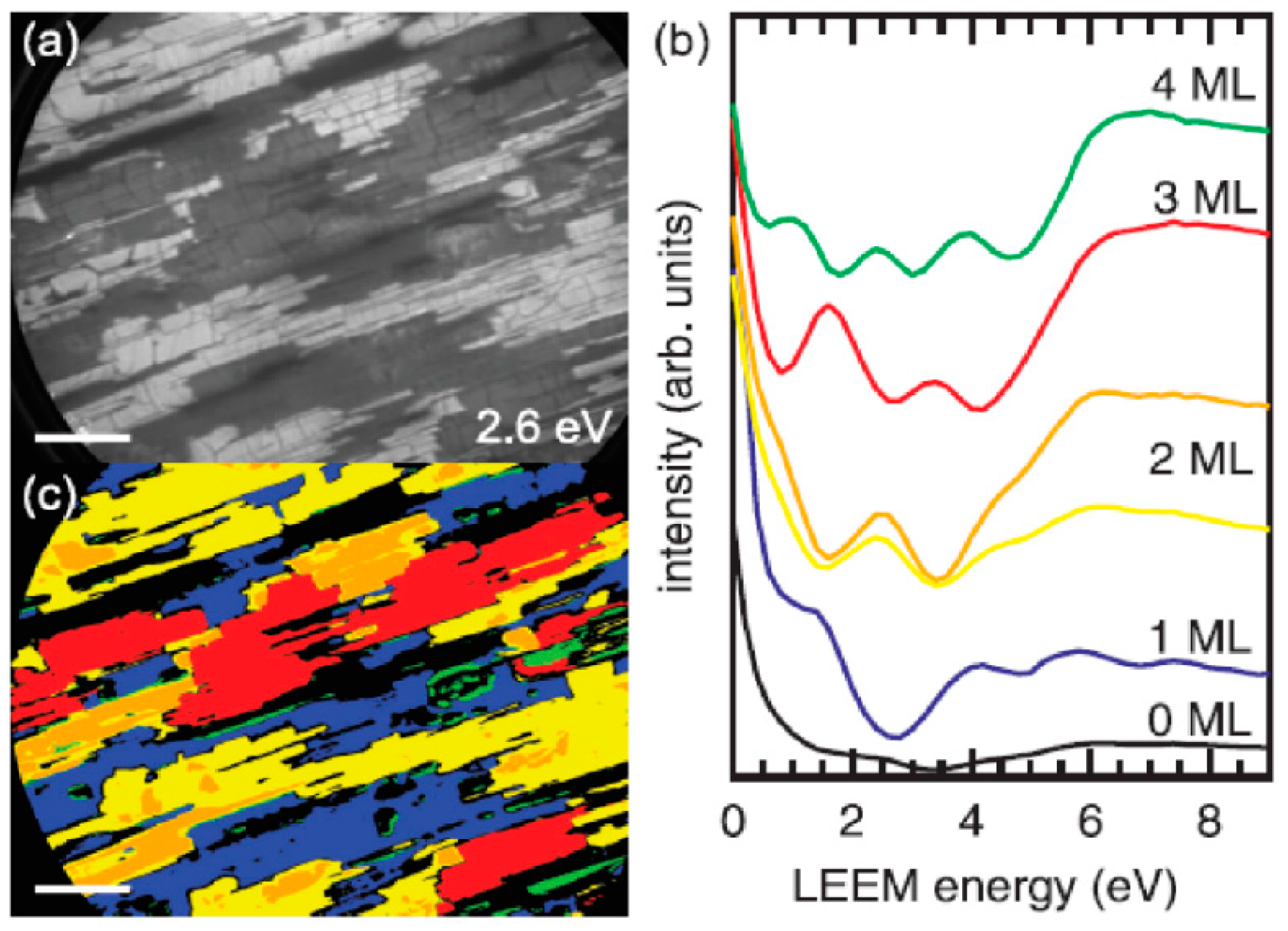
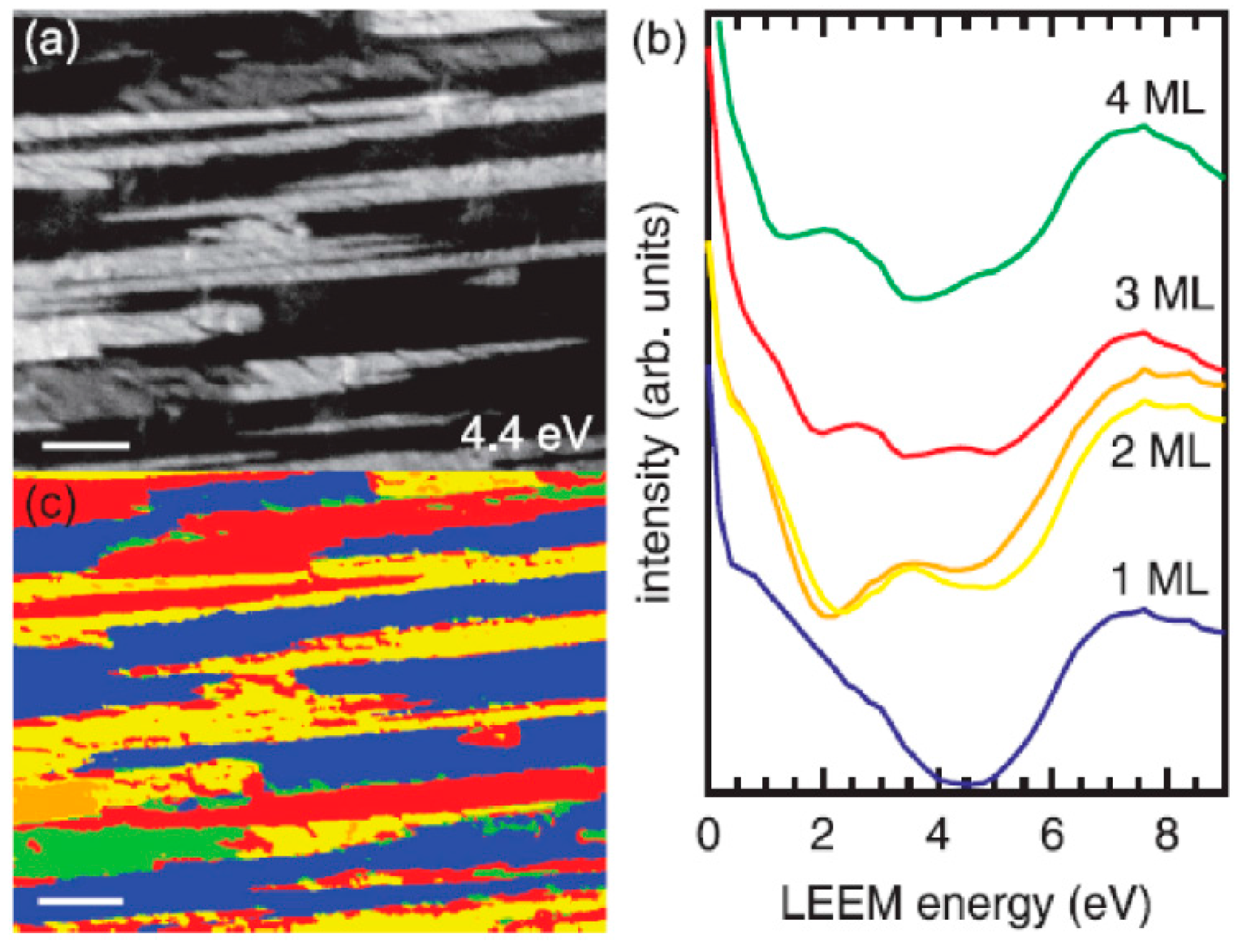
2.1. Low-Energy and Photoemission Electron Microscopy
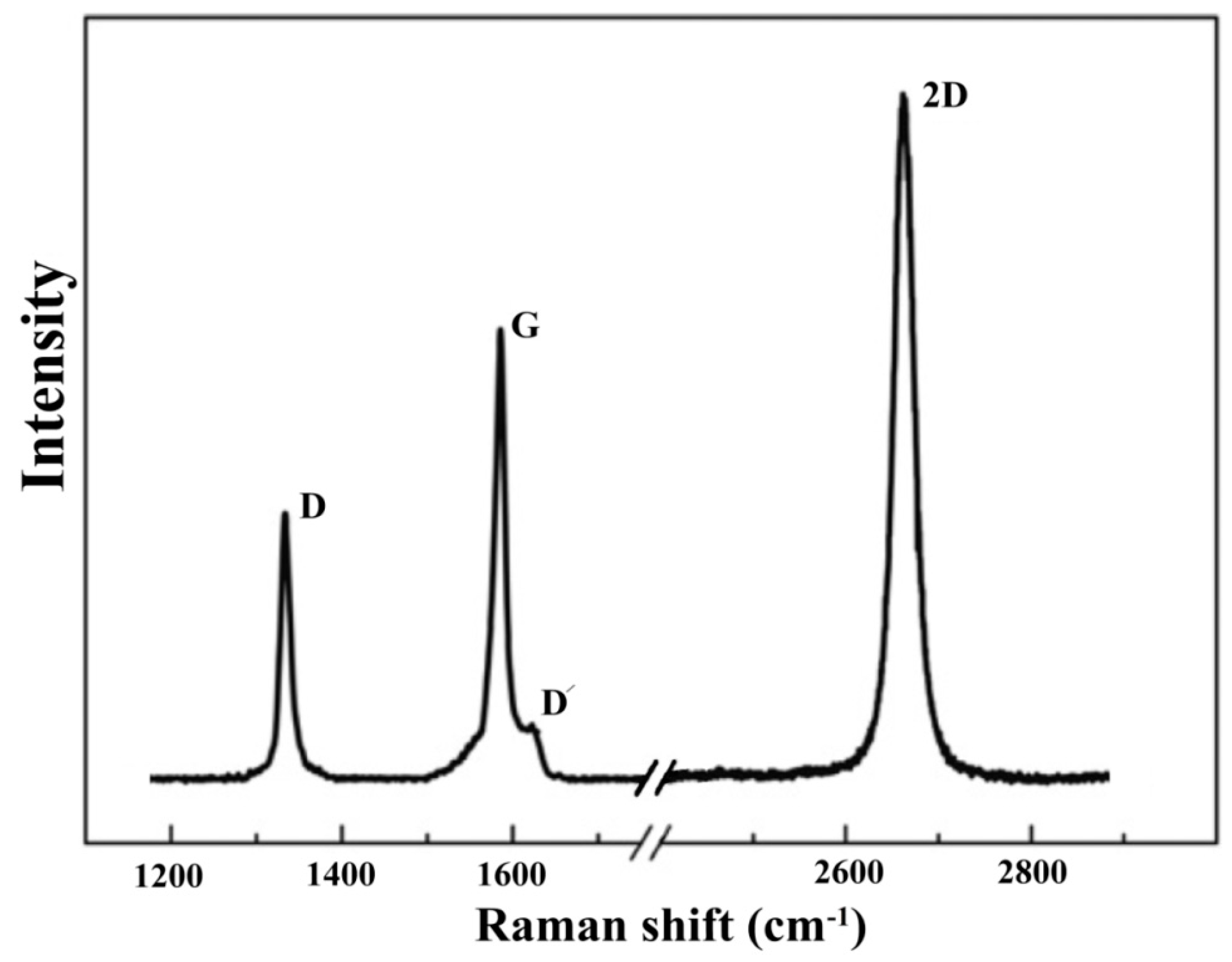
2.2. Raman Spectroscopy and Microscopy
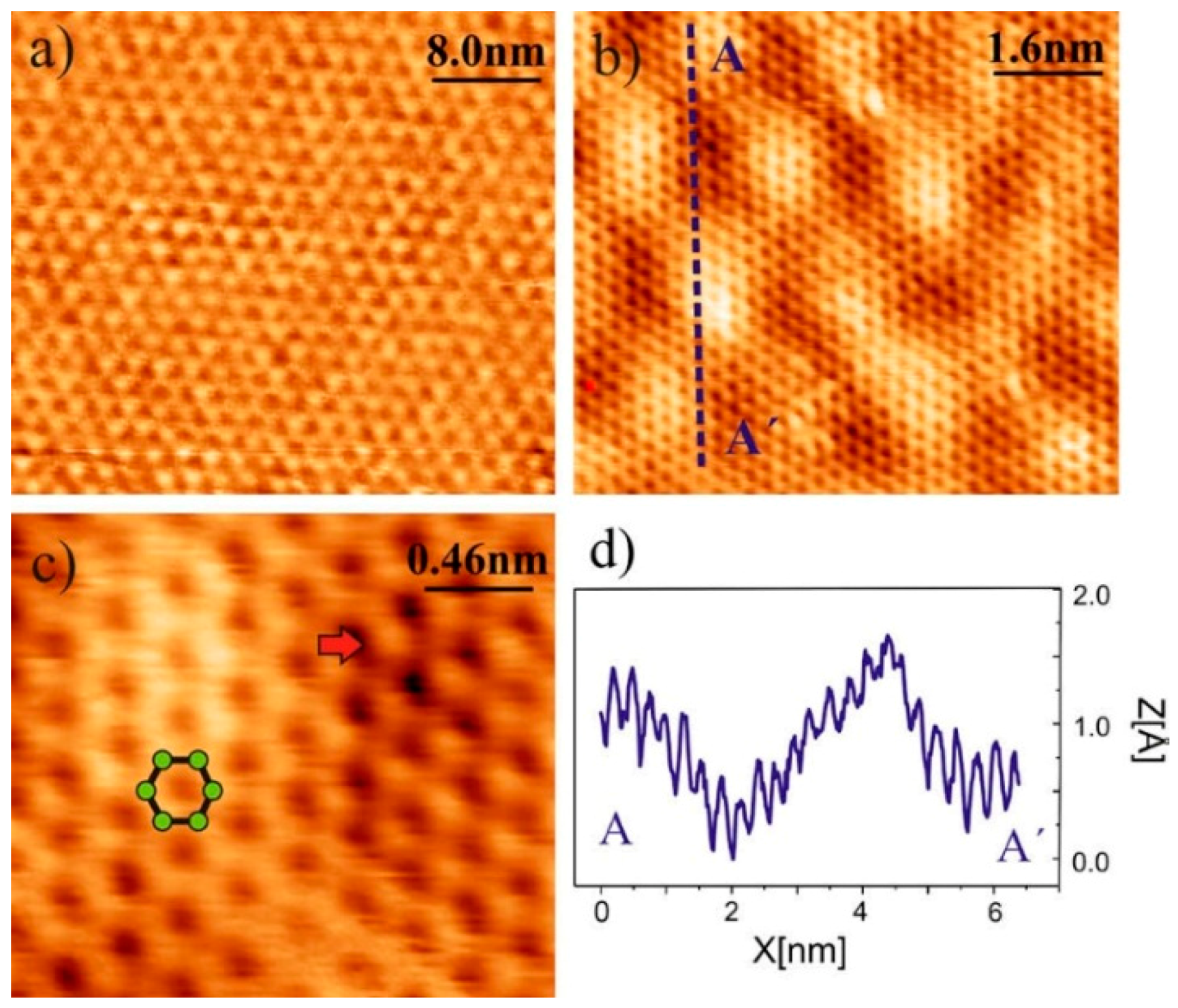
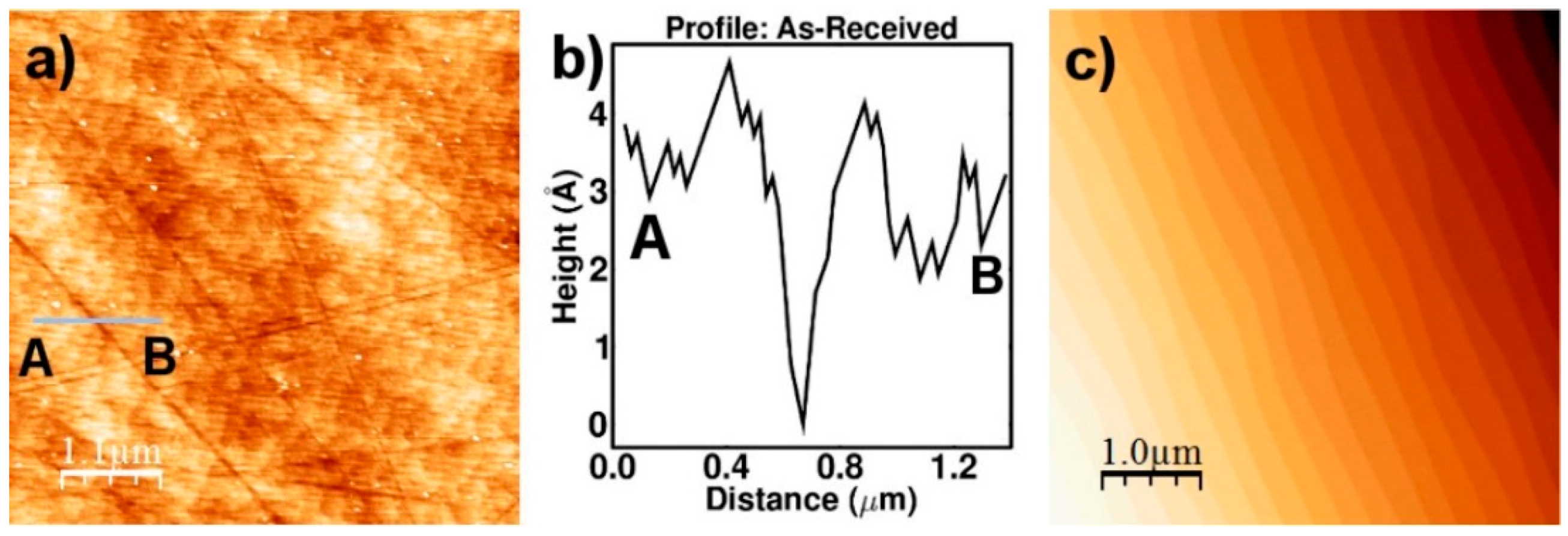
2.3. Scanning Tunneling Microscopy
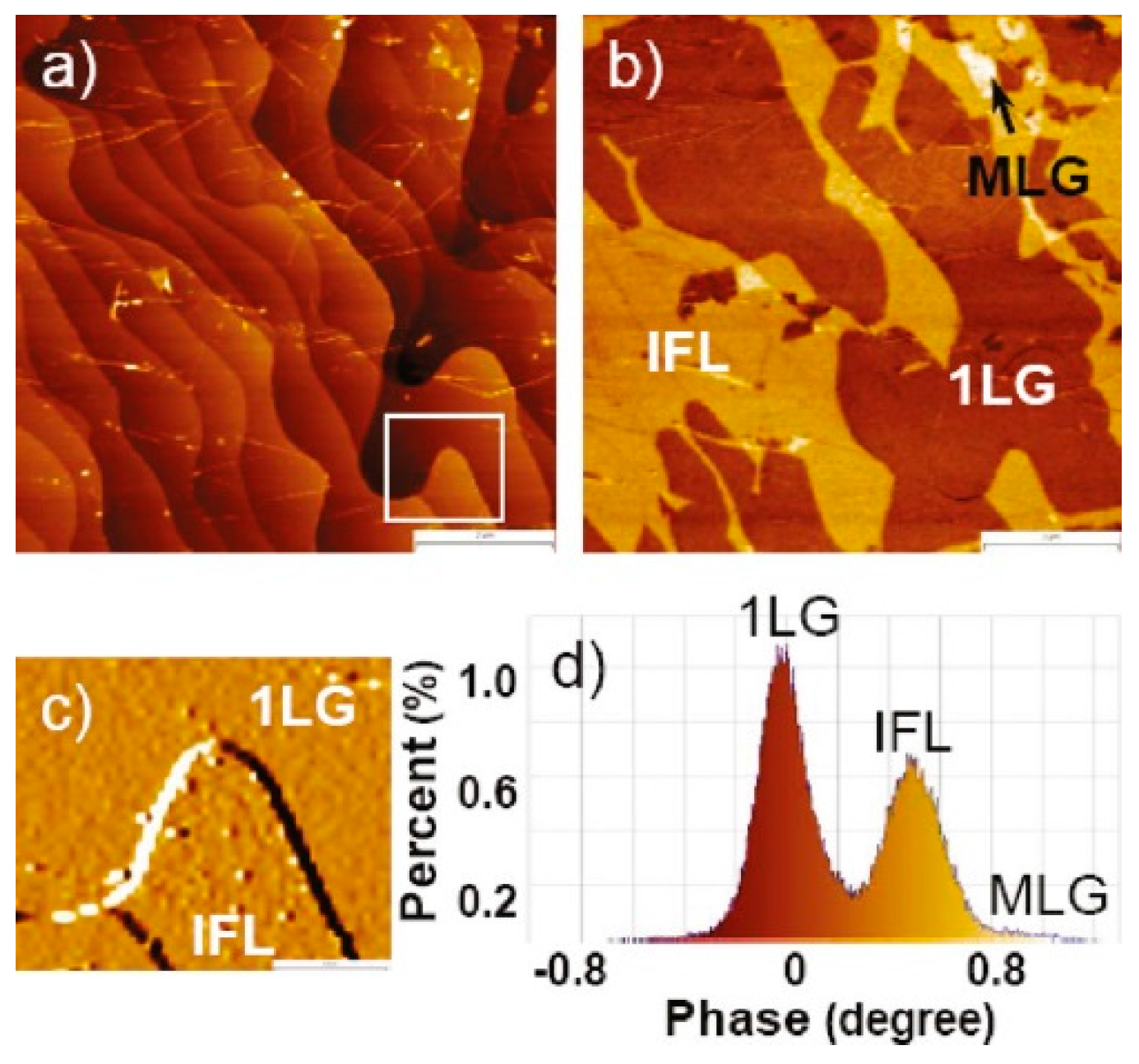
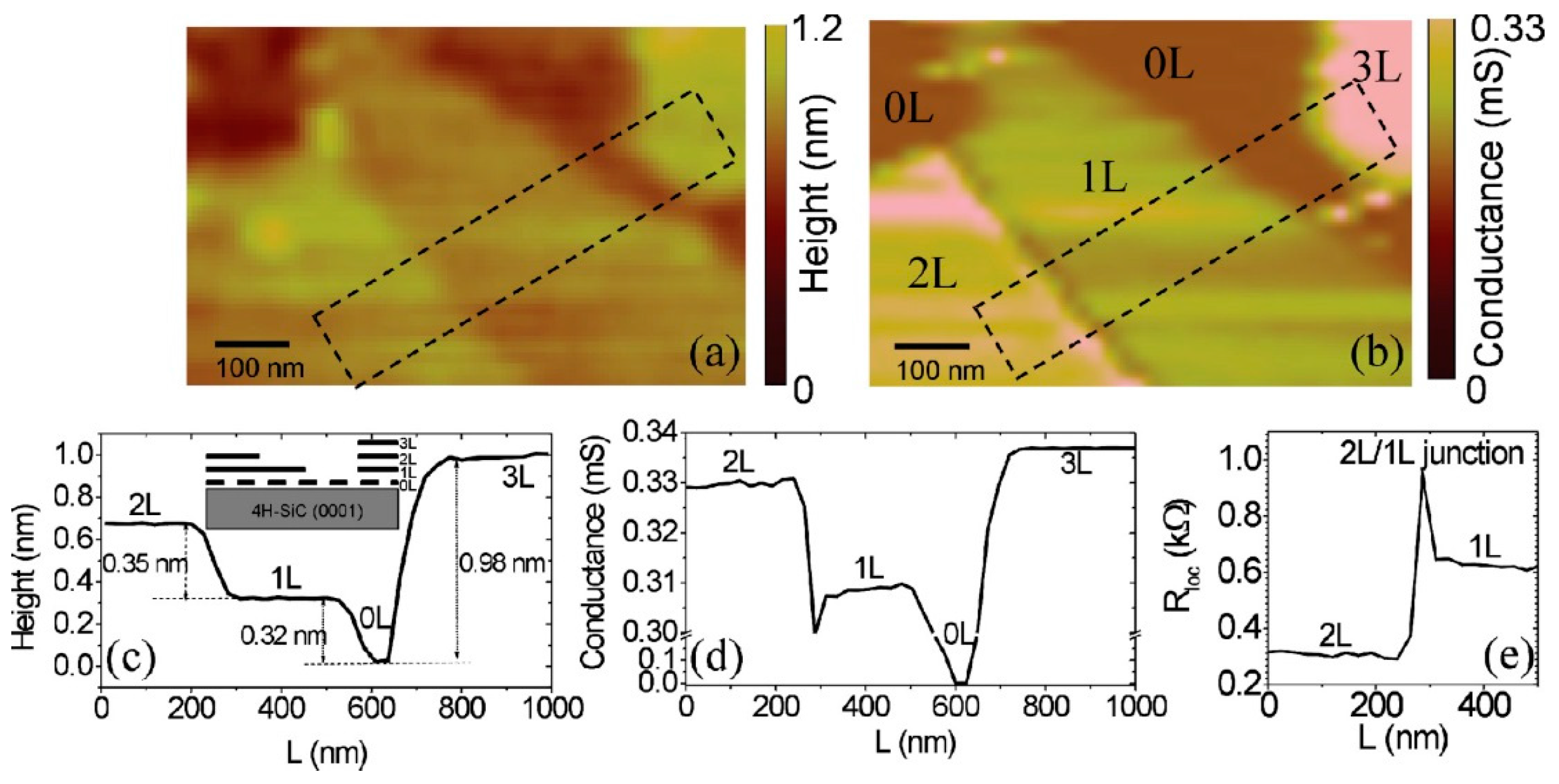
2.4. Atomic and Electrostatic Force Microscopy
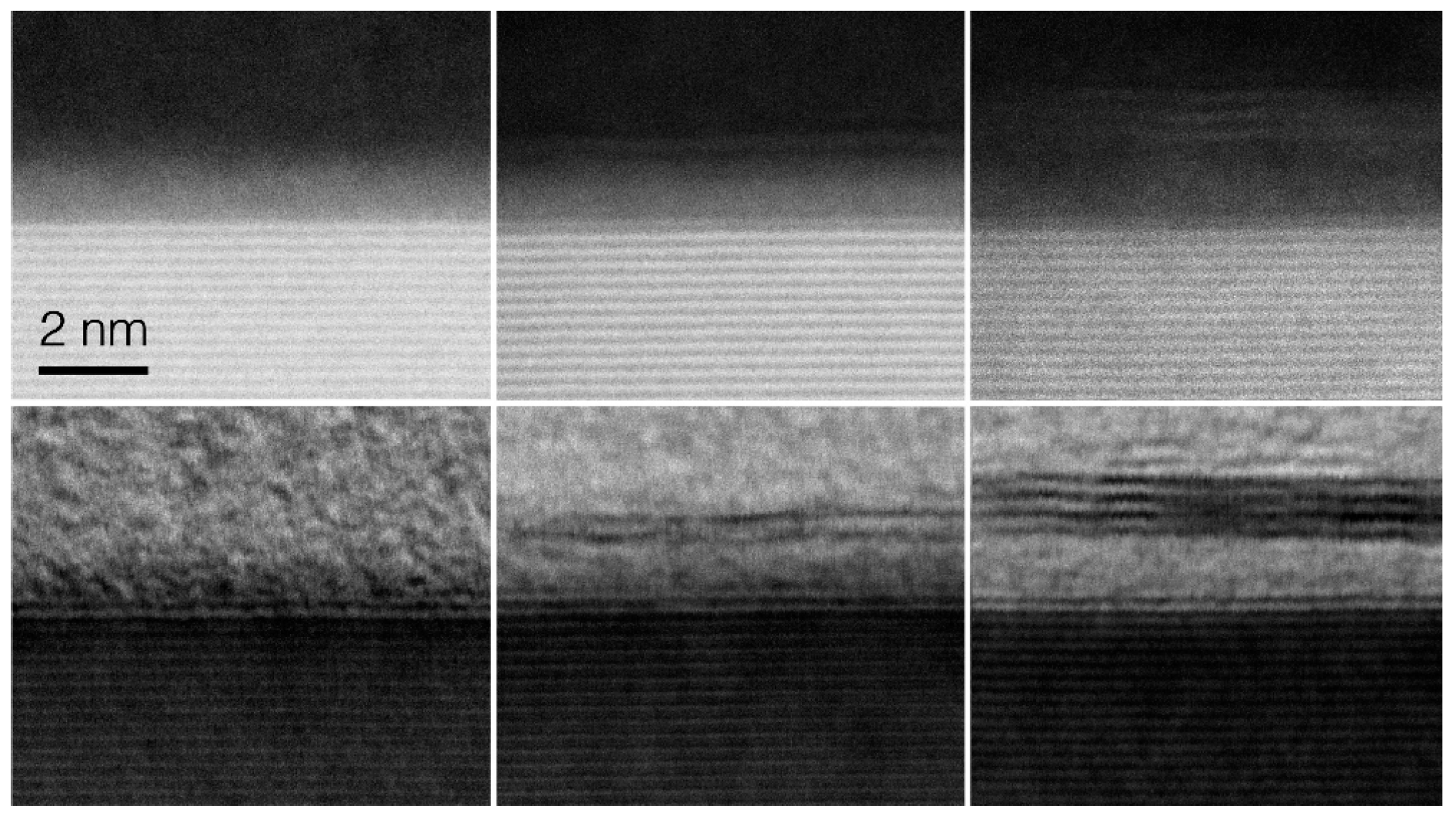
2.5. Transmission Electron Microscopy
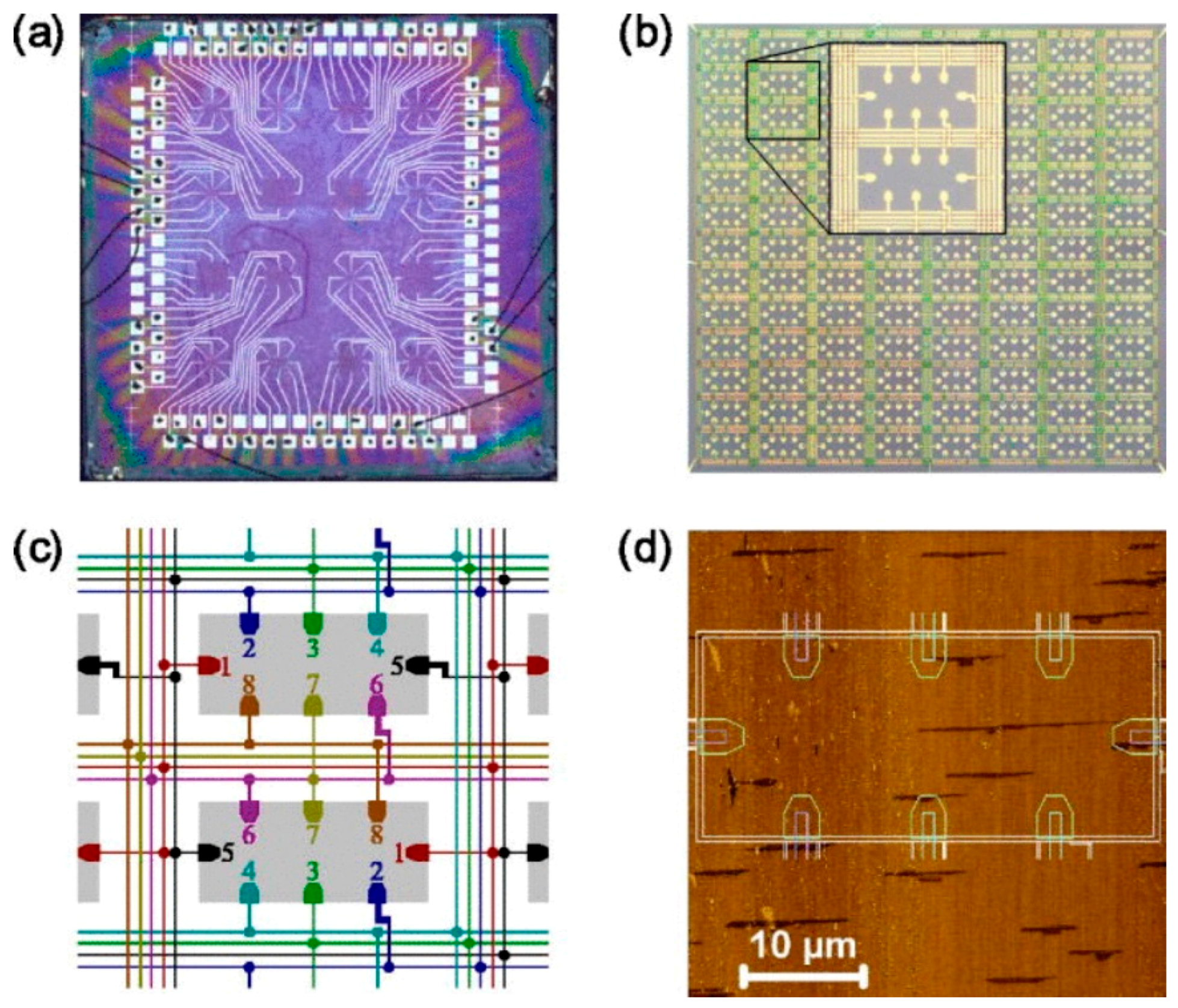
2.6. Scanning Electron Microscopy
3. Epitaxial Graphene on SiC Polytypes
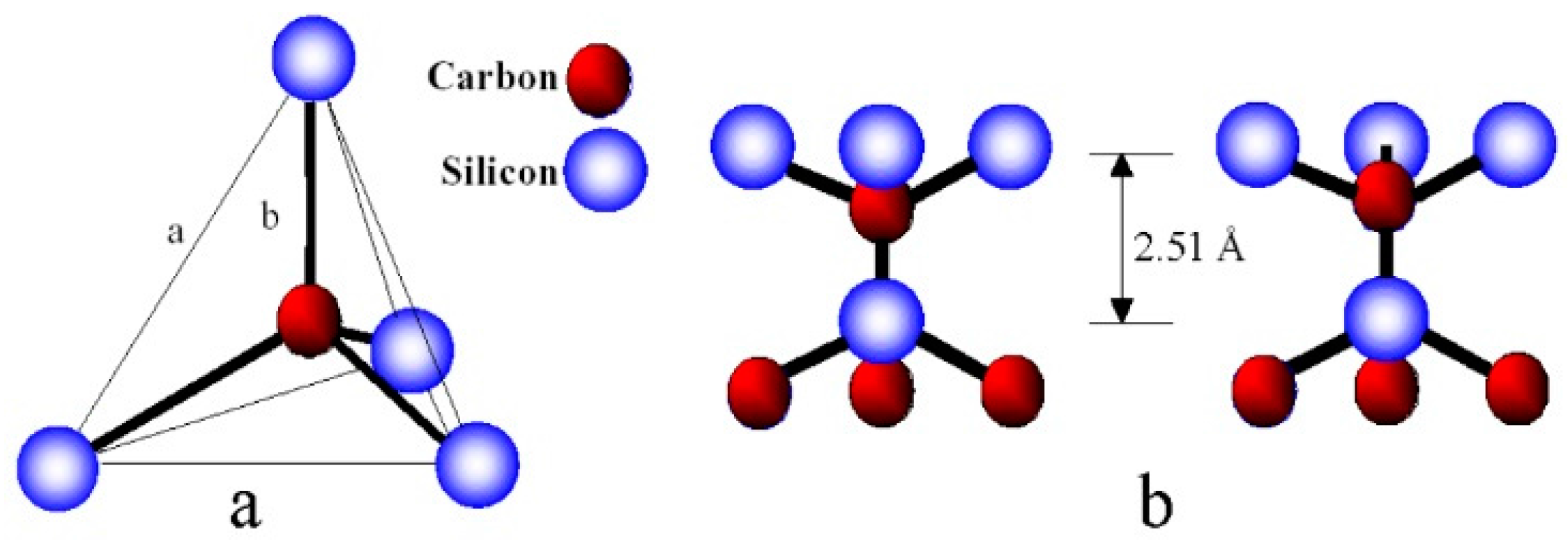
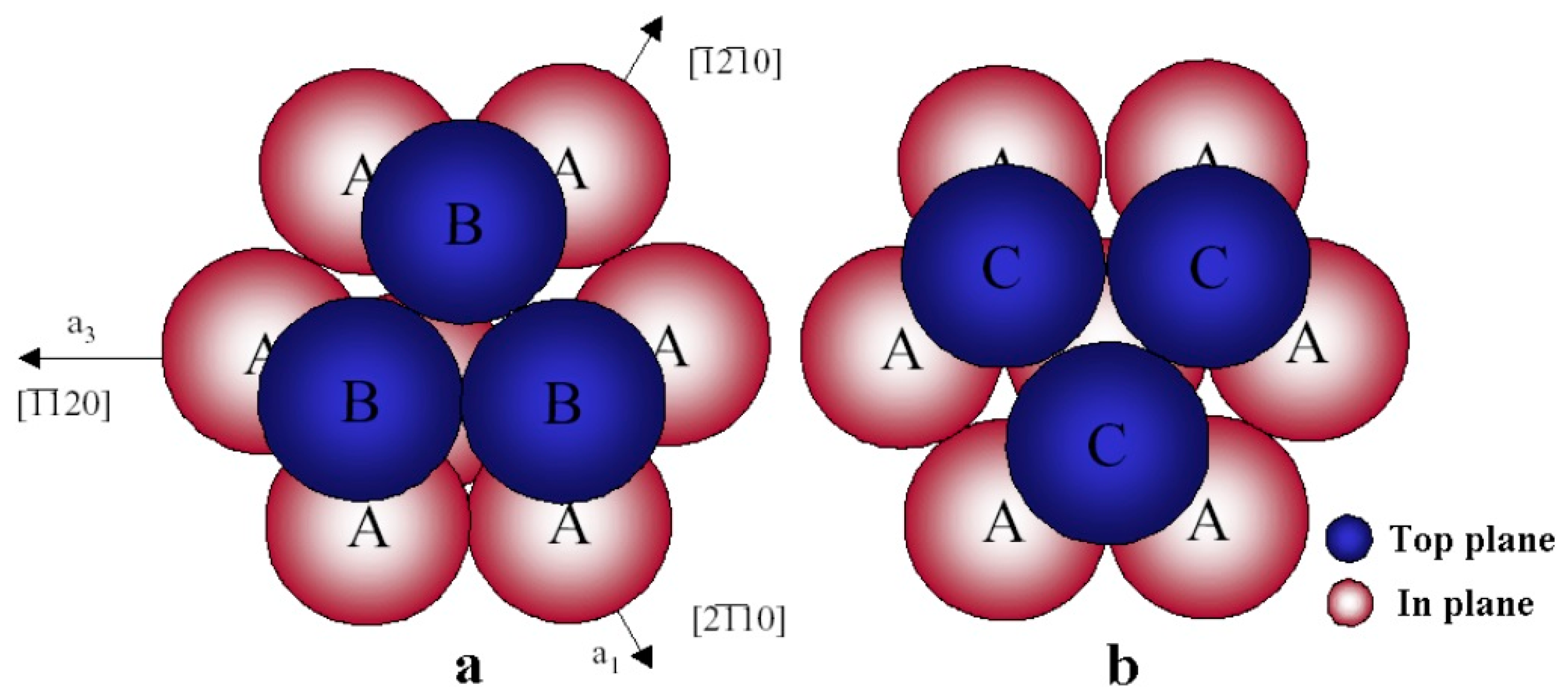
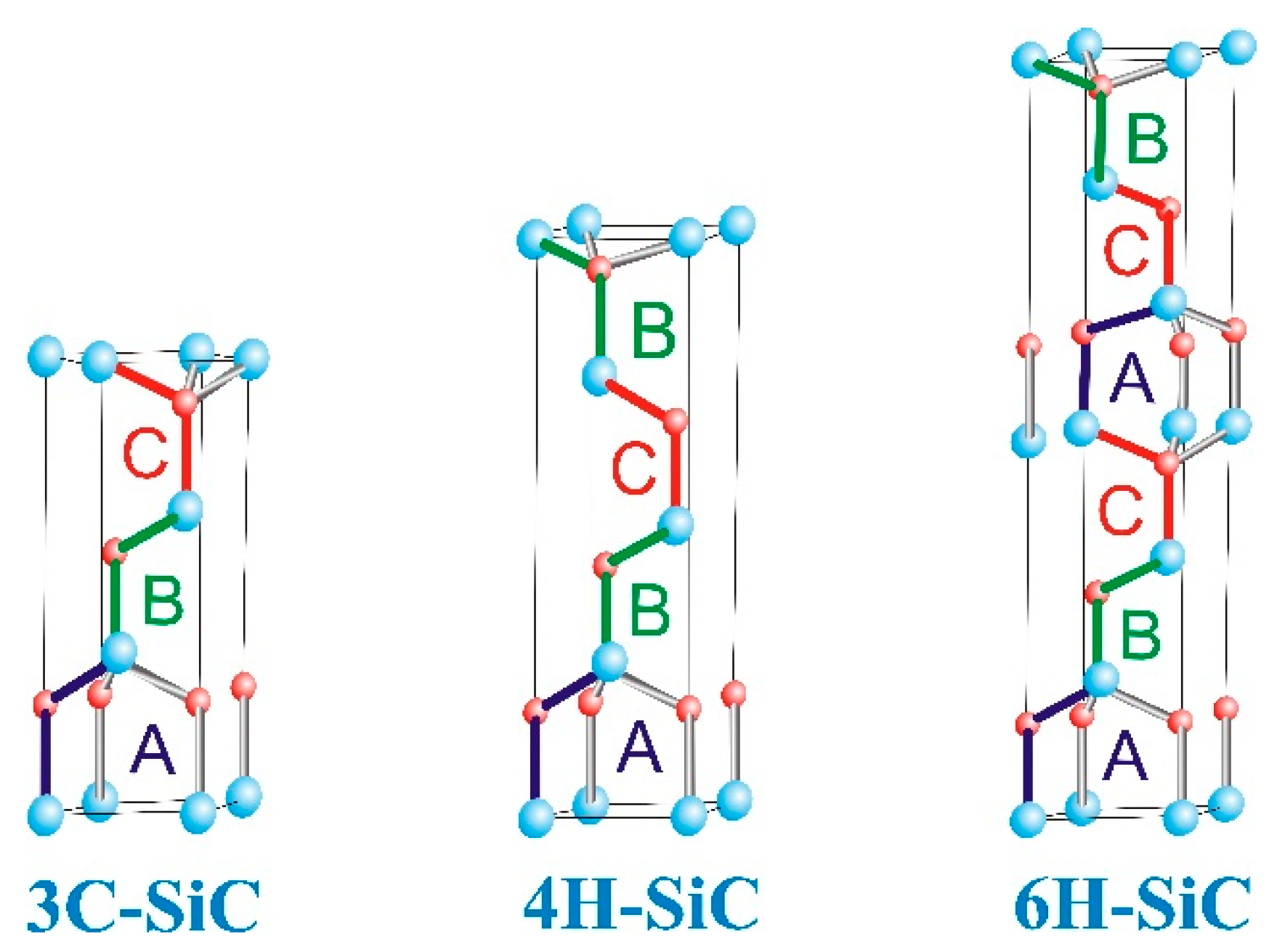
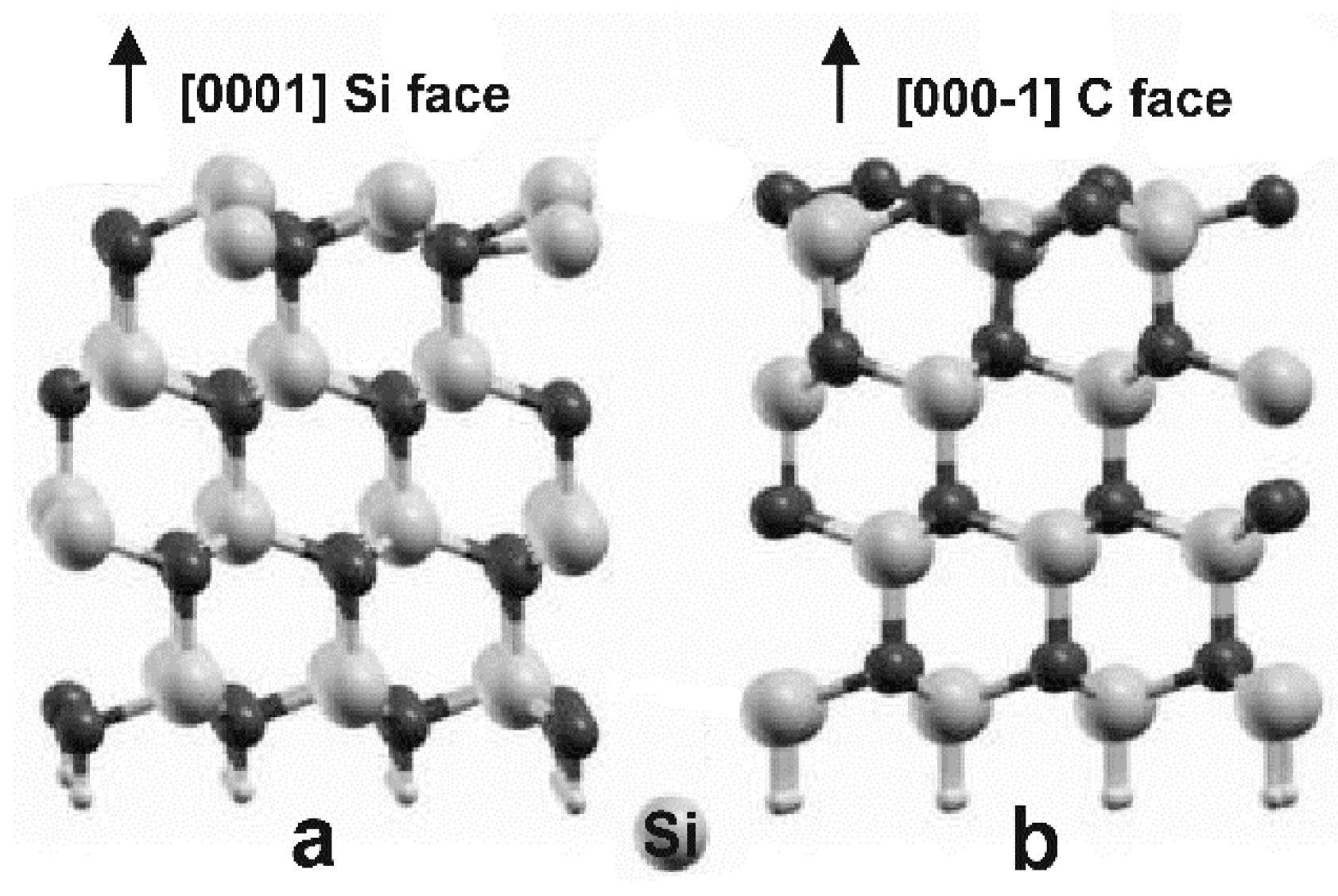
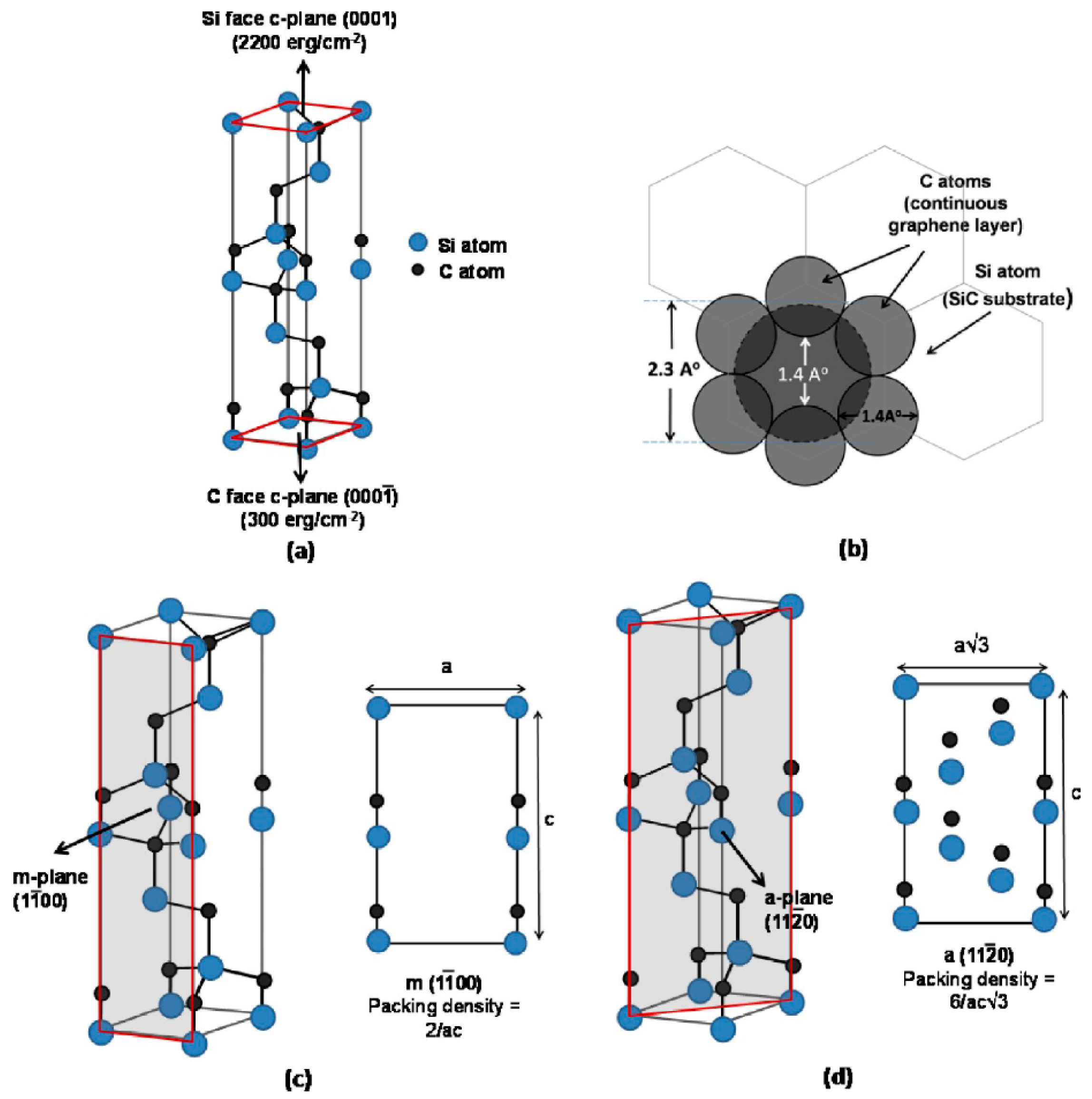
3.1. SiC as a Substrate
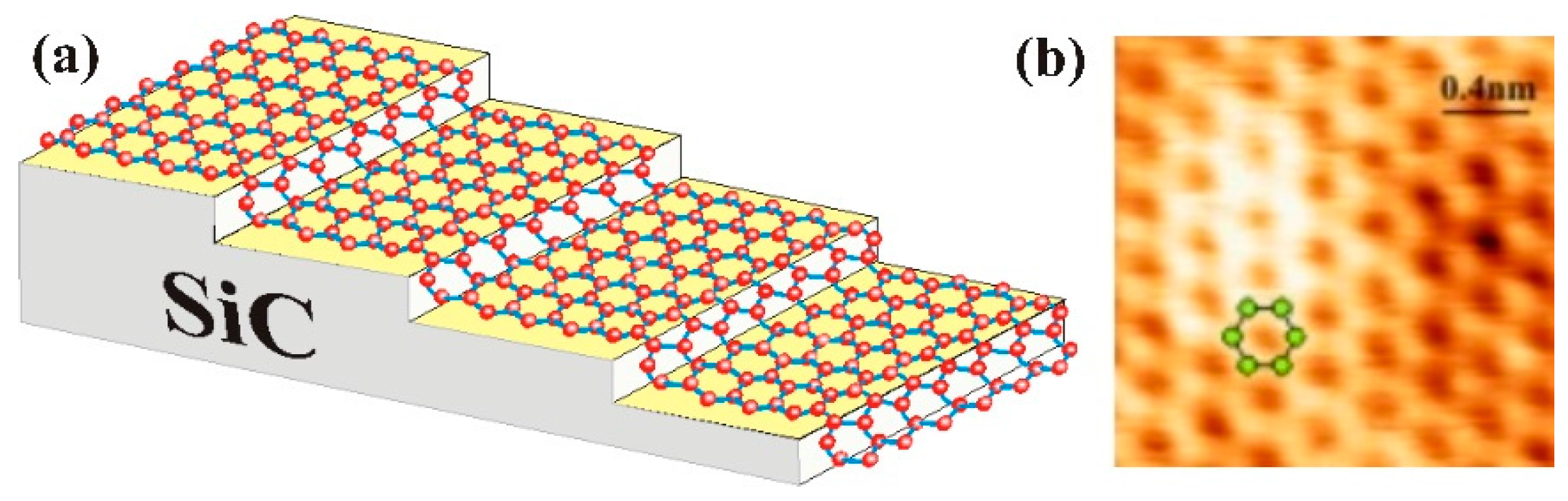
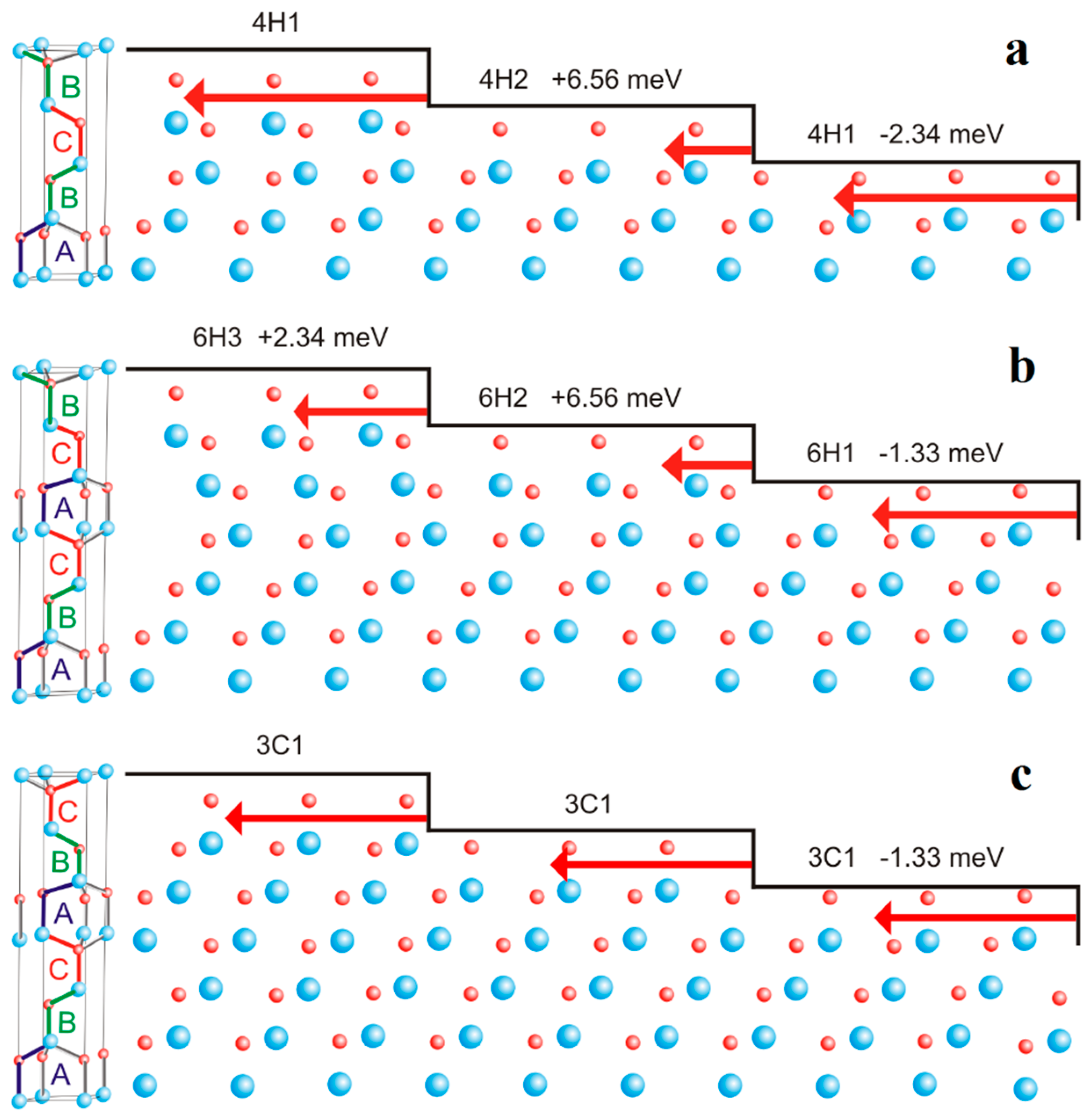
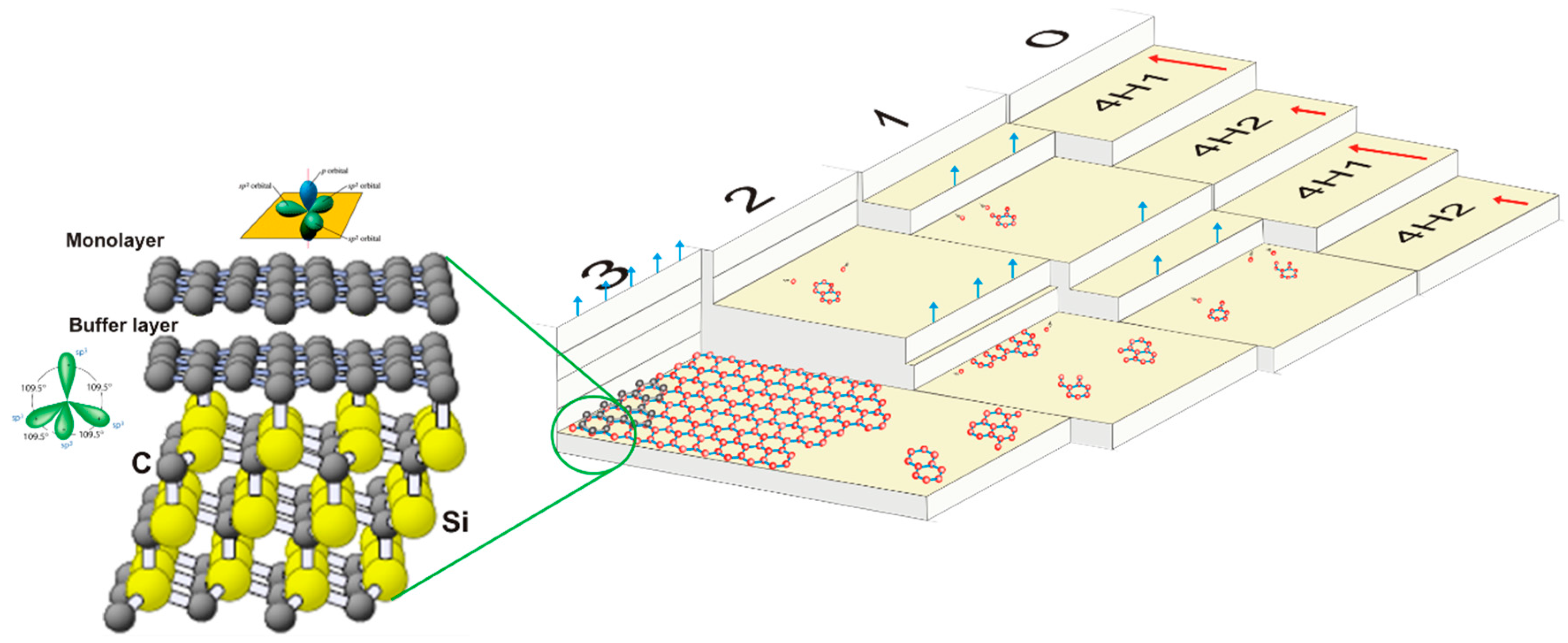
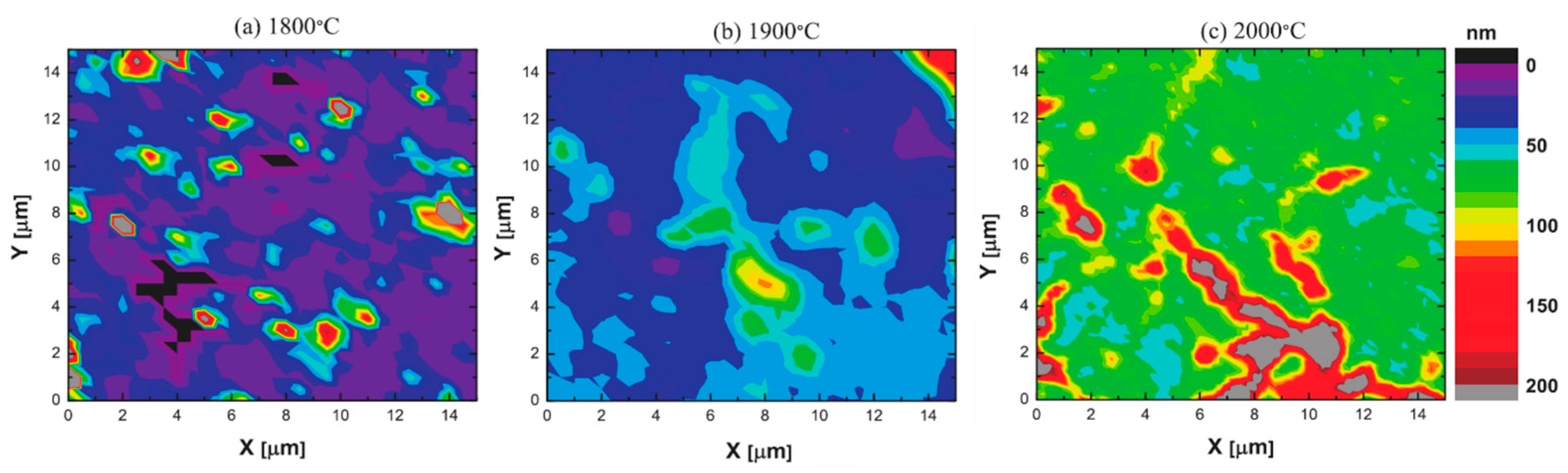
3.2. Graphitization Process of SiC Polytypes
3.3. Growth of Graphene on SiC Polar Faces
3.3.1. Effect of Ambient Conditions
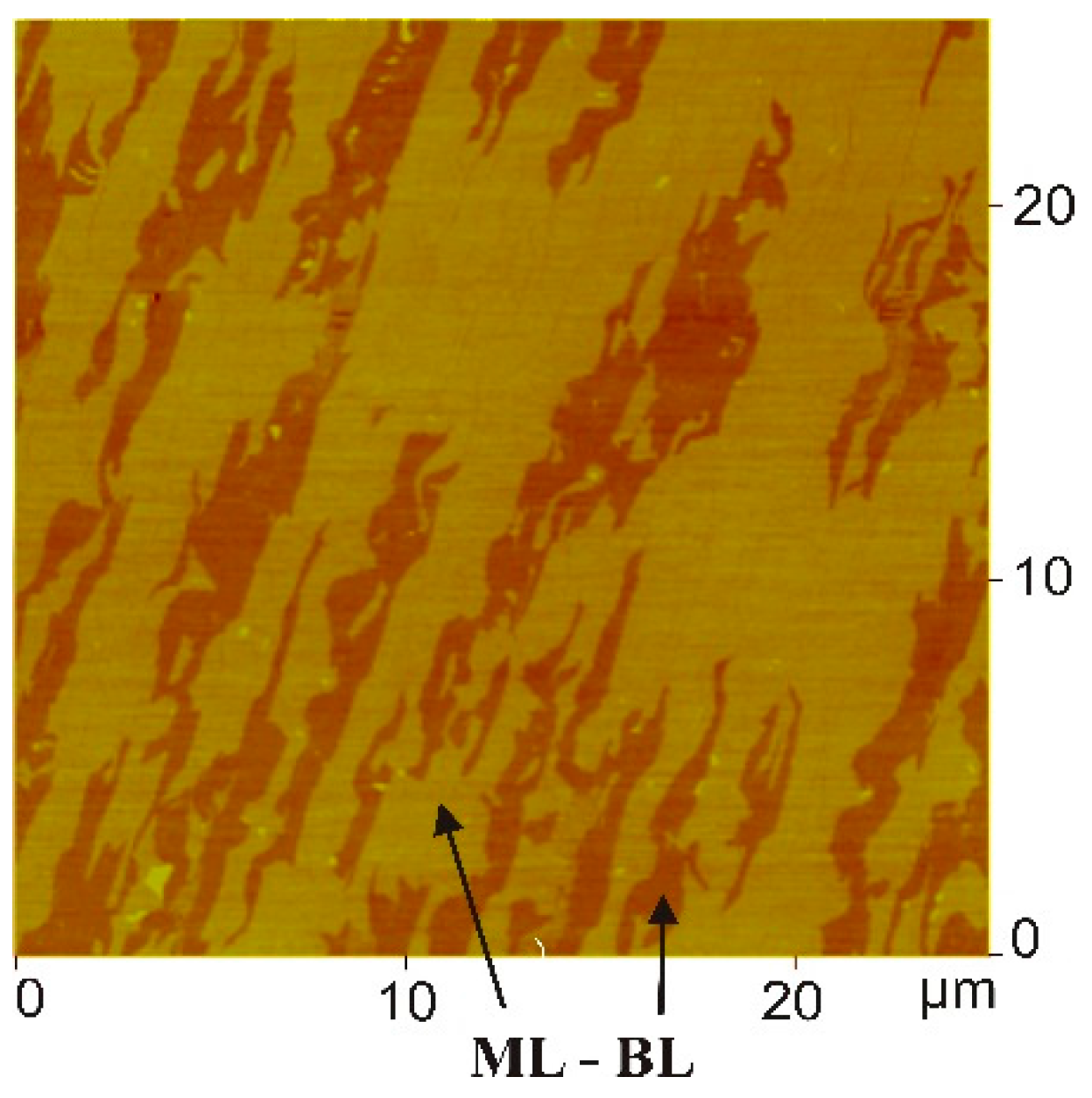
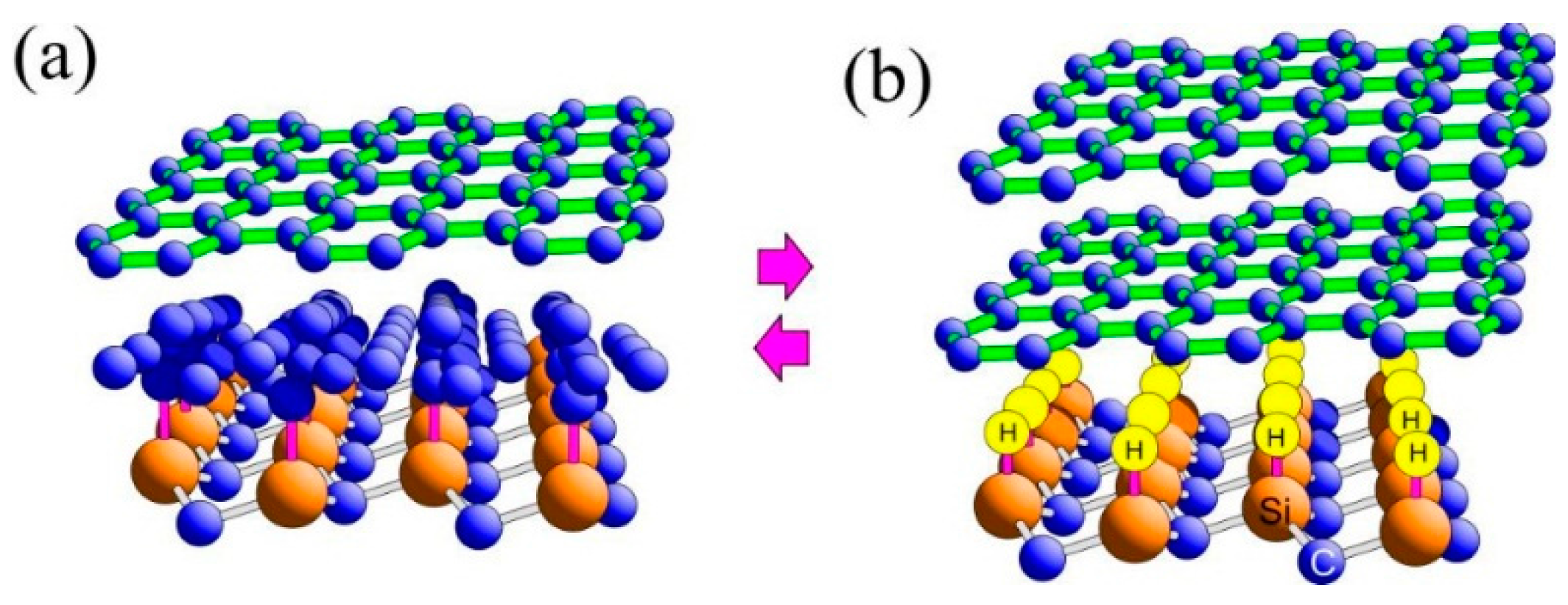
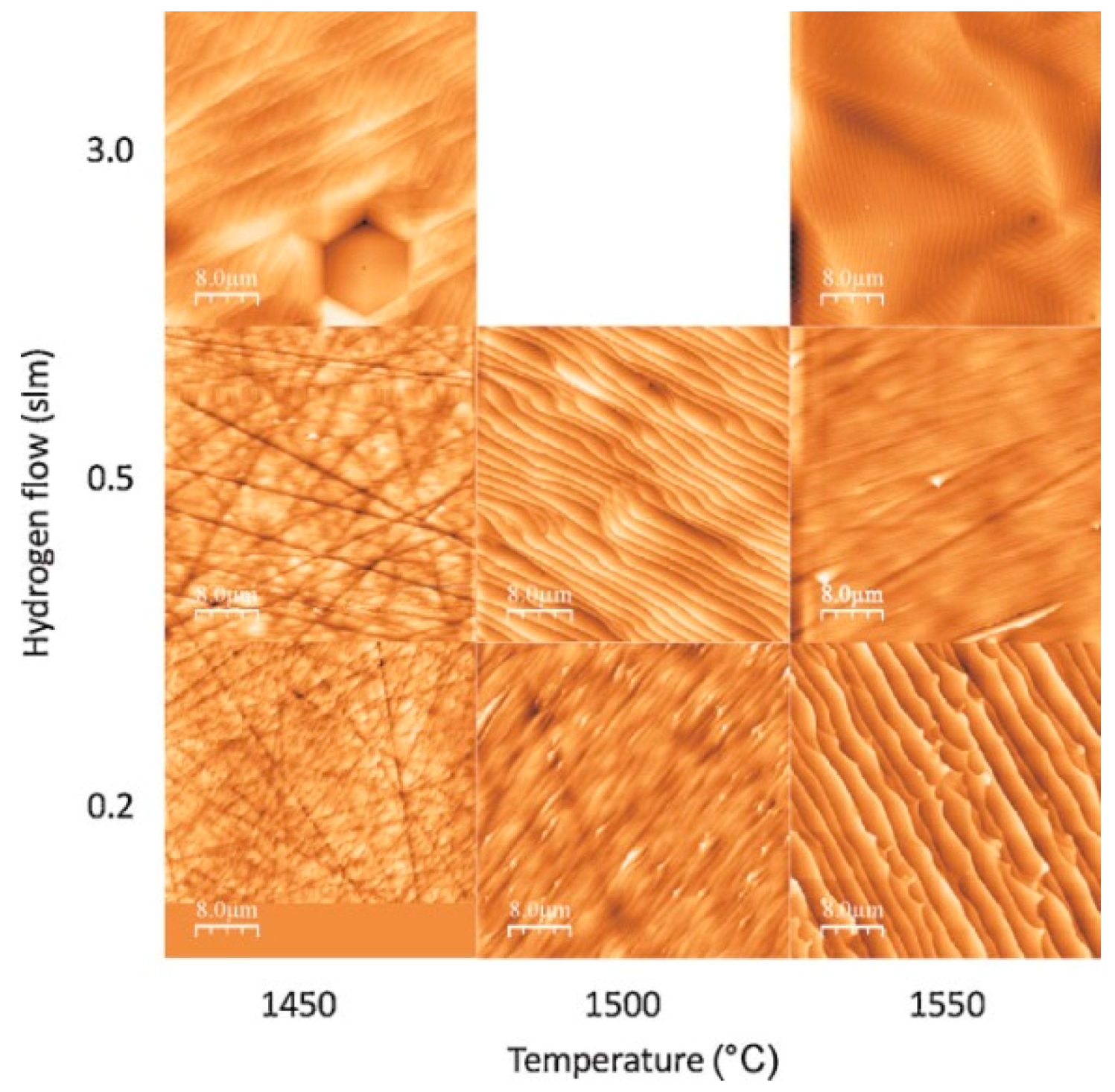
3.3.2. Growth of Graphene on Si Face
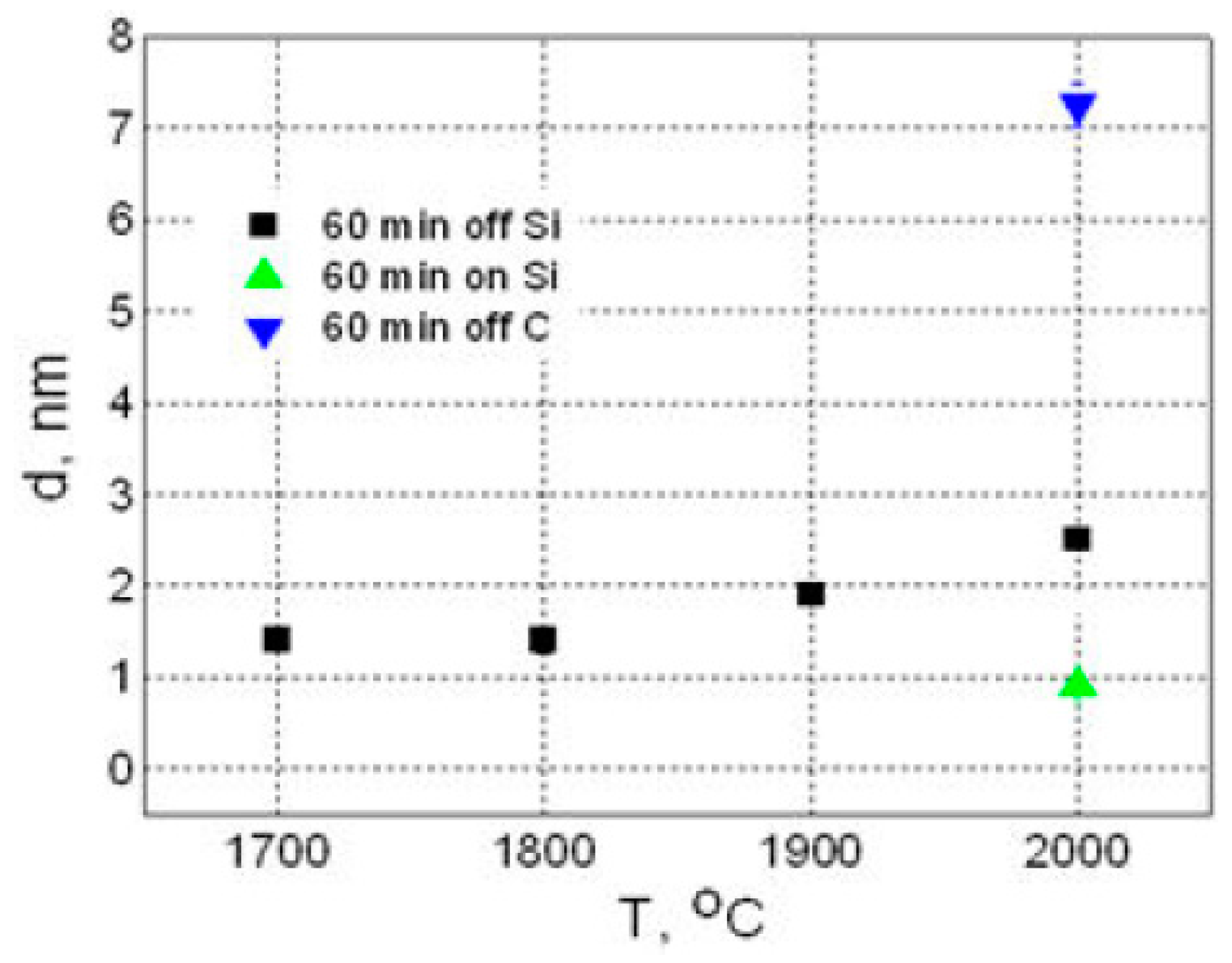
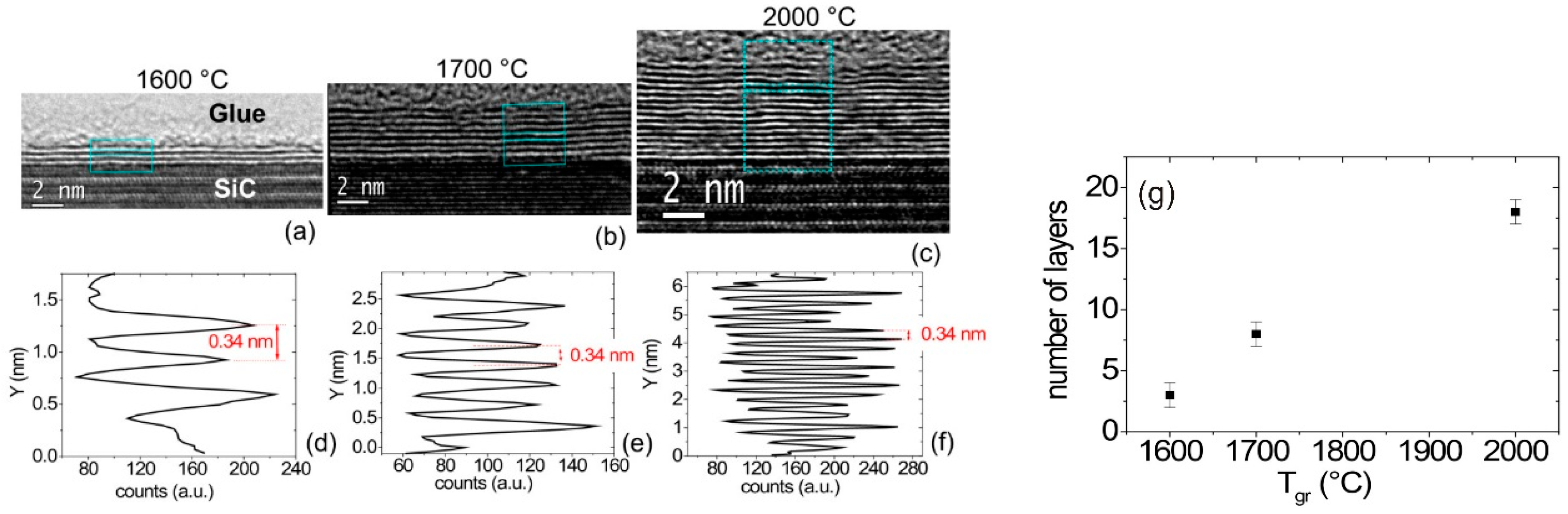
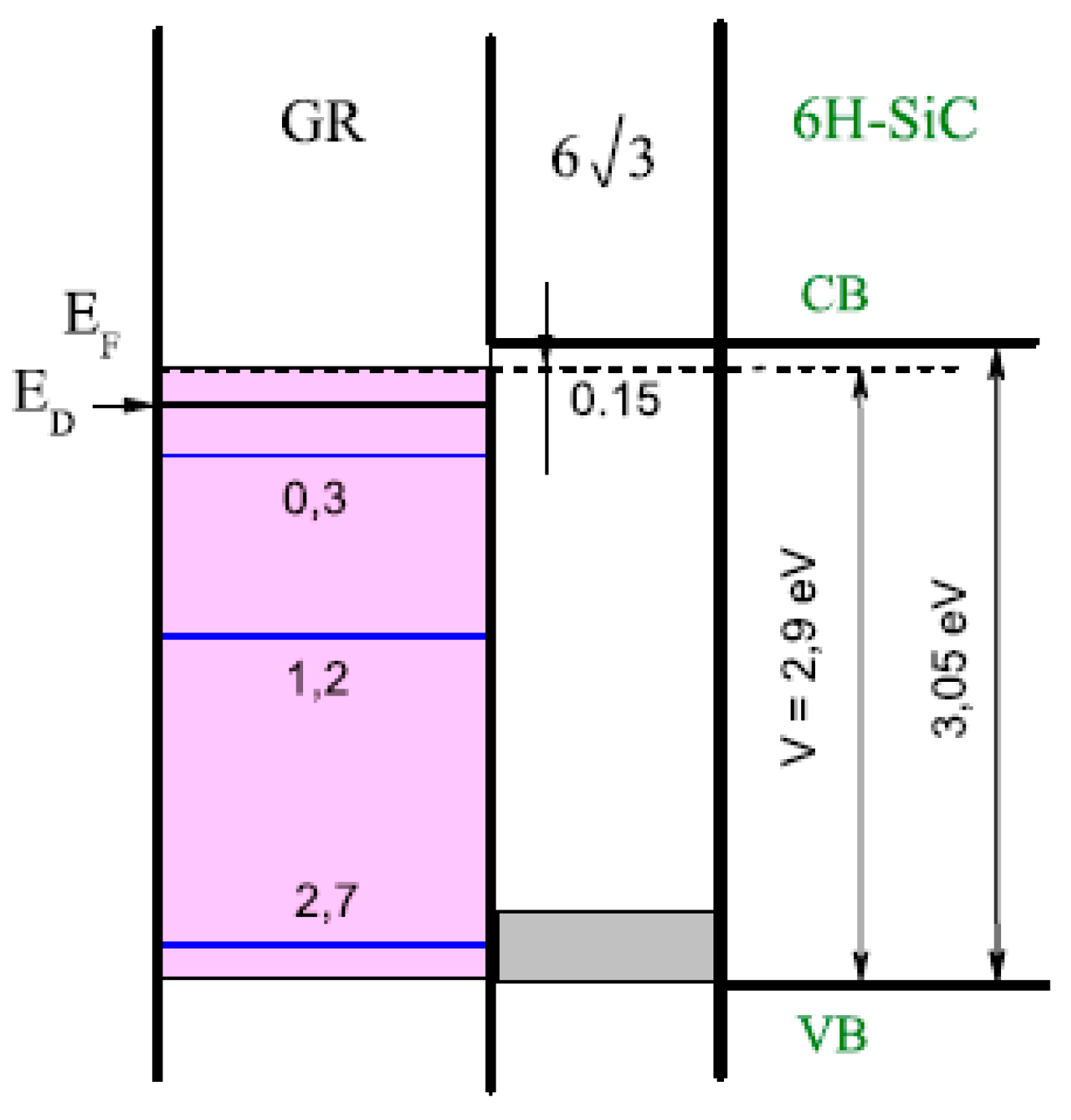
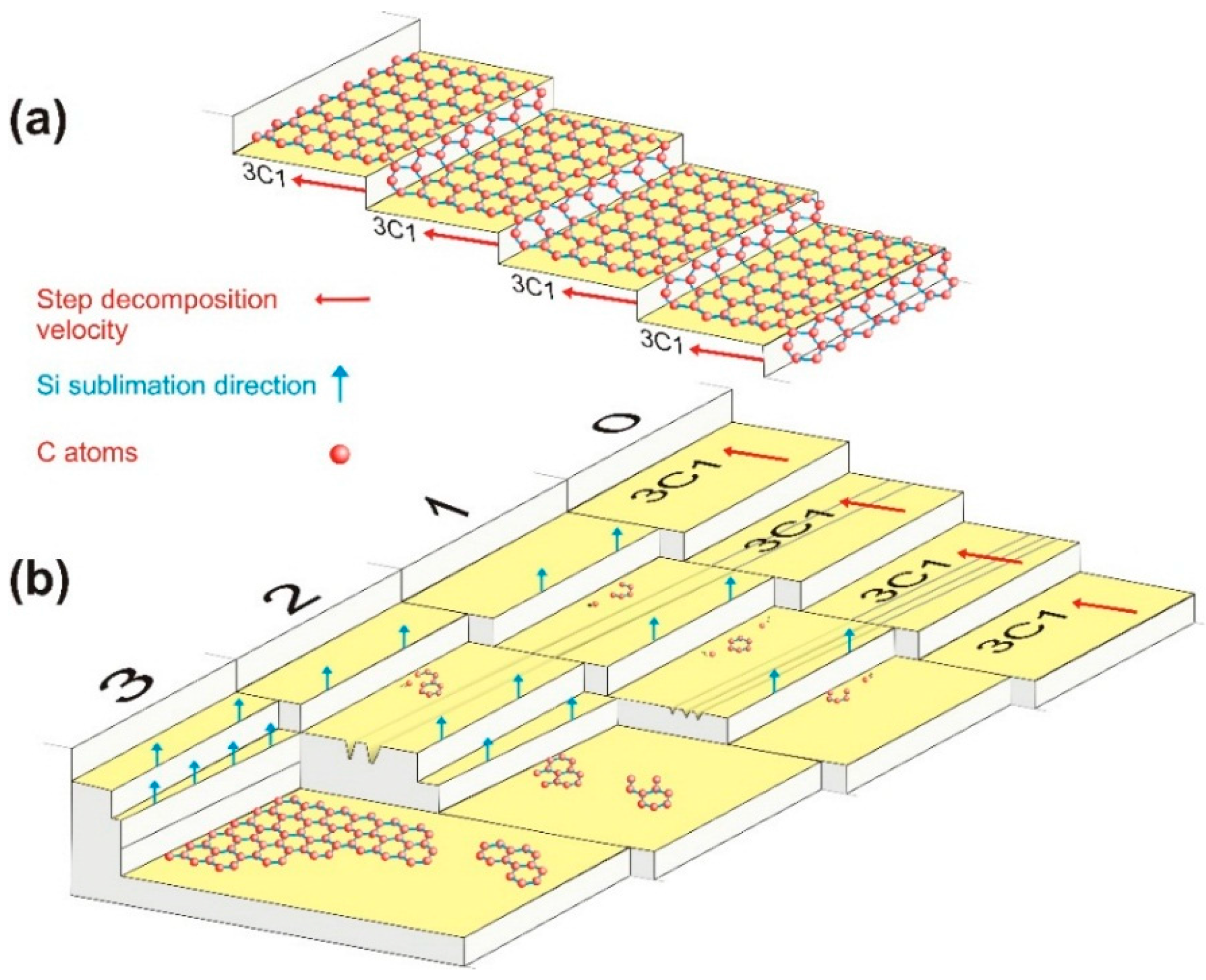
3.3.3. Growth of Graphene on C Face
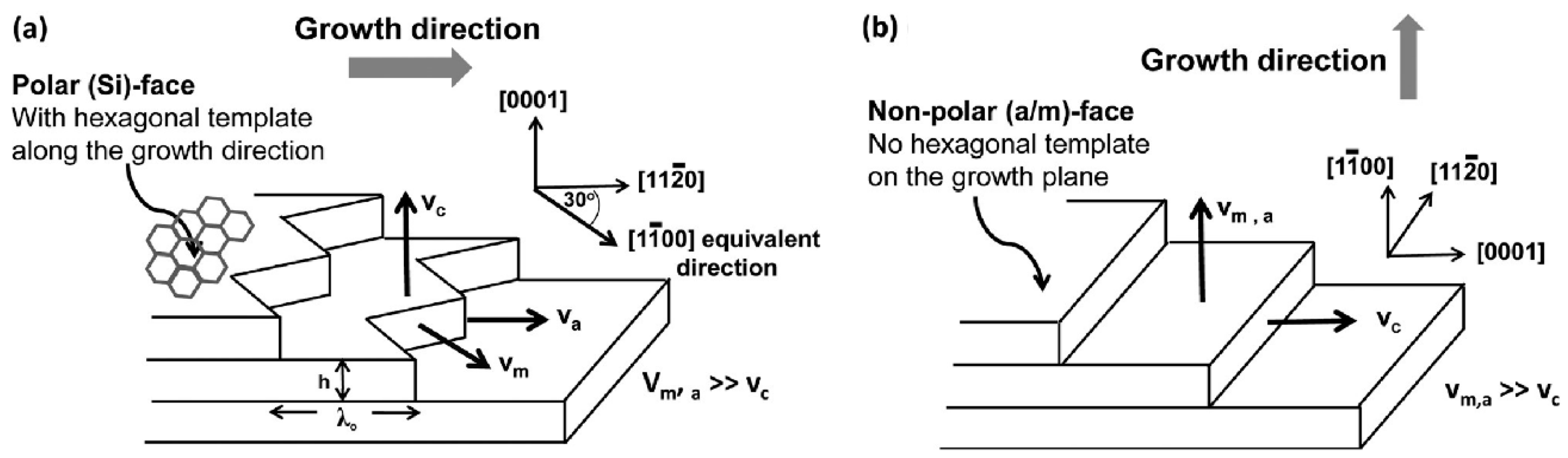
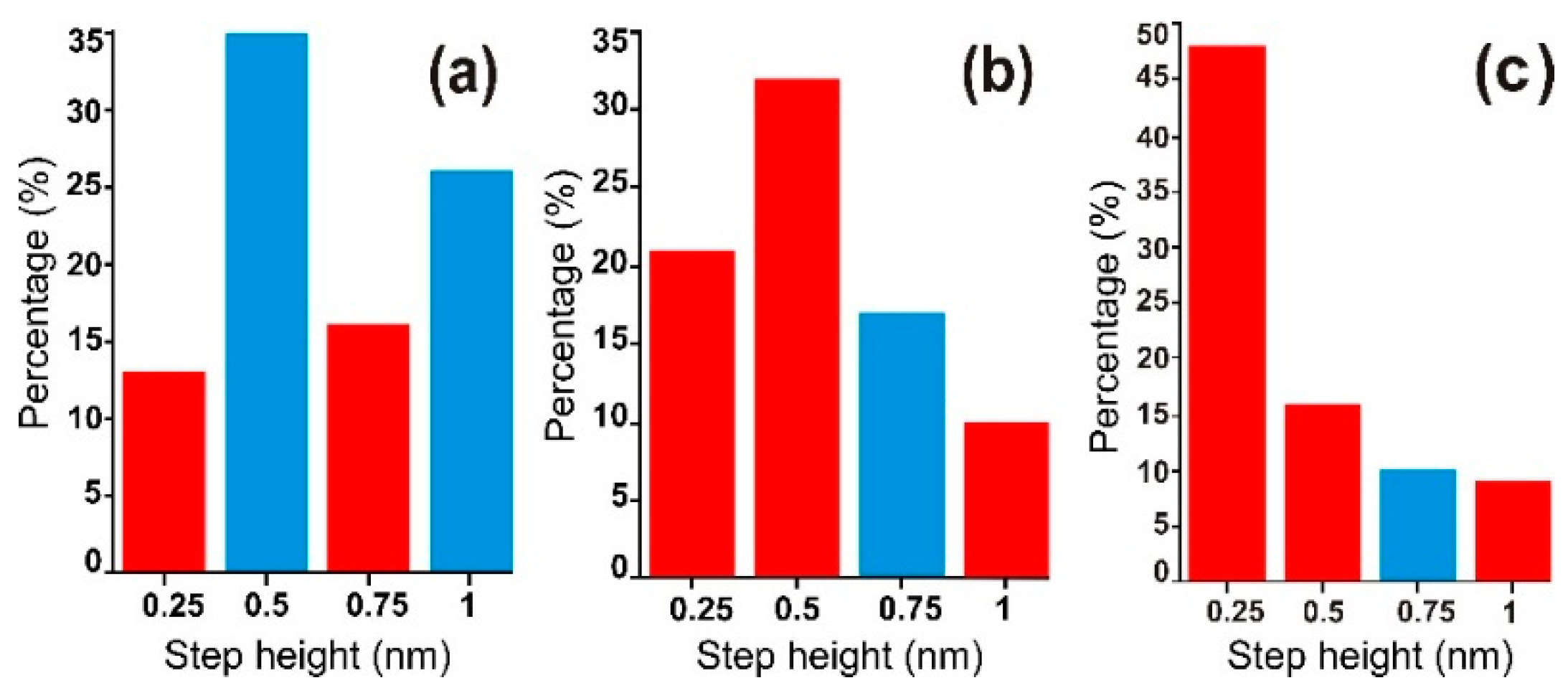
3.4. Growth of Graphene on SiC Nonpolar Faces
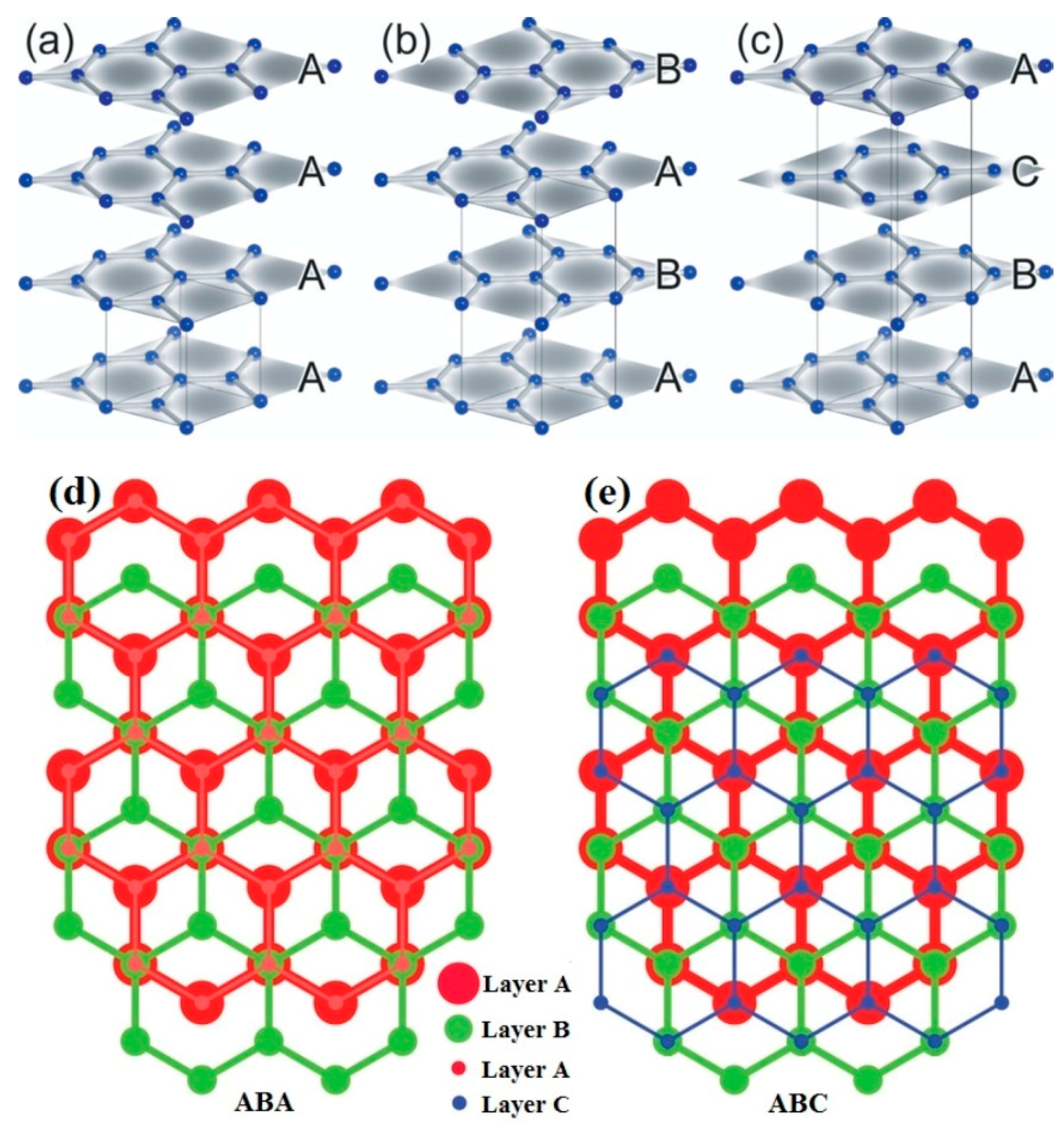
3.5. Epitaxial Graphene on 3C-SiC and Comparison with other Polytypes
4. Graphene Growth on Etched SiC Substrates
4.1. Substrate Preparation by Etching
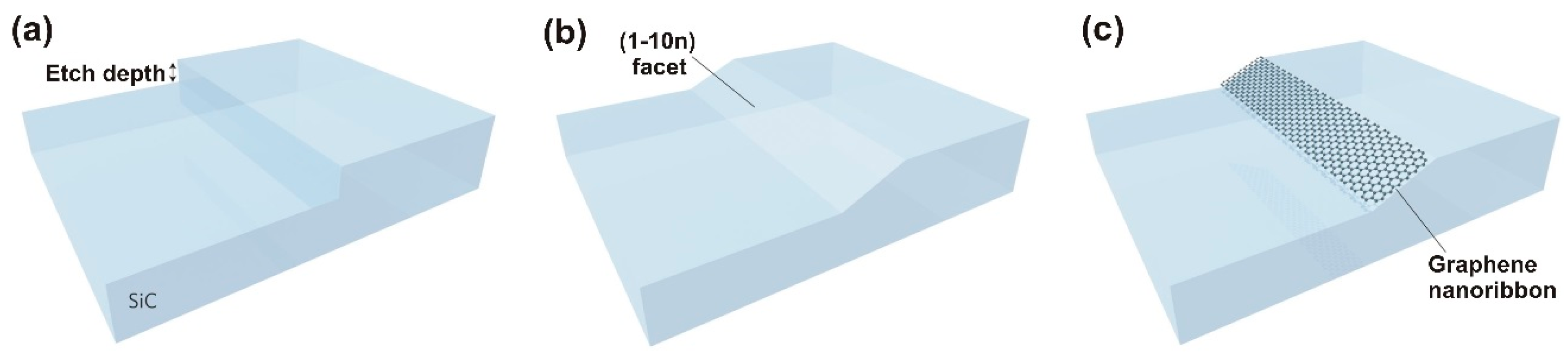
4.2. Graphene Nanoribbons (GNRs) on SiC
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Dreyer, D.R.; Ruoff, R.S.; Bielawski, C.W. From Conception to Realization: An Historial Account of Graphene and Some Perspectives for Its Future. Angew. Chem. Int. Ed 2010, 49, 9336–9344. [Google Scholar] [CrossRef] [PubMed]
- Schafhaeutl, C.; Prakt, J. Ueber die Verbindungen des Kohlenstoffes mit Silicium, Eisen und anderen Metallen, welche die verschiedenen Gallungen von Roheisen, Stahl und Schmiedeeisen bilden. Chemisty 1840, 21, 129–157. [Google Scholar] [CrossRef]
- Schafhaeutl, C. On the combinations of carbon with silicon and iron, and other metals, forming the different species of cast iron, steel, and malleable iron. Phil. Mag. 1840, 16, 570–590. [Google Scholar]
- Brodie, B.C. On the Atomic Weight of Graphite. Philos. Trans. R. Soc. Lond. 1859, 149, 249–259. [Google Scholar] [CrossRef]
- Brodie, B.C. Researches on the atomic weight of graphite. Q. J. Chem. Soc. 1860, 12, 261–268. [Google Scholar] [CrossRef]
- Boehm, H.P.; Clauss, A.; Fischer, G.O.; Hofmann, U. Dünnste kohlenstoff-folien. Z. Naturf. 1962, 17, 150–153. [Google Scholar] [CrossRef]
- Van Bommel, A.J.; Crombeen, J.E.; van Tooren, A. LEED and Auger electron observations of the SiC(0001) surface. Surf. Sci. 1975, 48, 463–472. [Google Scholar] [CrossRef]
- Lu, X.K.; Huang, H.; Nemchuk, N.; Ruoff, R.S. Tailoring graphite with the goal of achieving single sheets. Nanotechnology 1999, 10, 269–272. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Yiang, D.; Zhang, Y.; Dubonos, S.V. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Lin, Y.M.; Dimitrakopoulos, C.; Jenkins, K.A.; Farmer, D.B.; Chiu, H.-Y.; Grill, A.; Avouris, Ph. 100-GHz Transistors from Wafer-Scale Epitaxial Graphene. Science 2010, 327, 662. [Google Scholar] [CrossRef] [PubMed]
- Pearce, R.; Iakimov, T.; Andersson, M.; Hultman, L.; Lloyd Spetz, A.; Yakimova, R. Epitaxially grown graphene based gas sensors for ultra sensitive NO2 detection. Sens. Actuators B 2011, 155, 451–455. [Google Scholar] [CrossRef]
- Tzalenchuk, A.; Lara-Avila, S.; Kalaboukhov, A.; Paolillo, S.; Syväjärvi, M.; Yakimova, R.; Kazakova, O.; Janssen, T.J.B.M.; Fal’ko, V.; Kubatkin, S. Towards a quantum resistance standard based on epitaxial graphene. Nat. Nanotechnol. 2010, 5, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Lang, B. A LEED study of the deposition of carbon on platinum crystal surfaces. Surf. Sci. 1975, 53, 317–329. [Google Scholar] [CrossRef]
- Wu, Y.H.; Yu, T.; Shen, Z.X. Two-dimensional carbon nanostructures: Fundamental properties, synthesis, characterization, and potential applications. J. Appl. Phys. 2010, 108, 071301. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; Colombo, L.; Ruoff, R.S. Evolution of graphene growth on Ni and Cu by carbon isotope labeling. Nano Lett. 2009, 9, 4268–4272. [Google Scholar] [CrossRef] [PubMed]
- Sutter, P.W.; Flege, J.; Sutter, E.A. Epitaxial graphene on ruthenium. Nat. Mater. 2008, 7, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Somani, P.R.; Somani, S.P.; Umeno, M. Planer nano-graphenes from camphor by CVD. Chem. Phys. Lett. 2006, 430, 56–59. [Google Scholar] [CrossRef]
- Yakimova, R.; Virojanadara, C.; Gogova, D.; Syväjärvi, M.; Siche, D.; Larsson, K.; Johansson, L.J. Analysis of the Formation Conditions for Large Area Epitaxial Graphene on SiC Substrates. Mater. Sci. Forum 2010, 645–648, 565–568. [Google Scholar] [CrossRef]
- Yazdi, G.R.; Vasiliauskas, R.; Iakimov, T.; Zakharov, A.; Syväjärvi, M.; Yakimova, R. Growth of large area monolayer graphene on 3C-SiC and a comparison with other SiC polytypes. Carbon 2013, 57, 477–484. [Google Scholar] [CrossRef]
- Berger, C.; Song, Z.; Li, X.; Wu, X.; Brown, N.; Naud, C.; Mayou, D.; Li, T.; Hass, J.; Marchenkov, A.N.; et al. Electronic Confinement and Coherence in Patterned Epitaxial Graphene. Science 2006, 312, 1191–1196. [Google Scholar] [CrossRef] [PubMed]
- Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the electronic structure of bilayer graphene. Science 2006, 313, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Riedl, C.; Starke, U.; Bernhardt, J.; Franke, M.; Heinz, K. Structural properties of the graphene-SiC(0001) interface as a key for the preparation of homogeneous large-terrace graphene surfaces. Phys. Rev. B 2007, 76, 245406. [Google Scholar] [CrossRef]
- Emtsev, K.V.; Bostwick, A.; Horn, K.; Jobst, J.; Kellogg, G.L.; Ley, L.; McChesney, J.L.; Ohta, T.; Reshanov, S.A.; Rotenberg, E.; et al. Towards wafer-size graphene layers by atmospheric pressure graphitization of silicon carbide. Nat. Mater. 2009, 8, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Tairov, Y.M.; Tsvetkov, V.F. Investigation of growth processes of ingots of silicon carbide single crystals. J. Cryst. Growth 1978, 43, 209–212. [Google Scholar] [CrossRef]
- Tairov, Y.M.; Tsvetkov, V.F. General Principles of Growing Large-Size Single Crystals of Various Silicon Carbide Polytypes. J. Cryst. Growth 1981, 52, 146–150. [Google Scholar] [CrossRef]
- Lilov, S. Study of the equilibrium processes in the gas phase during silicon carbide sublimation. Mater. Sci. Eng. B 1993, 21, 65–69. [Google Scholar] [CrossRef]
- Jernigan, G.G.; VanMil, B.L.; Tedesco, J.L.; Tischler, J.G.; Glaser, E.R.; Davidson, A., III; Campbell, P.M.; Gaskill, D.K. Comparison of epitaxial graphene on Si face and C-face 4H SiC formed by ultrahigh vacuum and RF furnace production. Nano Lett. 2009, 9, 2605–2609. [Google Scholar] [CrossRef] [PubMed]
- Berger, C.; Song, Z.M.; Li, T.B.; Li, X.B.; Ogbazghi, A.Y.; Feng, R.; Dai, Z.T.; Marchenkov, A.N.; Conrad, E.H.; First, P.N.; et al. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics. J. Phys. Chem. B 2004, 108, 19912–19916. [Google Scholar] [CrossRef]
- Baringhaus, J.; Ruan, M.; dler, F.; Tejeda, A.; Sicot, M.; Taleb-Ibrahimi, A.; Li, A.P.; Jiang, Z.; Conrad, E.H.; Berger, C.; et al. Exceptional ballistic transport in epitaxial graphene nanoribbons. Nature 2014, 506, 349–354. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Dong, R.; Chakraborty, P.S.; Lourenco, N.; Palmer, J.; Hu, Y.; Ruan, M.; Hankinson, J.; Kunc, J.; Cressler, J.D.; et al. Record Maximum Oscillation Frequency in C-Face Epitaxial Graphene Transistors. Nano Lett. 2013, 13, 942–947. [Google Scholar] [CrossRef] [PubMed]
- Hicks, J.; Tejeda, A.; Taleb-Ibrahimi, A.; Nevius, M.S.; Wang, F.; Shepperd, K.; Palmer, J.; Bertran, F.; Le Fèvre, P.; Kunc, J.; et al. A wide-bandgap metal-semiconductor-metal nanostructure made entirely from graphene. Nat. Phys. 2013, 9, 49–54. [Google Scholar] [CrossRef]
- Turner, G.; Bauer, E. An ultrahigh vacuum electron microscope and its application to work function studies. In Proceedings of the Sixth International Congress on Electron Microscopy, Kyoto, Maruzen, Tokyo, 1966; Volume 1, pp. 163–164.
- Telieps, W.; Bauer, E. An analytical reflection and emission UHV surface electron microscope. Ultramicroscopy 1985, 17, 57–65. [Google Scholar] [CrossRef]
- Telieps, W.; Bauer, E. The (7 × 7) ↔ (1 × 1) phase transition on Si(111). Surf. Sci 1985, 162, 163–168. [Google Scholar] [CrossRef]
- Schmidt, T.; Heun, S.; Slezak, J.; Diaz, J.; Prince, K.C.; Lilienkamp, G.; Bauer, E. SPELEEM: combining LEEM and spectroscopic imaging. Surf. Rev. Lett. 1998, 5, 1287–1296. [Google Scholar] [CrossRef]
- Ohta, T.; Gabaly, F.E.; Bostwick, A.; McChesney, J.L.; Emtsev, K.V.; Schmid, A.K.; Seyller, T.; Horn, K.; Rotenberg, E. Morphology of graphene thin film growth on SiC(0001). New J. Phys. 2008, 10, 023034. [Google Scholar] [CrossRef]
- Virojanadara, C.; Syväjarvi, M.; Yakimova, R.; Johansson, L.I. Homogeneous large-area graphene layer growth on 6H-SiC(0001). Phys. Rev. B 2008, 78, 245403. [Google Scholar] [CrossRef]
- Forbeaux, I.; Themlin, J.M.; Debever, J.M. Heteroepitaxial graphite on 6HSiC(0001): Interface formation through conduction-band electronic structure. Phys. Rev. B 1998, 58, 16396–16406. [Google Scholar] [CrossRef]
- Fisher, P.J.; Luxmi; Srivastava, N.; Nie, S.; Feenstra, R.M. Thickness monitoring of graphene on Si C using low-energy electron diffraction. J. Vac. Sci. Technol. A 2010, 28, 958–962. [Google Scholar] [CrossRef]
- Raman, C.V.; Krishnan, K.S. A new class of spectra due to secondary radiation. Indian J. Phys. 1928, 2, 399–419. [Google Scholar]
- Raman, C.V.; Krishnan, K.S. A new type of secondary radiation. Nature 1928, 121, 501–502. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–58. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Righi, A.; Costa, S.D.; Chacham, H.; Fantini, C.; Venezuela, P.; Magnuson, C.; Colombo, L.; Bacsa, W.S.; Ruoff, R.S.; Pimenta, M.A. Graphene Moiré patterns observed by umklapp double-resonance Raman scattering. Phys. Rev. B 2011, 84, 241409. [Google Scholar] [CrossRef]
- Casiraghi, C. Doping dependence of the Raman peaks intensity of graphene close to the Dirac point. Phys. Rev. B 2009, 80, 233407. [Google Scholar] [CrossRef]
- Mohiuddin, T.M.G.; Lombardo, A.; Nair, R.R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.M.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 205433. [Google Scholar] [CrossRef]
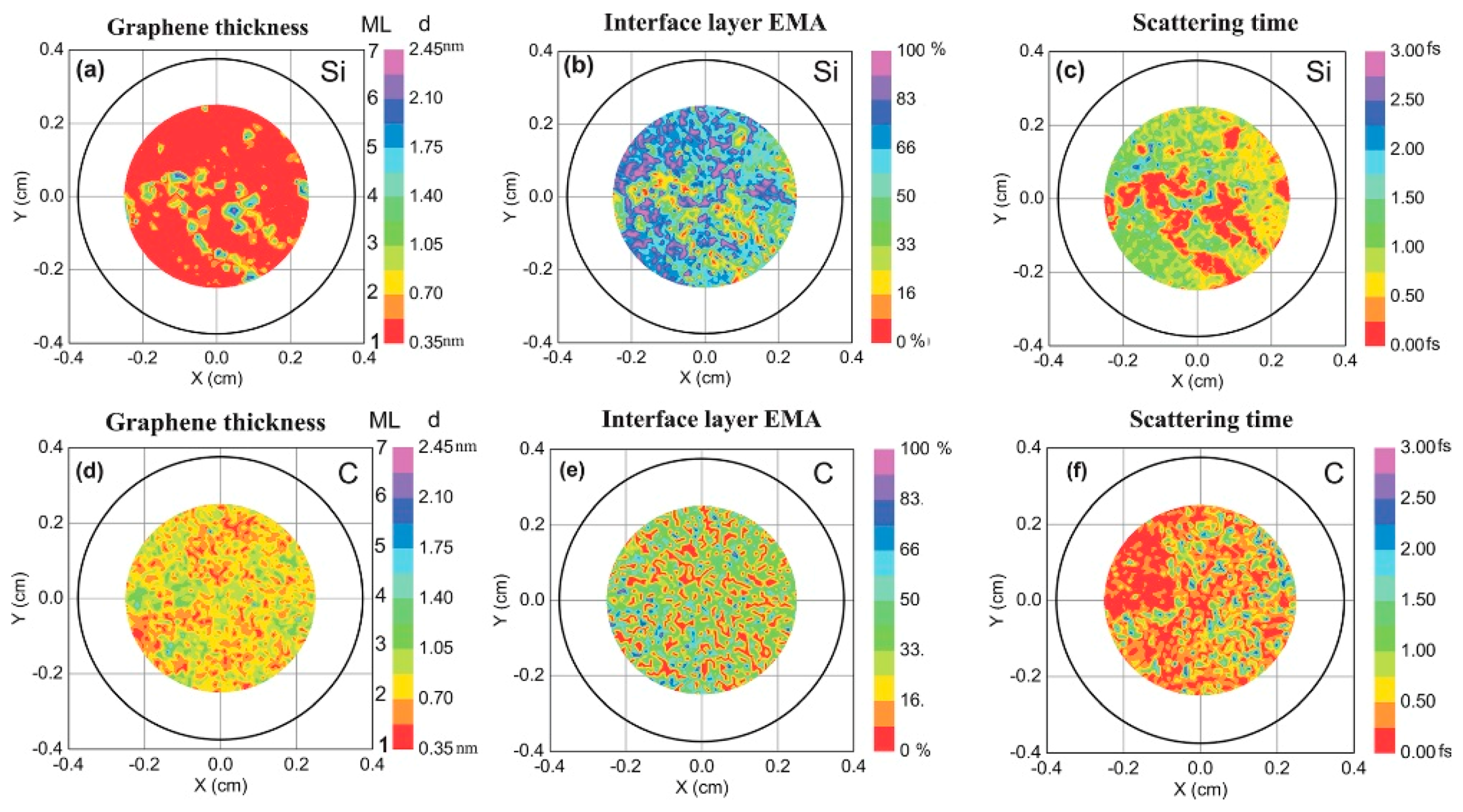
- Ivanov, I.G.; Hassan, J.U.; Iakimov, T.; Zakharov, A.A.; Yakimova, R.; Janzén, E. Layer-number determination in graphene on SiC by reflectance mapping. Carbon 2014, 77, 492–500. [Google Scholar] [CrossRef]
- Binnig, G.; Rohrer, H.; Gerber, C.; Weibel, E. Surface studies by scanning tunneling microscopy. Phys. Rev. Lett. 1985, 49, 57–61. [Google Scholar] [CrossRef]
- Hansma, P.K.; Tersoff, J. Scanning tunneling microscopy. J. Appl. Phys. 1987, 61, R1–R24. [Google Scholar] [CrossRef]
- Land, T.A.; Michely, T.; Behm, R.J.; Hemminger, J.C.; Comsa, G. STM investigation of single layer graphite structures produced on Pt(111) by hydrocarbon decomposition. Surf. Sci. 1992, 264, 261–270. [Google Scholar] [CrossRef]
- Biedermann, L.B.; Bolen, M.L.; Capano, M.A.; Zemlyanov, D.; Reifenberger, R.G. Insights into few-layer epitaxial graphene growth on 4H-SiC(0001) substrates from STM studies. Phys. Rev. B 2009, 79, 125411. [Google Scholar] [CrossRef]
- Virojanadara, C.; Yakimova, R.; Osiecki, J.R.; Syvajarvi, M.; Uhrberg, R.I.G.; Johansson, L.I.; Zakharov, A.A. Substrate orientation: A way towards higher quality monolayer graphene growth on 6H-SiC(0 0 0 1). Surf. Sci. 2009, 603, L87–L90. [Google Scholar] [CrossRef]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic force microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Hibino, H.; Kageshima, H.; Nagase, M. Epitaxial few-layer graphene: towards single crystal growth. J. Phys. D Appl. Phys. 2010, 43, 374005. [Google Scholar] [CrossRef]
- Burnett, T.; Yakimova, R.; Kazakova, O. Mapping of Local Electrical Properties in Epitaxial Graphene Using Electrostatic Force Microscopy. Nano Lett. 2011, 11, 2324–2328. [Google Scholar] [CrossRef] [PubMed]
- Ruska, E. The Early Development of Electron Lenses and Electron Microscopy. Microsc. Acta Suppl. 1980, 1–140. [Google Scholar]
- Haider, M.; Uhlemann, S.; Schwan, E.; Rose, H.; Kabius, B.; Urban, K. Electron microscopy image enhanced. Nature 1998, 392, 768–769. [Google Scholar] [CrossRef]
- Smith, B.W.; Luzzi, D.E. Electron irradiation effects in single wall carbon nanotubes. J. Appl. Phys. 2001, 90, 3509–3515. [Google Scholar] [CrossRef]
- Von Ardenne, M. Das elektronen-rastermikroskop. Z. Phys. 1938, 109, 553–572. [Google Scholar] [CrossRef]
- Grodecki, K.; Jozwik, I.; Baranowskia, J.M.; Teklinska, D.; Strupinski, W. SEM and Raman analysis of graphene on SiC(0001). Micron 2016, 80, 20–23. [Google Scholar] [CrossRef] [PubMed]
- Drowart, J.; De Maria, G.; Inghram, M.G. Thermodynamic Study of SiC Utilizing a Mass Spectrometer. J. Chem. Phys. 1958, 29, 1015–1021. [Google Scholar] [CrossRef]
- Berzelius, J.J. Untersuchungen über die Flusspath Faure und deren merkwürdige Verbindungen. Ann. Phys. Lpz 1 1824, 1, 169–230. (In German) [Google Scholar] [CrossRef]
- Acheson, A.G. England Patent 17911, 1892.
- Acheson, A.G. On Carborundum. Chem. News 1893, 68, 179. [Google Scholar]
- Round, H.J. A note on carborundum. Electr. World 1907, 19, 309–310. [Google Scholar]
- Lely, J.A. Darstellung von Einkristallen von Silicium carbid und Beherrschung von Art und Menge der eingebautem Verunreingungen. Ber. Deut. Keram. Ges 1955, 32, 229–250. [Google Scholar]
- Yazdi, G.R. Growth and Characterization of AlN: From Nano Structures to Bulk Material. Ph.D. Thesis, Linkoping University, Linköping, Sweden, 20 August 2008. [Google Scholar]
- Ramsdell, L.S. Studies on silicon carbide. Am. Min. 1947, 32, 64–82. [Google Scholar]
- Verma, A.R.; Krishna, P. Polymorphism and Polytypism in Crystals; John Wiley & Sons Inc.: New York, NY, USA, 1966. [Google Scholar]
- Yakimova, R.; Iakimov, T.; Yazdi, G.R.; Bouhafs, C.; Eriksson, J.; Zakharov, A.; Boosalis, A.; Schubert, M.; Darakchieva, V. Morphological and electronic properties of epitaxial graphene on SiC. Phys. B 2014, 439, 54–59. [Google Scholar] [CrossRef]
- Johansson, L.I.; Virojanadara, C. Properties of epitaxial graphene grown on C-face SiC compared to Si-face. J. Mater. Res. 2014, 29, 426–438. [Google Scholar] [CrossRef]
- Norimatsu, W.; Kusunoki, M. Structural features of epitaxial graphene on SiC{0001} surfaces. J. Phys. D. Appl. Phys. 2014, 47, 094017. [Google Scholar] [CrossRef]
- Chien, F.R.; Nutt, S.R.; Yoo, W.S.; Kimoto, T.; Matsunami, H. Terrace growth and polytype evelopment in epitaxial -SiC on –SiC (6H and 15R) substrates. J. Mater. Res. 1994, 9, 940–954. [Google Scholar] [CrossRef]
- Ohta, T.; Bartelt, N.C.; Nie, S.; Thurmer, K.; Kellogg, G.L. Role of carbon surface diffusion on the growth of epitaxial graphene on SiC. Phys. Rev. B 2010, 81, 121411. [Google Scholar] [CrossRef]
- Borovikov, V.; Zangwill, A. Step bunching of vicinal 6H-SiC{0001} surfaces. Phys. Rev. B 2009, 79, 245413. [Google Scholar] [CrossRef]
- Bolen, M.L.; Harrison, S.E.; Biedermann, L.B.; Capano, M.A. Graphene formation mechanisms on 4H-SiC(0001). Phys. Rev. B 2009, 80, 115433. [Google Scholar] [CrossRef]
- Ming, F.; Zangwill, A. Model for the epitaxial growth of graphene on 6H-SiC(0001). Phys. Rev. B 2011, 84, 115459. [Google Scholar] [CrossRef]
- Riedl, C.; Coletti, C.; Starke, U. Structural and electronic properties of epitaxial graphene on SiC(0 0 0 1): A review of growth, characterization, transfer doping and hydrogen intercalation. J. Phys. D 2010, 43, 374009. [Google Scholar] [CrossRef]
- de Heer, W.A.; Berger, C.; Ruan, M.; Sprinkle, M.; Li, X.; Hu, Y.; Zhang, B.; Hankinson, J.; Conrad, E. Large area and structured epitaxial graphene produced by confinement controlled sublimation of silicon carbide. Proc. Natl. Acad. Sci. USA 2011, 108, 16900–16905. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Guowei, He.; Luxmi; Feenstra, R.M. Interface structure of graphene on SiC(0001¯). Phys. Rev. B 2012, 85, 041404. [Google Scholar] [CrossRef]
- Badami, D.V. Graphitization of α-Silicon Carbide. Nature 1962, 193, 569–570. [Google Scholar] [CrossRef]
- Badami, D.V. X-Ray studies of graphite formed by decomposing silicon carbide. Carbon 1965, 3, 53–57. [Google Scholar] [CrossRef]
- Charrier, A.; Coati, A.; Argunova, T.; Thibaudau, F.; Garreau, Y.; Pinchaux, R.; Forbeaux, I.; Debever, J.M.; Sauvage-Simkin, M.; Themlin, J.M. Solid-state decomposition of silicon carbide for growing ultra-thin heteroepitaxial graphite films. J. Appl. Phys. 2002, 92, 2479–2481. [Google Scholar] [CrossRef]
- Nemec, L.; Blum, V.; Rinke, P.; Scheffler, M. Thermodynamic Equilibrium Conditions of Graphene Films on SiC. Phys. Rev. Lett 2013, 111, 065502. [Google Scholar] [CrossRef] [PubMed]
- Hibino, H.; Kageshima, H.; Maeda, F.; Nagase, M.; Kobayashi, Y.; Yamaguchi, H. Microscopic thickness determination of thin graphite films formed on SiC from quantized oscillation in reflectivity of low-energy electrons. Phys. Rev. B 2008, 77, 075413. [Google Scholar] [CrossRef]
- Hannon, J.B.; Tromp, R.M. Pit formation during graphene synthesis on SiC(0001): In situ electron microscopy. Phys. Rev. B 2008, 77, 241404. [Google Scholar] [CrossRef]
- Hupalo, M.; Conrad, E.H.; Tringides, M.C. Growth mechanism for epitaxial graphene on vicinal 6H-SiC(0001) surfaces: A scanning tunneling microscopy study. Phys. Rev. B 2008, 80, 041401. [Google Scholar] [CrossRef]
- Tromp, R.M.; Hannon, J.B. Thermodynamics and Kinetics of Graphene Growth on SiC(0001). Phys. Rev. Lett. 2009, 102, 106104. [Google Scholar] [CrossRef] [PubMed]
- Rutter, G.M.; Guisinger, N.P.; Crain, J.N.; Jarvis, E.A.A.; Stiles, M.D.; Li, T.; First, P.N.; Stroscio, J.A. Imaging the interface of epitaxial graphene with silicon carbide via scanning tunneling microscopy. Phys. Rev. B 2007, 76, 235416. [Google Scholar] [CrossRef]
- Nie, S.; Feenstra, R.M. Tunneling Spectroscopy of Graphene and related Reconstructions on SiC(0001). J. Vac. Sci. Technol. A 2009, 27, 1052. [Google Scholar] [CrossRef]
- Emtsev, K.V.; Speck, F.; Seyller, T.; Ley, L.; Riley, J.D. Interaction, growth, and ordering of epitaxial graphene on SiC{0001} surfaces: A comparative photoelectron spectroscopy study. Phys. Rev. B 2008, 77, 155303. [Google Scholar] [CrossRef]
- Darakchieva, V.; Boosalis, A.; Zakharov, A.A.; Hofmann, T.; Schubert, M.; Tiwald, T.E.; Iakimov, T.; Vasiliauskas, R.; Yakimova, R. Large-area microfocal spectroscopic ellipsometry mapping of thickness and electronic properties of epitaxial graphene on Si- and C-face of 3C-SiC(111). Appl. Phys. Lett 2013, 102, 213116. [Google Scholar] [CrossRef]
- Riedl, C.; Coletti, C.; Iwasaki, T.; Zakharov, A.A.; Starke, U. Quasi free-standing epitaxial graphene on SiC obtained by hydrogen intercalation. Phys. Rev. Lett. 2009, 103, 246804. [Google Scholar] [CrossRef] [PubMed]
- Mattausch, A.; Pankratov, O. Ab Initio Study of Graphene on SiC. Phys. Rev. Lett. 2007, 99, 076802. [Google Scholar] [CrossRef] [PubMed]
- Hannon, J.B.; Copel, M.; Tromp, R.M. Direct Measurement of the Growth Mode of Graphene on SiC(0001) and SiC(000). Phys. Rev. Lett. 2011, 107, 166101. [Google Scholar] [CrossRef] [PubMed]
- Starke, U.; Riedl, C. Epitaxial graphene on SiC(0001) and SiC(000): From surface reconstructions to carbon electronics. J. Phys. Condens. Matter 2009, 21, 134016. [Google Scholar] [CrossRef] [PubMed]
- De Lima, L.H.; de Siervo, A.; Landers, R.; Viana, G.A.; Goncalves, A.M.B.; Lacerda, R.G.; Häberle, P. Atomic surface structure of graphene and its buffer layer on SiC(0001): A chemical-specific photoelectron diffraction approach. Phys. Rev. B 2013, 87, 081403. [Google Scholar] [CrossRef]
- Norimatsu, W.; Kusunoki, M. Transitional structures of the interface between graphene and 6H–SiC (0001). Chem. Phys. Lett. 2009, 468, 52–56. [Google Scholar] [CrossRef]
- Borysiuk, J.; Bożek, R.; Strupiński, W.; Wysmołek, A.; Grodecki, K.; Stepniewski, R.; Baranowski, J.M. Transmission electron microscopy and scanning tunneling microscopy investigations of graphene on 4H-SiC(0001). J. Appl. Phys. 2009, 105, 023503. [Google Scholar] [CrossRef]
- Norimatsu, W.; Kusunoki, M. Selective formation of ABC-stacked graphene layers on SiC(0001). Phys. Rev. B 2010, 81, 161410. [Google Scholar] [CrossRef]
- Charlier, J.C.; Michenaud, J.P.; Gonze, X. First-principles study of the electronic properties of simple hexagonal graphite. Phys. Rev. B 1992, 46, 4531. [Google Scholar] [CrossRef]
- Aoki, M.; Amawashi, H. Dependence of band structures on stacking and field in layered graphene. Solid State Commun. 2007, 142, 123–127. [Google Scholar] [CrossRef]
- Latil, S.; Henrard, L. Charge Carriers in Few-Layer Graphene Films. Phys. Rev. Lett. 2006, 97, 036803. [Google Scholar] [CrossRef] [PubMed]
- Latil, S.; Meunier, V.; Henrard, L. Massless fermions in multilayer graphitic systems with misoriented layers: Ab initio calculations and experimental fingerprints. Phys. Rev. B 2007, 76, 201402. [Google Scholar] [CrossRef]
- Mak, K.; Shan, J.; Heinz, T. Electronic Structure of Few-Layer Graphene: Experimental Demonstration of Strong Dependence on Stacking Sequence. Phys. Rev. Lett. 2010, 104, 176404. [Google Scholar] [CrossRef] [PubMed]
- Ohta, T.; Bostwick, A.; McChesney, J.L.; Seyller, T.; Horn, K.; Rotenberg, E. Interlayer Interaction and Electronic Screening in Multilayer Graphene Investigated with Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2007, 98, 206802. [Google Scholar] [CrossRef] [PubMed]
- Daas, B.K.; Omar, S.U.; Shetu, S.; Daniels, K.M.; Ma, S.; Sudarshan, T.S.; Chandrashekhar, M.V.S. Comparison of Epitaxial Graphene Growth on Polar and Nonpolar 6H-SiC Faces: On the Growth of Multilayer Films. Cryst. Growth Des. 2012, 12, 3379–3387. [Google Scholar] [CrossRef]
- Berger, C.; Wu, X.; First, P.N.; Conrad, E.H.; Li, X.; Sprinkle, M.; Hass, J.; Varchon, F.; Magaud, L.; Sadowski, M.L.; et al. Dirac Particles in Epitaxial Graphene Films Grown on SiC. Adv. Solid State Phys. 2008, 47, 145–157. [Google Scholar]
- Virojanadara, C.; Zakharov, A.A.; Yakimova, R.; Johansson, L.I. Buffer layer free large area bi-layer graphene on SiC(0 0 0 1). Surf. Sci. 2010, 604, L4–L7. [Google Scholar] [CrossRef]
- Xia, C.; Watcharinyanon, S.; Zakharov, A.A.; Johansson, L.I.; Yakimova, R.; Virojanadara, C. Detailed studies of Na intercalation on furnace-grown graphene on 6H-SiC(0001). Surf. Sci. 2013, 613, 88–94. [Google Scholar] [CrossRef]
- Oliveira, M.H., Jr.; Schumann, T.; Fromm, F.; Koch, R.; Ostler, M.; Ramsteiner, M.; Seyller, T.; Lopes, J.M.J.; Riechert, H. Formation of high-quality quasi-free-standing bilayer graphene on SiC(0 0 0 1) by oxygen intercalation upon annealing in air. Carbon 2013, 52, 83–89. [Google Scholar] [CrossRef]
- Virojanadara, C.; Watcharinyanon, S.; Zakharov, A.A.; Johansson, L.J. Epitaxial graphene on 6H-SiC and Li intercalation. Phys. Rev. B 2010, 82, 205402. [Google Scholar] [CrossRef]
- Xia, C.; Watcharinyanon, S.; Zakharov, A.A.; Yakimova, R.; Hultman, L.; Johansson, L.J.; Virojanadara, C. Si intercalation/deintercalation of graphene on 6H-SiC(0001). Phsy. Rev. B 2012, 85, 045418. [Google Scholar] [CrossRef]
- Gierz, I.; Suzuki, T.; Weitz, R.T.; Lee, D.S.; Krauss, B.; Riedl, C.; Starke, U.; Höchst, H.; Smet, J.H.; Ast, C.R.; Kern, K. Electronic decoupling of an epitaxial graphene monolayer by gold intercalation. Phys. Rev. B 2010, 81, 235408. [Google Scholar] [CrossRef]
- Walter, A.L.; Jeon, K.J.; Bostwick, A.; Speck, F.; Ostler, M.; Seyller, T.; Moreschini, L.; Kim, Y.S.; Chang, Y.J.; Horn, K.; et al. Highly p-doped epitaxial graphene obtained by fluorine intercalation. Appl. Phys. Lett. 2011, 98, 184102. [Google Scholar] [CrossRef]
- Emtsev, K.V.; Zakharov, A.A.; Coletti, C.; Forti, S.; Starke, U. Ambipolar doping in quasifree epitaxial graphene on SiC(0001) controlled by Ge intercalation. Phys. Rev. B 2011, 84, 125423. [Google Scholar] [CrossRef]
- Tanabe, S.; Takamura, M.; Harada, Y.; Kageshima, H.; Hibino, H. Quantum Hall Effect and Carrier Scattering in Quasi-Free-Standing Monolayer Graphene. Appl. Phys. Exp. 2012, 5, 125101. [Google Scholar] [CrossRef]
- Caffrey, N.M.; Armiento, R.; Yakimova, R.; Abrikosov, I.A. Charge neutrality in epitaxial graphene on 6H-SiC(0001) via nitrogen intercalation. Phys. Rev. B 2015, 92, 081409. [Google Scholar] [CrossRef]
- Brar, V.W.; Zhang, Y.; Yayon, Y.; Bostwick, A.; Ohta, T.; McChesney, J.L.; Horn, K.; Rotenberg, E.; Crommie, M.F. Scanning tunneling spectroscopy of inhomogeneous electronic structure in monolayer and bilayer graphene on SiC. Appl. Phys. Lett. 2007, 91, 122102. [Google Scholar] [CrossRef]
- Lauffer, P.; Emtsev, K.V.; Graupner, R.; Seyller, T.; Ley, L.; Reshanov, S.A.; Weber, H.B. Atomic and electronic structure of few-layer graphene on SiC(0001) studied with scanning tunneling microscopy and spectroscopy. Phys. Rev. B 2008, 77, 155426. [Google Scholar] [CrossRef]
- Sonde, S.; Giannazzo, F.; Huntzinger, J.R.; Tiberj, A.; Syväjärvi, M.; Yakimova, R.; Raineri, V.; Camassel, J. Uniformity of Epitaxial Graphene on On-axis and Off-axis SiC Probed by Raman Spectroscopy and Nanoscale Current Mapping. Mater. Sci. Forum. 2010, 645–648, 607–610. [Google Scholar] [CrossRef]
- Sun, G.F.; Jia, J.F.; Xue, Q.K.; Li, L. Atomic-scale imaging and manipulation of ridges on epitaxial graphene on 6H-SiC(0001). Nanotechnology 2009, 20, 355701. [Google Scholar] [CrossRef] [PubMed]
- Vecchio, C.; Sonde, S.; Bongiorno, C.; Rambach, M.; Yakimova, R.; Raineri, V.; Giannazzo, F. Nanoscale structural characterization of epitaxial graphene grown on off-axis 4H-SiC (0001). Nanoscale Res. Lett. 2011, 6, 269. [Google Scholar] [CrossRef] [PubMed]
- Giannazzo, F.; Deretzis, I.; Magna, A.L.; Roccaforte, F.; Yakimova, R. Electronic transport at monolayer-bilayer junctions in epitaxial graphene on SiC. Phys. Rev. B 2012, 86, 235422. [Google Scholar] [CrossRef]
- Nicotra, G.; Ramasse, Q.M.; Deretzis, I.; La Magna, A.; Spinella, C.; Giannazzo, F. Delaminated Graphene at Silicon Carbide Facets: Atomic Scale Imaging and Spectroscopy. ACS Nano 2013, 7, 3045–3052. [Google Scholar] [CrossRef] [PubMed]
- Mikoushkin, V.M.; Shnitov, V.V.; Lebedev, A.A.; Lebedev, S.P.; Nikonov, S.Y.; Vilkov, O.Y.; Iakimov, T.; Yakimova, R. Size confinement effect in graphene grown on 6H-SiC (0001) substrate. Carbon 2015, 86, 139–145. [Google Scholar] [CrossRef]
- Lartsev, A.; Lara-Avila, S.; Danilov, A.; Kubatkin, S.; Tzalenchuk, A.; Yakimova, R. A prototype of R-K/200 quantum Hall array resistance standard on epitaxial graphene. J. Appl. Phys. 2015, 118, 044506. [Google Scholar] [CrossRef]
- Janssen, T.J.B.M.; Rozhko, S.; Antonov, I.; Tzalenchuk, A.; Williams, J.M.; Melhem, Z.; He, H.; Lara-Avila, S.; Kubatkin, S.; Yakimova, R. Operation of graphene quantum Hall resistance standard in a cryogen-free table-top system. 2D Materials 2015, 2, 035015. [Google Scholar] [CrossRef]
- Syvajarvi, M.; Yakimova, R.; Janźen, E. Interfacial properties in SiC liquid phase growth. J. Electrochem. Soc. 1999, 146, 1565–1569. [Google Scholar] [CrossRef]
- Borysiuk, J.; Bozek, R.; Grodecki, K.; Wysmołek, A.; Strupinski, W.; Stepniewski, R.; Baranowski, J.M. Transmission electron microscopy investigations of epitaxial graphene on C-terminated 4H–SiC. J. Appl. Phys. 2010, 108, 013518. [Google Scholar] [CrossRef]
- Hass, J.; Varchon, F.; Millán-Otoya, J.E.; Sprinkle, M.; Sharma, N.; de Heer, W.A.; Berger, C.; First, P.N.; Magaud, L.; Conrad, E.H. Why Multilayer Graphene on 4H−SiC(000) Behaves Like a Single Sheet of Graphene. Phys. Rev. Lett. 2008, 100, 125504. [Google Scholar] [CrossRef] [PubMed]
- Sprinkle, M.; Siege, D.; Hu, Y.; Hicks, J.; Tejeda, A.; Taleb-Ibrahimi, A.; Le Fèvre, P.; Bertran, F.; Vizzini, S.; Enriquez, H.; et al. First Direct Observation of a Nearly Ideal Graphene Band Structure. Phys. Rev. Lett. 2009, 103, 226803. [Google Scholar] [CrossRef] [PubMed]
- Sprinkle, M.; Hicks, J.; Tejeda, A.; Taleb-Ibrahimi, A.; Le Févre, P.; Bertran, F.; Tinkey, H.; Clark1, M.C.; Soukiassian, P.; Martinotti, D.; et al. Multilayer epitaxial graphene grown on the SiC(000) surface; structure and electronic properties. J. Phys. D: Appl. Phys. 2010, 43, 374006. [Google Scholar] [CrossRef]
- Lin, Y.M.; Dimitrakopoulos, C.; Farmer, D.B.; Han, S.J.; Wu, Y.; Zhu, W.; Gaskill, D.K.; Tedesco, J.L.; Myers-Ward, R.L.; Eddy, C.R., Jr.; et al. Multicarrier transport in epitaxial multilayer graphene. Appl. Phys. Lett. 2010, 97, 112107. [Google Scholar] [CrossRef]
- Johansson, L.I.; Watcharinyanon, S.; Zakharov, A.A.; Iakimov, T.; Yakimova, R.; Virojanadara, C. Stacking of adjacent graphene layers grown on C-face SiC. Phys. Rev. B 2011, 84, 125405. [Google Scholar] [CrossRef]
- Johansson, L.I.; Xia, C.; Hassan, J.U.; Iakimov, T.; Zakharov, A.A.; Watcharinyanon, S.; Yakimova, R.; Janzén, E.; Virojanadara, C. Is the Registry Between Adjacent Graphene Layers Grown on C-Face SiC Different Compared to That on Si-Face SiC. Crystals 2013, 3, 1–13. [Google Scholar] [CrossRef]
- Giusca, C.E.; Spencer, S.J.; Shard, A.G.; Yakimova, R.; Kazakova, O. Exploring graphene formation on the C-terminated face of SiC by structural, chemical and electrical methods. Carbon 2014, 69, 221–229. [Google Scholar] [CrossRef]
- Bouhafs, C.; Darakchieva, V.; Persson, I.L.; Tiberj, A.; Persson, P.O.Å.; Paillet, M.; Zahab, A.-A.; Landois, P.; Juillaguet, S.; Schoche, S.; et al. Structural properties and dielectric function of graphene grown by high-temperature sublimation on 4H-SiC(000). J. Appl. Phys. 2015, 117, 085701. [Google Scholar] [CrossRef]
- Nicotra, G.; Deretzis, I.; Scuderi, M.; Spinella, C.; Longo, P.; Yakimova, R.; Giannazzo, F.; La Magna, A. Interface disorder probed at the atomic scale for graphene grown on the C face of SiC. Phys. Rev. B 2015, 91, 155411. [Google Scholar] [CrossRef]
- Jabakhanji, B.; Camara, N.; Caboni, A.; Consejo, C.; Jouault, B.; Godignon, P.; Camassel, J. Almost free standing Graphene on SiC(000) and SiC(110). Mater. Sci. Forum 2012, 711, 235–241. [Google Scholar] [CrossRef]
- Ostler, M.; Deretzis, I.; Mammadov, S.; Giannazzo, F.; Nicotra, G.; Spinella, C.; Seyller, T.; La Magna, A. Direct growth of quasi-free-standing epitaxial graphene on nonpolar SiC surfaces. Phys. Rev. B 2013, 88, 085408. [Google Scholar] [CrossRef]
- Deretzis, I.; La Magna, A. A density functional theory study of epitaxial graphene on the (3 × 3)-reconstructed C-face of SiC. Appl. Phys. Lett. 2013, 102, 093101. [Google Scholar] [CrossRef]
- Beaucarne, G.; Brown, A.S.; Keevers, M.J.; Corkish, R.; Green, M.A. The impurity photovoltaic effect in wide- bandgap semiconductors: an opportunity for very-high-efficiency solar cells. Prog. Photovolt. Res. Appl. 2002, 10, 345–353. [Google Scholar] [CrossRef]
- Heine, V.; Cheng, C.; Needs, R.J. The preference of silicon carbide for growth in the metastable cubic form. J. Am. Ceram Soc. 1991, 74, 2630–2633. [Google Scholar] [CrossRef]
- Kimoto, T.; Itoh, A.; Matsunami, H. Step bunching in chemical vapor deposition of 6H– and 4H–SiC on vicinal SiC(0001) faces. Appl. Phys. Lett. 1995, 66, 3645–3647. [Google Scholar] [CrossRef]
- Low, T.; Perebeinos, V.; Tersoff, J.; Avouris, P.H. Deformation and scattering in graphene over substrate steps. Phys. Rev. Lett. 2012, 108, 096601. [Google Scholar] [CrossRef] [PubMed]
- Vasiliauskasa, R.; Marinovab, M.; Syväjärvia, M.; Liljedahla, R.; Zoulisc, G.; Lorenzzid, J.; Ferrod, G.; Juillaguetc, S.; Camasselc, J.; Polychroniadisb, E.K.; et al. Effect of initial substrate conditions on growth of cubic silicon carbide. J. Cryst. Growth 2011, 324, 7–14. [Google Scholar] [CrossRef]
- Jokubavicius, V.; Yazdi, G.R.; Liljedahl, R.; Ivanov, I.G.; Yakimova, R.; Syväjärvi, M. Lateral Enlargement Growth Mechanism of 3C-SiC on Off-Oriented 4H-SiC Substrates. Cryst. Growth Des. 2014, 14, 6514–6520. [Google Scholar] [CrossRef]
- Jokubavicius, V.; Yazdi, G.R.; Liljedahl, R.; Ivanov, I.G.; Jianwu, S.; Liu, X.; Schuh, P.; Wilhelm, M.; Wellmann, P.; Yakimova, R.; et al. Single Domain 3C-SiC Growth on Off-Oriented 4H-SiC Substrates. Cryst. Growth Des. 2015, 15, 2940–2947. [Google Scholar] [CrossRef]
- Chu, T.L.; Campbell, R.B. Chemical Etching of Silicon Carbide with Hydrogen. J. Electrochem. Soc. 1965, 112, 955–956. [Google Scholar] [CrossRef]
- Owman, F.; Hallin, C.; Mårtensson, P.; Janzen, E. Removal of polishing-induced damage from 6H-SiC(0001) substrates by hydrogen etching. J. Cryst. Growth 1996, 167, 391–395. [Google Scholar] [CrossRef]
- Robinson, Z.R.; Jernigan, G.G.; Currie, M.; Hite, J.K.; Bussmann, K.M.; Nyakiti, L.O.; Garces, N.Y.; Nath, A.; Rao, M.V.; Wheeler, V.D.; et al. Challenges to graphene growth on SiC(0001): Substrate effects, hydrogen etching and growth ambient. Carbon 2015, 81, 73–82. [Google Scholar] [CrossRef]
- Robinson, Z.R.; Jernigan, G.G.; Bussmann, K.M.; Nyakiti, L.O.; Garces, N.Y.; Nath, A.; Wheeler, V.D.; Myers-Ward, R.L.; Gaskill, D.K.; Eddy, C.R. Graphene Growth on SiC(000): Optimization of Surface Preparation and Growth Conditions. In Proceedings of Carbon Nanotubes, Graphene, and Emerging 2D Materials for Electronic and Photonic Devices VIII, 95520Y, San Diego, CA, USA, 16 September 2015.
- Ostler, M.; Speck, F.; Gick, M.; Seyller, T. Automated preparation of high-quality epitaxial graphene on 6H-SiC(0001). Phys. Status Solidi B 2010, 247, 2924–2926. [Google Scholar] [CrossRef]
- Swiderski, I. Thermal etching of α-SiC crystals in argon. J. Cryst. Growth 1972, 16, 1–9. [Google Scholar] [CrossRef]
- Nishiguchi, T.; Ohshima, S.; Nishino, S. Thermal Etching of 6H–SiC Substrate Surface. Jpn. J. Appl. Phys. 2003, 42, 1533–1537. [Google Scholar] [CrossRef]
- van der Berga, N.G.; Malherbea, J.B.; Bothab, A.J.; Friedlanda, E. Thermal etching of SiC. Appl. Surf. Sci. 2012, 258, 5561–5566. [Google Scholar] [CrossRef]
- Lebedev, S.P.; Petrov, V.N.; Kotousova, I.S.; Lavrentev, A.A.; Dementev, P.A.; Lebedev, A.A.; Titkov, N. Formation of Periodic Steps on 6H-SiC (0001) Surface by Annealing in a High Vacuum. Mater. Sci. Forum 2011, 679, 437–440. [Google Scholar] [CrossRef]
- Rana, T.; Chandrashekhar, M.V.S.; Sudarshan, T.S. Vapor phase surface preparation (etching) of 4H–SiC substrates using tetrafluorosilane (SiF4) in a hydrogen ambient for SiC epitaxy. J. Cryst. Growth. 2013, 380, 61–67. [Google Scholar] [CrossRef]
- Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954–17961. [Google Scholar] [CrossRef]
- Kan, E.; Li, Z.; Yang, J. Graphene nanoribbons: Geometric, electronic, and magnetic properties. Intech Open J. 2011, 331–348. [Google Scholar]
- Han, M.Y.; Brant, J.C.; Kim, P. Electron transport in disordered graphene nanoribbons. Phys. Rev. Lett. 2010, 104, 056801. [Google Scholar] [CrossRef] [PubMed]
- Tapaszto, L.; Dobrik, G.; Lambin, P.; Birό, L.P. Tailoring the atomic structure of graphene nanoribbons by scanning tunnelling microscope lithography. Nat. Nanotech. 2008, 3, 397–401. [Google Scholar] [CrossRef] [PubMed]
- Jiao, L.; Zhang, L.; Wang, X.; Diankov, G.; Dai, H. Narrow graphene nanoribbons from carbon nanotubes. Nature 2009, 458, 877–880. [Google Scholar] [CrossRef] [PubMed]
- Sprinkler, M.; Ruan, M.; Hu, Y.; Hankinson, J.; Rubio-Roy, M.; Zhang, B.; Wu, X.; Berger, C.; de Heer, W.A. Scalable templated growth of graphene nanoribbons on SiC. Nat. Nanotech. 2010, 5, 727–731. [Google Scholar] [CrossRef] [PubMed]
- Tongay, S.; Lemaitre, M.; Fridmann, J.; Hebard, A.F.; Gila, B.P.; Appleton, B.R. Drawing graphene nanoribbons on SiC by ion implantation. Appl. Phys. Lett 2012, 100, 073501. [Google Scholar]
- Zhang, Y.; Hui, C.; Sun, R.; Li, K.; He, K.; Ma, X.; Liu, F. A large-area 15 nm graphene nanoribbon array patterned by a focused ion beam. Nanotechnology 2014, 25, 135301. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, G.; Rothwell, S.; Nevius, M.S.; Mathieu, C.; Barrett, N.; Sala, A.; Mentes, T.O.; Locatelli, A.; Cohen, P.I.; et al. Pattern induced ordering of semiconducting graphene ribbons grown from nitrogen-seeded SiC. Carbon 2015, 82, 360–367. [Google Scholar] [CrossRef]















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yazdi, G.R.; Iakimov, T.; Yakimova, R. Epitaxial Graphene on SiC: A Review of Growth and Characterization. Crystals 2016, 6, 53. https://doi.org/10.3390/cryst6050053
Yazdi GR, Iakimov T, Yakimova R. Epitaxial Graphene on SiC: A Review of Growth and Characterization. Crystals. 2016; 6(5):53. https://doi.org/10.3390/cryst6050053
Chicago/Turabian StyleYazdi, Gholam Reza, Tihomir Iakimov, and Rositsa Yakimova. 2016. "Epitaxial Graphene on SiC: A Review of Growth and Characterization" Crystals 6, no. 5: 53. https://doi.org/10.3390/cryst6050053
APA StyleYazdi, G. R., Iakimov, T., & Yakimova, R. (2016). Epitaxial Graphene on SiC: A Review of Growth and Characterization. Crystals, 6(5), 53. https://doi.org/10.3390/cryst6050053




