Abstract
Saturated acyclic four-atom groups closed with a classic intramolecular hydrogen bond, generating planar five-membered rings (hydrogen-bridged quasi-rings), in which at least one of the ring atoms is bonded to other non-ring atoms that are not in the ring plane and, thus, capable to form intermolecular interactions, were studied in this work, in order to find the preferred mutual positions of these species in crystals and evaluate strength of intermolecular interactions. We studied parallel interactions of these rings by analysing crystal structures in the Cambridge Structural Database (CSD) and by quantum chemical calculations. The rings can have one hydrogen atom out of the ring plane that can form hydrogen bonds between two parallel rings. Hence, in these systems with parallel rings, two types of hydrogen bonds can be present, one in the ring, and the other one between two parallel rings. The CSD search showed that 27% of the rings in the crystal structures form parallel interactions. The calculations at very accurate CCSD(T)/CBS level revealed strong interactions, in model systems of thiosemicarbazide, semicarbazide and glycolamide dimers the energies are −9.68, −7.12 and −4.25 kcal/mol. The hydrogen bonds between rings, as well as dispersion interactions contribute to the strong interaction energies.
1. Introduction
The stacking interactions between aromatic rings are one of the well examined non-covalent interactions [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. However, not only aromatic, but other planar molecules and fragments can also form stacking (parallel) interactions [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]. Interestingly, several studies showed that stacking interactions of other planar molecules can be even stronger than stacking between aromatic molecules [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46], indicating the importance of these interactions. Analysis of the crystal structures from Cambridge Structural Database (CSD) have shown that planar chelate rings with delocalized π-bonds can form stackinginteractions with C6-aromatic rings, and with other chelate rings [24,25,26,27]. The interaction energies of nickel and copper six-membered chelate rings with benzene, calculated at very acurate CCSD(T)/CBS level, are −4.77 and −6.39 kcal/mol respectively [43,44], remarkably stronger than stacking interaction between two benzene molecules, −2.73 kcal/mol [10].
Supramolecular chemistry of hydrogen-bridged quasi-ring species becomes very interesting from the fundamental point of view, however, it could be also useful in molecular recognition, crystal engineering or biochemistry. Interactions of hydrogen-bridged rings in supramolecular arrangements are similar to interactions of classical rings formed by covalent bonding. For example, quasi-chelate rings can participate in C–H···π interactions similar to aromatic organic molecules [47]. Rings formed by resonance-assisted hydrogen bonding [45,48,49,50] can form π-stacking interactions. Moreover, hydrogen-bridged rings with saturated bonds can also form stacking interactions [46]. In our previous study, it was shown that, in crystal structures from Cambridge Structural Database (CSD), 27% of five-membered hydrogen-bridged rings form intermolecular stacking interactions [46]. Interaction energy calculated at very accurate CCSD(T)/CBS level are −4.89 kcal/mol and −2.95 kcal/mol, dependent on ring structure. These interactions are stronger than stacking between two benzene molecules (−2.73 kcal/mol) [10].
The aim of this work was to deepen the knowledge about intermolecular interactions of hydrogen-bridged rings by analyzing interaction of the saturated acyclic four-atom groups closed by a classic intramolecular hydrogen bond, generating planar five-membered quasi-rings, with at least one non-ring atom attached to the ring and situated out of the ring plane. This type of rings is observed quite frequently in crystal structures from the CSD. One example of such ring is presented in Figure 1a. The rings can have one hydrogen atom out of the ring plane that can form hydrogen bonds between two parallel rings. Hence, in these systems, two types of hydrogen bonds can be present, one in the ring, and the other one between two parallel rings. The parallel interactions of the rings were studied by searching Cambridge Structural Database (CSD) and by quantum chemical calculations.
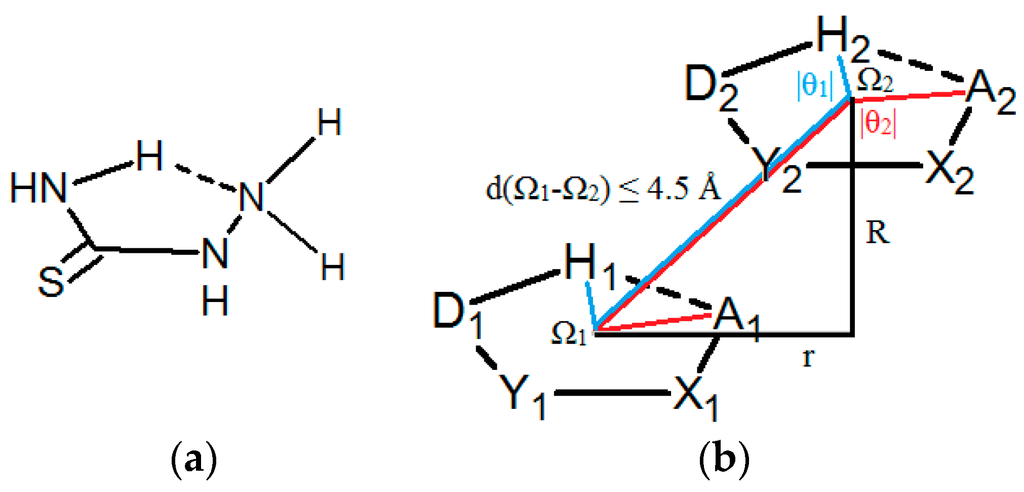
Figure 1.
(a) An example of a molecule with non–planar groups in the ring, that have hydrogen capable for hydrogen bond between two parallel rings. (b) Geometric parameters and atom labeling scheme used for the description of intermolecular interactions of saturated hydrogen-bridged rings, studied in this work; Ω marks the centroid of the ring, X and Y letters stand for any atoms adjacent to acceptor (A) and donor (D) atoms, respectively, R and r mark normal distance and offset value, respectively, θ1 and θ2-torsion angles H1Ω1Ω2H2 and A1Ω1Ω2A2, respectively; non–planar groups are omitted for simplicity.
2. Results
2.1. Search and Analysis of Crystal Structures from the CSD
To get an insight into the interactions of the hydrogen-bridged rings without multiple bonds that also have non-planar groups in the ring (Figure 1a), search and analysis of the data in crystal structures from the CSD were performed. Structures studied in this work are not limited to small molecules similar to the one presented in Figure 1a, but larger molecules which have structural fragments, as shown in Figure 1b, are included.
There are 1068 rings that satisfy Criteria 1–6, listed below in the Materials and Methods Section. There are 352 (33%) contacts of the two hydrogen-bridged quasi-rings that have distances between two centroids 4.5 Å or less, while 289 contacts (27%) have parallel orientation of the rings (interplanar angles smaller than 10°). Interestingly, in our previous search of hydrogen-bridged rings, with all planar groups in the ring, we found 978 rings in the CSD, while 27% (264) of the rings also formed parallel interactions [46].
The interplanar angle (π) distribution for contacts that have distances between two centroids less than 4.5 Å, indicating preferred parallel orientation of the middle ring planes, is given in Figure 2.
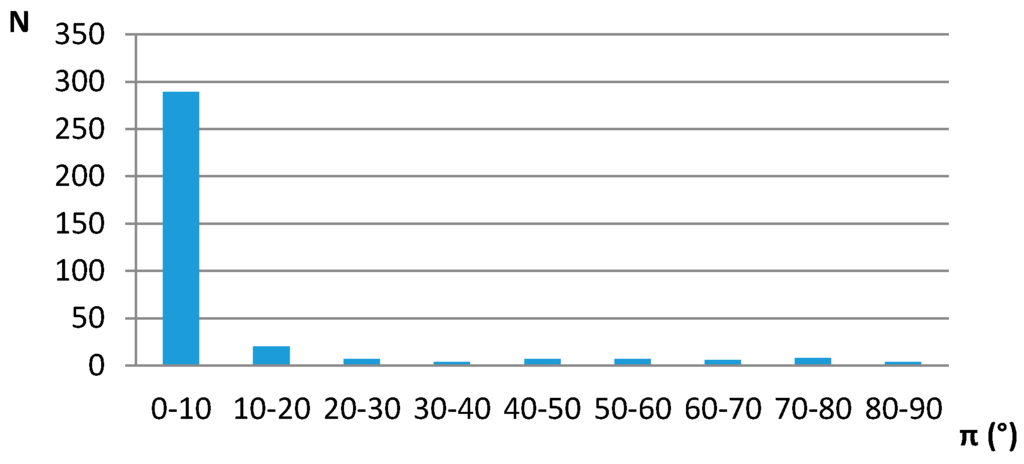
Figure 2.
Interplanar angle distributions of five-membered saturated hydrogen-bridged rings with non-planar groups in the rings in crystal structures. N—number of contacts.
The data in Figure 3 show that most of the parallel contacts have the normal distances between 3.0 and 3.5 Å. These are distances typical for stacking of organic aromatic rings (3–4 Å) [17,18,19,20,21,22] and other planar rings that form stacking interactions [24,25,26,27,43,44,45,46].
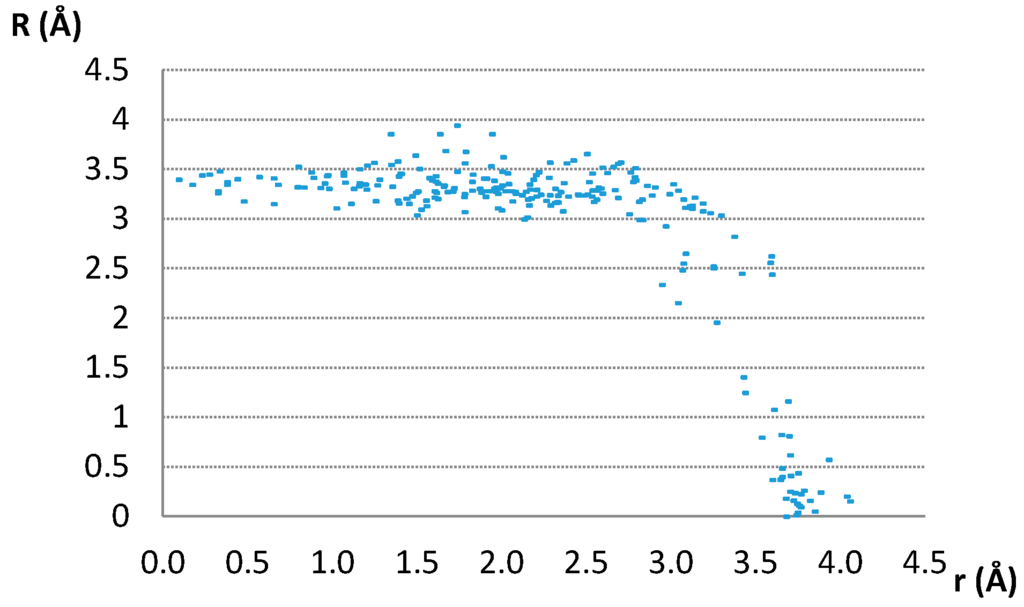
Figure 3.
Interplanar distances (R) of contacts having parallel ring planes, plotted as a function of offset values.
Analysis of distributions of torsion angles H1Ω1Ω2H2 (θ1) and A1Ω1Ω2A2 (θ2) (Figure 1) shows that the large majority of contacts has absolute torsion angles around 180° (Figure 4), indicating that the “head to tail” orientations are preferred.
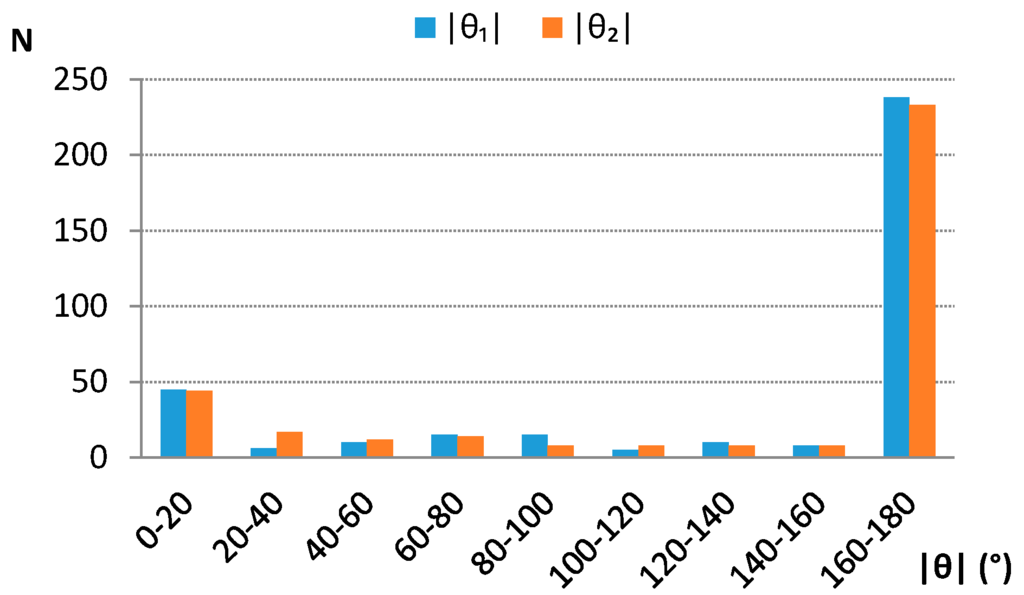
Figure 4.
Absolute torsion angle θ1 (H1Ω1Ω2H2) and θ2 (A1Ω1Ω2A2) distributions. Centroid and atom labeling is consistent with the scheme given in Figure 1. N—number of contacts.
Statistical analysis of elemental composition of the hydrogen-bridged rings studied in this work is given in Table 1.

Table 1.
Statistical analysis of elemental composition; the mark Z stands for halogen.
Many contacts (49.1%, or 173 contacts) involve rings containing N (as D, donor atom), C (as Y, atom adjacent to the donor), N (as X, atom adjacent to the acceptor), and N (as A acceptor atom), using atom labeling given in Figure 1. The majority of the contacts are between aminoguanidinium cation derivatives (55.5%, or 96 contacts), but crystal structures of aminoguanidinium salts are largely affected by ionic forces, so model systems containing aminoguanidinium cation were not used in the calculations.
Among the structures with NCNN sequence, relatively abundant are thiosemicarbazide derivatives (31.8%, or 55 contacts), with a sulfur atom doubly bonded to the carbon atom and semicarbazide derivatives (8.7%, or 15 contacts), with an oxygen atom doubly bonded to the carbon atom. In all contacts of these two groups, coordination number of D and X atoms is 3, i.e., these atoms belong to the planar groups (Figure 5). If a coordination number of D, Y or X atoms is 3, it means that these atoms belong to planar groups, since the ring itself is defined to be planar by constraints applied in CSD search (Materials and Methods Section). Coordination numbers of D, Y or X atoms larger than 3 indicate that these atoms belong to non-planar groups, mostly tetrahedral (or other geometries when Y or X are metals). Coordination number of A larger than 2 indicates that A belongs to the non-planar group, as well as in structures where coordination number of A is 2, A is oxygen atom and the substituent is hydrogen atom. Molecules 4 and 5, shown in Figure 5, are studied in our previous work, where all atoms in the ring belong to planar groups. In this work, however, at least one, or more, atoms in the ring should belong to non-planar groups. In molecules 1 and 2, A is part of non-planar group, while in 3, X is part of non-planar group.
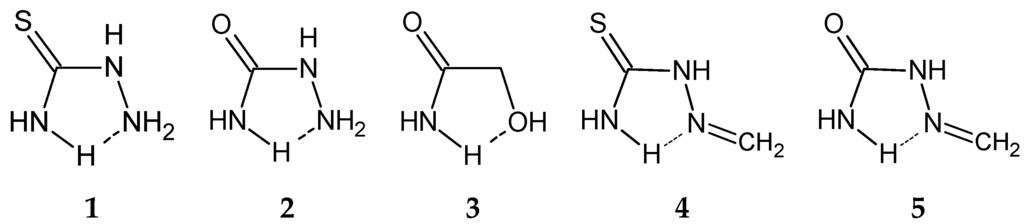
Figure 5.
Molecules chosen for the model systems for quantum chemical calculations of parallel interaction energies; 1–3 systems studied in this work; 4–5 similar systems from our previous work.
When A belongs to a non-planar group (Figure 1), it has a hydrogen atom as a substituent in almost all cases (98% of contacts of thiosemicarbazide (1) derivatives and 93% of contacts of semicarbazide (2) derivatives).
Another relatively numerous group of rings that form parallel interactions (18.8% of total number of contacts, or 66 contacts) has N, C, C and O atoms as D, X, Y and A atoms, respectively (Table 1). Most of them (87.9% or 58 contacts) are glycolamide (3) derivatives. In these structures, D atom always belongs to a planar group (coordination number is always 3), while X atom always belongs to a non-planar group with coordination number 4. Both substituents at X atom are hydrogen atoms in 79% of contacts. A large majority of contacts of this group (98%) has an A atom that belongs to a planar group or hydrogen atom as a substituent on A atom. This hydrogen atom is directed away from the area of the other molecule in the dimer, so it is not capable to form hydrogen bond with it (Figure 5).
It should be noted that D and A are donor and acceptor for intramolecular hydrogen bond, while they can have different roles in intermolecular hydrogen bonds between two rings (Figure 5, Figure 6 and Figure 7).
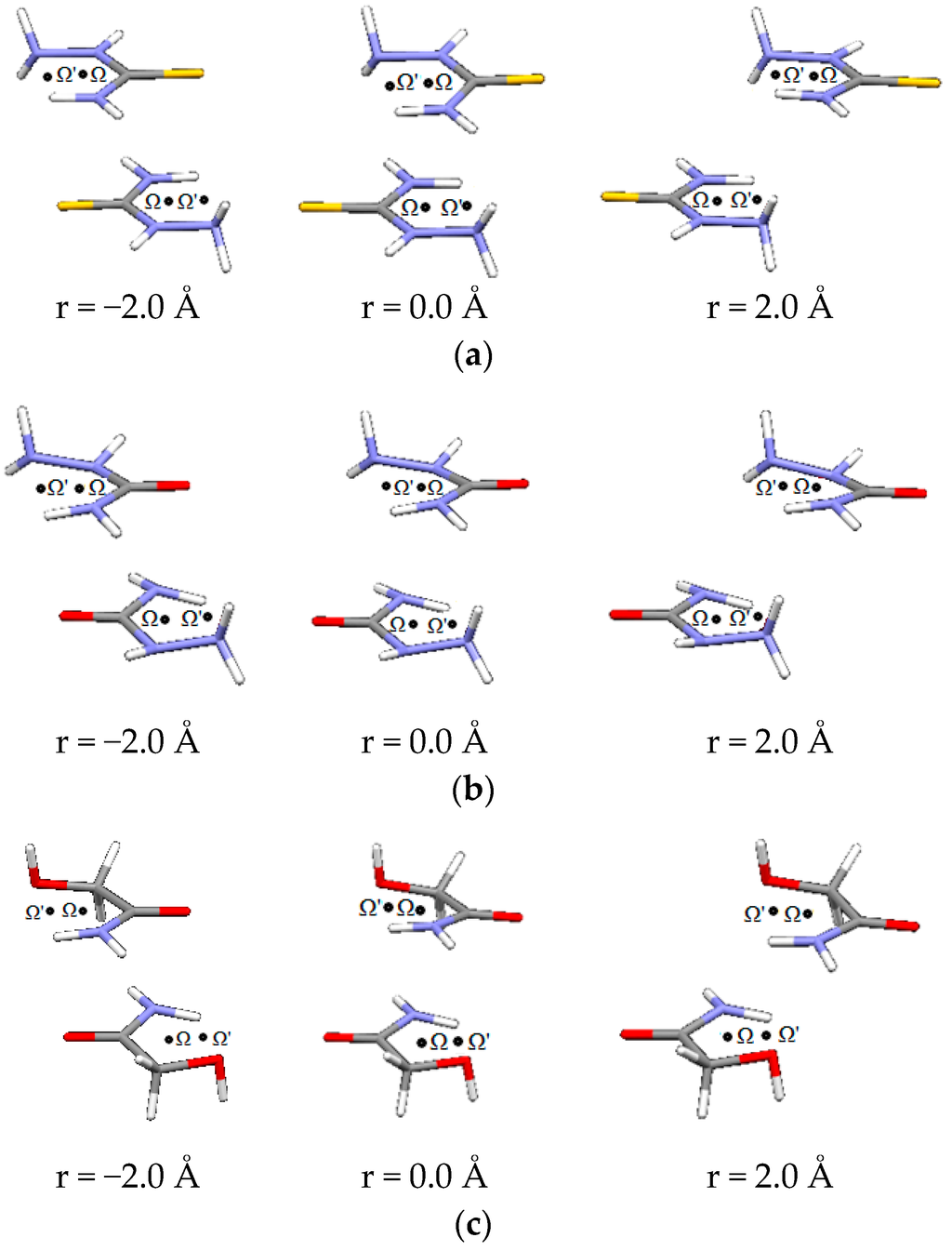
Figure 6.
Parallel interactions of (a) thiosemicarbazide, (b) semicarbazide and (c) glycolamide dimers, at three offset values along Ω-Ω’direction.
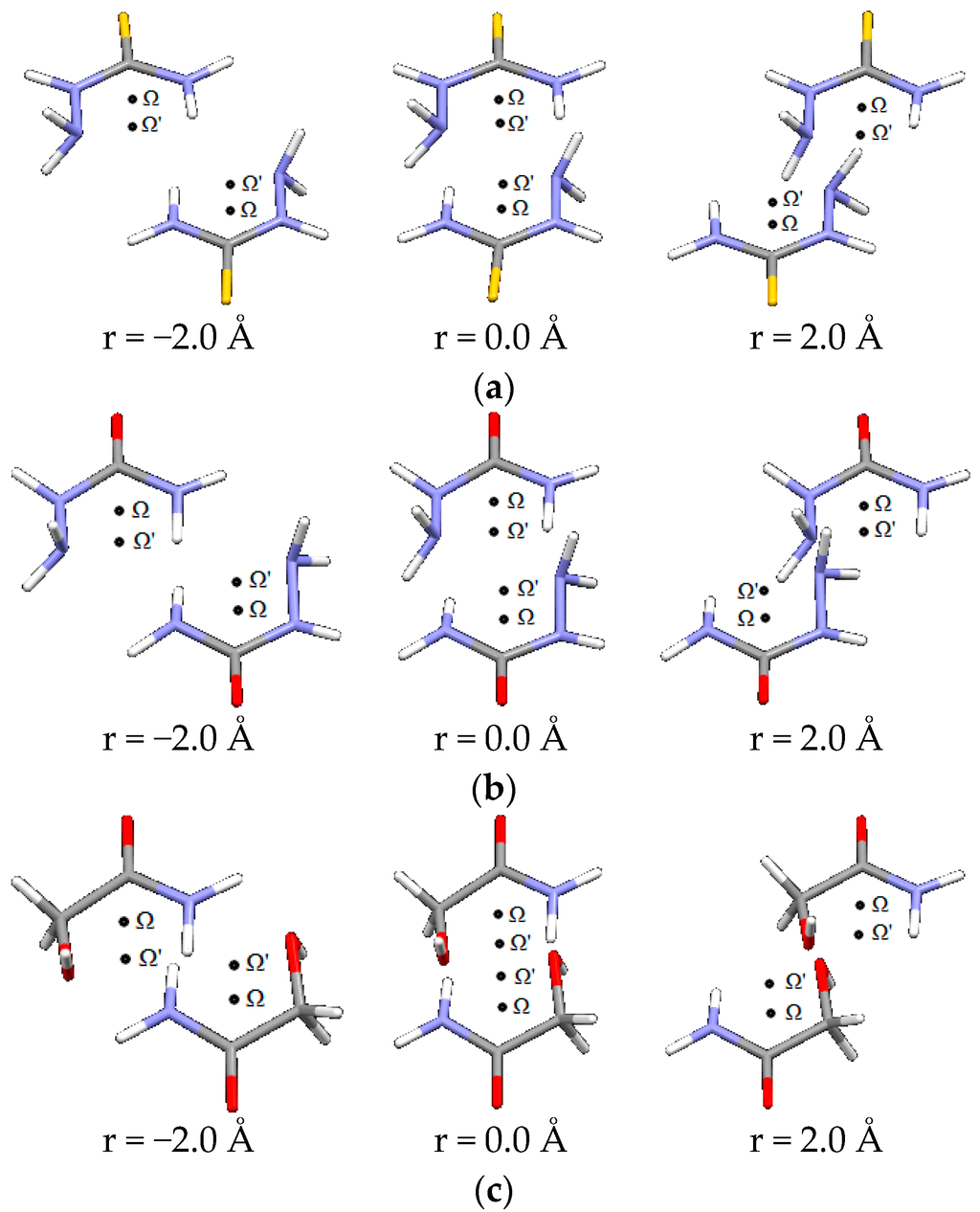
Figure 7.
Parallel interactions of (a) thiosemicarbazide, (b) semicarbazide and (c) glycolamide dimers, at three offset values along direction orthogonal to Ω-Ω’.
2.2. Quantum Chemical Calculations
Hydrogen-bridged rings, thiosemicarbazide (1), semicarbazide (2) and glycolamide (3), presented in Figure 5, were used in model systems to calculate stacking interactions. These rings were chosen since their derivatives occur quite frequently in crystal structures (Table 1). In order to show that these rings are appropriate representatives for whole set of rings studied in this work, we analyzed geometric parameters for derivatives of thiosemicarbazide, semicarbazide and glycolamide rings separately.
Trends concerning interactions of their derivatives in crystal structures are the same (Figures S1–S4) as overall trends (Figure 2, Figure 3 and Figure 4), justifying the use of these molecules in model system for quantum chemical calculations. Geometries of optimized dimers of thiosemicarbazide, semicarbazide and glycolamide in the gas phase, as well as some typical structural patterns in the crystals of thiosemicarbazide and derivatives of semicarbazide and glycolamide are also given in ESI (Figures S5 and S6).
In Figure 5, structures of two hydrogen-bridged rings, 4 and 5, that we used as model systems to calculate interaction energies in our previous study [46] are also presented. Model systems used for calculations are composed of two quasi-cyclic molecules in the antiparallel position (parallel alignment of the ring planes and torsion angles H1Ω1Ω2H2 and A1Ω1Ω2A2 of 180°) since data from the crystal structures showed antiparallel orientation of interacting rings (Figure 4).
Potential curves of interaction energies are obtained by moving molecules along two directions. The first is Ω-Ω’ direction, where Ω represents the centroid of the molecule, while Ω’ represents the centroid of the hydrogen-acceptor bond (Figure 6).
The second direction is orthogonal to the Ω-Ω’ direction. Representative geometries are shown in Figure 7.
The potential curves were calculated by varying offset values (r) in steps of 0.5 Å, while normal distances (R) were varied for every particular offset value in order to obtain the strongest energy.
For calculating potential curves, we used DFT methods, which are in good agreement with very accurate CCSD(T)/CBS method. Benchmark calculations are presented in Tables S1–S5. Model systems used for the benchmark analysis are shown in Figure S7. Potential curves are shown in Figure 8, while corresponding normal distances are shown in Figure S8, ESI.
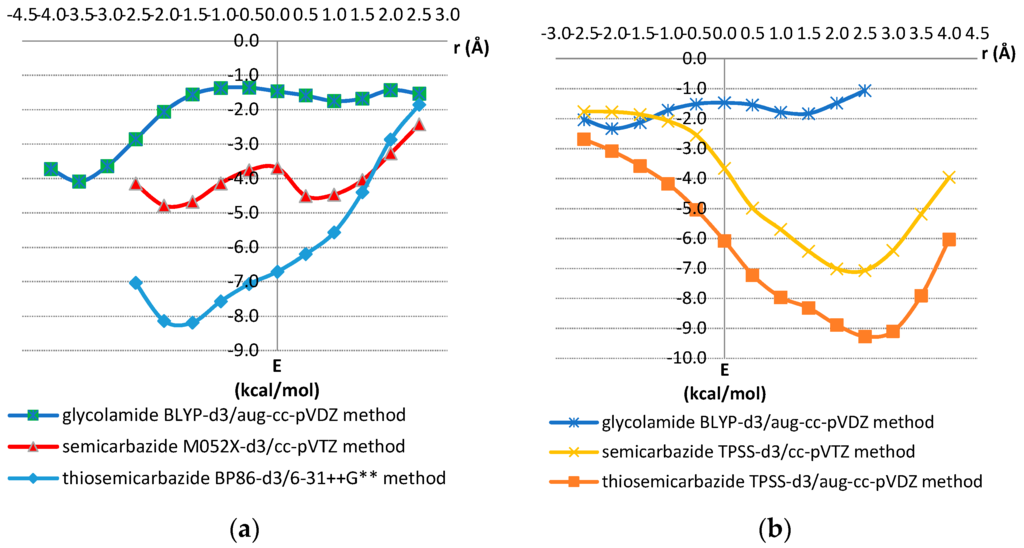
Figure 8.
(a) Potential curves for offset values varied in the Ω-Ω’direction; (b) Potential curves for offset values varied orthogonal to Ω-Ω’ direction. The interactions energies for each offset value r were calculated by varying the normal distance (R) between two molecules in a series of single point calculations. The strongest calculated energy for each offset value is presented. The selected geometries are shown in Figure 6 and Figure 7.
Potential curves in the Ω-Ω’ direction show minima for thiosemicarbazide, semicarbazide and glycolamide model systems at negative offset values of −1.5, −2.0, and −3.5 Å, respectively, with interaction energies, calculated at CCSD(T)/CBS level, of −7.66, −4.90 and −4.25 kcal/mol, respectively. The minima on potential curves orthogonal to the Ω-Ω’ direction are at positive offset values of 2.5 Å for thiosemicarbazide and semicarbazide model systems with energies of −9.68 and −7.12 kcal/mol, respectively (Figure 8, Table 2). The minimum for glycolamide model system is at offset of −2.0 Å with the energy of −2.21 kcal/mol.

Table 2.
Interaction energies and offsets of potential curves minima for molecules in Figure 5. Energies are in kcal/mol, distances are in Å.
Potential curves for thiosemicarbazide and semicarbazide model systems have similar shape, because of the similar molecular structure, however, the interaction energies are stronger for thiosemicarbazide, for almost all offsets. For all three model systems, the most stable interactions are calculated for the geometries with very favorable hydrogen bonds between rings, as shown in Figure 9. In dimers of thiosemicarbazide and semicarbazide (Figure 9a,b) intermolecular hydrogen bonds are bifurcated. Nitrogen atoms in position A (Figure 1b) are acceptor atoms of intramolecular hydrogen bonds and donors for the intermolecular hydrogen bonds. Acceptor atoms for the intermolecular hydrogen bonds are sulfur (Figure 9a) or oxygen atoms (Figure 9b), as well as nitrogen atoms in the position X (Figure 1b and Figure 9a,b). In the case of glycolamide, tetrahedral carbon atoms (position X, Figure 1b) are donors, while oxygen atoms of carbonyl groups are acceptors (Figure 9c) for intermolecular hydrogen bonds.
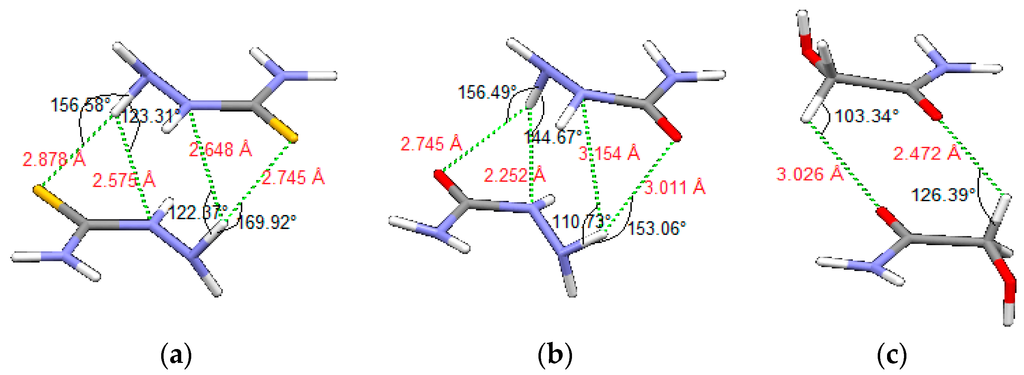
Figure 9.
Geometries of the strongest calculated interactions of (a) thiosemicarbazide, (b) semicarbazide and (c) glycolamide dimers, with presented intermolecular hydrogen bonds and CH–O interactions.
The data of potential curves and interaction energies calculated at very accurate CCSD(T)/CBS level show that interactions are quite strong (Figure 8, Table 2). The strongest are interactions in thiosemicarbazide dimer −9.68 kcal/mol, while interaction in semicarbazide dimer is weaker, however, still quite strong, −7.12 kcal/mol. Among the model systems used in this study, the weakest interaction was calculated in glycolamide dimer, −4.25 kcal/mol.
In the geometries of the minima on potential curves, there are two simultaneous hydrogen bonds between two quasi-rings that are in dimers of thiosemicarbazide and semicarbazide bifurcated (Figure 9). In order to evaluate the contribution of single hydrogen bond to the interaction energies, we performed calculations on model systems: thiosemicarbazide and semicarbazide molecules with ammonia and of glycolamide molecule with methanol (Figure 10). The position of NH and CH bonds that form intermolecular hydrogen bonds are the same as the position of the corresponding NH and CH bonds in geometries of minima shown in Figure 9, with identical bond lengths and valence angles. Energies are calculated using the same methods that are used for calculating potential curves (Figure 8), i.e., tpss-d3/aug-cc-pVDZ for thiosemicarbazide/ammonia, tpss-d3/cc-pVTZ for semicarbazide/ammonia, and blyp-d3/aug-cc-pVDZ for glycolamide/methanol. Evaluated energies of hydrogen bonds are −3.89, −1.80 and −1.67 kcal/mol, respectively. Although contributions of intermolecular hydrogen bonds to total interaction energies are considerable, the total interaction energies in Table 2 are more than energies of two hydrogen bonds, indicating the existence of additional contributions to total energies.
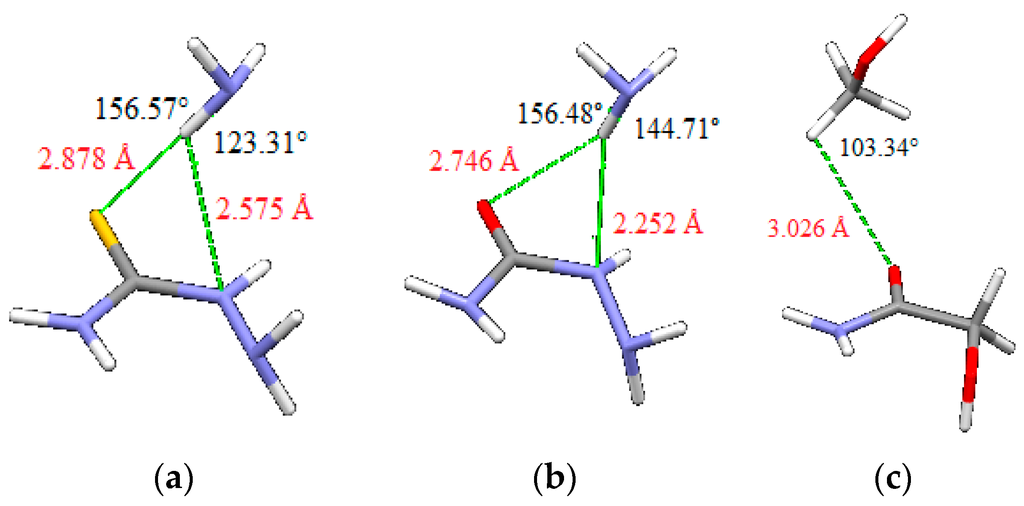
Figure 10.
Model systems for evaluating energies of hydrogen bonds (a) thiosemicarbazide and ammonia, (b) semicarbazide and ammonia, and (c) glycolamide and methanol. Positions and geometries of intermolecular hydrogen bonds are identical as in Figure 9. The calculated energies are (a) −3.89 kcal/mol, (b) −1.80 kcal/mol and (c) −1.67 kcal/mol.
Maps of electrostatic potentials for thiosemicarbazide, semicarbazide and glycolamide molecules (Figure 11) show that electron density is more localized on oxygen atom of semicarbazide than on the sulfur atom of thiosemicarbazide. In addition, the hydrogen atom in tiosemicarbazide is more positive than in semicarbazide. Electrostatic potential maps of glycolamide molecule show that hydrogen and oxygen involved in intermolecular interactions are less positive and less negative, respectively, than hydrogens and sulfur/oxygen atoms in thiosemicarbazide and semicarbazide.
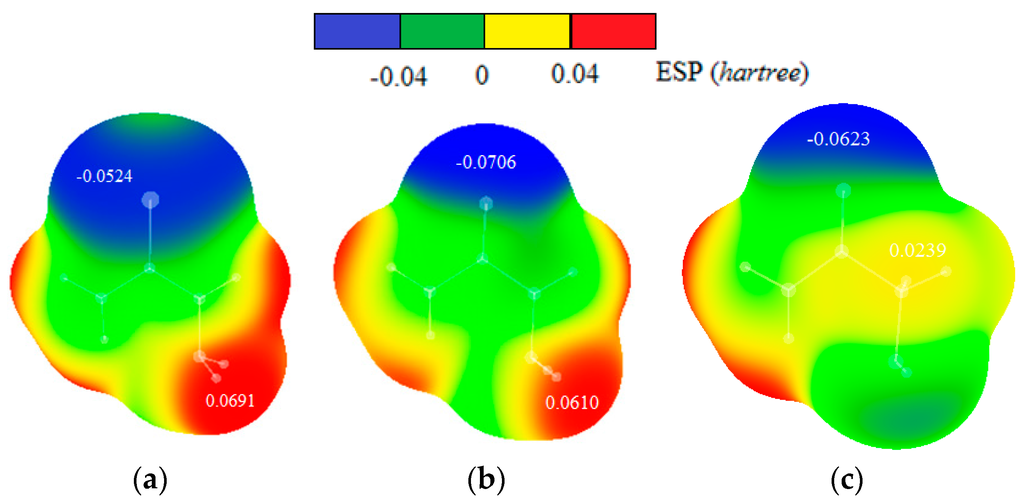
Figure 11.
Maps of electrostatic potentials for (a) thiosemicarbazide, (b) semicarbazide and (c) glycolamide molecules. The values of ESP maxima and minima in hartrees are indicated onto the surfaces of the maps.
3. Discussion
Orientations of the rings in crystal structures correspond to antiparallel arrangement (Figure 4, Figure 6 and Figure 7). In our previous work, we studied interactions of similar hydrogen-bridged rings, however, with all planar groups in the ring [46], as was mentioned above. The analysis of the data from crystal structures showed very similar trends as observed in this study.
Stacking interactions of similar systems without intermolecular hydrogen bonds (model systems of molecules 4 and 5, Figure 5) that were calculated in our previous work, −4.89 and −2.95 kcal/mol [46], are significantly weaker than interactions in model systems 1 and 2, studied in this work, −9.68 and −7.12 kcal/mol, at CCSD(T)/CBS level (Table 2). The geometries in the dimers are also quite different because of the hydrogen bonds. This indicates that the presence of hydrogen atoms between the ring planes that form hydrogen bonds, significantly influence the geometries and strengthen interactions between two parallel rings. In systems 1 and 2, there are double bifurcated intermolecular hydrogen bonds, NH–N and NH–S in the case of thiosemicarbazide (1) and NH–N and NH–O in case of semicarbazide (2) (Figure 9), which contribute to the strength of the interactions.
Evaluated energies of single hydrogen bonds (Figure 10) indicate significant contribution of hydrogen bonds to total interaction energy between two quasi-rings, however, indicate also other contributions to total energy. Namely total interaction energies for thiosemicarbazide, semicarbazide, and glycolamide (−9.27, −7.07 and −4.09 kcal/mol respectively) are larger than energies of two hydrogen bonds (−7.78, −3.60 and −3.34 kcal/mol, respectively). One can also notice that interaction energy in thiosemicarbazide and semicarbazide dimers is less than sum of hydrogen bonds (Figure 10) and interaction energies in dimers of 4 and 5 (Figure 5, Table 2), without intermolecular hydrogen bonds between quasi-rings.
The dimers of thiosemicarbazide and semicarbazide have similar geometries, so energy differences can be attributed mostly to the nature of sulfur and oxygen atoms. Stronger interaction in case of thiosemicarbazide is probably a consequence of stronger dispersion component that can be anticipated for larger sulfur atom. Indeed, electrostatic potential maps, discussed above, show larger sulfur atom with more delocalized negative charge (Figure 11). Besides, hydrogen atom involved in intermolecular interaction is slightly more acidic (more partially positive) in thiosemicarbazide than in semicarbazide (Figure 11), so that also contributes to the energy difference. Electrostatic potential maps can explain weaker interactions in glycolamide dimer. One reason for weaker interaction in the case of glycolamide is the type of hydrogen bonds between rings, which are in this case relatively weak CH–O interactions (Figure 10). Another reason is that CH–O bonds in glycolamide dimer are not bifurcated as in dimers of thiosemicarbazide and semicarbazide.
Curves of changing normal distances for various offset values presented in Figure S8, show that normal distances are shorter for thiosemicarbazide rings, in accordance with the strongest interaction energies.
The calculations on correlation energies show that correlation component is higher for thiosemirarbazide than for semicarbazide (Table S6), indicating that dispersion is also important in these interactions.
4. Materials and Methods
A CSD search (CSD version 5.35, November 2013. and updates, May 2014) is performed by using ConQuest 1.16 [51]. Constraints applied in search were: (1) distances between donor (D) and acceptor (A) atoms within the ring less than 4.0 Å; (2) angles between donor (D), hydrogen, and acceptor (A) atoms within the ring from 90° to 180°; (3) absolute torsions AXYD and XYDH (Figure 1) from 0 to 10°; (4) donor and acceptor atoms include N, O, Cl, S and F atoms, due to their considerable electronegativities; (5) all covalent bonds within the ring are set to be single acyclic; (6) structures where all atoms in the ring belong to planar groups (coordination number of D, Y and X atoms less than four and coordination number of A atom less than three are excluded from further considerations, since noncovalent interactions of these species were analyzed in our previous work [46]); and (7) intermolecular contacts having distances between two centroids 4.5 Å or less are considered in this work. The crystallographic R factor is set to be less than 10%, the error-free coordinates according to the criteria used in the CSD, the H-atom positions were normalized using the CSD default X–H bond lengths (O–H = 0.983 Å; C–H = 1.083 Å and N–H = 1.009 Å), no polymer structures and no powder structures were included.
Single-point calculations were used to evaluate interaction energy between two rings. Optimizations of monomers, thiosemicarbazide, semicarbazide, and glycolamide, are done at MP2/cc-pVTZ [52,53] level. The methods for calculation of interaction energy potential curves were chosen based on good agreement with CCSD(T)/CBS method [54] (Tables S1–S5, ESI). Interaction energy was determined as a difference of the dimer energy and the sum of energies of monomers, having included correction of basis set superposition error (BSSE) [55]. All calculations are done by using Gaussian09 series of programs [56].
Maps of electrostatic potentials for thiosemicarbazide, semicarbazide and glycolamide molecules, calculated and visualized from wavefunction files using the Wavefunction Analysis Program (WFA-SAS) [57,58]. The wavefunctions were calculated on MP2/cc-pVTZ level of theory.
5. Conclusions
Search and analysis of the crystal structures in the Cambridge Structural Database (CSD) show that saturated acyclic four-atom groups closed with a classic intramolecular hydrogen bond, generating planar five-membered rings (hydrogen-bridged quasi-rings), in which at least one of the ring atoms is bonded to other non-ring atoms that are not in the ring plane and, thus, capable to form intermolecular interactions, were observed quite frequently in crystal structures from the CSD. In the crystal structures, we found 1068 rings, while 289 (27%) of them form parallel interactions.
The rings can have one hydrogen atom out of the ring plane that gives possibility for hydrogen bonds between two parallel rings. Hence, in these systems, two types of hydrogen bonds can be present, one in the ring, and the other one between two parallel rings.
The strongest interaction energies, calculated at very accurate CCSD(T)/CBS level, are −9.68 and −7.12 kcal/mol for thiosemicarbazide and semicarbazide interactions, respectively. Similar rings that do not have possibility for hydrogen bonds between rings have significantly weaker interaction energies of −4.89 and −2.95 kcal/mol [46], indicating the importance of hydrogen bonds for the strength of the interactions. Evaluated energies of hydrogen bonds in thiosemicarbazide and semicarbazide are −7.78 and −3.60 kcal/mol, respectively.
The results presented in this paper recognize that interactions, and their strong interaction energies, can be important in all supramolecular systems.
Supplementary Materials
The supplementary materials are available online at http://www.mdpi.com/2073-4352/6/4/34/s1.
Acknowledgments
This work was supported by the Serbian Ministry of Education, Science and Technological Development (Grant 172065). The HPC resources and services used in this work were partially provided by the IT Research Computing group in Texas A&M University at Qatar. IT Research Computing is funded by the Qatar Foundation for Education, Science and Community Development (http://www.qf.org.qa).
Author Contributions
Snežana D. Zarić and Goran V. Janjić conceived and designed this study; Jelena P. Blagojević and Goran V. Janjić performed the study; Jelena P. Blagojević, Goran V. Janjić and Snežana D. Zarić analyzed the data; Jelena P. Blagojević and Snežana D. Zarić wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSD | Cambridge Structural Database |
| CCSD(T) | Coupled-Cluster with Single and Duble and Perturbative Triple excitations |
| CBS | Complete Basis Set |
| DFT | Density Functional Theory |
| ESI | Electronic Supporting Information |
| ESP | Electrostatic Potential |
| MP2 | Møller-Plesset Perturbation Theory of second order |
| cc-pVTZ | Correlation-Consistent Polarized Valence-only Triple-zeta basis set |
| BSSE | Basis Set Superposition Error |
| WFA-SAS | Wavefunction Analysis-Surface Analysis Suite |
References
- Salonen, L.M.; Ellermann, M.; Diederich, F. Aromatic rings in chemical and biological recognition: Energetics and structures. Angew. Chem. Int. Ed. 2011, 50, 4808–4842. [Google Scholar] [CrossRef] [PubMed]
- O’Sullivan, M.C.; Durham, T.B.; Valdes, H.E.; Dauer, K.L.; Karney, N.J.; Forrestel, A.C.; Bacchi, C.J.; Baker, J.F. Dibenzosuberyl substituted polyamines and analogs of clomipramine as effective inhibitors of trypanothione reductase; molecular docking, and assessment of trypanocidal activities. Bioorgan. Med. Chem. 2015, 23, 996–1010. [Google Scholar] [CrossRef] [PubMed]
- Woziwodzka, A.; Gołuński, G.; Wyrzykowski, D.; Kaźmierkiewicz, R.; Piosik, J. Caffeine and other methylxanthines as interceptors of food-borne aromatic mutagens: Inhibition of Trp-P-1 and Trp-P-2 mutagenic activity. Chem. Res. Toxicol. 2013, 26, 1660–1673. [Google Scholar] [CrossRef] [PubMed]
- Thio, Y.; Toh, S.W.; Xue, F.; Vittal, J.J. Self-assembly of a 15-nickel metallamacrocyclic complex derived from the l-glutamic acid Schiff base ligand. Dalton Trans. 2014, 43, 5998–6001. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Kuang, Y.; Gao, Y.; Zhang, Y.; Gao, P.; Xu, B. Aromatic-aromatic interactions induce the self-assembly of pentapeptidic derivatives in water to form nanofibers and supramolecular hydrogels. J. Am. Chem. Soc. 2010, 132, 2719–2728. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.-J. Binding mechanisms in supramolecular complexes. Angew. Chem. Int. Ed. 2009, 48, 3924–3977. [Google Scholar] [CrossRef] [PubMed]
- Schweizer, W.B.; Dunitz, J.D. Quantum Mechanical Calculations for Benzene Dimer Energies: Present Problems and Future Challenges. J. Chem. Theory Comput. 2006, 2, 288–291. [Google Scholar] [CrossRef] [PubMed]
- Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M.; Tanabe, K. Origin of Attraction and Directionality of the π/π Interaction: Model Chemistry Calculations of Benzene Dimer Interaction. J. Am. Chem. Soc. 2002, 124, 104–112. [Google Scholar] [CrossRef] [PubMed]
- Sinnokrot, M.O.; Valeev, E.F.; Sherrill, C.D. Estimates of the Ab Initio Limit for π−π Interactions: The Benzene Dimer. J. Am. Chem. Soc. 2002, 124, 10887–10893. [Google Scholar] [CrossRef] [PubMed]
- Rezáč, J.; Riley, K.E.; Hobza, P. S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures. J. Chem. Theory Comput. 2011, 7, 2427–2438. [Google Scholar] [CrossRef] [PubMed]
- Janowski, T.; Pulay, P. High accuracy benchmark calculations on the benzene dimer potential energy surface. Chem. Phys. Lett. 2007, 447, 27–32. [Google Scholar] [CrossRef]
- Bludský, O.; Rubes, M.; Soldán, P.; Nachtigall, P. Investigation of the benzene-dimer potential energy surface: DFT/CCSD(T) correction scheme. J. Chem. Phys. 2008, 128, 114102. [Google Scholar] [CrossRef] [PubMed]
- Hohenstein, E.G.; Sherrill, C.D. Effects of heteroatoms on aromatic π-π interactions: Benzene-pyridine and pyridine dimer. J. Phys. Chem. A 2009, 113, 878–886. [Google Scholar] [CrossRef] [PubMed]
- Geronimo, I.; Lee, E.C.; Singh, N.J.; Kim, K.S. How Different are Electron-Rich and Electron-Deficient π Interactions? J. Chem. Theory Comput. 2010, 6, 1931–1934. [Google Scholar] [CrossRef] [PubMed]
- Ninković, D.B.; Janjić, G.V.; Veljković, D.Ž.; Sredojević, D.N.; Zarić, S.D. What are the preferred horizontal displacements in parallel aromatic-aromatic interactions? Significant interactions at large displacements. Chemphyschem 2011, 12, 3511–3514. [Google Scholar] [CrossRef] [PubMed]
- Ninković, D.B.; Andrić, J.M.; Malkov, S.N.; Zarić, S.D. What are the preferred horizontal displacements of aromatic-aromatic interactions in proteins? Comparison with the calculated benzene-benzene potential energy surface. Phys. Chem. Chem. Phys. 2014, 16, 11173–11177. [Google Scholar] [CrossRef] [PubMed]
- Sinnokrot, M.O.; Sherrill, C.D. High-accuracy quantum mechanical studies of π-π interactions in benzene dimers. J. Phys. Chem. A 2006, 110, 10656–10668. [Google Scholar] [CrossRef] [PubMed]
- Podeszwa, R.; Bukowski, R.; Szalewicz, K. Potential energy surface for the benzene dimer and perturbational analysis of π-π interactions. J. Phys. Chem. A 2006, 110, 10345–10354. [Google Scholar] [CrossRef] [PubMed]
- Pitoňák, M.; Neogrády, P.; Řezáč, J.; Jurečka, P.; Urban, M.; Hobza, P. Benzene Dimer: High-Level Wave Function and Density Functional Theory Calculations. J. Chem. Theory Comput. 2008, 4, 1829–1834. [Google Scholar]
- Ninković, D.B.; Janjić, G.V.; Zarić, S.D. Crystallographic and ab Initio Study of Pyridine Stacking Interactions. Local Nature of Hydrogen Bond Effect in Stacking Interactions. Cryst. Growth Des. 2012, 12, 1060–1063. [Google Scholar] [CrossRef]
- Ninković, D.B.; Andrić, J.M.; Zarić, S.D. Parallel interactions at large horizontal displacement in pyridine-pyridine and benzene-pyridine dimers. Chemphyschem 2013, 14, 237–243. [Google Scholar] [CrossRef] [PubMed]
- Craven, E.; Zhang, C.; Janiak, C.; Rheinwald, G.; Lang, H. Synthesis, Structure and Solution Chemistry of (5, 5′-Dimethyl-2, 2′-bipyridine)(IDA)copper(II) and Structural Comparison With Aqua(IDA)(1, 10-phenanthroline)copper(II) (IDA = iminodiacetato). Z. Anorg. Allg. Chem. 2003, 629, 2282–2290. [Google Scholar] [CrossRef]
- Janjić, G.V.; Veljković, D.Z.; Zarić, S.D. Water/Aromatic Parallel Alignment Interactions. Significant Interactions at Large Horizontal Displacements. Cryst. Growth Des. 2011, 11, 2680–2683. [Google Scholar] [CrossRef]
- Sredojević, D.; Bogdanović, G.A.; Tomić, Z.D.; Zarić, S.D. Stacking vs. CH–π interactions between chelate and aryl rings in crystal structures of square-planar transition metal complexes. CrystEngComm 2007, 9, 793–798. [Google Scholar] [CrossRef]
- Sredojević, D.N.; Tomić, Z.D.; Zarić, S.D. Evidence of Chelate−Chelate Stacking Interactions in Crystal Structures of Transition-Metal Complexes. Cryst. Growth Des. 2010, 10, 3901–3908. [Google Scholar] [CrossRef]
- Tomić, Z.D.; Leovac, V.M.; Pokorni, S.V.; Zobel, D.; Zarić, S.D. Crystal Structure of Bis[acetone-1-naphthoylhydrazinato(−1)]copper(II) and Investigations of Intermolecular Interactions. Eur. J. Inorg. Chem. 2003, 6, 1222–1226. [Google Scholar] [CrossRef]
- Tomić, Z.D.; Sredojević, D.; Zarić, S.D. Stacking Interactions between Chelate and Phenyl Rings in Square-Planar Transition Metal Complexes. Cryst. Growth Des. 2006, 6, 29–31. [Google Scholar] [CrossRef]
- Wang, X.-J.; Jian, H.-X.; Liu, Z.-P.; Ni, Q.-L.; Gui, L.-C.; Tang, L.-H. Assembly molecular architectures based on structural variation of metalloligand [Cu(PySal)2] (PySal = 3-pyridylmethylsalicylideneimino). Polyhedron 2008, 27, 2634–2642. [Google Scholar] [CrossRef]
- Granifo, J.; Vargas, M.; Garland, M.T.; Ibáñez, A.; Gaviño, R.; Baggio, R. The novel ligand 4′-phenyl-3,2′:6′,3′′-terpyridine (L) and the supramolecular structure of the dinuclear complex [Zn2(μ-L)(acac)4]·H2O (acac = acetylacetonato). Inorg. Chem. Commun. 2008, 11, 1388–1391. [Google Scholar] [CrossRef]
- Philip, V.; Suni, V.; Prathapachandra Kurup, M.R.; Nethaji, M. Structural and spectral studies of nickel(II) complexes of di-2-pyridyl ketone N4,N4-(butane-1,4-diyl) thiosemicarbazone. Polyhedron 2004, 23, 1225–1233. [Google Scholar] [CrossRef]
- Konidaris, K.F.; Tsipis, A.C.; Kostakis, G.E. Shedding Light on Intermolecular Metal-Organic Ring Interactions by Theoretical Studies. ChemPlusChem 2012, 77, 354–360. [Google Scholar] [CrossRef]
- Konidaris, K.F.; Morrison, C.N.; Servetas, J.G.; Haukka, M.; Lan, Y.; Powell, A.K.; Plakatouras, J.C.; Kostakis, G.E. Supramolecular assemblies involving metal–organic ring interactions: Heterometallic Cu(II)–Ln(III) two-dimensional coordination polymers. CrystEngComm 2012, 14, 1842–1849. [Google Scholar] [CrossRef]
- Konidaris, K.F.; Powell, A.K.; Kostakis, G.E. Peculiar structural findings in coordination chemistry of malonamide–N,N′-diacetic acid. CrystEngComm 2011, 13, 5872–5876. [Google Scholar] [CrossRef]
- Tiekink, E.R.T. Molecular crystals by design? Chem. Commun. 2014, 50, 11079–11082. [Google Scholar] [CrossRef] [PubMed]
- Baul, T.S.B.; Kundu, S.; Mitra, S.; Höpfl, H.; Tiekink, E.R.T.; Linden, A. The influence of counter ion and ligand methyl substitution on the solid-state structures and photophysical properties of mercury(II) complexes with (E)-N-(pyridin-2-ylmethylidene)arylamines. Dalton Trans. 2013, 42, 1905–1920. [Google Scholar] [CrossRef] [PubMed]
- Khavasi, H.R.; Sadegh, B.M.M. Influence of N-heteroaromatic π-π stacking on supramolecular assembly and coordination geometry; effect of a single-atom change in the ligand. Dalton Trans. 2015, 44, 5488–5502. [Google Scholar] [CrossRef] [PubMed]
- Hosseini-Monfared, H.; Pousaneh, E.; Sadighian, S.; Ng, S.W.; Tiekink, E.R.T. Syntheses, Structures, and Catalytic Activity of Copper(II)-Aroylhydrazone Complexes. Z. Anorg. Allg. Chem. 2013, 639, 435–442. [Google Scholar] [CrossRef]
- Ni, Q.-L.; Jiang, X.-F.; Gui, L.-C.; Wang, X.-J.; Yang, K.-G.; Bi, X.-S. Synthesis, structures and characterization of a series of Cu(I)-diimine complexes with labile N,N′-bis((diphenylphosphino)methyl)naphthalene-1,5-diamine: Diverse structures directed by π–π stacking interactions. New J. Chem. 2011, 35, 2471–2476. [Google Scholar] [CrossRef]
- Molčanov, K.; Jurić, M.; Kojić-Prodić, B. Stacking of metal chelating rings with π-systems in mononuclear complexes of copper(II) with 3,6-dichloro-2,5-dihydroxy-1,4-benzoquinone (chloranilic acid) and 2,2’-bipyridine ligands. Dalton Trans. 2013, 42, 15756–15765. [Google Scholar] [CrossRef] [PubMed]
- Akine, S.; Varadi, Z.; Nabeshima, T. Synthesis of Planar Metal Complexes and the Stacking Abilities of Naphthalenediol-Based Acyclic and Macrocyclic Salen-Type Ligands. Eur. J. Inorg. Chem. 2013, 35, 5987–5998. [Google Scholar] [CrossRef]
- Melnic, E.; Coropceanu, E.B.; Kulikova, O.V.; Siminel, A.V.; Anderson, D.; Rivera-Jacquez, H.J.; Masunov, A.E.; Fonari, M.S.; Kravtsov, V.C. Robust Packing Patterns and Luminescence Quenching in Mononuclear [Cu(II)(phen)2] Sulfates. J. Phys. Chem. C 2014, 118, 30087–30100. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, X.-H.; Liu, G.-Z.; Ma, L.-F.; Wang, L.-Y. Five Mn(II) Coordination Polymers Based on 2,3′,5,5′-Biphenyl Tetracarboxylic Acid: Syntheses, Structures, and Magnetic Properties. Cryst. Growth Des. 2015, 15, 966–974. [Google Scholar] [CrossRef]
- Malenov, D.P.; Ninković, D.B.; Sredojević, D.N.; Zarić, S.D. Stacking of benzene with metal chelates: Calculated CCSD(T)/CBS interaction energies and potential-energy curves. Chemphyschem 2014, 15, 2458–2461. [Google Scholar] [CrossRef] [PubMed]
- Malenov, D.P.; Ninković, D.B.; Zarić, S.D. Stacking of metal chelates with benzene: Can dispersion-corrected DFT be used to calculate organic-inorganic stacking? Chemphyschem 2015, 16, 761–768. [Google Scholar] [CrossRef] [PubMed]
- Karabıyık, H.; Karabıyık, H.; Ocak İskeleli, N. Hydrogen-bridged chelate ring-assisted π-stacking interactions. Acta Cryst. B 2012, 68, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Blagojević, J.P.; Zarić, S.D. Stacking interactions of hydrogen-bridged rings—Stronger than the stacking of benzene molecules. Chem. Commun. 2015, 51, 12989–12991. [Google Scholar] [CrossRef] [PubMed]
- Yeo, C.I.; Halim, S.N.A.; Ng, S.W.; Tan, S.L.; Zukerman-Schpector, J.; Ferreira, M.A.B.; Tiekink, E.R.T. Investigation of putative arene-C-H···π(quasi-chelate ring) interactions in copper(I) crystal structures. Chem. Commun. 2014, 50, 5984–5986. [Google Scholar] [CrossRef] [PubMed]
- Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Interrelation between H-bond and Pi-electron delocalization. Chem. Rev. 2005, 105, 3513–3560. [Google Scholar] [CrossRef] [PubMed]
- Lyssenko, K.A.; Antipin, M.Y. The nature and energy characteristics of intramolecular hydrogen bonds in crystals. Russ. Chem. Bull. 2006, 55, 1–15. [Google Scholar] [CrossRef]
- Sanz, P.; Mó, O.; Yañez, M.; Elguero, J. Resonance-assisted hydrogen bonds: A critical examination. Structure and stability of the enols of beta-diketones and beta-enaminones. J. Phys. Chem. A 2007, 111, 3585–3591. [Google Scholar] [CrossRef] [PubMed]
- Bruno, I.J.; Cole, J.C.; Edgington, P.R.; Kessler, M.; Macrae, C.F.; McCabe, P.; Pearson, J.; Taylor, R. New software for searching the Cambridge Structural Database and visualizing crystal structures. Acta Cryst. Sect. B—Struct. Sci. 2002, 58, 389–397. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 (Revision D.01); Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Bulat, F.A.; (Fable Theory & Computation LLC, Washington, DC, USA); Toro-Labbe, A.; (Pontificia Universidad Católica de Chile, Santiago, Chile). Personal communication, 2013.
- Bulat, F.A.; Toro-Labbé, A.; Brinck, T.; Murray, J.S.; Politzer, P. Quantitative analysis of molecular surfaces: Areas, volumes, electrostatic potentials and average local ionization energies. J. Mol. Model. 2010, 16, 1679–1691. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).