Novel S = 1/2 Kagome Lattice Materials: Cs2TiCu3F12 and Rb2TiCu3F12
Abstract
:1. Introduction
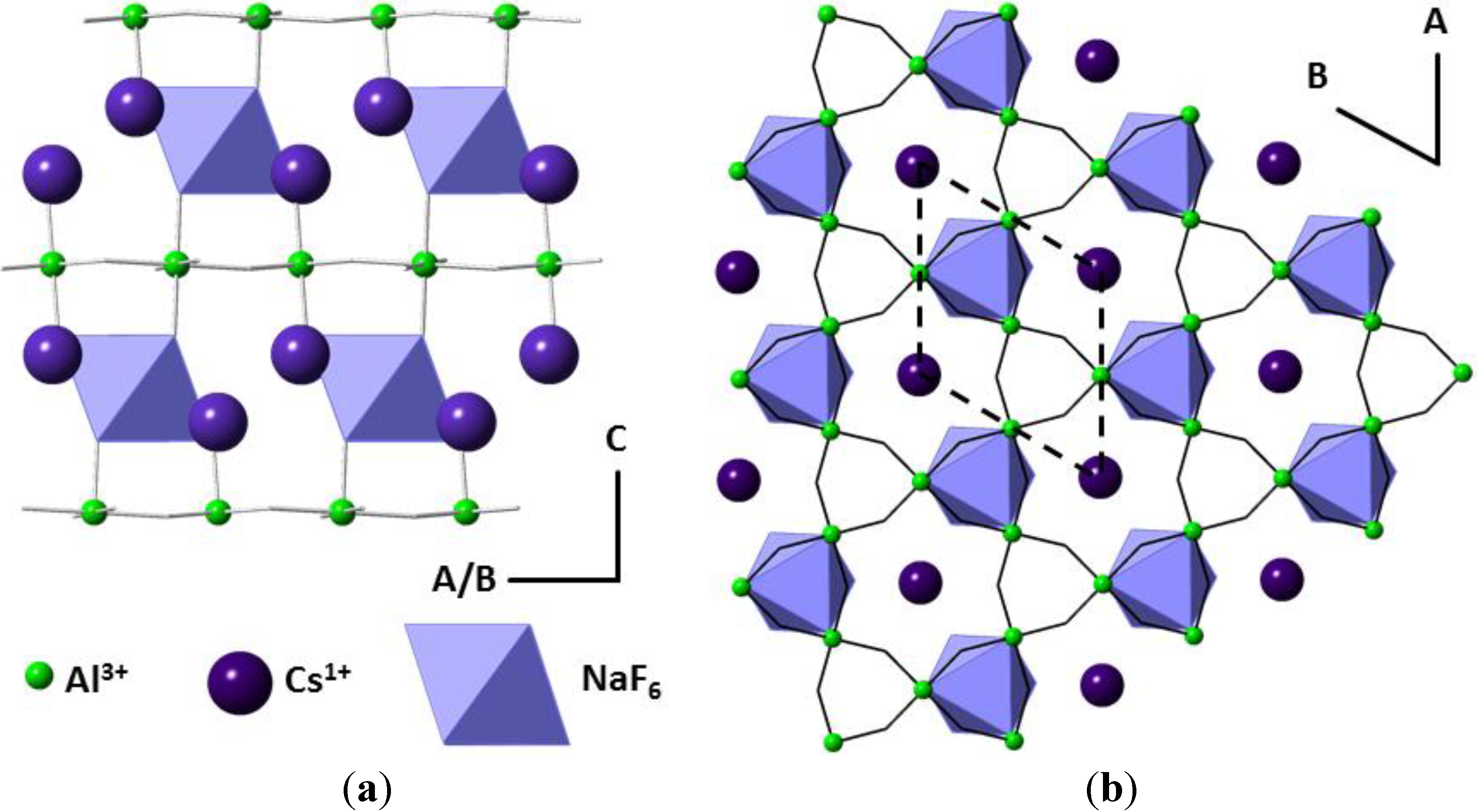
2. Results and Discussion
2.1. Single Crystal X-ray Diffraction of Cs2TiCu3F12
| M4+ | Ionic Radius [16] | a (Å) | c (Å) |
|---|---|---|---|
| Ti4+ | 0.605 | 7.1014(14) | 19.955(2) |
| Sn4+ (11) | 0.69 | 7.142(4) | 20.381(14) |
| Hf4+ (11) | 0.71 | 7.163 | 20.49 |
| Zr4+ (11) | 0.72 | 7.166 | 20.46 |
| Bond | Cs2TiCu3F12 | Cs2SnCu3F12 [11] |
|---|---|---|
| Cs–F1 (×3) | 3.101(4) | 3.124(2) |
| Cs–F2 (×3) | 3.352(4) | 3.411(2) |
| Cu–F1 (×4) | 1.9037(14) | 1.8969(11) |
| Cu–F2 (×2) | 2.333(4) | 2.346(2) |
| M4+–F2 (×6) | 1.864(4) | 1.9527(15) |
| Cu–Cu (×4) | 3.551 | 3.571 |
| RT | 125 K | ||
|---|---|---|---|
| Bond | Distance (Å) | Bond | Distance (Å) |
| Ti1–F2 (×6) | 1.864(4) | Ti1–F5 (×6) | 1.863(9) |
| Ti2–F7 (×2) | 1.871(9) | ||
| Ti2–F6 (×2) | 1.871(7) | ||
| Ti2–F8 (×2) | 1.872(8) | ||
| Atom | BVS | Atom | BVS |
| Ti1 | 4.53 | Ti1 | 4.72 |
| Ti2 | 4.33 | ||
| Average | 4.53 | Average | 4.43 |
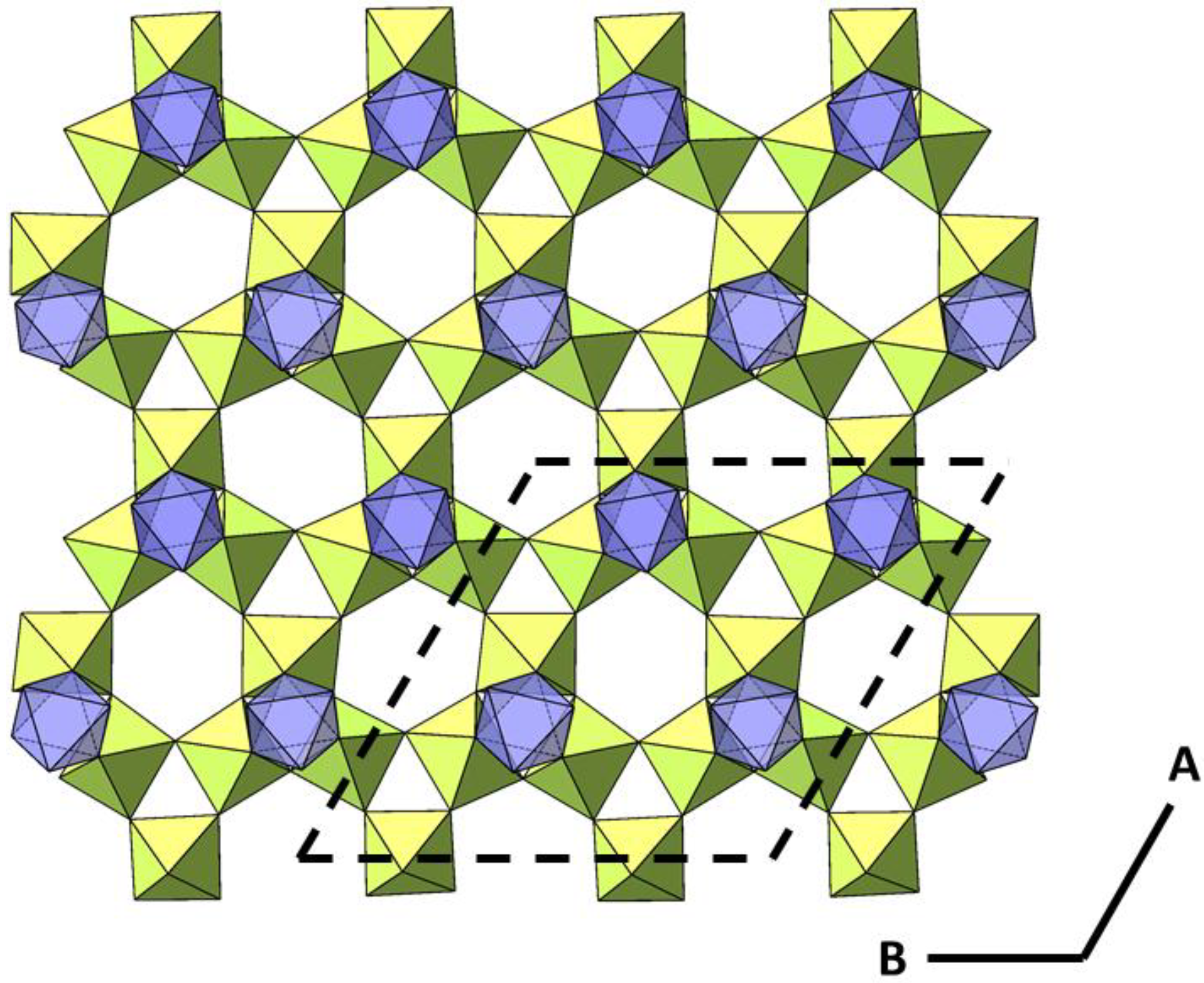
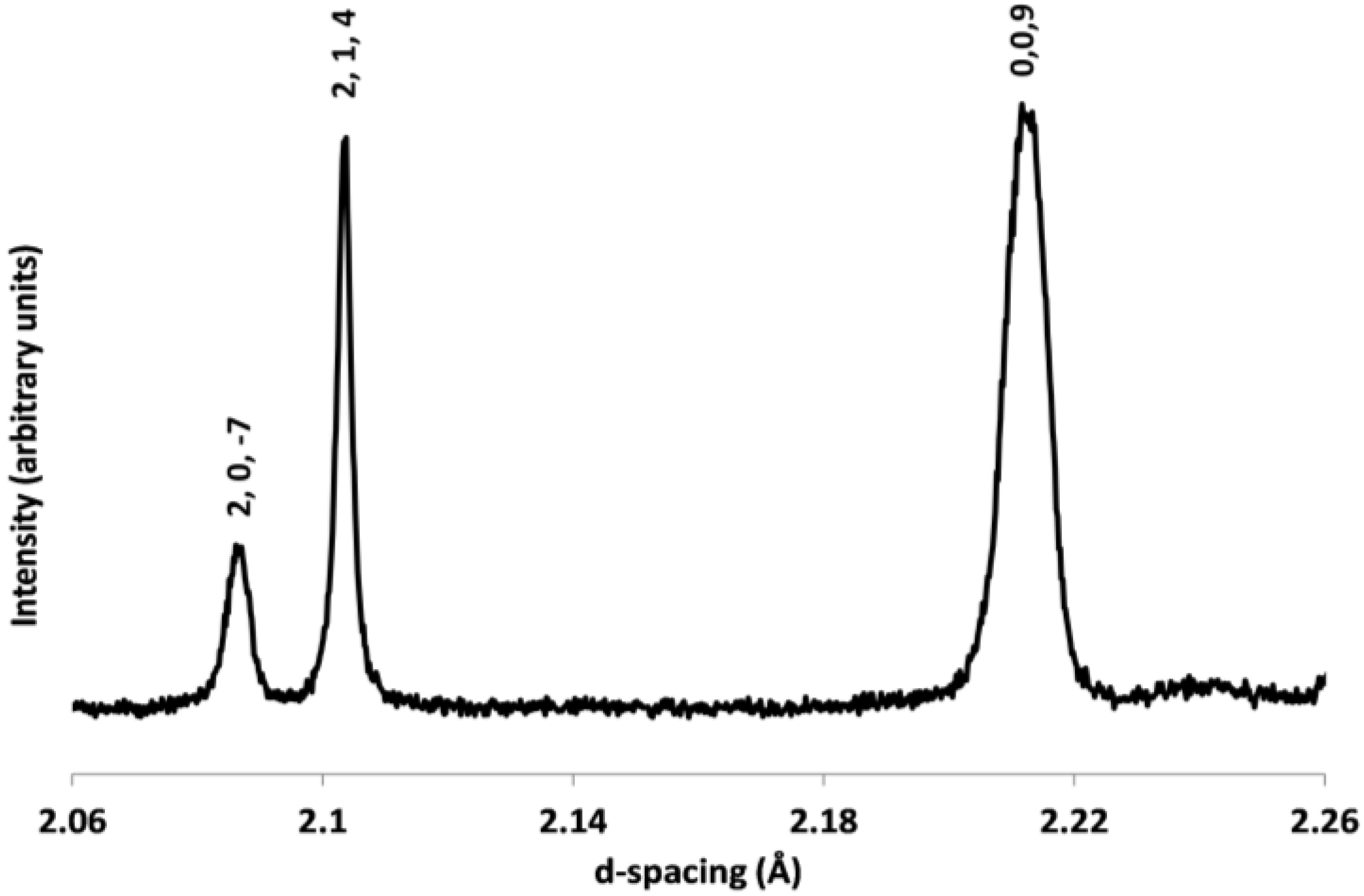
2.2. Powder Diffraction Study of Cs2TiCu3F12
| Metal—Fluoride Bond | Bond Length (Å) |
|---|---|
| Cs–F3 | 3.051(4) |
| Cs–F1 | 3.086(5) |
| Cs–F2 | 3.102(5) |
| Cs–F4 | 3.185(5) |
| Cs–F5 | 3.201(5) |
| Cs–F5 | 3.242(5) |
| Cs–F6 | 3.275(5) |
| Cu1–F2 (×2) | 1.912(6) |
| Cu1–F1 (×2) | 1.917(6) |
| Cu1–F6 (×2) | 2.310(6) |
| Cu2–F3 | 1.875(5) |
| Cu2–F1 | 1.903(6) |
| Cu2–F2 | 1.921(6) |
| Cu2–F3 | 1.952(5) |
| Cu2–F4 | 2.319(6) |
| Cu2–F5 | 2.325(6) |
| Ti–F6 (×2) | 1.835(4) |
| Ti–F4 (×2) | 1.843(5) |
| Ti–F5 (×2) | 1.896(5) |
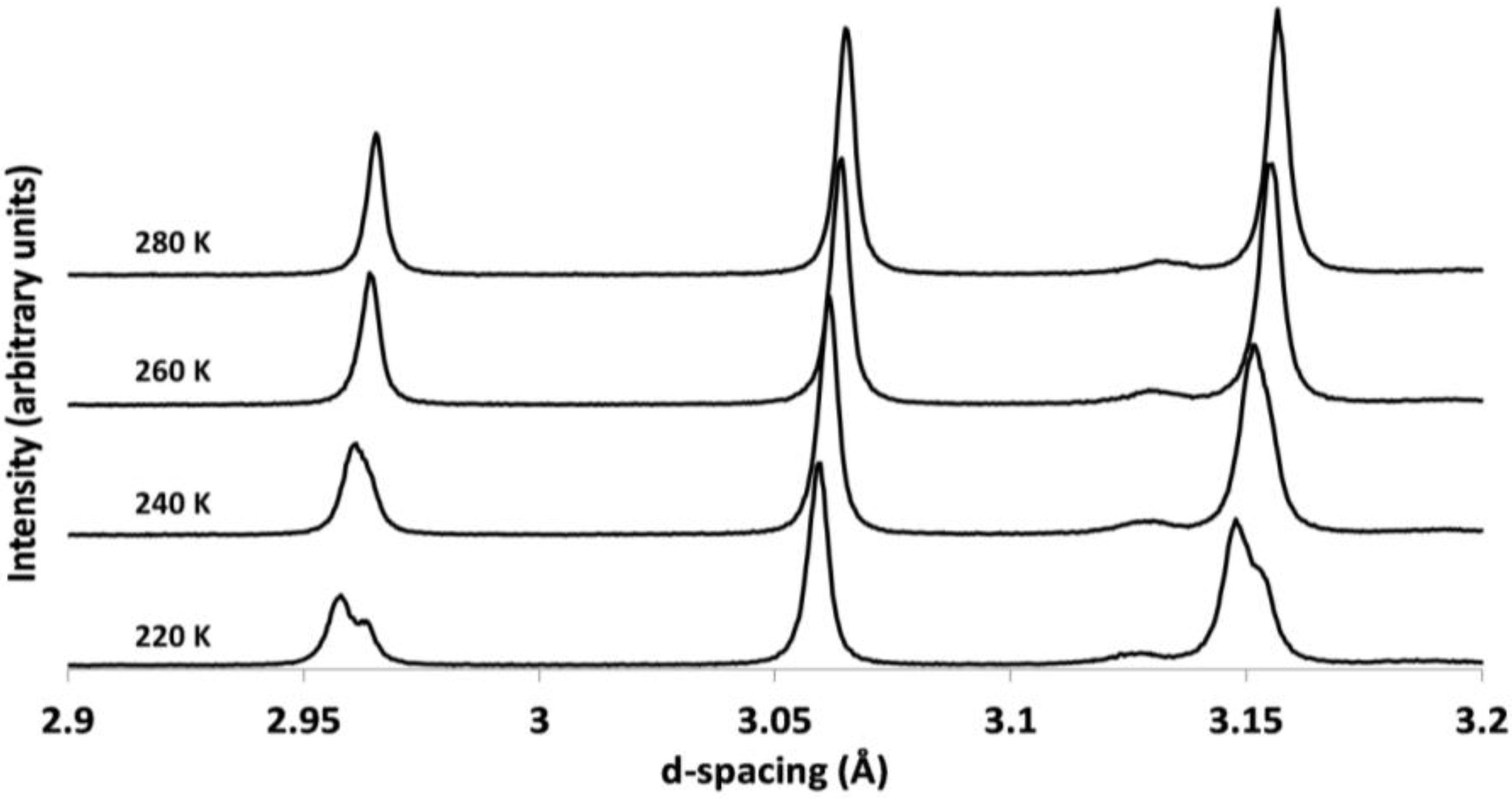
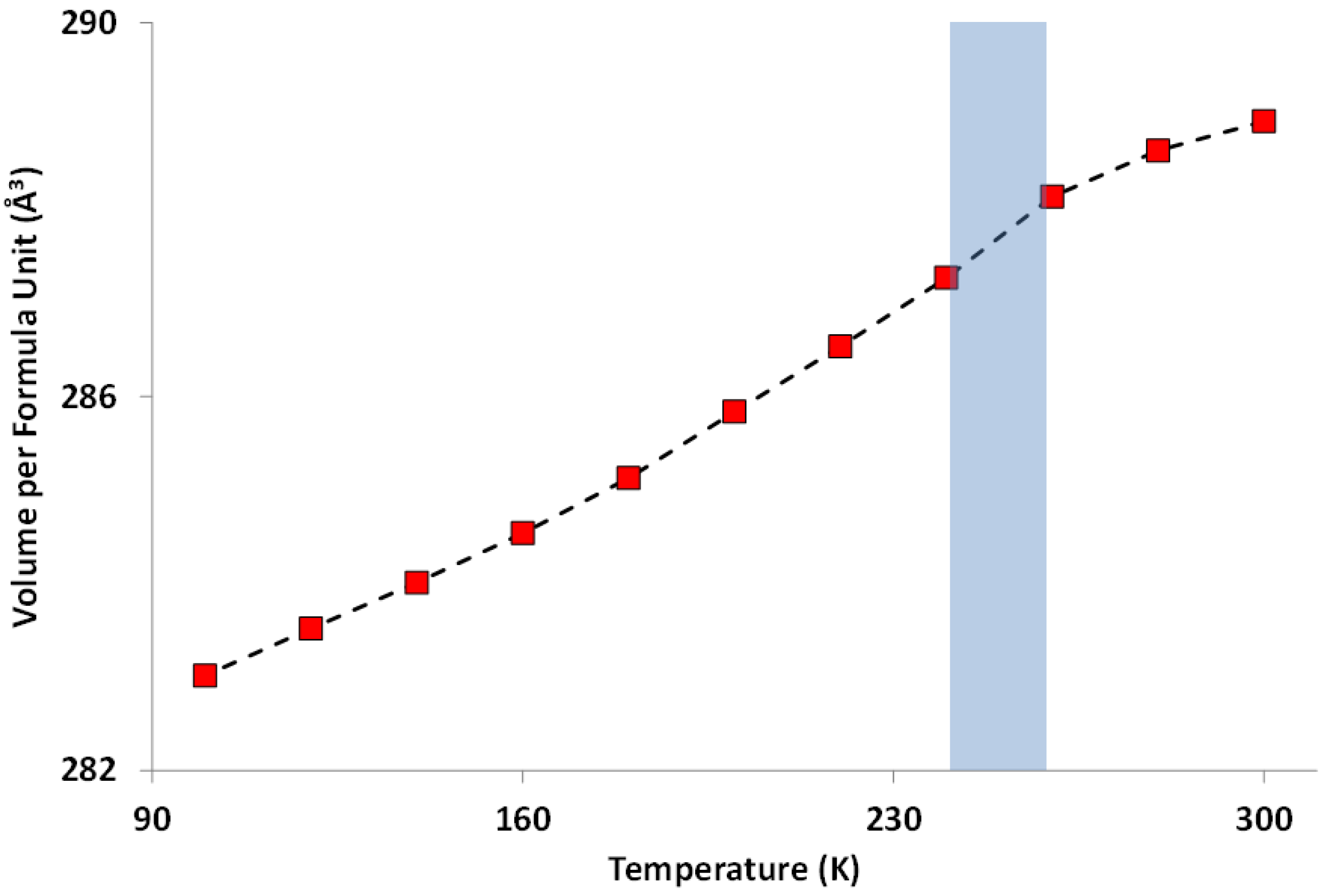
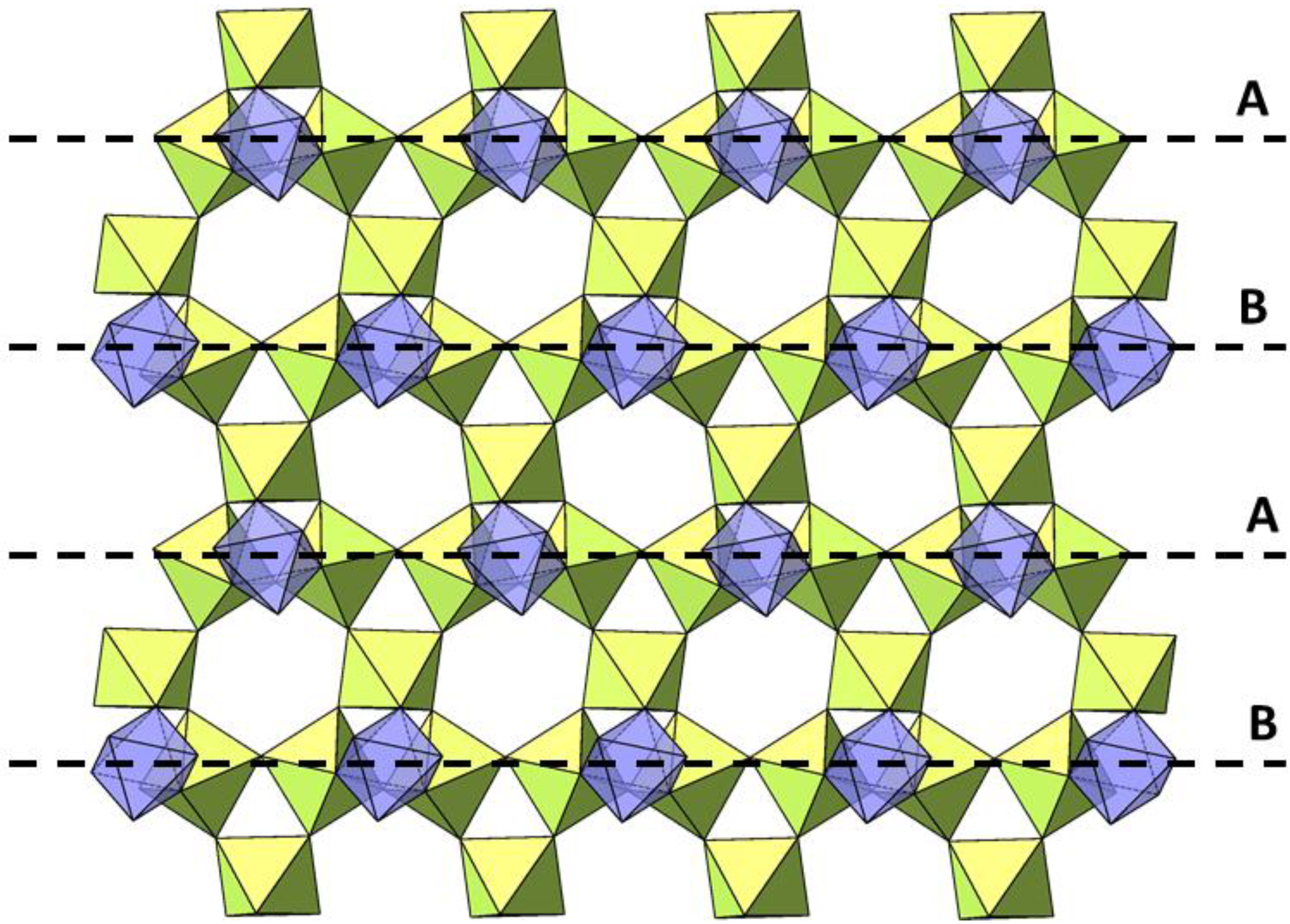
| Temperature (K) | BVS | |||
|---|---|---|---|---|
| Ti4+ | Cu12+ | Cu22+ | Cs+ | |
| 300 | 4.884 | 2.016 | 0.858 | |
| 280 | 4.884 | 2.012 | 0.867 | |
| 260 | 4.884 | 2.014 | 0.870 | |
| 240 | 4.934 | 1.990 | 2.037 | 0.919 |
| 220 | 4.714 | 1.950 | 2.009 | 0.946 |
| 200 | 4.676 | 1.954 | 2.002 | 0.961 |
| 100 | 4.616 | 1.970 | 1.975 | 1.019 |
2.3. Comparison of Single Crystal and Powder Samples of Cs2TiCu3F12
2.4. Powder X-ray Diffraction of Rb2TiCu3F12
| Unit Cell Parameter | SXPD | NPD |
|---|---|---|
| a (Å) | 10.3592(8) | 10.3703(15) |
| b (Å) | 10.3506(9) | 10.3521(19) |
| c (Å) | 10.3440(3) | 10.3369(14) |
| α (°) | 83.838(8) | 83.717(17) |
| β (°) | 83.832(8) | 83.635(14) |
| γ (°) | 83.9111(15) | 83.921(8) |
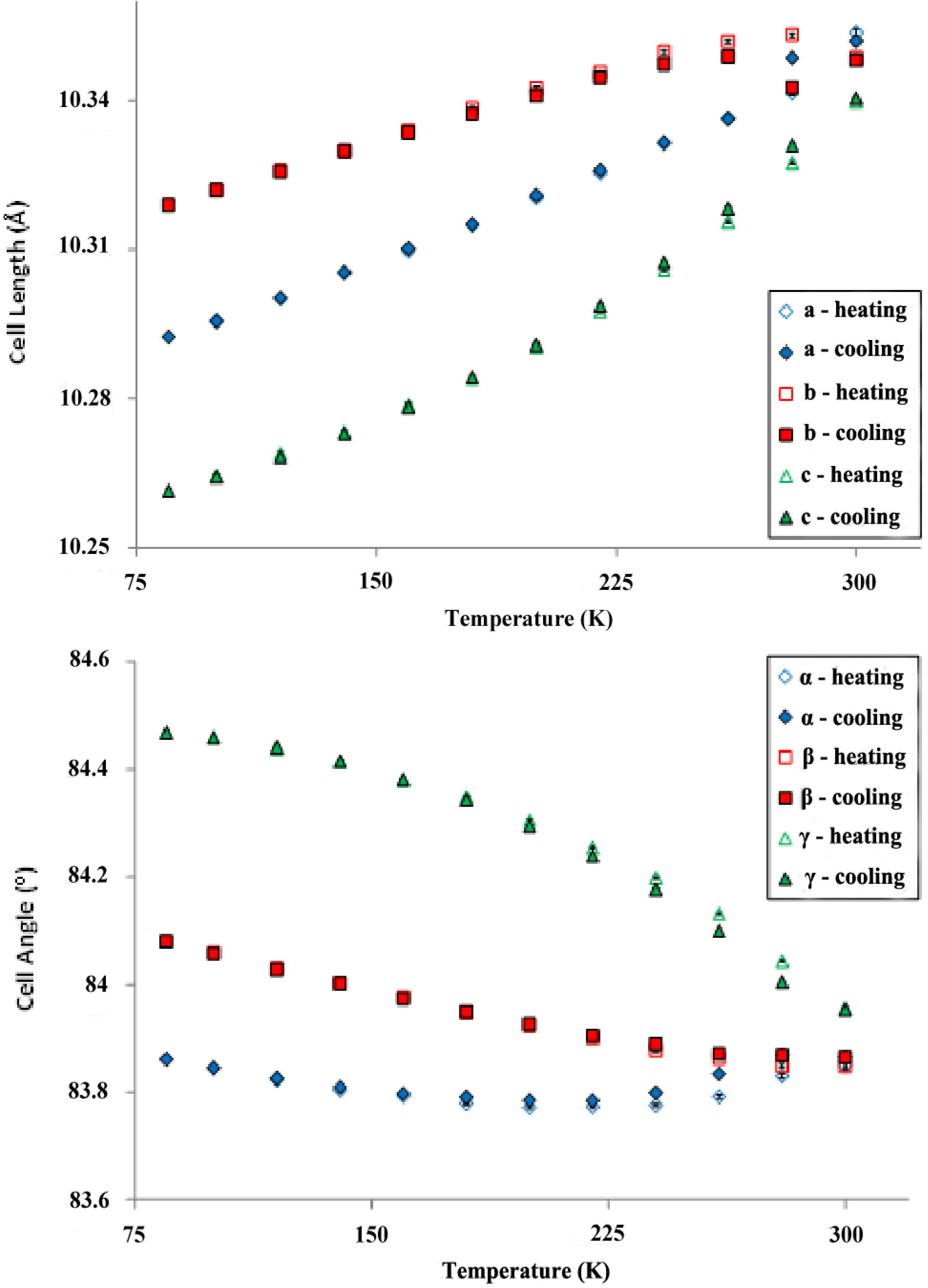
2.5. Magnetic Properties of Cs2TiCu3F12
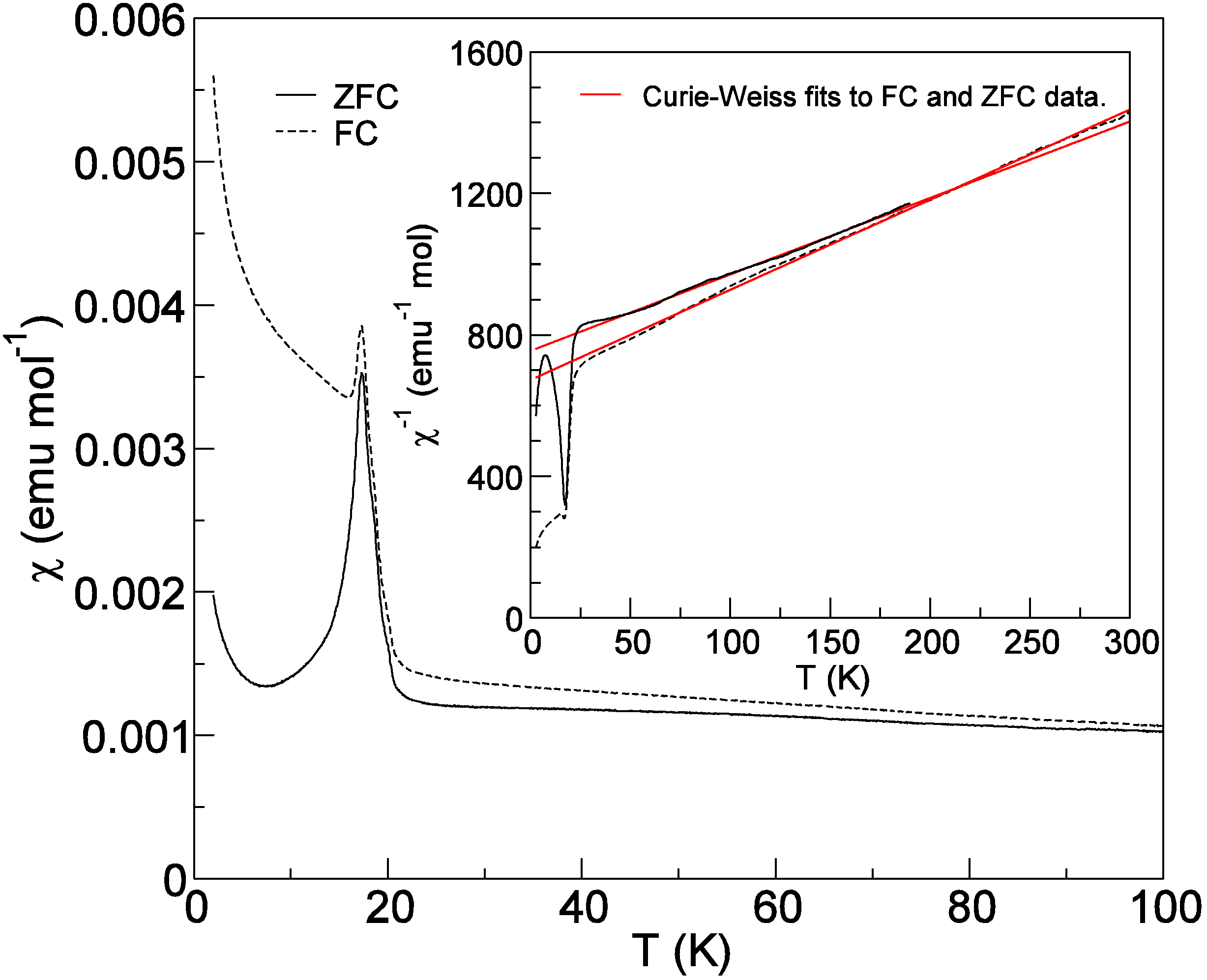
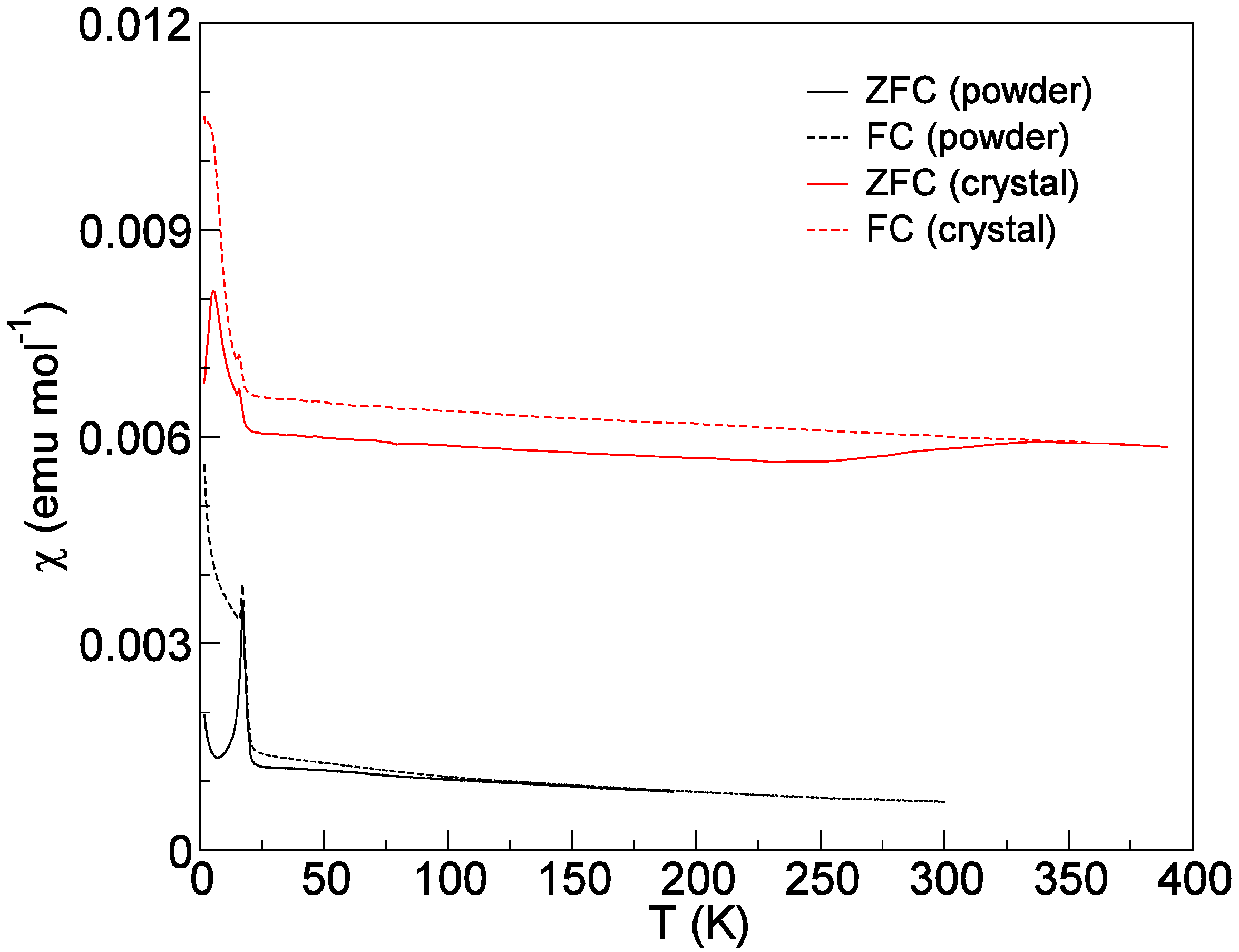
3. Experimental Section
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Harrison, A. First catch your hare: The design and synthesis of frustrated magnets. J. Phys. 2004, 16, S553–S572. [Google Scholar]
- Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 1973, 8, 153–160. [Google Scholar] [CrossRef]
- Mendels, P.; Bert, F.; de Vries, M.A.; Olariu, A.; Harrison, A.; Duc, F.; Trombe, J.C.; Lord, J.S.; Amato, A.; Baines, C. Quantum magnetism in the paratacamite family: Towards an ideal kagome lattice. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef] [PubMed]
- Fak, B.; Kermarrec, E.; Messio, L.; Bernu, B.; Lhuillier, C.; Bert, F.; Mendels, P.; Koteswararao, B.; Bouquet, F.; Ollivier, J.; et al. Kapellasite: A kagome quantum spin liquid with competing interactions. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed]
- Aidoudi, F.H.; Aldous, D.W.; Goff, R.J.; Slawin, A.M.Z.; Attfield, J.P.; Morris, R.E.; Lightfoot, P. An ionothermally-prepare S = ½ vanadium oxyfluoride kagome lattice. Nat. Chem. 2011, 3, 801–806. [Google Scholar] [CrossRef] [PubMed]
- Clark, L.; Orain, J.C.; Bert, F.; de Vries, M.A.; Aidoudi, F.H.; Morris, R.E.; Lightfoot, P.; Lord, J.S.; Telling, M.T.F.; Bonville, P.; et al. Gapless spin liquid ground state in the S = ½ vanadium oxyfluoride kagome antiferromagnet [NH4]2[C7H14N][V7O6F18]. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef] [PubMed]
- Courbion, G.; Jacoboni, C.; Depape, R. Crystal structure of Cs2NaAl3F12. Acta Crystallogr Sect. B 1976, 32, 3190–3193. [Google Scholar] [CrossRef]
- Matan, K.; Ono, T.; Fukumoto, Y.; Sato, T.J.; Yamaura, J.; Yano, M.; Morita, K.; Tanaka, H. Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice. Nat. Phys. 2010, 6, 865–869. [Google Scholar] [CrossRef]
- Müller, M.; Müller, B.G. Cs2M(IV)Cu3F12 (M(IV) = Zr, Hf)—Crystal structure and magnetic behaviour. Z. Anorg. Allg. Chem. 1995, 621, 993–1000. [Google Scholar] [CrossRef]
- Reisinger, S.A.; Tang, C.C.; Thompson, S.P.; Morrison, F.D.; Lightfoot, P. Structural phase transition in the S = ½ kagome system Cs2ZrCu3F12 and a comparison to the valence-bond solid phase in Rb2SnCu3F12. Chem. Mater. 2011, 23, 4234–4240. [Google Scholar] [CrossRef]
- Ono, T.; Morita, K.; Yano, M.; Tanaka, H.; Fujii, K.; Uekusa, H.; Narumi, Y.; Kindo, K. Magnetic susceptibilities in a family of S = ½ kagome antiferromagnets. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Downie, L.J.; Black, C.; Ardashnikova, E.I.; Tang, C.C.; Vasiliev, A.N.; Golovanov, A.N.; Berdonosov, P.S.; Dolgikh, V.A.; Lightfoot, P. Structural phase transitions in the kagome lattice based materials Cs2−xRbxSnCu3F12 (x = 0, 0.5, 1.0, 1.5). CrystEngComm 2014, 16, 7419–7425. [Google Scholar] [CrossRef]
- Downie, L.J.; Thompson, S.P.; Tang, C.C.; Parsons, S.; Lightfoot, P. Re-entrant structural phase transition in a frustrated kagome magnet, Rb2SnCu3F12. CrystEngComm 2013, 15, 7426–7429. [Google Scholar] [CrossRef]
- Morita, K.; Yano, M.; Ono, T.; Tanaka, H.; Fujii, K.; Uekusa, H.; Narumi, Y.; Kindo, K. Singlet ground state and spin gap in the of S = ½ kagome antiferromagnet Rb2SnCu3F12. J. Phys. Soc. Jpn. 2008, 77, 043707:1–043707:4. [Google Scholar]
- Amemiya, T.; Yano, M.; Morita, K.; Umegaki, I.; Ono, T.; Tanaka, H.; Fujii, K.; Uekusa, H. Partial ferromagnetic ordering and indirect exchange interaction in the spatially anisotropic kagome antiferromagnet Cs2Cu3CeF12. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic-radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A Found Crystallogr. 1976, 32, 751–767. [Google Scholar]
- Wills, A.S. Program VaList for Windows. Available online: http://www.ccp14.ac.uk/ (accessed on 1 October 2014).
- Stephens, P.W. Phenomenological model of anisotropic peak broadening in powder diffraction. J. Appl. Crystallogr. 1999, 32, 281–289. [Google Scholar] [CrossRef]
- Boultif, A.; Louer, D. Indexing of powder diffraction patterns for low-symmetry lattices by the successive dichotomy method. J. Appl. Crystallogr. 1991, 24, 987–993. [Google Scholar] [CrossRef]
- Campbell, B.J.; Stokes, H.T.; Tanner, D.E.; Hatch, D.M. ISODISPLACE: A web-based tool for exploring structural distortions. J. Appl. Crystallogr. 2006, 39, 607–614. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Banfield, J.F. Thermodynamic analysis of phase stability of nanocrystalline titania. J. Mater. Chem. 1998, 8, 2073–2076. [Google Scholar] [CrossRef]
- Tolbert, S.H.; Alivisatos, P. Size dependence of a first-order solid-solid phase transition: The wurzite to rock-salt transformation in CdSe nanocrystals. Science 1994, 265, 373–376. [Google Scholar] [CrossRef] [PubMed]
- McHale, J.M.; Auroux, A.; Perrotta, A.J.; Navrotsky, A. Surface energies and thermodynamic phase stability in nanocrystalline aluminas. Science 1997, 277, 788–791. [Google Scholar] [CrossRef]
- Ardelean, I.; Peteanu, M.; Burzo, E.; Ciorcas, F.; Filip, S. EPR and magnetic susceptibility studies of Cu2+ ions in TeO2-B2O3-PbO glasses. Solid State Commun. 1996, 98, 351–355. [Google Scholar] [CrossRef]
- Aldous, D.W. Solvothermal Chemistry of Early Transition Metal Fluorides. Ph.D. Thesis, University of St Andrews, St Andrews, UK, 2008. [Google Scholar]
- Thompson, S.P.; Parker, J.E.; Potter, J.; Hill, T.P.; Birt, A.; Cobb, T.M.; Yuan, F.; Tang, C.C. Beamline I11 at Diamond: A new instrument for high resolution powder diffraction. Rev. Sci. Instrum. 2009, 80. [Google Scholar] [CrossRef]
- Larson, A.C.; von Dreele, R.B. General Structure Analysis System (GSAS); Report No. 88–748; Los Alamos Natl. Lab.: Los Alamos, NM, USA, 1994. [Google Scholar]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Cryst. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Farrugia, L.J. J. WinGX and ORTEP for Windows: an update. Appl. Crystallogr. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Jain, P.; Dalal, N.S.; Toby, B.H.; Kroto, H.W.; Cheetham, A.K. Order-disorder antiferroelectric phase transition in a hybrid inorganic-organic framework with the perovskite architecture. J. Am. Chem. Soc. 2008, 130, 10450–10451. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Downie, L.J.; Ardashnikova, E.I.; Tang, C.C.; Vasiliev, A.N.; Berdonosov, P.S.; Dolgikh, V.A.; De Vries, M.A.; Lightfoot, P. Novel S = 1/2 Kagome Lattice Materials: Cs2TiCu3F12 and Rb2TiCu3F12. Crystals 2015, 5, 226-243. https://doi.org/10.3390/cryst5020226
Downie LJ, Ardashnikova EI, Tang CC, Vasiliev AN, Berdonosov PS, Dolgikh VA, De Vries MA, Lightfoot P. Novel S = 1/2 Kagome Lattice Materials: Cs2TiCu3F12 and Rb2TiCu3F12. Crystals. 2015; 5(2):226-243. https://doi.org/10.3390/cryst5020226
Chicago/Turabian StyleDownie, Lewis J., Elena I. Ardashnikova, Chiu C. Tang, Alexandre N. Vasiliev, Peter S. Berdonosov, Valery A. Dolgikh, Mark A. De Vries, and Philip Lightfoot. 2015. "Novel S = 1/2 Kagome Lattice Materials: Cs2TiCu3F12 and Rb2TiCu3F12" Crystals 5, no. 2: 226-243. https://doi.org/10.3390/cryst5020226
APA StyleDownie, L. J., Ardashnikova, E. I., Tang, C. C., Vasiliev, A. N., Berdonosov, P. S., Dolgikh, V. A., De Vries, M. A., & Lightfoot, P. (2015). Novel S = 1/2 Kagome Lattice Materials: Cs2TiCu3F12 and Rb2TiCu3F12. Crystals, 5(2), 226-243. https://doi.org/10.3390/cryst5020226









