Light-Induced Heating of Microsized Nematic Volumes

Abstract

The experimental study has been carried out using advanced computer vision methods in order to visualize the moment of excitation and further propagation of a non stationary isotropic domain in a hybrid aligned nematic (HAN) microsized volume under the effect of a laser beam focused on a bounding liquid crystal surface. It has been shown that, when the laser power exceeds a certain threshold value, in bulk of the HAN microvolume, an isotropic circular domain is formed. We also observed a structure of alternating concentric rings around the isotropic circular region, which increases with distance from the center of the isotropic domain. The formation of a sequence of rings in a polarizing microscopic image indicates the formation of a complex topology of the director field in the HAN cell under study. The following evolution of the texture can be represented by two modes. Firstly, the “fast” heating mode, which is responsible for the formation and explosive expansion of an isotropic zone in bulk of the HAN microvolume with characteristic time ${\tau }_1$ due to a laser spot heating on the upper indium tin oxide (ITO) layer. Secondly, the “slow” heating mode, when an isotropic zone and concentric rings slowly expand with characteristic time ${\tau }_2$ mainly due to the finite thermoconductivity of ITO layer. When the laser power significantly exceeds the threshold value, damped oscillations of the isotropic domain are observed. We also introduced the metrics that allows quantitatively estimate the behavior of texture observed. The results obtained form an experimental basis for further investigation of thermomechanical force appearing in the LC system with coupled gradients of temperature and director fields.

1. Introduction

With the current sustained demand for further miniaturization in the drug delivery devices, as well as techniques for biomolecules manipulation and biosensing, there is considerable interest in understanding the mentioned systems behavior from a technological implementation point of view. Robust and accurate experimental techniques for controlling the movement of molecular liquids and liquid crystals (LCs) make it possible to quickly and cost-effectively simulate hypothetical devices. This, in turn, can lead to the development of new and potentially improved designs for biotechnology devices and approaches. Thus, the investigation of complex dynamics in organic fluids including anisotropic materials is still of a high demand of modern soft matter physics. Microfluidics has appeared as a scientific field which is devoted to the approach how to manipulate, control and analyses tiny amounts of molecular liquids and LCs in channels ranging in size from tens to hundreds of micrometers [1,2,3]. Microfluidics has become a paradigm in various fields from chemical synthesis and biological analysis to optics and information technology [1,4,5]. Central to the success in microfluidics is development of innovative methods of manipulation of molecular liquids or LC systems in microchannels. Complex fluids, such as LCs or systems with biological materials, are characterized by a non-trivial coupling between fluid flow and structural deformations [4,5,6,7,8]. The channel size up to nanoscale ensures a close connection between nematic and biological fluids [4]. As for LC, an external electric field is traditionally used for controlling fluid motion [1]. On the other hand, in the significantly reduced LC volume, a number of other factors affect the flow dynamics. Among those factors is the temperature gradient, which starts to play an important role.

A liquid crystal drop of micro- sized volume is extremely sensitive to both the temperature gradient, $\nabla T$, and boundary conditions. Consequently, these factors can influence the nature of hydrodynamic flow $\mathbf{v}$ in micro- or nanosized LC channels. One of the nonmechanical methods for producing flow in a nematic microfluidic channel is based on the coupling between the temperature, $\nabla T$ , and the director field, $\nabla \widehat{\mathbf{n}}$, gradients. The problem of motion associated with an ultra-small (a few microliters) isotropic and LC drop, under the influence of the temperature gradient, caused by a laser beam, has drawn considerable attention [9,10,11,12,13]. The possibility of using a nearly infrared laser as a microfluidic heat source has been addressed by several groups [9,10,11,12,13]. Lasers provide the opportunity of precise tunable spatial and temporal properties of optical irradiation, providing controllable heating of the LC system [13]. Understanding of how the liquid crystal material can be manipulating by the temperature gradient is also a matter of great fundamental interest, as well as an essential part of knowledge in the field of soft-matter science.

If the laser beam is focused on the volume of the LC droplet or channel, as well as on the bounding surfaces, then an isotropic domain can form in the volume of the LC phase, or near the bounding surfaces, for some long time. Coupling between $\nabla T$ and $\nabla \widehat{\mathbf{n}}$ is responsible for the excitation of an additional force in the LC phase called the thermomechanical force [14], (TMF) ${\mathcal{F}}_i=\partial {\sigma }_{\mathrm{ki}}^{\mathrm{TM}}/\partial x_k$. Here ${\sigma }_{\mathrm{ki}}^{\mathrm{TM}}={\xi }_{\mathrm{kijlp}}\left({\nabla }_{j}T\right)\left({\nabla }_l{n}_p\right)$ is the thermomechanical stress tensor, which is one of the main factors that distinguish the LC system from isotropic molecular liquids, while ${\xi }_{\mathrm{kijlp}}$ is the thermomechanical coupling tensor and equal indexes are summed up. The magnitude of the hydrodynamic flow $\mathbf{v}$ excited by $\nabla T$ in a hybrid aligned nematic volume (HAN) is proportional to the tangential component of the thermomechanical stress tensor, ${\sigma }_{\mathrm{zx}}^{\mathrm{TM}}$, and has the form $\sim {\displaystyle \frac{d}{\eta }}{\sigma }_{\mathrm{zx}}^{\mathrm{TM}}$, where d and $\eta$ are the thickness and viscosity of the liquid crystal material [8,9], respectively. Thus, the development of physically controlled systems is required to accurately study the thermomechanical force. As is known, the director gradient, $\nabla \widehat{\mathbf{n}}$, can be formed by hybrid alignment of the LC volume on the bounding surfaces or near the isotropic domain-LC interface, or by taking into account both these mechanisms. At the same time, the temperature gradient $\nabla T$ can be excited by local laser heating. A recent analysis of the numerical results showed that due to the interaction of the gradients of the director’s field, $\nabla \widehat{\mathbf{n}}$ with $\nabla T$, the heating pattern of the microscopic HAN cell in the direction perpendicular to the laser spot on the bounding surface (in the direction of $\mathrm{z}$) is such that only a small part of the nematic volume is involved in the heating process, while most of the liquid crystal is not heated (see reference [15]). At the same time, this numerical investigation showed that the heating of the micro-sized volume of HAN caused by laser radiation spreads much wider in the $\mathrm{xy}$-plane. Thus, heating of a micro-sized HAN cell in the $\mathrm{xy}$-plane requires a detailed study of both the structure and dynamics of this system. For further development of concepts and models describing the thermomechanical force and energy dissipation modes in micro-volumes of HAN, we must find out, firstly, what typical dynamic modes can be observed in the HAN cell when exposed to a focused laser beam and, secondly, the typical evolution time of the director field disturbance. For this purpose, as the first step, an experimental study will be carried out using advanced computer vision methods that make it possible to capture the moment of excitation of the non-stationary isotropic domain in the HAN volume under the effect of temperature gradient. Thus, the main goal of our research is to develop experimental routines for a comprehensive study of the dynamics of formation of the isotropic domain that occurs in the nematic volume under laser radiation.

The outline of this paper is as follows: the experimental details are given in Section 2. Results and discussions are given in Section 3. Conclusions are summarized in Section 4.

2. Experimental Details

2.1. Sample Preparation

Let us begin with the consideration of the nematic sample exposed to laser radiation. The principal scheme of the LC cell is shown in Figure 1. To prepare LC cell, a standard indium tin oxide (ITO)-coated glass substrates are used. In our case, the ITO electrodes play the role of a light-absorbing layer, which is heated in the area of laser exposure. In the present study, we used the LC cell with a hybrid alignment. To provide a planar orientation on one of the bounding substrates, we used a polyimide alignment layer. A polyimide layer was deposited from solutions in 1-Methyl-2-pyrrolidinone (NMP, MACKLIN, Shanghai, China, ≥99%) to a pre-cleaned substrate, followed by spin-coating and drying at 220 °C for one hour. After drying, the polyimide layer was mechanically rubbed. To provide homeotropic anchoring on the ITO-coated glass plate, we used an adsorbed molecular monolayer of the surfactant CTAB (cetriltrimethylammonium bromide, Sigma-Aldrich, Saint Louis, MO, USA, ≥99%). The prepared substrates are fixed with glue. The thickness of a gap between substrates is set by teflon spacers. In the prepared cell, the thickness is equal to 15 µm , which is determined by the interference pattern in the transmission spectra of the cell before filling it with LC material. After the glue was completely dry, the LC cell was filled under the action of capillary forces. For the study, we use 4-pentyl-$4^{\prime }$-cyanobiphenyl (5CB) nematic liquid crystals (Sigma Aldrich, $98\%$) with nematic-isotropic phase transition near 35 °C. In Figure 1 we schematically showed the heating of the upper ITO electrode by 1064 nm laser beam with following isotropic domain formation (“isotropic bubble”, shown in grey color) and the initiation of a complex director field topology. In further discussion, we admit, that the plane of substrate is a xy-plane, the direction perpendicular to the substrate is along z-axis. The coordinate system is also shown in Figure 1.

2.2. Optical Setup and Measurement Routine

A developed experimental setup is shown in Figure 2. As a source of heating radiation we used a laser (VENUS, Connet Laser Technology, Shanghai, China) with a wavelength ${\lambda }_L=1064$ nm in continuous mode (Laser 1064 in the Figure 2). To ensure the Gaussian distribution of the laser beam intensity profile, the spatial filter consisted of two lenses (L1, L2), as well as a pin-hole diaphragm (Ph) were used. Then, the laser beam after reflecting from the dichroic mirror (DM) is introduced into the objective (O), which focuses the beam on the upper electrode of the LC cell. The objective used in the scheme allows ×50 magnification with a relatively longer working distance, which is $6\mathrm{mm}$. The laser spot in the plane of focus ($\mathrm{xy}$-plane) is approximately of 20 µm .

To obtain the texture of the LC layer, the polarized microscopic branch is used in the same setup. The white light from the LED source passes through the polarizer (P1, Figure 2). The linearly polarized light is focused on the LC cell using a lens (L3). The texture was observed using the same lens (O) and a CCD camera located after the color filter (F) and the cross analyzer (P2). The dichroic mirrors used have a high transmission coefficient in the visible spectrum and reflect in the near-infrared region of the spectrum. A CCD camera with a frame rate of 80 fps and a resolution of 640 × 480 pixels was used. We used a PC to collect the raw data (Figure 2).

Initially, we started by considering a HAN cell filled with 5CB molecules at a temperature of ∼300 K followed by exposure to a laser beam. The LC material was confined between two glass substrates with ITO layers and alignment layers. One variant of the hybrid aligned LC cell assumed that the upper bounding surface on which the laser beam is focused is aligned planar in the $\mathrm{xy}$ plane, while the lower bounding surface is aligned homeotropically, i.e., along $\mathrm{z}$ axis. This will be $\mathbf{case}\mathbf{I}$ . Another variant of the hybrid aligned LC cell assumed that the upper bounding surface is aligned homeotropically, while the lower one is aligned planar. This will be $\mathbf{case}\mathbf{II}$. The LC cell with uniform thickness of 15 μm was placed horizontally (in $\mathrm{xy}$-plane) in the optical setup (Figure 2). The tightly focused laser beam was used to effectively interact with the hybrid aligned 5CB sample through the ITO absorbing layer (see Figure 1). A number of heating regimes are considered, in which the laser radiation power P ranged from 0.5 to 15.5 $\mathrm{mW}$ with the corresponding laser energy exposition time ${\tau }_{\mathrm{in}}=8$ s. Here, we have to highlight one important aspect. In our setup using the HAN cell, focused laser radiation acts most effectively on the upper electrode. However, part of the de-focused transmitted laser light also interacts with lower electrode and can lead to “parasitic” heating of lower part of the LC cell. However, the temperature of the bottom electrode would be lower, which would allow the formation of the temperature gradient using laser radiation.

Thus, the measurement routine looks as follows:

• The LC cell is arranged in the microscopic scheme between crossed polarizers. The position of the LC cell in the polarized optical microscopy branch is adjusted at 45 degrees to the plane of incident light polarization to ensure maximum transmittance before exposure to laser radiation.
• First of all, we focus a low-power laser beam ($1\mathrm{MW}$) at the upper electrode. Secondly, we scan the cell position along the z axes. As will be shown in the next section, at low laser power, a stationary texture is quickly formed. During the z-scanning process, as the laser beam approaches the heated electrode, the texture begins to form. When focusing on the electrode, the texture will have the smallest size with the most pronounced intensity changes. After setting up the optical setup, the laser turns off to allow the LC cell to relax before measuring again.
• Then we focus the laser on the electrode of the LC cell, which provides the planar alignment. In our work, we used several laser power levels from $0.5\mathrm{mW}$ to $15.5\mathrm{mW}$.
• For each certain power, we record a video footage of texture formation and evolution within 8 s after turning on the laser and 3 s before turning on the laser. For each power used, a full cycle of heating under the influence of the laser and cooling after the laser is turned off is performed.
• The LC cell was rotated in the opposite direction. The laser radiation was focused on the electrode with the homeotropic boundary alignment. The video recording of texture formation was performed in accordance with the previous step.

3. Results and Discussion

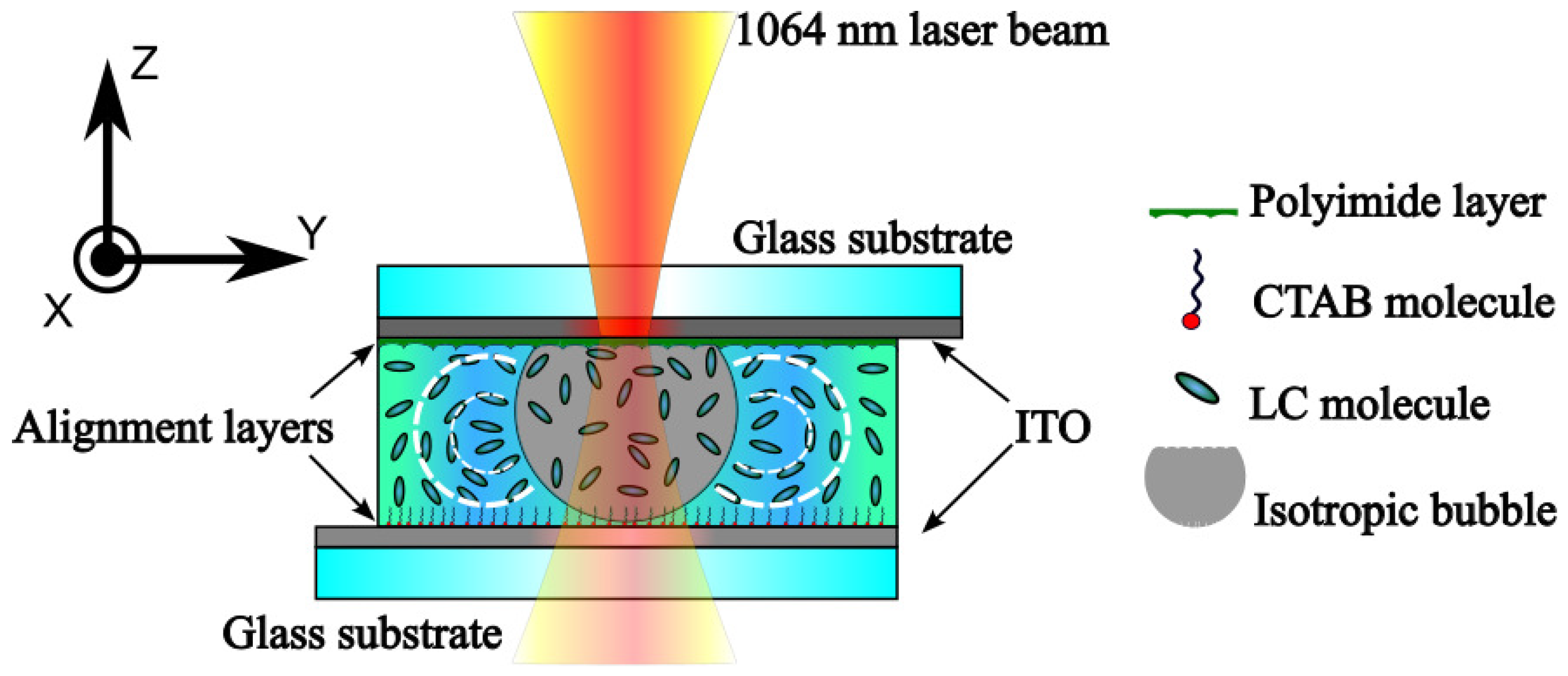
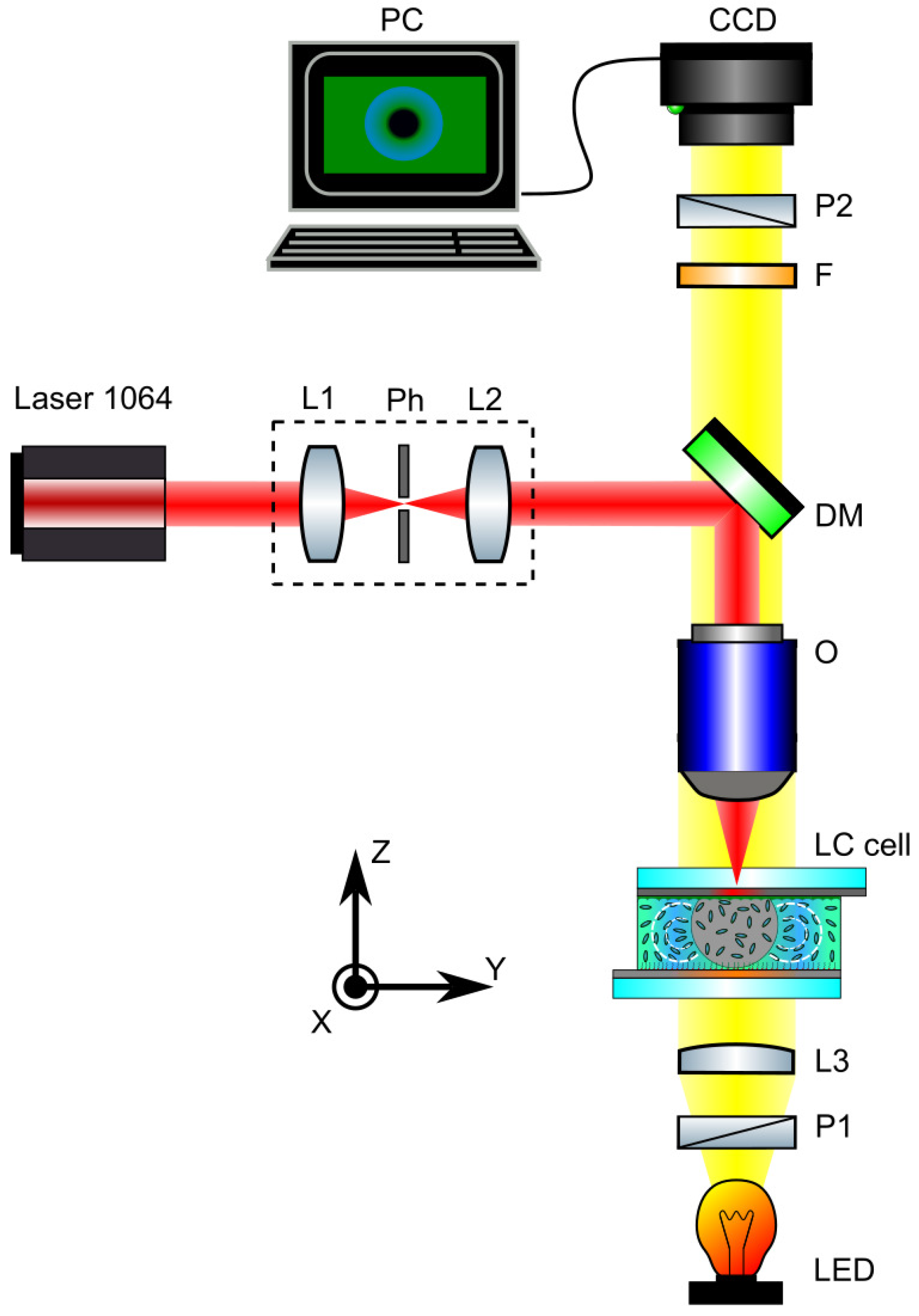
3.1. Laser Beam Heating of Nematic Sample

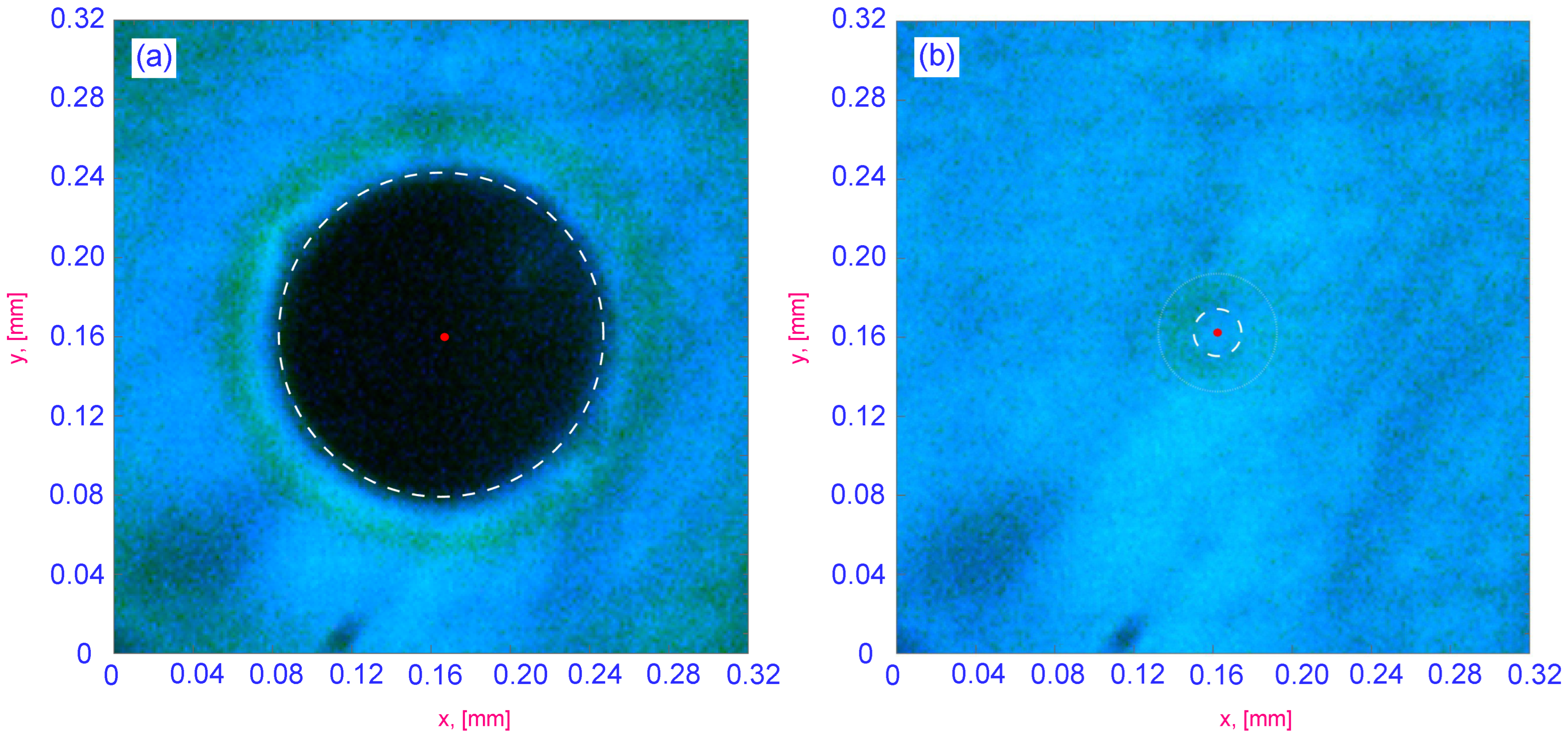
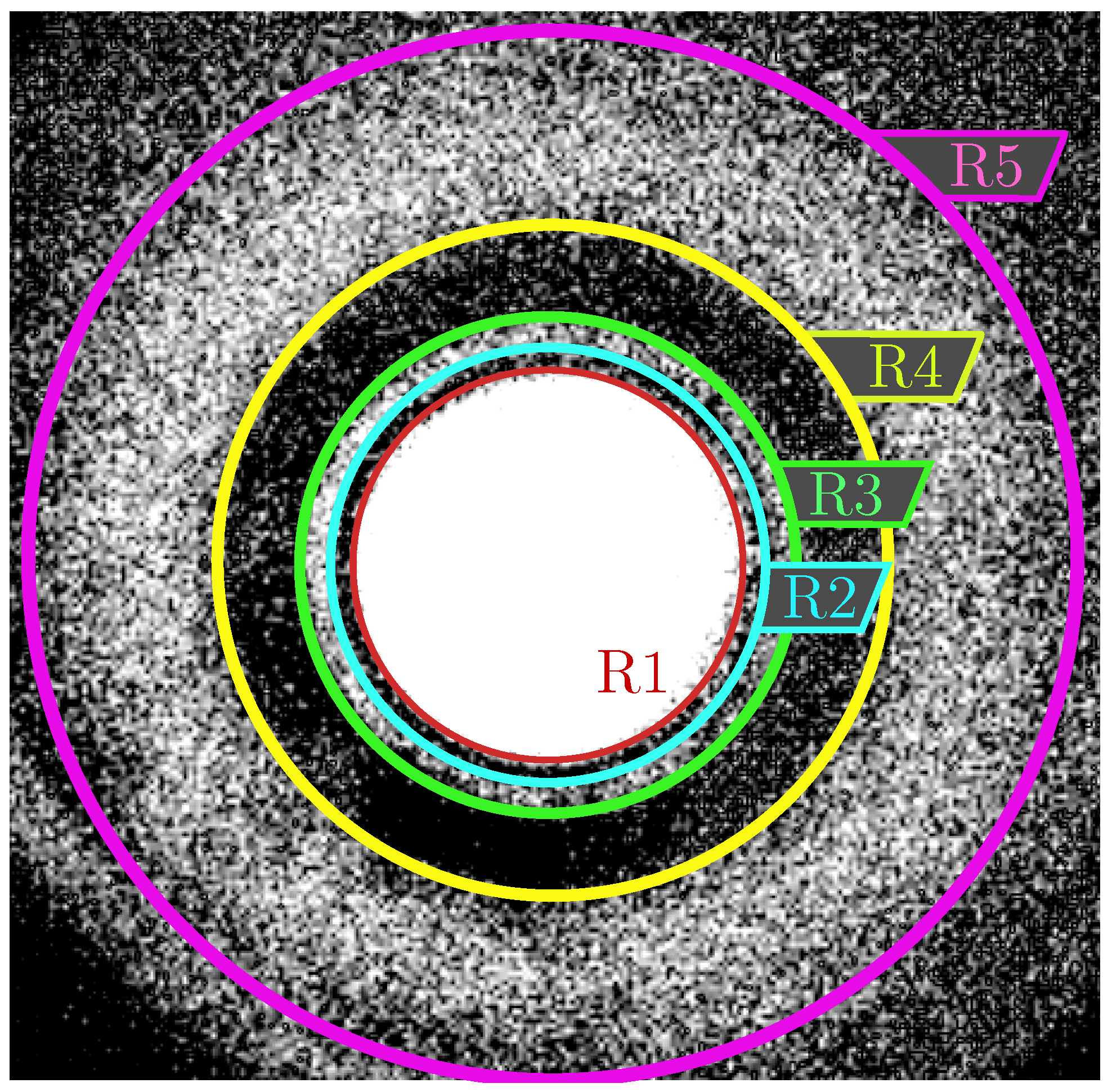
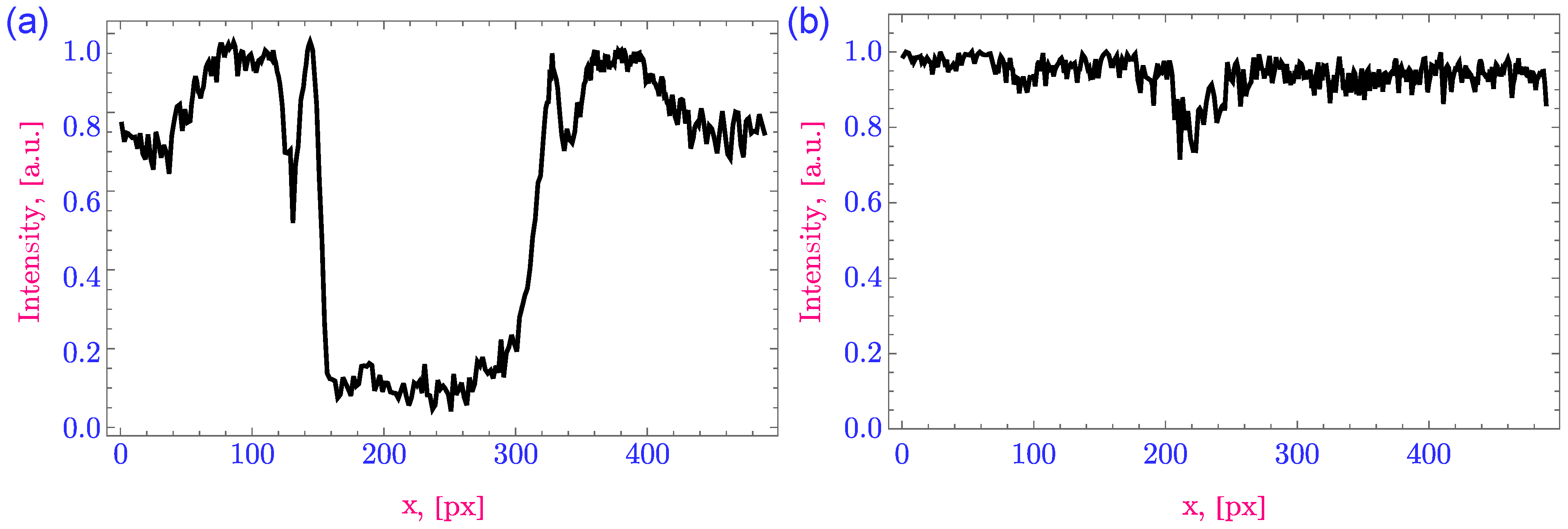
Under the effect of the electrode heating with the laser power $\mathrm{P}$ exceeding a threshold value of approximately ≈2.5 mW, the “fast” formation of a texture consisting of a black circular region corresponding to an isotropic domain with concentric colored rings is observed. The typical texture is shown in Figure 3a for optical power equal to $15.5\mathrm{mW}$. In Figure 3a we marked the center of texture with red dot and the revealed boundary of black area with dashed white line. To highlight the texture profile we provided an intensity cut section in Figure 4a at which there is clearly observed the central black area with following sequence of zones with high and low intensity.

We must emphasize that the textures are formed at a high speed, which apparently exceeds the frame rate used. However, after formation textures two modes of expansion are formed, namely the fast explosive expansion mode and the slow transition to a stationary state. The features of the evolution of the texture formed at the laser power exceeding the threshold volume will be discussed in the following subsections. Using the laser with the power below the threshold value (≈2.5 mW), we observed the formation of a slightly distinguishable colored ring without signs of an isotropic domain. The example of such a texture is shown in Figure 3b, where the laser power is $\mathrm{P}=1.0\mathrm{mW}$. The red dot corresponds to the center of the detected texture. A slightly observed colored ring is bounded by white lines. The corresponding intensity cut section is shown in Figure 4b.

Such a texture is completely formed at a rate much higher than the frame rate used per second, and can be characterized as static, since there is no sign of a change in the second time scale. As discussed in the previous section, we used this texture to provide focus on the electrode. The formation of the black domain in the $\mathrm{xy}$-plane with a sequence of rings in the polarizing microscopic image indicates the formation of a complex topology of the director field in the HAN cell. This topology was caused by local heating and a corresponding change in the temperature gradient. Although these texture features are visible to the naked eye, and the radii of the observed rings can be estimated by the intensity of cut sections, we used computer vision methods to recognize the texture and analyze its morphology. The approach of computer vision techniques allow us to fast automatic process the obtained video-footage frame-by-frame and makes it possible to reduce the number of operator errors during manual processing. For this purpose, frame-by-frame preprocessing of the image was performed. At the first stage, we divided the source frame into RGB color channels and obtained 3 matrices with dimension $640\times 480$ images containing information about the red, green and blue channels for each frame, respectively. For further data processing, it is sufficient to use only the blue channel matrices. In the second step, we removed the background matrix from each blue channel matrix, which corresponds to the averaging of blue channel data for frames taken 3 s before laser heating. At the next stage, each matrix was binarized and inverted for ease of further processing. Then, for each received preprocessed frame, a morphological closure operation was applied. The morphological detection algorithm was used to identify circular elements in each frame. The algorithm of morphological detection is described in Ref. [16]. The example of the preprocessing results is shown in Figure 5.

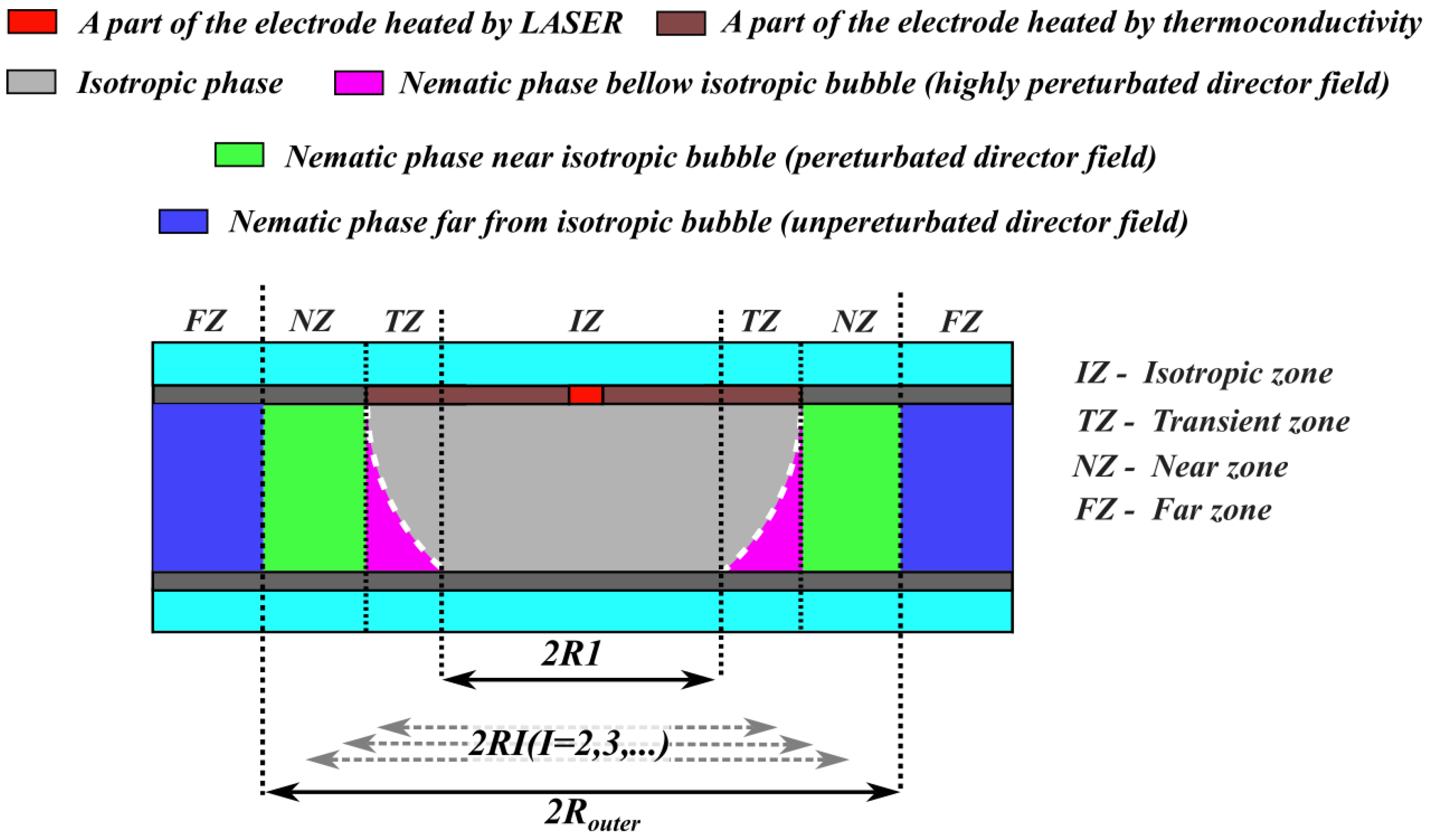
In the inverted binarized Figure 5, several circular elements can be observed when the circle with a radius $\mathrm{R}1$ corresponds to the black isotropic area in Figure 3a. Other circular elements indicate the sequence of rings that appeared as a result of heating processes. Before we go any further, we need to clarify the physical nature of the texture formed in the polarized microscopic branch. Since the light from the LED propagates from bottom, perpendicular to the substrate, we represent the structure of the LC cell from the optical point of view as a series of vertically oriented zones, as shown in Figure 6.

To observe the black area in the polarized microscopic image (Figure 3a), the whole path from the bottom to the top of the substrate must correspond to a completely isotropic area. Thus, the black circular area in Figure 3a corresponds to the cylindrical volume of the isotropic domain, which contains only an isotropic liquid between substrates. Such a cylindrical zone is labeled as IZ in Figure 6. However, the total isotropic domain has a shape different from that of the cylinder. Thus, a part of the LC cell can be represented by a vertical zone containing both isotropic and nematic phases. Such a zone is designated as the transition zone (TZ) in Figure 6. Now it is clear that the radius of $\mathrm{R}1$ from Figure 6 corresponds to the radius of the mentioned cylinder base, i.e., corresponds to the IZ-TZ boundary. We can assume that the director field in the nematic part of such zones can be strongly perturbed due to anchoring at the interface with an isotropic volume, possible fluid flows, and temperature gradient effects. Moreover, the thickness of the nematic phase in the TZ zone varies, as schematically shown in Figure 6. After TZ, we can introduce a zone called the near zone (NZ), with radius $R_{\mathrm{outer}}$, which has a perturbed director field but no isotropic volume.

As seen in Figure 3a, in the texture the number of bright and dark rings are observed. From polarized optical microscopy point of view it means that the polarization of light after passing through the cell varied in the xy-plane. Indeed, after passing through a LC cell with induced complex director field topologies, phase transformations and hydrodynamic flows, the light from the LED is characterized by a complex spatial distribution of polarization depending on the local anisotropy. Thus, the textures carry information about the director field perturbation. Such a perturbation is attributed to changes in the director field topology, which determines the birefringence, and to changes in the nematic phase thickness, which determines the optical path through the anisotropic phases. The usage of crossed polarizers allows to transfer spatial topology of light polarization to the spatial topology of light intensity which is captured with CCD camera. Taking into account those thoughts, we can claim that all textural rings with radii $RI$ starting from R2 are belonged to the TZ and NZ parts of cell between $R_1$ and $R_{\mathrm{outer}}$, respectively (Figure 6).

Finally, the rest of the LC cell has no perturbations and can be designated as far zone (FZ). Since in FZ there is no spatial perturbation of director field and no isotropic phases, no textural features can be observed in FZ. Thus, the boundary between NZ and FZ (${\mathrm{R}}_{\mathrm{outer}}$ in Figure 6) is an outer boundary of all textural features that can be observed. We can assume that number of rings as well as their thicknesses depend on following factors including thickness of the cell, initial configuration of director field, optical and material properties of LC used, parameters of laser irradiation. Further investigations may shed light on the influence of all these factors on formed texture properties.

Here we need to clarify another physical point. Despite the fact that the area of the laser spot on the upper ITO electrodes does not exceed ∼20 µm, the heating area of the electrode is significantly larger due to the limited thermal conductivity of the electrode materials, which is also shown in Figure 6. We would like to mention, that we have shown the typical textures observed for a given experimental condition; the reproducibility of texture formation features verified on several cells via measuring several times during a week.

3.2. Dynamics of the LC Textures

Now we can go further and focus our attention to the dynamics of texture evolution. As we said previously, the texture formed under the action of laser with power higher than ≈2.5 mW is not static and expands during the radiation exposure. First, we observe the “fast” mode characterized by explosive texture expansion over a typical period of time ${\tau }_1$. We believe that this mode is mainly influenced by the heating of LC materials by a laser spot on the ITO layer and a less pronounced effect of thermal conductivity. Secondly, the “slow” mode, when the isotropic domain slowly increases due to the thermal conductivity of the electrode. This slow mode is characterized by a characteristic time period of ${\tau }_2$.

As can be seen, the boundary between IZ and TZ is defined by a circle with radius $\mathrm{R}1$. The first light ring in Figure 3a corresponds to the area of space between circles with radius $\mathrm{R}1$ and $\mathrm{R}2$ in the inverted binarized Figure 6, the second light ring corresponds to the area of space between the circle with radius $\mathrm{R}3$ and $\mathrm{R}4$, etc. 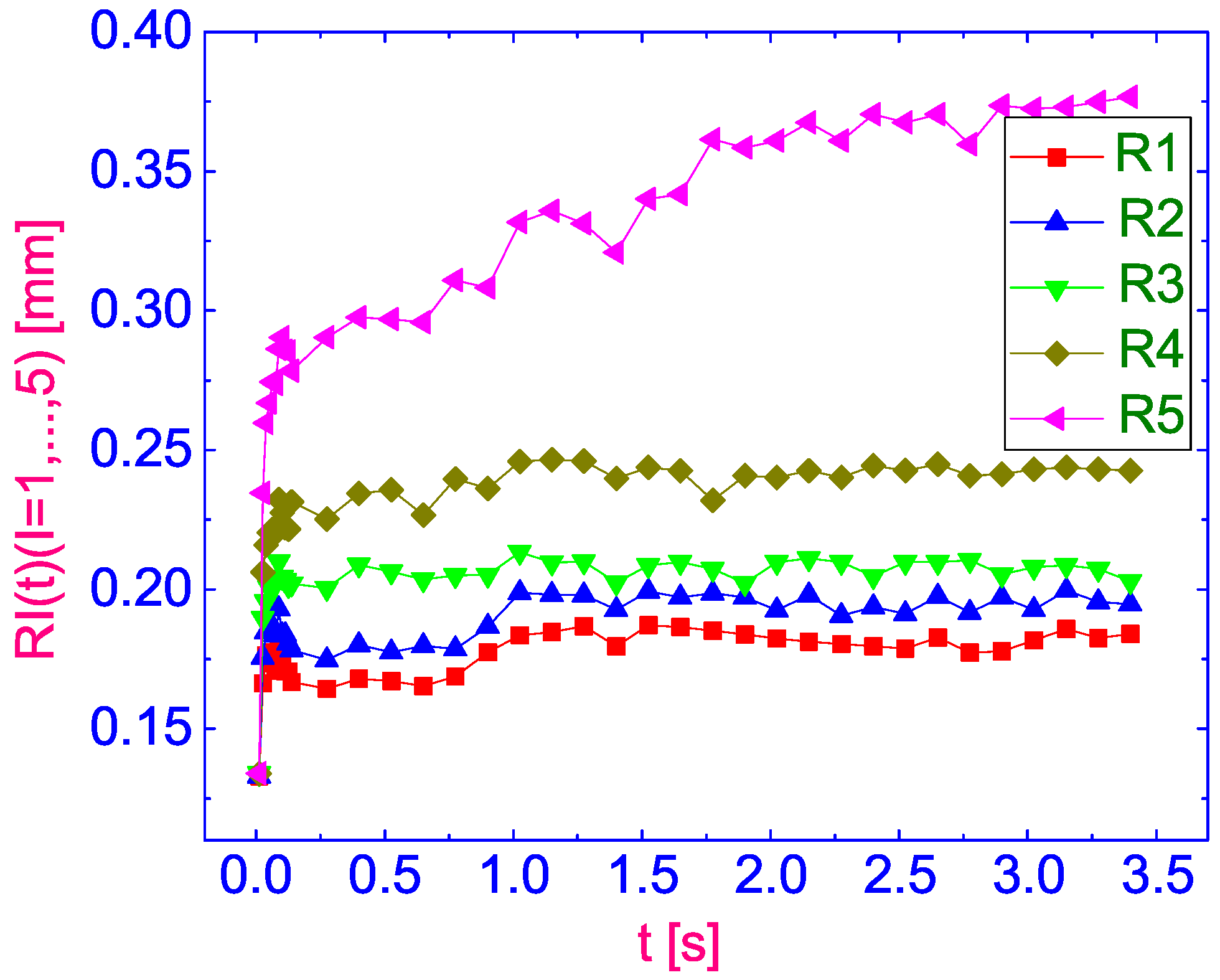All the bright ring structures observed in Figure 3a and characterized with R2, R3, etc are attributed to the TZ and NZ where the optical anisotropic properties of LC film is varying as discussed previously. When the laser is turned on, the observed textures and their radii expand. An example of the time dependence of the characteristic radii of a texture is shown in Figure 7 for $\mathbf{case}\mathbf{I}$ and for optical laser power $15.5\mathrm{mW}$.

The data presented in Figure 7 highlighted an explosive increase in the radius of the isotropic domain and the accompanying concentric rings, followed by a slow transition to a stationary state. The typical explosive growth time is about 0.1–0.2 s. When the laser radiation power is much higher than the threshold value, damped oscillations of the isotropic domain are observed.

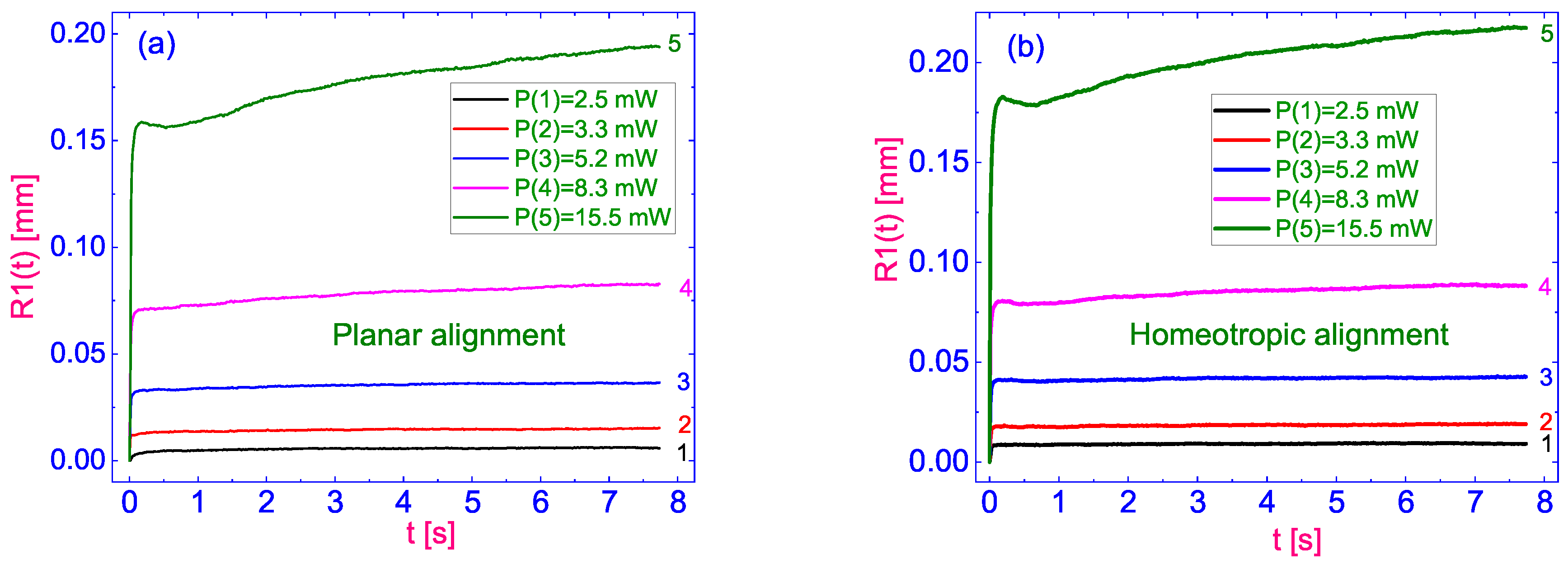
Since, depending on the power of the laser radiation, the textures formed have different characteristic radii, and, generally speaking, the rings can extend beyond the frame, it is most advisable to compare the dynamics of texture expansion along the boundary of an isotropic zone. Figure 8 shows the dynamics of the isotropic zone expansion (the dependence of its radius $R1\left(t\right)$ on time t when the laser beam is focused on a planar ($\mathbf{case}\mathbf{I}$) (Figure 8a) and homeotropic ($\mathbf{case}\mathbf{II}$) (Figure 8b) substrates, depending on the power P of the laser radiation. As we can see from Figure 8a,b, the typical behavior of changing of the radius of zone IZ is the same for both $\mathbf{case}\mathbf{I}$ and $\mathbf{case}\mathbf{II}$, consisting in explosive expansion and further slow growth. Moreover, damped oscillations are clearly observed at higher optical power values.

However, this phenomenon should be considered in detail in future work, by capturing the dynamics with higher frame rate and camera resolution, as well as by developing a hydrodynamic theoretical description.

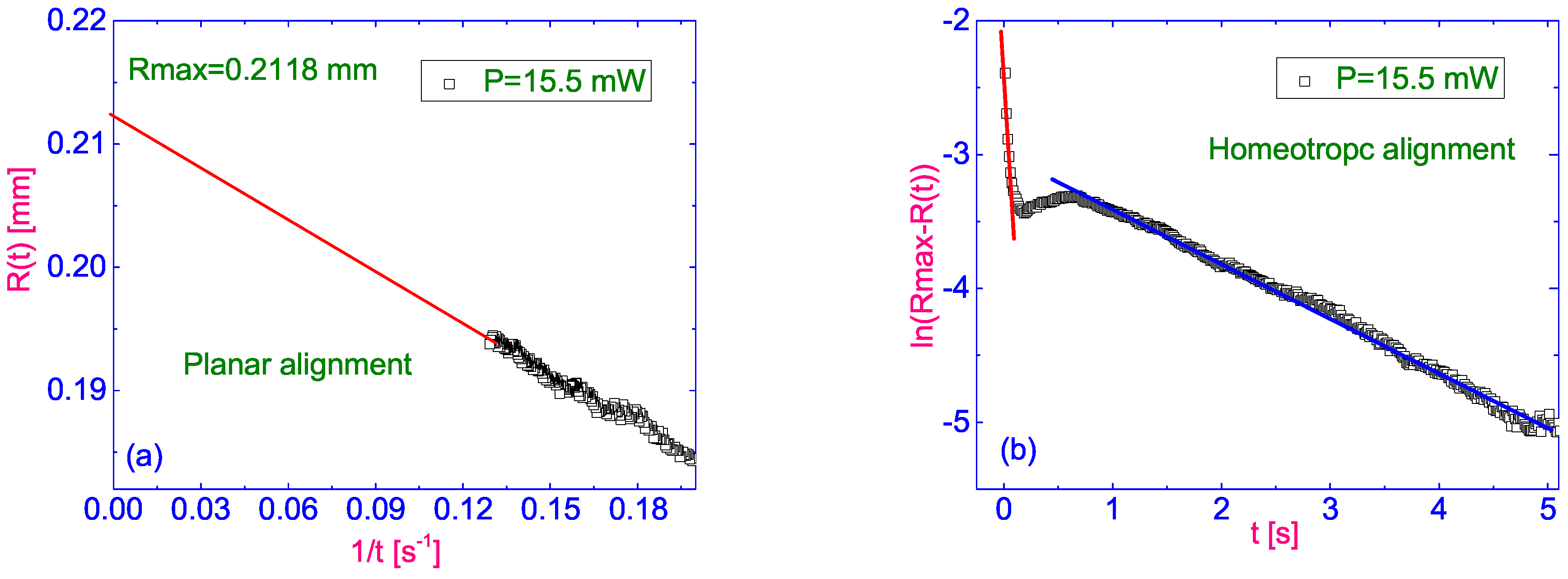
At this stage, we intend to introduce some indicators that allow us to assess the dynamics of evolution more quantitatively. First, we need to estimate the stationary radii of the isotropic zones $R_{\max }$ that are formed when thermal stabilization in our dynamical system is achieved. To estimate $R_{\max }$, we propose to plot the obtained dependencies $R1\left(t\right)$ in coordinates of $1/t$ for $t>5\mathrm{s}$. The example of such plotting is shown in Figure 9a. The dependence of $R1\left(t\right)$ in this given time range t takes a linear form and can be extrapolated to the ordinate axis. The ordinate of the intersection point of such a linear approximation with the ordinate axis allows us to estimate the maximum radius of the circular domain $R_{\max }$. The example of $R_{\max }$ determination is shown in Figure 9a.

Then, it is necessary to propose an algorithm for estimation of the characteristic time periods of the expansion dynamics. We can presume, that dynamics of expansion have multi-exponential behavior. Thus, the characteristic time can be obtained by plotting the time dependence of the IZ radii on logarithmic scale. For plotting convenience it is much easy to work with $\Delta R\left(t\right)$ which is $\Delta R1\left(t\right)=R_{\max }-R1\left(t\right)$. As can be seen in Figure 9b linear dependence intervals can be observed using such a logarithmic scale when plotting $ln(R_{\max }-R1\left(t\right))$ on t. Two areas with linear dependencies are clearly distinguished: first, corresponding to the time just after switching on the laser radiation and, second, in the time interval between the $2\mathrm{nd}$ and $5\mathrm{th}$ seconds. The slope coefficients of the linear approximations correspond to the inverse of the characteristic times ${\tau }_1$ and ${\tau }_2$. Accordingly, the expected value of the first characteristic of the “fast” time, ${\tau }_1$, is much less than the corresponding values of the “slow”, time ${\tau }_2$.

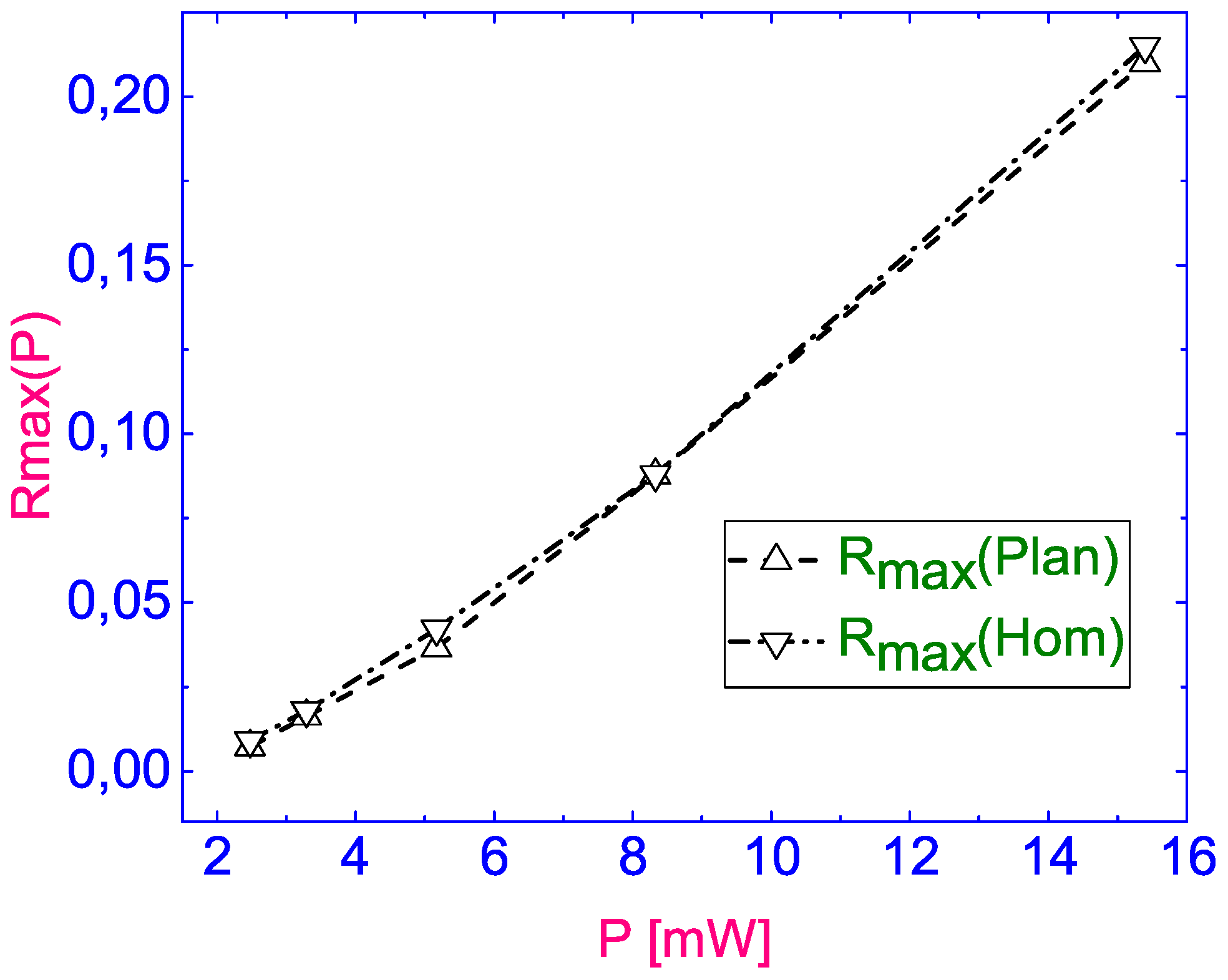
Comparison of the limiting radius $R_{\max }\left(P\right)\equiv R1$ of an isotropic zone depending on the power of P laser radiation when it focuses on both planar ($\mathbf{case}\mathbf{I}$) (triangles up) and homeotropically ($\mathbf{case}\mathbf{II}$) (down triangles) aligned substrates are shown in Figure 10. As can be seen from Figure 10, the two dependencies almost coincide. This dependence seems logical, since, as a result, the volume of the liquid that has passed into the isotropic phase should be determined by the amount of energy pumped into the system.

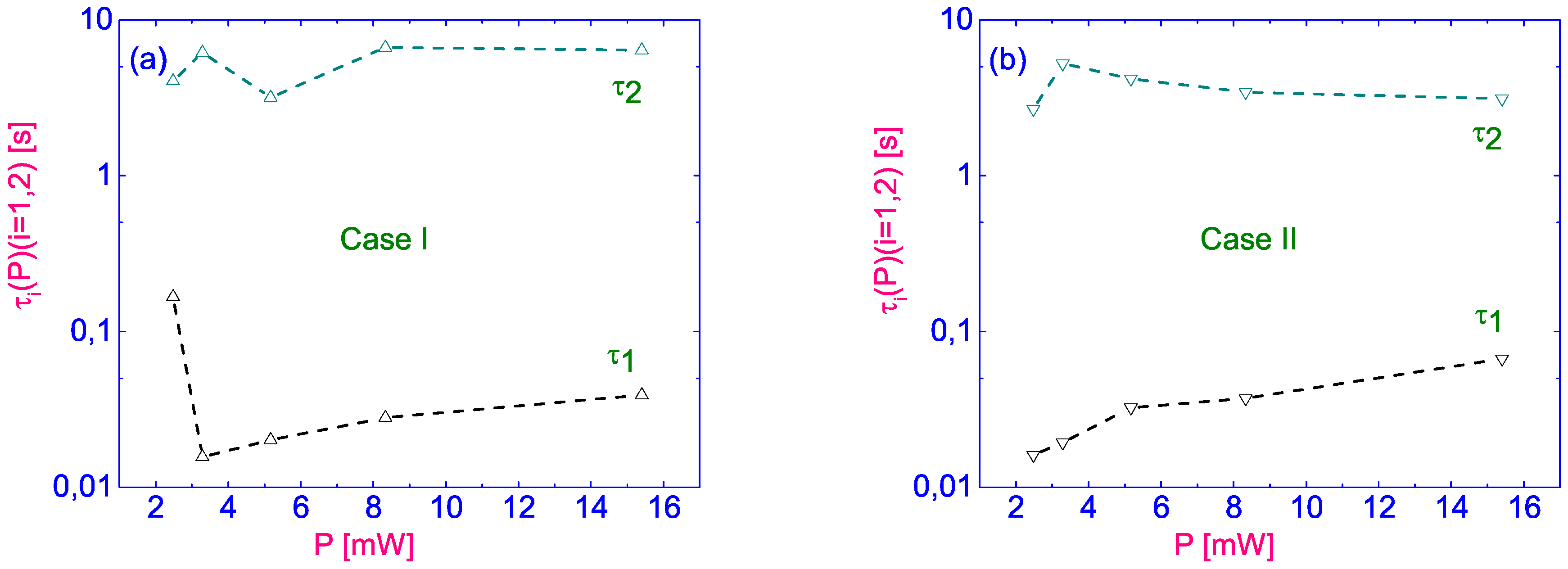
Figure 11 shows the dependences of “fast” (${\tau }_1\left(P\right)$) and “slow” (${\tau }_2\left(P\right)$) expansion time of the isotropic circular domain depending on the power P of the laser radiation when it is focused as on the planar, $\mathbf{case}\mathbf{I}$, (Figure 11a) and on homeotropic $\mathbf{case}\mathbf{II}$, (Figure 11b), substrates. In all cases, we see that ${\tau }_2$ is several orders of magnitude higher than ${\tau }_1$. Moreover, at this stage we have not identified a clear dependence of ${\tau }_2$ of the laser power. In future work, we intend to obtain data with a smaller power step, which will allow us to investigate the dependence of ${\tau }_2$ on the laser power and the initial configuration of the director’s field. With a lower power P (less than $3\mathrm{mW}$) and focusing on the planar aligned bounding surface ($\mathbf{case}\mathbf{I}$), a point appears that deviates sharply from the dependence ${\tau }_1\left(P\right)$. The observed flaw is caused by a technical error that occurred due to the limitation of the maximum time resolution of the CCD camera used ($1/80$ s). To improve the results of measuring the “fast” time ${\tau }_1$, in the following studies it is necessary to reduce the power step and shoot at a higher frame rate, which will allow for a more accurate linear approximation. Nevertheless, starting with the power of P exceeding $3\mathrm{mW}$, both dependencies tend to monotonous growth.

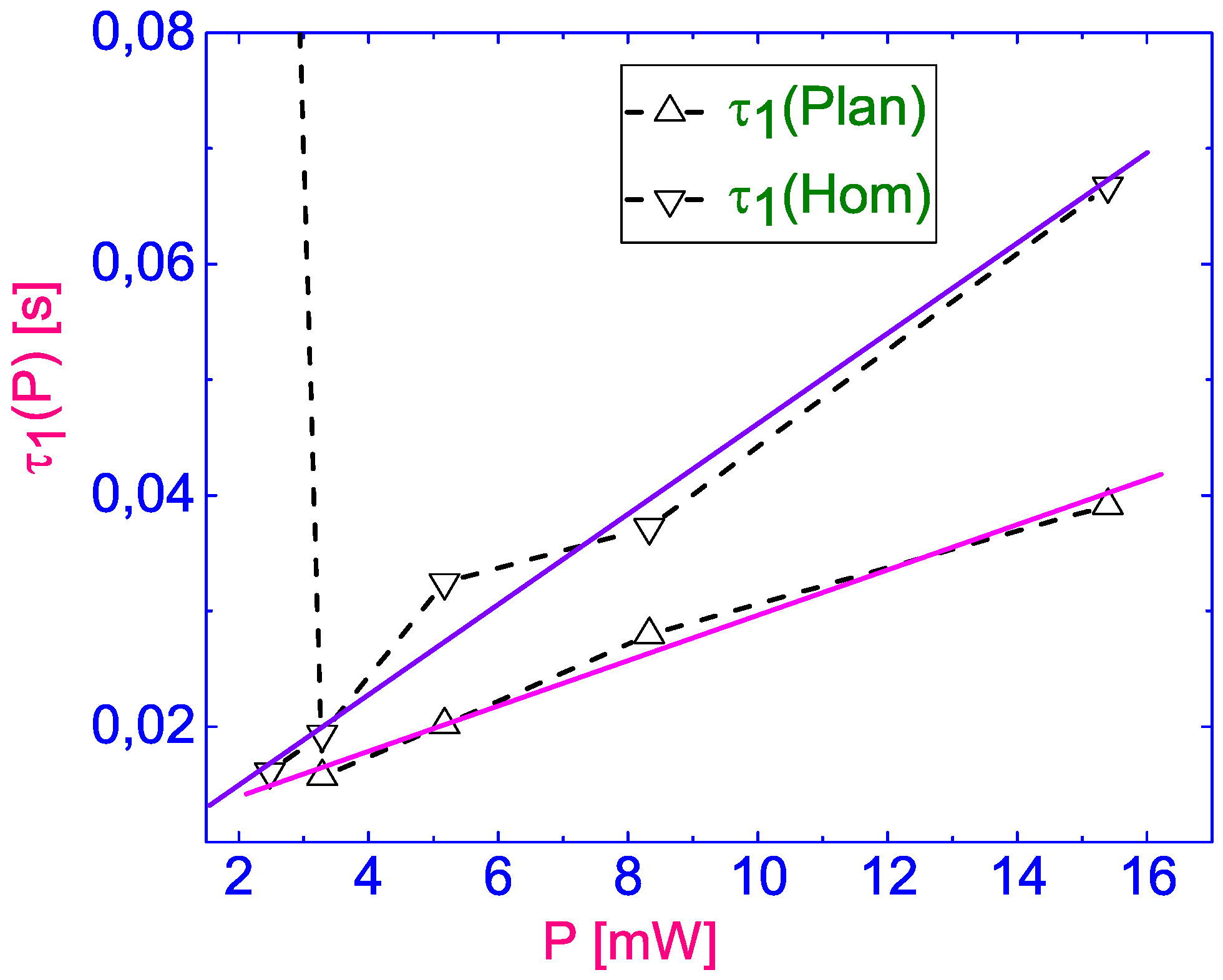
In Figure 12 we compare the dependence of the “fast” time ${\tau }_1$ on the laser power for both $\mathbf{case}\mathbf{I}$ and $\mathbf{case}\mathbf{II}$. It can be seen that the growth rates of these dependencies vary markedly. In the case of laser beam focusing on the homeotropically aligned bounding surface ($\mathbf{case}\mathbf{II}$), the dependence slope is almost twice as high as in the case of focusing on the planar aligned surface. This difference in the growth rates of these dependencies ${\tau }_1\left(\mathbf{case}\mathbf{I}\right)$ and ${\tau }_1\left(\mathbf{case}\mathbf{II}\right)$ can be explained by the difference in thermal conductivity coefficients ${\lambda }_{\Vert }\left(5\mathrm{CB}\right)\sim 0.24$ and ${\lambda }_{\perp }\left(5\mathrm{CB}\right)\sim 0.13$ (in units $\mathrm{W}/\mathrm{mK}$) [17] corresponding to the parallel and perpendicular direction of the director $\widehat{\mathbf{n}}$.

Despite the fact that this stage of our experimental studies is the first attempt, we can assert that the presented techniques and metrics are sufficient for a comprehensively study of the dynamics of texture evolution in the context of the thermomechanical force in the LC cells with the gradient of both the director’s field and temperature distribution.

4. Conclusions

Thus, we experimentally investigated the effect of laser heating on the formation and evolution of phase transformations in a hybrid aligned nematic cell (HAN). For this purpose, we have implemented an optical setup based on a polarized optical microscopic scheme with laser radiation injected. Then, an advanced computer vision method was used to visualize the moment of excitation and further propagation of an unsteady isotropic domain in the HAN micro-sized volume under the effect of a laser beam focused on the bounding LC (LC) surface. It has been shown that when the laser power exceeds a certain threshold value, in bulk of the HAN micro-volume an isotropic circular domain is formed. The structure of alternating concentric rings around the isotropic circular region was also observed, which increased with distance from the center of the isotropic domain. The formation of a sequence of rings in a polarizing microscopic image indicates the formation of a complex topology of the director field in the studied HAN cell. The following evolution of the texture can be represented by two modes. Firstly, the ”fast” heating mode, which is responsible for the formation and explosive expansion of the isotropic zone in bulk of the HAN micro-volume with characteristic time ${\tau }_1$ due to laser spot heating of the upper indium tin oxide (ITO) layer. It is shown that in the case of focusing the laser beam on the homeotropically aligned bounding surface ($\mathbf{case}\mathbf{II}$), the slope dependence of ${\tau }_1$ is almost twice as high as in the case of focusing on the planar aligned surface ($\mathbf{case}\mathbf{I}$). Secondly, the ”slow” heating mode, when the isotropic zone and concentric rings slowly expand with a characteristic time ${\tau }_2$ mainly due to the finite thermoconductivity of the ITO layer. It is also shown that for both cases ($\mathbf{case}\mathbf{I}$ and $\mathbf{case}\mathbf{II}$) the values ${\tau }_2$ is an order of magnitude higher than ${\tau }_1$. When the laser power significantly exceeds the threshold value, damped oscillations of the isotropic domain are observed. We have also introduced the metrics that allows us to quantify the behavior of the observed texture. The results obtained form the experimental basis for further investigation of the thermomechanical force appears in the LC system with coupled gradients of temperature and director fields. It should be noted that the study of the dynamics of laser heating in a microsized nematic volume consisting of cyanobiphenyl molecules can be extended to ferroelectric nematic materials [18,19].

We believe that the present study may shed some light on the problem of the micro-fluids dynamics in a micro-sized nematic volume under the heating effect of a focusing laser beam. The setup, image processing algorithms as well as metrics introduced in the present work may be become a basement of experimental routines for the investigation of thermomechanical force in LC cells stem from the coupling between the temperature and director field gradients. In turn, such studies will lead to the appearance of new microfluidic and micro cargo devices.