Oriented-Attachment-Driven Heteroepitaxial Growth During Early Coalescence of Single-Crystal Diamond on Iridium: A Combined Multiscale Simulation and Experimental Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. First-Principles Calculations
2.1.1. Interface Analysis
2.1.2. Diamond Nucleation Growth
2.2. Molecular Dynamics Simulations
2.3. Experimental Details
2.3.1. Substrate Preparation
2.3.2. Diamond Deposition
- H2 Cleaning (25 min): Pure hydrogen plasma at 700 °C removed surface contaminants.
- Stabilization (5 min): Introduction of 3% CH4/H2 at reduced power enabled plasma equilibrium.
- Bias-Enhanced Nucleation (BEN) (60 min): Critical nucleation phase (−250 V bias at 800 °C) with 3% CH4.
- Growth (120 min): Diamond expansion at 900 °C with 2% CH4 and increased power.
2.3.3. Characterization
3. Results and Discussion
3.1. Ir(100)/Dia(100) Interfacial Interactions
3.1.1. Adhesive Energy and Interfacial Stress
3.1.2. Electronic Properties
3.2. Stepwise Growth of Diamond Nuclei
3.2.1. Interfacial Geometry and Bond Evolution
3.2.2. Electron Transfer Kinetics
3.2.3. Formation Energetics and Growth Mode Transition
3.3. Molecular Dynamics Simulation of Diamond Grain Connection
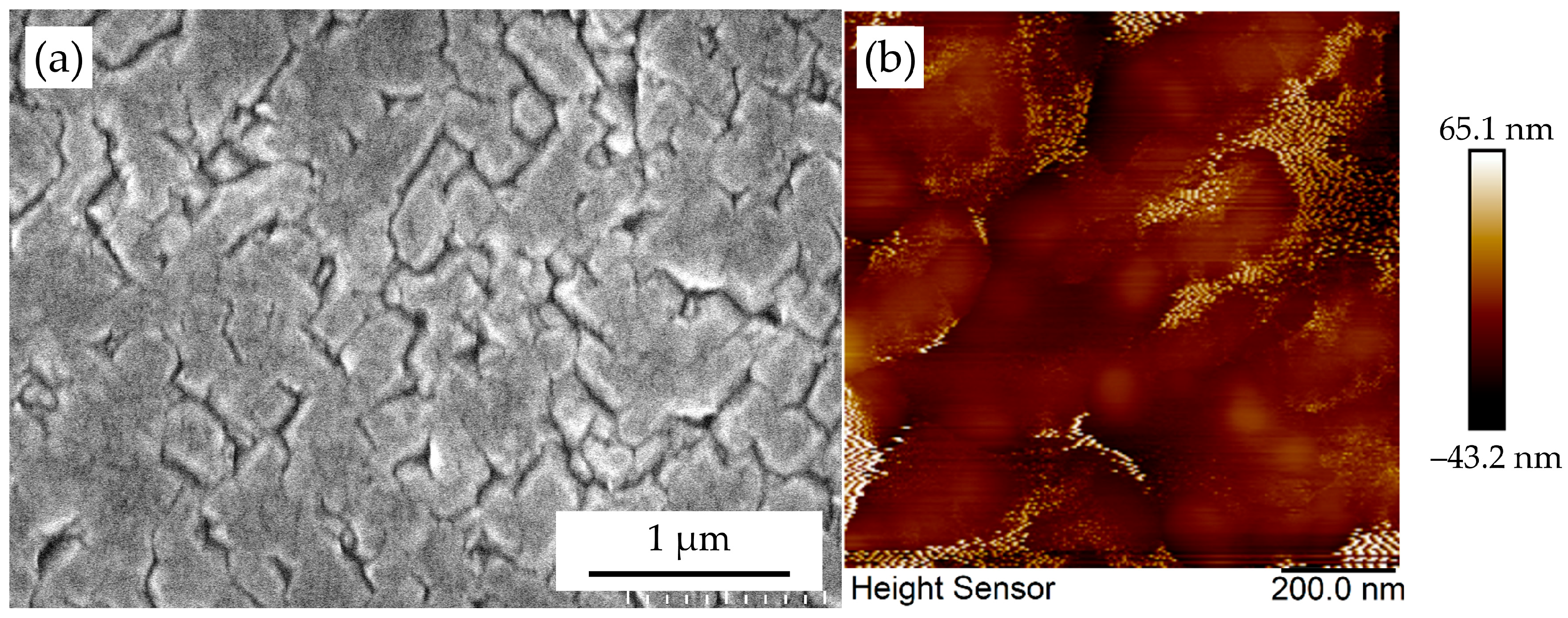
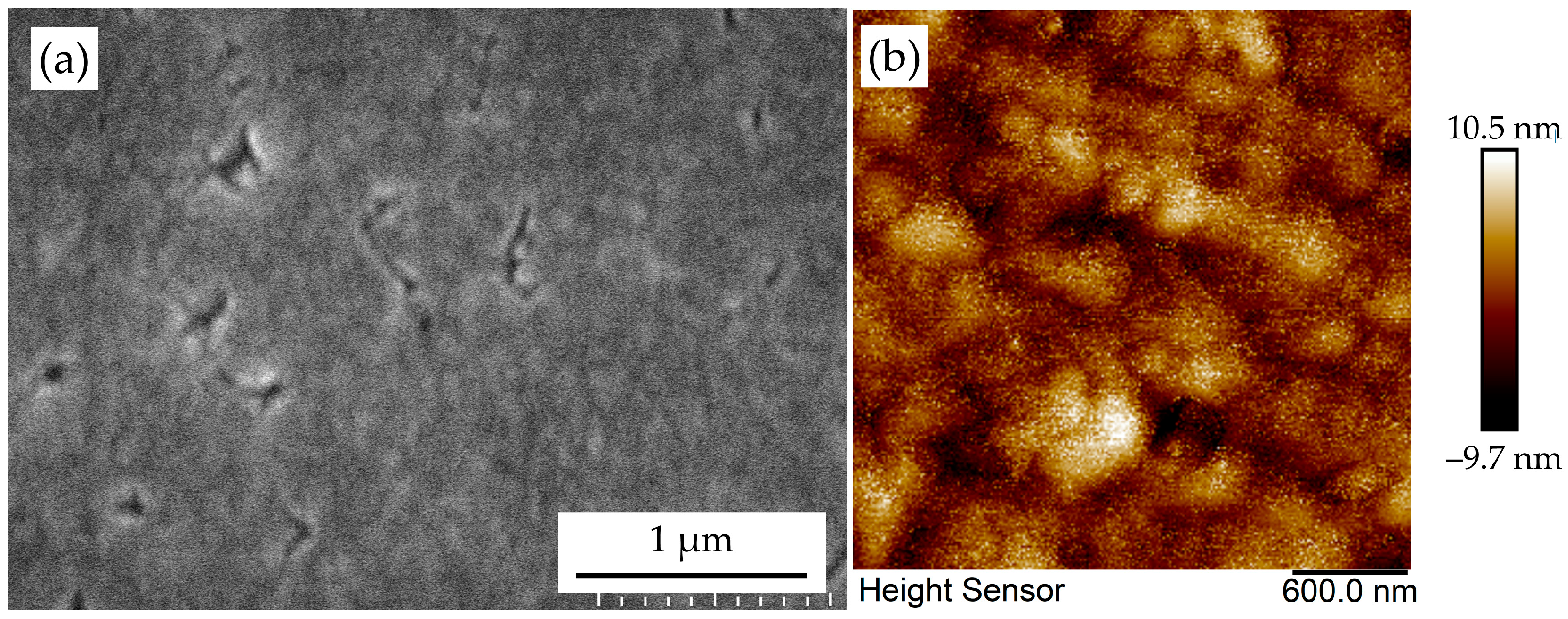
3.4. Coalescence Behavior of Epitaxial Diamond Nuclei: Normal Versus Defective Regimes
3.5. Grain Boundary Annihilation During Coalescence
3.6. Formation of Epitaxial Diamond Thin Films
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Y.L.; Ding, Y.; Sun, Z.G.; Ren, J.; Zhao, J.L.; Zhou, Q.Q. Achieving uniform diamond distribution in impregnated bits through multi-stage encapsulation and stage-by-stage sieving: A pathway to enhanced drilling performance. Int. J. Refract. Met. Hard Mater. 2025, 133, 107338. [Google Scholar] [CrossRef]
- Hao, X.; Liu, B.; Li, Y.; Zhao, J.; Zhang, S.; Wen, D.; Liu, K.; Dai, B.; Han, J.; Zhu, J. Diamond single crystal-polycrystalline hybrid microchannel heat sink strategy for directional heat dissipation of hot spots in power devices. Diam. Relat. Mater. 2023, 135, 109858. [Google Scholar] [CrossRef]
- Augustine, R.; Kalva, S.N.; Dalvi, Y.B.; Varghese, R.; Chandran, M.; Hasan, A. Air-jet spun tissue engineering scaffolds incorporated with diamond nanosheets with improved mechanical strength and biocompatibility. Colloids Surf. B 2023, 221, 112958. [Google Scholar] [CrossRef] [PubMed]
- Cesaroni, S.; Bombarda, F.; Bollanti, S.; Cianfarani, C.; Claps, G.; Cordella, F.; Flora, F.; Marinelli, M.; Mezi, L.; Milani, E.; et al. Conceptual design of CVD diamond tomography systems for fusion devices. Fusion Eng. Des. 2023, 197, 114037. [Google Scholar] [CrossRef]
- Cheng, C.; Li, R.; Gui, Q.; Wu, G.; Liang, K.; Dong, F.; Guo, Y.; Zhang, Z.; Liu, S. Structural design and electronic performance at MOx/diamond (M = Hf, Zr, Ti, Al, Sc, Y) interfaces for MOS device applications. Appl. Surf. Sci. 2025, 679, 161231. [Google Scholar] [CrossRef]
- Rusevich, L.L.; Kotomin, E.A.; Popov, A.I.; Aiello, G.; Scherer, T.A.; Lushchik, A. The electronic, vibrational and dielectric properties of diamond crystals with neutral vacancies: First principles study. Opt. Mater. 2024, 150, 115222. [Google Scholar] [CrossRef]
- Tian, Y.; Meng, F.; Wu, D.; Yang, D.; Tao, X.; Li, Z.; Tang, J.; Sun, X.; Pan, J. First-principles investigation of excited-state lattice dynamics and mechanical properties in diamond. Micromachines 2025, 16, 668. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Bi, T.; Yuan, X.; Chang, Y.; Zhang, R.; Fu, Y.; Tu, J.; Huang, Y.; Liu, J.; Li, C.; et al. C-Si interface on SiO2/(111) diamond p-MOSFETs with high mobility and excellent normally-off operation. Appl. Surf. Sci. 2022, 593, 153368. [Google Scholar] [CrossRef]
- Abdelrahman, A.; Ohmagari, S.; Yoshitake, T. Reverse characterization prediction of diamond Schottky barrier power devices using machine learning: Predicting breakdown voltage and Baliga figure of merit. Diam. Relat. Mater. 2024, 149, 111645. [Google Scholar] [CrossRef]
- Yu, C.; He, Z.Z.; Zhou, C.J.; Guo, J.C.; Song, X.B.; Cai, S.J.; Feng, Z.H. High frequency hydrogen-terminated diamond MESFET with an fmax of 103GHz. Mater. Today Commun. 2021, 28, 102489. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Danilov, P.A.; Vins, V.G.; Pomazkin, D.A.; Gorevoy, A.V.; Skorikov, M.L.; Chen, J.; Smirnov, N.A.; Paholchuk, P.P.; Kornilov, N.V.; et al. Resonant and non-resonant ultrafast non-linear photonics of quantum NV− emitters in diamond. Diam. Relat. Mater. 2025, 153, 112081. [Google Scholar] [CrossRef]
- Song, Z.; Yuan, H.; Fan, P.; Li, M.; Shen, J.; Wang, S.; Bian, G. Enhancing fluorescence of diamond NV− centers for quantum sensing: A multi-layer optical antireflection coating. Diam. Relat. Mater. 2024, 141, 110584. [Google Scholar] [CrossRef]
- Schirru, F.; Chokheli, D.; Kiš, M. Thin single crystal diamond detectors for alpha particle detection. Diam. Relat. Mater. 2014, 49, 96–102. [Google Scholar] [CrossRef]
- Chan, S.; Tu, J.; Huang, K.; Yang, Z.; Liu, P.; Zheng, L.; Liu, J.; Chen, L.; Wei, J.; Li, C. Oriented growth of 5-inch optical polycrystalline diamond films by suppressing dark features. Ceram. Int. 2024, 50 Pt 8, 37111–37118. [Google Scholar] [CrossRef]
- Li, Y.; Dai, B.; Ralchenko, V.G.; Lyu, J.; Hao, X.; Zhao, J.; Zhang, S.; Liu, K.; Han, J.; Bolshakov, A.P.; et al. Growth of single-crystal diamond by microwave plasma CVD with high precursor utilization using cyclic gas injection and control of carbonaceous species content with optical emission spectroscopy. Vacuum 2022, 206, 111529. [Google Scholar] [CrossRef]
- Banik, S.; Indhu, R.; Arunachalam, N.; Rao, M.S.R. Femtosecond laser-induced surface structuring for improved surface characteristics of single crystal diamond. Diam. Relat. Mater. 2025, 154, 112240. [Google Scholar] [CrossRef]
- Hu, X.; Li, M.; Wang, Y.; Peng, Y.; Tang, G.; Wang, X.; Li, B.; Yang, Y.; Xu, M.; Xu, X.; et al. Growth of 2-inch diamond films on 4H–SiC substrate by microwave plasma CVD for enhanced thermal performance. Vacuum 2023, 211, 111895. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, Y.; Weng, C.; Zhu, W.; Lou, L.; Wang, G. The quality of epitaxial lateral overgrown diamond on substrate with laser-cut holes of varying shapes and side orientations. Diam. Relat. Mater. 2024, 148, 111488. [Google Scholar] [CrossRef]
- Ralchenko, V.; Bolshakov, A.; Sovyk, D.; Artemov, V.; Vasiliev, A.; Krylov, Y.; Martyanov, A.; Fedorova, I.; Masalov, V.; Popovich, A.; et al. Epitaxial lateral overgrowth of single crystal diamond through self-assembled highly ordered porous colloidal SiO2 opal mask. Mater. Sci. Semicond. Process. 2025, 196, 109642. [Google Scholar] [CrossRef]
- Li, D.; Lv, X.; Wang, Q.; Wu, X.; Sun, G.; Xu, S.; Han, S.; Li, L.; Zou, G. Epitaxial lateral overgrowth of single crystalline diamond with different periodic trench geometries fabricated by laser cutting. Appl. Surf. Sci. 2025, 702, 163361. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Shu, G.; Fang, S.; Dai, B.; Zhu, J. Virtues of Ir(100) substrate on diamond epitaxial growth: First-principle calculation and XPS study. J. Cryst. Growth 2021, 560–561, 126047. [Google Scholar] [CrossRef]
- Dong, C.; Zhang, K.; He, L.; Liu, J.; Zhang, Z.; Lv, X.; Wang, Q.; Li, L.; Zou, G. Interfacial improvement of Ir/MgO substrate by post-deposition annealing for heteroepitaxial growth of single crystal diamond. J. Alloys Compd. 2025, 1036, 182174. [Google Scholar] [CrossRef]
- Fischer, M.; Gsell, S.; Schreck, M.; Brescia, R.; Stritzker, B. Preparation of 4-inch Ir/YSZ/Si(001) substrates for the large-area deposition of single-crystal diamond. Diam. Relat. Mater. 2008, 17, 1035–1038. [Google Scholar] [CrossRef]
- Li, J.; Zhou, B.; Piliptsou, D.G.; Sun, H.; Wu, Y.; Hei, H.; Gao, J.; Yu, S. Pre-planting amorphous carbon films based on Ir composite substrates for diamond nucleation. J. Cryst. Growth 2025, 649, 127945. [Google Scholar] [CrossRef]
- Lee, J.; Konaté, A.; Guibert, C.; Landoulsi, J. Biomimetic mineral layer over layer-by-layer assemblies: Growth mechanism directed by collagen fibrils. Surf. Interfaces 2023, 40, 103059. [Google Scholar] [CrossRef]
- Singh, C.P.; Ghosh, K. Two-stage superlattice growth approach integrating two-dimensional polarization enhancement mechanism for optimized p-type heterostructures in AlGaN DUV-LEDs. Mat. Sci. Eng. B-Adv. 2025, 322, 118601. [Google Scholar] [CrossRef]
- Chen, P.; Shen, W.; Chen, Z.; Li, C.; Han, S.; Wu, Y.; Hang, T.; Li, M. Surface atom migration-involved two-dimensional nucleation and growth of nanotwinned copper in DC electrodeposition. Acta Mater. 2024, 262, 119468. [Google Scholar] [CrossRef]
- Kazantsev, D.M.; Akhundov, I.O.; Rudaya, N.S.; Kozhukhov, A.S.; Alperovich, V.L.; Latyshev, A.V. Thermal roughening of GaAs surface by unwinding dislocation-induced spiral atomic steps during sublimation. Appl. Surf. Sci. 2020, 529, 147090. [Google Scholar] [CrossRef]
- Li, F.-Y.; Song, G.-Y.; Zhang, Q.-X.; Hou, M.-H.; Zhou, L.; Tai, J.-C. Understanding the growth mechanism of Al-bearing hematite nanoparticles via two-dimensional oriented attachment. J. Cryst. Growth 2023, 620, 127360. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Chen, X.; Liu, D.; Zhang, L.; Zhai, X.; Li, M. Fabrication of single crystal molybdate: A new protocol of coupling metal ion interaction and oriented-attachment with assistance of supercritical CO2. Mat. Sci. Eng. B-Adv. 2025, 319, 118379. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, X.; Jiao, F.; Xu, R.; Hao, S.; Li, H.; Zhang, Q. Oriented Attachment Growth of 2,6-Diamino-3,5-dinitropyrazine-1-oxide Mesocrystals: Morphological Evolution, Regulation, and Mechanism. Cryst. Growth Des. 2024, 24, 2764–2774. [Google Scholar] [CrossRef]
- Meshina, K.; Barabanov, N.; Tkachenko, D.; Vorontsov-Velyaminov, P.; Bobrysheva, N.; Voznesenskiy, M.; Osmolowsky, M.; Osmolovskaya, O. Zinc oxide nanoobjects for dye removal: Effective photocatalyst design via oriented attachment process. Surf. Interf. 2025, 60, 106006. [Google Scholar] [CrossRef]
- Aguilar-Chan, G.; Flores, E.; Alvarado-Gil, J.J.; Rodríguez-Gattorno, G. Oriented attachment of silver nanoparticles in DMSO by collapsing under thermal stress. Colloids Surf. A 2024, 703, 135210. [Google Scholar] [CrossRef]
- Ma, J.; Guo, Z.; Dai, S.; Liu, Y.; Hu, H.; Li, P.; Jin, L.; Ao, Y. Sizing agent induces the oriented attachment of 2D nanosheets for preparing high-performance carbon fiber composites. Surf. Interf. 2024, 51, 104549. [Google Scholar] [CrossRef]
- Fu, Y.S.; Song, Y.F.; Kulinich, S.A.; Sun, J.; Liu, J.; Du, X.W. Single-crystal ZnO flocky sphere formed by three-dimensional oriented attachment of nanoparticles. J. Phys. Chem. Solids 2008, 69, 880–883. [Google Scholar] [CrossRef]
- Dideikin, A.T.; Eidelman, E.D.; Kidalov, S.V.; Kirilenko, D.A.; Meilakhs, A.P.; Shakhov, F.M.; Shvidchenko, A.V.; Sokolov, V.V.; Babunz, R.A.; Vul, A.Y. Oriented-attachment growth of diamond single crystal from detonation nanodiamonds. Diam. Relat. Mater. 2017, 75, 85–90. [Google Scholar] [CrossRef]
- Ren, Y.; Lv, W.; Li, X.; Dong, H.; Wöhrl, N.; Yang, X.; Li, Z.; Wang, T. Effect of nitrogen on growth and optical properties of single-crystal diamond synthesized by chemical vapor deposition. Materials 2024, 17, 1311. [Google Scholar] [CrossRef]
- Arnault, J.-C.; Saada, S.; Ralchenko, V. Chemical vapor deposition single-crystal diamond: A review. Phys. Status Solidi-Rapid Res. Lett. 2022, 16, 2100354. [Google Scholar] [CrossRef]
- Yang, T.-I.; Chuang, C.-Y.; Chang, L. Enhancement of crystalline quality of homoepitaxial (100) diamond by microwave plasma chemical vapor deposition with a tungsten wire. Diam. Relat. Mater. 2025, 154, 112237. [Google Scholar] [CrossRef]
- Yoshikawa, T.; Kodama, H.; Kono, S.; Suzuki, K.; Sawabe, A. Wafer bowing control of free-standing heteroepitaxial diamond (100) films grown on Ir(100) substrates via patterned nucleation growth. Thin Solid Films. 2015, 594, 120–128. [Google Scholar] [CrossRef]
- Schreck, M.; Gsell, S.; Brescia, R.; Fischer, M. Ion bombardment induced buried lateral growth: The key mechanism for the synthesis of single crystal diamond wafers. Sci. Rep. 2017, 7, 44462. [Google Scholar] [CrossRef] [PubMed]

















| Aspect | Vapor–Solid (VS) | Step-Flow (SF) | Oriented Attachment (OA) |
|---|---|---|---|
| Physical essence | Gas–solid phase transition | Surface kinetic migration | Rotation-induced lattice matching |
| Key process | CH4 → C(ad) → Random | C(ad) + kink → Lateral spreading | Nanodisk rotation → Coherent merging stacking |
| Lattice control | Thermodynamic disorder | Template-guided by steps | Spontaneous nematic alignment |
| Crystal quality | Polycrystalline | Single crystal (needs perfect steps) | Near-single crystal |
| Defect reduction | Defect proliferation | Vertical blocking | Dislocation annihilation |
| Step dependence | Non-essential | Mandatory (else 3D islands) | Self-generates atomic terraces |
| Carbon coverage | Insensitive | >1 ML (monolayer) | 0.3–0.7 ML |
| Heteroepitaxy fitness | Universal but defective | Only homo/quasi-homo | Optimized for heterointerface |
| Limiting factor | High defect density | Step preparation complexity | Critical angle tolerance |
| Nucleation Stage | Growth Stage | |||
|---|---|---|---|---|
| H2 Cleaning | Stabilization | BEN * | ||
| CH4/% | 0 | 3 | 3 | 2 |
| Pressure/Torr | 20 | 20 | 20 | 20 |
| MW Power/W | 1500 | 1200 | 1200 | 2000 |
| Bias/V | 0 | 0 | −250 | 0 |
| Temp./°C | 700 | 700 | 800 | 900 |
| Time/min | 25 | 5 | 60 | 120 |
| Coverage (ML) | Layer Spacing (Å) | Bond Length (Å) | ||
|---|---|---|---|---|
| dIr-Ir-uncovered | dIr-Ir-C atop | dIr-Ir-C hollow | dIr-C | |
| 0.125 | 1.94 | 2.21 | — | 1.739 |
| 0.25 | 1.93 | 2.24 | — | 1.736 |
| 0.375 | 1.94 | 2.24 | — | 1.740 |
| 0.50 | 1.91 | 2.21 | — | 1.737 |
| 0.625 | — | 5.81 | 2.00 | 1.712–1.862 |
| 0.75 | — | 2.27 | 1.94 | 1.739–1.919 |
| 0.875 | — | 2.46 | 1.95 | 1.736–1.949 |
| 1.00 | — | 2.14 | — | 1.759 |
| Coverage (ML) | Adsorption Site | Charge on C (e) |
|---|---|---|
| 0.125 | Atop | −0.08 |
| 0.25 | Atop | −0.08 |
| 0.375 | Atop | −0.08 |
| 0.50 | Atop | −0.07 |
| 0.625 | Atop | −0.10 |
| Hollow | −0.29 | |
| 0.75 | Atop | −0.06 |
| Hollow | −0.24 | |
| 0.875 | Atop | −0.05 |
| Hollow | −0.22 | |
| 1.00 | Atop | −0.06 |
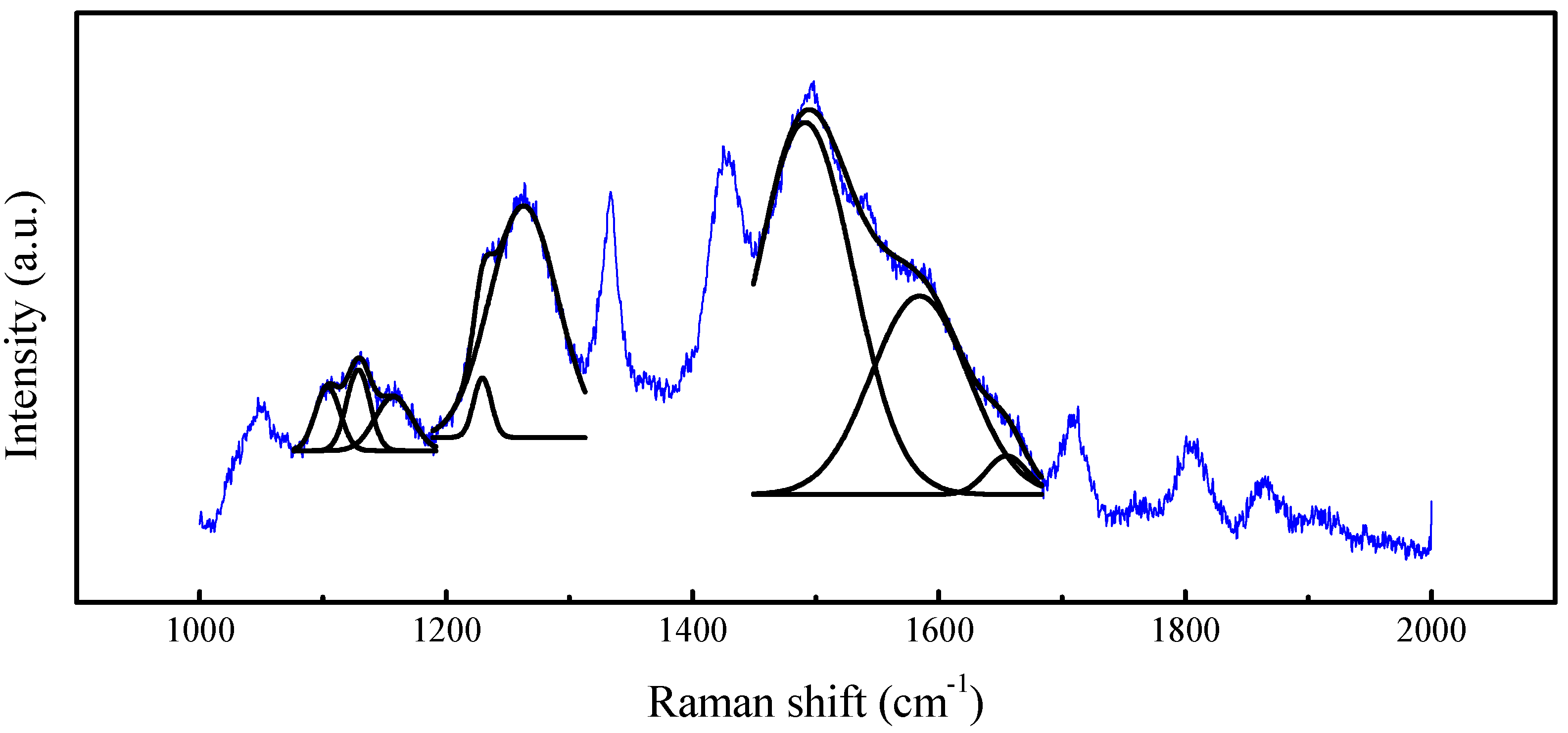
| Parameter | Coalesced Region | Non-Coalesced Region |
|---|---|---|
| Diamond (perfect sp3) | ||
| Center (°) | 1329.74 | 1333.09 |
| FWHM (°) | 21.97 | 25.49 |
| Analytic Area | 43,054.61 | 78,519.59 |
| Shift (°) * | −3.26 | +0.09 |
| sp3-dominant DLC (unperfect sp3) | ||
| Center (°) | 1461.36 | 1456.73 |
| FWHM (°) | 61.11 | 61.05 |
| Analytic Area | 20,372.04 | 44,398.25 |
| Graphite (D-bands) | ||
| Center (°) | 1358.27 | 1359.51 |
| FWHM (°) | 33.46 | 22.65 |
| Analytic Area | 19,667.63 | 22,495.26 |
| Graphite (G-bands, sp2) | ||
| Center (°) | 1578.92 | 1578.41 |
| FWHM (°) | 61.11 | 61.05 |
| Analytic Area | 29,389.18 | 67,261.60 |
| ID/IG | 0.67 | 0.33 |
| sp2/perfect sp3 ratio | 0.68 | 0.86 |
| DLC/perfect sp3 ratio | 0.47 | 0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, J.; Li, Z.; Yang, S.; Zhu, J. Oriented-Attachment-Driven Heteroepitaxial Growth During Early Coalescence of Single-Crystal Diamond on Iridium: A Combined Multiscale Simulation and Experimental Validation. Crystals 2025, 15, 803. https://doi.org/10.3390/cryst15090803
Wang Y, Chen J, Li Z, Yang S, Zhu J. Oriented-Attachment-Driven Heteroepitaxial Growth During Early Coalescence of Single-Crystal Diamond on Iridium: A Combined Multiscale Simulation and Experimental Validation. Crystals. 2025; 15(9):803. https://doi.org/10.3390/cryst15090803
Chicago/Turabian StyleWang, Yang, Junhao Chen, Zhe Li, Shilin Yang, and Jiaqi Zhu. 2025. "Oriented-Attachment-Driven Heteroepitaxial Growth During Early Coalescence of Single-Crystal Diamond on Iridium: A Combined Multiscale Simulation and Experimental Validation" Crystals 15, no. 9: 803. https://doi.org/10.3390/cryst15090803
APA StyleWang, Y., Chen, J., Li, Z., Yang, S., & Zhu, J. (2025). Oriented-Attachment-Driven Heteroepitaxial Growth During Early Coalescence of Single-Crystal Diamond on Iridium: A Combined Multiscale Simulation and Experimental Validation. Crystals, 15(9), 803. https://doi.org/10.3390/cryst15090803






