Reconfigurable GeTe’s Planar RGB Resonator Filter–Absorber
Abstract
1. Introduction
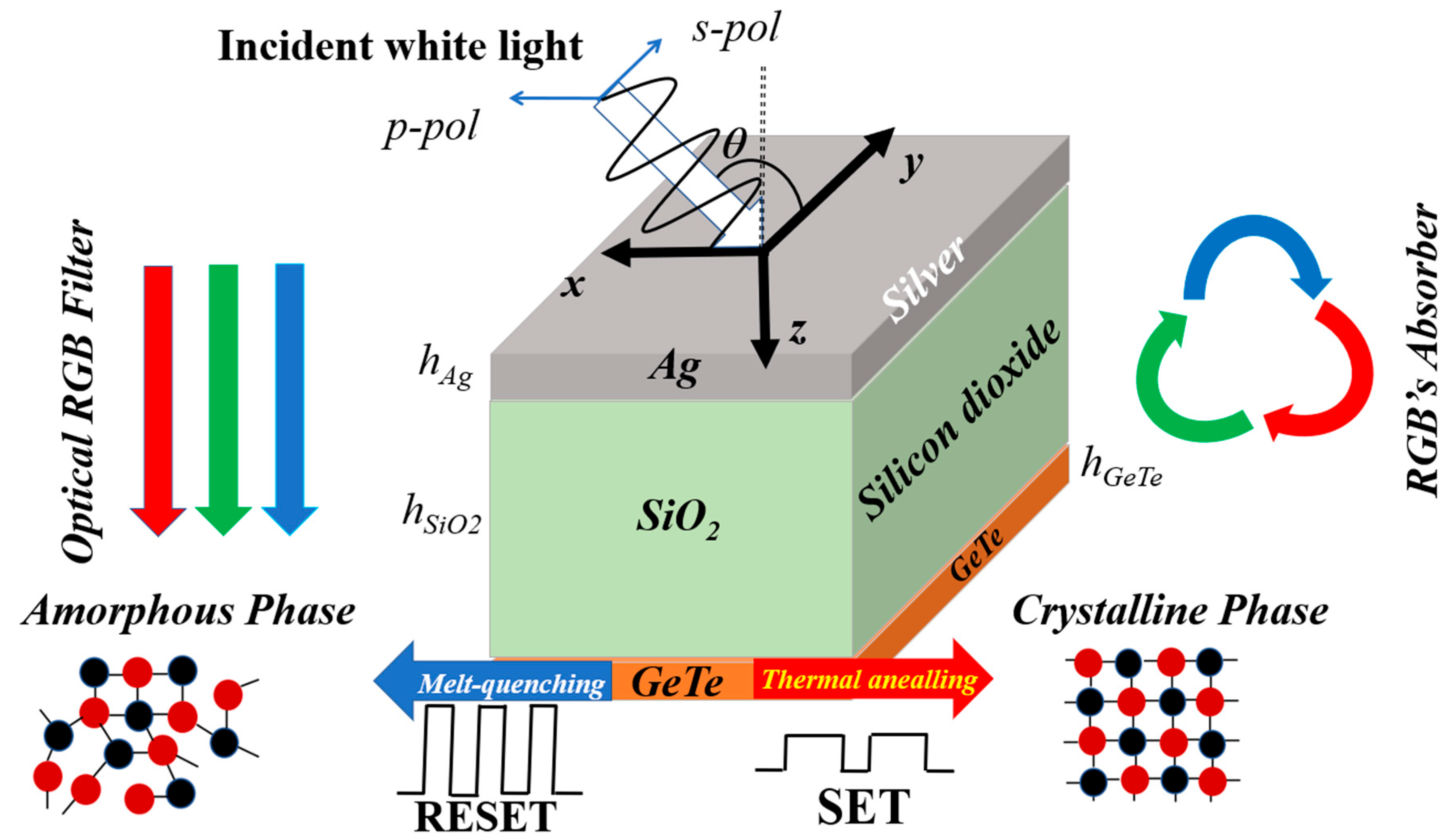
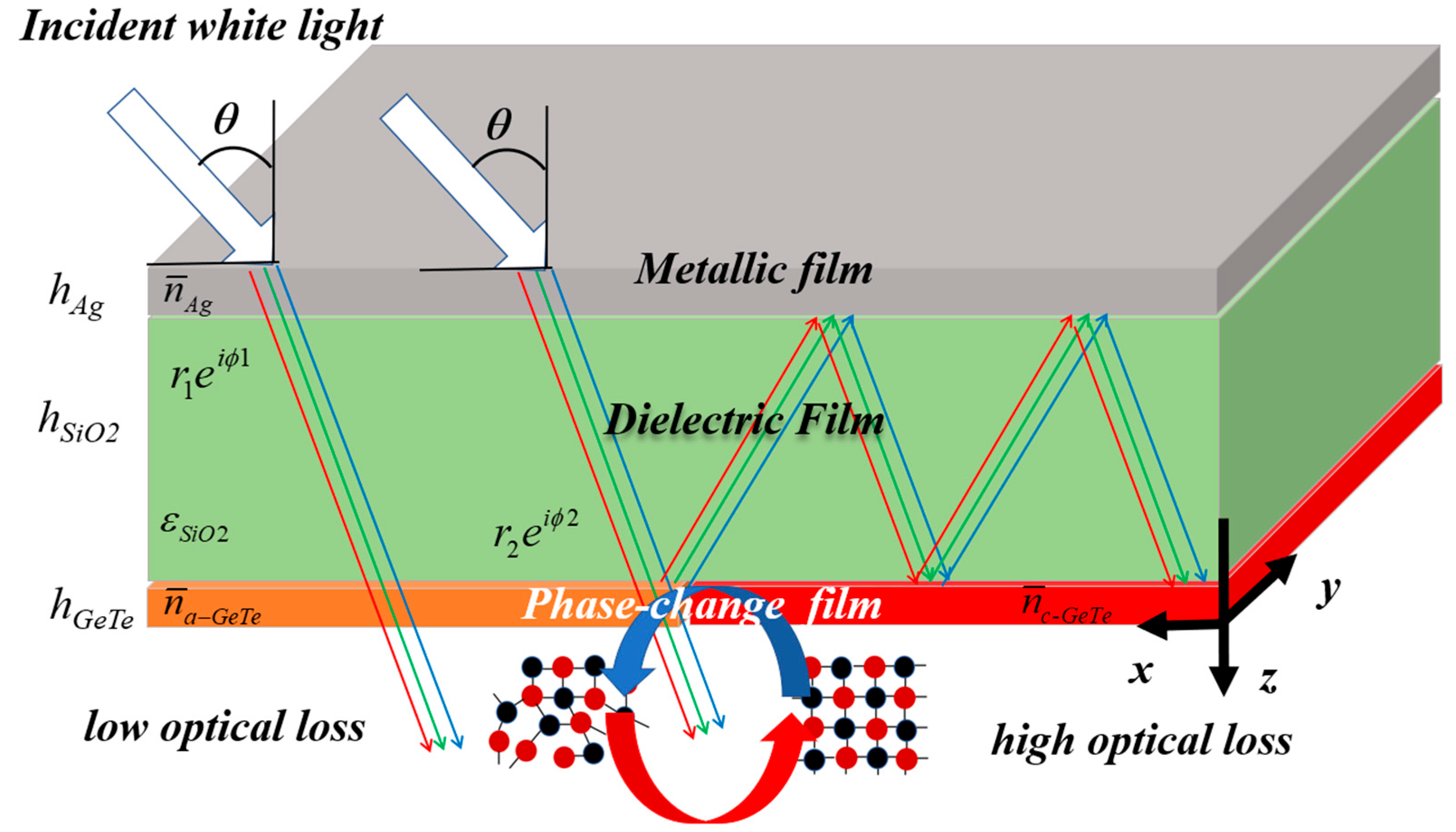
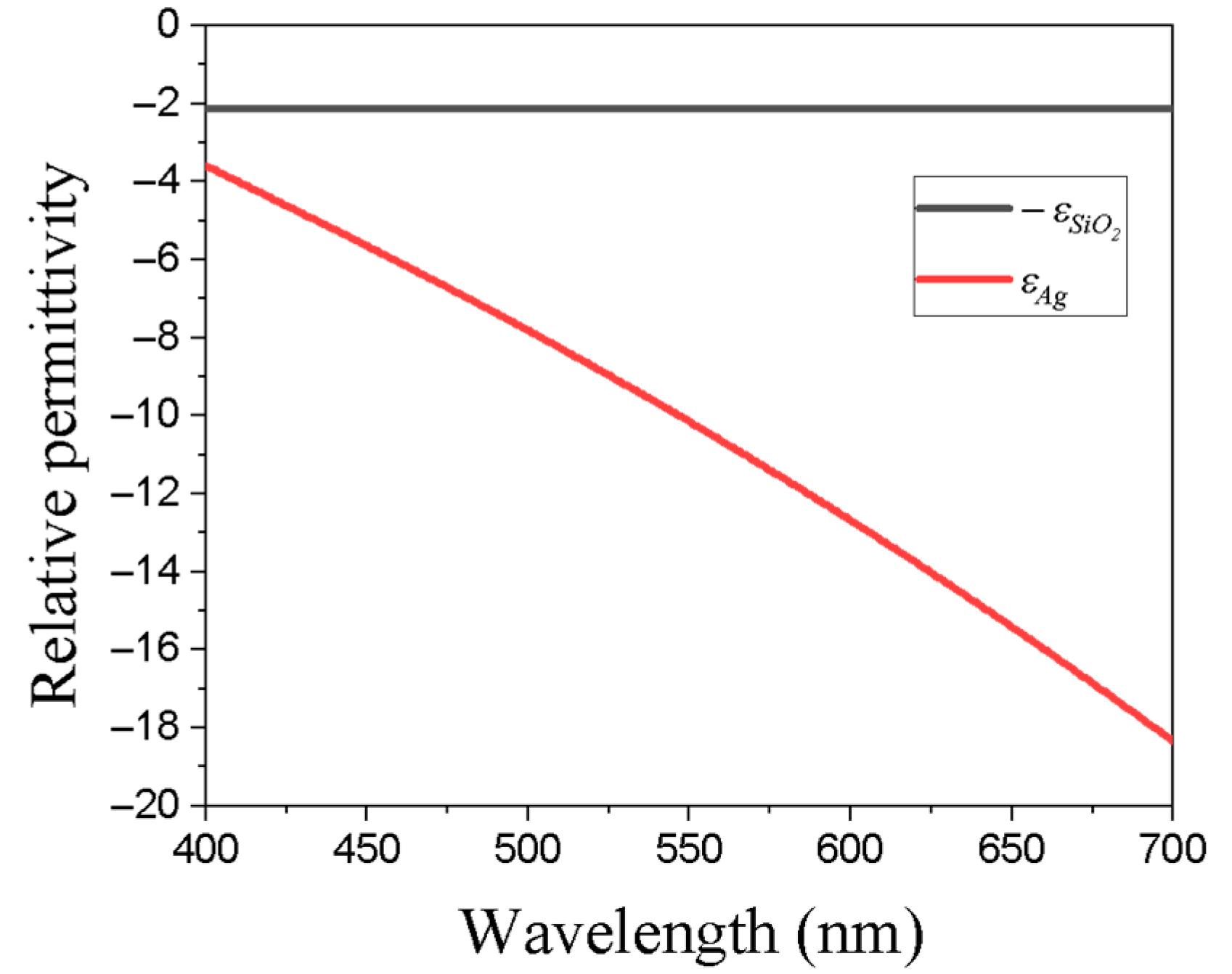
2. Device’s Configuration and Methods
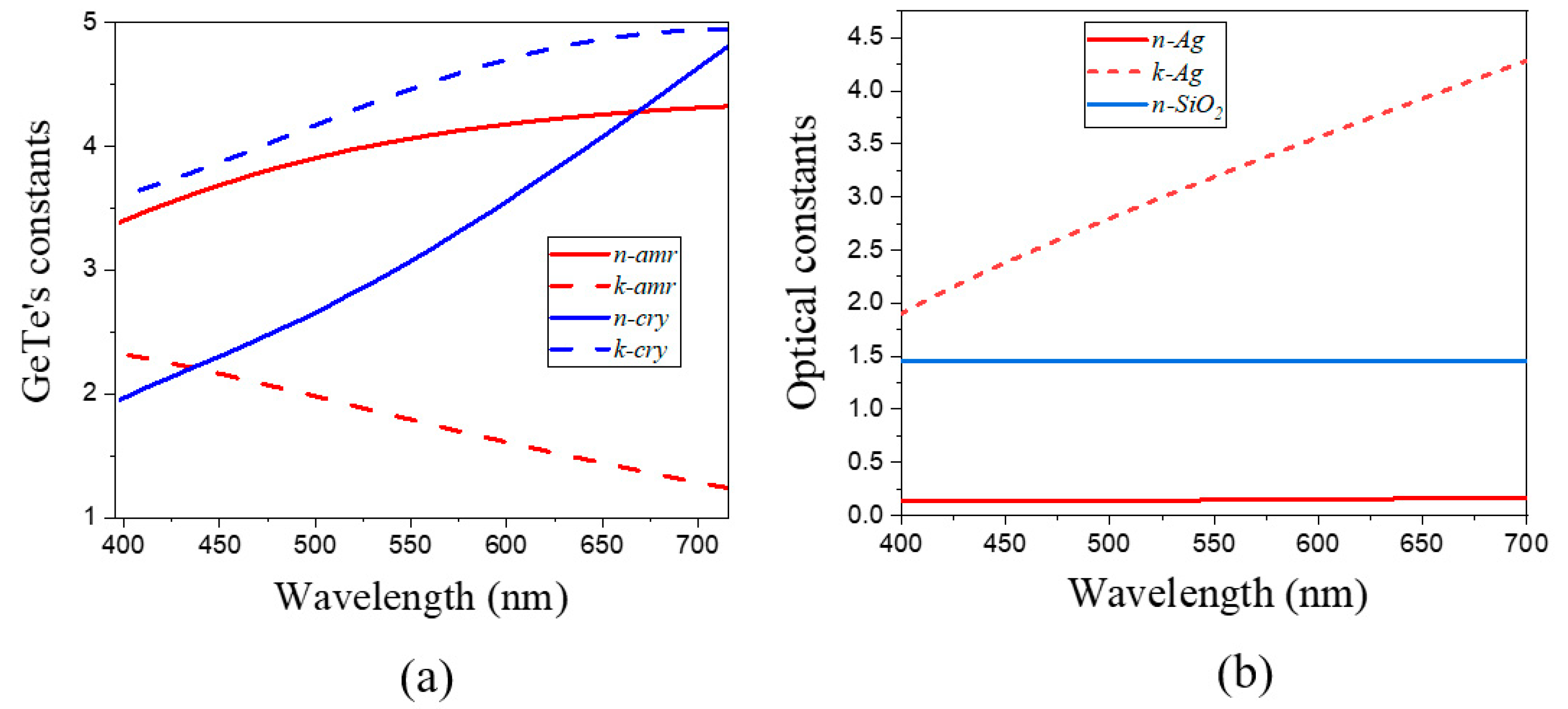
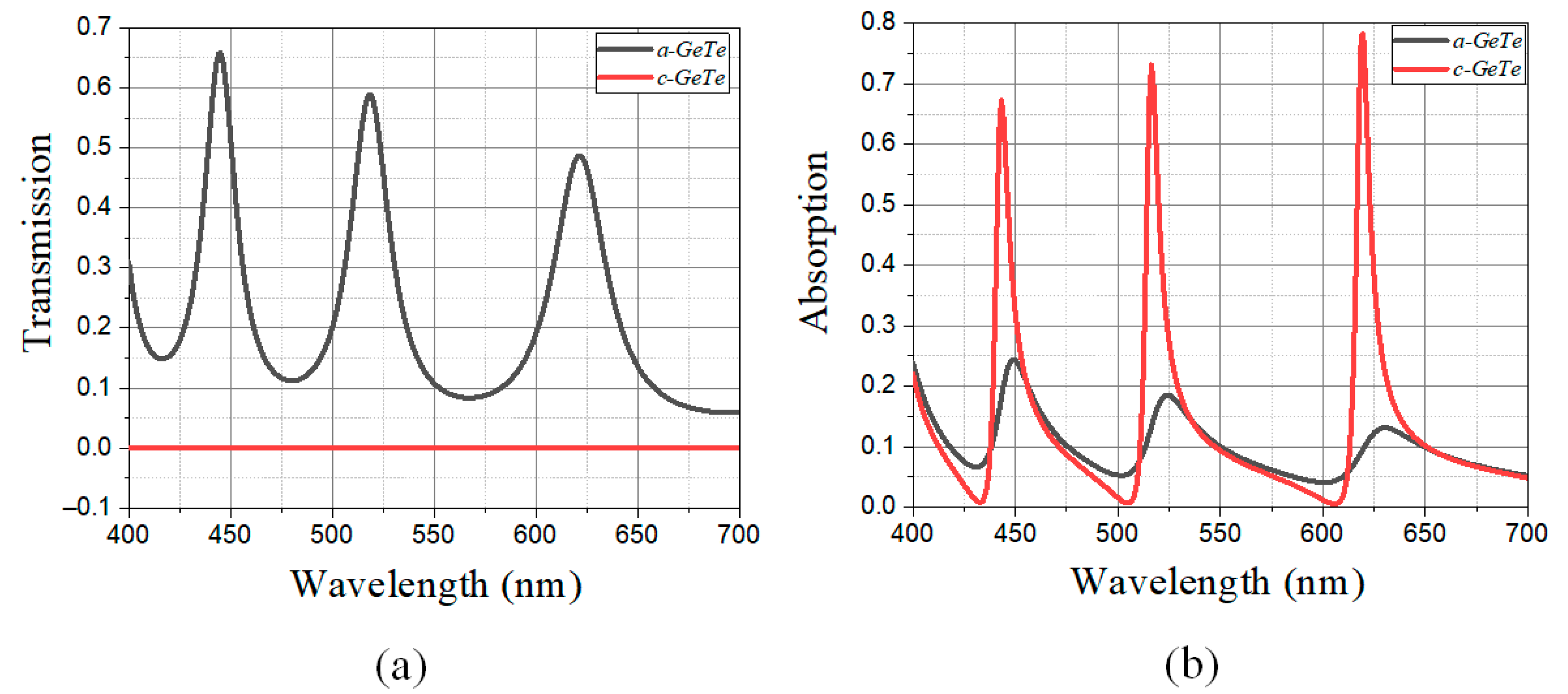
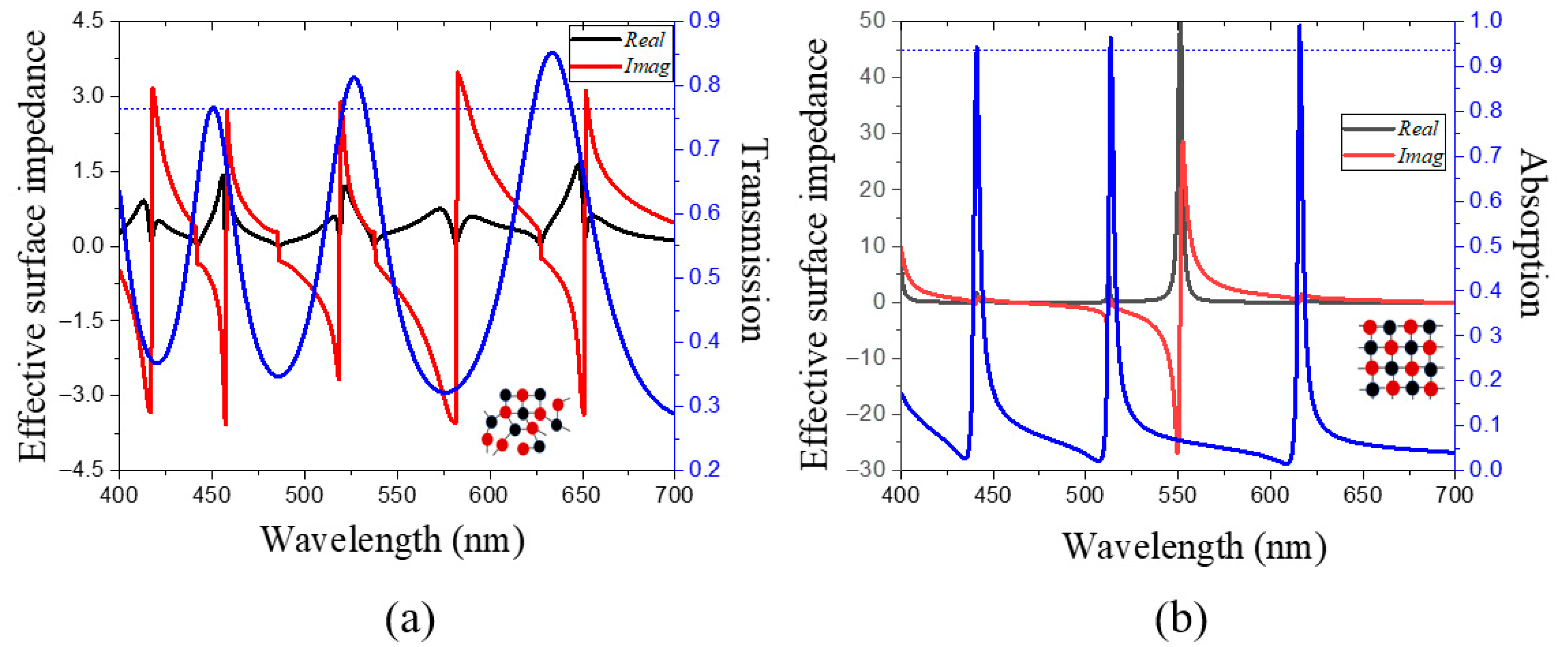
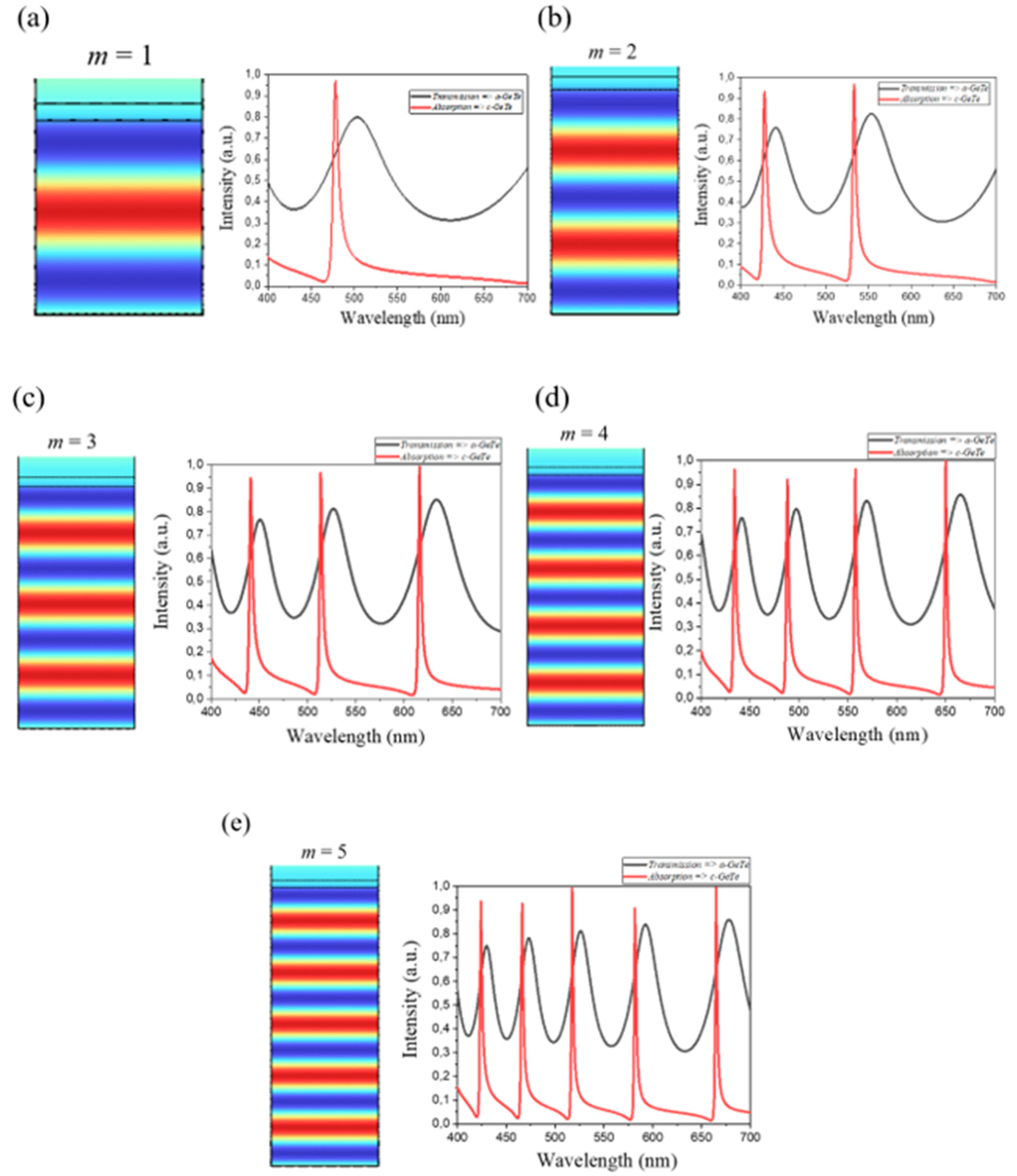
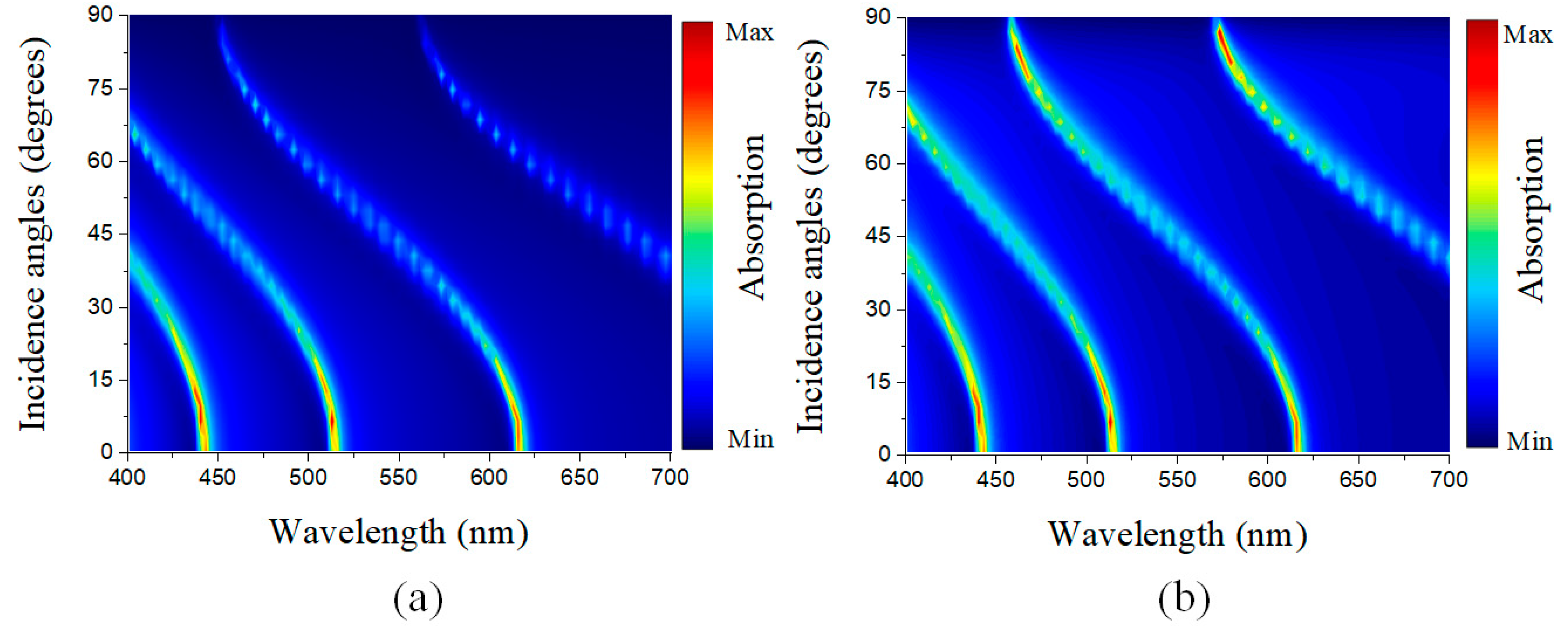
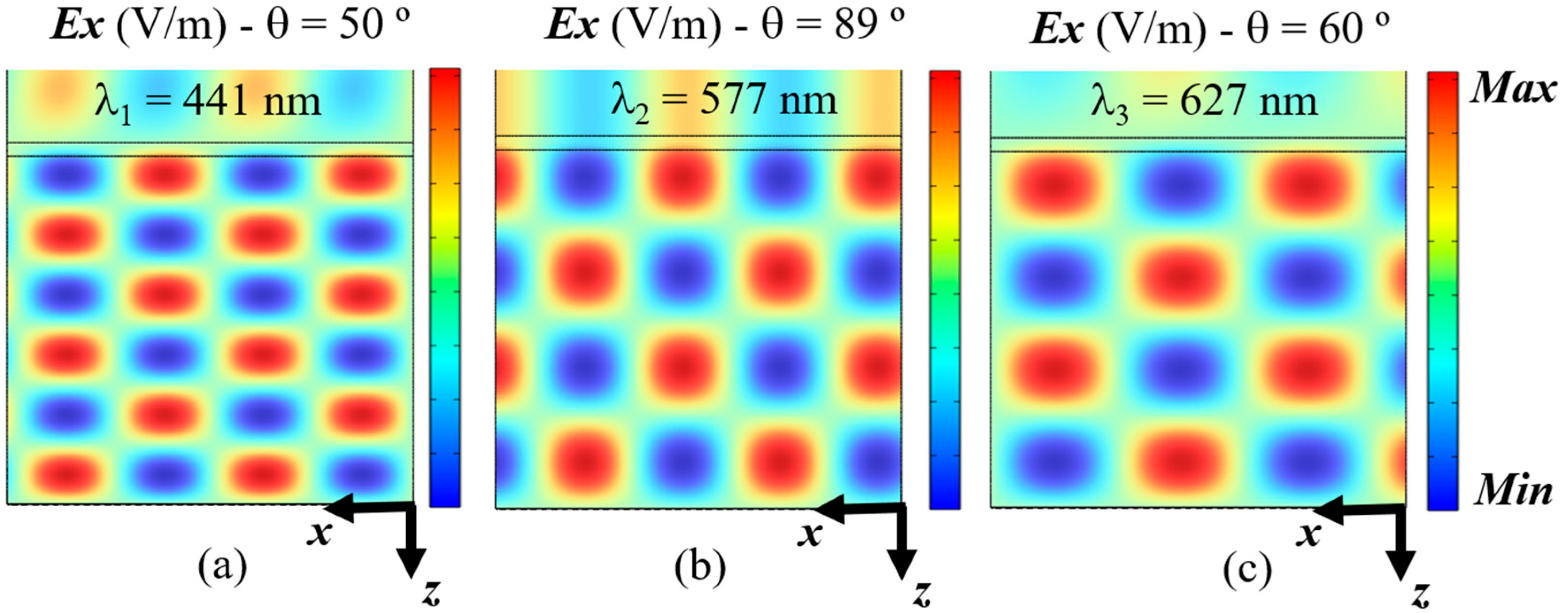
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kwak, H.; Jung, I.; Kim, D.; Ju, S.; Choi, S.; Kang, C.; Kim, H.; Baac, H.W.; Ok, J.G.; Lee, K.-T. Resonant-mode engineering for additive reflective structural colors with high brightness and high color purity. Sci. Rep. 2024, 14, 13694. [Google Scholar] [CrossRef] [PubMed]
- de Souza, I.L.G.; Rodriguez-Esquerre, V.F. Design of planar and wideangle resonant color absorbers for applications in the visible spectrum. Sci. Rep. 2019, 9, 7045. [Google Scholar] [CrossRef] [PubMed]
- ElKabbash, M.; Hoffman, N.; Lininger, A.R.; Jalil, S.A.; Letsou, T.; Hinczewski, M.; Strangi, G.; Guo, C. Fano resonant optical coatings platform for full gamut and high purity structural colors. Nat. Commun. 2023, 14, 3960. [Google Scholar] [CrossRef]
- Lee, K.; Seo, S.; Guo, L.J. High-Color-Purity Subtractive Color Filters with a Wide Viewing Angle Based on Plasmonic Perfect Absorbers. Adv. Opt. Mater. 2015, 3, 347–352. [Google Scholar] [CrossRef]
- de Souza, I.L.G.; Rodriguez-Esquerre, V.F.; Rêgo, D.F. Wide-angle filters based on nanoresonators for the visible spectrum. Appl. Opt. 2018, 57, 6755–6759. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Xiang, X.; Wang, T.; Yang, H.; Wang, X.; Gong, Y.; Gao, J. Tunable Perfect Narrow-Band Absorber Based on a Metal-Dielectric-Metal Structure. Coatings 2019, 9, 393. [Google Scholar] [CrossRef]
- Li, Z.; Butun, S.; Aydin, K. Large-Area, Lithography-Free Super Absorbers and Color Filters at Visible Frequencies Using Ultrathin Metallic Films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- de Souza, I.L.G.; Rodriguez-Esquerre, V.F. Wavelength-Selective Near Unity Absorber Based on Fabry-Pérot Nanoresonators. J. Microw. Optoelectron. Electromagn. Appl. 2021, 20, 219–227. [Google Scholar] [CrossRef]
- Kim, Y.-G.; Quan, Y.-J.; Kim, M.-S.; Cho, Y.; Ahn, S.-H. Lithography-free and Highly Angle Sensitive Structural Coloration Using Fabry–Perot Resonance of Tin. Int. J. Precis. Eng. Manuf. Green Technol. 2021, 8, 997–1006. [Google Scholar] [CrossRef]
- Rahman, A.; Kim, D.K.; Lee, J.-K.; Byun, J.Y. To realize a variety of structural color adjustments via lossy-dielectric-based Fabry–Perot cavity structure. Nanophotonics 2022, 11, 4855–4868. [Google Scholar] [CrossRef]
- Prakash, S.R.; Kumar, R.; Mitra, A. Reconfigurable and spectrally switchable perfect absorber based on a phase-change material. Appl. Opt. 2022, 61, 2888–2897. [Google Scholar] [CrossRef]
- Ghobadi, A.; Hajian, H.; Butun, B.; Ozbay, E. Strong Light–Matter Interaction in Lithography-Free Planar Metamaterial Perfect Absorbers. ACS Photonics 2018, 5, 4203–4221. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, Y.; Chen, Y.; Wang, Y.; Dai, P.; Zhang, Z.; Duan, H. Reflective Color Filters and Monolithic Color Printing Based on Asymmetric Fabry–Perot Cavities Using Nickel as a Broadband Absorber. Adv. Opt. Mater. 2016, 4, 1196–1202. [Google Scholar] [CrossRef]
- Zhan, Y.; Wu, K.; Zhang, C.; Wu, S.; Li, X. Infrared hot-carrier photodetection based on planar perfect absorber. Opt. Lett. 2015, 40, 4261–4264. [Google Scholar] [CrossRef]
- Yang, R.; Dai, C.; Wan, C.; Zheng, G.; Li, Z. Planar ultrathin omni-directional perfect absorber utilizing amorphous silicon for photovoltaics. Opt. Mater. Express 2020, 10, 532–539. [Google Scholar] [CrossRef]
- Mkhitaryan, V.K.; Ghosh, D.S.; Rudé, M.; Canet-Ferrer, J.; Maniyara, R.A.; Gopalan, K.K.; Pruneri, V. Tunable Complete Optical Absorption in Multilayer Structures Including Ge2Sb2Te5 without Lithographic Patterns. Adv. Opt. Mater. 2016, 5, 1600452. [Google Scholar] [CrossRef]
- Wuttig, M.; Bhaskaran, H.; Taubner, T. Phase-change materials for non-volatile photonic applications. Nat. Photonics 2017, 11, 465–476. [Google Scholar] [CrossRef]
- Abdollahramezani, S.; Hemmatyar, O.; Taghinejad, H.; Krasnok, A.; Kiarashinejad, Y.; Zandehshahvar, M.; Alù, A.; Adibi, A. Tunable nanophotonics enabled by chalcogenide phase-change materials. Nanophotonics 2020, 9, 1189–1241. [Google Scholar] [CrossRef]
- Gong, Z.; Yang, F.; Wang, L.; Chen, R.; Wu, J.; Grigoropoulos, C.P.; Yao, J. Phase change materials in photonic devices. J. Appl. Phys. 2021, 129, 030902. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Liu, J. Overview of Phase-Change Materials Based Photonic Devices. IEEE Access 2020, 8, 121211–121245. [Google Scholar] [CrossRef]
- Cao, T.; Cen, M. Fundamentals and Applications of Chalcogenide Phase-Change Material Photonics. Adv. Theory Simul. 2019, 2, 1900094. [Google Scholar] [CrossRef]
- Simpson, R.E.; Yang, J.K.W.; Hu, J. Are phase change materials ideal for programmable photonics?: Opinion. Opt. Mater. Express 2022, 12, 2368–2373. [Google Scholar] [CrossRef]
- Behera, J.K.; Zhou, X.; Tominaga, J.; Simpson, R.E. Laser switching and characterisation of chalcogenides: Systems, measurements, and applicability to photonics. Opt. Mater. Express 2017, 7, 3741–3759. [Google Scholar] [CrossRef]
- Raeis-Hosseini, N.; Rho, J. Metasurfaces based on phase-change material as a reconfigurable platform for multifunctional devices. Materials 2017, 10, 1046. [Google Scholar] [CrossRef] [PubMed]
- Ferrera, M.; Kinsey, N.; Shaltout, A.; DeVault, C.; Shalaev, V.; Boltasseva, A. Dynamic nanophotonics. J. Opt. Soc. Am. B 2017, 34, 95–103. [Google Scholar] [CrossRef]
- Miller, K.J.; Haglund, R.F.; Weiss, S.M. Optical phase change materials in integrated silicon photonic devices. Opt. Mater. Express 2018, 8, 2415–2429. [Google Scholar] [CrossRef]
- Bang, S.; Kim, J.; Yoon, G.; Tanaka, T.; Rho, J. Recent advances in tunable and reconfigurable metamaterials. Micromachines 2018, 9, 560. [Google Scholar] [CrossRef]
- Nemati, A.; Wang, Q.; Hong, M.; Teng, J. Tunable and reconfigurable metasurfaces and metadevices. Opto-Electron. Adv. 2018, 1, 180009. [Google Scholar] [CrossRef]
- Krasnok, A.; Alù, A. Active nanophotonics. Proc. IEEE 2019, 108, 628–654. [Google Scholar] [CrossRef]
- He, Q.; Sun, S.; Zhou, L. Tunable/reconfigurable metasurfaces: Physics and applications. Research 2019, 2019, 1849272. [Google Scholar] [CrossRef]
- Taghinejad, M.; Cai, W. All-optical control of light in micro- and nanophotonics. ACS Photonics 2019, 6, 1082–1093. [Google Scholar] [CrossRef]
- Ding, F.; Yang, Y.; Bozhevolnyi, S.I. Dynamic metasurfaces using phase-change chalcogenides. Adv. Opt. Mater. 2019, 7, 1801709. [Google Scholar] [CrossRef]
- Pérez, D.; Gasulla, I.; Capmany, J. Programmable multifunctional integrated nanophotonics. Nanophotonics 2018, 7, 1351–1371. [Google Scholar] [CrossRef]
- Harris, N.C.; Carolan, J.; Bunandar, D.; Prabhu, M.; Hochberg, M.; Baehr-Jones, T.; Fanto, M.L.; Smith, A.M.; Tison, C.C.; Alsing, P.M.; et al. Linear programmable nanophotonic processors. Optica 2018, 5, 1623–1631. [Google Scholar] [CrossRef]
- Wright, C.D.; Bhaskaran, H.; Pernice, W.H. Integrated phase-change photonic devices and systems. MRS Bull. 2019, 44, 721–727. [Google Scholar] [CrossRef]
- Qiu, Z.; Jin, G.; Tang, B. Thermally Controlled Broadband Ge2Sb2Te5-Based Metamaterial Absorber for Imaging Applications. Photonics 2024, 11, 272. [Google Scholar] [CrossRef]
- Jin, G.; Ren, Y.; Tang, B. Numerical Simulations of Circular Dichroism and Polarization Conversion in VO2-Based Terahertz Metamaterials. Crystals 2023, 13, 437. [Google Scholar] [CrossRef]
- Lin, Z.; Tang, B. A thermochromic material VO2-based metamaterial device for efficient temperature-adaptive radiative cooling. J. Mater. Chem. C 2025, 13, 13255–13261. [Google Scholar] [CrossRef]
- Wang, J.N.; Xiong, B.; Peng, R.W.; Li, C.Y.; Hou, B.Q.; Chen, C.W.; Liu, Y.; Wang, M. Flexible Phase Change Materials for Electrically-Tuned Active Absorbers. Small 2021, 17, 2101282. [Google Scholar] [CrossRef]
- Oliveira, I.A.; de Souza, I.L.G.; Rodriguez-Esquerre, V.F. Design of hybrid narrow-band plasmonic absorber based on chalcogenide phase change material in the infrared spectrum. Sci. Rep. 2021, 11, 21919. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, S.; Jin, K.; He, Y.; Yang, X.; Xu, J. Tunable multiple narrowband polarization stable metamaterial terahertz absorbers based on dirac semi metal and phase change material VO2. Alex. Eng. J. 2025, 116, 104–111. [Google Scholar] [CrossRef]
- Kumar, A.; Varshney, G. Thermally switchable metal-free THz electromagnetic shield using phase change material. Mater. Today Commun. 2024, 38, 108007. [Google Scholar] [CrossRef]
- de Souza, I.L.G.; Rodriguez-Esquerre, V.F.; Oliveira, I.A. Design of Planar Reconfigurable, Tunable, and Wide Angle Resonant Absorbers for Applications in the IR Spectrum. Adv. Theory Simul. 2021, 4, 2100002. [Google Scholar] [CrossRef]
- Du, K.-K.; Li, Q.; Lyu, Y.-B.; Ding, J.-C.; Lu, Y.; Cheng, Z.-Y.; Qiu, M. Control over Emissivity of Zero-Static-Power Thermal Emitters Based on Phase-Changing Material GST. Light Sci. Appl. 2016, 6, e16194. [Google Scholar] [CrossRef] [PubMed]
- Abdollahramezani, S.; Hemmatyar, O.; Taghinejad, M.; Taghinejad, H.; Kiarashinejad, Y.; Zandehshahvar, M.; Fan, T.; Deshmukh, S.; Eftekhar, A.A.; Cai, W.; et al. Dynamic Hybrid Metasurfaces. Nano Lett. 2021, 21, 1238–1245. [Google Scholar] [CrossRef]
- He, J.; Shi, Z.; Ye, S.; Li, M.; Dong, J. Reconfigurable All-Dielectric Metasurface Based on GSST. Results Phys. 2022, 42, 106017. [Google Scholar] [CrossRef]
- De Galarreta, C.R.; Sinev, I.; Alexeev, A.M.; Trofimov, P.; Ladutenko, K.; Carrillo, S.G.-C.; Gemo, E.; Baldycheva, A.; Bertolotti, J.; Wright, C.D. Reconfigurable Multilevel Control of Hybrid All-Dielectric Phase-Change Metasurfaces. Optica 2020, 7, 476. [Google Scholar] [CrossRef]
- Conrads, L.; Bontke, F.; Mathwieser, A.; Buske, P.; Wuttig, M.; Schmitt, R.; Holly, C.; Taubner, T. Infrared beam-shaping on demand via tailored geometric phase metasurfaces employing the plasmonic phase-change material In3SbTe2. Nat. Commun. 2025, 16, 3698. [Google Scholar] [CrossRef]
- Bai, W.; Yang, P.; Huang, J.; Chen, D.; Zhang, J.; Zhang, Z.; Yang, J.; Xu, B. Near-Infrared Tunable Metalens Based on Phase Change Material Ge2Sb2Te5. Sci. Rep. 2019, 9, 5368. [Google Scholar] [CrossRef]
- Tan, J.; Zhao, Z.; Chen, R.; Yu, F.; Chen, J.; Wang, J.; Li, G.; Xing, H.; Chen, X.; Lu, W. Polarization-Controlled Varifocal Metalens with a Phase Change Material GSST in Mid-Infrared. Opt. Express 2022, 30, 32501–32508. [Google Scholar] [CrossRef]
- Oliveira, I.A.; de Souza, I.L.G.; Rodriguez-Esquerre, V.F. Programmable nanophotonic planar resonator filter-absorber based on phase-change InSbTe. Sci. Rep. 2023, 13, 13225. [Google Scholar] [CrossRef] [PubMed]
- Pries, J.; Yu, Y.; Kerres, P.; Häser, M.; Steinberg, S.; Gladisch, F.; Wei, S.; Lucas, P.; Wuttig, M. Approaching the Glass Transition Temperature of GeTe by Crystallizing Ge15Te85. Phys. Status Solidi (RRL)—Rapid Res. Lett. 2020, 15, 2000478. [Google Scholar] [CrossRef]
- Chen, B.; de Wal, D.; Brink, G.H.T.; Palasantzas, G.; Kooi, B.J. Resolving Crystallization Kinetics of GeTe Phase-Change Nanoparticles by Ultrafast Calorimetry. Cryst. Growth Des. 2017, 18, 1041–1046. [Google Scholar] [CrossRef]
- Yarema, O.; Perevedentsev, A.; Ovuka, V.; Baade, P.; Volk, S.; Wood, V.; Yarema, M. Colloidal Phase-Change Materials: Synthesis of Monodisperse GeTe Nanoparticles and Quantification of Their Size-Dependent Crystallization. Chem. Mater. 2018, 30, 6134–6143. [Google Scholar] [CrossRef]
- Polycarpou, A.C. Introduction to the Finite Element Method in Electromagnetics; Springer International Publishing: Cham, Switzerland, 2006. [Google Scholar] [CrossRef]
- COMSOL. Available online: https://www.comsol.com/ (accessed on 23 July 2025).
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef]
- Bahl, S.K.; Chopra, K.L. Amorphous Versus Crystalline GeTe Films. II. Optical Properties. J. Appl. Phys. 1969, 40, 4940–4947. [Google Scholar] [CrossRef]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic Parameter Retrieval from Inhomogeneous Metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef]
- Amiri, M.; Tofigh, F.; Shariati, N.; Lipman, J.; Abolhasan, M. Review on Metamaterial Perfect Absorbers and Their Applications to IoT. IEEE Internet Things J. 2021, 8, 4105–4131. [Google Scholar] [CrossRef]
- Tittl, A.; Harats, M.G.; Walter, R.; Yin, X.; Schäferling, M.; Liu, N.; Rapaport, R.; Giessen, H. Quantitative Angle-Resolved Small-Spot Reflectance Measurements on Plasmonic Perfect Absorbers: Impedance Matching and Disorder Effects. ACS Nano 2014, 8, 10885–10892. [Google Scholar] [CrossRef]
- Zhang, J.-L.; Shen, W.-D.; Gu, P.; Zhang, Y.-G.; Jiang, H.-T.; Liu, X. Omnidirectional narrow bandpass filter based on metal-dielectric thin films. Appl. Opt. 2008, 47, 6285–6290. [Google Scholar] [CrossRef] [PubMed]
- Macleod, H.A. Thin-Film Optical Filters, 5th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Jian, A.; Wu, Y.; Ji, J.; Li, D.; Zhang, Y.; Xue, X.; Sang, S. Low cell concentration detection by Fabry-Pérot resonator with sensitivity enhancement by dielectrophoresis. Sensors Actuators A: Phys. 2021, 331, 112297. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]

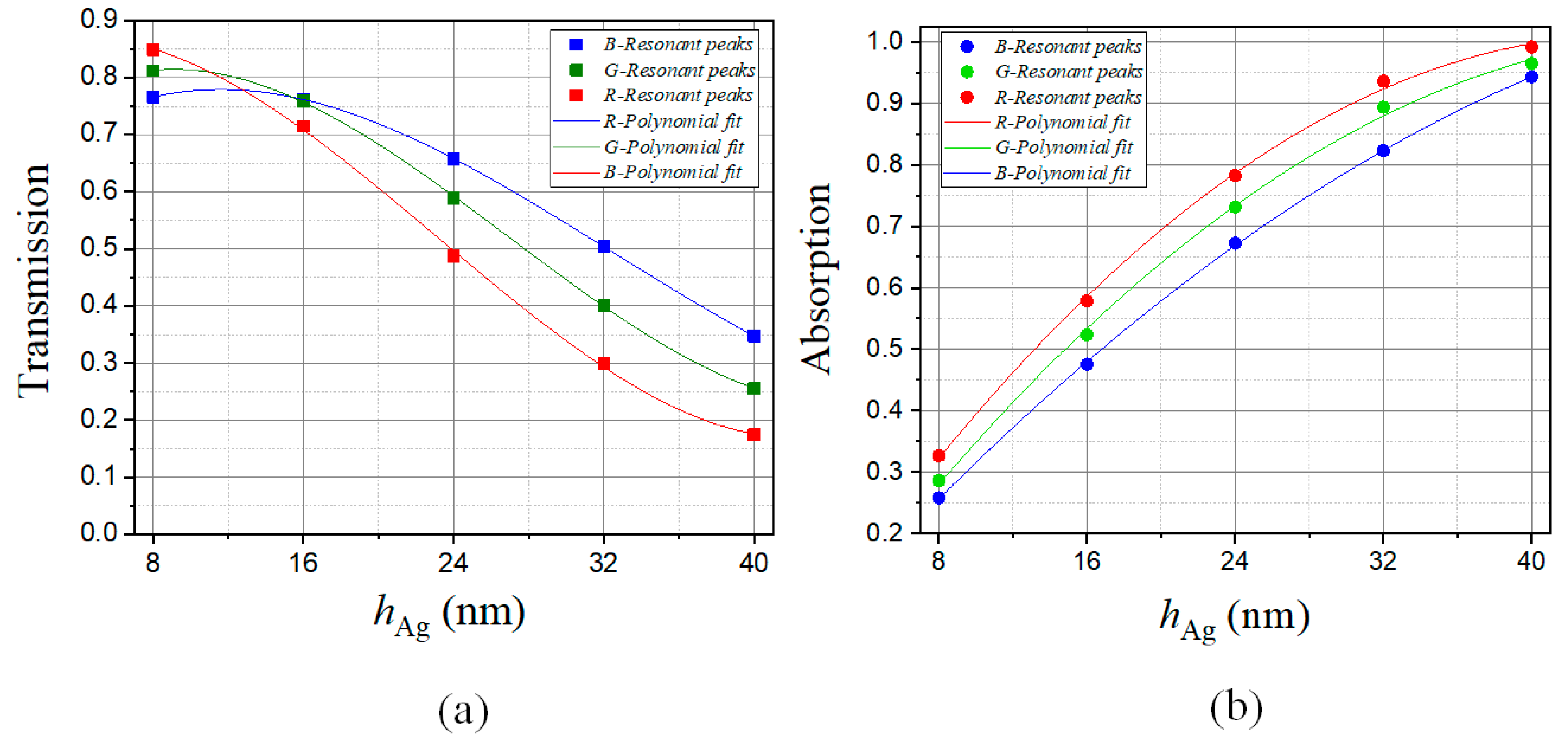

| Amorphous Phase | Polinomial Expression | |
|---|---|---|
| Blue | (3) | |
| Green | (4) | |
| Red | (5) | |
| Crystalline Phase | Polinomial Expression | |
| Blue | (6) | |
| Green | (7) | |
| Red | (8) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, I.A.; Rodriguez-Esquerre, V.F.; Gomes de Souza, I.L. Reconfigurable GeTe’s Planar RGB Resonator Filter–Absorber. Crystals 2025, 15, 789. https://doi.org/10.3390/cryst15090789
Oliveira IA, Rodriguez-Esquerre VF, Gomes de Souza IL. Reconfigurable GeTe’s Planar RGB Resonator Filter–Absorber. Crystals. 2025; 15(9):789. https://doi.org/10.3390/cryst15090789
Chicago/Turabian StyleOliveira, Israel Alves, Vitaly F. Rodriguez-Esquerre, and Igor L. Gomes de Souza. 2025. "Reconfigurable GeTe’s Planar RGB Resonator Filter–Absorber" Crystals 15, no. 9: 789. https://doi.org/10.3390/cryst15090789
APA StyleOliveira, I. A., Rodriguez-Esquerre, V. F., & Gomes de Souza, I. L. (2025). Reconfigurable GeTe’s Planar RGB Resonator Filter–Absorber. Crystals, 15(9), 789. https://doi.org/10.3390/cryst15090789





