Abstract
By analyzing atomic force microscopy images, we studied the spatial distribution of nanoholes etched by InAl droplets in In0.52Al0.48As surfaces, employing molecular beam epitaxy. We identified two temperature regimes, which exhibit significantly different droplet aggregation behavior. The droplet density shows an exponential decrease with increasing temperature in the low-temperature regime (300–390 °C), which is characterized by an activation energy of 0.34 eV, whereas for the high-temperature regime (435–505 °C), the exponential decrease persists but with a much larger activation energy of 2.20 eV. The increased activation energy is accompanied by a strong elongation of the denuded zone around the nanoholes in the distribution of the nearest neighbors along the [011] direction, whereas the distribution is almost isotropic in the low-temperature regime. In both temperature regimes, we observe a narrowing of the capture-zone size distribution with increasing temperature; however, the distribution broadens with the transition to the high-temperature regime before narrowing again with further increasing temperature. By employing nucleation theory, we find that the critical nucleus size does not appear to be significantly different between the two temperature regimes. However, Ostwald ripening is probably relevant, so nucleation theory does not describe our experiments completely. We propose a change in the surface reconstruction, with a more anisotropic arrangement in the high-temperature regime as the underlying reason for the significantly different behavior in the two regimes.
1. Introduction
Semiconductor quantum dots (QDs) are prime candidates for the on-demand generation of single photons and entangled photon pairs, crucial processes for quantum information technologies [1,2]. In particular, local droplet-etched (LDE) QDs in the system have shown very low fine-structure splitting [3] due to the very good circular in-plane symmetry of the electron and hole wave functions, allowing for the generation of photon pairs with a high degree of polarization entanglement [4]. To also achieve this for QDs that emit in the optical C band, one can try to transfer the process of LDE to the system for QD generation. Cao et al. demonstrated LDE QDs in layers [5]. Deutsch and co-workers reported on the fabrication of droplet-etched QDs in layers, lattice-matched to InP, emitting in the optical C band [6,7]. In this paper, we analyze the spatial distribution of nanoholes in layers etched by InAl droplets as in the latter.
The LDE process in molecular beam epitaxy (MBE) can be divided into two parts [8,9]: First, the group-III material is deposited under strongly reduced group-V flux. This results in the formation of metallic droplets on the surface. In the second step, these droplets etch nanometer-sized holes. Consequently, the final arrangement of the holes mirrors the distribution of the droplets before the etching started. The spatial distribution of droplets has already been analyzed by Tuktamyshev et al. [10,11] for Ga droplets on a GaAs(111)A vicinal surface. They employed nucleation theory [12] to evaluate the droplets’ spatial distribution in their experiments. Although initially only intended for sub-monolayer coverage growth of islands, this approach describes their results reasonably well. In this contribution, we discuss a different material system—an on-axis surface, i.e., a system with no intrinsic anisotropy induced by steps—and, for the first time, a droplet that is composed of two different metals (In and Al). Following the approach proposed by Tuktamyshev and co-workers, we compare our results from the analysis of the nanoholes’ spatial distribution to predictions from the theoretical description of island nucleation and growth. Therefore, we discuss the relevant formulas briefly in the following paragraphs.
Standard mean-field nucleation theory [13] predicts that the density (N) of stable 2D islands formed by adatoms diffusing on a structureless substrate varies with temperature and flux as follows:
where F is the atom flux onto the substrate, D the adatom diffusivity, is an activation energy containing the diffusion activation energy and the nucleation energy for a stable cluster, the Boltzmann constant, and T the substrate temperature. Furthermore,
is an exponent containing information about the adatom aggregation process given by the parameter, where i the critical size of the stable nucleus, i.e., the number of atoms that form a stable nucleus. Equation (1) is an analytical solution for the case of sub-monolayer coverage, provided the island size distribution satisfies the scaling law:
where is an ‘unknown’ distribution function that depends on the island size (s), the average island size (), and the critical coverage before island coalescence () [12]. It must be mentioned that, for problems like diffusion and aggregation, scaling analysis, in general, only offers a qualitative description. However, the conceptual understanding gained from scaling is invaluable for interpreting and making sense of computer simulations and experimental results [12].
Mulheran and Blackman [14] have discussed the connection between island size scaling and the size distribution of the adatom capturing zones (CZs), i.e., the region of the surface from which emerging islands capture additional adatoms for their growth, with the assumption that the atoms from the material flux deposited onto the substrate instantly agglomerate to either form an island or diffuse to the nearest island, emptying the region in which every adatom is closer to the central island than to any other one. These CZs are often approximated by a Voronoi tessellation of the surface, a mathematical construct that creates regions in which any point is closer to its nucleus than to any other one on the surface [15,16,17] by connecting the central nuclei to their nearest neighbors and drawing the perpendicular bisectors of each connecting line. These bisectors form a polygon around the central point, defining a Voronoi cell. Mulheran and Blackman also showed that the island size distribution follows the same distribution function as the CZ size distribution, i.e., one can investigate the Voronoi cell size distribution instead of the island size distribution. This is especially advantageous in cases where it is hard to determine the island size, e.g., for 3D islands or, in our case, a situation in which the original droplets vanished and only the resulting holes can be observed. A commonly—but not the only—employed scaling function for the Voronoi cell size distribution in thin-film growth is the generalized Wigner distribution (GWD) [10,11,18,19].
The GWD is given by
with the two -dependent parameters of and , , with s being the area of a Voronoi cell, being the average Voronoi cell area, and
Fitting the GWD and its only parameter () provides insight into the critical nucleus size if is known. As pointed out, for example, by Pimpinelli and co-workers, is related to the adatom aggregation of the islands, e.g., in the case of 2D diffusion and for 1D diffusion [12,19]. These two cases have been observed experimentally for Ga droplets [10,11]. In fact, Pimpinelli and co-workers derived relations between p and i for different situations, e.g., two- and three-dimensional islands, fractal islands, and vicinal surfaces [12]. Later, Pimpinelli introduced the parameter to write the different relations in a compact form (Equation (5)) [19]; however, there is no deeper physical interpretation for the parameter. Earlier, Kandel [20] pointed out that the energy barriers at island edges might also play an important role in the island formation stage, leading to . Furthermore, Pimpinelli states that for restricted adatom diffusion, where is a function of the concentration of blocking impurities [19]. Nevertheless, without any a priori knowledge of the dominant process, information about and i can only be gained via cross-evaluation of two experimentally accessible datasets, e.g., the exponent (p) (Equation (2)) and the fit parameter () of the capture zone distribution (Equation (6)). However, this approach is only valid if the critical coverage for coalescence itself is not a function of the island density (this might be the case for fractal clusters [12], but it is not valid in our material system). Then, one finds
as has been stated by Pimpinelli et al. when analyzing pentacene molecules on sputter-amorphized mica surfaces [19].
In this work, we investigate the spatial distribution of the nanoholes etched in In0.52Al0.38As layers by InAl droplets. We vary the etching temperature and material flux of the etchant and determine the spatial distribution from atomic force microscopy (AFM) images. We perform Voronoi tessellation of the images and determine the distribution function for the sizes of the Voronoi cells. In addition, we determine the density of the nanoholes as a function of temperature for a fixed flux, as well as for a varying fluxes at two selected temperatures. The analysis also includes a determination of the nanoholes’ nearest-neighbor distribution.
2. Materials and Methods
All samples were grown on semi-insulating InP(100) substrates from AXT (on-axis orientation better than 0.5° according to the manufacturer) in a standard solid-source MBE system, an Octoplus 500 from Dr. Eberl MBE-Komponenten GmbH, equipped with standard effusion cells for group-III elements and a valved cracker source for As. We do not believe that the small, unintentional miscut of the wafers plays any role in experimental observations because all anisotropies we observe are along a specific crystal direction. This seems very improbably induced by an unintentional miscut over several wafer batches.
The substrates were first heated to 540 °C for deoxidation—10 min under an environment. Afterwards, the substrate temperature was lowered to 505 °C, and a 100 nm In0.52Al0.48As layer was grown at an flux of mbar, measured ∼40 mm above the wafer surface by a standard Bayard–Alpert ionization gauge. In the next step, the substrate temperature was lowered to the value at which droplet etching was performed (300–505 °C), and the flux was reduced to mbar. Then, the group-III shutters were opened briefly to deposit ∼1.4 ML InAl. This was followed by an etching step of 3 min, nd following that, the flux was increased back to mbar. Afterwards, the substrate temperature was increased again to 505 °C. At last, after waiting one minute for stabilization (usually, the holes are filled after this step), the sample was cooled down again and removed from the system. The ramp back to 505 °C is only included to exactly match our recipes for the full structure with QDs emitting at 1550 nm [6]. The temperatures given throughout this paper were determined by band-edge thermometry using a BandiT system from ksA. More details on the fabrication process of the nanoholes can be found in [6,7].
The droplet-etched holes were investigated by AFM, employing a Bruker Icon Dimension XR SPM. The center coordinates of the individual holes were determined from the AFM images, employing the open-source software Gwyddion [21]. Based on these coordinates, the density of the holes, the direction in which the nearest neighbor occurs, the Voronoi tessellation, and all consecutive calculations were carried out by employing Python code. We scanned regions of different sizes, depending on the hole density, with a resolution of 2048 × 2048 pixels and a scan time of 2 s per line (∼80 min per image). For each density, we analyzed multiple images to obtain significant statistical relevance. The exact details can be found in Table 1.

Table 1.
Key parameters of the AFM images forming the basis for the analysis of the spatial distribution of the nanoholes.
3. Results and Discussion
First, we analyzed the hole density as a function of the etching temperature for a constant InAl flux of 0.7 ML/s in an Arrhenius-like manner. As can be seen in Figure 1, we observe two regimes in which the exponential dependence from Equation (1) can be fitted quite well by a linear regression on the logarithmic density values, albeit with two significantly different slopes. This corresponds to different activation energies for the two temperature ranges: from 300 °C up to ca. 390 °C, an activation energy of eV is found, whereas for the high-temperature regime (ca. 435 °C to 505 °C), the temperature dependence is much stronger with eV. This change in activation energy is a clear indication that the mechanism of droplet aggregation is different in these two temperature regimes.
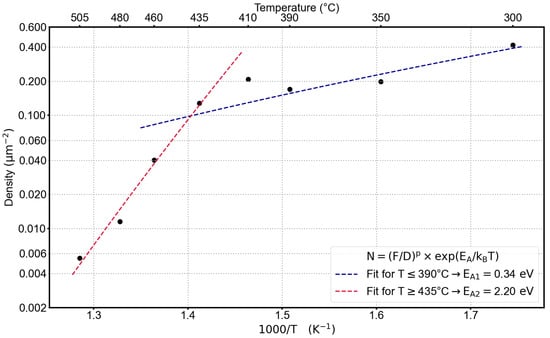
Figure 1.
Temperature-dependent change of the average hole density determined from AFM images. The InAl flux was constant for all samples at 0.7 ML/s.
When analyzing the AFM images, we did not observe any evidence for different droplet types over the entire temperature range that we investigated, i.e., no indication of a separation into pure In and Al droplets. Different droplet types would manifest themselves in different types of nanoholes, e.g., with different depths and diameters, as shown in [7]. Therefore, we assume that the ones in our experiments are InAl droplets with the same composition as the flux ratio (52% In content) but cannot exclude slight variations of the droplet composition. Of course, In and Al atoms will show different surface diffusion and binding energies in a few-atom island, i.e., the critical nucleus size depends on the exact composition. Therefore, one has to interpret results of comparisons with nucleation theory with some precaution because the theory takes only one material type into account. The results, e.g., the activation energies or the critical nucleus size, can be interpreted as an average value.
To get more insight into the aggregation process, we analyzed the CZ distribution of the InAl droplets by applying Voronoi tessellations to our AFM images as discussed in Section 1. We determined the parameter for all AFM images by fitting the GWD (Equation (4)) to the Voronoi cell size distribution. An exemplary Voronoi tessellation superimposed on the AFM image of the sample with an etching temperature of 350 °C is shown in Figure 2a. In Figure 2b, the corresponding distribution of Voronoi cell sizes and the best fit using the GWD function from Equation (5) are shown.
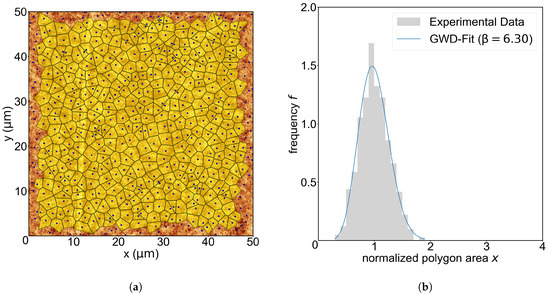
Figure 2.
(a) Application of the Voronoi tessellation to a AFM image for an etching temperature of 350 °C. The Voronoi polygons are colored yellow, and the corresponding nanoholes are depicted with a blue spot. Note that the outermost holes are rejected due to their incomplete or infinitely large Voronoi polygons at the edges. (b) Distribution of the normalized Voronoi cell size. The y-axis is the frequency, i.e., , with being the number of polygons with a size of per bin and a width of , and is the total number of valid Voronoi cells (yellow polygons). The blue curve is a fit of the GWD (Equation (5)) to the value of f at the bin centers.
From the set of parameters at a given etching temperature, we calculate the average value and its standard error. The values and their error as function of temperature are shown in Figure 3. As seen before, differences between the two temperature regions can be observed, as shown in Figure 1. The value of monotonically increases in the low-temperature region from ∼5 at 300 °C to ∼7 at 390 °C. For a substrate temperature of 410 °C, drops to a value of ∼4, then starts to monotonically increase again in the high-temperature region to a value of ∼9 at 505 °C. An increasing value of corresponds to a narrowing of the Voronoi cell size distribution. A narrowing distribution with increasing temperature seems to be reasonable because the adatom diffusion length generally increases with increasing temperature and Ostwald ripening becomes more relevant with increasing temperature [22]. However, we do not observe a monotonic increase over the whole temperature range, as expected from such a ripening process; instead, two temperature regions monotonically increase, with a rather abrupt drop to a lower -value around 410 °C. The temperature at which the sudden drop in appears corresponds to the temperature at which the activation energy () changes (see Figure 1).
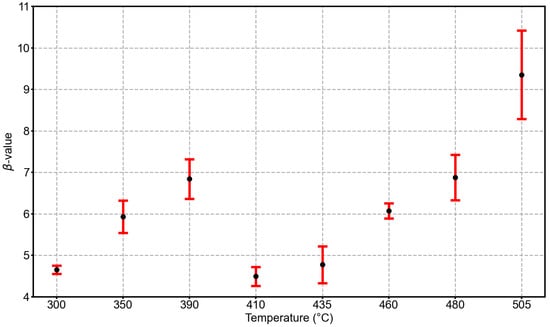
Figure 3.
Average parameter from the GWD fits to the Voronoi cell size distributions as a function of the etching temperature. The error bars represent the standard error of the mean at the given temperature.
Neither the hole density nor the size distribution of the CZs contains any directional information. To elaborate on this, we investigated both the distribution of the nearest nanoholes and the average shape of the Voronoi cells. For the nearest-neighbor distribution, we repositioned each hole in an AFM image to the origin () and mapped the relative coordinates of all other holes as in [10,11]. Then, we aggregated the data from all AFM images at a given temperature and displayed them in a 2D histogram so that each pixel represents the number of holes at these coordinates. Basically, those 2D histograms visualize the spatial distribution of the frequency of nearest-neighbor occurrences. Figure 4 displays the resulting exemplary histograms for etching temperatures of (a) 350 °C (low-temperature regime, ∼0.2 holes/μm2) and (b) 480 °C (high-temperature regime, ∼0.02 holes/μm2).
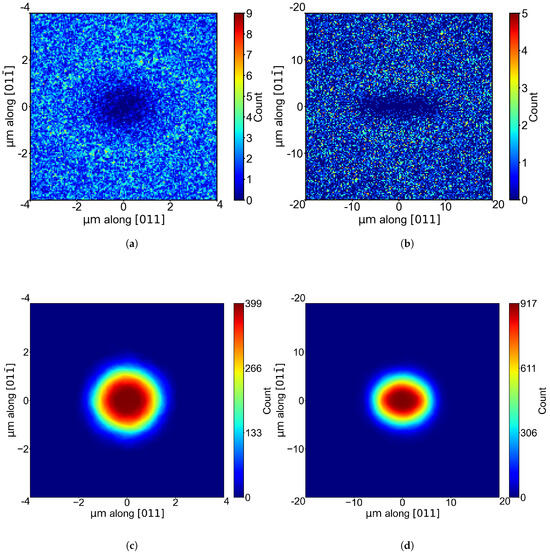
Figure 4.
A 2D histogram of the nearest nanohole neighbor in the AFM images at substrate temperatures of (a) 350 °C and (b) 480 °C with pixel sizes of and , respectively. (c,d) The average shape of the corresponding Voronoi polygons in the same AFM images.
As expected, the zone without nearest neighbors is significantly larger for the experiment at the higher temperature due to the much lower density. Notably, we observe a pronounced elongation of the denuded zone along the [011] direction for 480 °C, whereas the denuded zone is nearly circular in shape at 350 °C. The 2D histograms for the other temperatures show the same tendency: We observe a nearly isotropic denuded zone in the low-temperature regime below 410 °C, whereas the denuded zone in the high-temperature regime above 410 °C is strongly anisotropic, with an elongation along [011]. Please note that these temperature regimes also agree with the two ranges for which we find the two different activation energies (see Figure 1). To support our findings, we also investigated the average shape of the Voronoi cells by shifting all holes with their corresponding Voronoi cell to the center of the image. The number of Voronoi cells overlapping on a pixel is color-coded. In Figure 4c,d, the 2D histograms for 350 °C and 480 °C are shown. The same behavior regarding the elongation along [011] as in the nearest-neighbor distribution is observed. The elongation at high temperatures is not as pronounced, but this is expected because many Voronoi cells with different shapes are superimposed. Interestingly, an elongation along [011] is also observed in the shape of the individual holes for the high-temperature region [6,7]. However, this does not necessarily have to be caused by elliptically shaped droplets or the adatom agglomeration process but may be due to an anisotropy in the etching process.
Our observations clearly point towards a change in the adatom agglomeration process when going from the low-temperature to the high-temperature regime. According to nucleation theory, this should be reflected in the parameter (see Equations (2) and (5)). To also exploit Equation (2) for the determination of , we performed flux-dependent depositions at 350 °C (low-temperature regime) and 460 °C (high-temperature regime). In Figure 5, a double-logarithmic plot of the hole density as a function of the InAl flux is shown. The power-law behavior predicted by Equation (2) is evident, and by fitting the experimental data, we obtain a value for the exponent (p) at the two deposition temperatures. With the corresponding values determined earlier (Figure 3), we can now determine and i by calculating i according to Equation (6) and solving Equation (2) or (5) for . Our results for , p, and the corresponding values for i and are summarized in Table 2.
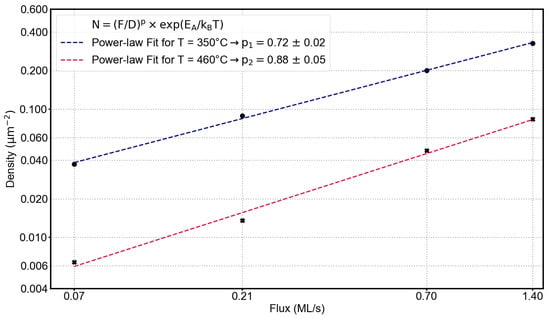
Figure 5.
Flux-dependent change of the hole density at 350 °C and 460 °C. The flux was varied from 1.4 ML/s over 0.7 ML/s and 0.21 ML/s to 0.07 ML/s.

The parameter changes from ∼0.93 at 350 °C to ∼0.73 at 460 °C, while the critical size of the nucleus does not appear to change significantly. It seems that the transition between the low-temperature and high-temperature regime does not coincide with a significant change in the critical nucleus size. The interpretation of is not straightforward: For dominating 2D diffusion, should be 1, whereas it should be 2 for 1D diffusion. However, we observe values smaller than 1, which indicates that the processes of attachment to the islands play a role [19,20]. We do not want to overstretch the interpretation of because we think that Ostwald ripening plays a role in our experiments, which is not included in the aforementioned nucleation theories from which emerged. They are strictly applicable only under specific conditions, e.g., instantaneous nucleation and low coverage. For all the equations given in Section 1, ripening is not included. However, Brune [22] states that Ostwald ripening might be relevant for metal clusters if . He also points out that Ostwald ripening results in a narrower island size distribution with increasing temperature, as mentioned earlier when discussing the changes in the parameter. We find , and we also clearly observe a narrowing of the Voronoi cell size distribution. This indicates that Ostwald ripening might, in fact, play a role in our experiments. However, if such ripening is the only important factor, we would not observe the different adatom aggregation behaviors in the two temperature regimes, i.e., the significantly different activation energies, the drop in the values around the transition temperature between the low- and high-temperature regimes, and the change in the denuded zone’s shape around the holes. For textbook Ostwald ripening, we would expect a monotonic temperature dependence. Therefore, a second effect must play a role. We speculate that this might be a change in the surface reconstruction around the transition temperature of 410 °C between the low- and high-temperature regimes. We propose that in the high-temperature regime, the reconstruction is more anisotropic. Although we could not verify this experimentally due to the lack of a suitable RHEED system in our MBE, the proposal seems to be reasonable. For example, Kim [23] investigated the formation of Ga droplets on GaAs surfaces and pointed out that the reconstruction of the surface will, in general, change from an As-rich to a Ga-rich surface reconstruction in the first phase of the deposition in the droplet formation stage. So, the metal-rich surface reconstruction is relevant for the droplet formation process. Stevens and co-workers [24] also found a change in the In diffusion behavior that coincides with a change in the surface reconstruction when investigating the crystallization behavior of In droplets on In0.53Ga0.47As, a material system that is very similar to ours, which could therefore exhibit a similar surface reconstruction. They also discussed the variation of activation energies for different material systems, for different temperature ranges, and for different experimental methods. This supports our idea that a change in the surface reconstruction is responsible for the two different adatom agglomeration behaviors in low- and high-temperature droplet formation.
4. Conclusions
We performed a comprehensive statistical analysis of the spatial distribution of nanoholes etched by InAl droplets in In0.52Al0.48As as a function of temperature and material flux. The investigation clearly identifies two distinct temperature regimes with significantly different adatom aggregation behavior. In the low-temperature regime (300 °C to 390 °C), the exponential decrease in the nanohole density with temperature is characterized by an activation energy of 0.34 eV. In contrast, in the high-temperature regime (435 °C to 505 °C), a much larger activation energy of 2.20 eV is found. This transition is accompanied by a strong change in the spatial arrangement of the nanoholes. While the nearest-neighbor distribution is almost isotropic at low temperatures, it shows a pronounced elongation along the [011] direction in the high-temperature regime. Analysis of the Voronoi cell size distributions revealed that within both regimes, the distribution narrows with increasing temperature, as indicated by an increasing parameter. However, a distinct drop in the value, i.e., a broadening of the size distribution, marks the transition to the high-temperature regime around ∼410 °C. By employing nucleation theory and analyzing flux-dependent data, we determined that the critical nucleus size is approximately 4 and does not appear to change significantly between the two regimes. The observed narrowing of the size distributions and the large critical nucleus size suggest that Ostwald ripening is a relevant process in our experiments. However, Ostwald ripening alone cannot account for the abrupt shift in the activation energy and the onset of anisotropy in the agglomeration process. We propose that the reason for the two distinct behaviors in the two temperature regimes is a change in the surface reconstruction, which becomes more anisotropic for the high-temperature regime. These findings offer crucial insight into the self-assembly mechanisms of droplets, which is essential to unlock their potential for next-generation quantum information systems. Further experiments could investigate the spatial distribution of nanoholes in In0.52Al0.48As etched by pure In droplets or pure Al droplets for comparison.
Author Contributions
Conceptualization, N.A. and D.R.; Data curation, N.A.; Formal analysis, N.A. and D.R.; Funding acquisition, D.R.; Investigation, N.A.; Methodology, N.A. and D.R.; Project administration, D.R.; Resources, D.D. and D.R.; Software, N.A.; Supervision, D.R.; Validation, N.A. and D.R.; Visualization, N.A.; Writing—original draft, N.A.; Writing—review and editing, D.R. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—SFB-Geschäftszeichen TRR142/3-2022—Projektnummer 231447078.
Data Availability Statement
The data supporting this study’s findings are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors have no conflicts to disclose.
Abbreviations
The following abbreviations are used in this manuscript:
| QD | Quantum Dot |
| LDE | Local Droplet-Etched |
| MBE | Molecular Beam Epitaxy |
| AFM | Atomic Force Microscopy |
| CZ | Capture Zone |
| GWD | Generalized Wigner Distribution |
References
- Michler, P. Single Semiconductor Quantum Dots; NanoScience and Technology; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Michler, P.; Portalupi, S. Semiconductor Quantum Light Sources: Fundamentals, Technologies and Devices; De Gruyter Textbook; De Gruyter: Berlin, Germany, 2024. [Google Scholar]
- Zhai, L.; Löbl, M.C.; Nguyen, G.N.; Ritzmann, C.T.; Javadi, A.; Wieck, A.D.; Ludwig, A.; Warburton, R.J. Low-noise GaAs quantum dots for quantum photonics. Nat. Commun. 2020, 11, 4745. [Google Scholar] [CrossRef]
- Schimpf, C.; Reindl, M.; Basso Basset, F.; Jöns, K.D.; Trotta, R.; Rastelli, A. Quantum dots as potential sources of strongly entangled photons: Perspectives and challenges for applications in quantum networks. Appl. Phys. Lett. 2021, 118, 100502. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, Y.; Ma, C.; Wang, Y.; Brechtken, B.; Haug, R.J.; Rugeramigabo, E.P.; Zopf, M.; Ding, F. Local droplet etching on InAlAs/InP surfaces with InAl droplets. AIP Adv. 2022, 12, 055302. [Google Scholar] [CrossRef]
- Deutsch, D.; Buchholz, C.; Zolatanosha, V.; Jöns, K.D.; Reuter, D. Telecom C-band photon emission from (In,Ga)As quantum dots generated by filling nanoholes in In0.52Al0.48As layers. AIP Adv. 2023, 13, 055009. [Google Scholar] [CrossRef]
- Deutsch, D.; Zolatanosha, V.; Reuter, D. Local droplet etching with In, Al and InAl in In0.52Al0.48As layers for generation of quantum dots emitting in the optical C-band. J. Cryst. Growth 2025, 668, 128247. [Google Scholar] [CrossRef]
- Stemmann, A.; Heyn, C.; Köppen, T.; Kipp, T.; Hansen, W. Local droplet etching of nanoholes and rings on GaAs and AlGaAs surfaces. Appl. Phys. Lett. 2008, 93, 123108. [Google Scholar] [CrossRef]
- Heyn, C.; Sonnenberg, D.; Hansen, W. Local Droplet Etching: Self-assembled Nanoholes for Quantum Dots and Nanopillars. In Nanodroplets; Springer: New York, NY, USA, 2013; pp. 363–384. [Google Scholar] [CrossRef]
- Tuktamyshev, A.; Fedorov, A.; Bietti, S.; Semenov, A.V.; Chaldyshev, V.V.; Sanguinetti, S. Temperature Activated Dimensionality Crossover in the Nucleation of Quantum Dots by Droplet Epitaxy on GaAs(111)A Vicinal Substrates. Sci. Rep. 2019, 9, 14520. [Google Scholar] [CrossRef] [PubMed]
- Tuktamyshev, A.; Fedorov, A.; Bietti, S.; Chaldyshev, V.V.; Sanguinetti, S. Nucleation of Ga droplets self-assembly on GaAs(111)A substrates. Sci. Rep. 2021, 11, 6833. [Google Scholar] [CrossRef] [PubMed]
- Pimpinelli, A.; Villain, J.; Wolf, D.E. Scaling and Crossovers in Models for Thin Film Growth. In Morphological Organization in Epitaxial Growth and Removal; Zheng, Z., Lagally, M.G., Eds.; Series on Directions in Condensed Matter Physics; World Scientific: Singapore, 1998; Volume 14, pp. 121–148. [Google Scholar]
- Venables, J.A.; Spiller, G.D.T.; Hanbücken, M. Nucleation and growth of thin films. Rep. Prog. Phys. 1984, 47, 399–459. [Google Scholar] [CrossRef]
- Mulheran, P.A.; Blackman, J.A. The origins of island size scaling in heterogeneous film growth. Philos. Mag. Lett. 1995, 72, 55–60. [Google Scholar] [CrossRef]
- Voronoï, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites. J. Für Die Reine Und Angew. Math. 1908, 133, 97–178. [Google Scholar] [CrossRef]
- Kiang, T. Random fragmentation in two and three dimensions. Z. Für Astrophys. 1966, 64, 433. [Google Scholar]
- Mulheran, P. On the statistical properties of the two-dimensional random Voronoi network. Philos. Mag. Lett. 1992, 66, 219–224. [Google Scholar] [CrossRef]
- Pimpinelli, A.; Einstein, T.L. Capture-Zone Scaling in Island Nucleation: Universal Fluctuation Behavior. Phys. Rev. Lett. 2007, 99, 226102. [Google Scholar] [CrossRef] [PubMed]
- Pimpinelli, A.; Tumbek, L.; Winkler, A. Scaling and Exponent Equalities in Island Nucleation: Novel Results and Application to Organic Films. J. Phys. Chem. Lett. 2014, 5, 995–998. [Google Scholar] [CrossRef] [PubMed]
- Kandel, D. Initial Stages of Thin Film Growth in the Presence of Island-Edge Barriers. Phys. Rev. Lett. 1997, 78, 499–502. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Brune, H. Growth of Metal Clusters at Surfaces. In Metal Clusters at Surfaces: Structure, Quantum Properties, Physical Chemistry; Springer: Berlin/Heidelberg, Germany, 2000; pp. 67–105. [Google Scholar] [CrossRef]
- Kim, J.S. Ga-migration on a Ga-rich and As-stabilized surfaces: Ga-droplet and GaAs- nanostructure formation. Mater. Sci. Semicond. Process. 2017, 57, 70–76. [Google Scholar] [CrossRef]
- Stevens, M.A.; Tomasulo, S.; Maximenko, S.; Vandervelde, T.E.; Yakes, M.K. Surface diffusion measurements of In on InGaAs enabled by droplet epitaxy. J. Appl. Phys. 2017, 121, 195302. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).