Coarse-Graining and Classifying Massive High-Throughput XFEL Datasets of Crystallization in Supercooled Water
Abstract
1. Introduction
2. Approach
2.1. Experimental Background
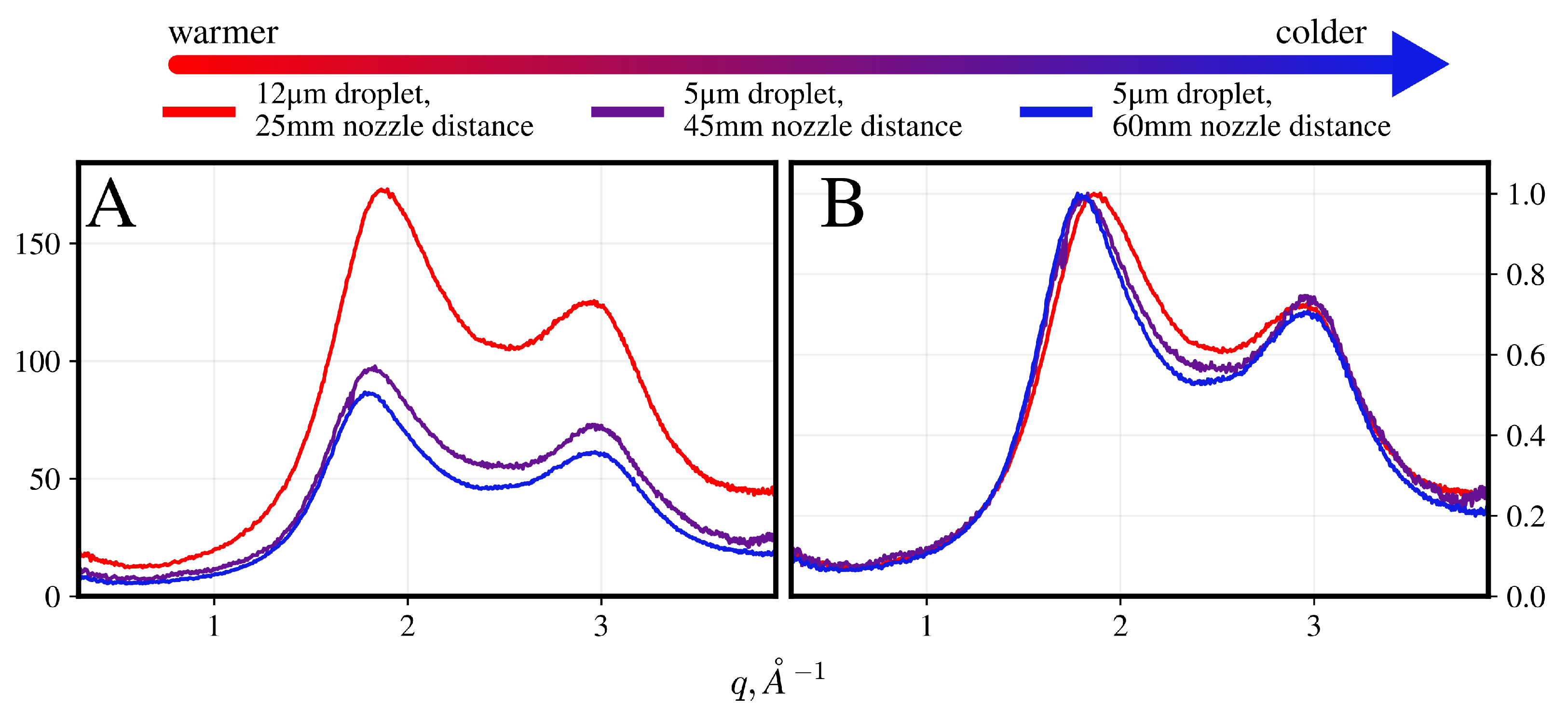
2.2. Data Description and Processing
2.3. Considerations for Classification
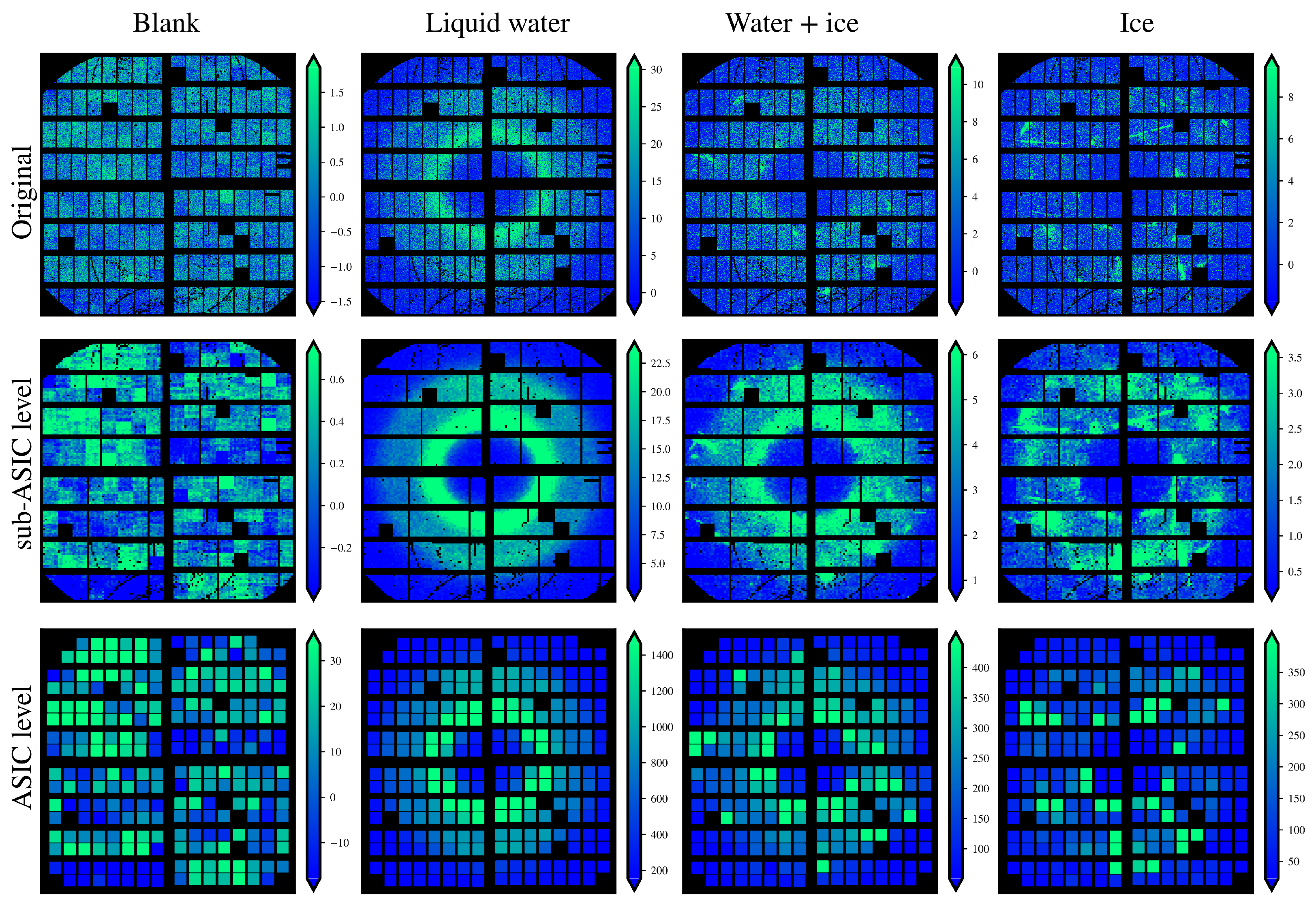
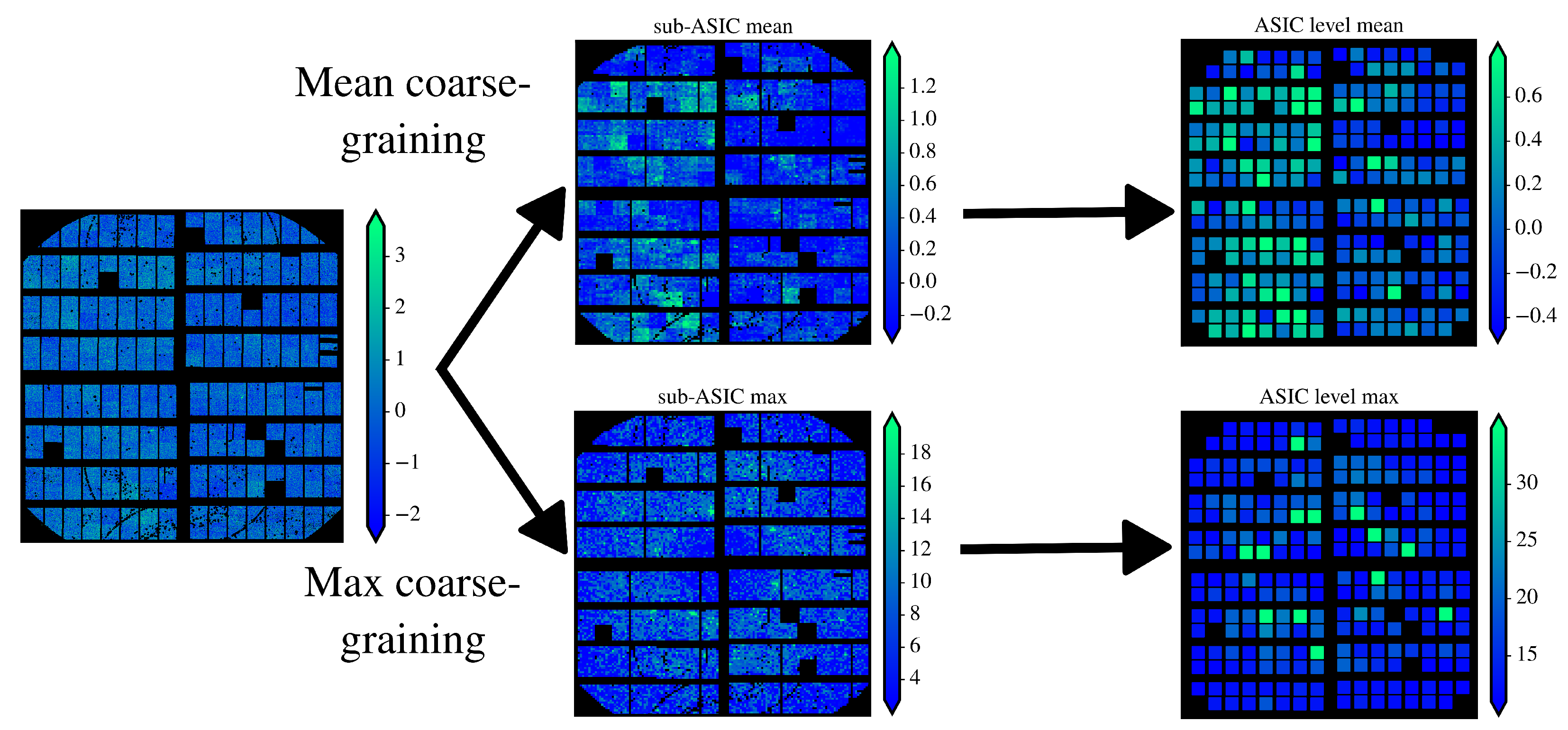
2.4. Angular Coarse-Graining with Means and Maxes
2.5. Covariance as a Statistical Criterion for Feature Attention
3. Results
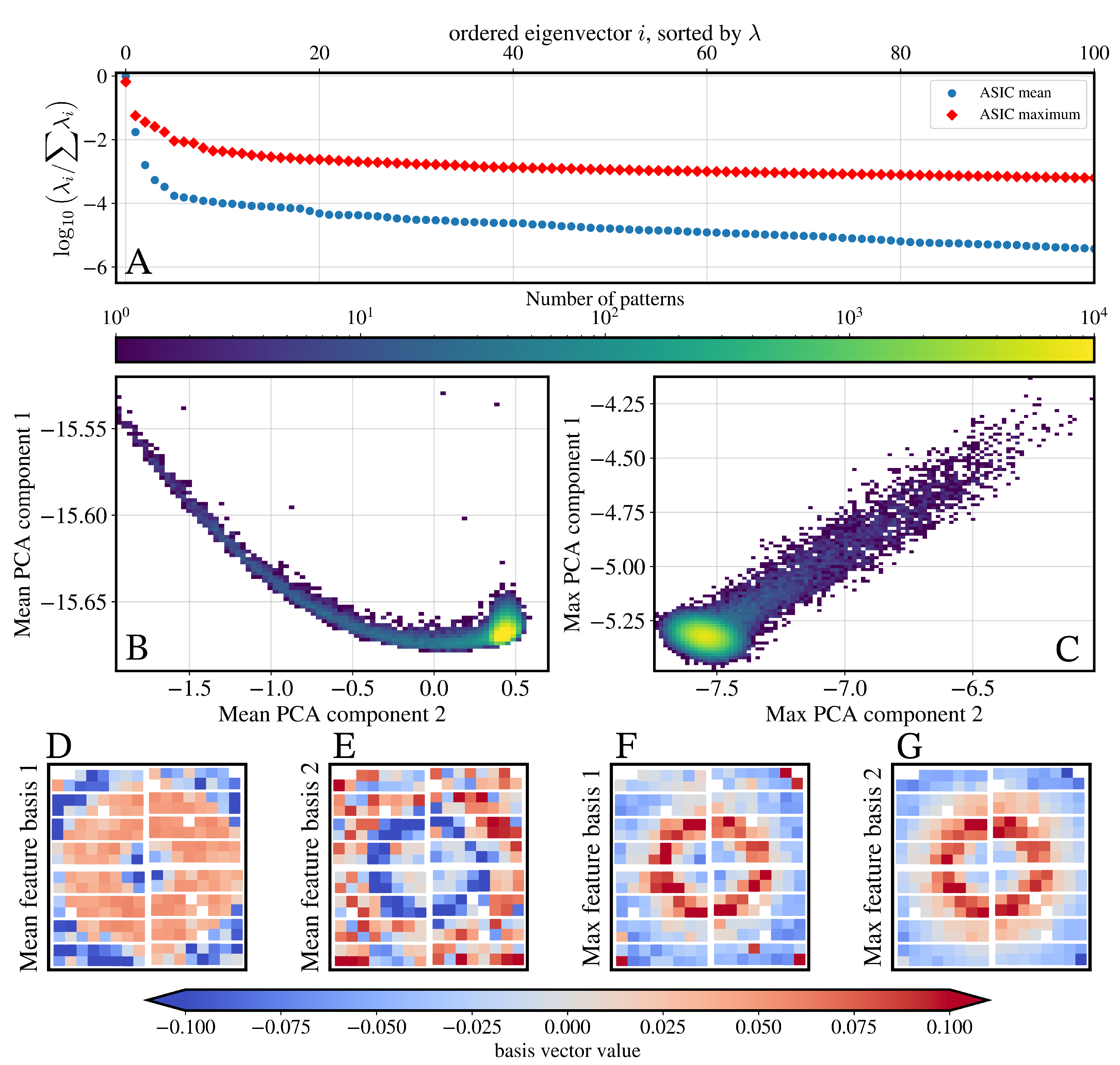
3.1. Impact of Coarse-Graining
3.2. Principal Component Analysis
3.3. Outlier Statistics on Ice-Sensitive ASICs for Classification
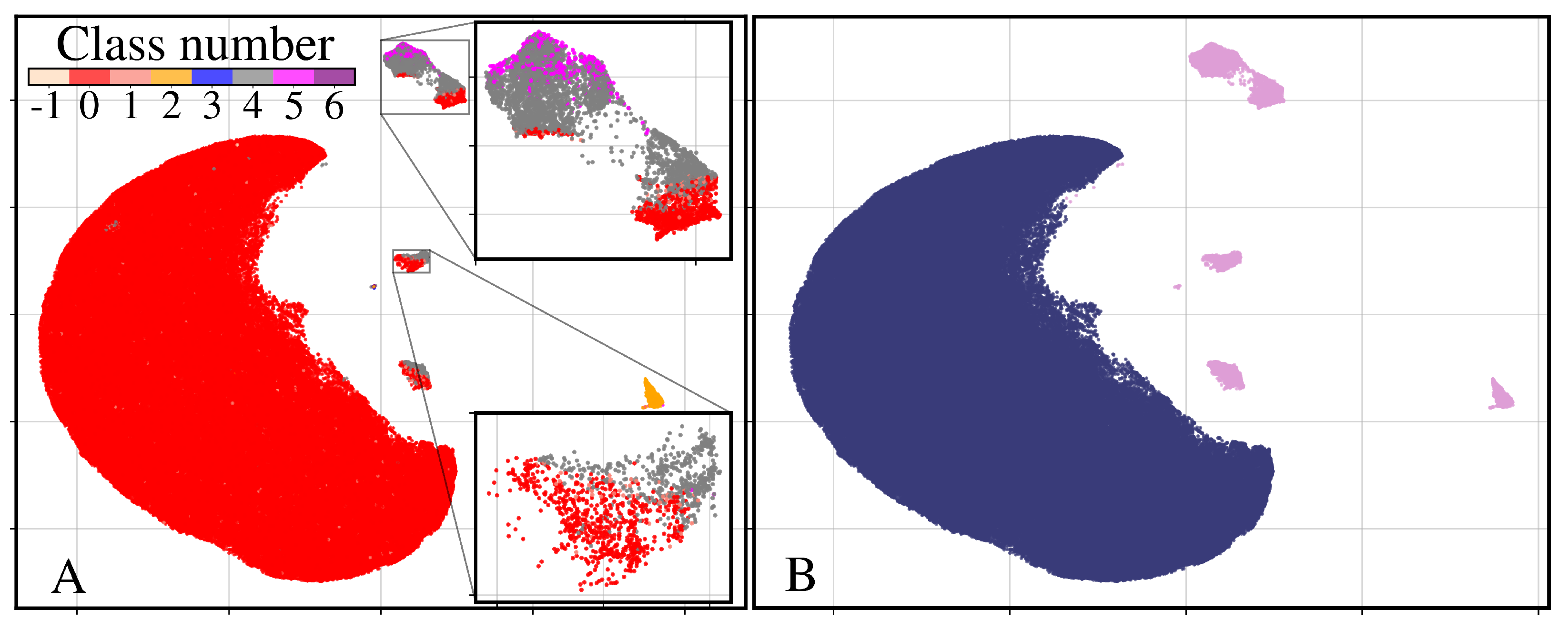
3.4. Massive Hit-Finding and Hit-Classification
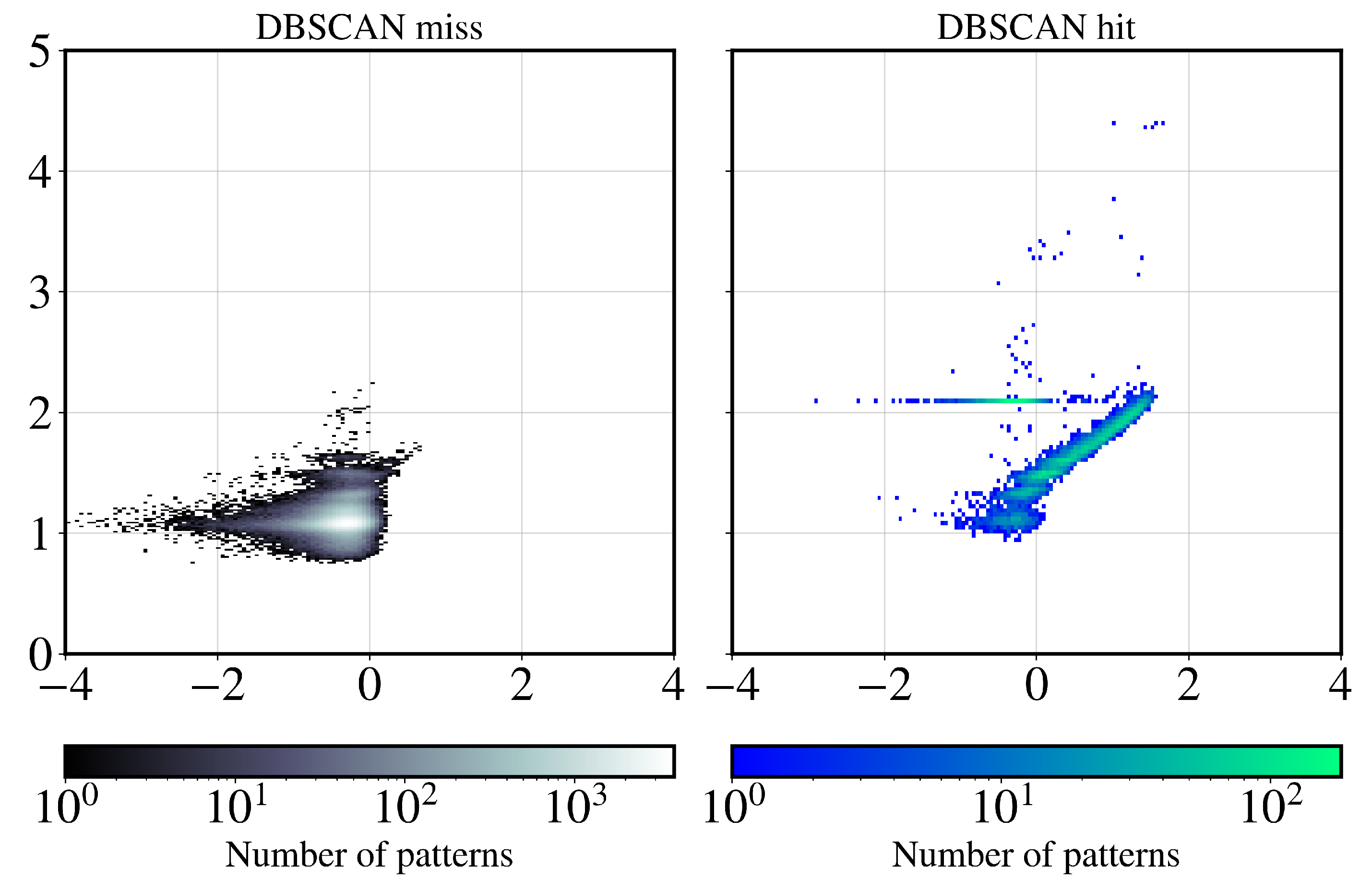
3.5. Cross-Validating Hits and Blanks
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Loh, N.D.; Hampton, C.Y.; Martin, A.V.; Starodub, D.; Sierra, R.G.; Barty, A.; Aquila, A.; Schulz, J.; Lomb, L.; Steinbrener, J.; et al. Fractal morphology, imaging and mass spectrometry of single aerosol particles in flight. Nature 2012, 486, 513–517. [Google Scholar] [CrossRef]
- Hantke, M.F.; Hasse, D.; Maia, F.R.N.C.; Ekeberg, T.; John, K.; Svenda, M.; Loh, N.D.; Martin, A.V.; Timneanu, N.; Larsson, D.S.D.; et al. High-throughput imaging of heterogeneous cell organelles with an X-ray laser. Nat. Photonics 2014, 8, 943–949. [Google Scholar] [CrossRef]
- Sellberg, J.A.; Huang, C.; McQueen, T.A.; Loh, N.D.; Laksmono, H.; Schlesinger, D.; Sierra, R.G.; Nordlund, D.; Hampton, C.Y.; Starodub, D.; et al. Ultrafast X-ray probing of water structure below the homogeneous ice nucleation temperature. Nature 2014, 510, 381–384. [Google Scholar] [CrossRef]
- Shen, Z.; Xavier, P.L.; Bean, R.; Bielecki, J.; Bergemann, M.; Daurer, B.J.; Ekeberg, T.; Estillore, A.D.; Fangohr, H.; Giewekemeyer, K.; et al. Resolving Nonequilibrium Shape Variations among Millions of Gold Nanoparticles. ACS Nano 2024, 18, 15576–15589. [Google Scholar] [CrossRef] [PubMed]
- Cramer, S.P. Free-Electron Lasers. In X-Ray Spectroscopy with Synchrotron Radiation; Springer International Publishing: Cham, Switzerland, 2020; pp. 295–310. [Google Scholar]
- Sobolev, E.; Zolotarev, S.; Giewekemeyer, K.; Bielecki, J.; Okamoto, K.; Reddy, H.K.N.; Andreasson, J.; Ayyer, K.; Barak, I.; Bari, S.; et al. Megahertz single-particle imaging at the European XFEL. Commun. Phys. 2020, 3, 97. [Google Scholar] [CrossRef]
- Ayyer, K.; Xavier, P.L.; Bielecki, J.; Shen, Z.; Daurer, B.J.; Samanta, A.K.; Awel, S.; Bean, R.; Barty, A.; Bergemann, M.; et al. 3D diffractive imaging of nanoparticle ensembles using an x-ray laser. Optica 2021, 8, 15–23. [Google Scholar] [CrossRef]
- Gallo, P.; Amann-Winkel, K.; Angell, C.A.; Anisimov, M.A.; Caupin, F.; Chakravarty, C.; Lascaris, E.; Loerting, T.; Panagiotopoulos, A.Z.; Russo, J.; et al. Water: A Tale of Two Liquids. Chem. Rev. 2016, 116, 7463–7500. [Google Scholar] [CrossRef]
- Pettersson, L.G.M.; Nilsson, A. The structure of water; from ambient to deeply supercooled. J. Non-Cryst. Solids 2015, 407, 399–417. [Google Scholar] [CrossRef]
- Nilsson, A.; Schreck, S.; Perakis, F.; Pettersson, L.G.M. Probing water with X-ray lasers. Adv. Phys. X 2016, 1, 226–245. [Google Scholar] [CrossRef]
- Gallo, P.; Stanley, H.E. Supercooled water reveals its secrets. Science 2017, 358, 1543–1544. [Google Scholar] [CrossRef]
- Pathak, H.; Späh, A.; Kim, K.H.; Tsironi, I.; Mariedahl, D.; Blanco, M.; Huotari, S.; Honkimäki, V.; Nilsson, A. Intermediate range O–O correlations in supercooled water down to 235 K. J. Chem. Phys. 2019, 150, 224506. [Google Scholar] [CrossRef] [PubMed]
- Chris Benmore, L.C.G.; Soignard, E. Intermediate range order in supercooled water. Mol. Phys. 2019, 117, 2470–2476. [Google Scholar] [CrossRef]
- Mason, B. The supercooling and nucleation of water. Adv. Phys. 1958, 7, 221–234. [Google Scholar] [CrossRef]
- Kalita, A.; Mrozek-McCourt, M.; Kaldawi, T.F.; Willmott, P.R.; Loh, N.D.; Marte, S.; Sierra, R.G.; Laksmono, H.; Koglin, J.E.; Hayes, M.J.; et al. Microstructure and crystal order during freezing of supercooled water drops. Nature 2023, 620, 557–561. [Google Scholar] [CrossRef]
- Esmaeildoost, N.; Jönsson, O.; McQueen, T.A.; Ladd-Parada, M.; Laksmono, H.; Loh, N.T.D.; Sellberg, J.A. Heterogeneous Ice Growth in Micron-Sized Water Droplets Due to Spontaneous Freezing. Crystals 2022, 12, 65. [Google Scholar] [CrossRef]
- Mancuso, A.P.; Aquila, A.; Batchelor, L.; Bean, R.J.; Bielecki, J.; Borchers, G.; Doerner, K.; Giewekemeyer, K.; Graceffa, R.; Kelsey, O.D.; et al. The Single Particles, Clusters and Biomolecules and Serial Femtosecond Crystallography instrument of the European XFEL: Initial installation. J. Synchrotron Radiat. 2019, 26, 660–676. [Google Scholar] [CrossRef]
- DePonte, D.P.; Weierstall, U.; Schmidt, K.; Warner, J.; Starodub, D.; Spence, J.C.H.; Doak, R.B. Gas dynamic virtual nozzle for generation of microscopic droplet streams. J. Phys. D Appl. Phys. 2008, 41, 195505. [Google Scholar] [CrossRef]
- Vakili, M.; Bielecki, J.; Knoška, J.; Otte, F.; Han, H.; Kloos, M.; Schubert, R.; Delmas, E.; Mills, G.; de Wijn, R.; et al. 3D printed devices and infrastructure for liquid sample delivery at the European XFEL. J. Synchrotron Radiat. 2022, 29, 331–346. [Google Scholar] [CrossRef]
- Henrich, B.; Becker, J.; Dinapoli, R.; Goettlicher, P.; Graafsma, H.; Hirsemann, H.; Klanner, R.; Krueger, H.; Mazzocco, R.; Mozzanica, A.; et al. The adaptive gain integrating pixel detector AGIPD a detector for the European XFEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 633, S11–S14. [Google Scholar] [CrossRef]
- Mezza, D.; Allahgholi, A.; Arino-Estrada, G.; Bianco, L.; Delfs, A.; Dinapoli, R.; Goettlicher, P.; Graafsma, H.; Greiffenberg, D.; Hirsemann, H.; et al. Characterization of AGIPD1.0: The full scale chip. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 838, 39–46. [Google Scholar] [CrossRef]
- Ayyer, K.; Lan, T.Y.; Elser, V.; Loh, N.D. Dragonfly: An implementation of the expand-maximize-compress algorithm for single-particle imaging. J. Appl. Crystallogr. 2016, 49, 1320–1335. [Google Scholar] [CrossRef]
- Loh, N.D.; Bogan, M.J.; Elser, V.; Barty, A.; Boutet, S.; Bajt, S.; Hajdu, J.; Ekeberg, T.; Maia, F.R.N.C.; Schulz, J.; et al. Cryptotomography: Reconstructing 3D Fourier Intensities from Randomly Oriented Single-Shot Diffraction Patterns. Phys. Rev. Lett. 2010, 104, 225501. [Google Scholar] [CrossRef]
- White, T.A.; Kirian, R.A.; Martin, A.V.; Aquila, A.; Nass, K.; Barty, A.; Chapman, H.N. CrystFEL: A software suite for snapshot serial crystallography. J. Appl. Crystallogr. 2012, 45, 335–341. [Google Scholar] [CrossRef]
- Jönsson, H.O.; Caleman, C.; Andreasson, J.; Tîmneanu, N. Hit detection in serial femtosecond crystallography using X-ray spectroscopy of plasma emission. IUCrJ 2017, 4, 778–784. [Google Scholar] [CrossRef]
- Liu, J.; van der Schot, G.; Engblom, S. Supervised classification methods for flash X-ray single particle diffraction imaging. Opt. Express 2019, 27, 3884–3899. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, V.; Nawaz, S.; Pennicard, D.; Setty, S.P.R.; Graafsma, H. Data reduction for X-ray serial crystallography using machine learning. J. Appl. Crystallogr. 2023, 56, 200–213. [Google Scholar] [CrossRef] [PubMed]
- Galchenkova, M.; Tolstikova, A.; Klopprogge, B.; Sprenger, J.; Oberthuer, D.; Brehm, W.; White, T.A.; Barty, A.; Chapman, H.N.; Yefanov, O. Data reduction in protein serial crystallography. IUCrJ 2024, 11, 190–201. [Google Scholar] [CrossRef]
- Hadian-Jazi, M.; Messerschmidt, M.; Darmanin, C.; Giewekemeyer, K.; Mancuso, A.P.; Abbey, B. A peak-finding algorithm based on robust statistical analysis in serial crystallography. J. Appl. Crystallogr. 2017, 50, 1705–1715. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Daurer, B.J.; Sala, S.; Hantke, M.F.; Reddy, H.K.N.; Bielecki, J.; Shen, Z.; Nettelblad, C.; Svenda, M.; Ekeberg, T.; Carini, G.A.; et al. Ptychographic wavefront characterization for single-particle imaging at x-ray lasers. Optica 2021, 8, 551–562. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar] [CrossRef]
- Cruz-Chú, E.R.; Hosseinizadeh, A.; Mashayekhi, G.; Fung, R.; Ourmazd, A.; Schwander, P. Selecting XFEL single-particle snapshots by geometric machine learning. Struct. Dyn. 2021, 8, 014701. [Google Scholar] [CrossRef]
- Assalauova, D.; Ignatenko, A.; Isensee, F.; Trofimova, D.; Vartanyants, I.A. Classification of diffraction patterns using a convolutional neural network in single-particle-imaging experiments performed at X-ray free-electron lasers. J. Appl. Crystallogr. 2022, 55, 444. [Google Scholar] [CrossRef]
- Martin, A.V. Orientational order of liquids and glasses via fluctuation diffraction. IUCrJ 2017, 4, 24–36. [Google Scholar] [CrossRef]
- Mahajan, M.; Nimbhorkar, P.; Varadarajan, K. The planar k-means problem is NP-hard. Theoret. Comput. Sci. 2012, 442, 13–21. [Google Scholar] [CrossRef]
- Schlesinger, D.; Sellberg, J.A.; Nilsson, A.; Pettersson, L.G.M. Evaporative cooling of microscopic water droplets in vacuo: Molecular dynamics simulations and kinetic gas theory. J. Chem. Phys. 2016, 144. [Google Scholar] [CrossRef] [PubMed]
- Robinson, I.K. Crystal truncation rods and surface roughness. Phys. Rev. B 1986, 33, 3830–3836. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.P. Probabilistic Machine Learning: An introduction; MIT Press: 2022. Available online: http://probml.github.io/book1 (accessed on 14 August 2025).

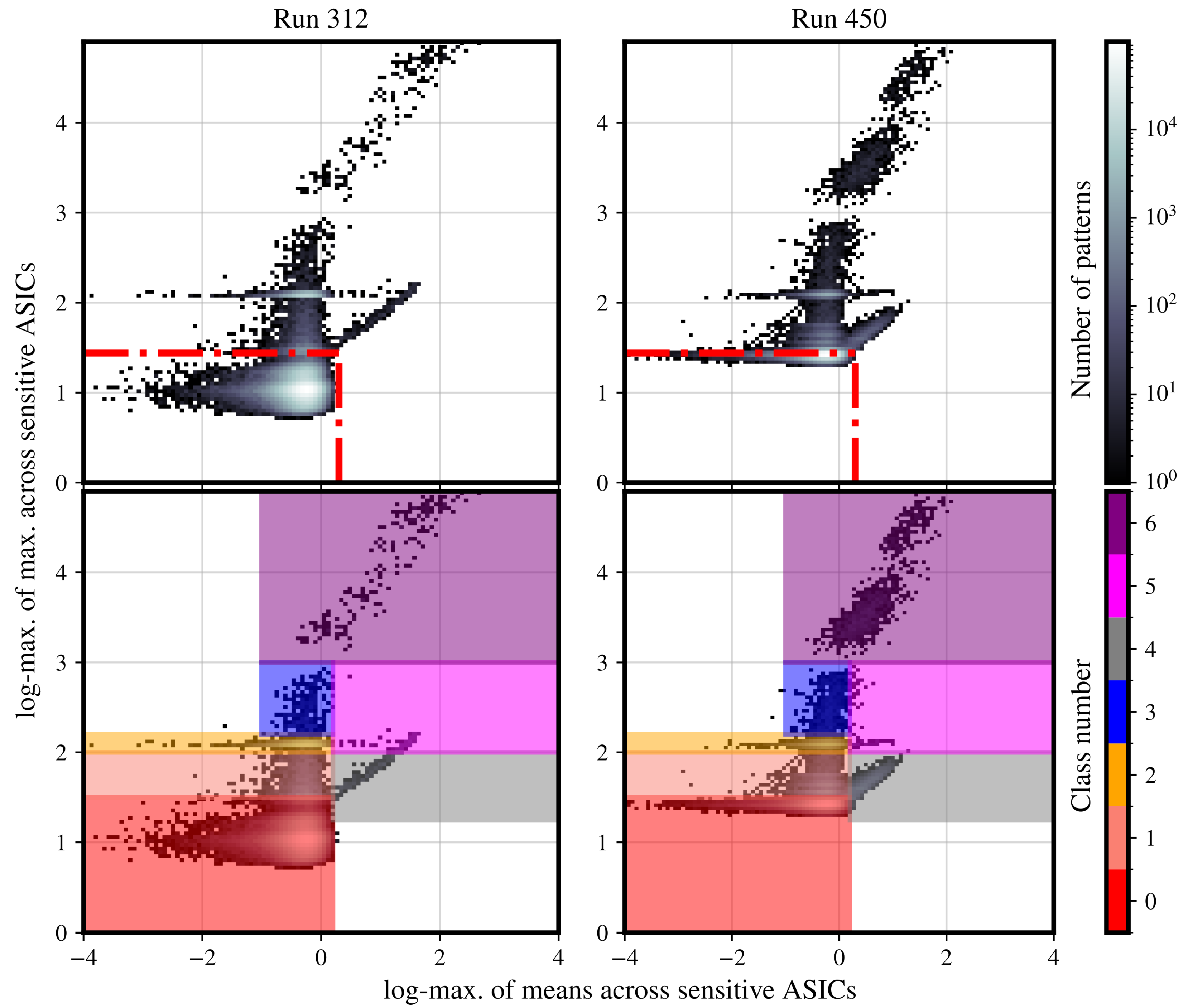

| Class Label | Num. Patterns | Mean Limits (Photons) | Max Limits (Photons) | Interpretation |
|---|---|---|---|---|
| 0 | 4.21 × 108 (92.69%) | [10−5, 0.17] | [0.1, 3.4] | blanks (high-confidence) |
| 1 | 4.32 × 106 (0.98%) | [10−5, 0.17] | [3.4, 10.8] | blanks with high thermal noise |
| 2 | 1.75 × 107 (3.80%) | [10−5, 0.17] | [10.8, 17.0] | blanks (hot pixels activated) |
| 3 | 2.62 × 105 (0.06%) | [10−5, 0.17] | [17.0, 107.5] | weak hits |
| 4 | 5.01 × 106 (1.12%) | [0.17, 1075] | [1.9, 10.8] | strong liquid water hits |
| 5 | 5.94 × 106 (1.28%) | [0.17, 1075] | [10.8, 108] | liquid water and ice hits |
| 6 | 2.61 × 105 (0.06%) | [0.01, 1075] | [108, 10800] | strong ice hits |
| Hit (Outlier Statistics) | Miss (Outlier Statistics) | |
|---|---|---|
| Hit (UMAP-DBSCAN) | 2.86 × 104, 2.21% | 9.31 × 103, 0.72% |
| Miss (UMAP-DBSCAN) | 1.67 × 104, 1.29% | 1.24 × 106, 95.79% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chia, E.S.H.; Berberich, T.B.; Sobolev, E.; Koliyadu, J.C.P.; Adams, P.; André, T.; Antonia, F.D.; Cardoch, S.; De Santis, E.; Formosa, A.; et al. Coarse-Graining and Classifying Massive High-Throughput XFEL Datasets of Crystallization in Supercooled Water. Crystals 2025, 15, 734. https://doi.org/10.3390/cryst15080734
Chia ESH, Berberich TB, Sobolev E, Koliyadu JCP, Adams P, André T, Antonia FD, Cardoch S, De Santis E, Formosa A, et al. Coarse-Graining and Classifying Massive High-Throughput XFEL Datasets of Crystallization in Supercooled Water. Crystals. 2025; 15(8):734. https://doi.org/10.3390/cryst15080734
Chicago/Turabian StyleChia, Ervin S. H., Tim B. Berberich, Egor Sobolev, Jayanath C. P. Koliyadu, Patrick Adams, Tomas André, Fabio Dall Antonia, Sebastian Cardoch, Emiliano De Santis, Andrew Formosa, and et al. 2025. "Coarse-Graining and Classifying Massive High-Throughput XFEL Datasets of Crystallization in Supercooled Water" Crystals 15, no. 8: 734. https://doi.org/10.3390/cryst15080734
APA StyleChia, E. S. H., Berberich, T. B., Sobolev, E., Koliyadu, J. C. P., Adams, P., André, T., Antonia, F. D., Cardoch, S., De Santis, E., Formosa, A., Hammarström, B., Hassett, M. P., Kim, S., Kloos, M., Letrun, R., Malka, J., Melo, D., Paporakis, S., Sato, T., ... Loh, N.-t. D. (2025). Coarse-Graining and Classifying Massive High-Throughput XFEL Datasets of Crystallization in Supercooled Water. Crystals, 15(8), 734. https://doi.org/10.3390/cryst15080734







