ANN-Based Prediction of OSL Decay Curves in Quartz from Turkish Mediterranean Beach Sand

Abstract

Quartz is a widely used mineral in dosimetric and geochronological applications due to its stable luminescence properties under ionizing radiation. This study presents an artificial neural network (ANN)-based approach to predict the optically stimulated luminescence (OSL) decay curves of quartz extracted from Mediterranean beach sand samples in Turkey. Experimental OSL signals were obtained from quartz samples irradiated with beta doses ranging from 0.1 Gy to 1034.9 Gy. The dataset was used to train ANN models with three different learning algorithms: Levenberg–Marquardt (LM), Bayesian Regularization (BR), and Scaled Conjugate Gradient (SCG). Forty-seven decay curves were used for training and three for testing. The ANN models were evaluated based on regression accuracy, training–validation–test performance, and their predictive capability for low, medium, and high doses (1 Gy, 72.4 Gy, 465.7 Gy). The results showed that BR achieved the highest overall regression (R = 0.99994) followed by LM (R = 0.99964) and SCG (R = 0.99820), confirming the superior generalization and fits across all dose ranges. LM performs optimally at low-to-moderate doses, and SCG delivers balanced yet slightly noisier predictions. The proposed ANN-based method offers a robust and effective alternative to conventional kinetic modeling approaches for analyzing OSL decay behavior and holds considerable potential for advancing luminescence-based retrospective dosimetry and OSL dating applications.

1. Introduction

Quartz (SiO₂) is one of the most widely used minerals in luminescence dating due to its abundance, stable crystalline structure, and favorable optically stimulated luminescence (OSL) properties [1,2]. OSL measurements of quartz are primarily based on the detection of light emitted during the release of trapped charge carriers when the mineral is stimulated by light, most commonly by blue LEDs [3]. The resulting OSL decay curves provide crucial information for determining the equivalent dose, which is essential for age estimation in geological and archeological studies [4,5,6].

However, the complex behavior of OSL decay curves, which often exhibit multi-exponential characteristics due to various trapping and recombination centers, poses challenges for precise modeling and interpretation [7]. Conventional analytical approaches, such as fitting decay curves with predefined mathematical models (e.g., first-order, second order or general-order kinetic models), can sometimes fail to adequately capture the non-linear and multi-component nature of the signals, especially when measurement noise or mineral heterogeneity are significant [8,9].

In recent years, artificial neural networks (ANNs) have emerged as a powerful computational tool to model non-linear relationships in various fields of physics and engineering [10]. ANNs have shown promising capabilities in recognizing complex patterns within luminescence data, including the prediction and deconvolution of TL glow curves [11,12,13].

Training ANNs with experimental OSL datasets enables the estimation of decay behaviors under various irradiation and preheat conditions, as well as the prediction of complete luminescence decay curves from given dose values. Conversely, ANNs can estimate radiation doses from measured OSL decay data, potentially improving dose estimation accuracy and deepening the understanding of quartz luminescence properties.

To ensure the robust and efficient training of ANNs, various learning algorithms can be implemented. Among these, the Levenberg–Marquardt (LM) algorithm is widely recognized for its fast convergence in training moderate-sized feedforward networks by combining the advantages of the Gauss–Newton method and gradient descent. The Bayesian Regularization (BR) algorithm extends standard backpropagation by introducing regularization parameters to reduce overfitting and enhance generalization capability, especially when dealing with noisy experimental data. The Scaled Conjugate Gradient (SCG) algorithm, on the other hand, is suitable for large datasets and provides a balance between computational efficiency and convergence stability by avoiding time-consuming line search steps during training [14,15,16].

Previous studies have demonstrated that combining ANNs with various training algorithms, such as LM, BR, and SCG, can significantly improve the modeling and prediction of TL glow curves, enabling more accurate dose–response estimations and kinetic analyses [11,13,17].

Although significant progress has been made in applying machine learning to luminescence research, the complex structure of OSL decay curves has received relatively limited attention in studies utilizing advanced approaches such as artificial neural networks (ANNs) or deep learning. Considering the inherently multi-exponential and strongly non-linear characteristics of OSL decay behavior, the integration of data-driven modeling techniques holds great promise for improving the accuracy and interpretability of dose estimations. A more comprehensive understanding of OSL signal dynamics through machine learning could substantially contribute to the advancement of luminescence dating, retrospective dosimetry, and other fields where OSL serves as a critical diagnostic indicator.

This study aims to investigate the applicability of an ANN-based approach to analyze the OSL decay behavior of quartz samples extracted from beach sand collected along the Mediterranean coast of Turkey, to predict the OSL decay curves of quartz minerals exposed to different radiation doses, and to forecast their general dose–response behavior.

2. Materials and Methods

The quartz mineral, which is the subject of this study, was obtained by separating sand samples through chemical and physical methods from an open access public beach (36°36′30.6″ N, 34°19′25.8″ E) located in Erdemli district, Mersin province, Turkey.

Quartz grains were separated from the collected beach sand samples by following standard preparation procedures [1] and using a protocol similar to the soil-based method applied by Yüksel [18], which is commonly adapted by many researchers. The process involved sequential chemical and physical treatments, including sieving, acid etching to remove carbonates and organic matter, and magnetic separation to eliminate heavy minerals. To further enhance the separation of feldspar and ensure higher quartz purity, an additional heavy liquid separation step was performed using sodium polytungstate (SPT) adjusted to a density of approximately 2.62 g/cm³. At this density, feldspar grains, being less dense, floated to the surface, while the denser quartz grains settled at the bottom. The quartz fraction was carefully extracted, thoroughly rinsed with deionized water and ethanol to remove any residual heavy liquid, and subsequently dried at low temperature.

Powdered quartz samples of 8.0 ± 0.2 mg with a particle size in the range of 90–140 µm were glued to rimmed disks using silicone oil and five aliquots were prepared for OSL measurements. β-irradiation was carried out using an internal strontium radioisotope (⁹⁰Sr) beta source with an activity of 1.85 GBq (50 mCi), delivering a dose rate of 0.10 Gy/s and a maximum energy of 2.2 MeV.

All luminescence measurements (OSL and TL) were performed using a lexsyg smart TL/OSL reader (Freiberg Instruments GmbH, Freiberg, Germany), and OSL decay curves were recorded for fifty different radiation doses ranging from 0.1 Gy to 1034.9 Gy. Data acquisition and signal analysis of the recorded OSL signals were carried out using LexStudio2 software (version 2.8.2). Before recording the OSL decay curves of the quartz samples irradiated at the selected radiation doses, the samples were subjected to a preheat treatment at 220 °C for 10 s. This preheating step was applied after each irradiation. After each irradiation–OSL measurement cycle, the aliquots were bleached by subjecting them to controlled annealing and sequential TL measurements up to 450 °C to verify the complete emptying of charge traps. Following preheating, the quartz samples were heated up to 125 °C at a heating rate of 5 °C/s and held at this temperature and then stimulated for 60 s using blue light-emitting diodes (458 nm, 40 mW/cm²). The OSL decay curves were recorded through a BSL TL-365 nm detection window equipped with a Hoya U-340 glass filter (2.5 mm) and a Delta BP 365/50 EX interference filter (5 mm).

Out of the experimental OSL signals obtained at 50 different radiation doses ranging from 0.1 Gy to 1034.9 Gy, 47 were selected and trained using artificial neural networks (ANNs) in MATLAB software (R2023b) with the Neural Net Fitting (NNF) toolbox (23.2), employing Levenberg–Marquardt (LM), Bayesian Regularization (BR), and Scaled Conjugate Gradient (SCG) backpropagation algorithms, while the OSL decay curves from the remaining 3 doses, which were not used for training, were utilized to compare with the decay curves generated by the mathematical function produced by the ANN.

3. Results and Discussions

This section presents the experimental findings, including the OSL dose–response behavior of quartz samples, their reusability under repeated irradiation cycles, and the predictive performance of the developed ANN models. The results are discussed in the context of luminescence mechanisms and ANN-based approaches that capture the relationship between absorbed dose and luminescence intensity, providing accurate predictions relevant to dosimetric applications.

3.1. OSL Dose–Response

The OSL decay curve represents the time-dependent luminescence emitted as trapped charge carriers are released from energy traps within the crystal lattice under optical stimulation, providing a direct relationship between the measured luminescence intensity and the absorbed radiation dose [1,7]. This dose–response behavior enables a detailed characterization of the trapping and recombination processes [19] and is crucial for precise dose estimation and retrospective dosimetry in both geological and synthetic materials [6,20].

In this study, systematic dose–response experiments were conducted on quartz samples using the OSL method over a wide dose interval ranging from 0.1 Gy to 1034.9 Gy. For each dose point, the samples were irradiated with a calibrated beta source, preheated to remove unstable signal components, and subsequently stimulated under controlled conditions using blue LEDs to record the corresponding OSL decay curves. The OSL decay curves recorded as a function of absorbed dose are shown in Figure 1, plotted as OSL intensity versus time on both linear and log–log scales to demonstrate the signal behavior more clearly.

Figure 1a,b illustrate the OSL decay curves of the quartz samples plotted as a function of time for various radiation dose values ranging from 0.1 Gy to 1034.9 Gy. As shown in Figure 1a,b, the overall shape of the OSL decay curves remains consistent across different doses (exponential decay curves), whereas the initial OSL intensities systematically increase with increasing absorbed dose. This increase in OSL signal with dose is a well-documented behavior in the literature and is mainly attributed to the higher population of charge carriers trapped in luminescence centers (electron traps) as the irradiation dose increases [1,8,21]. This dose–response relationship is generally linear over low-to-moderate dose ranges but may exhibit supralinearity or saturation at higher doses due to limitations in trap filling or recombination mechanisms [22,23]. Studies have shown that quartz and other silicate minerals demonstrate a predictable increase in OSL intensity with increasing dose, making them suitable for dosimetric applications in geological and archeological contexts [6,19]. The proportional growth in OSL intensity with dose reflects the larger number of trapped electrons that are released during optical stimulation, emitting luminescence as they recombine [21,24].

The initial OSL intensities as a function of the corresponding ionizing radiation dose are shown on a log–log scale in Figure 2. Each data point represents the mean initial OSL value measured from five identical aliquots mounted on rimmed stainless-steel disks, with error bars indicating the standard deviation of the replicate measurements.

The dose–response behavior of the quartz samples, as presented in Figure 2, demonstrates that the initial OSL intensities increase proportionally with the absorbed beta dose up to approximately 10 Gy, indicating a well-defined linear region suitable for precise dosimetric and dating applications [1,4,8]. This linearity at low-to-moderate doses is consistent with previous studies on quartz OSL properties, which have shown that the intensity of the fast OSL component increases linearly with dose due to the steady accumulation of charge carriers in stable traps [6]. Beyond about 20 Gy, the data points gradually deviate from the extrapolated linear trend and begin to fall below it, indicating the onset of a sublinear region. It is worth noting that the dose–response behavior observed in this study displays a relatively extended linear range up to approximately 20 Gy before entering a sublinear growth region. Although some quartz samples in the literature are reported to reach saturation at significantly lower doses, or even show signal reduction at high doses due to competition among trapping and recombination centers, the quartz used in this study exhibited stable and gradual signal growth up to several hundred Gray. This variation is consistent with findings by Feathers and Pagonis (2015) [25], who emphasized the role of different bleaching components and their interactions in determining the saturation characteristics of quartz OSL signals. This sublinear behavior is attributed to the progressive filling of available traps and recombination centers, which limits the further accumulation of trapped charge carriers and thus reduces the growth rate of the luminescence signal [19,22]. Similar sublinear trends have been widely reported in quartz OSL studies, confirming that saturation effects and trap competition can occur at higher doses [23,26]. No significant supralinearity was observed in the dose range analyzed, suggesting that no additional deeper or new traps are activated under these irradiation conditions [6]. Overall, this response supports the suitability of the studied quartz samples for reliable OSL dosimetry and dating within the low-to-moderate dose range, which is a key requirement for retrospective dosimetric applications in geology and archeology [19,23,27].

3.2. Reusability

Reusability is a fundamental requirement for any reliable OSL dosimeter material. A quartz sample cannot be considered suitable for practical dosimetric applications if its OSL sensitivity changes significantly with repeated irradiation and readout cycles. In this study, the reusability of the quartz samples was thoroughly evaluated under controlled laboratory conditions. Prepared aliquots were repeatedly irradiated with a fixed 10 Gy test dose using a beta source, then quickly cooled to room temperature and read out using identical preheat and optical stimulation protocols for each cycle. This irradiation–readout sequence was repeated for a total of 15 cycles while keeping all other experimental parameters constant. 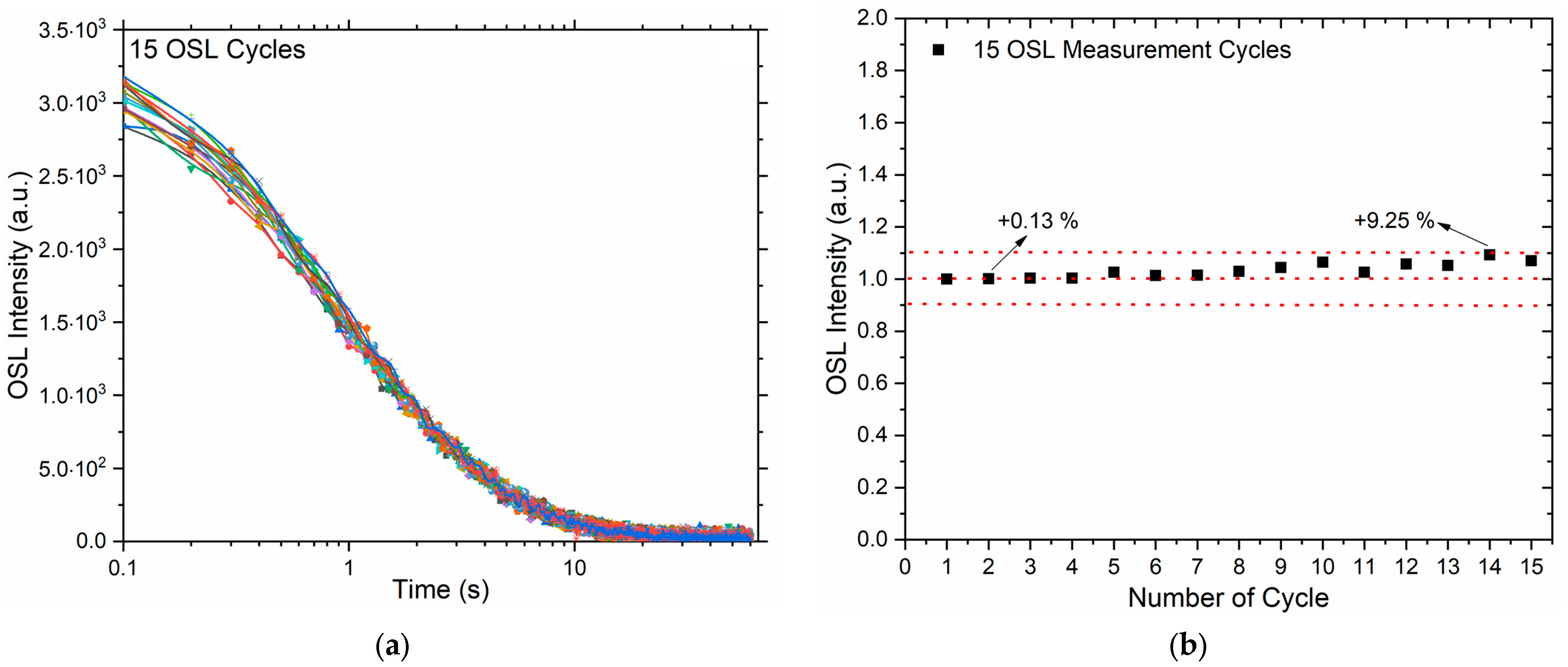The relationship between the OSL intensity and the number of reuse cycles obtained from these measurements is presented in Figure 3.

Figure 3a shows the OSL decay curves recorded during each measurement cycle, plotted as OSL intensity versus time. The curves exhibit consistent exponential decay behavior across all cycles, with no significant variation in the overall shape or decay rate.

This behavior is in agreement with many studies showing the high reproducibility of quartz OSL lifetime determinations under repeated isothermal decay and dose recovery experiments.

Buylaert et al. demonstrated that isothermal decay and dose recovery protocols yield highly reproducible quartz OSL lifetimes, supporting signal stability [28]. Similarly, Preusser et al. analyzed variations in OSL sensitivity across dose ranges and highlighted consistent behavior in quartz samples, reinforcing their suitability for dose estimation and repeated usage [21].

Figure 3b summarizes the relationship between the normalized initial OSL intensities and the number of reuse cycles. The plot shows that the OSL signal intensity remains remarkably stable over 15 cycles, with the maximum observed deviation being approximately 9.25% relative to the initial measurement. This minor variation is within acceptable experimental uncertainty and further confirms the excellent reusability of the quartz samples for multiple OSL measurements. Previous studies by Truscott et al. [29] and McKeever et al. [30] have similarly reported that natural quartz can maintain stable OSL sensitivity across repeated cycles when consistent preheat and stimulation conditions are applied.

Taken together, these results demonstrate that the tested quartz samples exhibit excellent reusability under repeated irradiation and readout, supporting their suitability for retrospective dosimetry, dose recovery experiments, and routine quality control in luminescence dating applications.

3.3. Artificial Neural Network (ANN)

OSL measurements require the accurate modeling of dose–response relationships to characterize the behavior of materials exposed to varying levels of ionizing radiation. Quartz is widely studied in various scientific fields, including dosimetric applications, geological dating, and archeological research, due to its ability to store radiation energy and its stable luminescence properties. Understanding and modeling the general behavior of the OSL decay curves recorded in response to absorbed radiation doses is therefore crucial for reliable dose estimation. In this study, an artificial neural network (ANN) model was developed to predict the OSL decay curves of quartz samples using varying beta radiation dose values as input. The input dataset consisted of 45 distinct radiation dose values, and each corresponding output dataset was represented by an OSL decay curve comprising 200 data points. Prior to training, all data were preprocessed and normalized using min–max scaling to ensure stable convergence. The normalized dataset was then divided into training (70%), validation (15%), and testing (15%) subsets using a stratified partitioning technique to ensure representative sampling across the full dose range. The ANN architecture, as shown in Figure 4, was designed with an input layer containing one neuron to receive the radiation dose, a hidden layer with ten neurons to capture non-linear relationships, and an output layer of two hundred neurons corresponding to the OSL decay curve points. The entire model was developed and implemented using the Deep Learning Toolbox 23.2 (with Neural Net Fitting app) in MATLAB 2023b for data preparation, training, and performance evaluation.

In this study, the prediction performance of ANN models developed using three different training algorithms—Levenberg–Marquardt (LM), Bayesian Regularization (BR), and Scaled Conjugate Gradient (SCG)—was systematically investigated to estimate the OSL decay curves of quartz samples. To ensure sufficient convergence and performance stability, the training process was carried out with a maximum of 1000 epochs. The comparative evaluation was based on three main criteria: (i) the performance trends illustrated by the training–validation–test mean squared error (MSE) plots, (ii) the regression analysis results including correlation coefficients (R values), and (iii) the accuracy of the predicted OSL decay curves at three representative dose levels: low (1 Gy), medium (72.4 Gy), and high (465.7 Gy).

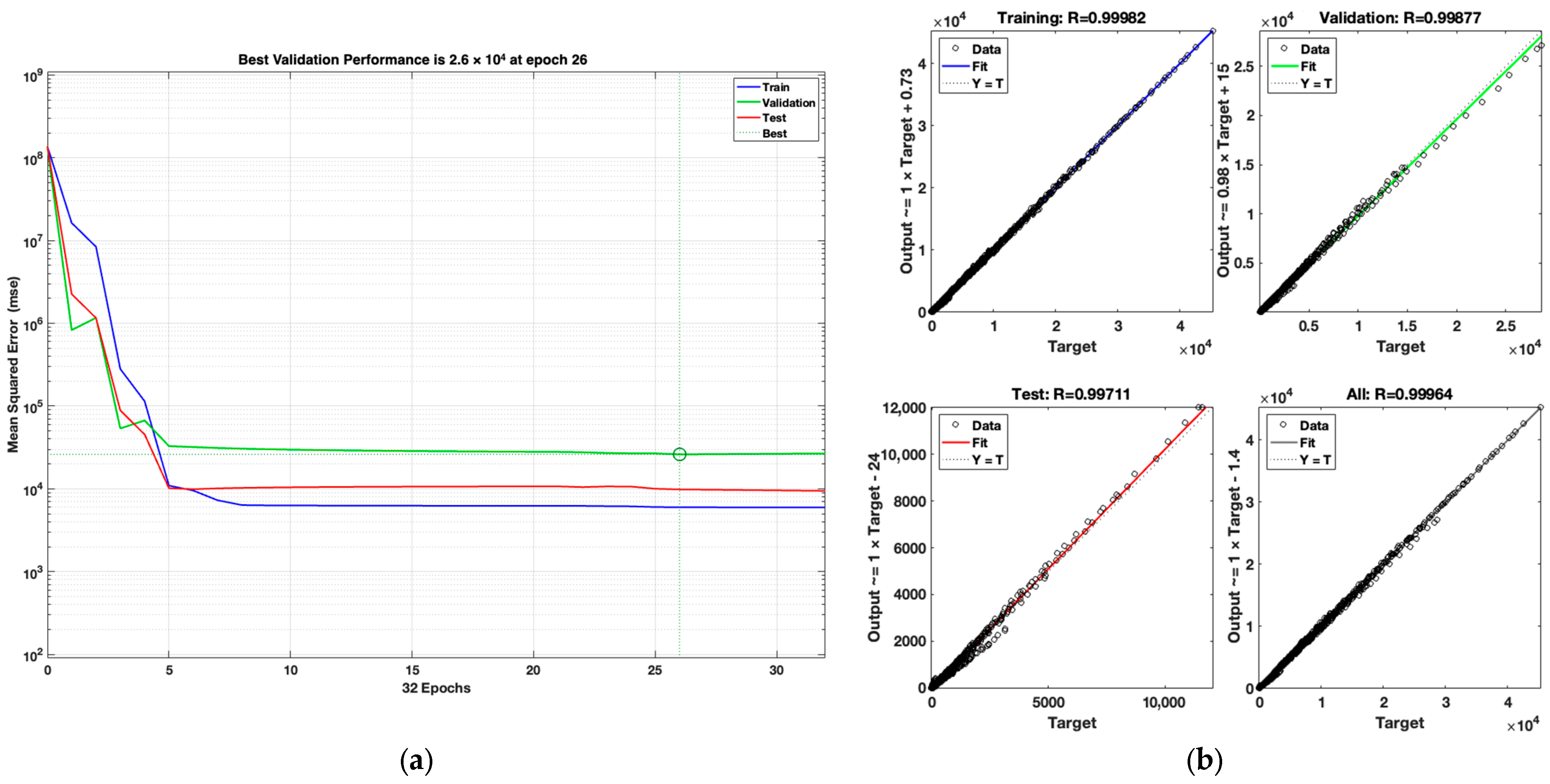
Figure 5 shows the performance of the LM optimization algorithm’s simulation and regression results.

The performance plot for the LM algorithm shows that the MSE rapidly decreases within the first few epochs and reaches its minimum validation value of 26,048.34 at epoch 26. After this point, the training, validation, and test curves remain nearly parallel, indicating that the model does not suffer from overfitting. The regression results demonstrate high prediction accuracy with correlation coefficients of R = 0.99982 (training), R = 0.99877 (validation), R = 0.99711 (test), and R = 0.99964 (overall).

Figure 6 shows the performance of the BR optimization algorithm’s simulation and the results of its regression.

The BR algorithm demonstrates robust generalization capability with a longer training time, reaching its best training MSE of 1477.85 at epoch 921. The regression results indicate excellent model fit with R = 0.99995 (training), R = 0.99974 (test), and R = 0.99994 (overall), verifying that BR effectively minimizes overfitting.

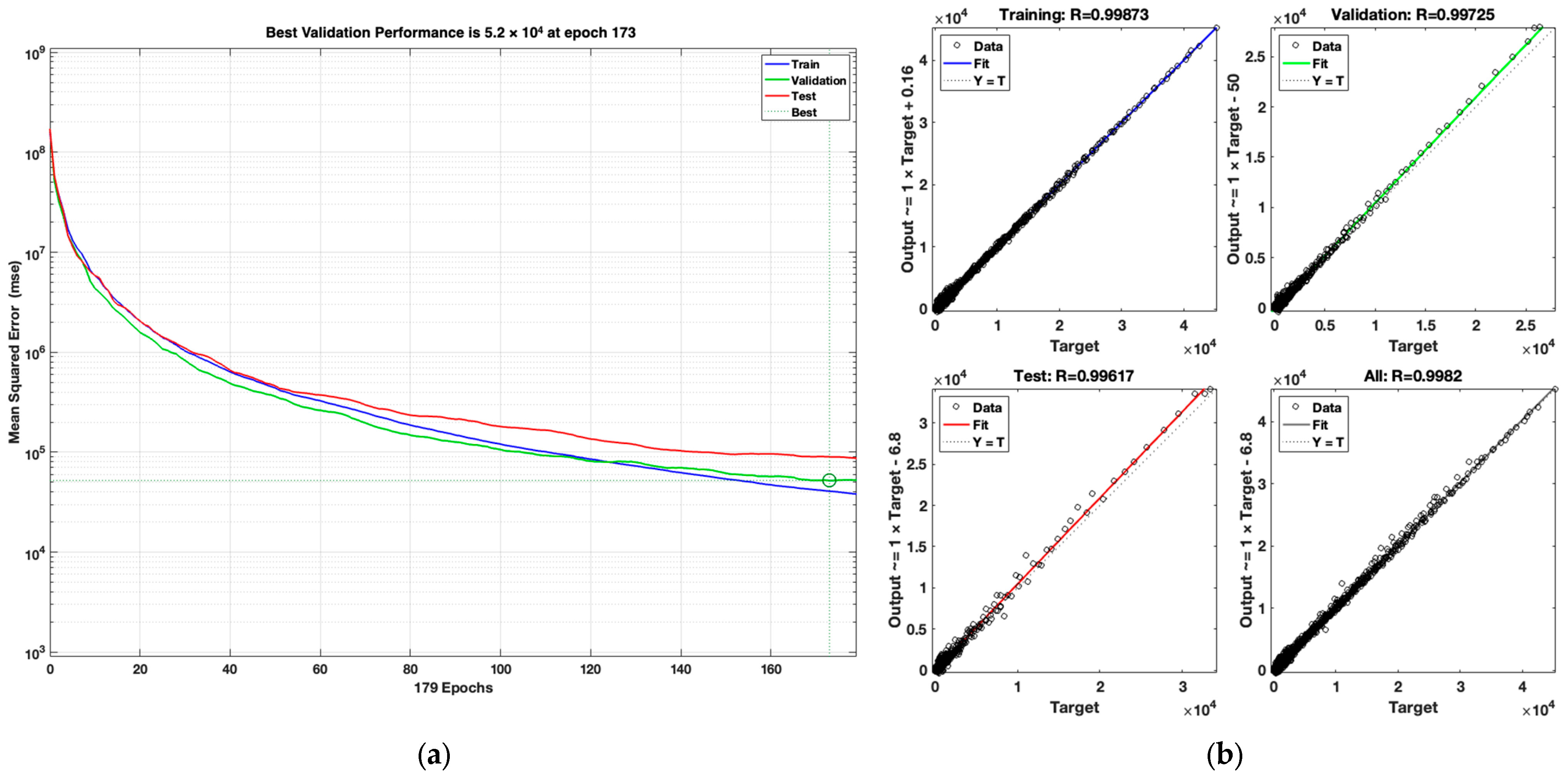
Figure 7 shows the performance of the SCG optimization algorithm’s simulation and the results of its regression.

The SCG performance plot reveals slower convergence than LM, with the best validation MSE of 51,979.40 obtained at epoch 173. The R values are slightly lower than those for LM and BR, with R = 0.99873 (training), R = 0.99725 (validation), R = 0.99617 (test), and R = 0.9982 (overall).

In this part of the study, comparisons are presented between the experimentally obtained OSL decay curves and those generated by the ANN model for three different radiation doses—low (1 Gy), medium (72.4 Gy), and high (465.7 Gy)—which were not used during the training of the LM, BR, and SCG algorithms.

Figure 8 presents a set of semi-logarithmic plots comparing the experimentally obtained OSL decay curves of quartz irradiated with 1, 72.4, and 465.7 Gy radiation doses and those generated by the ANN model optimized using the LM, BR, and SCG algorithms, with time plotted on a logarithmic x-axis and OSL intensity on a linear y-axis.

In the low-dose comparison (1 Gy), the LM algorithm’s predicted curve generally follows the experimental curve but exhibits slightly more deviation compared to BR, particularly in the late decay region. For the medium dose (72.4 Gy), LM achieves excellent alignment with the experimental decay curve, accurately capturing both the initial intensity and the tailing portion. However, in the high-dose range (465.7 Gy), the LM prediction shows minor mismatches at the initial high-intensity region, suggesting that local minima might limit its prediction accuracy for complex high-dose behavior. Overall, LM is most effective for low-to-moderate dose ranges due to its fast convergence and high accuracy.

For the low dose (1 Gy), the BR-predicted curve closely matches the experimental decay curve and shows better fit than LM and SCG, especially in the tailing region. In the medium dose (72.4 Gy), BR performs almost identically to LM, achieving near-perfect agreement with the experimental data. For the high dose (465.7 Gy), BR outperforms LM and SCG, providing smoother predictions and maintaining closer alignment with the initial high-intensity region. This confirms that the BR algorithm’s strong regularization capability enhances its reliability when modeling complex and noisy luminescence data.

For the low dose (1 Gy), the SCG predictions show greater scatter and higher noise, deviating from the experimental decay behavior, especially in the later part of the curve. In the medium dose (72.4 Gy), SCG produces reliable results, closely following the experimental curve and matching the performance of LM and BR. At the high dose (465.7 Gy), SCG provides acceptable predictions but slightly underperforms BR, especially in modeling the steep initial decay region. These results confirm that SCG offers balanced but relatively slower convergence and may be more sensitive to local variations at extreme dose levels.

The combined results indicate the following.

For low-dose conditions (1 Gy), the BR algorithm provides the most accurate fit to experimental data, benefiting from its inherent overfitting control and robust generalization. For the medium-dose range (72.4 Gy), all three algorithms deliver highly reliable predictions with minimal discrepancies, with LM and BR producing almost identical results. In the high-dose range (465.7 Gy), BR maintains superior prediction accuracy, LM shows acceptable performance with minor deviations, and SCG yields reasonable but slightly noisier outputs. Therefore, the BR algorithm is recommended for applications where dose levels span a wide and complex range and where noise minimization is critical. LM remains an effective option for rapid and accurate modeling at low-to-moderate doses due to its faster convergence. SCG provides balanced performance with relatively stable generalization but requires careful parameter tuning for extreme dose conditions.

These observations are consistent with findings in the literature: LM’s efficiency in moderate-sized feedforward networks has been widely reported [16], BR’s strong generalization and regularization have been confirmed for noisy datasets [31], and SCG has been noted for its computational efficiency and acceptable accuracy in large-scale problems [18].

4. Conclusions

This study highlights the robustness and predictive capability ANN architectures for modeling the OSL decay behavior of quartz samples collected from Mediterranean beach sand in Turkey. A comprehensive dataset, comprising experimental OSL signals corresponding to a wide range of beta irradiation doses (0.1–1034.9 Gy), was used to train and evaluate ANN models using three different optimization algorithms including LM, BR, and SCG. The results demonstrate that ANN models are capable of capturing the inherently non-linear, multi-exponential characteristics of OSL decay curves, which are often challenging to model accurately using conventional kinetic approaches.

Among the tested algorithms, the BR-based ANN model exhibited the best generalization performance and higher robustness across all dose intervals, including high-dose regimes where signal saturation and supralinear responses typically impair classical fitting techniques. The LM algorithm yielded efficient and highly accurate predictions in low-to-intermediate dose ranges due to its fast convergence characteristics, while the SCG algorithm provided stable, but slightly less precise, performance across the full dose range, with greater sensitivity to signal variance under extreme conditions.

Furthermore, the trained ANN models can not only predict OSL decay curves from given dose values but also infer absorbed doses from measured decay behavior, demonstrating their bidirectional applicability in luminescence-based dosimetric reconstructions. This dual functionality opens pathways for the integration of ANN-based modeling frameworks into automated, high-throughput dose estimation systems, particularly in retrospective dosimetry and luminescence dating applications where the rapid and accurate interpretation of complex decay data is essential.

It is important to note that the trained ANN model presented in this study is specifically tailored to the quartz samples obtained from Mediterranean beach sand. However, the ANN-based methodology is broadly applicable and can be adapted to other quartz sources, provided that a new training dataset is generated to capture their distinct luminescence characteristics. This approach is not intended to replace conventional protocols such as the single-aliquot regenerative-dose (SAR) method but to complement them by offering a flexible and automated tool for modeling OSL decay behavior and dose–response trends. Future studies may explore the generalizability of the model by applying the same framework to different quartz types with varying bleaching characteristics and trap structures.

Future research may focus on varying preheat conditions, incorporating temperature-dependent effects such as thermal quenching, and exploring hybrid ANN–physical modeling approaches to further enhance model interpretability, physical consistency, and predictive scalability.