Previous Article in Journal
RETRACTED: Hosni Mahmoud, H.A. Computerized Detection of Calcium Oxalate Crystal Progression. Crystals 2022, 12, 1450
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 15
Issue 8
10.3390/cryst15080714
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Revisiting Mn4Al11: Growth of Stoichiometric Single Crystals and Their Structural and Magnetic Properties

by
Roman A. Khalaniya
1,
Andrei V. Mironov
1,
Alexander N. Samarin
2,
Alexey V. Bogach
1,2,
Aleksandr N. Kulchu
1 and
Andrei V. Shevelkov
1,*
1
Department of Chemistry, Lomonosov Moscow State University, Moscow 119991, Russia
2
Prokhorov General Physics Institute of the Russian Academy of Sciences, Moscow 119991, Russia
*
Author to whom correspondence should be addressed.
Crystals 2025, 15(8), 714; https://doi.org/10.3390/cryst15080714 (registering DOI)
Submission received: 4 July 2025 / Revised: 23 July 2025 / Accepted: 2 August 2025 / Published: 4 August 2025
(This article belongs to the Section Crystalline Metals and Alloys)
Browse Figures
Versions Notes

Abstract

Stoichiometric single crystals of Mn4Al11 were synthesized from the elements using Sn as a flux. The crystal structure of Mn4Al11 was investigated using single crystal X-ray diffraction and showed a complex triclinic structure with a relatively small unit cell and interpenetrating networks of Mn and Al atoms. While our results generally agree with the previously reported data in the basic structure features such as triclinic symmetry and structure type, the atomic parameters differ significantly, likely due to different synthetic techniques producing off-stoichiometry or doped crystals used in the previous works. Our structural analysis showed that the view of the Mn substructure as isolated zigzag chains is incomplete. Instead, the Mn chains are coupled in corrugated layers by long Mn-Mn bonds. The high quality of the crystals with the stoichiometric composition also enabled us to study magnetic behavior in great detail and reveal previously unobserved magnetic ordering. Our magnetization measurements showed that Mn4Al11 is an antiferromagnet with TN of 65 K. The presence of the maximum above TN also suggests strong local interactions indicative of low-dimensional magnetic behavior, which likely stems from lowered dimensionality of the Mn substructure.

1. Introduction

Strong interactions between transition metal T and main group element E atoms often promote T-E intermetallic compounds to display unusual crystal structures and physical properties [1,2,3,4,5,6,7,8,9]. The crystal structures often deviate from the simple ordered close packing of atoms and exhibit large voids [2,4,8,10], two-center covalent bonds [1,11,12], and non-commensurate [13,14] or quasicrystalline order [15,16,17]. Unique electronic structures can also emerge from the d-p interactions resulting in non-trivial topological properties [8,9,18,19], superconductivity [20,21,22,23], or non-metallic behavior atypical for intermetallic compounds [5,7,11,13,24]. Strong T-E interactions can also result in the competition of magnetic interactions leading to a range of unusual magnetic properties, which can include magnetic frustration [8,10,25,26], spin reorientation [10,25], and non-collinear ordering [10,25,26].
The structure and properties of these compounds depend strongly on the number of valence electrons per transition metal atoms, or valence electron concentration (VEC) [1,2]. By changing the number of valence electrons in the intermetallic phase, one can significantly change the structural, electronic, and magnetic order. In some cases, one can induce a metal-insulator transition [24,27,28,29,30] or turn a ferromagnetic phase into an antiferromagnetic one or vice versa [31,32,33].
One of the examples of such a behavior is Mn4Al11, which features an unusual, even for the T-E compounds, low symmetry triclinic structure, where electronic and magnetic behavior can be significantly altered by controlling the number of valence electrons [34,35,36]. Using Cr-doping, weak ferro- or ferrimagnetism was achieved in the Mn4−xCrxAl11 solid solution [36], while the Ge doping leads to non-metallic behavior [35].
Despite the unique crystal structure and tunability of chemical properties, Mn4Al11 remains somewhat poorly studied. The information about its crystal structure presented in the literature is inconsistent [37,38], with the structural experiments performed on either Zn-doped or low-quality, or non-stochiometric crystals, with one of the reports indicating a significant number of Mn vacancies [37,38]. The electron diffraction also showed that Mn4Al11 are often formed as twinned crystals and can exhibit stacking faults [39,40]. Previous investigations of magnetization and electronic transport were performed on the impure powder sample, where magnetic ordering was not observed, but both magnetic susceptibility and electrical resistivity exhibited a noticeable maximum around 100 K indicative of low-dimensional behavior [34].
Given the complex crystal structure and twinning patterns, obtaining high quality single crystals of Mn4Al11 is necessary to resolve the disagreements between the literature data and to establish the proper structure and properties of this compound. In this paper, we present a new approach to grow and isolate pure and stoichiometric Mn4Al11 single crystals from a Sn flux, which allowed us to perform a detailed structural analysis of Mn4Al11 and characterization of its magnetic behavior. Our results show new notable features, such as the presence of Mn layers in the structure and the existence of magnetic ordering, both of which were not observed previously. We discuss these results and analyze them in comparison with the previous reports and the studies of related compounds.

2. Materials and Methods

Stoichiometric single crystals of Mn4Al11 were grown using a Sn flux. The samples were prepared from the high purity elements: Mn chips (99.9%, Merck, Darmstadt, Germany), Al pieces (99.99%, Sigma-Aldrich, Steinheim, Germany), and Sn pieces (99.999%, Sigma-Aldrich, Steinheim, Germany). Since both Mn and Al are highly reactive at elevated temperatures, several precautions were employed to prevent the oxidation of the sample in the course of the synthesis. Initial mixtures of the elements were placed in the Al2O3 crucibles, while the crucibles themselves were contained inside evacuated and sealed silica tubes during the annealing. For the single crystal growth, we tested two initial compositions: Mn4Al11Sn22 and Mn4Al11Sn44, the former resulting in large well-formed crystals. To check for the previously reported off-stoichiometry, we also performed synthesis of one Mn-deficient sample Mn3.8Al11Sn44.
The annealing was performed using the following temperature profile. Initially, the samples were heated up to 1000 °C, held at this temperature for 24 h, and then slowly cooled down to 600 °C at a rate of 1 °C/h. After that, the furnace was turned off. To remove the Sn flux, the samples were first centrifuged at 600 °C through the graphite wool, and then the remaining tin flux was removed using nitric acid. At first, the crystals were submerged in the concentrated (65%) nitric acid for half an hour to passivate the surface. Then, the acid was diluted in half by distilled water. The crystals were kept in this solution for several hours until the remaining Sn flux was fully oxidized. The crystals were then rinsed several times in distilled water. To remove the hydrated tin oxide, the crystals were cleaned in the acetone using ultrasonic bath. As a result of the synthesis, several small dark plate-like crystals (up to 3 mm in length) or needle-shaped twins were observed (Figure S1 in Supporting Information).
Although the crystals are highly resistant to nitric acid, in some cases, signs of etching were observed. Thus, the exposure of the crystals to the acid should not be left unsupervised. The purity of distilled water is also essential, since the presence of chloride ions in the acid solution can quickly lead to full dissolution of target crystals. Non-oxidizing acids were also tested as solvents for the Sn flux; however, they either failed to dissolve the flux, or dissolved the crystals themselves, the latter being the case for the hydrochloric acid.
The elemental composition of the crystals was studied by EDX analysis. The elemental analysis was performed using an electron microscope JEOL JSM 6490LV (JEOL, Tokyo, Japan) equipped with an Oxford Instruments Analytical INCA X-Sight system (Abingdon, UK) for the EDX analysis. The recorded spectra were analyzed using the INCA Microanalysis Suite (Oxford Instruments Analytical, Abingdon, UK).
Due to the low atomic number of Al and high absorption of its characteristic X-ray, the intensity of the Al Kα signal is heavily affected by the tilt of the studied edge. Thus, the apparent Al concentration can vary in the range from 68 to 78 at. %, depending on the tilt angle. The EDX measurements performed on clean and even surfaces show an even Mn:Al distribution (Figures S2 and S3 in Supporting Information) and a low variation in the intensities of the spectral lines, meaning that the variation of the composition within the crystals is negligible. In order to achieve more accurate EDX results, the tilt of the surface should be close to 0°. This was performed for the small single crystals later picked for the X-ray diffraction experiments, resulting in the calculated Al concentration being close to the expected value of 73.33 at. % (Table 1 and Table S1 in Supporting Information).
Despite the use of the Sn flux, the presence of Sn in the bulk of the crystals was not detected in our EDX measurements. Clean surfaces and chipped crystals show an even level of background noise at energies where the Sn L-lines are located (Figure S2 in Supporting Information). Highest calculated Sn concentration from an individual spectrum was around 0.05 at. %, which is close to the expected detection limit of Sn in a lighter element matrix [41]. The EDX analysis however, showed the presence of microscopic chunks of Sn covered in a tin oxide scattered on the surface of some of the crystals (Figures S3 and S4 in Supporting Information). As tin is superconducting below 3.7 K [42], special care needs to be taken in order to fully remove Sn flux from the surface of the crystals for magnetic measurements.
In order to confirm the stoichiometric composition of the obtained crystals and to determine their crystal structure, the crystals were studied by means of single crystal X-ray diffraction. The structural analysis was performed on the crystals from the Mn4Al11Sn44 and Mn3.8Al11Sn44 samples, and one plate-like crystal was selected from each sample. The diffraction studies were performed at room temperature using a Enraf-Nonius CAD-4 diffractometer (Ag Kα radiation, λ = 0.56083 Å, Enraf-Nonius, Delft, The Netherlands). The collected Bragg peaks were indexed in the triclinic cell of the P-1 space group, with both crystals showing practically identical unit cell parameters.
The crystal structure was solved by the Superflip program [43] implemented in the Jana2006 package [43]. The latter was also used for crystal structure refinement. To check for vacancies or anti-site defects, the occupancies of the individual sites were initially refined. The refined occupancies were within the error from the full occupancy. Thus, the site occupancies were fixed at unity in the final refinement. The refinement for the two crystals converged to practically identical atomic parameters with similar residuals.
Crystallographic data and refinement details for the Mn4Al11 single crystal obtained from the Mn4Al11Sn44 sample are given in Table 1, while the corresponding atomic parameters are presented in Table 2. Due to the similarity between the two crystals, the data regarding the Mn4Al11 single crystal obtained from the Mn-deficient Mn3.8Al11Sn44 sample is given in Tables S1 and S2 in Supporting Information. The comparison of the most important interatomic distances between the present study and the literature data is given in Table S3 in Supporting Information. The crystallographic information files are deposited in the CCDC (ref. numbers 2469767, 2469768). For the visualization of the crystallographic data, the VESTA 3 software was used [44].
Several crystals from the Mn4Al11Sn44 batch were also crushed and studied using powder X-ray diffraction using a Bruker D8 Advance diffractometer (Cu Kα, λ = 1.54184 Å, Bruker, Karlsruhe, Germany) equipped with a LYNXEYE detector (Bruker, Karlsruhe, Germany). Due to the plate-like shape of the crystals, the diffraction showed a pronounced texture in the powdered sample. Thus, only the le Bail fit using Jana2006 could be performed yielding cell parameters (a = 5.08751(9), b = 8.84822(17), c = 5.05519(11), α = 89.7961(14), β = 100.5194(11), γ = 105.3556(12)) that are consistent with the single crystal data (Table 1 and Table S1 in Supporting Information). Minor amounts of residual Sn flux and Mn5Al8 were also detected in the sample (Figure S5 in Supporting Information).
Magnetization of Mn4Al11 single crystals was measured using a Squid-type magnetometer MPMS3 (Quantum Design, San Diego, CA, USA) in various magnetic fields up to 5 T in the temperature range of 2–380 K. The magnetizations measurements of the crystals showed some of those to experience superconducting transition around 3 K. The examination of such crystals using the EDX analysis showed small chunks of Sn, scattered on the surface of the crystals (Figure S2 in Supporting Information). Only Sn-free crystals were selected for measuring the magnetic properties of Mn4Al11.

3. Results and Discussion

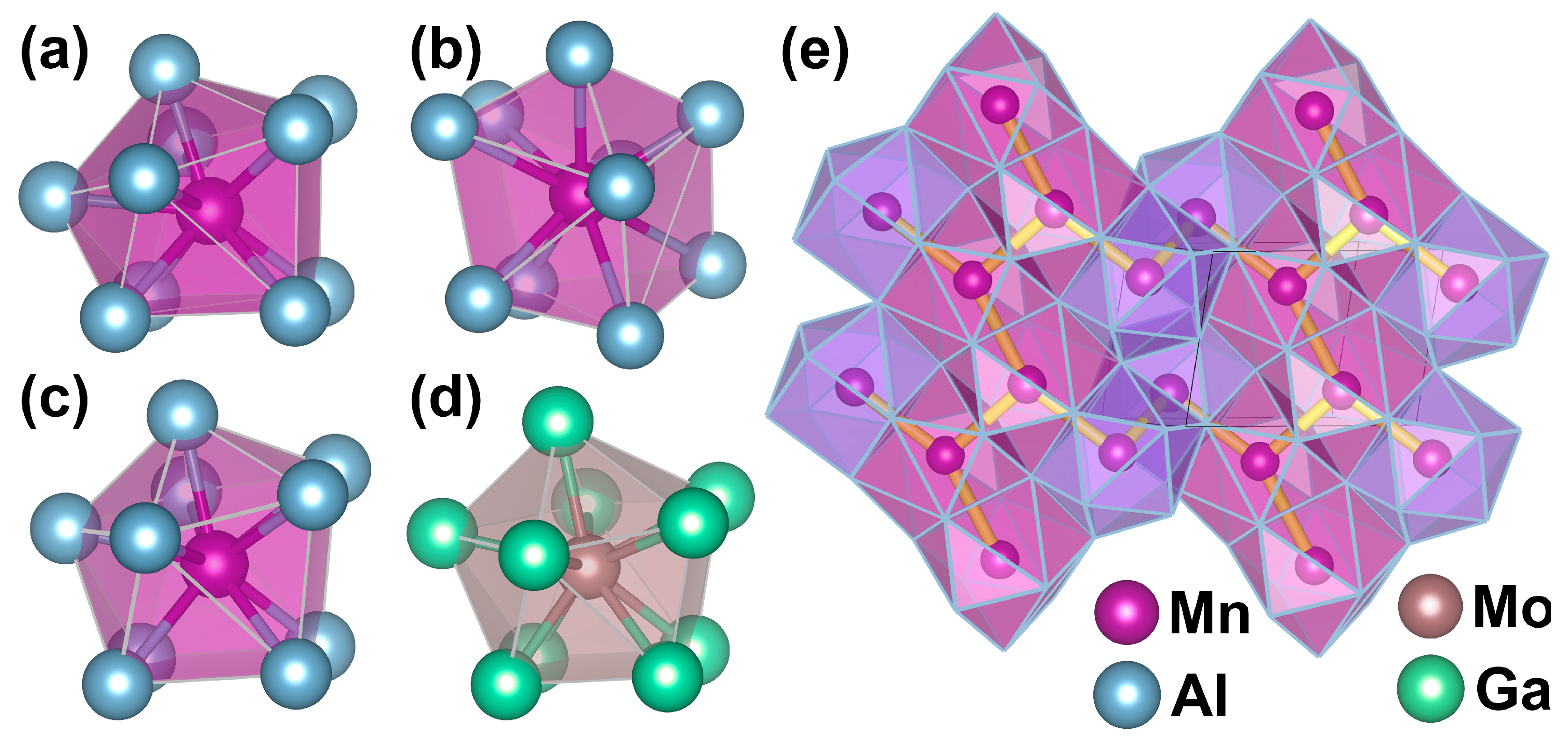
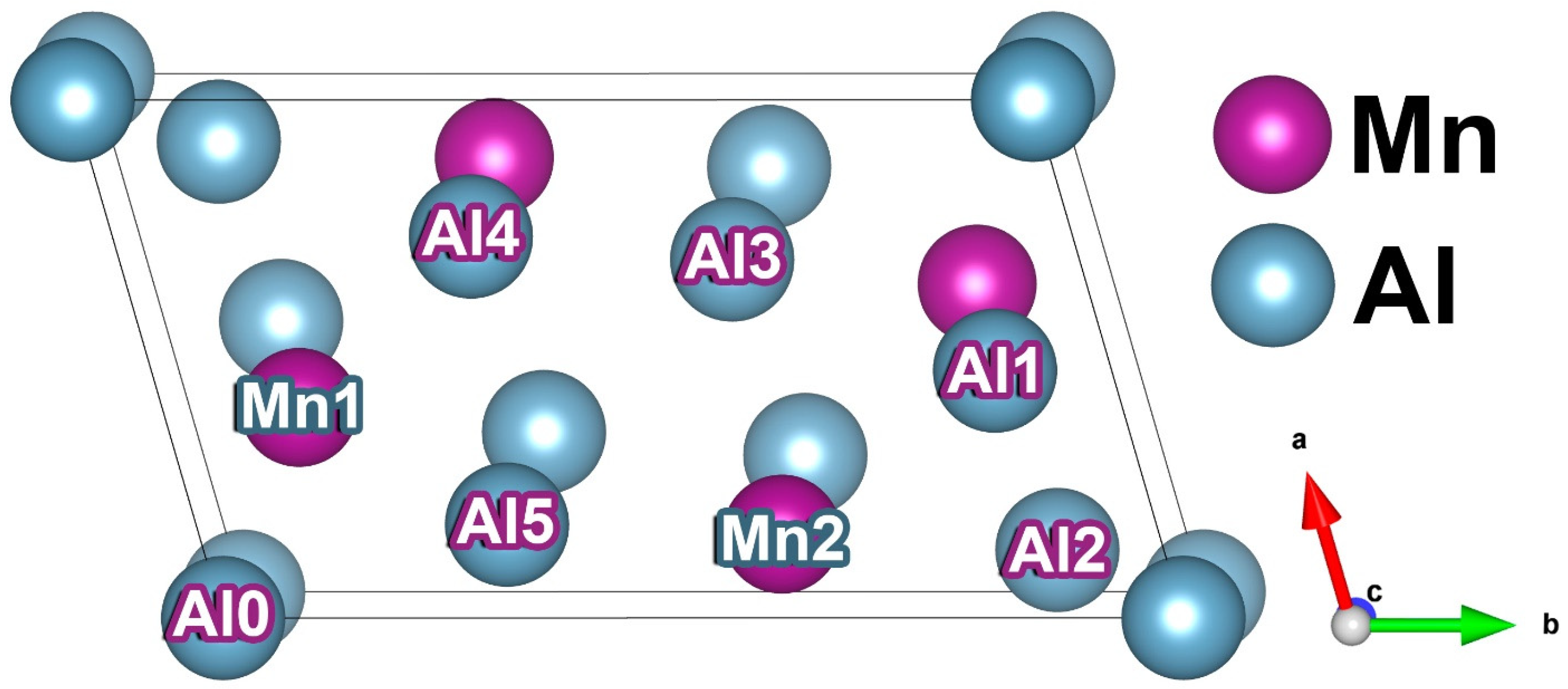
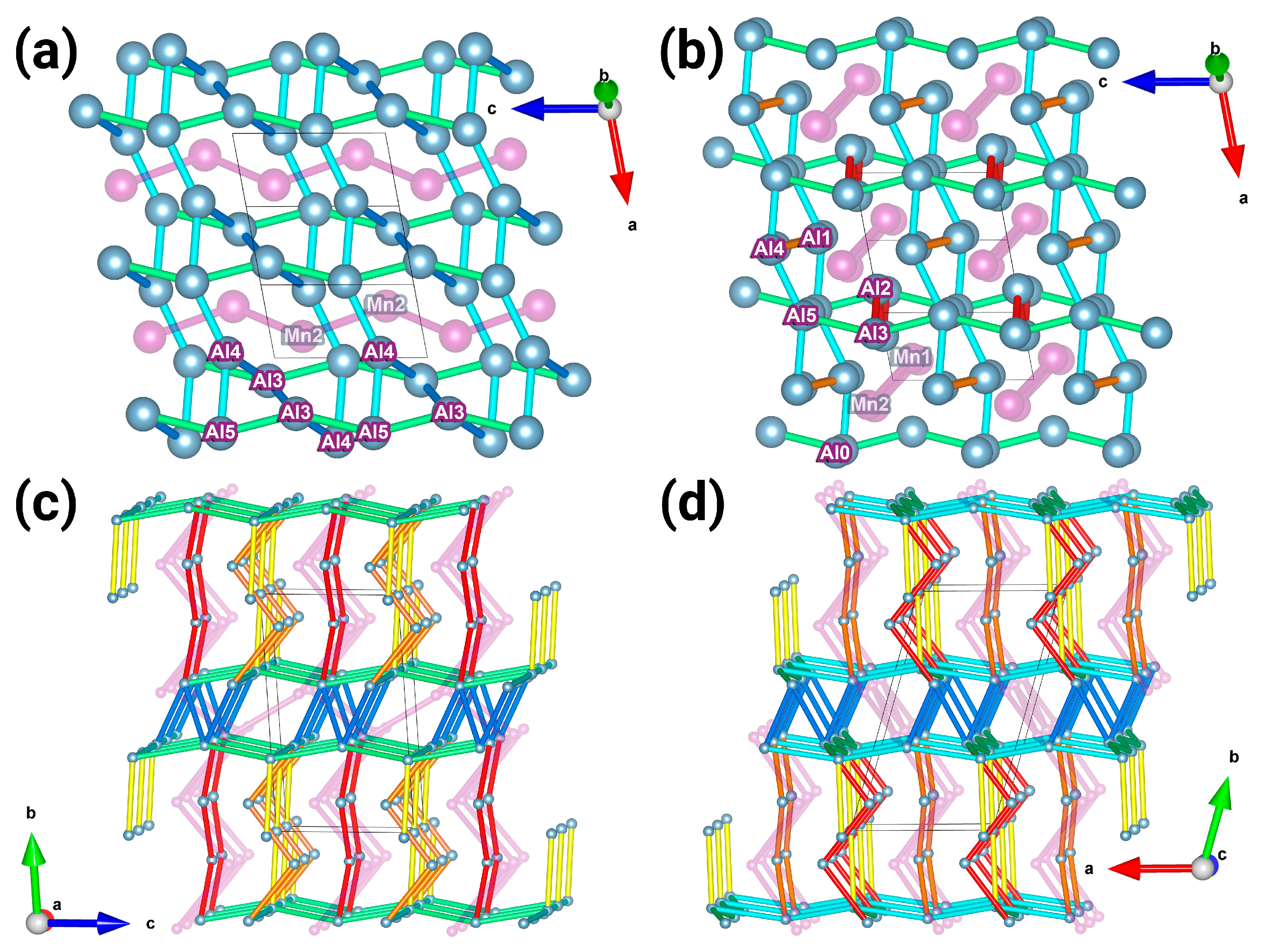
3.1. Crystal Structure of Mn4Al11

Our single crystal X-ray diffraction studies showed that Mn4Al11 crystallizes in the triclinic structure of the P-1 space group (a = 5.0876(12) Å, b = 8.8438(17) Å, c = 5.0562(11) Å, α = 89.800(16)°, β = 100.548(16)°, γ = 105.358(16)°, Z = 1). The crystal structure consists of eight crystallographic sites: two for Mn atoms and six for Al atoms. A unit cell of Mn4Al11 is presented in Figure 1.
No abnormalities were observed during our refinement of the structure. No appreciable variation of the occupancies of the individual sites was observed. Our refinement also yielded similar atomic displacement parameters (ADPs) for all atomic sites, most of Ueq lying in the range of 0.007–0.010 Å2 with Ueq of Mn1 being slightly lower. The calculated interatomic distances (Table S3 in Supporting Information) are also well within the common ranges for Mn-Al, Mn-Mn, and Al-Al contacts [45,46,47,48,49,50,51,52,53,54,55,56,57]. Given the large number of crystallographic sites and the triclinic unit cell, it seems reasonable to first dissect the crystal structure into individual Mn and Al substructures in order to simplify its description.
The Mn substructure is represented by corrugated layers (Figure 2), with each layer being stacked on top of the other. Inside these layers, the Mn atoms are connected through long 3.1–3.3 Å Mn-Mn bonds. These Mn bonds are much longer than typical metallic Mn-Mn bonds in elemental Mn [44,45] and are supported by four bridging Al atoms (Figure 2d). Despite long separations between Mn atoms, such bonds between transition metal atoms (T) with bridging p-element atoms are considered equivalent or isolobal to σ T-T bonds [1,2]. Mn1 atoms form three isolobal bonds: two longer bonds between each other and one shorter bond with a Mn2 atom, while Mn2 atoms form only two isolobal bonds: one between each other and one with a Mn1 atom.
The Al atoms surround Mn atoms creating 10-vertex polyhedra, which can be viewed as distorted 2-capped cubes (Figure 3a,b). Such a polyhedron can be also viewed as a centaur polyhedron [57] that combines one half of an icosahedron and one half of a cube. Due to the formation of isolobal bonds, MnAl10 polyhedra are fused by their rectangular edges, thus forming layers of MnAl10 polyhedra, which are joined through their Al vertices (Figure 3e).
Icosahedral coordination of transition element atoms is one of the characteristic features of the Al-based intermetallics [16,17,46,47,48,49,50,51,52,53,54,55], including the Al-rich compounds in the Mn-Al system [47,48,49,50,51,52,53,54,55,56,58], with Al-based quasicrystalline phases being one of the well-known results of such a coordination [16,17]. The cubic coordination of a transition metal is also quite frequent in intermetallic compounds as a whole [1,4,59,60,61,62,63,64,65,66,67,68,69], including several Al-based alloys of the CsCl or anti-CaF2 structure types [61,64,65,69]. Similar MnAl10 polyhedra can be also found in MnAl6 (Figure 3c) [47], although the rectangular Al edges do not act as bridges that support the Mn network, since the Mn atoms are practically isolated, with the shortest Mn-Mn distance being 4.472 Å [47]. Similar centaur polyhedra TGa10 can be also found in Ga-based compounds, where they act as a structural basis for the Ga-rich family of superconductors and are often referred to as endohedral clusters [21,22,23,70].
The Mn-Al distances vary quite noticeably within the MnAl10 polyhedra. Each polyhedron contains one short Mn-Al bond of 2.40–2.41 Å, several longer contacts of 2.50–2.65 Å, and a few longest Mn-Al bonds of 2.70–2.78. It is interesting to note that the average Mn-Al distances are longer for Mn2 atoms, which could be due to the formation of the additional Mn-Mn isolobal bond, which Mn1 atoms lack.
Crystals 15 00714 g003
Figure 3. MnAl10 polyhedra in the crystal structure of Mn4Al11 (a,b) and MnAl6 (c); MoGa10 polyhedra in the crystal structure of Mo4Ga20Se (d); fragment of one layer of fused MnAl10 polyhedra in Mn4Al11 (e) with Mn-Mn isolobal bonds shown in yellow. The crystallographic data for MnAl6 and Mo4Ga20Se were taken from the literature [48,70] and visualized using VESTA 3 [44].
Figure 3. MnAl10 polyhedra in the crystal structure of Mn4Al11 (a,b) and MnAl6 (c); MoGa10 polyhedra in the crystal structure of Mo4Ga20Se (d); fragment of one layer of fused MnAl10 polyhedra in Mn4Al11 (e) with Mn-Mn isolobal bonds shown in yellow. The crystallographic data for MnAl6 and Mo4Ga20Se were taken from the literature [48,70] and visualized using VESTA 3 [44].
Crystals 15 00714 g003
Since there are no Al-Al bonds located outside of the Mn-centered polyhedra, the geometry of Al network seems to be mostly guided by the Mn-Al interactions and the formation of the Mn-Mn isolobal bonds. However, the Al atoms are not isolated in the structure and provide an array of relatively short Al-Al bonds forming quite a unique network.
This substructure can be subdivided into several zigzag or linear Al chains. Two of the zigzag chains (Al3-Al5 and Al4-Al5) are infinite and intersect forming layers at y~0.35 and 0.65 (Figure 4a,c,d). These layers are located close to each other and form double layers through the formation of finite Al4-Al3-Al3-Al4 chains. Two other finite zigzag chains (Al3-Al2-Al2-Al3 and Al4-Al1-Al1-Al4) are located between y = 0.62 and 1.38 and run along the b-axis (Figure 4b). The linear Al5-Al0-Al5 chain is also located in the layer between y = 0.62 and 1.38. Together, these three chains connect the double layers composed of Al3, Al4, and Al5 atoms (Figure 4c,d).
The Al-Al distances in these chains are significantly shorter than the Al-Al distances in the pure Al (2.863 Å) [56]. In the case of the zigzag chains, the distances vary from 2.592 Å (the shorter Al3-Al5 bond) to 2.697 Å (the longer Al3-Al5 bond), while the linear Al5-Al0-Al5 chain shows two identical long Al0-Al5 bonds of 2.750 Å.
By combining the Mn and Al substructures, an alternative description of the Mn4Al11 structure can be made as two interpenetrating networks of Mn and Al atoms (Figure 4). The layered Mn network can be seen as connected zigzag chains weaving through the 3-dimensional Al network, with the Mn2-Mn2 infinite chains running through the Al3–Al5 double layers (Figure 4a) and finite Mn2-Mn1-Mn1-Mn2 chains going along the Al chains in the Al0–Al2 layer (Figure 4b).
Several structural studies of Mn4Al11 and its doped derivatives were reported previously [35,36,37,38,39,40], including the X-ray structural analyses in the reports of Bland [37], Kontio et al. [38], Singh et al. [35], and Noor et al. [36]. While the basic features of the crystal structure determined in our work, such as crystal symmetry, cell parameters and the number of crystallographic sites, are consistent with the previous reports, the atomic parameters differ between the works leading in some cases to the different description of the structure as a whole.
The first structural analysis of Mn4Al11 performed by Bland [37] was made on crystals obtained from a Zn flux, which resulted in a small amount of Zn incorporated in the crystal. Despite the observed presence of Zn in the crystals, the report of Bland did not include Zn atoms in the refinement. Surprisingly, both the position of Mn atoms and Mn-Mn distances are comparable to the present work. The coordinates of some Al sites, however, noticeably differ, which could be due to Zn for Al substitution.
The second structural investigation was performed by Kontio et al. [49], where the crystals were obtained mechanically from the solidified and annealed arc-melted Mn4Al11 lump. Most of the differences with the work by Kontio et al. [49] lie in the description of the Mn2 site, which is not fully occupied in the earlier report and shifted in the z direction leading to the large difference in calculated Mn2-Mn2 distances of around 0.1 Å (see Table S1 in Supporting Information).
This difference between Mn-Mn distances in the structural model by Kontio et al. [49] suggests that Mn1 and Mn2 atoms form isolated infinite Mn chains Mn1-Mn1-Mn2-Mn2, with long separations between Mn2 atoms in the different chains. In our study, we found that there is much less difference between intrachain and interchain Mn-Mn distances in the stoichiometric Mn4Al11. Specifically, intrachain and interchain Mn2-Mn2 distances differ by only 0.25 Å, and not by 0.45 Å, as inferred from the previously reported data [49] (see Table S1 in Supporting Information).
Given the similarities in the description of the Mn2 site between our work and the work of Bland, it seems that the flux techniques used in the present work and by Bland [48] yield crystals with the stoichiometric Mn content, while the technique used by Kontio et al. [49] indeed yields non-stoichiometric crystals, likely due to the loss of volatile Mn during the arc-melting stage. Unfortunately, we were unable to verify the effect of Mn vacancies on the interatomic distances, since our attempt of synthesis of Mn-deficient crystals from the Sn flux using a lower initial Mn content yielded perfectly stoichiometric crystals virtually identical to those obtained from the samples with the initially stoichiometric Mn:Al ratio (Tables S1 and S2 in Supporting Information).
Since the crystal used by Kontio et al. [38] was mechanically extracted from the annealed arc-melted lump, the difference in the atomic parameters could also be due to the lower quality of the crystal itself. The recent report by Xian et al. [39] showed that the crystals of the Mn4Al11 can be twinned along the b*-axis and the (1 0 −1) direction, while the electron diffraction studies performed by Yoshida [40] shows possible stacking faults. This view is also supported by a high value of the R-factor (0.067) achieved by Kontio et al. [38] and large differences in the atomic displacement parameters, despite the refinement of the occupancies of the sites.
Two recent structural investigations by Singh et al. [35] and Noor et al. [36]. were performed on the samples heavily doped by Ge and Cr, namely Mn4Al10Ge and Mn2.26Cr1.74Al11, respectively. Due to the high level of doping and different synthetic techniques used in these works, it is difficult to draw any conclusions based on the comparison between the structural models. It should be noted that Singh et al. [46] use different naming of the Al sites and present the atomic parameters for only five out of six Al sites.

3.2. Magnetic Properties of Mn4Al11

Magnetization measurements of Mn4Al11 single crystals showed relatively low magnetization throughout the entire measured temperature range (Figure 5 and Figure S6 in Supporting Information). The magnetic moment per one Mn atom did not exceed 0.01 μB even in 5 T field.
Above 170 K, the compound exhibits Curie–Weiss behavior. Approximation by the Curie–Weiss law yielded the effective moment μeff of 1.2 μB per one Mn atom and negative Weiss temperature θW ranging from −92 to −96 K depending on the orientation of a crystal (Figure S7 in Supporting Information).
The magnetic susceptibility χ(T) reaches a local maximum at 100 K, after which it starts decreasing slowly upon further cooling. A sign of the phase transition, however, only appears at a lower temperature of 65 K, where we observe a pronounced kink in the susceptibility in all fields up to 5 T (Figure 5a,b and Figure S6a,b in Supporting Information). This temperature also marks an onset of a divergence between the susceptibility curves for different orientations of the crystal. The susceptibility perpendicular to the b*-axis χ⟂(T) experiences a noticeable drop right below 65 K, while this effect is much less pronounced for the susceptibility along the b*-axis χ||(T). This suggests the antiferromagnetic ordering of the magnetic moments in the ac plane.
At 50 K, susceptibility begins to increase again upon cooling, suggesting changes in the magnetic structure or the presence of paramagnetic centers. Since the magnetic susceptibility increases with the magnetic field in this region, indicating field-induced spin reorientation processes, the former appears to be more likely.
The presence of the susceptibility maximum above the Neel temperature is a characteristic sign of low-dimensional magnetic systems with strong local antiferromagnetic interactions [71,72,73]. In the intermetallic compounds, similar behavior was previously observed in our studies of the Fe32+δGe35−xEx (E = Si, P, As) family of compounds, which showed a low-dimensional transition metal substructure [25,74,75,76]. In the case of Fe32+δGe33As2 and Fe32+δGe35−xPx, we also observed an increase in the magnetic susceptibility at low temperatures, which was suggested to be a result of the establishment of a non-collinear order [74,75,76]. It is worth noting, however, that all Fe32+δGe35−xEx (E = Si, P, As) compounds exhibited a large degree of magnetic frustration with the frustration parameter f = TN/|θW|~3 [25,74,75,76]. In the case of Mn4Al11, the values of TN and |θW| are much closer to each other (f~1.5), indicating the absence of strong magnetic frustration.
Previous magnetization studies of Mn4Al11 performed by Dunlop and Grüner [34] using powder samples showed an overall similar shape of the magnetic susceptibility curve with a clear maximum at 100 K and an upturn, which starts below 40 K. Dunlop and Grüner [34] concluded the latter to be a result of an off-stoichiometry or an impurity; on the contrary, our results show that the upturn is very likely to be an intrinsic property of the compound. However, the susceptibility curves obtained by Dunlop and Grüner [34] are smooth in the vicinity of 65 K, and no other anomalies in the magnetic susceptibility indicating the magnetic ordering were observed in the earlier report.
The paper by Dunlop and Grüner [34] also mentions magnetic diffraction studies performed at 4.2 and 300 K, which corroborate the absence of a long-range magnetic order. According to the authors [34], the diffraction pattern collected at 4.2 K did not display any additional Bragg peaks or noticeable changes in the intensities of structural reflections compared to the diffraction pattern at 300 K. Since no additional details were provided about the neutron diffraction results, and the neutron diffraction patterns themselves were not presented in the paper [34], we can only speculate on whether the long-range order was really absent in the samples of Dunlop and Grüner.
Given the low effective magnetic moment of about 1.2 μB/Mn estimated from the Curie–Weiss fit and the metallic nature of the system, the Mn magnetic moment in the ordered state may be in the range of a few tenths of the Bohr magneton. In the cases of complex low symmetry magnetic structures with low magnetic moments, magnetic reflections may have very low intensities with long exposure times and large amounts of compounds that are required to obtain the complete diffraction pattern [76].
The absence of any magnetic susceptibility anomaly near 65 K also does not exclude the formation of the long-range magnetic order. Similar smooth behavior of magnetic susceptibility near the TN was observed for previously mentioned Fe32+δGe35−xEx (E = Si, P, As) [25,74,75,76]. A clear indication of the phase transition in these cases could only be obtained by comparing the curves obtained in different magnetic fields or orientations of the crystals, or by heat capacity and neutron diffraction measurements [25,74,75,76].
The second possibility is that the properties of the compound are very sensitive to the changes in the composition and the presence of off-stoichiometric structural defects, which were observed in some similar compounds. In the case of Al-based intermetallic alloys, one of the most well-known examples is the FeAl alloy, where magnetic ordering is absent in the structurally ordered alloy but can turn up due to the anti-site defects [66], for instance, if the sample is obtained through rapid quenching. Analogous Ga-based CoGa alloy also shows similar behavior, with anti-site defects being responsible for the magnetic ordering [67,68].
In the cases of related p-element-rich compounds such as Mn4Si7, Fe2Ge3 and FeGa3, which are known to display off-stoichiometry, different samples can show noticeably different magnetic behavior [29,77,78,79,80,81,82]. Mn4Si7 can exhibit excess in Mn, which can lead to weak ferromagnetism [29,77], while stoichiometric Mn4Si7 is diamagnetic [29]. In the case of FeGa3, the presence of additional Fe in the interstitial positions or in one of the Ga sites results in weak ferromagnetic behavior [78,79], which the stoichiometric compound lacks showing diamagnetic response [78]. Different samples of Fe2Ge3 prepared by similar techniques demonstrate either temperature-dependent paramagnetism [80], or temperature-independent paramagnetism [81], or even weak ferromagnetism [82].
Given the lack of data on the characterization of samples presented by Dunlop and Grüner [34], additional studies aimed at reproduction of their results are necessary to correctly determine the origin of the observed discrepancies between the works.

4. Conclusions

Single crystals of Mn4Al11 were grown using Sn as a flux and characterized comprehensively by X-ray diffraction, energy dispersion spectroscopy, and magnetization measurements. Despite the use of Sn, both elemental analysis and crystal structure refinement showed the crystals to be stoichiometric and Sn-free. A high quality of the obtained crystals shows that the use of an additional element as a flux does not necessarily lead to contamination of target crystals with the impurity element and may even be preferable over the self-flux techniques.
While our results confirm the general view of the crystal structure and the magnetic behavior, we observed notable discrepancies with the literature data, which can be due to the structural defects in the samples used in previous works. Atomic coordinates and consequently interatomic distances determined in this study differ noticeably from the literature data leading to the different description of the Mn substructure. Magnetic measurements showed low magnetization and the appearance of the antiferromagnetic transition at 65 K, which was not previously reported for off-stoichiometric or lightly doped samples.
Given the lack of information presented in the literature and the observed discrepancies between our results and the literature data, additional experiments are required to evaluate and properly compare the results presented in the different works. Specifically, additional experiments are needed to verify the results obtained on the arc-melted samples to determine to which extent the properties of compound are affected by structural defects and possible off-stoichiometry. New synthetic techniques for Mn4Al11 also need to be developed, which will enable one to control both the presence of structural defects and the composition.
However, the results presented and discussed in this paper illustrate that, while the T-E intermetallic compounds present a great platform for tailoring physical behavior, their structure and properties can be quite sensitive to the quality of the samples and the choice of a preparation technique; therefore, special attention needs to be paid to the thorough characterization of the samples and further to relate the observed properties with fine details of the crystal structure. In the case of Mn4Al11, this is exemplified by the possible dependence of magnetic properties upon the occupancy of the Mn positions and the concomitant substructure of manganese.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15080714/s1; Table S1: Crystallographic and refinement parameters for the Mn4Al11 single crystal obtained from the Mn3.8Al11Sn44 sample; Table S2: Atomic coordinates and displacement parameters for the Mn4Al11 single crystal obtained from the Mn3.8Al11Sn44 sample. The occupancies of the sites were constrained at unity (see text); Table S3: Comparison between interatomic distances in the crystal structure of Mn4Al11 calculated using our data (the crystal from the Mn4Al11Sn44 sample) and the data published by Bland [37] and Kontio et al. [38]. Differences in the reported distances that are above 0.03 Å are marked in bold; Figure S1: Optical microphotograph of the Mn4Al11 crystals; Figures S2: EDX element mapping of a Mn4Al11 single crystal: backscattered electron image (a), images in Al Kα (b), Mn Kα (c), combined spectrum from all measured points (d,e), close up of the region containing Sn L-lines, which are shown in green (e) The recorded spectrum is shown in yellow, the calculated spectrum is shown in red; Figure S3: EDX element mapping of a Mn4Al11 single crystal with small Sn chunks attached to it: backscattered electron image (a), images in Al Kα (b), Mn Kα (c) and Sn Lα (d); Figure S4: EDX spectrum of a Mn4Al11 single crystal with a Sn chunk attached to it. The recorded spectrum (Spectrum 1) is shown in yellow, the calculated spectrum is shown in red. The inset shows backscattered electron image of the crystal; Figure S5: Powder X-ray diffraction pattern of the crushed Mn4Al11 crystals from the Mn4Al11Sn44 sample. The inset shows the region between 39.5 and 46.4 degrees. The upper black dots represent the experimental diffraction pattern, and the red line shows the calculated pattern obtained from a le Bail fit. Peak positions are given by the ticks. The difference plot is shown by the black line in the bottom part. The X-ray pattern shows minor amounts of Mn5Al8 and residual Sn flux; Figure S6: Magnetic properties of Mn4Al11: magnetic susceptibility of a single crystal along the b*-axis (a) and perpendicular to it (b); magnetic moment as a function of the magnetic field at different temperatures of a single crystal along the b*-axis (c) and perpendicular to it (d); Figure S7: The inverse magnetic susceptibility of Mn4Al11: the inverse magnetic susceptibility of a single crystal along the b*-axis (a) and perpendicular to it (b). The red line represents the Curie–Weiss fit above 170 K using the Curie–Weiss law χ = C/(T − θW). The refined Curie–Weiss parameters are shown on the graph. The effective moment per Mn atom μeff/Mn was calculated as μeff/Mn = 3 k B C n M n N A μ B , where nMn is the number of Mn atoms in the formula unit, kB is the Boltzmann constant, NA is the Avogadro number, and μB is the Bohr magneton.

Author Contributions

Conceptualization, R.A.K. and A.V.S.; methodology, R.A.K., A.V.M. and A.V.B.; validation, R.A.K., A.V.M. and A.V.B.; formal analysis, R.A.K., A.V.M. and A.V.B.; investigation, R.A.K., A.V.M., A.N.S., A.V.B. and A.N.K.; resources, A.V.S.; data curation, R.A.K.; writing—original draft preparation, R.A.K.; writing—review and editing, R.A.K. and A.V.S.; visualization, R.A.K. and A.V.B.; supervision, A.V.S.; project administration, A.V.S.; funding acquisition, A.V.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Russian Science Foundation, grant number 25-13-00005.

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.

Acknowledgments

We thank the Lomonosov Moscow State University Program of Development for the use of LYNXEYE detector. The authors also thank Valery Yu. Verchenko for his help during the powder diffraction experiment.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Yannello, V.J.; Fredrickson, D.C. Generality of the 18−n rule: Intermetallic structural chemistry explained through isolobal analogies to transition metal complexes. Inorg. Chem. 2015, 54, 11385–11398. [Google Scholar] [CrossRef]
  2. Yannello, V.J.; Lu, E.; Fredrickson, D.C. At the limits of isolobal bonding: π-based covalent magnetism in Mn2Hg5. Inorg. Chem. 2020, 59, 12304–12313. [Google Scholar] [CrossRef]
  3. Häussermann, U.; Viklund, P.; Boström, M.; Norrestam, R.; Simak, S.I. Bonding and physical properties of Hume-Rothery compounds with the PtHg4 structure. Phys. Rev. B 2001, 63, 125118. [Google Scholar] [CrossRef]
  4. Khalaniya, R.A.; Shevelkov, A.V. When two is enough: On the origin of diverse crystal structures and physical properties in the Fe-Ge system. J. Solid State Chem. 2019, 270, 118–128. [Google Scholar] [CrossRef]
  5. Likhanov, M.S.; Shevelkov, A.V. Intermetallic compounds with non-metallic properties. Rus. Chem. Bull. 2020, 69, 2231–2255. [Google Scholar] [CrossRef]
  6. Rimmler, B.H.; Pal, B.; Parkin, S.S. Non-collinear antiferromagnetic spintronics. Nat. Rev. Mater. 2025, 10, 109–127. [Google Scholar] [CrossRef]
  7. Verchenko, V.Y.; Tsirlin, A.A. Semiconducting and Metallic Compounds within the IrIn3 Structure Type: Stability and Chemical Bonding. Inorg. Chem. 2022, 61, 3274–3280. [Google Scholar] [CrossRef] [PubMed]
  8. Wang, Q.; Lei, H.; Qi, Y.; Felser, C. Topological quantum materials with Kagome lattice. Acc. Mater. Res. 2024, 5, 786–796. [Google Scholar] [CrossRef]
  9. Yin, J.X.; Lian, B.; Hasan, M.Z. Topological Kagome magnets and superconductors. Nature 2022, 612, 647–657. [Google Scholar] [CrossRef]
  10. Teng, X.; Oh, J.S.; Tan, H.; Chen, L.; Huang, J.; Gao, B.; Yin, J.-X.; Chu, J.-H.; Hashimoto, M.; Lu, D.; et al. Magnetism and charge density wave order in kagome FeGe. Nat. Phys. 2023, 19, 814–822. [Google Scholar] [CrossRef]
  11. Likhanov, M.S.; Khalaniya, R.A.; Verchenko, V.Y.; Gippius, A.A.; Zhurenko, S.V.; Tkachev, A.V.; Fazlizhanova, D.I.; Kuznetsov, A.N.; Shevelkov, A.V. ReGaGe2: An intermetallic compound with semiconducting properties and localized bonding. Chem. Comm. 2019, 55, 5821–5824. [Google Scholar] [CrossRef] [PubMed]
  12. Armbrüster, M.; Schnelle, W.; Cardoso-Gil, R.; Grin, Y. Chemical bonding in compounds of the CuAl2 family: MnSn2, FeSn2 and CoSn2. Chem. A Eur. J. 2010, 16, 10357–10365. [Google Scholar] [CrossRef] [PubMed]
  13. Sato, N.; Ouchi, H.; Takagiwa, Y.; Kimura, K. Glass-like lattice thermal conductivity and thermoelectric properties of incommensurate chimney-ladder compound FeGeγ. Chem. Mater. 2016, 28, 529–533. [Google Scholar] [CrossRef]
  14. Khalaniya, R.A.; Verchenko, V.Y.; Bogach, A.V.; Likhanov, M.; Shevelkov, A.V. Itinerant ferromagnet Re4−xMnxGe7−δ (x = 0.9 − 1.5, δ = 0.42 − 0.44) with incommensurate chimney-ladder structure stabilised at ambient pressure. Dalton Trans. 2023, 52, 10657–10661. [Google Scholar] [CrossRef]
  15. Elser, V.; Henley, C.L. Crystal and quasicrystal structures in Al-Mn-Si alloys. Phys. Rev. Lett. 1985, 55, 2883–2886. [Google Scholar] [CrossRef]
  16. Yamamoto, A.; Hiraga, K. Structure of an icosahedral Al-Mn quasicrystal. Phys. Rev. B 1988, 37, 6207–6215. [Google Scholar] [CrossRef]
  17. Kimura, K.; Hashimoto, T.; Suzuki, K.; Nagayama, K.; Ino, H.; Takeuchi, S. Structure and stability of quasicrystalline Al–Mn alloys. J. Phys. Soc. Jpn. 1986, 55, 534–543. [Google Scholar] [CrossRef]
  18. Li, H.; Ding, B.; Chen, J.; Li, Z.; Hou, Z.; Liu, E.; Zhang, H.; Xi, X.; Wu, G.; Wang, W. Large topological Hall effect in a geometrically frustrated Kagome magnet Fe3Sn2. Appl. Phys. Lett. 2019, 114, 192408. [Google Scholar] [CrossRef]
  19. Samanta, S.; Park, H.; Lee, C.; Jeon, S.; Cui, H.; Yao, Y.X.; Hwang, J.; Choi, K.-Y.; Kim, H.S. Emergence of flat bands and ferromagnetic fluctuations via orbital-selective electron correlations in Mn-based kagome metal. Nat. Comm. 2024, 15, 5376. [Google Scholar] [CrossRef]
  20. Banno, N. Low-temperature superconductors: Nb3Sn, Nb3Al, and NbTi. Superconductivity 2023, 6, 100047. [Google Scholar] [CrossRef]
  21. Verchenko, V.Y.; Shevelkov, A.V. Endohedral cluster intermetallic superconductors: At the frontier between chemistry and physics. Dalton Trans. 2021, 50, 5109–5114. [Google Scholar] [CrossRef]
  22. Xie, W.; Luo, H.; Phelan, B.F.; Klimczuk, T.; Cevallos, F.A.; Cava, R.J. Endohedral gallide cluster superconductors and superconductivity in ReGa5. Proc. Nat. Acad. Sci. USA 2015, 112, E7048–E7054. [Google Scholar] [CrossRef]
  23. Ryżyńska, Z.; Wiśniewski, P.; Kaczorowski, D.; Xie, W.; Cava, R.J.; Klimczuk, T.; Winiarski, M.J. Superconductivity in the endohedral Ga cluster compound PdGa5. J. Phys. Chem. C 2021, 125, 11294–11299. [Google Scholar] [CrossRef]
  24. Häussermann, U.; Boström, M.; Viklund, P.; Rapp, Ö.; Björnängen, T. FeGa3 and RuGa3: Semiconducting intermetallic compounds. J. Solid State Chem. 2002, 165, 94–99. [Google Scholar] [CrossRef]
  25. Khalaniya, R.A.; Verchenko, V.; Mironov, A.V.; Samarin, A.N.; Bogach, A.; Kulchu, A.N.; Polevik, A.O.; Wei, Z.; Dikarev, E.V.; Stern, R.; et al. Spin reorientation and magnetic frustration in Fe32+δGe35−xSix with a kagome lattice broken by crystallographic intergrowth. Dalton Trans. 2025, 54, 8317–8330. [Google Scholar] [CrossRef]
  26. Khalaniya, R.A.; Verchenko, V.Y.; Sobolev, A.V.; Presniakov, I.A.; Wei, Z.; Dikarev, E.V.; Shevelkov, A.V. Intricate magnetic behavior of Fe6Ge5 and its origin within a complex iron framework: The magnetic and 57Fe Mössbauer study. J. Alloy Compd. 2022, 902, 163759. [Google Scholar] [CrossRef]
  27. Kotur, B.; Babizhetskyy, V.; Bauer, E.; Kneidinger, F.; Danner, A.; Leber, L.; Michor, H. Metal Site Doping in the Narrow-Gap FeGa3 Semiconductor. Mater. Sci. 2013, 49, 211–219. [Google Scholar] [CrossRef]
  28. Ramachandran, B.; Syu, K.Z.; Kuo, Y.K.; Gippius, A.A.; Shevelkov, A.V.; Verchenko, V.Y.; Lue, C.S. Thermoelectric performance of intermetallic FeGa3 with Co doping. J. Alloys Compd. 2014, 608, 229–234. [Google Scholar] [CrossRef]
  29. Hammura, K.; Udono, H.; Ohsugi, I.J.; Aono, T.; De Ranieri, E. Magnetisation of bulk Mn11Si19 and Mn4Si7. Thin Solid Film. 2011, 519, 8516–8519. [Google Scholar] [CrossRef]
  30. Adams, T.; Mühlbauer, S.; Neubauer, A.; Münzer, W.; Jonietz, F.; Georgii, R.; Böni, P.; Pedersen, B.; Schmidt, M.; Rosch, A.; et al. Skyrmion lattice domains in Fe1−xCoxSi. Phys. Rev. B Cond. Matter Mater. Phys. 2010, 81, 041203. [Google Scholar] [CrossRef]
  31. Kitagawa, J.; Yakabe, G.; Nakayama, A.; Nishizaki, T.; Tsubota, M. Competition between ferromagnetic and antiferromagnetic states in Al8.5−xFe23Ge12.5+x (0 ≤ x ≤ 3). J. Solid State Chem. 2020, 284, 121188. [Google Scholar] [CrossRef]
  32. Venturini, G. Magnetic study of the HfFe6Ge6-type solid solutions ScMn6Ge6−xGax and LuMn6Ge6−xGax (0.25≤ x≤ 1.50). J. Alloys Compd. 2000, 309, 20–25. [Google Scholar] [CrossRef]
  33. Venturini, G. Antiferro-to ferromagnetic transition in HfFe6Ge6-type solid solution YMn6Ge6−xGax (0.25≤ x ≤ 2.00). J. Alloys Compd. 2000, 311, 101–108. [Google Scholar] [CrossRef]
  34. Dunlop, J.B.; Grüner, G. One-dimensional effects in the intermetallic compound Al11Mn4. Solid State Comm. 1976, 18, 827–829. [Google Scholar] [CrossRef]
  35. Singh, P.; Del Rose, T.; Mudryk, Y.; Pecharsky, V.K.; Johnson, D.D. Designed metal-insulator transition in low-symmetry magnetic intermetallics. Phys. Rev. B 2024, 109, 064207. [Google Scholar] [CrossRef]
  36. Noor, M.; Law, K.; Yasmin, N.; Hauser, A.; Besara, T. Ferrimagnetism and half-metallicity in Cr-substituted Mn4–xCrxAl11. J. Phys. Cond. Matter 2025, 37, 235704. [Google Scholar] [CrossRef] [PubMed]
  37. Bland, J.A. Studies of aluminum-rich alloys with the transition metals manganese and tungsten. II. The crystal structure of δ (Mn-Al)-Mn4Al11. Acta Crystallogr. 1958, 11, 236–244. [Google Scholar] [CrossRef]
  38. Kontio, A.; Stevens, E.D.; Coppens, P.; Brown, R.D.; Dwight, A.E.; Williams, J.M. New investigation of the structure of Mn4Al11. Acta Crystallogr. Sect. B 1980, 36, 435–436. [Google Scholar] [CrossRef]
  39. Xian, J.W.; Peng, L.; Zeng, G.; Wang, D.; Gourlay, C.M. Al11Mn4 formation on Al8Mn5 during the solidification and heat treatment of AZ-series magnesium alloys. Materialia 2021, 19, 101192. [Google Scholar] [CrossRef]
  40. Yoshida, K. One-Dimensionally Disordered δ (Mn-Al) Structure in Vacuum Co-Deposited Film. J. Phys. Soc. Jpn. 1972, 32, 431–440. [Google Scholar] [CrossRef]
  41. Boato, G.; Gallinaro, G.; Rizzuto, C. Effect of transition-metal impurities on the critical temperature of superconducting Al, Zn, In, and Sn. Phys. Rev. 1966, 148, 353–361. [Google Scholar] [CrossRef]
  42. Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallogr.-Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
  43. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  44. Goldstein, J.I.; Newbury, D.E.; Michael, J.R.; Ritchie, N.W.; Scott, J.H.J.; Joy, D.C. Scanning Electron Microscopy and X-Ray Microanalysis, 4th ed.; Springer: New York, NY, USA, 2017; pp. 341–357. [Google Scholar]
  45. Fedotov, V.K.; Antonov, V.E.; Cornell, K.; Grosse, G.; Kolesnikov, A.I.; Sikolenko, V.V.; Sumin, V.V.; Wagner, F.E.; Wipf, H. Neutron scattering studies of the structure and lattice dynamics of a solid solution of hydrogen in-manganese. J. Phys. Cond. Matter 1998, 10, 5255–5266. [Google Scholar] [CrossRef]
  46. Shoemaker, C.B.; Shoemaker, D.P.; Hopkins, T.E.; Yindepit, S. Refinement of the structure of β-manganese and of a related phase in the Mn–Ni–Si system. Acta Crystallogr. Sect. B 1978, 34, 3573–3576. [Google Scholar] [CrossRef]
  47. Nicol, A.D.I. The structure of MnAl6. Acta Crystallogr. Sect. B 1953, 6, 285–293. [Google Scholar] [CrossRef]
  48. Kontio, A.; Coppens, P. New study of the structure of MnAl6. Acta Crystallogr. Sect. B 1981, 37, 433–435. [Google Scholar] [CrossRef]
  49. Onishi, T.; Nakatani, Y. Crystal Structures of MnAl6 and MnAl4. J. Japan Inst. Light Metals 1975, 25, 253–258. [Google Scholar] [CrossRef]
  50. Kreiner, G.; Franzen, H.F. The crystal structure of λ-Al4Mn. J. Alloys Compd. 1997, 261, 83–104. [Google Scholar] [CrossRef]
  51. Shoemaker, C.B.; Keszler, D.A.; Shoemaker, D.P. Structure of μ-MnAl4 with composition close to that of quasicrystal phases. Acta Crystallogr. Sect. B 1989, 45, 13–20. [Google Scholar] [CrossRef]
  52. Pavlyuk, V.V.; Yanson, T.I.; Bodak, O.I.; Černý, R.; Gladyshevskii, R.E.; Yvon, K.; Stepien-Damm, J. Structure refinement of orthorhombic MnAl3. Cryst. Struct. Comm. 1995, 51, 792–794. [Google Scholar] [CrossRef]
  53. Hiraga, K.; Kaneko, M.; Matsuo, Y.; Hashimoto, S. The structure of Al3Mn: Close relationship to decagonal quasicrystais. Phil. Mag. B 1993, 67, 193–205. [Google Scholar] [CrossRef]
  54. Shi, N.C.; Li, X.Z.; Ma, Z.S.; Kuo, K.H. Crystalline phases related to a decagonal quasicrystal. I. A single-crystal X-ray diffraction study of the orthorhombic Al3Mn phase. Acta Crystallogr. Sect. B 1994, 50, 22–30. [Google Scholar] [CrossRef]
  55. Thimmaiah, S.; Tener, Z.; Lamichhane, T.N.; Canfield, P.C.; Miller, G.J. Crystal structure, homogeneity range and electronic structure of rhombohedral γ-Mn5Al8. Z. Kristallogr.-Cryst. Mater. 2017, 232, 601–610. [Google Scholar] [CrossRef]
  56. Moze, O.; Pareti, L.; Ermakov, A.E. Neutron diffraction and magnetic investigations of Ga substituted MnAl permanent magnet materials. J. Appl. Phys. 1988, 63, 4616–4619. [Google Scholar] [CrossRef]
  57. Bandyopadhyay, J.; Gupta, K.P. Low temperature lattice parameters of Al and Al-Zn alloys and Grüneisen parameter of Al. Cryogenics 1978, 18, 54–55. [Google Scholar] [CrossRef]
  58. Schnepf, A.; Schenk, C. Na6[Ge10{Fe(CO)4}8]∙18THF: A Centaur Polyhedron of Germanium Atoms. Angew. Chem. Int. Ed. 2006, 45, 5373–5376. [Google Scholar] [CrossRef]
  59. Barlock, J.G.; Mondolfo, L.F. Structure of some aluminium-iron-magnesium-manganese-silicon alloys. Int. J. Mater. Res. 1975, 66, 605–611. [Google Scholar] [CrossRef]
  60. Wells, A.F. Structural Inorganic Chemistry, 4th ed.; Oxford University Press: Oxford, UK, 1975; pp. 1008–1059. [Google Scholar]
  61. Gross, N.; Kotzyba, G.; Künnen, B.; Jeitschko, W. Binary Compounds of Rhodium and Zinc: RhZn, Rh2Zn11, and RhZn13. Z. Anorg. Allg. Chem. 2001, 627, 155–163. [Google Scholar] [CrossRef]
  62. Sidorenko, F.; Kotov, A.P.; Zelenin, L.P.; Gel’d, P.V. Physical properties of mutual FeAl-CoAl solid solutions. Fiz. Met. Metalloved. 1973, 35, 209–211. [Google Scholar]
  63. Feschotte, P.; Bass, P. A new, very shy intermetallic compound: AgGa. J. Less-Common Met. 1991, 171, 157–162. [Google Scholar] [CrossRef]
  64. Lecocq, P.; Michel, A. Proprietes magnetiques et structurales des solutions solides de substitution de germanium dans le fer α. Bull. Soc. Chim. Fr. 1962, 7, 1412–1416. [Google Scholar]
  65. Dutchak, Y.I.; Chekh, V.G. High temperature x-ray diffraction study of the lattice dynamics of the compounds AlCo and AlNi. Russ. J. Phys. Chem. 1981, 55, 1326–1328. [Google Scholar]
  66. Bogner, J.; Steiner, W.; Reissner, M.; Mohn, P.; Blaha, P.; Schwarz, K.; Krachler, R.; Ipser, H.; Sepiol, B. Magnetic order and defect structure of FexAl1−x alloys around x = 0.5: An experimental and theoretical study. Phys. Rev. B 1998, 58, 14922. [Google Scholar] [CrossRef]
  67. Cascio, D.L.; Bakker, H. Change in magnetisation of Co50Ga50 due to atomic disorder induced by quenching from high temperatures. Phys. Status Solidi 1993, 135, 611–619. [Google Scholar] [CrossRef]
  68. Whittle, G.L.; Clark, P.E.; Cywinski, R.A. Mössbauer effect study of the structural and magnetic properties of Co-Ga alloys. J. Magn. Magn. Mater. 1982, 28, 64–76. [Google Scholar] [CrossRef]
  69. Straumanis, M.E.; Chopra, K.S. Lattice Parameters, Expansion Coefficients and Extent of the Al2Au Phase. Z. Phys. Chem. 1964, 42, 344–350. [Google Scholar] [CrossRef]
  70. Verchenko, V.Y.; Zubtsovskii, A.O.; Plenkin, D.S.; Bogach, A.V.; Wei, Z.; Tsirlin, A.A.; Dikarev, E.V.; Shevelkov, A.V. Family of Mo4Ga21-based superconductors. Chem. Mater. 2020, 32, 6730–6735. [Google Scholar] [CrossRef]
  71. Pchelkina, Z.V.; Mazurenko, V.V.; Volkova, O.S.; Deeva, E.B.; Morozov, I.V.; Shutov, V.V.; Troyanov, S.I.; Werner, J.; Koo, C.; Klingeler, R.; et al. Electronic structure and magnetic properties of the strong-rung spin-1 ladder compound Rb3Ni2(NO3)7. Phys. Rev. B 2018, 97, 144420. [Google Scholar] [CrossRef]
  72. Vorobyova, A.A.; Shilov, A.I.; Spiridonov, F.M.; Knotko, A.V.; Danilovich, I.L.; Vasiliev, A.N.; Morozov, I.V. One-dimensional magnet basic copper (ii) dihydroxoborate Cu2{BO(OH)2}(OH)3: Synthesis and properties. Russ. Chem. Bull. 2020, 69, 704–711. [Google Scholar] [CrossRef]
  73. Vorobyova, A.; Danilovich, I.; Morozov, I.; Ovchenkov, Y.; Vasiliev, A.; Volkova, O.; Iqbal, A.; Rahaman, B.; Saha-Dasgupta, T. Square lattice antiferromagnets (NO)M(NO3)3 (M= Co, Ni): Effects of anisotropy. J. Alloys Compd. 2022, 929, 167197. [Google Scholar] [CrossRef]
  74. Khalaniya, R.A.; Mironov, A.V.; Verchenko, V.Y.; Jesche, A.; Tsirlin, A.A.; Shevelkov, A.V. Nontrivial recurrent intergrowth structure and unusual magnetic behavior of intermetallic compound Fe32+δGe33As2. Inorg. Chem. 2016, 55, 12953–12961. [Google Scholar] [CrossRef]
  75. Khalaniya, R.A.; Verchenko, V.Y.; Wei, Z.; Dikarev, E.V.; Heinmaa, I.; Stern, R.; Jesche, A.; Tsirlin, A.A.; Shevelkov, A.V. From Fe32+δGe35-xPx to Fe32+δGe35-x-yPxAsy: Fine geometry optimization in new intergrowth structures. J. Alloys Compd. 2019, 779, 229–236. [Google Scholar] [CrossRef]
  76. Khalaniya, R.A.; Sobolev, A.V.; Verchenko, V.Y.; Tsirlin, A.A.; Senyshyn, A.; Damay, F.; Presniakov, I.A.; Shevelkov, A.V. Magnetic structures of Fe32+δGe33As2 and Fe32+δ′Ge35−xPx intermetallic compounds: A neutron diffraction and 57Fe Mössbauer spectroscopy study. Dalton Trans. 2021, 50, 2210–2220. [Google Scholar] [CrossRef] [PubMed]
  77. Gottlieb, U.; Sulpice, A.; Lambert-Andron, B.; Laborde, O. Magnetic properties of single crystalline Mn4Si7. J. Alloys Compd. 2003, 361, 13–18. [Google Scholar] [CrossRef]
  78. Wagner, F.R.; Cardoso-Gil, R.; Boucher, B.; Wagner-Reetz, M.; Sichelschmidt, J.; Gille, P.; Baenitz, M.; Grin, Y. On Fe–Fe dumbbells in the ideal and real structures of FeGa3. Inorg. Chem. 2018, 57, 12908–12919. [Google Scholar] [CrossRef] [PubMed]
  79. Ribeiro, C.K.; Rabello, A.F.; Martelli, V.; Zivkovic, I.; Fogh, E.; Rønnow, H.M.; Cornejo, D.; Jiménez, J.L. Electrical and Magnetic Properties of FeGa3 with Antisite Disorder. New Phys. Sae Mulli 2023, 73, 1149–1154. [Google Scholar] [CrossRef]
  80. Verchenko, V.Y.; Wei, Z.; Tsirlin, A.A.; Callaert, C.; Jesche, A.; Hadermann, J.; Dikarev, E.V.; Shevelkov, A.V. Crystal growth of the Nowotny chimney ladder phase Fe2Ge3: Exploring new Fe-based narrow-gap semiconductor with promising thermoelectric performance. Chem. Mater. 2017, 29, 9954–9963. [Google Scholar] [CrossRef]
  81. Xu, Y.; Wu, Y.; Cao, H.; Guo, S.; Yan, J.; Chen, X. Single crystal growth and thermoelectric properties of Nowotny chimney-ladder compound Fe2Ge3. Phys. Rev. Mater. 2023, 7, 125404. [Google Scholar] [CrossRef]
  82. Chen, Y.Q.; Wu, W.B.; He, Y.X.; Zhang, J.Y.; He, T.; Li, Z.; Xiao, Q.-L.; Ge, J.Y. Extremely large magnetoresistance in high quality magnetic Fe2Ge3 single crystals. Commun. Phys. 2025, 8, 116. [Google Scholar] [CrossRef]
Crystals 15 00714 g001
Figure 1. Single unit cell in the crystal structure of Mn4Al11.
Figure 1. Single unit cell in the crystal structure of Mn4Al11.
Crystals 15 00714 g001
Crystals 15 00714 g002
Figure 2. Different projections showing the Mn layers in the crystal structure of Mn4Al11: projection along the direction of Mn1-Mn2 chains (a); projection along the c-axis (b); slightly tilted view along the c-axis (c). The formation of Mn-Mn isolobal bonds in the crystal structure of Mn4Al11 (d), the bridging Al atoms are represented by smaller blue balls, and the isolobal Mn-Mn bonds are shown in yellow.
Figure 2. Different projections showing the Mn layers in the crystal structure of Mn4Al11: projection along the direction of Mn1-Mn2 chains (a); projection along the c-axis (b); slightly tilted view along the c-axis (c). The formation of Mn-Mn isolobal bonds in the crystal structure of Mn4Al11 (d), the bridging Al atoms are represented by smaller blue balls, and the isolobal Mn-Mn bonds are shown in yellow.
Crystals 15 00714 g002
Crystals 15 00714 g004
Figure 4. The Al network in the crystal structure of Mn4Al11: top view of the fragment between y = 0.32 and 0.68 composed of Al3–Al5 atoms (a); top view of the fragment between y = 0.62 and 1.38 composed of Al0–Al5 atoms (b); slightly tilted view along the c-axis (c); slightly tilted view along the a-axis (d). The Al atoms are shown in grey. Different Al chains are marked with different colors to visually differentiate them. The Mn atoms are semitransparent and shown in purple.
Figure 4. The Al network in the crystal structure of Mn4Al11: top view of the fragment between y = 0.32 and 0.68 composed of Al3–Al5 atoms (a); top view of the fragment between y = 0.62 and 1.38 composed of Al0–Al5 atoms (b); slightly tilted view along the c-axis (c); slightly tilted view along the a-axis (d). The Al atoms are shown in grey. Different Al chains are marked with different colors to visually differentiate them. The Mn atoms are semitransparent and shown in purple.
Crystals 15 00714 g004
Crystals 15 00714 g005
Figure 5. Magnetic properties of Mn4Al11: magnetic susceptibility of a single crystal in different orientations (a) and of several randomly oriented single crystals (b); magnetic moment as a function of the magnetic field at different temperatures of a single crystal (c) in different orientations and of several randomly oriented single crystals (d).
Figure 5. Magnetic properties of Mn4Al11: magnetic susceptibility of a single crystal in different orientations (a) and of several randomly oriented single crystals (b); magnetic moment as a function of the magnetic field at different temperatures of a single crystal (c) in different orientations and of several randomly oriented single crystals (d).
Crystals 15 00714 g005
Table 1. Crystallographic and refinement parameters for the Mn4Al11 single crystal obtained from the Mn4Al11Sn44 sample.
Table 1. Crystallographic and refinement parameters for the Mn4Al11 single crystal obtained from the Mn4Al11Sn44 sample.
refined compositionMn4Al11
EDX compositionMn4.18(2)Al10.82(2)
molar weight516.6
structure typeMn4Al11
crystal systemTriclinic
space groupP-1
a, Å5.0876(12)
b, Å8.8438(17)
c, Å5.0562(11)
A89.800(16)
β, °100.548(16)
Γ105.358(16)
V, Å3215.42(8)
Z1
ρcalc, g/cm33.9817
crystal size0.21 × 0.13 × 0.03
radiationAg Kα
wavelength, Å0.56083 Å
temperature, K293
2θ range, °3.24–25.95
number of parameters71
number of reflections1700
GoF1.03
Δρmax/min, e−/Å30.86/−0.66
R[F2 > 3σ(F2)]/Rw(F2)0.0304/0.0436
Table 2. Atomic coordinates and displacement parameters for the Mn4Al11 single crystal obtained from the Mn4Al11Sn44 sample. The occupancies of the sites were constrained at unity (see text).
Table 2. Atomic coordinates and displacement parameters for the Mn4Al11 single crystal obtained from the Mn4Al11Sn44 sample. The occupancies of the sites were constrained at unity (see text).
AtomWyck.xYzUeq, Å2
Mn12i0.38941(8)0.13305(5)0.33559(9)0.00564(11)
Mn22i0.85296(9)0.40131(5)0.70820(9)0.00707(12)
Al01a0000.0103(3)
Al12i0.53059(18)0.12593(10)0.84570(19)0.0087(2)
Al22i0.89478(17)0.12552(10)0.4907(2)0.0088(2)
Al32i0.33000(17)0.37389(10)0.57031(19)0.0082(3)
Al42i0.72648(18)0.36785(11)0.1925(2)0.0093(2)
Al52i0.17738(18)0.32225(11)0.05353(19)0.0104(3)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Khalaniya, R.A.; Mironov, A.V.; Samarin, A.N.; Bogach, A.V.; Kulchu, A.N.; Shevelkov, A.V. Revisiting Mn4Al11: Growth of Stoichiometric Single Crystals and Their Structural and Magnetic Properties. Crystals 2025, 15, 714. https://doi.org/10.3390/cryst15080714

AMA Style

Khalaniya RA, Mironov AV, Samarin AN, Bogach AV, Kulchu AN, Shevelkov AV. Revisiting Mn4Al11: Growth of Stoichiometric Single Crystals and Their Structural and Magnetic Properties. Crystals. 2025; 15(8):714. https://doi.org/10.3390/cryst15080714

Chicago/Turabian Style

Khalaniya, Roman A., Andrei V. Mironov, Alexander N. Samarin, Alexey V. Bogach, Aleksandr N. Kulchu, and Andrei V. Shevelkov. 2025. "Revisiting Mn4Al11: Growth of Stoichiometric Single Crystals and Their Structural and Magnetic Properties" Crystals 15, no. 8: 714. https://doi.org/10.3390/cryst15080714

APA Style

Khalaniya, R. A., Mironov, A. V., Samarin, A. N., Bogach, A. V., Kulchu, A. N., & Shevelkov, A. V. (2025). Revisiting Mn4Al11: Growth of Stoichiometric Single Crystals and Their Structural and Magnetic Properties. Crystals, 15(8), 714. https://doi.org/10.3390/cryst15080714

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop