Modulation of Protein Dynamics by Glycerol in Water-Soluble Chlorophyll-Binding Protein (WSCP)
Abstract
1. Introduction
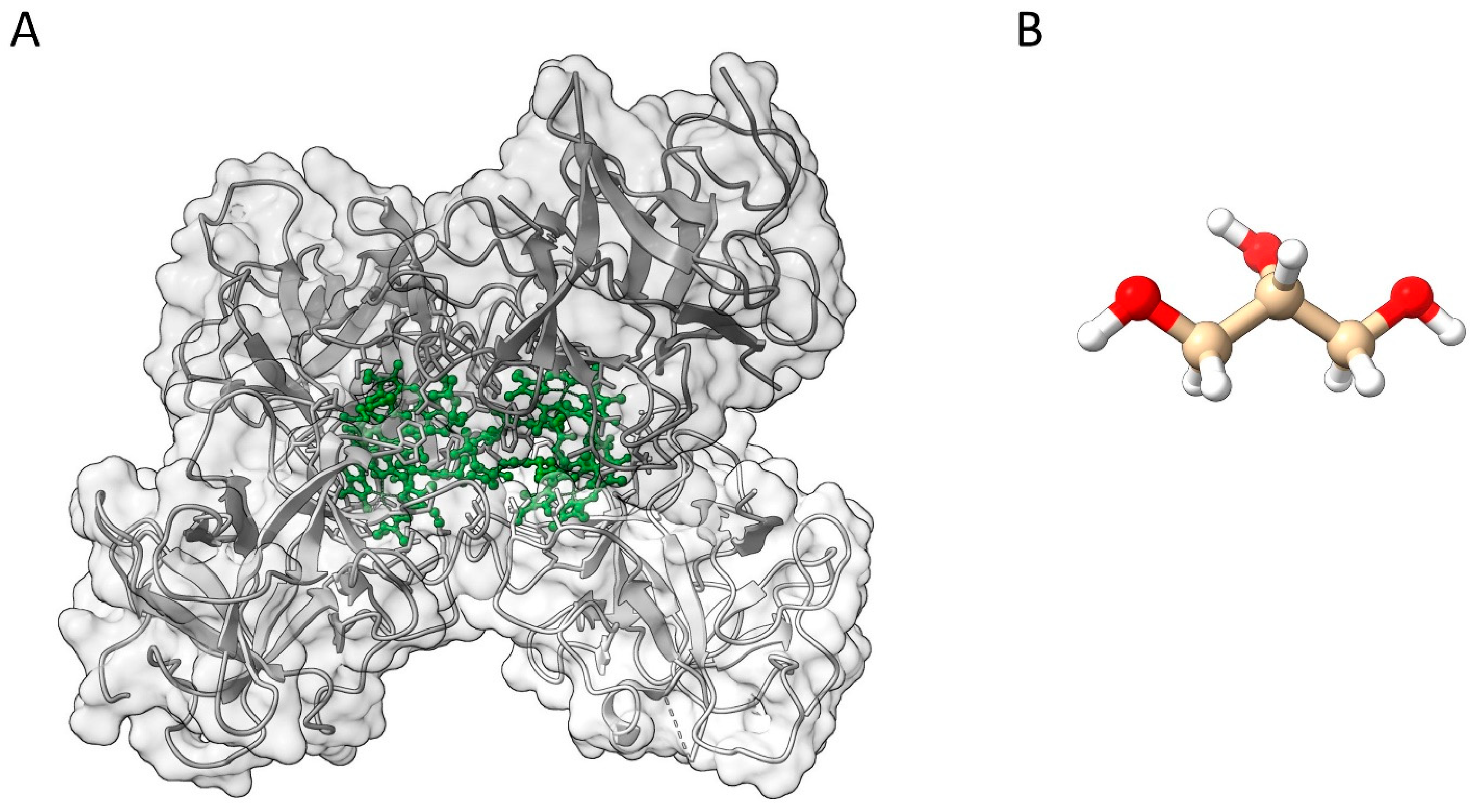
2. Materials and Methods
2.1. Sample Preparation
2.2. QENS Experiments
2.3. INS Experiments
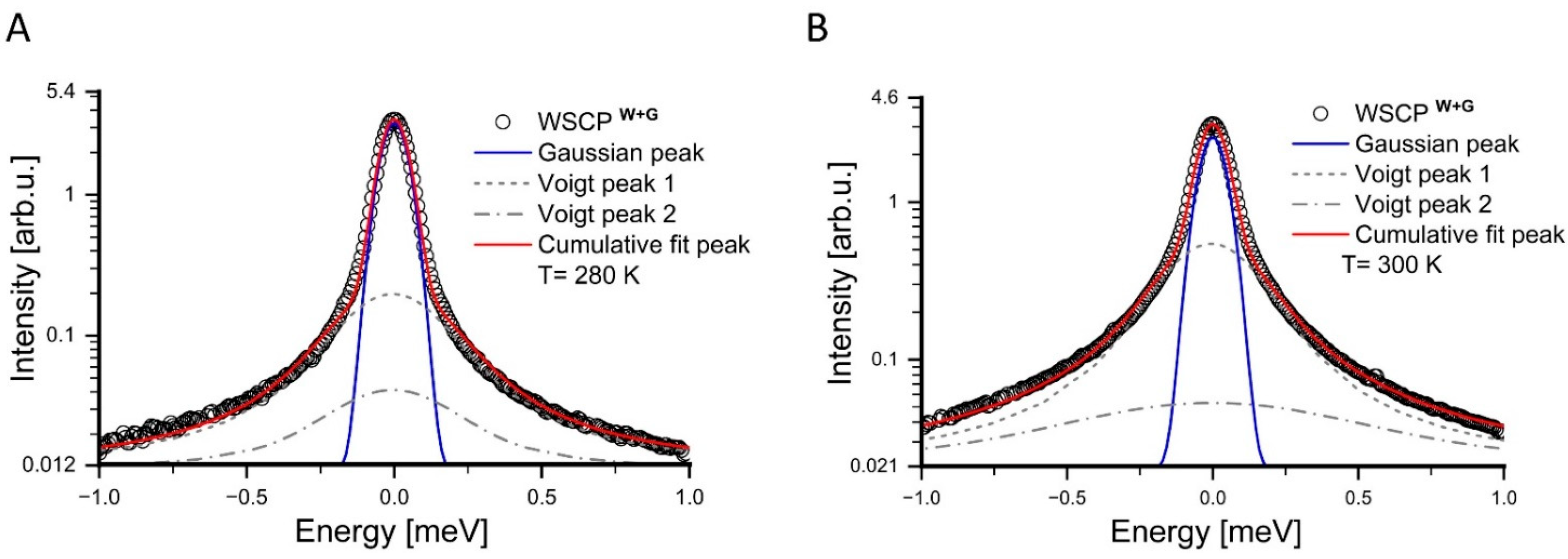
2.4. QENS Data Analysis
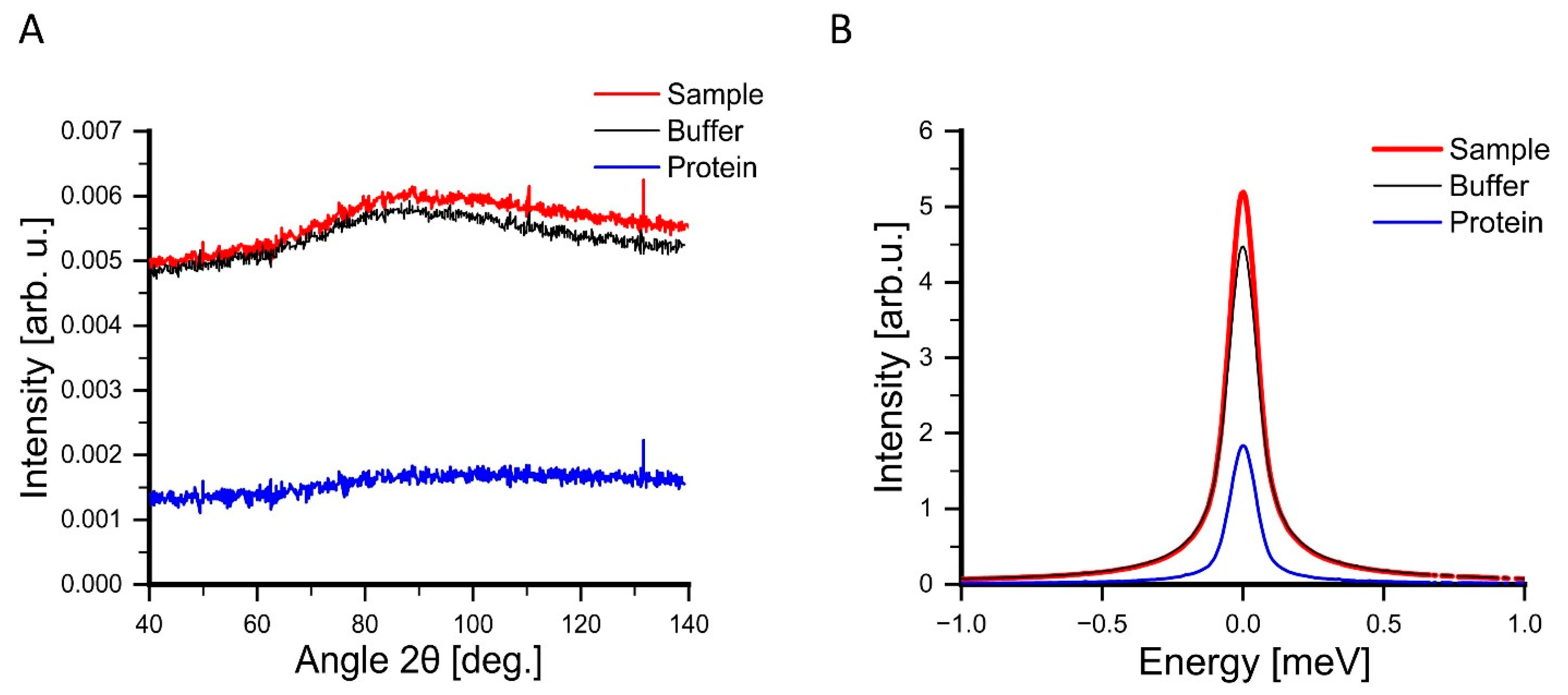
2.5. Buffer Subtraction
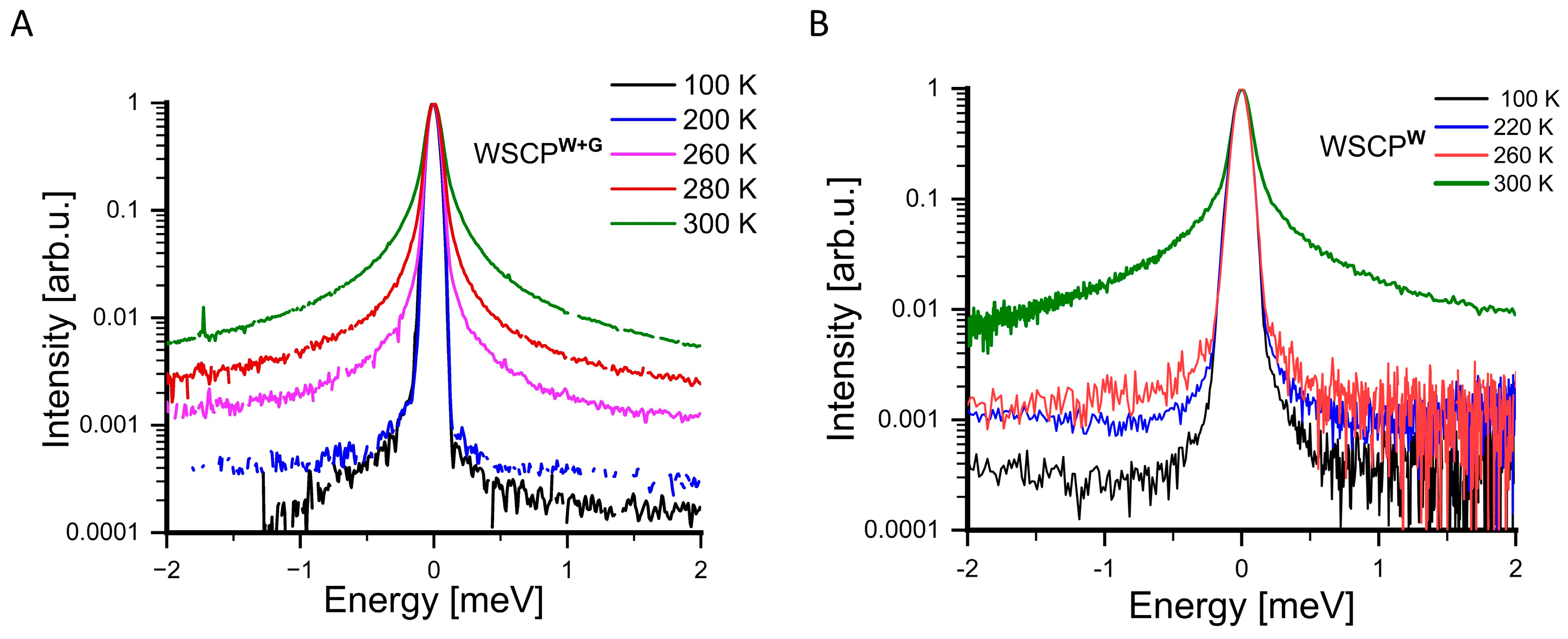
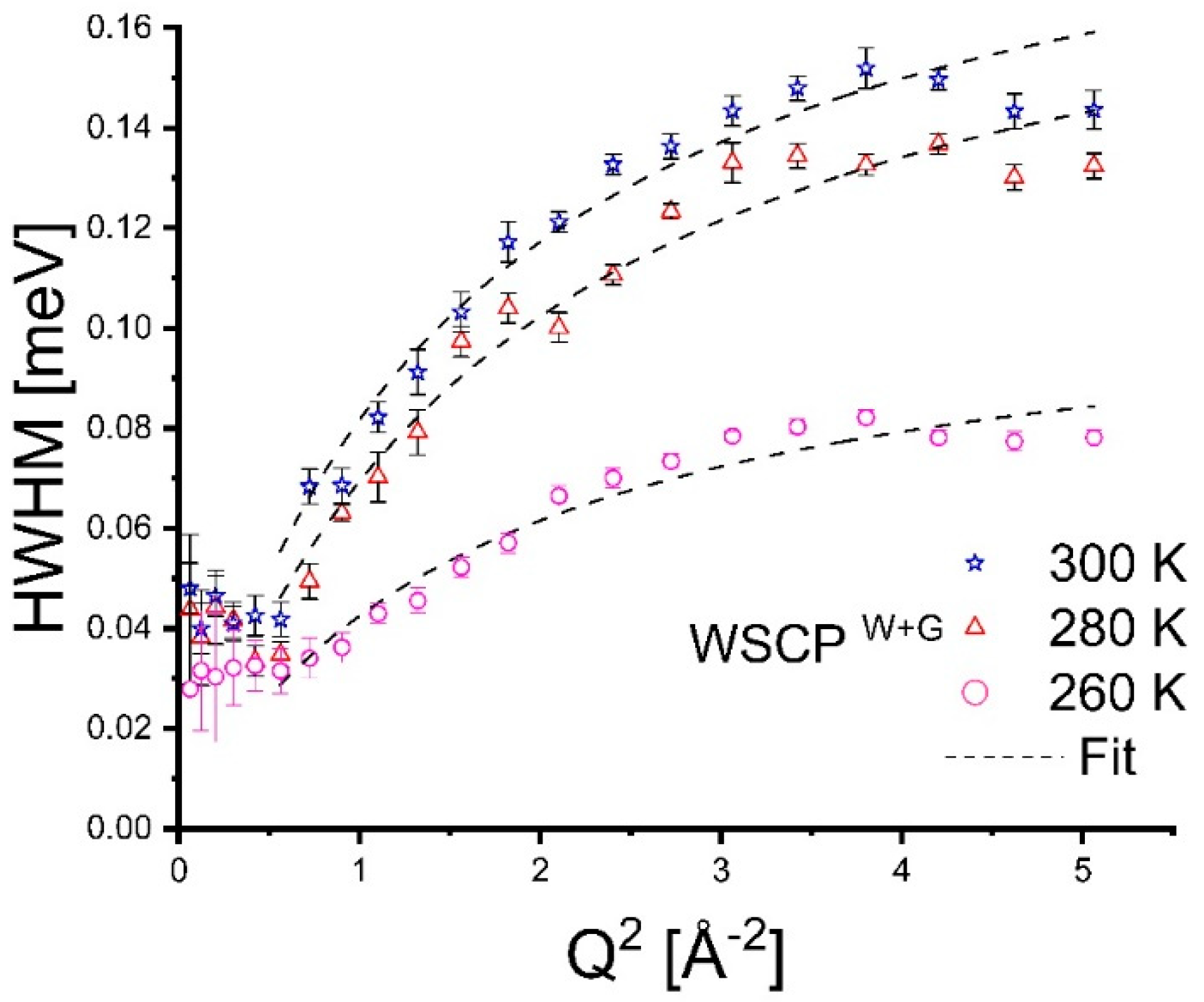
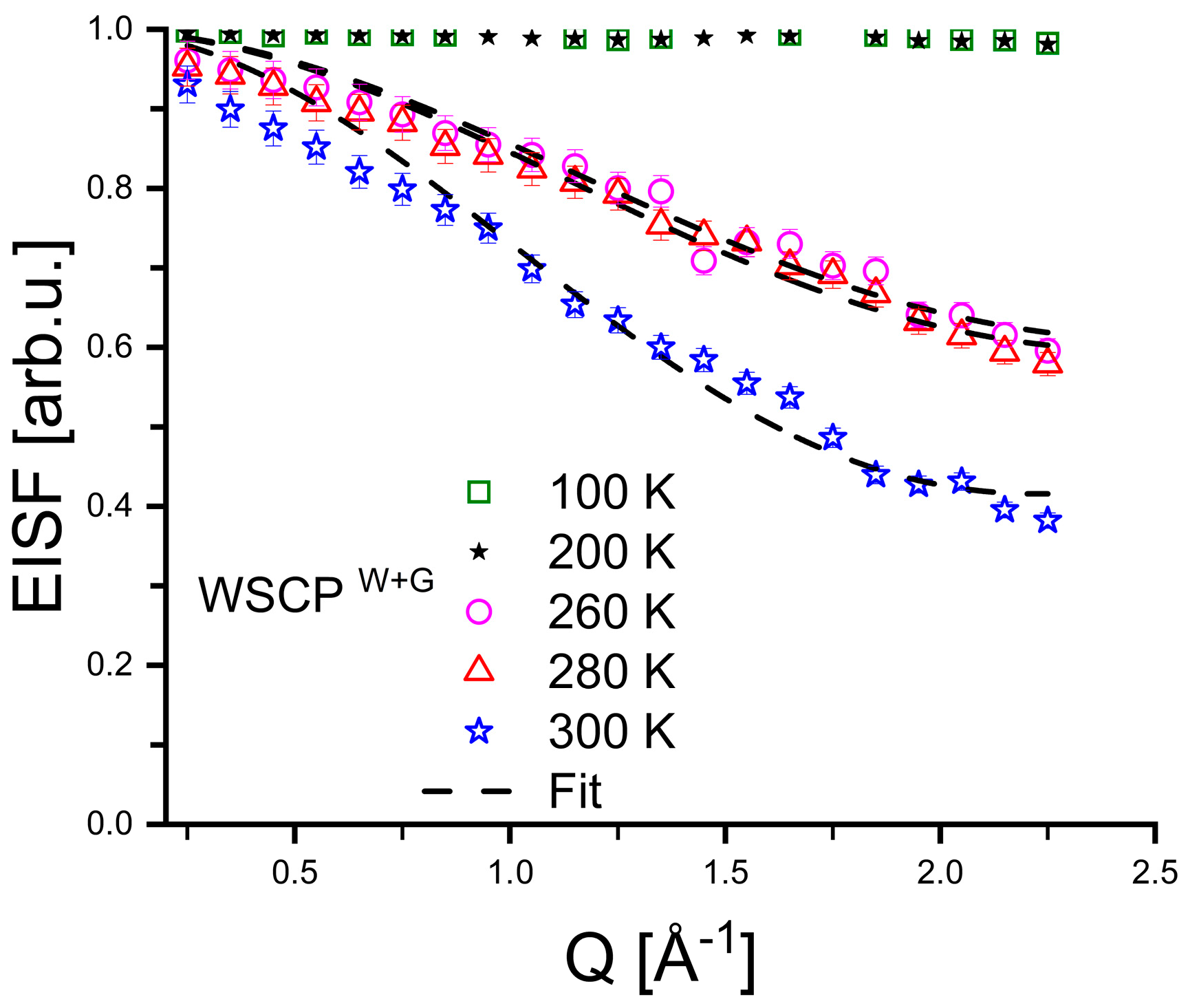
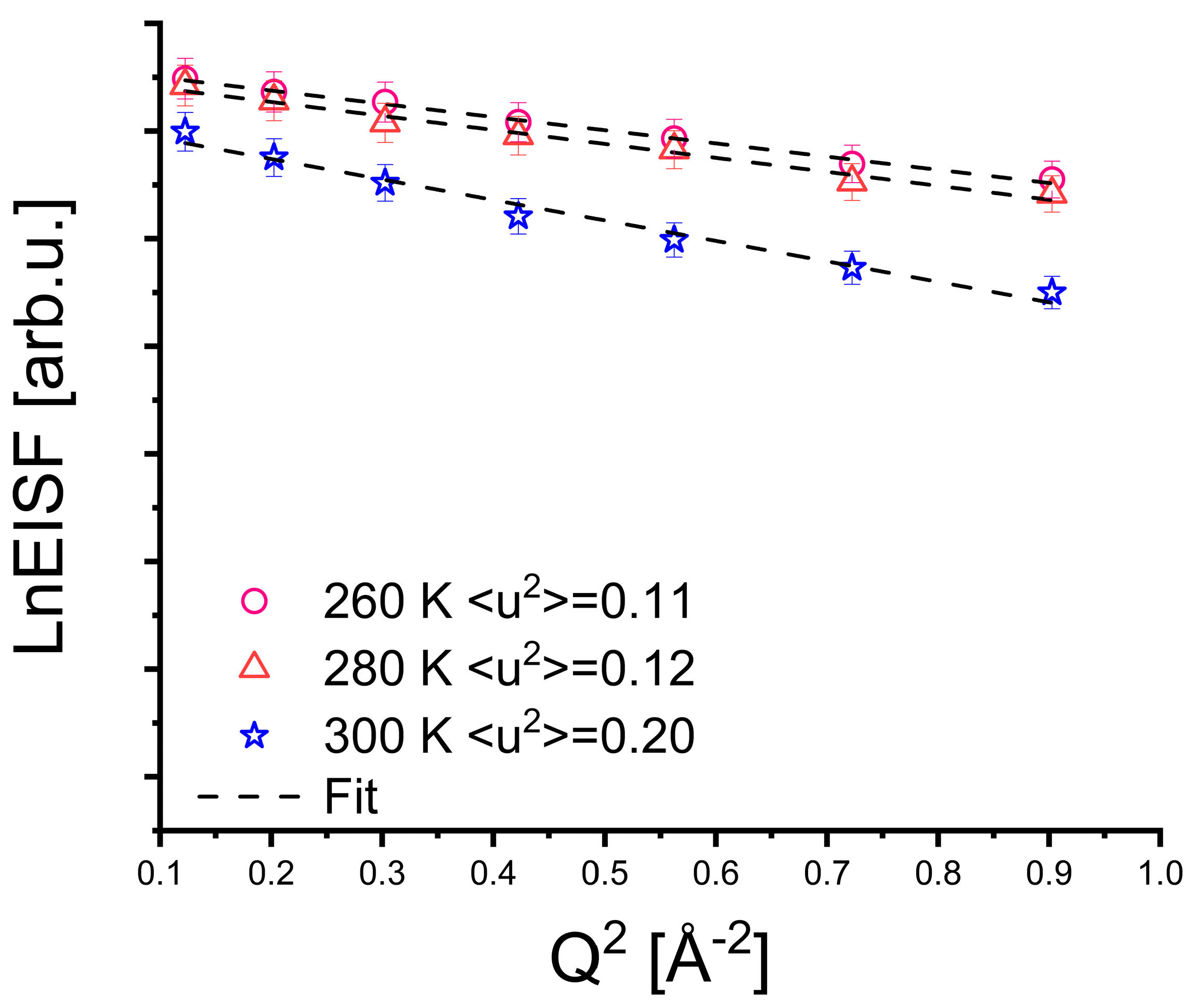
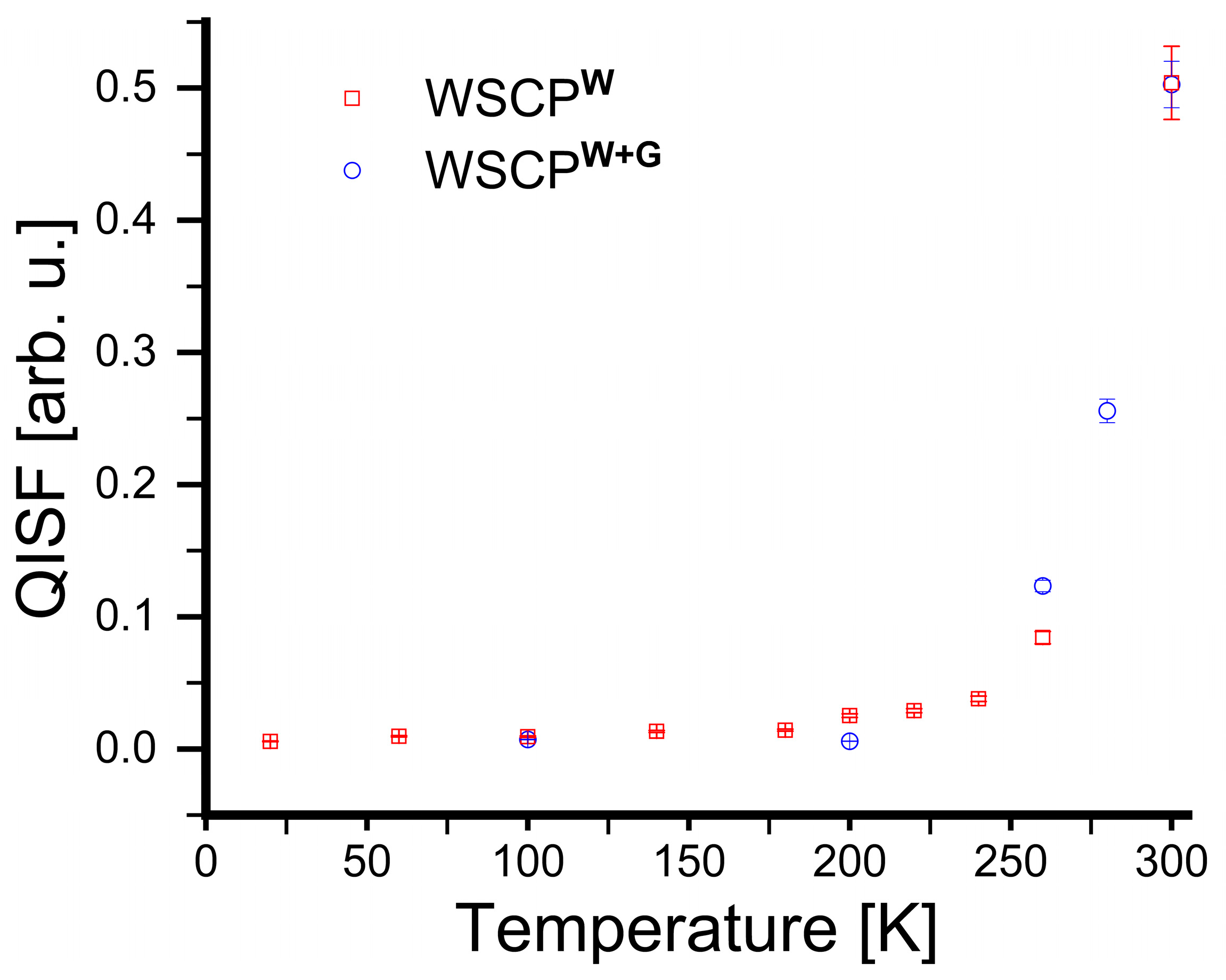
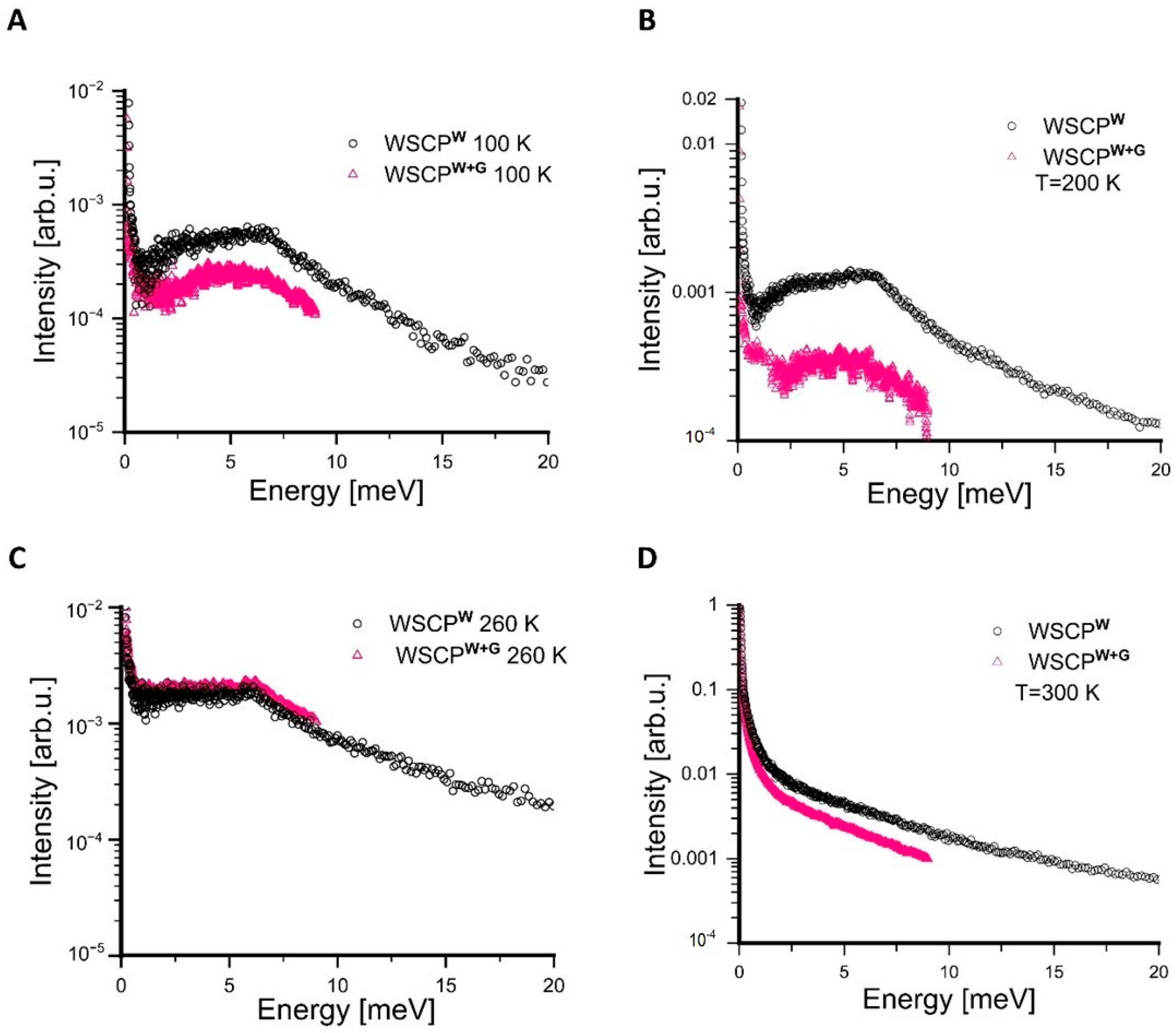
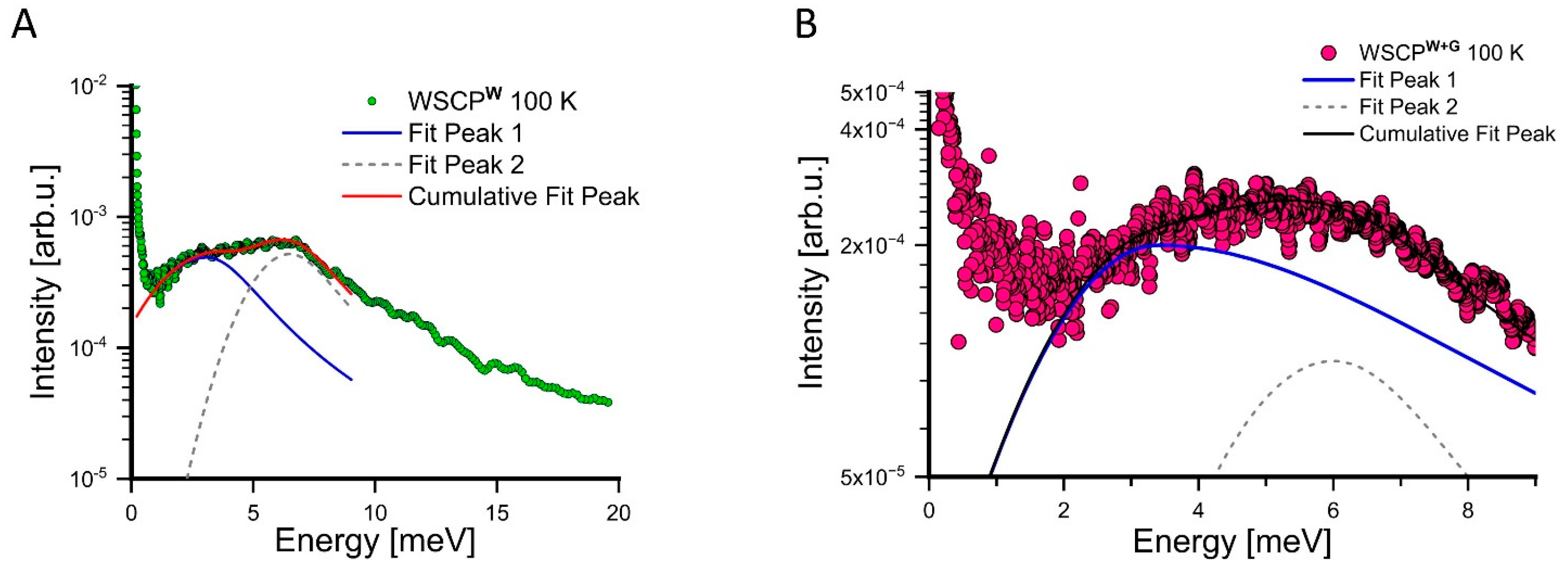
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NS | neutron scattering |
| MSD | mean square displacement |
| WSCP | Water-Soluble Chlorophyll-Binding Protein |
| WSCPW | WSCP in water |
| WSCPW+G | WSCP in water and glycerol |
| INS | Inelastic Neutron Scattering |
| QENS | Quasielastic Neutron Scattering |
| FWHM | full width at half maximum |
| HWHM | half width at half maximum |
| EISF | elastic incoherent structure factor |
| QISF | quasielastic incoherent structure factor |
| τ | residence time |
| D | jump diffusion constant |
| f | fraction of hydrogen atoms involved in motion |
| r | radius of motion |
| lnEISF | logarithm of the EISF |
| Chl | chlorophyll |
References
- Nam, K.; Wolf-Watz, M. Protein dynamics: The future is bright and complicated! Struct. Dyn. 2023, 10, 014301. [Google Scholar] [CrossRef] [PubMed]
- Cornicchi, E.; Cinelli, S.; Natali, F.; Onori, G.; Paciaroni, A. Elastic neutron scattering study of proton dynamics in glycerol. Phys. B Condens. Matter 2004, 350, E951–E954. [Google Scholar] [CrossRef]
- Matveev, Y.I.; Grinberg, V.Y.; Tolstoguzov, V. The plasticizing effect of water on proteins, polysaccharides and their mixtures. Glassy state of biopolymers, food and seeds. Food Hydrocoll. 2000, 14, 425–437. [Google Scholar] [CrossRef]
- Kaushik, J.K.; Bhat, R. Thermal stability of proteins in aqueous polyol solutions: Role of the surface tension of water in the stabilizing effect of polyols. J. Phys. Chem. B 1998, 102, 7058–7066. [Google Scholar] [CrossRef]
- Pieper, J.; Trapp, M.; Skomorokhov, A.; Natkaniec, I.; Peters, J.; Renger, G. Temperature–dependent vibrational and conformational dynamics of photosystem II membrane fragments from spinach investigated by elastic and inelastic neutron scattering. Biochim. Biophys. Acta (BBA)-Bioenerg. 2012, 1817, 1213–1219. [Google Scholar] [CrossRef]
- Jang, K.; Kim, H.G.; Hlaing, S.H.S.; Kang, M.; Choe, H.-W.; Kim, Y.J. A short review on cryoprotectants for 3D protein structure analysis. Crystals 2022, 12, 138. [Google Scholar] [CrossRef]
- De Graaf, L.A. Denaturation of proteins from a non-food perspective. J. Biotechnol. 2000, 79, 299–306. [Google Scholar] [CrossRef]
- Levine, H.; Slade, L. Water as a plasticizer: Physico-chemical aspects of low-moisture polymeric systems. Water Sci. Rev. 1988, 3, 79–185. [Google Scholar]
- Gabel, F.; Bicout, D.; Lehnert, U.; Tehei, M.; Weik, M.; Zaccai, G. Protein dynamics studied by neutron scattering. Q. Rev. Biophys. 2002, 35, 327–367. [Google Scholar] [CrossRef]
- Fitter, J. Conformational dynamics of a protein in the folded and the unfolded state. Chem. Phys. 2003, 292, 405–411. [Google Scholar] [CrossRef]
- Sacquin-Mora, S.; Sebban, P.; Derrien, V.; Frick, B.; Lavery, R.; Alba-Simionesco, C. Probing the flexibility of the bacterial reaction center: The wild-type protein is more rigid than two site-specific mutants. Biochemistry 2007, 46, 14960–14968. [Google Scholar] [CrossRef] [PubMed]
- Lehnert, U.; Reat, V.; Weik, M.; Zaccai, G.; Pfister, C. Thermal motions in bacteriorhodopsin at different hydration levels studied by neutron scattering: Correlation with kinetics and light-induced conformational changes. Biophys. J. 1998, 75, 1945–1952. [Google Scholar] [CrossRef] [PubMed]
- Krieger-Liszkay, A.; Fufezan, C.; Trebst, A. Singlet oxygen production in photosystem II and related protection mechanism. Photosynth. Res. 2008, 98, 551–564. [Google Scholar] [CrossRef] [PubMed]
- Hill, J.J.; Shalaev, E.Y.; Zografi, G. Thermodynamic and dynamic factors involved in the stability of native protein structure in amorphous solids in relation to levels of hydration. J. Pharm. Sci. 2005, 94, 1636–1667. [Google Scholar] [CrossRef]
- Ali, F.; Manzoor, U.; Khan, F.I.; Lai, D.; Khan, M.K.A.; Chandrashekharaiah, K.; Singh, L.R.; Dar, T.A. Effect of polyol osmolytes on the structure-function integrity and aggregation propensity of catalase: A comprehensive study based on spectroscopic and molecular dynamic simulation measurements. Int. J. Biol. Macromol. 2022, 209, 198–210. [Google Scholar] [CrossRef]
- Paciaroni, A.; Orecchini, A.; Cinelli, S.; Onori, G.; Lechner, R.; Pieper, J. Protein dynamics on the picosecond timescale as affected by the environment: A quasielastic neutron scattering study. Chem. Phys. 2003, 292, 397–404. [Google Scholar] [CrossRef]
- Gekko, K.; Timasheff, S.N. Thermodynamic and kinetic examination of protein stabilization by glycerol. Biochemistry 1981, 20, 4677–4686. [Google Scholar] [CrossRef]
- Zachariassen, K.E. The mechanism of the cryoprotective effect of glycerol in beetles tolerant to freezing. J. Insect Physiol. 1979, 25, 29–32. [Google Scholar] [CrossRef]
- Mitchell, D.E.; Fayter, A.E.; Deller, R.C.; Hasan, M.; Gutierrez-Marcos, J.; Gibson, M.I. Ice-recrystallization inhibiting polymers protect proteins against freeze-stress and enable glycerol-free cryostorage. Mater. Horiz. 2019, 6, 364–368. [Google Scholar] [CrossRef]
- Ye, Y.; Zheng, L.; Hong, L.; García Sakai, V.; de Souza, N.R.; Teng, D.; Wu, B.; Xu, Y.; Cai, J.; Liu, Z. Direct Observation of the Mutual Coupling Effect in the Protein–Water–Glycerol Mixture by Combining Neutron Scattering and Selective Deuteration. J. Phys. Chem. B 2024, 128, 405–414. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, W.; Wei, H.; Deng, S.; Yu, X.; Huang, T. The mechanisms and applications of cryoprotectants in aquatic products: An overview. Food Chem. 2023, 408, 135202. [Google Scholar] [CrossRef] [PubMed]
- Chéron, N.; Naepels, M.; Pluhařová, E.; Laage, D. Protein preferential solvation in water: Glycerol mixtures. J. Phys. Chem. B 2020, 124, 1424–1437. [Google Scholar] [CrossRef] [PubMed]
- Gekko, K.; Timasheff, S.N. Mechanism of protein stabilization by glycerol: Preferential hydration in glycerol-water mixtures. Biochemistry 1981, 20, 4667–4676. [Google Scholar] [CrossRef] [PubMed]
- Hirai, M.; Ajito, S.; Sugiyama, M.; Iwase, H.; Takata, S.-i.; Shimizu, N.; Igarashi, N.; Martel, A.; Porcar, L. Direct evidence for the effect of glycerol on protein hydration and thermal structural transition. Biophys. J. 2018, 115, 313–327. [Google Scholar] [CrossRef] [PubMed]
- Vagenende, V.; Yap, M.G.; Trout, B.L. Mechanisms of protein stabilization and prevention of protein aggregation by glycerol. Biochemistry 2009, 48, 11084–11096. [Google Scholar] [CrossRef]
- Caliskan, G.; Briber, R.M.; Thirumalai, D.; Garcia-Sakai, V.; Woodson, S.A.; Sokolov, A.P. Dynamic transition in tRNA is solvent induced. J. Am. Chem. Soc. 2006, 128, 32–33. [Google Scholar] [CrossRef]
- Davis-Searles, P.R.; Saunders, A.J.; Erie, D.A.; Winzor, D.J.; Pielak, G.J. Interpreting the effects of small uncharged solutes on protein-folding equilibria. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 271–306. [Google Scholar] [CrossRef]
- Rösgen, J.; Pettitt, B.M.; Bolen, D.W. An analysis of the molecular origin of osmolyte-dependent protein stability. Protein Sci. 2007, 16, 733–743. [Google Scholar] [CrossRef]
- Daniel, R.M.; Peterson, M.E.; Danson, M.J.; Price, N.C.; Kelly, S.M.; Monk, C.R.; Weinberg, C.S.; Oudshoorn, M.L.; Lee, C.K. The molecular basis of the effect of temperature on enzyme activity. Biochem. J. 2010, 425, 353–360. [Google Scholar] [CrossRef]
- Ringe, D.; Petsko, G.A. The ‘glass transition’in protein dynamics: What it is, why it occurs, and how to exploit it. Biophys. Chem. 2003, 105, 667–680. [Google Scholar] [CrossRef]
- Grimaldo, M.; Roosen-Runge, F.; Zhang, F.; Schreiber, F.; Seydel, T. Dynamics of proteins in solution. Q. Rev. Biophys. 2019, 52, e7. [Google Scholar] [CrossRef]
- Vural, D.; Hu, X.; Lindner, B.; Jain, N.; Miao, Y.; Cheng, X.; Liu, Z.; Hong, L.; Smith, J.C. Quasielastic neutron scattering in biology: Theory and applications. Biochim. Biophys. Acta (BBA)-Gen. Subj. 2017, 1861, 3638–3650. [Google Scholar] [CrossRef] [PubMed]
- Ahlgren, K.; Olsson, C.; Ermilova, I.; Swenson, J. New insights into the protein stabilizing effects of trehalose by comparing with sucrose. Phys. Chem. Chem. Phys. 2023, 25, 21215–21226. [Google Scholar] [CrossRef] [PubMed]
- Naidu, K.T.; Prabhu, N.P. Polyols, increasing global stability of cytochrome c, destabilize the thermal unfolding intermediate. J. Biomol. Struct. Dyn. 2022, 40, 11216–11228. [Google Scholar] [CrossRef]
- Paciaroni, A.; Cinelli, S.; Onori, G. Effect of the environment on the protein dynamical transition: A neutron scattering study. Biophys. J. 2002, 83, 1157–1164. [Google Scholar] [CrossRef]
- Rosi, B.P.; D’Angelo, A.; Buratti, E.; Zanatta, M.; Tavagnacco, L.; Natali, F.; Zamponi, M.; Noferini, D.; Corezzi, S.; Zaccarelli, E. Impact of the environment on the pnipam dynamical transition probed by elastic neutron scattering. Macromolecules 2022, 55, 4752–4765. [Google Scholar] [CrossRef]
- GhattyVenkataKrishna, P.K.; Carri, G.A. Effect of glycerol–water binary mixtures on the structure and dynamics of protein solutions. J. Biomol. Struct. Dyn. 2014, 32, 424–437. [Google Scholar] [CrossRef]
- Lerbret, A.; Affouard, F. Molecular packing, hydrogen bonding, and fast dynamics in lysozyme/trehalose/glycerol and trehalose/glycerol glasses at low hydration. J. Phys. Chem. B 2017, 121, 9437–9451. [Google Scholar] [CrossRef]
- Golub, M.; Rusevich, L.; Irrgang, K.D.; Pieper, J. Rigid versus Flexible Protein Matrix: Light-Harvesting Complex II Exhibits a Temperature-Dependent Phonon Spectral Density. J. Phys. Chem. B 2018, 122, 7111–7121. [Google Scholar] [CrossRef]
- Renger, G.; Pieper, J.; Theiss, C.; Trostmann, I.; Paulsen, H.; Renger, T.; Eichler, H.; Schmitt, F.-J. Water soluble chlorophyll binding protein of higher plants: A most suitable model system for basic analyses of pigment–pigment and pigment–protein interactions in chlorophyll protein complexes. J. Plant Physiol. 2011, 168, 1462–1472. [Google Scholar] [CrossRef]
- Maleeva, Y.V.; Neverov, K.; Obukhov, Y.N.; Kritsky, M. Water soluble chlorophyll-binding proteins of plants: Structure, properties and functions. Mol. Biol. 2019, 53, 876–888. [Google Scholar] [CrossRef]
- Palm, D.M.; Agostini, A.; Pohland, A.-C.; Werwie, M.; Jaenicke, E.; Paulsen, H. Stability of water-soluble chlorophyll protein (WSCP) depends on phytyl conformation. ACS Omega 2019, 4, 7971–7979. [Google Scholar] [CrossRef] [PubMed]
- Satoh, H.; Uchida, A.; Nakayama, K.; Okada, M. Water-soluble chlorophyll protein in Brassicaceae plants is a stress-induced chlorophyll-binding protein. Plant Cell Physiol. 2001, 42, 906–911. [Google Scholar] [CrossRef] [PubMed]
- Horigome, D.; Satoh, H.; Itoh, N.; Mitsunaga, K.; Oonishi, I.; Nakagawa, A.; Uchida, A. Structural mechanism and photoprotective function of water-soluble chlorophyll-binding protein. J. Biol. Chem. 2007, 282, 6525–6531. [Google Scholar] [CrossRef]
- Agostini, A.; Meneghin, E.; Gewehr, L.; Pedron, D.; Palm, D.M.; Carbonera, D.; Paulsen, H.; Jaenicke, E.; Collini, E. How water-mediated hydrogen bonds affect chlorophyll a/b selectivity in Water-Soluble Chlorophyll Protein. Sci. Rep. 2019, 9, 18255. [Google Scholar] [CrossRef]
- Theiss, C.; Trostmann, I.; Andree, S.; Schmitt, F.; Renger, T.; Eichler, H.; Paulsen, H.; Renger, G. Pigment-pigment and pigment-protein interactions in recombinant water-soluble chlorophyll proteins (WSCP) from cauliflower. J. Phys. Chem. B 2007, 111, 13325–13335. [Google Scholar] [CrossRef]
- Schmitt, F.-J.; Trostmann, I.; Theiss, C.; Pieper, J.; Renger, T.; Fuesers, J.; Hubrich, E.; Paulsen, H.; Eichler, H.; Renger, G. Excited state dynamics in recombinant water-soluble chlorophyll proteins (WSCP) from cauliflower investigated by transient fluorescence spectroscopy. J. Phys. Chem. B 2008, 112, 13951–13961. [Google Scholar] [CrossRef]
- Pieper, J.; Rätsep, M.; Trostmann, I.; Schmitt, F.-J.; Theiss, C.; Paulsen, H.; Eichler, H.; Freiberg, A.; Renger, G. Excitonic energy level structure and pigment-protein interactions in the recombinant water-soluble chlorophyll protein. II. Spectral hole-burning experiments. J. Phys. Chem. B 2011, 115, 4053–4065. [Google Scholar] [CrossRef]
- Alster, J.; Lokstein, H.; Dostál, J.; Uchida, A.; Zigmantas, D. 2D spectroscopy study of water-soluble chlorophyll-binding protein from Lepidium virginicum. J. Phys. Chem. B 2014, 118, 3524–3531. [Google Scholar] [CrossRef]
- Damaraju, S.; Schlede, S.; Eckhardt, U.; Lokstein, H.; Grimm, B. Functions of the water soluble chlorophyll-binding protein in plants. J. Plant Physiol. 2011, 168, 1444–1451. [Google Scholar] [CrossRef]
- Meng, E.C.; Goddard, T.D.; Pettersen, E.F.; Couch, G.S.; Pearson, Z.J.; Morris, J.H.; Ferrin, T.E. UCSF ChimeraX: Tools for structure building and analysis. Protein Sci. 2023, 32, e4792. [Google Scholar] [CrossRef] [PubMed]
- Arnold, O.; Bilheux, J.-C.; Borreguero, J.M.; Buts, A.; Campbell, S.I.; Chapon, L.; Doucet, M.; Draper, N.; Leal, R.F.; Gigg, M.A. Mantid—Data Analysis and Visualization Package for Neutron Scattering and μ SR Experiments; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Berrod, Q.; Lagrené, K.; Ollivier, J.; Zanotti, J.-M. Inelastic and quasi-elastic neutron scattering. Application to soft-matter. EPJ Web Conf. 2018, 188, 05001. [Google Scholar] [CrossRef][Green Version]
- Azuah, R.T.; Kneller, L.R.; Qiu, Y.; Tregenna-Piggott, P.L.; Brown, C.M.; Copley, J.R.; Dimeo, R.M. DAVE: A comprehensive software suite for the reduction, visualization, and analysis of low energy neutron spectroscopic data. J. Res. Natl. Inst. Stand. Technol. 2009, 114, 341. [Google Scholar] [CrossRef] [PubMed]
- Golub, M.; Moldenhauer, M.; Schmitt, F.J.; Lohstroh, W.; Maksimov, E.G.; Friedrich, T.; Pieper, J. Solution Structure and Conformational Flexibility in the Active State of the Orange Carotenoid Protein. Part II: Quasielastic Neutron Scattering. J. Phys. Chem. B 2019, 123, 9536–9545. [Google Scholar] [CrossRef]
- Singwi, K.; Sjölander, A. Diffusive motions in water and cold neutron scattering. Phys. Rev. 1960, 119, 863. [Google Scholar] [CrossRef]
- Rodriguez-Velamazan, J.A.; Gonzalez, M.A.; Real, J.A.; Castro, M.; Munoz, M.C.; Gaspar, A.B.; Ohtani, R.; Ohba, M.; Yoneda, K.; Hijikata, Y.; et al. A switchable molecular rotator: Neutron spectroscopy study on a polymeric spin-crossover compound. J. Am. Chem. Soc. 2012, 134, 5083–5089. [Google Scholar] [CrossRef]
- Stevenson, K.J. Review of OriginPro 8.5. J. Am. Chem. Soc. 2011, 133, 5621. [Google Scholar] [CrossRef]
- Telling, M.T. Quasi-Elastic Neutron Scattering-A Tool for the Study of Biological Molecules and Processes. In Dynamics of Biological Macromolecules by Neutron Scattering; Bentham Science Publishers: Sharjah, United Arab Emirates, 2012; pp. 4–21. [Google Scholar]
- Suetake, I.; Sharma, R.K.; Hojo, H. Analytical Techniques for the Elucidation of Protein Function; John Wiley & Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Russo, D.; Wurm, F.; Teixeira, J. Unlocking complexity through neutron scattering: Structure and dynamics of protein–polymer conjugates. Protein Sci. 2025, 34, e70137. [Google Scholar] [CrossRef]
- Fitter, J.; Lechner, R.; Buldt, G.; Dencher, N. Internal molecular motions of bacteriorhodopsin: Hydration-induced flexibility studied by quasielastic incoherent neutron scattering using oriented purple membranes. Proc. Natl. Acad. Sci. USA 1996, 93, 7600–7605. [Google Scholar] [CrossRef]
- Roh, J.; Curtis, J.; Azzam, S.; Novikov, V.; Peral, I.; Chowdhuri, Z.; Gregory, R.; Sokolov, A.P. Influence of hydration on the dynamics of lysozyme. Biophys. J. 2006, 91, 2573–2588. [Google Scholar] [CrossRef]
- Shirley, W.M.; Bryant, R.G. Proton-nuclear spin relaxation and molecular dynamics in the lysozyme-water system. J. Am. Chem. Soc. 1982, 104, 2910–2918. [Google Scholar] [CrossRef]
- Golub, M.; Pieper, J. The Unusual Functional Role of Protein Flexibility in Photosynthetic Light Harvesting: Protein Dynamics Studied Using Neutron Scattering. Crystals 2024, 14, 743. [Google Scholar] [CrossRef]
- Doster, W.; Settles, M. The dynamical transition in proteins: The role of hydrogen bonds. NATO ASI Ser. A Life Sci. 1999, 305, 177–194. [Google Scholar]
- Pieper, J.; Hauss, T.; Buchsteiner, A.; Renger, G. The Effect of Hydration on Protein Flexibility in Photosystem II of Green Plants Studied by Quasielastic Neutron Scattering. Eur. Biophys. J. EBJ 2008, 37, 657–663. [Google Scholar] [CrossRef] [PubMed]
- Golub, M.; Koppel, M.; Pikma, P.; Frick, B.; Pieper, J. Dynamics-Function Correlation in Photosystem II: Molecular Dynamics in Solution. Crystals 2023, 13, 1441. [Google Scholar] [CrossRef]
- Hajizadeh, M.; Golub, M.; Moldenhauer, M.; Lohstroh, W.; Friedrich, T.; Pieper, J. The Dynamical Properties of Three Different Variants of the Orange Carotenoid Protein: A Quasielastic Neutron Scattering Study. Crystals 2024, 14, 361. [Google Scholar] [CrossRef]
- Caliskan, G.; Mechtani, D.; Roh, J.; Kisliuk, A.; Sokolov, A.; Azzam, S.; Cicerone, M.T.; Lin-Gibson, S.; Peral, I. Protein and solvent dynamics: How strongly are they coupled? J. Chem. Phys. 2004, 121, 1978–1983. [Google Scholar] [CrossRef]
- Jansson, H.; Bergman, R.; Swenson, J. Protein and solvent dynamics as studied by QENS and dielectric spectroscopy. J. Non-Cryst. Solids 2006, 352, 4410–4416. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, C.; Yao, X.; Benmore, C.J.; Yu, L. Structures of glass-forming liquids by X-ray scattering: Glycerol, xylitol, and D-sorbitol. J. Chem. Phys. 2021, 155, 244508. [Google Scholar] [CrossRef]
- Bischof, J.C.; He, X. Thermal stability of proteins. Ann. N. Y. Acad. Sci. 2006, 1066, 12–33. [Google Scholar] [CrossRef]
- Yannopoulos, S.; Andrikopoulos, K.; Ruocco, G. On the analysis of the vibrational Boson peak and low-energy excitations in glasses. J. Non-Cryst. Solids 2006, 352, 4541–4551. [Google Scholar] [CrossRef]
- Pieper, J.; Rätsep, M.; Trostmann, I.; Paulsen, H.; Renger, G.; Freiberg, A. Excitonic energy level structure and pigment-protein interactions in the recombinant water-soluble chlorophyll protein. I. Difference fluorescence line-narrowing. J. Phys. Chem. B 2011, 115, 4042–4052. [Google Scholar] [CrossRef] [PubMed]
- Lutz, M. Resonance Raman spectra of chlorophyll in solution. J. Raman Spectrosc. 1974, 2, 497–516. [Google Scholar] [CrossRef]
- Gryliuk, G.; Rätsep, M.; Hildebrandt, S.; Irrgang, K.-D.; Eckert, H.-J.; Pieper, J. Excitation energy transfer and electron-vibrational coupling in phycobiliproteins of the cyanobacterium Acaryochloris marina investigated by site-selective spectroscopy. Biochim. Biophys. Acta (BBA)-Bioenerg. 2014, 1837, 1490–1499. [Google Scholar] [CrossRef]
- Coquillat, D.; O’Connor, E.; Brouillet, E.V.; Meriguet, Y.; Bray, C.; Nelson, D.J.; Faulds, K.; Torres, J.; Dyakonova, N. Investigating the low-frequency vibrations of chlorophyll derivatives using terahertz spectroscopy. In Proceedings of the Terahertz Emitters, Receivers, and Applications XII, San Diego, CA, USA, 1–5 August 2021; pp. 30–33. [Google Scholar]
- Du, J.; Teramoto, T.; Nakata, K.; Tokunaga, E.; Kobayashi, T. Real-time vibrational dynamics in chlorophyll a studied with a few-cycle pulse laser. Biophys. J. 2011, 101, 995–1003. [Google Scholar] [CrossRef]
- Morris, G.J.; Goodrich, M.; Acton, E.; Fonseca, F. The high viscosity encountered during freezing in glycerol solutions: Effects on cryopreservation. Cryobiology 2006, 52, 323–334. [Google Scholar] [CrossRef]
- Tsai, A.M.; Udovic, T.J.; Neumann, D.A. The inverse relationship between protein dynamics and thermal stability. Biophys. J. 2001, 81, 2339–2343. [Google Scholar] [CrossRef]
- Towey, J.; Soper, A.; Dougan, L. Molecular insight into the hydrogen bonding and micro-segregation of a cryoprotectant molecule. J. Phys. Chem. B 2012, 116, 13898–13904. [Google Scholar] [CrossRef]
- Capaccioli, S.; Ngai, K.; Ancherbak, S.; Paciaroni, A. Evidence of coexistence of change of caged dynamics at T g and the dynamic transition at T d in solvated proteins. J. Phys. Chem. B 2012, 116, 1745–1757. [Google Scholar] [CrossRef]
- Tarek, M.; Tobias, D. Role of protein-water hydrogen bond dynamics in the protein dynamical transition. Phys. Rev. Lett. 2002, 88, 138101. [Google Scholar] [CrossRef]
- Kruteva, M. Dynamics studied by quasielastic neutron scattering (QENS). Adsorption 2021, 27, 875–889. [Google Scholar] [CrossRef]
| 260 K | 280 K | 300 K | |
|---|---|---|---|
| f | 0.39 ± 0.02 a | 0.41 ± 0.02 a | 0.59 ± 0.02 c |
| r [Å] | 0.92 ± 0.05 a | 0.95 ± 0.05 a | 1.06 ± 0.04 c |
| D [meVÅ2] | 0.07 ± 0.01 a | 0.11 ± 0.01 b | 0.14 ± 0.02 c |
| Γ [meV−1] | 9.0 ± 0.5 a | 5.1 ± 0.3 b | 4.8 ± 0.3 b |
| D [10−5 cm2/s] | 1.05 ± 0.1 a | 1.6 ± 0.2 b | 2.1 ± 0.2 c |
| τ [ps] | 5.9 ± 0.3 a | 3.3 ± 0.2 b | 3.1 ± 0.2 b |
| ⟨u2⟩ [Å−2] | 0.11 ± 0.01 a | 0.12 ± 0.01 b | 0.20 ± 0.01 c |
| T (K) | Xc1 (meV) | Wl1 (meV) | A1 (%) |
|---|---|---|---|
| 20 | 3.1 ± 0.1 a | 3.6 ± 0.3 a | 54 |
| 60 | 3.1 ± 0.1 a | 3.6 ± 0.2 a | 54 |
| 100 | 3.1 ± 0.1 a | 4.3 ± 0.1 b | 55 |
| 140 | 3.0 ± 0.1 b | 4.7 ± 0.1 c | 58 |
| 180 | 2.9 ± 0.1 c | 5.2 ± 0.1 d | 60 |
| 200 | 2.8 ± 0.1 d | 6.4 ± 0.1 e | 66 |
| 220 | 2.8 ± 0.1 e | 7.0 ± 0.1 f | 69 |
| 240 | 2.6 ± 0.1 f | 8.0 ± 0.1 g | 73 |
| 260 | 2.4 ± 0.1 g | 8.1 ± 0.1 h | 77 |
| T (K) | Xc1 (meV) | Wl1 (meV) | A1 (%) |
|---|---|---|---|
| 100 | 3.4 ± 0.1 a | 9.3 ± 0.3 a | 75.5 |
| 200 | 3.2 ± 0.1 b | 10 ± 0.6 b | 82.7 |
| 260 | 2.5 ± 0.1 c | 6.7 ± 0.9 b | 91 |
| 280 | 1.8 ± 0.1 d | 7.5 ± 0.1 b | 92 |
| 300 | 1.5 ± 0.1 e | 7.8 ± 0.2 b | 95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajizadeh, M.; Golub, M.; Bektas, I.; Rusevich, L.L.; Embs, J.P.; Lohstroh, W.; Paulsen, H.; Pieper, J. Modulation of Protein Dynamics by Glycerol in Water-Soluble Chlorophyll-Binding Protein (WSCP). Crystals 2025, 15, 569. https://doi.org/10.3390/cryst15060569
Hajizadeh M, Golub M, Bektas I, Rusevich LL, Embs JP, Lohstroh W, Paulsen H, Pieper J. Modulation of Protein Dynamics by Glycerol in Water-Soluble Chlorophyll-Binding Protein (WSCP). Crystals. 2025; 15(6):569. https://doi.org/10.3390/cryst15060569
Chicago/Turabian StyleHajizadeh, Mina, Maksym Golub, Inga Bektas, Leonid L. Rusevich, Jan P. Embs, Wiebke Lohstroh, Harald Paulsen, and Jörg Pieper. 2025. "Modulation of Protein Dynamics by Glycerol in Water-Soluble Chlorophyll-Binding Protein (WSCP)" Crystals 15, no. 6: 569. https://doi.org/10.3390/cryst15060569
APA StyleHajizadeh, M., Golub, M., Bektas, I., Rusevich, L. L., Embs, J. P., Lohstroh, W., Paulsen, H., & Pieper, J. (2025). Modulation of Protein Dynamics by Glycerol in Water-Soluble Chlorophyll-Binding Protein (WSCP). Crystals, 15(6), 569. https://doi.org/10.3390/cryst15060569






