Mechanical and Electronic Properties of Fe(II) Doped Calcite: Ab Initio Calculations
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
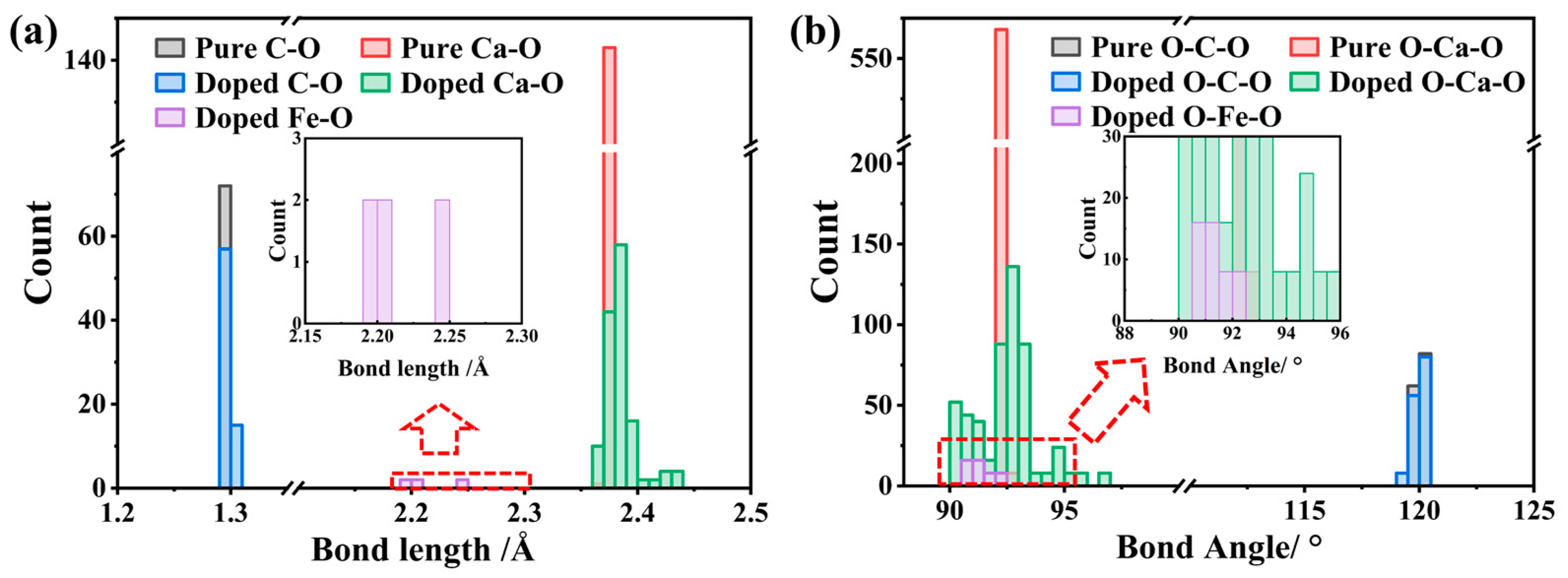
3.1. Relaxation of Structure
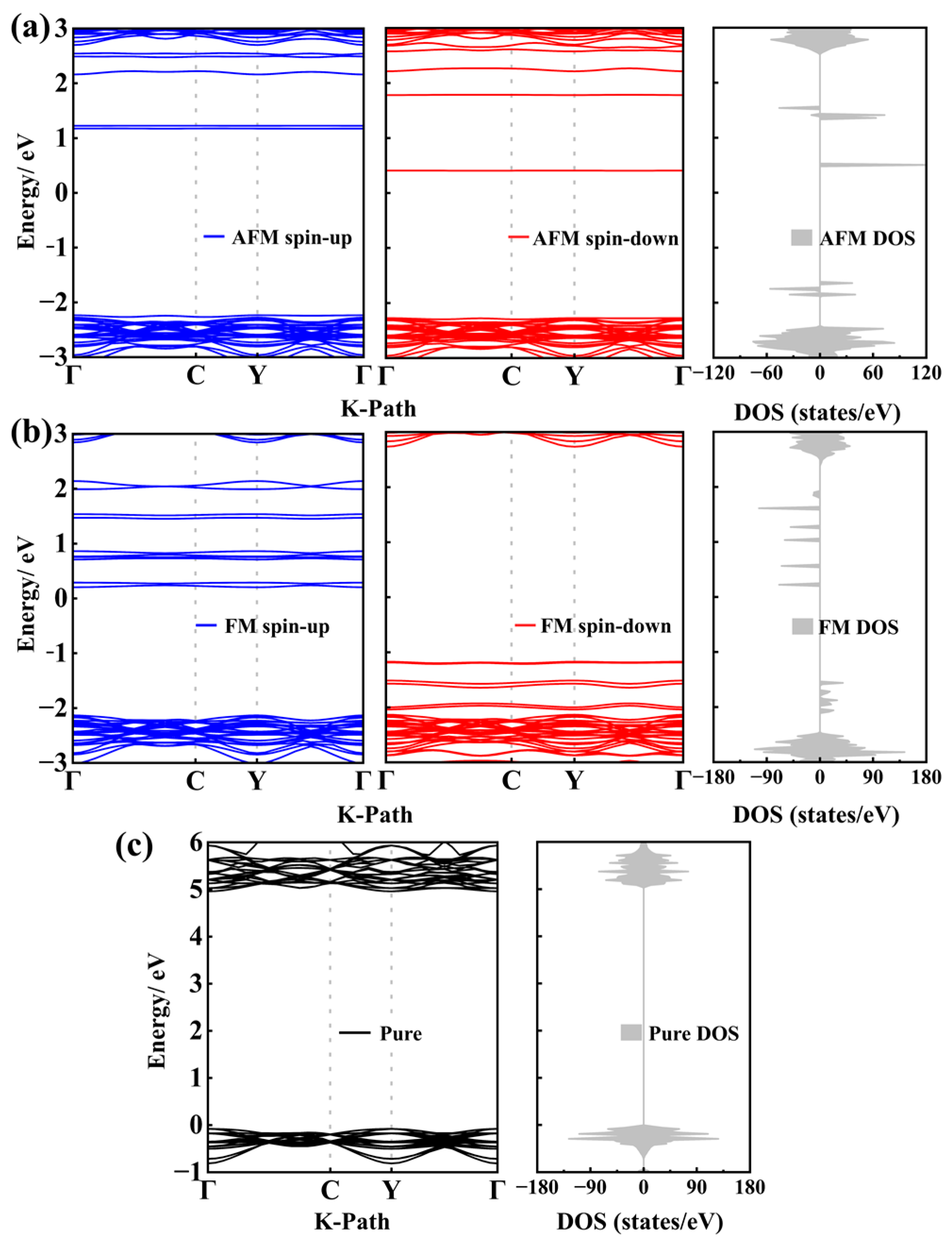
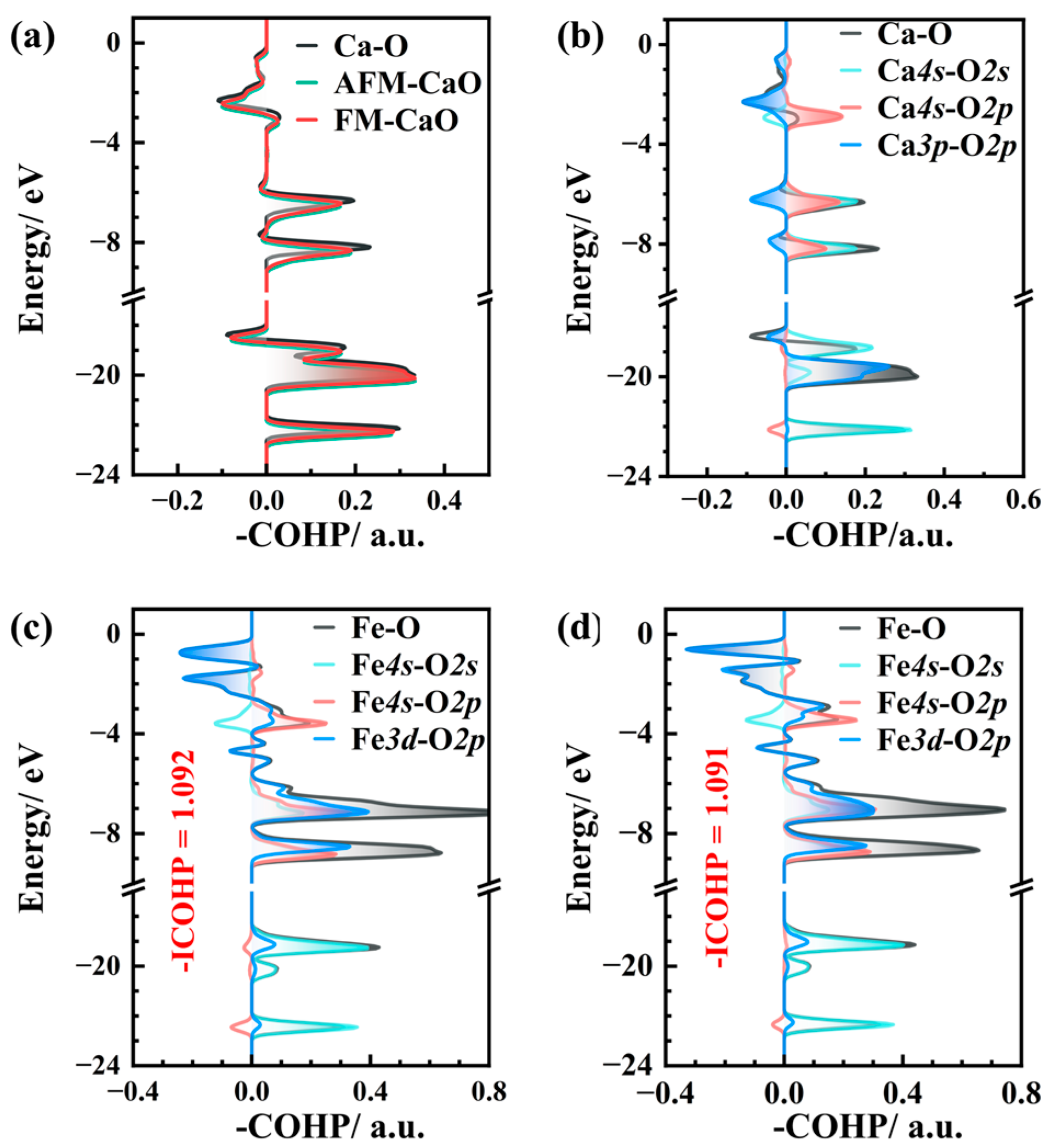
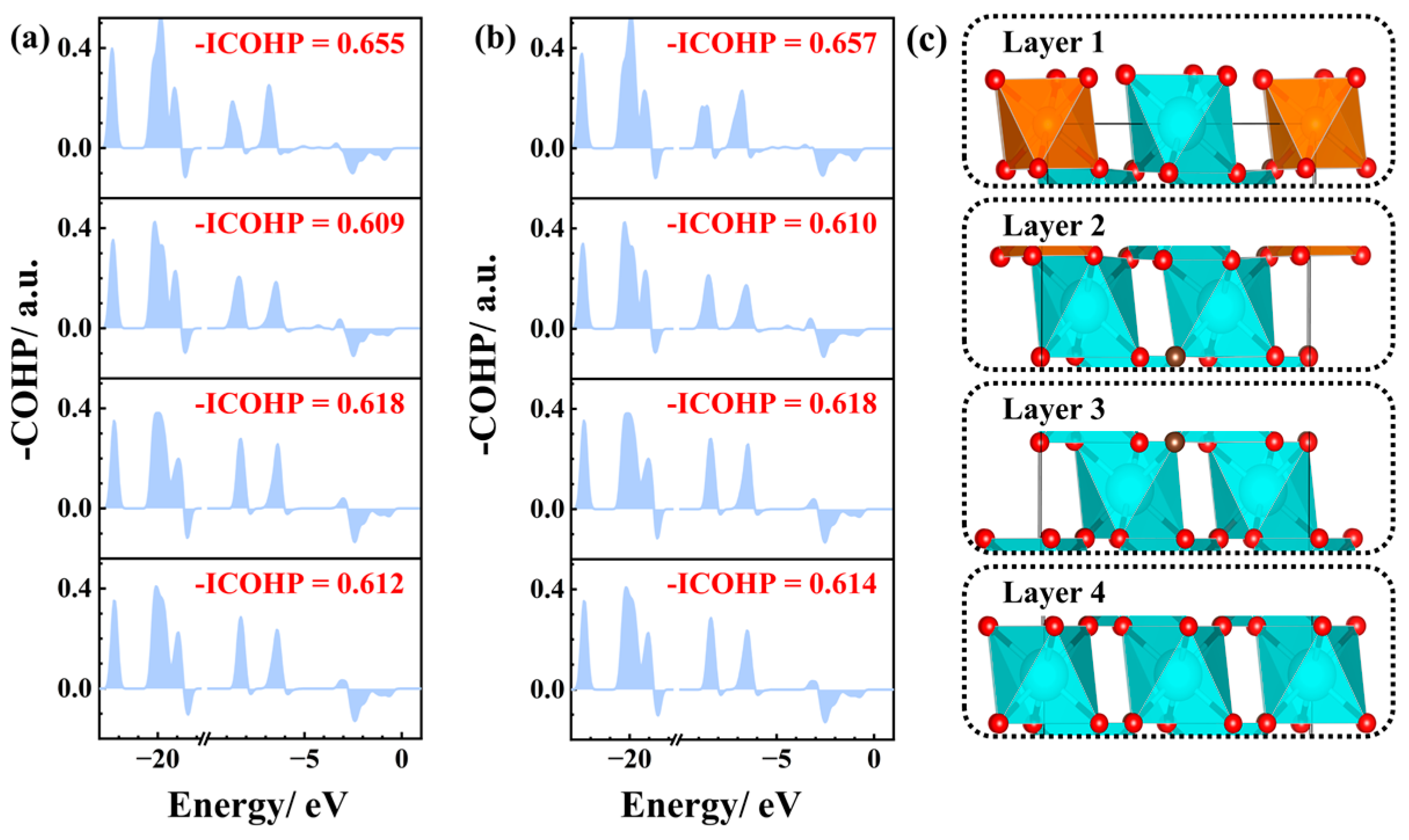
3.2. Electronic Structure
3.3. Elastic Property
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qian, C.; Ren, X.; Rui, Y.; Wang, K. Characteristics of bio-CaCO3 from microbial bio-mineralization with different bacteria species. Biochem. Eng. J. 2021, 176, 108180. [Google Scholar] [CrossRef]
- Staudigel, P.T.; Swart, P.K. Isotopic behavior during the aragonite-calcite transition: Implications for sample preparation and proxy interpretation. Chem. Geol. 2016, 442, 130–138. [Google Scholar] [CrossRef]
- Yoshioka, S.; Kitano, Y. Transformation of aragonite to calcite through heating. Geochem. J. 1985, 19, 245–249. [Google Scholar] [CrossRef]
- Reimer, T.; Dempster, T.; Warren-Myers, F.; Jensen, A.J.; Swearer, S.E. High prevalence of vaterite in sagittal otoliths causes hearing impairment in farmed fish. Sci. Rep. 2016, 6, 25249. [Google Scholar] [CrossRef] [PubMed]
- Pracheil, B.M.; George, R.; Chakoumakos, B.C. Significance of otolith calcium carbonate crystal structure diversity to microchemistry studies. Rev. Fish Biol. Fish. 2019, 29, 569–588. [Google Scholar] [CrossRef]
- Elgalhud, A.A.; Dhir, R.K.; Ghataora, G. Limestone addition effects on concrete porosity. Cem. Concr. Compos. 2016, 72, 222–234. [Google Scholar] [CrossRef]
- Wan, J.; Liu, B.; Wang, H.; Chen, W.; Wang, F.; Yue, Y.; Li, N. High-strength and -toughness calcite through hybridization with amino acids by sp2 to sp3 transformation. Cell Rep. Phys. Sci. 2024, 5, 102106. [Google Scholar] [CrossRef]
- Ihli, J.; Clark, J.N.; Kanwal, N.; Kim, Y.Y.; Holden, M.A.; Harder, R.J.; Tang, C.C.; Ashbrook, S.E.; Robinson, I.K.; Meldrum, F.C. Visualization of the effect of additives on the nanostructures of individual bio-inspired calcite crystals. Chem. Sci. 2019, 10, 1176–1185. [Google Scholar] [CrossRef]
- Ulian, G.; Valdre, G. Study of the variation of the optical properties of calcite with applied stress, useful for specific rock and material mechanics. Sci. Rep. 2022, 12, 299. [Google Scholar] [CrossRef]
- Choi, S.-G.; Chang, I.; Lee, M.; Lee, J.-H.; Han, J.-T.; Kwon, T.-H. Review on geotechnical engineering properties of sands treated by microbially induced calcium carbonate precipitation (MICP) and biopolymers. Constr. Build. Mater. 2020, 246, 118415. [Google Scholar] [CrossRef]
- Shakeri, M.R.; Haeri, S.M.; Shahrabi, M.M.; Khosravi, A.; Sajadi, A.A. An Experimental Study on Mechanical Behavior of a Calcite Cemented Gravelly Sand. Geotech. Test. J. 2018, 41, 494–507. [Google Scholar] [CrossRef]
- Stipp, S.L.; Hochella, M.F. Structure and bonding environments at the calcite surface as observed with X-ray photoelectron spectroscopy (XPS) and low energy electron diffraction (LEED). Geochim. Cosmochim. Acta 1991, 55, 1723–1736. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, K.; Yao, Y.; Xue, F.; Lu, F.; Yan, W.; Yuan, F.; Wang, X. Ferromagnetic Fe-TiO2 spin catalysts for enhanced ammonia electrosynthesis. Nat. Commun. 2025, 16, 1129. [Google Scholar] [CrossRef]
- Dos Santos, G.; Meyer, R.; Tramontina, D.; Bringa, E.M.; Urbassek, H.M. Spin-lattice-dynamics analysis of magnetic properties of iron under compression. Sci. Rep. 2023, 13, 14282. [Google Scholar] [CrossRef]
- Zhao, J.; He, M.-C.; Hu, X.-X.; Gao, W. Density functional theory investigation of carbon monoxide adsorption on the kaolinite (001) surface. Chin. Phys. B 2017, 26, 079101. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Jain, A.; Hautier, G.; Ong, S.P.; Moore, C.J.; Fischer, C.C.; Persson, K.A.; Ceder, G. Formation enthalpies by mixing GGA and GGA+Ucalculations. Phys. Rev. B 2011, 84, 045115. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, Y.; Ding, X.; Sun, J.; Butterfield, N.J.; Aufort, J.; Salje, E.K.H. 1 citation on Dimensions. {101¯4} twin boundary in calcite: Structure and physical properties. Phys. Rev. B 2024, 110, 144112. [Google Scholar] [CrossRef]
- Campbell, S.; Poduska, K.M. Incorporating far-infrared data into carbonate mineral analyses. Minerals 2020, 10, 628. [Google Scholar] [CrossRef]
- Grau-Crespo, R.; Hamad, S.; Catlow, C.R.A.; Leeuw, N.H.d. Symmetry-adapted configurational modelling of fractional site occupancy in solids. J. Phys. Condens. Matter 2007, 19, 256201. [Google Scholar] [CrossRef]
- Hossain, F.M.; Murch, G.E.; Belova, I.V.; Turner, B.D. Electronic, optical and bonding properties of CaCO3 calcite. Solid State Commun. 2009, 149, 1201–1203. [Google Scholar] [CrossRef]
- Nityananda, R.; Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Resonance 2017, 22, 809–811. [Google Scholar] [CrossRef]
- Brik, M.G. First-principles calculations of structural, electronic, optical and elastic properties of magnesite MgCO3 and calcite CaCO3. Phys. B Condens. Matter 2011, 406, 1004–1012. [Google Scholar] [CrossRef]
- Stashans, A.; Chamba, G.; Pinto, H. Electronic structure, chemical bonding, and geometry of pure and Sr-doped CaCO3. J. Comput. Chem. 2008, 29, 343–349. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougreeff, A.L.; Dronskowski, R. Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef]
- Nelson, R.; Ertural, C.; George, J.; Deringer, V.L.; Hautier, G.; Dronskowski, R. LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory. J. Comput. Chem. 2020, 41, 1931–1940. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Guran, A.; Atanackovic, T.M.; Guran, A. Hooke’s law. In Theory of Elasticity for Scientists and Engineers; Birkhäuser: Basel, Switzerland, 2000; pp. 85–111. [Google Scholar] [CrossRef]
- Gusev, A.; Sadovnikov, S. Conditions of elastic mechanical stability and elastic properties of crystal structures with different symmetry. Phys. Solid State 2022, 64, 659. [Google Scholar] [CrossRef]
- Chen, C.-C.; Lin, C.-C.; Liu, L.-G.; Sinogeikin, S.V.; Bass, J.D. Elasticity of single-crystal calcite and rhodochrosite by Brillouin spectroscopy. Am. Mineral. 2001, 86, 1525–1529. [Google Scholar] [CrossRef]
- Hearmon, R.F.S. The Elastic Constants of Anisotropic Materials. Rev. Mod. Phys. 1946, 18, 409–440. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.; Qiao, Y.; Luan, Z. Effect of Mg(II), Mn(II), and Fe(II) doping on the mechanical properties and electronic structure of calcite. Mater. Today Commun. 2022, 31, 103725. [Google Scholar] [CrossRef]
- Zhang, C.; Li, L.; Yuan, Z.; Xu, X.; Song, Z.; Zhang, Y.R. Mechanical properties of siderite and hematite from DFT calculation. Miner. Eng. 2020, 146, 106107. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Li, X.T.; Li, R.H.; Liu, R.; Qu, Z.; Sheinerman, A.G.; Zhang, Z.F. Prediction for the elastic modulus of polycrystalline materials: Theoretical derivation, verification, and application. Phys. Rev. B 2023, 108, 174104. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Und Mech. 2006, 9, 49–58. [Google Scholar] [CrossRef]
- Liao, M.; Liu, Y.; Min, L.; Lai, Z.; Han, T.; Yang, D.; Zhu, J. Alloying effect on phase stability, elastic and thermodynamic properties of Nb-Ti-V-Zr high entropy alloy. Intermetallics 2018, 101, 152–164. [Google Scholar] [CrossRef]
- Liao, M.; Liu, Y.; Cui, P.; Qu, N.; Zhou, F.; Yang, D.; Han, T.; Lai, Z.; Zhu, J. Modeling of alloying effect on elastic properties in BCC Nb-Ti-V-Zr solid solution: From unary to quaternary. Comput. Mater. Sci. 2020, 172, 109289. [Google Scholar] [CrossRef]
- Xu, L.; Tian, J.; Wu, H.; Fang, S.; Lu, Z.; Ma, C.; Sun, W.; Hu, Y. Anisotropic surface chemistry properties and adsorption behavior of silicate mineral crystals. Adv. Colloid. Interface Sci. 2018, 256, 340–351. [Google Scholar] [CrossRef]
- Li, X.T.; Liu, Z.Q.; Zhang, Z.J.; Zhang, P.; Zhang, Z.F. Ductile-to-brittle transition criterion of metallic glasses. Phys. Rev. Mater. 2024, 8, 093608. [Google Scholar] [CrossRef]



| Exp [34] | Exp [33] | Fe-Doped [34] | Pure | Fe-Doped | Siderite [35] | |
|---|---|---|---|---|---|---|
| C11 | 149.4 | 144 | 93.0 | 146.9 | 160.9 | 278.0 |
| C12 | 57.9 | 53.9 | 39.1 | 53.6 | 71.2 | 95.5 |
| C13 | 53.5 | 51.1 | 26.5 | 57.0 | 60.3 | 84.1 |
| C33 | 85.2 | 84 | 74.1 | 87.6 | 83.1 | 144.0 |
| C44 | 34.1 | 33.5 | 25.5 | 30.5 | 35.7 | 48.0 |
| C66 | 45.8 | 45.1 | 42.2 | 43.4 | 44.8 | 91.3 |
| Exp | Pure | Fe-Doped | Fe-Doped [34] | Siderite [35] | Unit | |
|---|---|---|---|---|---|---|
| B | 74.6 ± 2.0 | 77.88 | 82.50 | 48.23 | 129.18 | GPa |
| E | 81.0 ± 0.8 | 82.55 | 87.56 | 72.21 | 154.67 | GPa |
| G | 30.7 ± 0.2 | 31.19 | 33.09 | 28.87 | 59.47 | GPa |
| ν | 0.32 | 0.32 | 0.32 | 0.25 | 0.30 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhi, X.; Jia, F.; Ye, J.; Li, N. Mechanical and Electronic Properties of Fe(II) Doped Calcite: Ab Initio Calculations. Crystals 2025, 15, 566. https://doi.org/10.3390/cryst15060566
Wu Z, Zhi X, Jia F, Ye J, Li N. Mechanical and Electronic Properties of Fe(II) Doped Calcite: Ab Initio Calculations. Crystals. 2025; 15(6):566. https://doi.org/10.3390/cryst15060566
Chicago/Turabian StyleWu, Zhangci, Xiao Zhi, Fujie Jia, Jiayuan Ye, and Neng Li. 2025. "Mechanical and Electronic Properties of Fe(II) Doped Calcite: Ab Initio Calculations" Crystals 15, no. 6: 566. https://doi.org/10.3390/cryst15060566
APA StyleWu, Z., Zhi, X., Jia, F., Ye, J., & Li, N. (2025). Mechanical and Electronic Properties of Fe(II) Doped Calcite: Ab Initio Calculations. Crystals, 15(6), 566. https://doi.org/10.3390/cryst15060566






