Anisotropic Fracture Energy of Boron-Doped P-Type Silicon by Microindentation: Influence of Temperature and Crystallographic Orientation
Abstract
1. Introduction
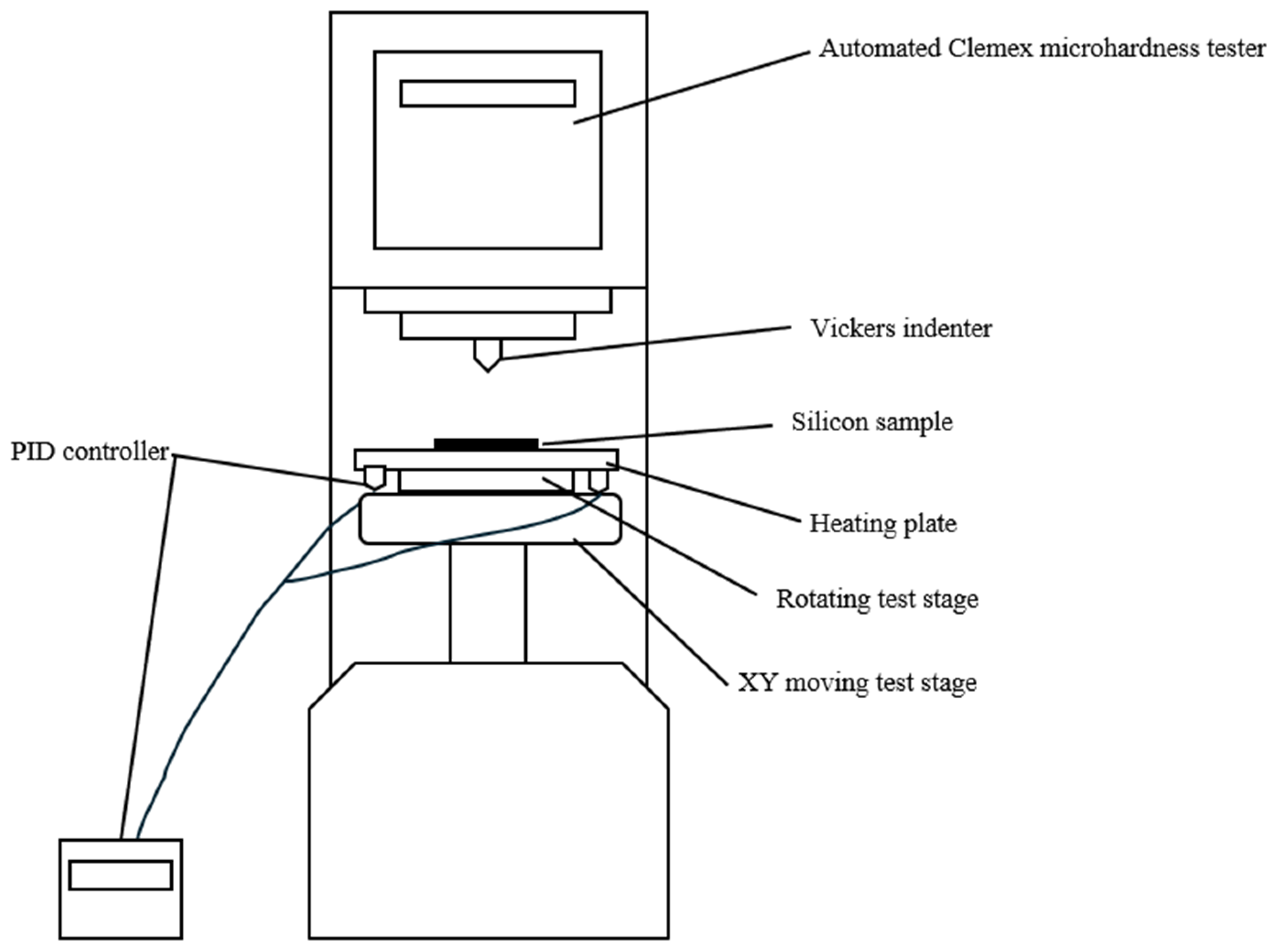
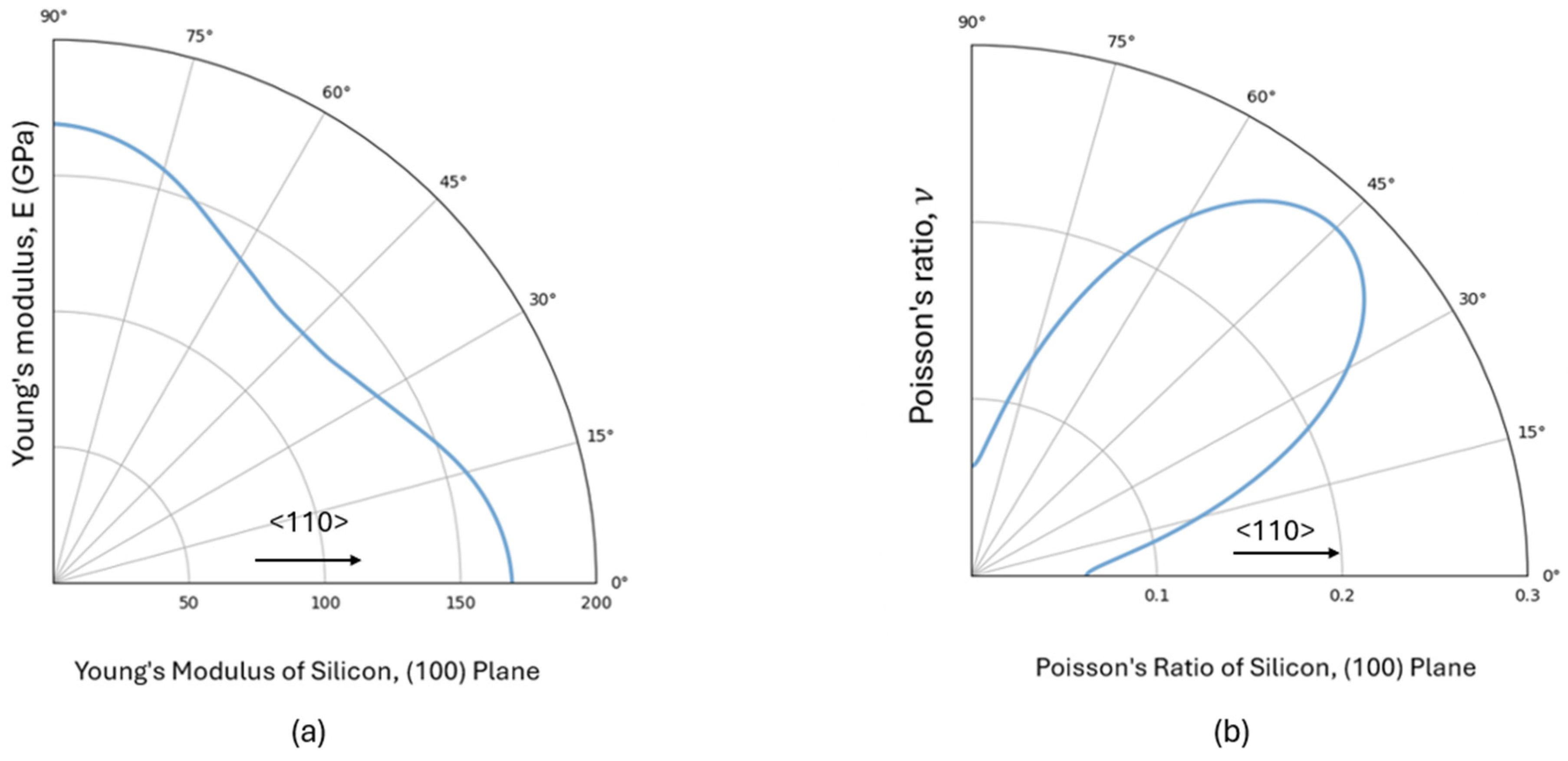
2. Materials and Methods
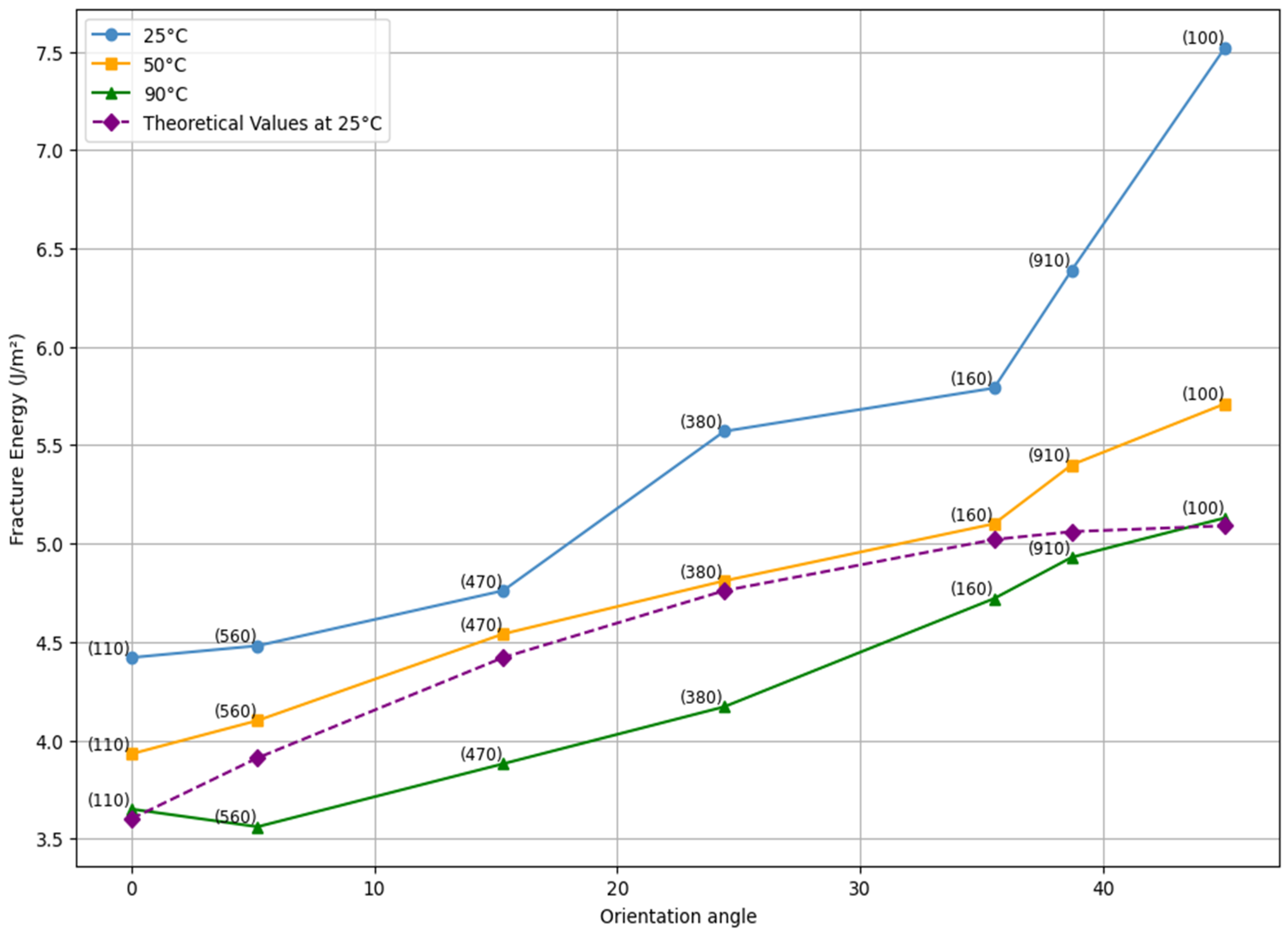
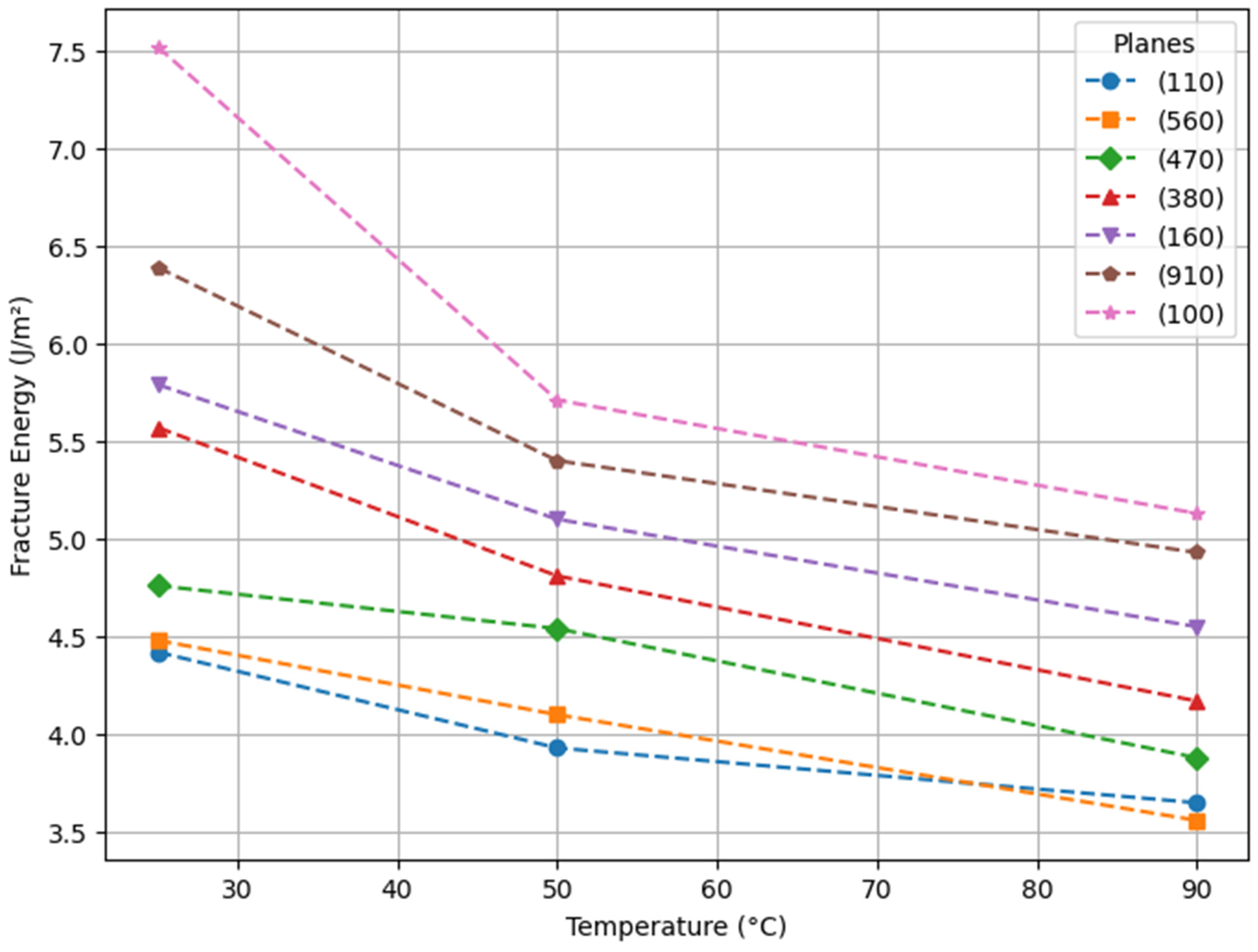
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, S. (Ed.) Advanced Material and Device Applications with Germanium; InTech: London, UK, 2018. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Meng, F.; Liu, D.; Huang, S.; Cui, J.; Wang, J.; Wen, W. Origin and evolution of a crack in silicon induced by a single grain grinding. J. Manuf. Process. 2022, 75, 617–626. [Google Scholar] [CrossRef]
- Masolin, A.; Bouchard, P.-O.; Martini, R.; Bernacki, M. Thermo-mechanical and fracture properties in single-crystal silicon. J. Mater. Sci. 2013, 48, 979–988. [Google Scholar] [CrossRef]
- Hintsala, E.D.; Bhowmick, S.; Yueyue, X.; Ballarini, R.; Asif, S.A.S.; Gerberich, W.W. Temperature dependent fracture initiation in microscale silicon. Scr. Mater. 2017, 130, 78–82. [Google Scholar] [CrossRef]
- Armstrong, D.E.J.; Tarleton, E. Bend Testing of Silicon Microcantilevers from 21 °C to 770 °C. JOM 2015, 67, 2914–2920. [Google Scholar] [CrossRef]
- Korte, S.; Barnard, J.S.; Stearn, R.J.; Clegg, W.J. Deformation of silicon—Insights from microcompression testing at 25–500 °C. Int. J. Plast. 2011, 27, 1853–1866. [Google Scholar] [CrossRef]
- Jaya, B.N.; Wheeler, J.M.; Wehrs, J.; Best, J.P.; Soler, R.; Michler, J.; Kirchlechner, C.; Dehm, G. Microscale Fracture Behavior of Single Crystal Silicon Beams at Elevated Temperatures. Nano Lett. 2016, 16, 7597–7603. [Google Scholar] [CrossRef]
- Nakao, S.; Ando, T.; Shikida, M.; Sato, K. Effect of temperature on fracture toughness in a single-crystal-silicon film and transition in its fracture mode. J. Micromech. Microeng. 2008, 18, 015026. [Google Scholar] [CrossRef]
- Li, X.; Fan, Z.; Huang, S.; Lu, M.; Huang, H. Brittle-to-ductile transition in nanoscratching of silicon and gallium arsenide using Berkovich and Conical tips. Appl. Surf. Sci. 2023, 637, 157934. [Google Scholar] [CrossRef]
- Lauener, C.M.; Petho, L.; Chen, M.; Xiao, Y.; Michler, J.; Wheeler, J.M. Fracture of Silicon: Influence of rate, positioning accuracy, FIB machining, and elevated temperatures on toughness measured by pillar indentation splitting. Mater. Des. 2018, 142, 340–349. [Google Scholar] [CrossRef]
- Norton, A.D.; Falco, S.; Young, N.; Severs, J.; Todd, R.I. Microcantilever investigation of fracture toughness and subcritical crack growth on the scale of the microstructure in Al2O3. J. Eur. Ceram. Soc. 2015, 35, 4521–4533. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Y.A.; Li, Y.J.; Wang, X.F.; Yue, Y.J. Cleavage anisotropy of boron doped cracks in crystalline silicon. Microelectron. Reliab. 2022, 138, 114653. [Google Scholar] [CrossRef]
- Guolin Yu, G.Y.; Junji Watanabe, J.W.; Katsutoshi Izumi, K.I.; Kenshiro Nakashima, K.N.; Takashi Jimbo, T.J.; Masayoshi Umeno, M.U. Mechanical Property Characterization of Boron-Doped Silicon by Berkovich-Type Indenter. Jpn. J. Appl. Phys. 2001, 40, L183. [Google Scholar] [CrossRef]
- Sakakima, H.; Izumi, S. Carrier-doping effect on strength and deformations in group-IV crystals. Int. J. Mech. Sci. 2025, 293, 110169. [Google Scholar] [CrossRef]
- Hirakata, H.; Homma, S.; Noda, H.; Sakaguchi, S.; Shimada, T. Effects of excess electrons/holes on fracture toughness of single-crystal Si. J. Appl. Phys. 2023, 133, 035101. [Google Scholar] [CrossRef]
- Moulins, A.; Andrusyszyn, F.; Dugnani, R.; Zednik, R.J. Indentation fracture toughness of semiconducting gallium arsenide at elevated temperatures. Eng. Fail. Anal. 2022, 137, 106417. [Google Scholar] [CrossRef]
- Niihara, K.; Morena, R.; Hasselman, D.P.H. Evaluation ofK Ic of brittle solids by the indentation method with low crack-to-indent ratios. J. Mater. Sci. Lett. 1982, 1, 13–16. [Google Scholar] [CrossRef]
- Palmqvist, S. A method to determine the toughness of brittle materials, especially hard metals. Jernkontorets Ann. 1957, 141, 300–306. [Google Scholar]
- Moradkhani, A.; Panahizadeh, V.; Hoseinpour, M. Indentation fracture resistance of brittle materials using irregular cracks: A review. Heliyon 2023, 9, e19361. [Google Scholar] [CrossRef]
- Ponton, C.B.; Rawlings, R.D. Vickers indentation fracture toughness test Part 2 Application and critical evaluation of standardised indentation toughness equations. Mater. Sci. Technol. 1989, 5, 961–976. [Google Scholar] [CrossRef]
- Anstis, G.R.; Chantikul, P.; Lawn, B.R.; Marshall, D.B. A Critical Evaluation of Indentation Techniques for Measuring Fracture Toughness: I, Direct Crack Measurements. J. Am. Ceram. Soc. 1981, 64, 533–538. [Google Scholar] [CrossRef]
- Lemaitre, P. Fracture toughness of germanium determined with the Vickers indentation technique. J. Mater. Sci. Lett. 1988, 7, 895–896. [Google Scholar] [CrossRef]
- Tanaka, M.; Higashida, K.; Nakashima, H.; Takagi, H.; Fujiwara, M. Fracture Toughness Evaluated by Indentation Methods and Its Relation to Surface Energy in Silicon Single Crystals. Mater. Trans. 2003, 44, 681–684. [Google Scholar] [CrossRef][Green Version]
- Ebrahimi, F.; Kalwani, L. Fracture anisotropy in silicon single crystal. Mater. Sci. Eng. A 1999, 268, 116–126. [Google Scholar] [CrossRef]
- Rickhey, F.; Marimuthu, K.P.; Lee, K.; Lee, H. Indentation cracking of monocrystalline silicon considering fracture anisotropy. Theor. Appl. Fract. Mech. 2019, 100, 128–138. [Google Scholar] [CrossRef]
- Moulins, A.; Dugnani, R.; Zednik, R.J. Anisotropic fracture energy and toughness of single crystal gallium arsenide by microindentation. Eng. Fract. Mech. 2023, 292, 109631. [Google Scholar] [CrossRef]
- Wachtman, J.B., Jr. Determination of Elastic Constants Required for Application of Fracture Mechanics to Ceramics. In Concepts, Flaws and Fractography, 2nd ed.; Fracture Mechanics of Ceramics; Springer: Boston, MA, USA, 1973; pp. 49–68. [Google Scholar]
- McSkimin, H.J.; Bond, W.L.; Buehler, E.; Teal, G.K. Measurement of the Elastic Constants of Silicon Single Crystals and Their Thermal Coefficients. Phys. Rev. 1951, 83, 1080. [Google Scholar] [CrossRef]
- Sih, G.C.; Paris, P.C.; Irwin, G.R. On cracks in rectilinearly anisotropic bodies. Int. J. Fract. Mech. 1965, 1, 189–203. [Google Scholar] [CrossRef]
- Flügge, S. Elasticity and Plasticity/Elastizität und Plastizität; Springer: Berlin/Heidelberg, Germany, 1958; pp. 551–590. [Google Scholar] [CrossRef]
- Brantley, W.A. Calculated elastic constants for stress problems associated with semiconductor devices. J. Appl. Phys. 1973, 44, 534–535. [Google Scholar] [CrossRef]
- Tanaka, M.; Higashida, K.; Nakashima, H.; Takagi, H.; Fujiwara, M. Orientation dependence of fracture toughness measured by indentation methods and its relation to surface energy in single crystal silicon. Int. J. Fract. 2006, 139, 383–394. [Google Scholar] [CrossRef]
- Wolff, G.A.; Broder, J.D. Microcleavage, bonding character and surface structure in materials with tetrahedral coordination. Acta Crystallogr. 1959, 12, 313–323. [Google Scholar] [CrossRef]
- DelRio, F.W.; Cook, R.F.; Boyce, B.L. Fracture strength of micro- and nano-scale silicon components. Appl. Phys. Rev. 2015, 2, 021303. [Google Scholar] [CrossRef]
- Pérez, R.; Gumbsch, P. Directional Anisotropy in the Cleavage Fracture of Silicon. Phys. Rev. Lett. 2000, 84, 5347–5350. [Google Scholar] [CrossRef]
- King, S.W.; Antonelli, G.A. Simple bond energy approach for non-destructive measurements of the fracture toughness of brittle materials. Thin Solid Films 2007, 515, 7232–7241. [Google Scholar] [CrossRef]
- Nejati, M.; Bahrami, B.; Ayatollahi, M.R.; Driesner, T. On the anisotropy of shear fracture toughness in rocks. Theor. Appl. Fract. Mech. 2021, 113, 102946. [Google Scholar] [CrossRef]

| (J/m2) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Angle (±1°) | Plane | 25 °C | 50 °C | 90 °C | 25 °C | 50 °C | 90 °C | 25 °C | 50 °C | 90 °C |
| 0° | (110) | 11.05 | 10.55 | 10.16 | 0.81 | 0.77 | 0.74 | 4.42 | 3.93 | 3.65 |
| 5° | (560) | 11.31 | 11.03 | 9.84 | 0.82 | 0.78 | 0.73 | 4.48 | 4.10 | 3.56 |
| 15° | (470) | 11.74 | 11.13 | 10.33 | 0.85 | 0.83 | 0.77 | 4.76 | 4.54 | 3.88 |
| 25° | (380) | 12.00 | 11.52 | 10.85 | 0.93 | 0.86 | 0.80 | 5.57 | 4.81 | 4.17 |
| 35° | (160) | 12.42 | 11.97 | 11.11 | 0.96 | 0.90 | 0.87 | 5.79 | 5.10 | 4.72 |
| 40° | (910) | 12.75 | 12.30 | 11.54 | 1.01 | 0.93 | 0.89 | 6.39 | 5.40 | 4.93 |
| 45° | (100) | 13.06 | 12.59 | 11.80 | 1.10 | 0.97 | 0.90 | 7.52 | 5.71 | 5.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guettouche, W.e.; Zednik, R.J. Anisotropic Fracture Energy of Boron-Doped P-Type Silicon by Microindentation: Influence of Temperature and Crystallographic Orientation. Crystals 2025, 15, 533. https://doi.org/10.3390/cryst15060533
Guettouche We, Zednik RJ. Anisotropic Fracture Energy of Boron-Doped P-Type Silicon by Microindentation: Influence of Temperature and Crystallographic Orientation. Crystals. 2025; 15(6):533. https://doi.org/10.3390/cryst15060533
Chicago/Turabian StyleGuettouche, Wala eddine, and Ricardo J. Zednik. 2025. "Anisotropic Fracture Energy of Boron-Doped P-Type Silicon by Microindentation: Influence of Temperature and Crystallographic Orientation" Crystals 15, no. 6: 533. https://doi.org/10.3390/cryst15060533
APA StyleGuettouche, W. e., & Zednik, R. J. (2025). Anisotropic Fracture Energy of Boron-Doped P-Type Silicon by Microindentation: Influence of Temperature and Crystallographic Orientation. Crystals, 15(6), 533. https://doi.org/10.3390/cryst15060533






