Interface Effect in Ir-Nb-Zr Alloy
Abstract
1. Introduction
2. Calculation Methods
3. Results and Discussion
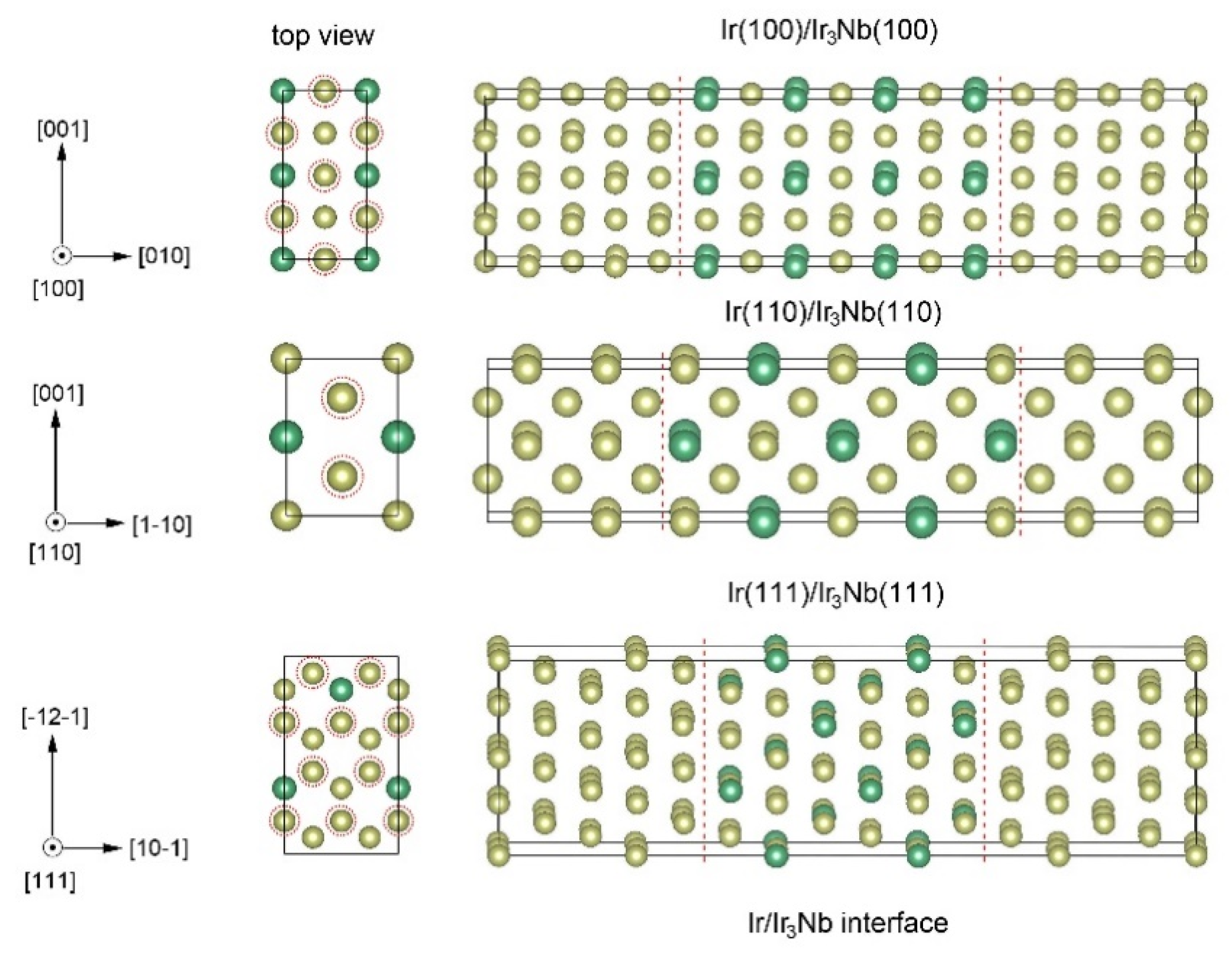
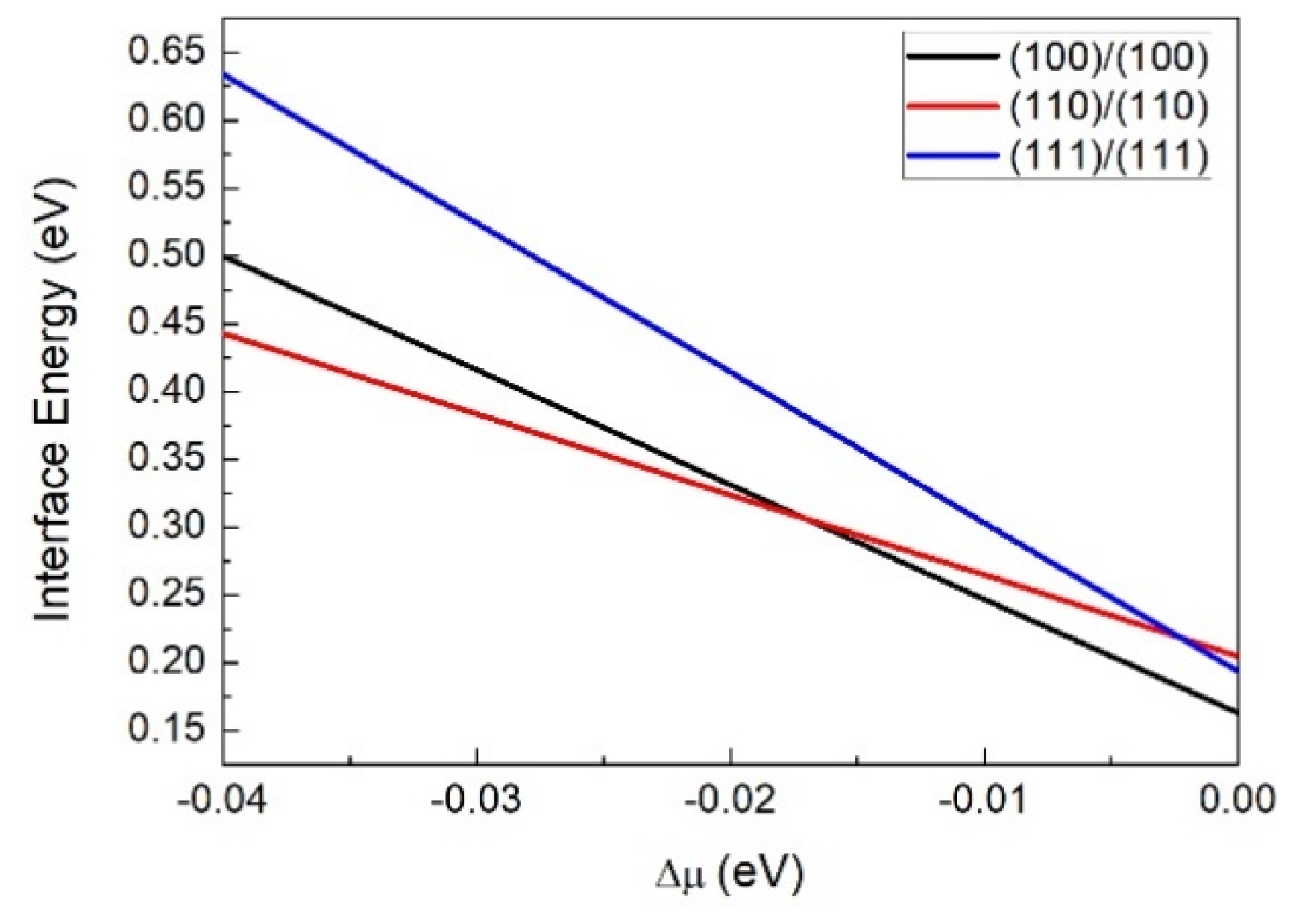
3.1. Interface Structure and Stability
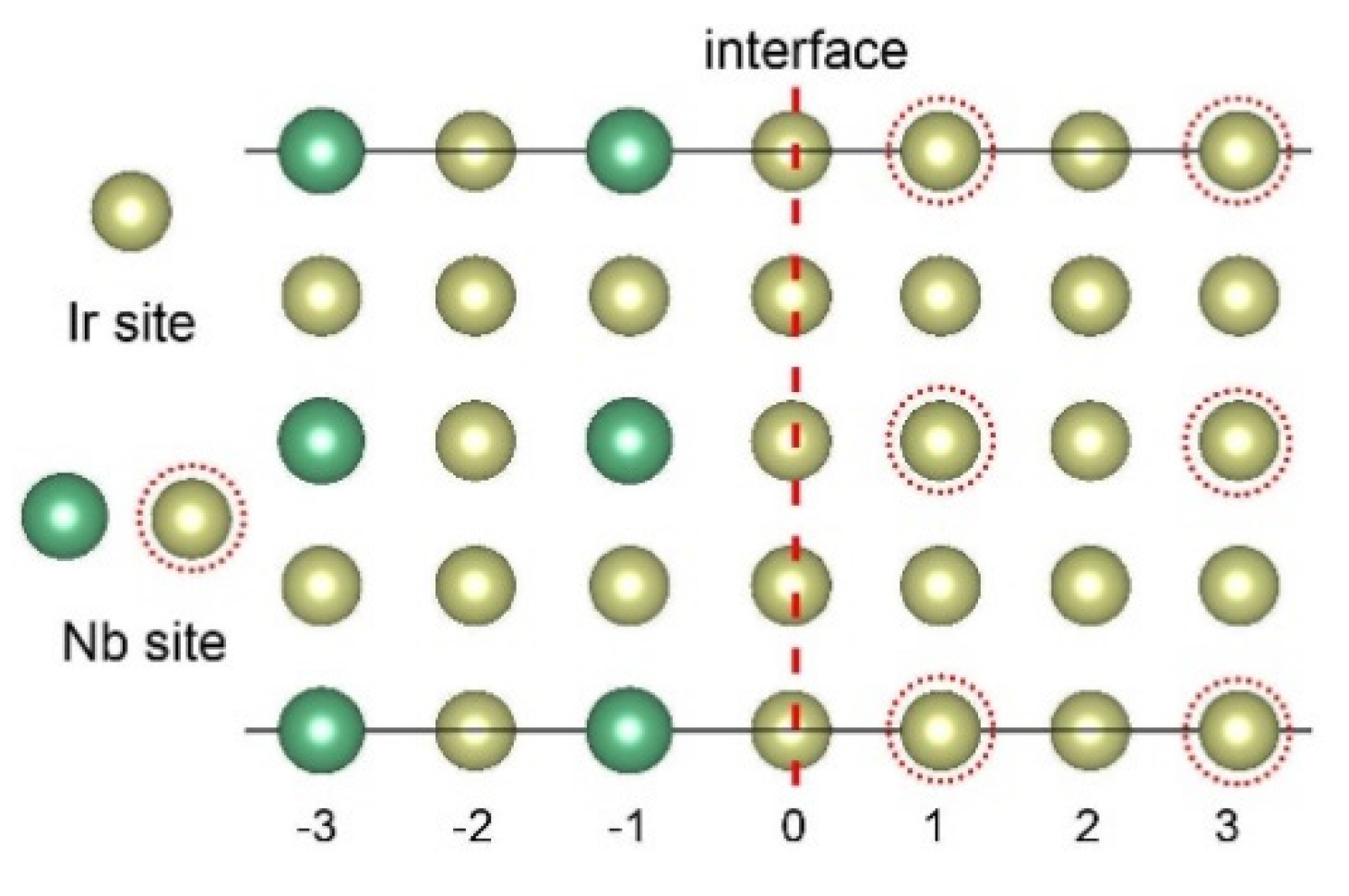
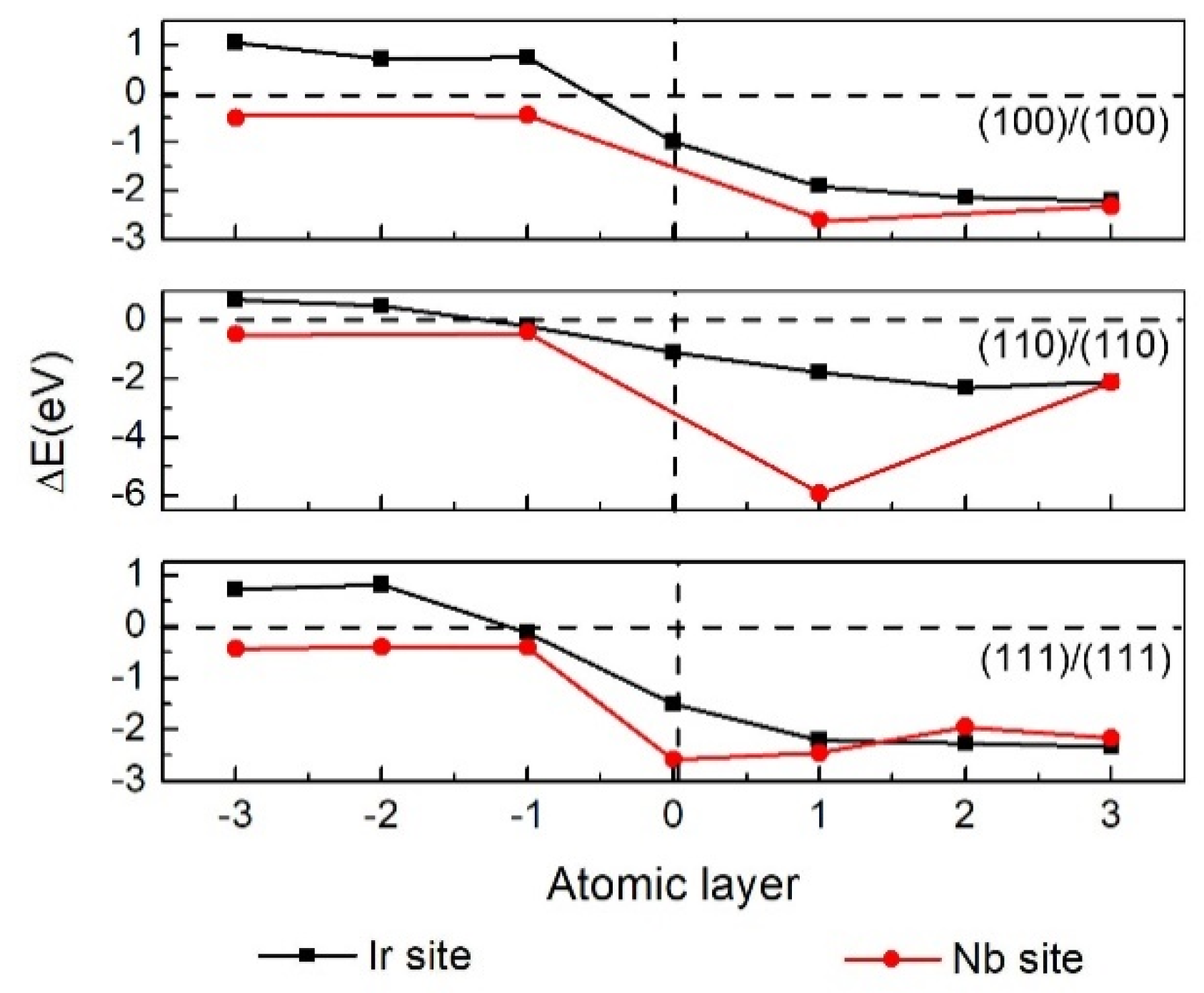
3.2. Interface Segregation
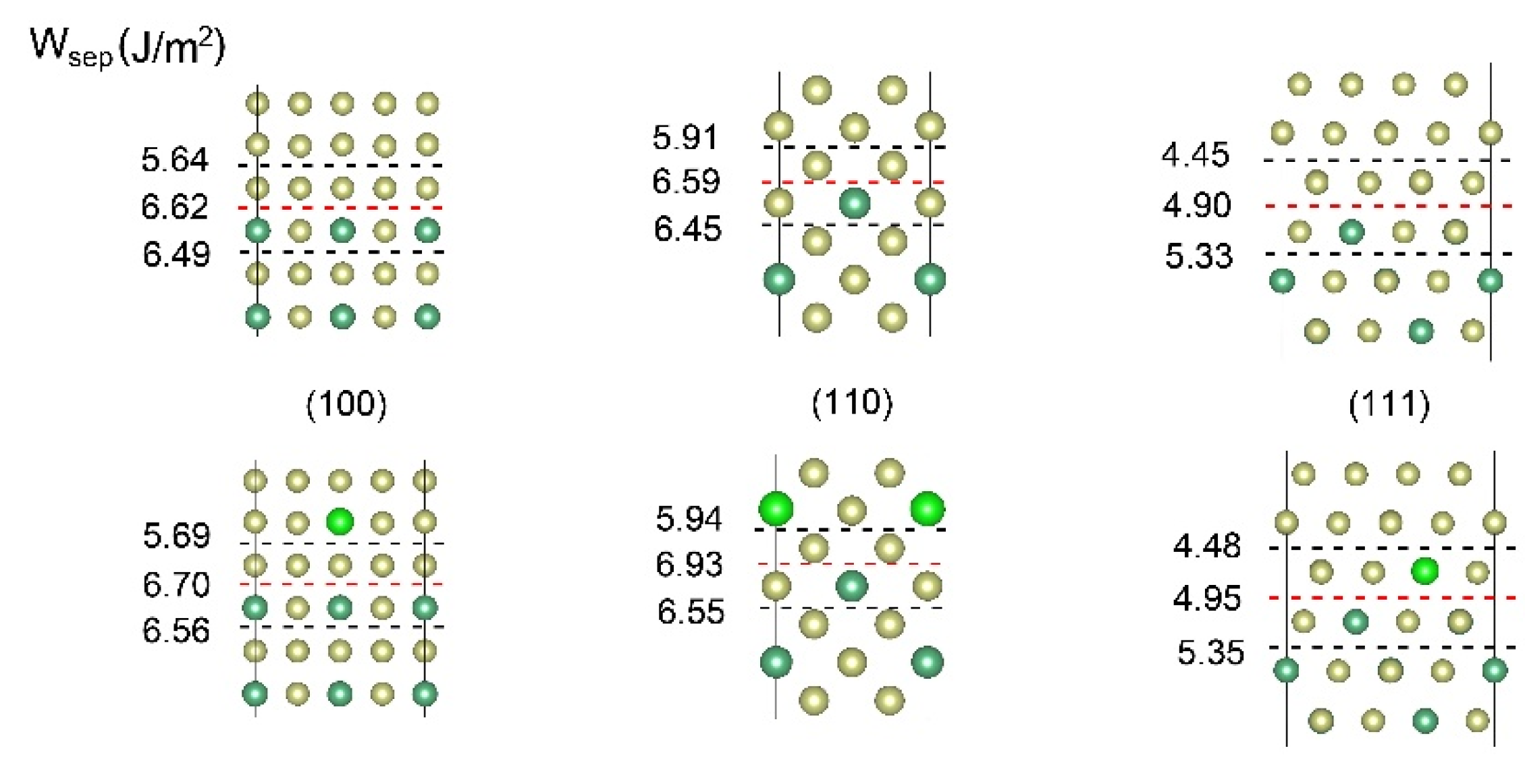
3.3. Interface Strength
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balk, T.J.; Hemker, K.J.; Kubin, L.P. On anomalous strain hardening in iridium crystals. Scr. Mater. 2007, 56, 389–392. [Google Scholar] [CrossRef]
- Stevanovic, V.; Sljivancanin, Z.; Baldereschi, A. Effect of carbon adsorption on the isomer stability of Ir4 clusters. Phys. Rev. Lett. 2007, 99, 165501. [Google Scholar] [CrossRef] [PubMed]
- Gornostyrev, Y.N.; Katsnelson, M.I.; Medvedeva, N.I.; Mryasov, O.N.; Freeman, A.J.; Trefilov, A.V. Peculiarities of defect structure and mechanical properties of iridium: Results of ab initio electronic structure calculations. Phys. Rev. B 2000, 62, 7802–7808. [Google Scholar] [CrossRef]
- Yamabe, Y.; Koizumi, Y.; Murakami, H.; Ro, Y.; Maruko, T.; Harada, H. Development of Ir-base refractory superalloys. Scr. Mater. 1996, 35, 211–215. [Google Scholar] [CrossRef]
- Yamabe, Y.; Ro, Y.; Maruko, T.; Harada, H. Ir-base refractory superalloys for ultra-high temperatures. Metall. Mater. Trans. A 1998, 29, 537–549. [Google Scholar] [CrossRef]
- Gengsen, X.; Xiaoyu, C. Effects of the alloying element on the stacking fault energies of dilute Ir-based superalloys: A comprehensive first-principles study. J. Mater. Res. 2020, 35, 2718–2725. [Google Scholar]
- Gu, Y.F.; Yamabe, Y.; Harada, H. Development of quaternary Ir-Ta-Ni-Al refractory superalloys. Scr. Mater. 1999, 41, 651–657. [Google Scholar]
- Gu, Y.F.; Yamabe, Y.; Harada, H. Effects of carbon addition on the microstructure and mechanical properties of Ir85Nb15 two-phase refractory superalloy. Mater. Sci. Eng. A 2003, 339, 216–219. [Google Scholar] [CrossRef]
- Huang, C.; Yamabe, Y.; Nakazawa, S. Mechanical properties of Ir–Nb–Pt–Al quaternary alloys. Mater. Lett. 2004, 58, 483–488. [Google Scholar] [CrossRef]
- Yu, X.H.; Yamabe, Y.; Ro, Y.; Harada, H. Design of quaternary Ir-Nb-Ni-Al refractory superalloys. Metall. Mater. Trans. A 2000, 31, 173–178. [Google Scholar] [CrossRef]
- Gyurko, A.M.; Sanchez, J.M. Characterization of mechanical properties in the Ir–Nb–Zr intermetallic system. Mater. Sci. Eng. A 1993, 170, 169–175. [Google Scholar] [CrossRef]
- Yamabe, Y.; Gu, Y.F.; Harada, H. Compressive Strength and Creep Properties of Ir-Nb-Zr Alloys between 1473 and 2073 K. Metall. Mater. Trans. A 2003, 34, 2207–2215. [Google Scholar] [CrossRef]
- Yamabe, Y.; Harada, H. Face centered cubic and L12 two-phase structure of Ir–Nb–Zr alloys. J. Alloy. Compd. 2003, 361, 169–179. [Google Scholar] [CrossRef]
- Royset, J.; Ryum, N. Kinetics and mechanisms of precipitation in an Al–0.2 wt.% Sc alloy. Mater. Sci. Eng. A 2005, 396, 409–422. [Google Scholar] [CrossRef]
- Kanresky, R.A.; Dunand, D.C.; Seidman, D.N. Evolution of nanoscale precipitates in Al microalloyed with Sc and Er. Acta Mater. 2009, 57, 4022–4031. [Google Scholar]
- Krug, M.E.; Dunand, D.C.; Seidman, D.N. Effects of Li additions on precipitation-strengthened Al–Sc and Al–Sc–Yb alloys. Acta Mater. 2011, 59, 1700–1715. [Google Scholar] [CrossRef]
- Ovri, H.; Lilleodden, E.T. New insights into plastic instability in precipitation strengthened Al–Li alloys. Acta Mater. 2015, 89, 88–97. [Google Scholar] [CrossRef]
- Rösner, H.; Kalogeridis, A.; Liu, W.; Pesicka, J.; Nembach, E. Dislocation mechanisms in Al-rich Al-Li alloys. Mater. Sci. Eng. A 1997, 234, 298–301. [Google Scholar] [CrossRef]
- Clouet, E.; Lae, L.; Epicier, T.; Lefebvre, W.; Nastar, M.; Deschamps, A. Complex precipitation pathways in multicomponent alloys. Nat. Mater. 2006, 5, 482–488. [Google Scholar] [CrossRef]
- Knipling, K.E.; Seidman, D.N.; Dunand, D.C. Ambient- and high-temperature mechanical properties of isochronally aged Al–0.06Sc. Al–0.06Zr and Al–0.06Sc–0.06Zr (at.%) alloys. Acta Mater. 2011, 59, 943–954. [Google Scholar]
- Knipling, K.E.; Karnesky, R.A.; Lee, C.P.; Dunand, D.C.; Seidman, D.N. Precipitation evolution in Al–0.1Sc, Al–0.1Zr and Al–0.1Sc–0.1Zr (at.%) alloys during isochronal aging. Acta Mater. 2010, 58, 5184–5195. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, Y.; Cao, F.; Hu, T.; Wang, Y.; Yin, D. Formation of coherent, core-shelled nano-particles in dilute Al-Sc-Zr alloys from the first-principles. J. Mater. Sci. Technol. 2019, 35, 930–938. [Google Scholar] [CrossRef]
- Gong, H.R. Ideal mechanical strength and interface cohesion property of Ir-base superalloys from first principles calculation. Mater. Chem. Phys. 2011, 126, 284–288. [Google Scholar] [CrossRef]
- Bai, X.; Li, Y.; Wang, Y.; Zheng, Q.; Fang, X.; Liu, Q.; Yan, B.; Gao, Y. A comparative study on the stability of six Ir/Ir3X (X = Ti, V, Zr, Nb, Hf, Ta) interfaces by first-principle and AIMD calculations. Appl. Surf. Sci. 2023, 630, 157502. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.M.; Emzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Jiang, Y.; Smith, J.R.; Evans, A.G. Temperature dependence of the activity of Al in dilute Ni(Al) solid solutions. Phys. Rev. B 2006, 74, 224110. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, W.; Seidman, D.N.; Wolverton, C. First-principles study of the nucleation and stability of ordered precipitates in ternary Al–Sc–Li alloys. Acta Mater. 2011, 59, 3012–3023. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, C. First-Principles Interface Thermodynamics of Core-Shelled Nano-Phase Precipitation in Alloys. Mater. Chin. 2019, 38, 748–758. [Google Scholar]
| Ir/Ir3Nb | Al/Al3X | ||||||
|---|---|---|---|---|---|---|---|
| 100 | 110 | 111 | 100 | 110 | 111 | ||
| Present | 0.25 | 0.27 | 0.30 | Al3Sc [29] | 0.165 | 0.178 | 0.189 |
| Others [22] | −0.25 | −0.09 | 1.07 | Al3Li [29] | 0.012 | 0.017 | 0.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.-G.; Jiang, Y.; Zhao, M.-C.; Yin, D.-F. Interface Effect in Ir-Nb-Zr Alloy. Crystals 2025, 15, 519. https://doi.org/10.3390/cryst15060519
Yao J-G, Jiang Y, Zhao M-C, Yin D-F. Interface Effect in Ir-Nb-Zr Alloy. Crystals. 2025; 15(6):519. https://doi.org/10.3390/cryst15060519
Chicago/Turabian StyleYao, Jian-Gang, Yong Jiang, Ming-Chun Zhao, and Deng-Feng Yin. 2025. "Interface Effect in Ir-Nb-Zr Alloy" Crystals 15, no. 6: 519. https://doi.org/10.3390/cryst15060519
APA StyleYao, J.-G., Jiang, Y., Zhao, M.-C., & Yin, D.-F. (2025). Interface Effect in Ir-Nb-Zr Alloy. Crystals, 15(6), 519. https://doi.org/10.3390/cryst15060519








