Geometric Characterizations of Non-Uniform Structure I Methane Hydrate Behaviors Under Pressure
Abstract
1. Introduction
2. Materials and Methods
2.1. DFT Simulations and Computational Methods
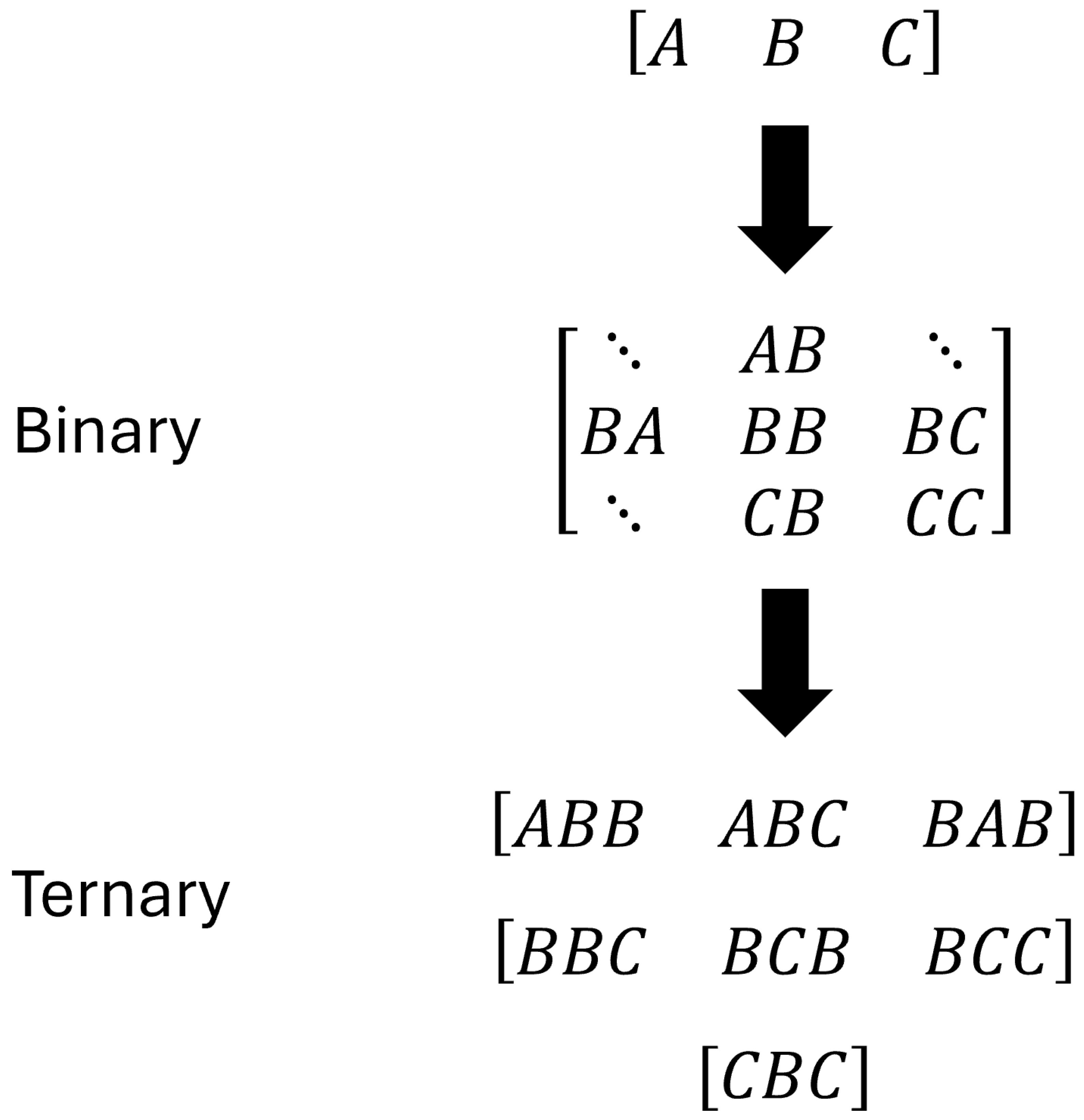
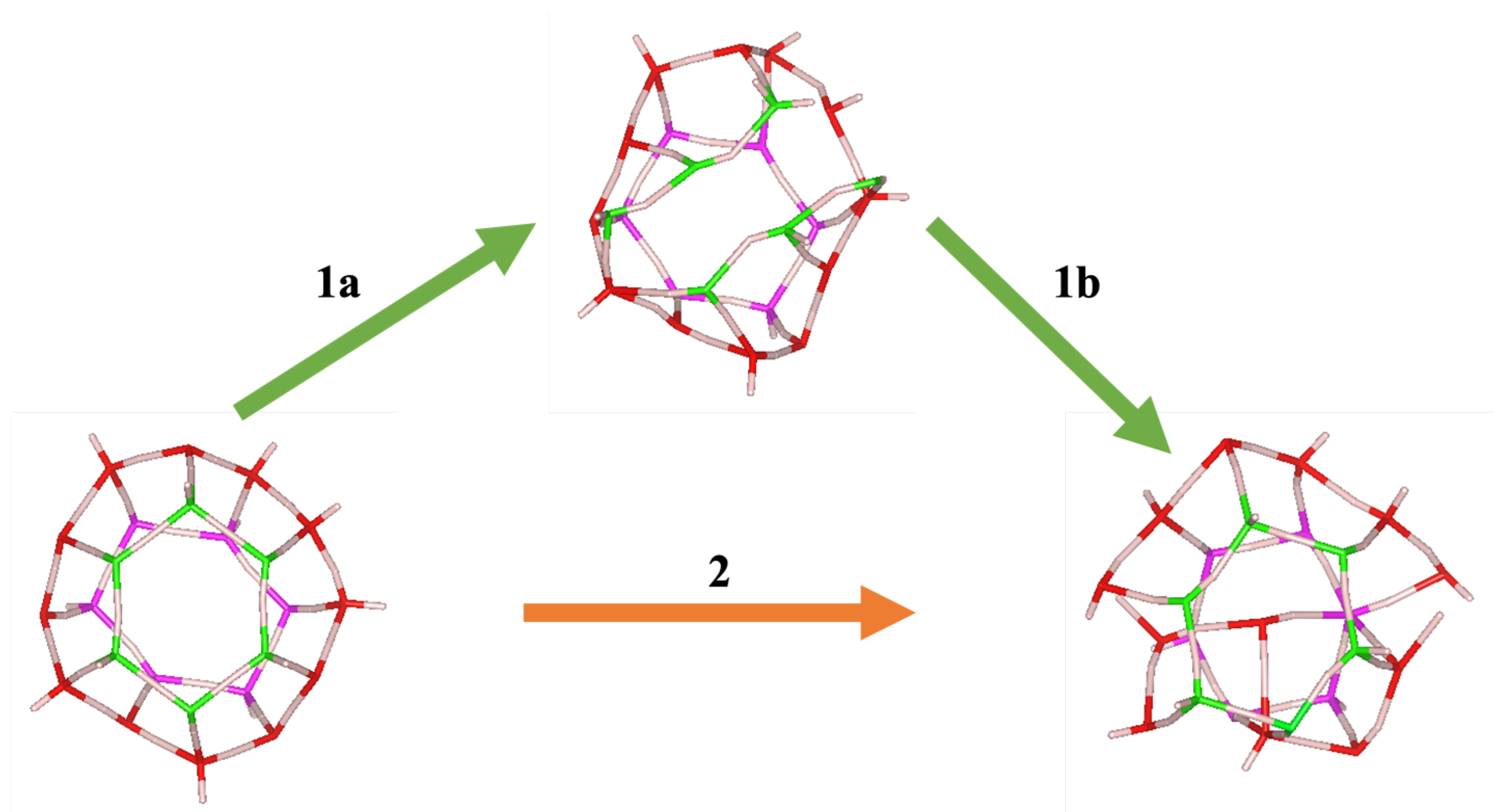
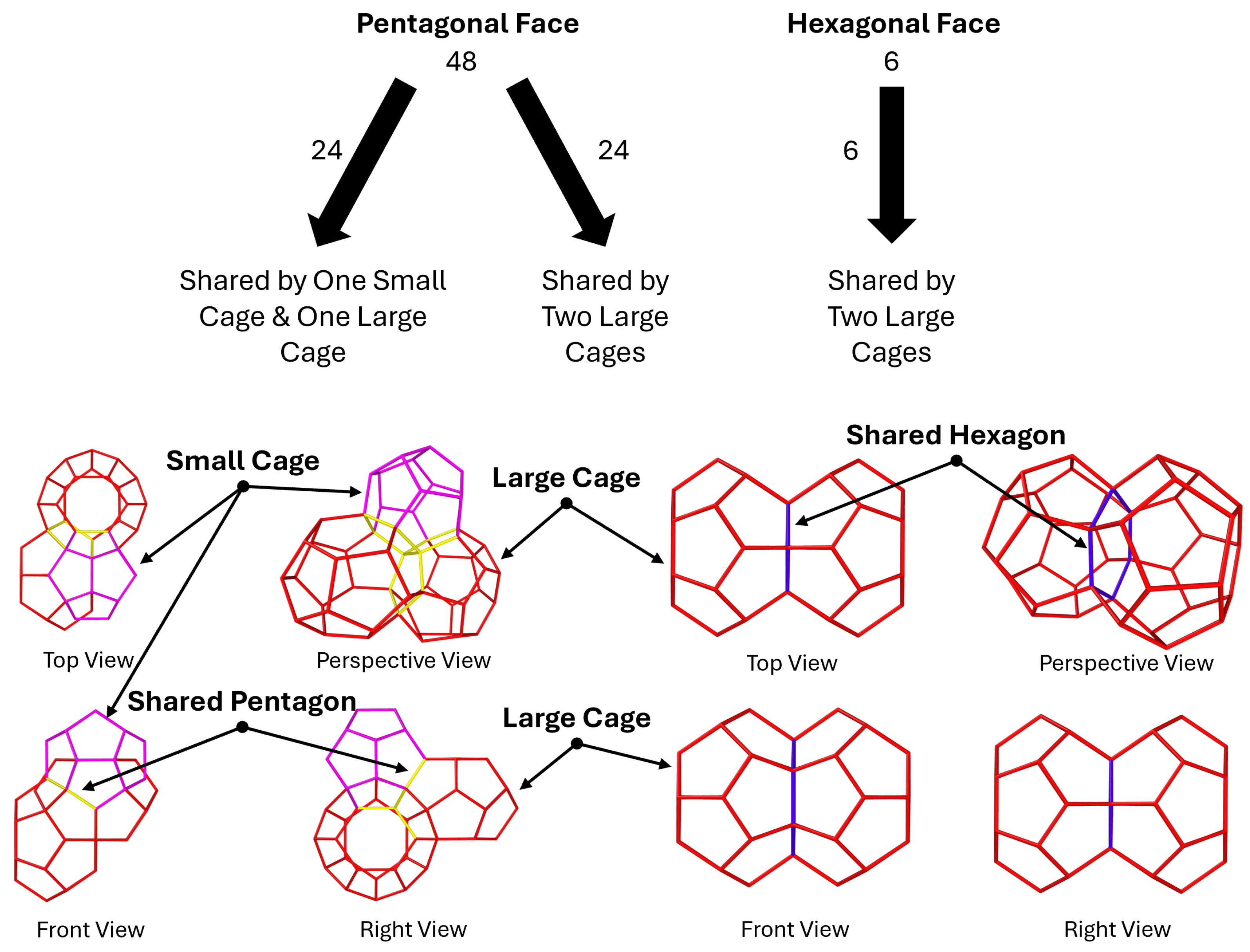
2.2. Classification Scheme of Water Oxygen Atoms
2.3. Bond Length and Angle Calculations
3. Results
3.1. Fracture Mechanisms Under Pressure
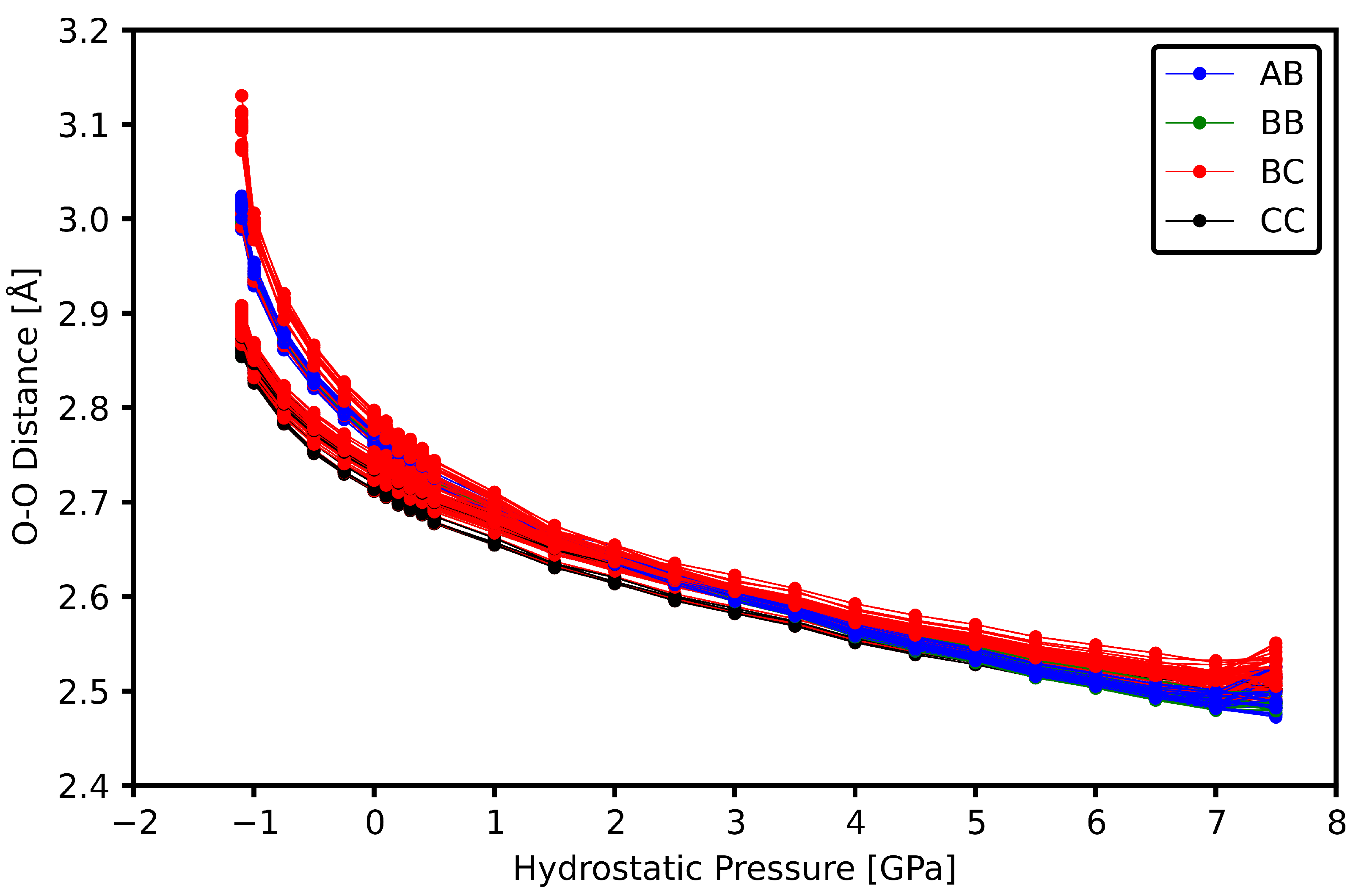
3.2. Intermolecular Bonds
3.3. Intermolecular Angles
3.4. Structural Breakdowns
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carroll, J. Natural Gas Hydrates: A Guide for Engineers, 3rd ed.; Gulf Professional Publishing: Houston, TX, USA, 2014. [Google Scholar]
- Koh, C.A.; Sloan, E.D.; Sum, A.K.; Wu, D.T. Fundamentals and Applications of Gas Hydrates. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 237–257. [Google Scholar] [CrossRef]
- Sloan, E.D. Fundamental Principles and Applications of Natural Gas Hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef]
- Mathews, S.; Daghash, S.; Rey, A.; Servio, P. Recent Advances in Density Functional Theory and Molecular Dynamics Simulation of Mechanical, Interfacial, and Thermal Properties of Natural Gas Hydrates in Canada. Can. J. Chem. Eng. 2022, 100, 2557–2571. [Google Scholar] [CrossRef]
- Cannone, S.F.; Lanzini, A.; Santarelli, M. A Review on CO2 Capture Technologies with Focus on CO2-Enhanced Methane Recovery from Hydrates. Energies 2021, 14, 387. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, F.; Tian, Y.; Wu, X.; Zheng, J.; Zhang, J.; Li, L.; Yang, P.; Zhao, J. Review and Prospects of Hydrate Cold Storage Technology. Renew. Sustain. Energy Rev. 2020, 117, 109492. [Google Scholar] [CrossRef]
- Das, S.; Tadepalli, K.M.; Roy, S.; Kumar, R. A Review of Clathrate Hydrate Nucleation, Growth and Decomposition Studied Using Molecular Dynamics Simulation. J. Mol. Liq. 2022, 348, 118025. [Google Scholar] [CrossRef]
- Gambelli, A.M.; Presciutti, A.; Rossi, F. Review on the Characteristics and Advantages Related to the Use of Flue-Gas as CO2/N2 Mixture for Gas Hydrate Production. Fluid Phase Equilibria 2021, 541, 113077. [Google Scholar] [CrossRef]
- Sayani, J.K.S.; Lal, B.; Pedapati, S.R. Comprehensive Review on Various Gas Hydrate Modelling Techniques: Prospects and Challenges. Arch. Comput. Methods Eng. 2022, 29, 2171–2207. [Google Scholar] [CrossRef]
- Chen, W.; Pinho, B.; Hartman, R.L. Flash Crystallization Kinetics of Methane (sI) Hydrate in a Thermoelectrically-Cooled Microreactor. Lab Chip 2017, 17, 3051–3060. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, Z.; Khan, S.A.; Li, S.; Li, Q.; Liu, X.; Linga, P. Path-Dependent Morphology of CH4 Hydrates and Their Dissociation Studied with High-Pressure Microfluidics. Lab Chip 2024, 24, 1602–1615. [Google Scholar] [CrossRef]
- Feng, Y.; Li, M.; Han, Y.; Li, Q.; Lv, X.; Zhao, J.; Yang, L.; Liu, Y.; Song, Y. Gas Hydrate Nucleation and Growth in a Micro-Reactor: Effect of Individual Component Separated from the Crude Oil in the South China Sea. Chem. Eng. J. 2023, 459, 141483. [Google Scholar] [CrossRef]
- Demirbas, A. Methane Gas Hydrate; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Sun, Z.; Wang, H.; Yao, J.; Sun, Z.; Bongole, K.; Zhu, X.; Liu, L.; Wang, J. Effect of Cage-Specific Occupancy on the Dissociation Rate of a Three-Phase Coexistence Methane Hydrate System: A Molecular Dynamics Simulation Study. J. Nat. Gas Sci. Eng. 2018, 55, 235–242. [Google Scholar] [CrossRef]
- Balcı, F.M.; Uras-Aytemiz, N. Exploring Vacancy Defects in S-I Clathrate Hydrates. J. Mol. Graph. Model. 2025, 136, 108969. [Google Scholar] [CrossRef]
- Yanes-Rodríguez, R.; Prosmiti, R. Analysing the Stability of He-filled Hydrates: How Many He Atoms Fit in the sII Crystal? Phys. Chem. Chem. Phys. 2024, 26, 2519–2528. [Google Scholar] [CrossRef]
- Zhang, Z.; Kusalik, P.G.; Guo, G.J.; Ning, F.; Wu, N. Insight on the Stability of Polycrystalline Natural Gas Hydrates by Molecular Dynamics Simulations. Fuel 2021, 289, 119946. [Google Scholar] [CrossRef]
- Vlasic, T.M.; Servio, P.D.; Rey, A.D. Effect of Guest Size on the Mechanical Properties and Molecular Structure of Gas Hydrates from First-Principles. Cryst. Growth Des. 2017, 17, 6407–6416. [Google Scholar] [CrossRef]
- Daghash, S.M.; Servio, P.; Rey, A.D. Elastic Properties and Anisotropic Behavior of Structure-H (sH) Gas Hydrate from First Principles. Chem. Eng. Sci. 2020, 227, 115948. [Google Scholar] [CrossRef]
- Daghash, S.M.; Servio, P.; Rey, A.D. From Infrared Spectra to Macroscopic Mechanical Properties of sH Gas Hydrates through Atomistic Calculations. Molecules 2020, 25, 5568. [Google Scholar] [CrossRef] [PubMed]
- Mathews, S.L.; Servio, P.D.; Rey, A.D. Heat Capacity, Thermal Expansion Coefficient, and Grüneisen Parameter of CH4, CO2, and C2H6 Hydrates and Ice Ih via Density Functional Theory and Phonon Calculations. Cryst. Growth Des. 2020, 20, 5947–5955. [Google Scholar] [CrossRef]
- Jia, J.; Liang, Y.; Tsuji, T.; Murata, S.; Matsuoka, T. Elasticity and Stability of Clathrate Hydrate: Role of Guest Molecule Motions. Sci. Rep. 2017, 7, 1290. [Google Scholar] [CrossRef]
- Mirzaeifard, S.; Servio, P.; Rey, A.D. Multiscale Modeling and Simulation of Water and Methane Hydrate Crystal Interface. Cryst. Growth Des. 2019, 19, 5142–5151. [Google Scholar] [CrossRef]
- Mathews, S.; Servio, P.; Rey, A. Multiscale Interfacial Structure and Organization of sII Gas Hydrate Interfaces Using Molecular Dynamics. Nanomaterials 2025, 15, 464. [Google Scholar] [CrossRef]
- Guerra, A.; Mathews, S.; Marić, M.; Servio, P.; Rey, A.D. All-Atom Molecular Dynamics of Pure Water–Methane Gas Hydrate Systems under Pre-Nucleation Conditions: A Direct Comparison between Experiments and Simulations of Transport Properties for the Tip4p/Ice Water Model. Molecules 2022, 27, 5019. [Google Scholar] [CrossRef]
- Kuo, I.F.W.; Mundy, C.J.; Eggimann, B.L.; McGrath, M.J.; Siepmann, J.I.; Chen, B.; Vieceli, J.; Tobias, D.J. Structure and Dynamics of the Aqueous Liquid-Vapor Interface: A Comprehensive Particle-Based Simulation Study. J. Phys. Chem. B 2006, 110, 3738–3746. [Google Scholar] [CrossRef]
- Tanaka, R.; Sakemoto, R.; Ohmura, R. Crystal Growth of Clathrate Hydrates Formed at the Interface of Liquid Water and Gaseous Methane, Ethane, or Propane: Variations in Crystal Morphology. Cryst. Growth Des. 2009, 9, 2529–2536. [Google Scholar] [CrossRef]
- Asserson, R.B.; Hoffmann, A.C.; Hø iland, S.; Asvik, K.M. Interfacial Tension Measurement of Freon Hydrates by Droplet Deposition and Contact Angle Measurements. J. Pet. Sci. Eng. 2009, 68, 209–217. [Google Scholar] [CrossRef]
- Zhu, X.; Rey, A.D.; Servio, P. Piezo-Elasticity and Stability Limits of Monocrystal Methane Gas Hydrates: Atomistic-continuum Characterization. Can. J. Chem. Eng. 2023, 101, 639–650. [Google Scholar] [CrossRef]
- Zhu, X.; Guerra, A.; Servio, P.; Rey, A.D. Atomistic-Geometric Simulations to Investigate the Mechanical Stability of Monocrystalline sI Methane Hydrates under Pressure. Sci. Rep. 2023, 13, 1907. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, F.; Cheng, D.; Liu, L.; Xia, F.; Liu, X.; Hou, J.; Ni, H. The Key Role of CO2 Molecules’ Rotation on the Shear Mechanical Properties of CO2-N2 Hydrates. Fuel 2025, 381, 133581. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Shi, Q.; Qu, Y.; Hao, Y.; Fu, Y.; Wu, J.; Zhang, Z. Mechanical Properties and Cage Transformations in CO2-CH4 Heterohydrates: A Molecular Dynamics and Machine Learning Study. J. Phys. D Appl. Phys. 2024, 57, 465302. [Google Scholar] [CrossRef]
- Arzbacher, S.; Rahmatian, N.; Ostermann, A.; Massani, B.; Loerting, T.; Petrasch, J. Macroscopic Defects upon Decomposition of CO2 Clathrate Hydrate Crystals. Phys. Chem. Chem. Phys. 2019, 21, 9694–9708. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Liang, D.; Wu, N.; Yi, L.; Hu, G. Transient Translational and Rotational Water Defects in Gas Hydrates. J. Phys. Chem. C 2017, 121, 17595–17602. [Google Scholar] [CrossRef]
- Uras-Aytemiz, N.; Balcı, F.M. Bjerrum Defects in S-II Gas Hydrate. J. Mol. Graph. Model. 2024, 133, 108878. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Takeuchi, F.; Hiratsuka, M.; Ohmura, R.; Alavi, S.; Sum, A.K.; Yasuoka, K. Water Proton Configurations in Structures I, II, and H Clathrate Hydrate Unit Cells. J. Chem. Phys. 2013, 138, 124504. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Kosyakov, V.I. Gas Hydrate Frameworks of Allen’s Polyhedra. 1. Frameworks on 3–5 Nets. J. Struct. Chem. 2002, 43, 622–631. [Google Scholar] [CrossRef]
- Komarov, V.Y.; Solodovnikov, S.F.; Kurnosov, A.V.; Kosyakov, V.I.; Manakov, A.Y. Design of Tetrahedral Frameworks as Layered Packings of Uniform Polyhedral Cavities. J. Struct. Chem. 2005, 46, S181–S187. [Google Scholar] [CrossRef]
- Komarov, V.U.; Solodovnikov, S.F.; Grachev, E.V.; Kosyakov, V.I.; Manakov, A.Y.; Kurnosov, A.V.; Shestakov, V.A. Phase Formation and Structure of High-Pressure Gas Hydrates and Modeling of Tetrahedral Frameworks with Uniform Polyhedral Cavities. Crystallogr. Rev. 2007, 13, 257–297. [Google Scholar] [CrossRef]
- Keutsch, F.N.; Cruzan, J.D.; Saykally, R.J. The Water Trimer. Chem. Rev. 2003, 103, 2533–2578. [Google Scholar] [CrossRef]
- Huš, M.; Urbic, T. Strength of Hydrogen Bonds of Water Depends on Local Environment. J. Chem. Phys. 2012, 136, 144305. [Google Scholar] [CrossRef]
- Petrucci, R.H. General Chemistry: Principles and Modern Applications, 10th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]


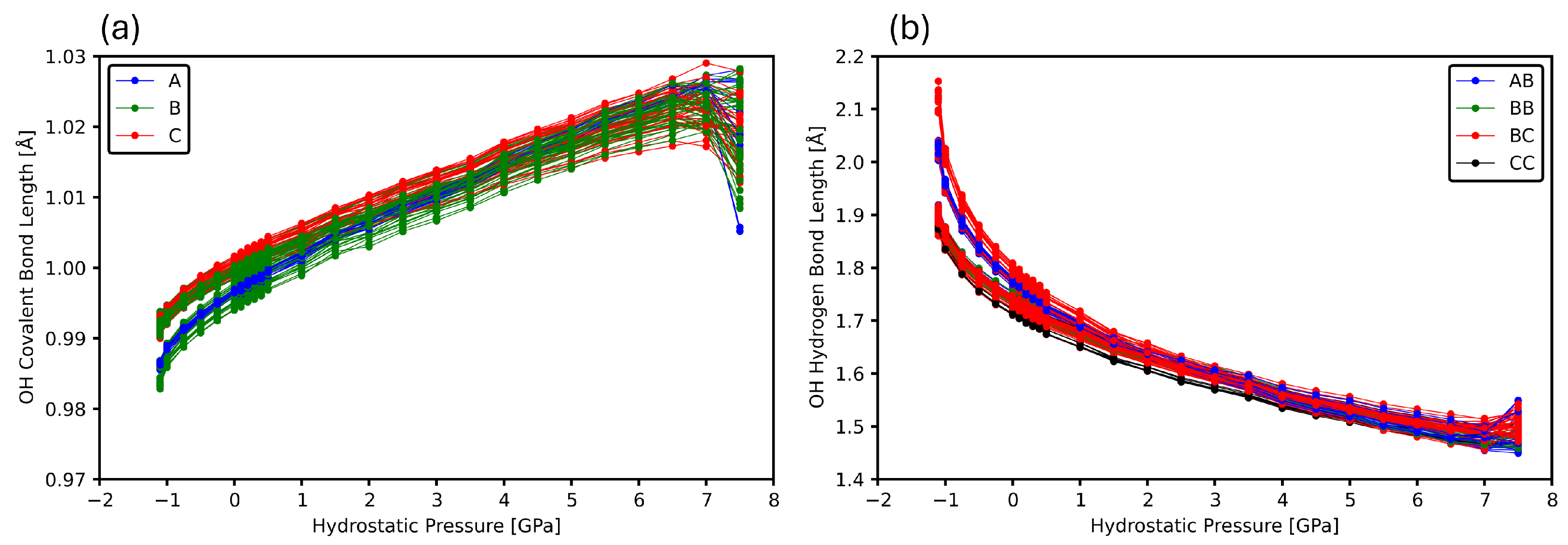

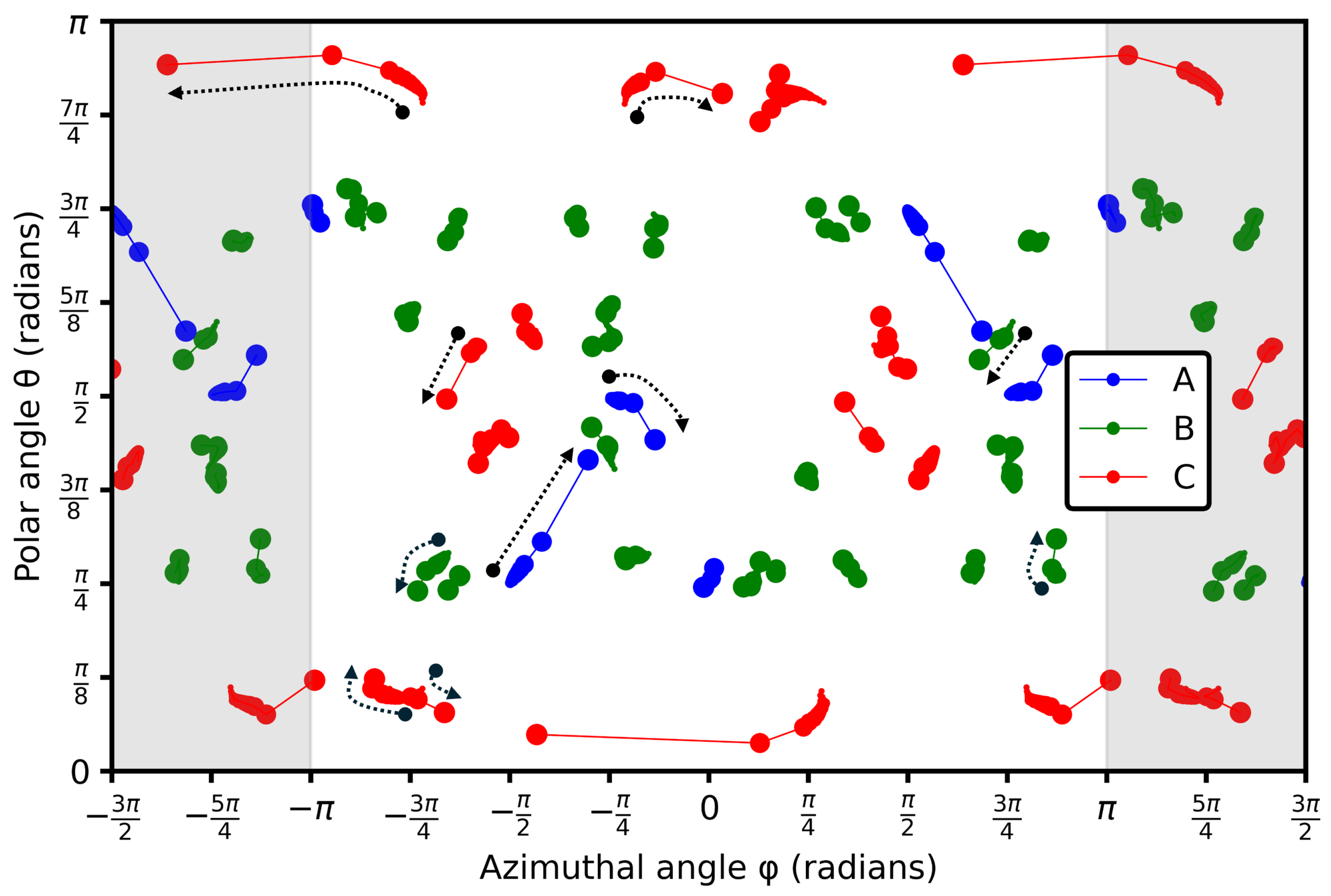
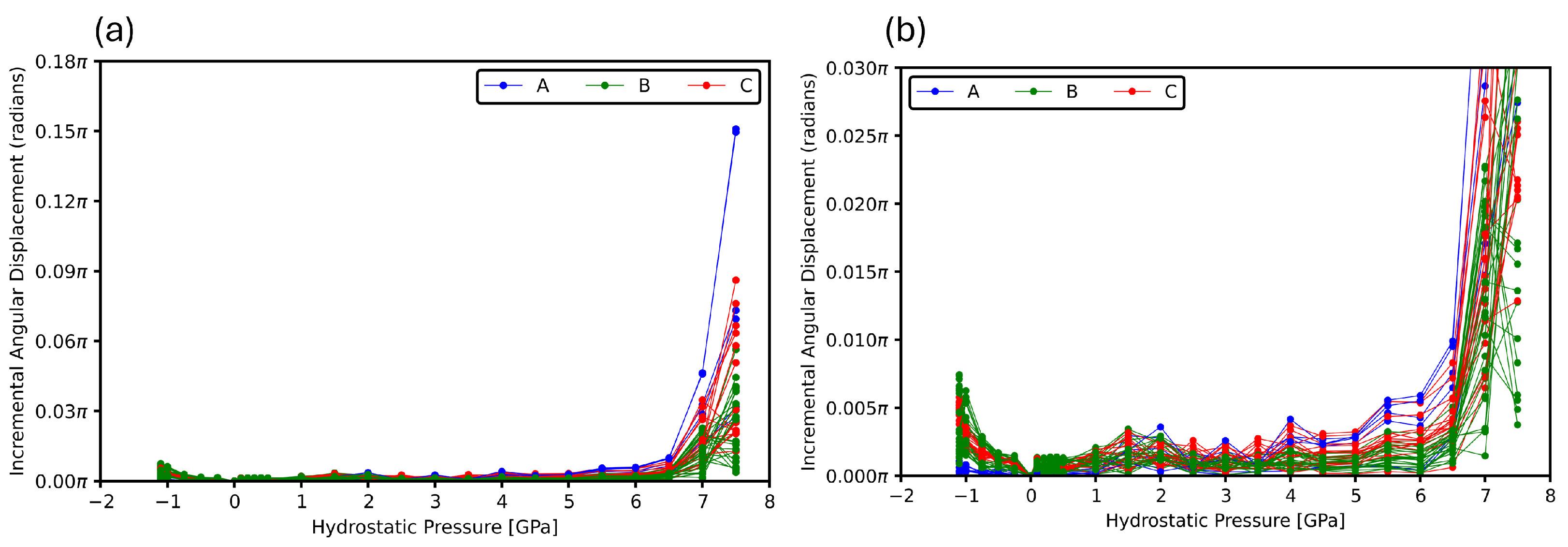
| Location | Label | Start | End | Widest | |||
|---|---|---|---|---|---|---|---|
| O-O Distance | FZ1 | GPa | GPa | ||||
| Å | Å | Å | |||||
| OH Covalent Bond Length | FZ2 | GPa | GPa | ||||
| Å | Å | Å | |||||
| OH Hydrogen Bond Length | FZ3 | GPa | GPa | ||||
| Å | Å | Å | |||||
| HOH Angle | FZ4 | GPa | GPa | ||||
| rad | rad | rad | |||||
| OOO Angle | FZ5 | GPa | GPa | ||||
| rad | rad | rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathews, S.; Zhu, X.; Guerra, A.; Servio, P.; Rey, A. Geometric Characterizations of Non-Uniform Structure I Methane Hydrate Behaviors Under Pressure. Crystals 2025, 15, 518. https://doi.org/10.3390/cryst15060518
Mathews S, Zhu X, Guerra A, Servio P, Rey A. Geometric Characterizations of Non-Uniform Structure I Methane Hydrate Behaviors Under Pressure. Crystals. 2025; 15(6):518. https://doi.org/10.3390/cryst15060518
Chicago/Turabian StyleMathews, Samuel, Xiaodan Zhu, André Guerra, Phillip Servio, and Alejandro Rey. 2025. "Geometric Characterizations of Non-Uniform Structure I Methane Hydrate Behaviors Under Pressure" Crystals 15, no. 6: 518. https://doi.org/10.3390/cryst15060518
APA StyleMathews, S., Zhu, X., Guerra, A., Servio, P., & Rey, A. (2025). Geometric Characterizations of Non-Uniform Structure I Methane Hydrate Behaviors Under Pressure. Crystals, 15(6), 518. https://doi.org/10.3390/cryst15060518







