Study of the Electrical Conduction Mechanism in Low-Frequency Field for CuMnO2 Crednerite-Type Materials Obtained by Microwave-Assisted Hydrothermal Synthesis
Abstract
1. Introduction
2. Materials and Methods
2.1. Microwave-Assisted Hydrothermal Synthesis (MWH)
2.2. Characterization Techniques
3. Results and Discussion
3.1. Structural and Morphological Analysis
3.2. Complex Impedance
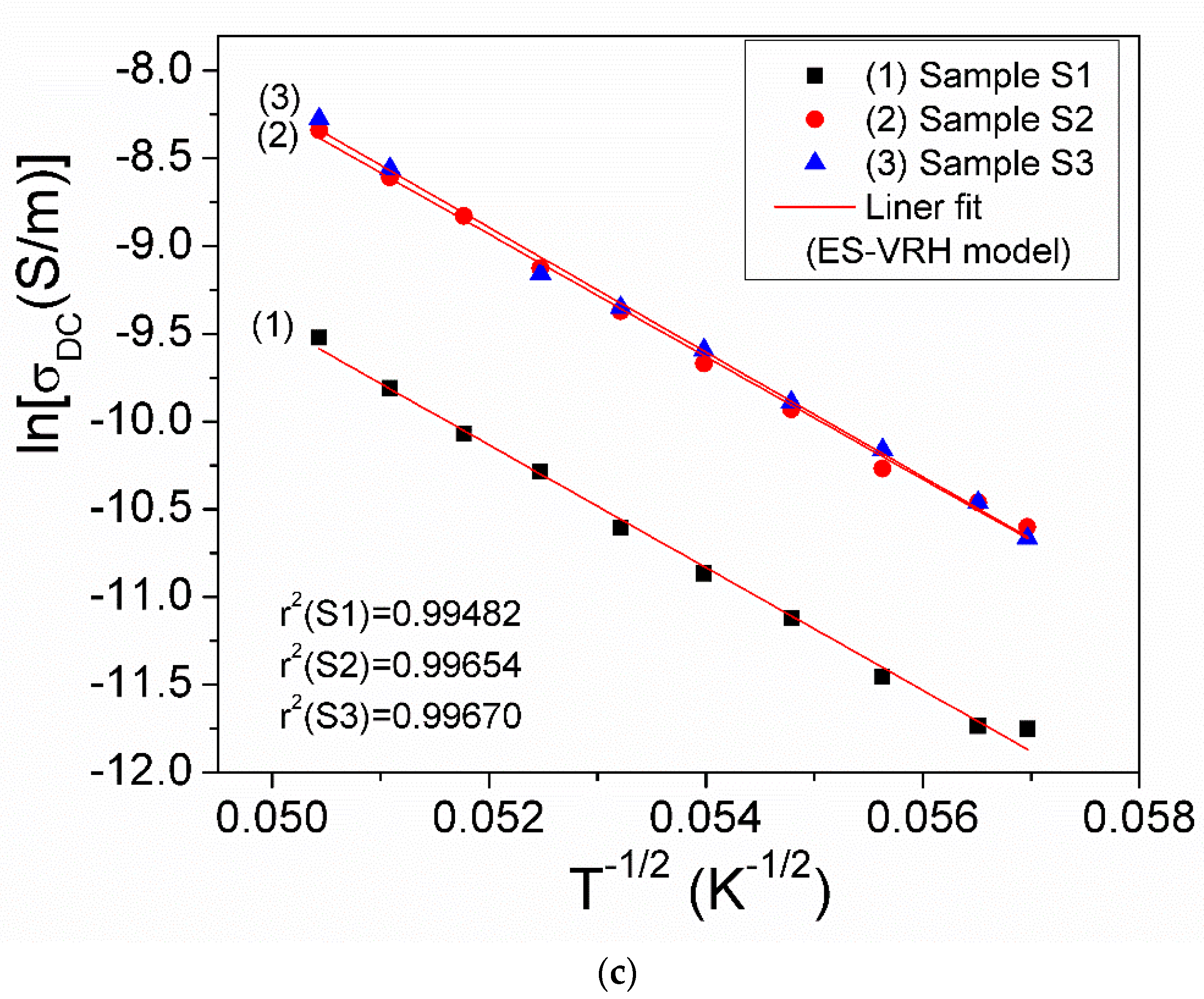
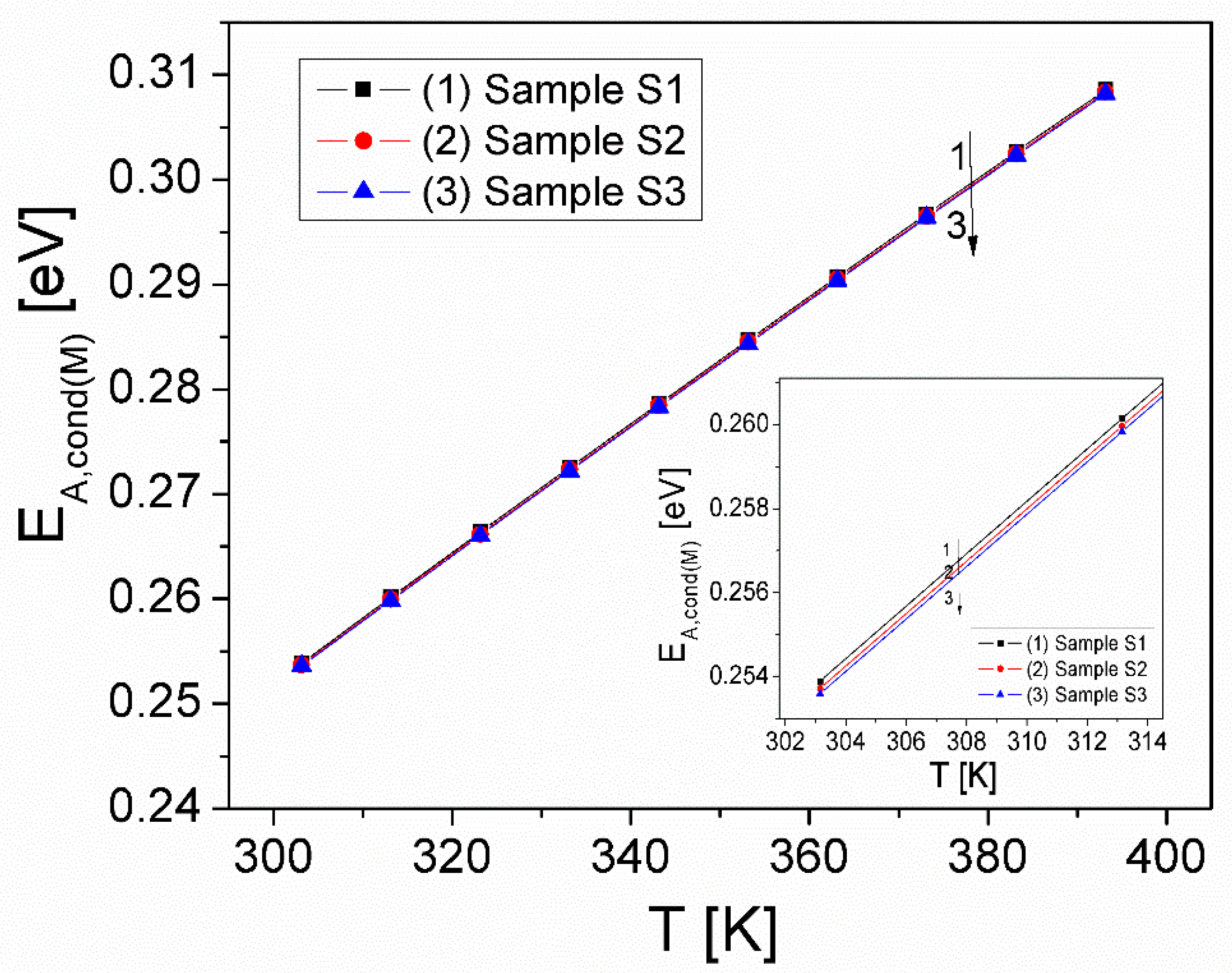
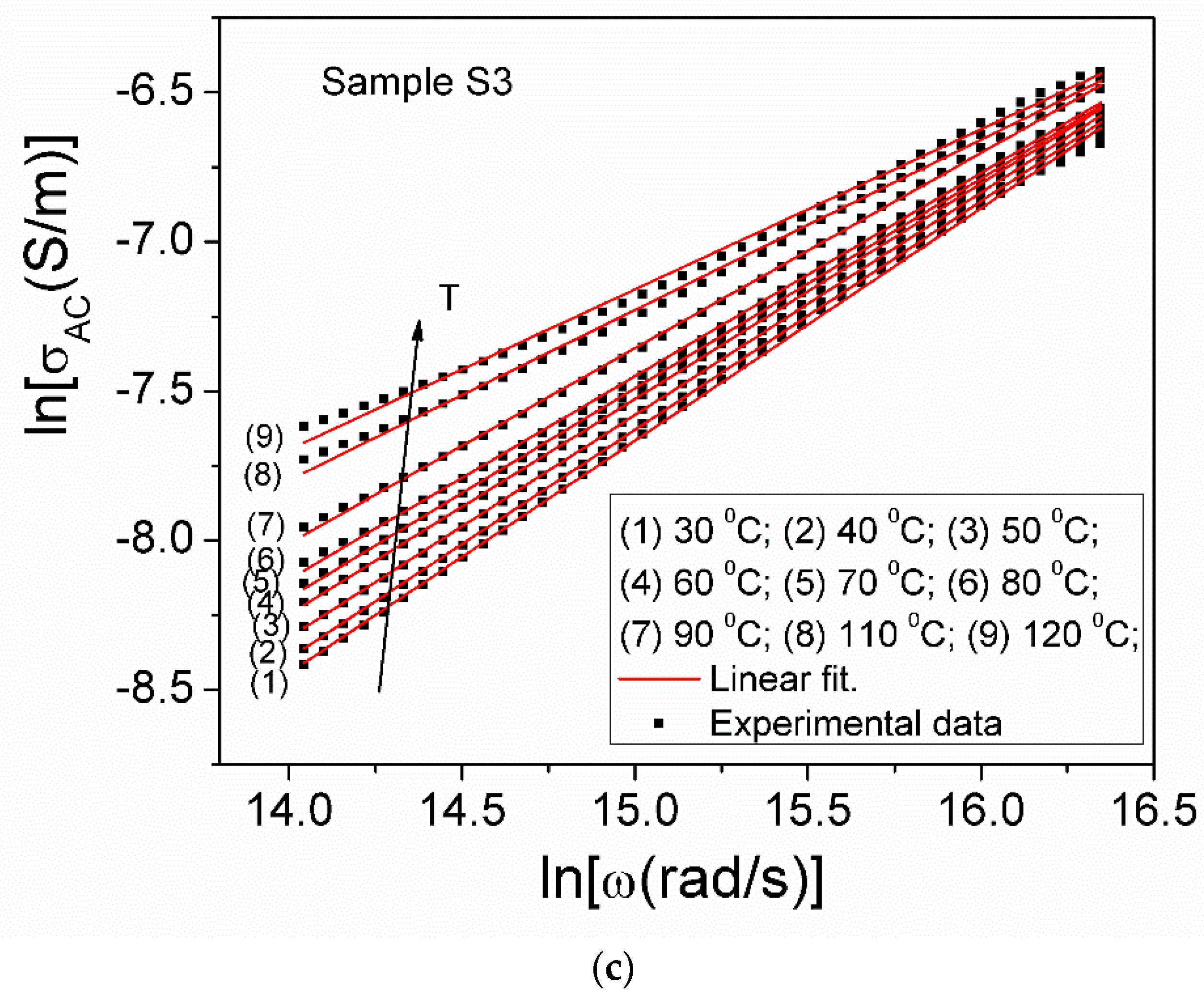
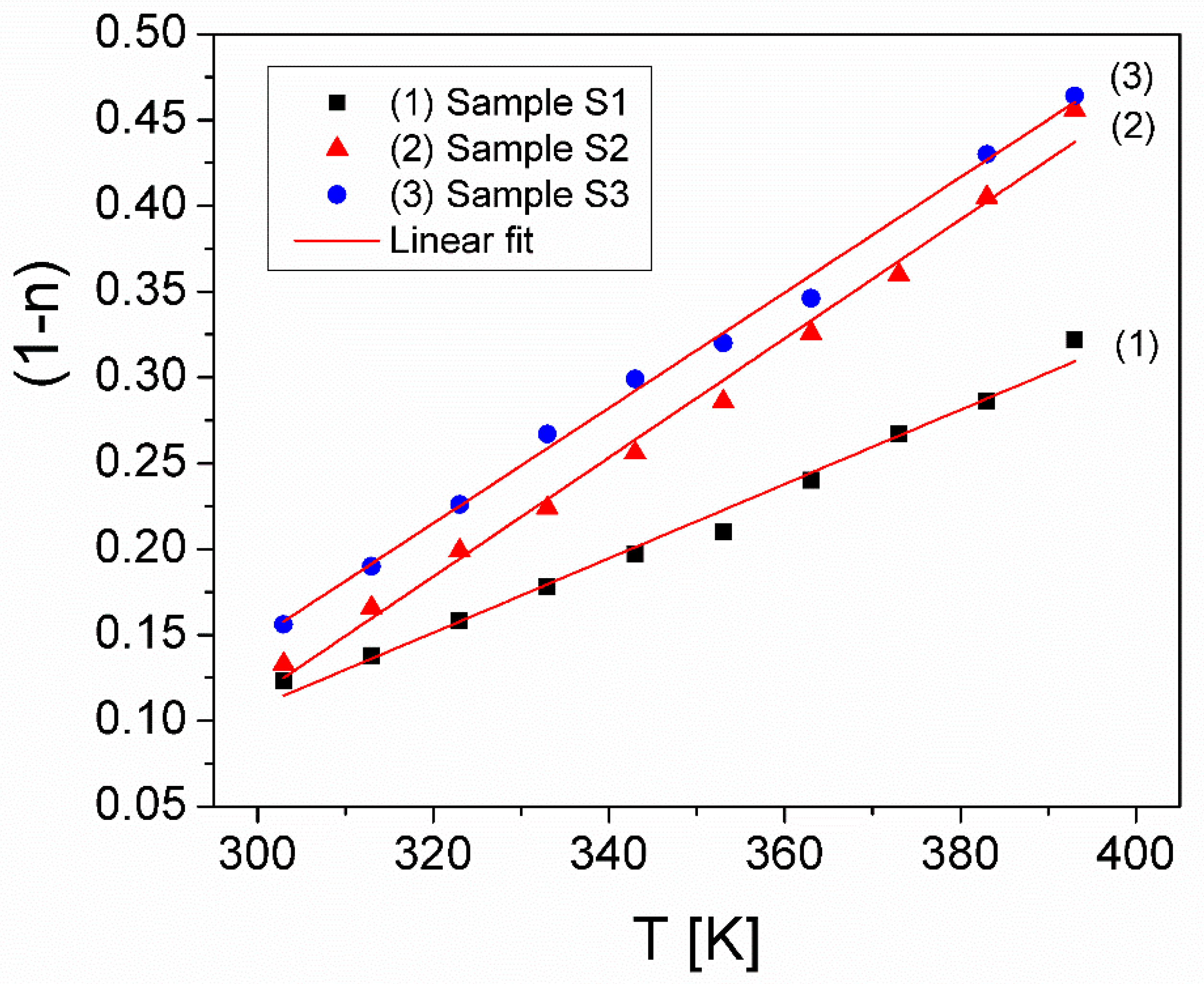
3.3. Electrical Conductivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.X.; Zhao, Z.Y. A comprehensive review on the preparation and applications of delafossite CuAlO2 optoelectronic functional materials. Mat. Sci. Semicond. Proces. 2023, 167, 107819. [Google Scholar] [CrossRef]
- Moreira, M.; Afonso, J.; Crepelliere, J.; Lenoble, D.; Lunca-Popa, P. A review on the p-type transparent Cu–Cr–O delafossite materials. J. Mater. Sci. 2022, 57, 3114–3142. [Google Scholar] [CrossRef]
- Seki, S.; Onose, Y.; Tokura, Y. Spin-Driven Ferroelectricity in Triangular Lattice Antiferromagnets ACrO2 (A = Cu, Ag, Li, or Na). Phys. Rev. Lett. 2008, 101, 067204. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, P.; Zhu, H.; Zhu, H.; Li, X.; Zhao, J.; Xu, C.; Xiang, H. Mechanism of Type-II Multiferroicity in Pure and Al-Doped CuFeO2. Phys. Rev. Lett. 2025, 134, 066801. [Google Scholar] [CrossRef]
- Nandjou, F.; Haussener, S. Degradation in photoelectrochemical devices: Review with an illustrative case study. J. Phys. D Appl. Phys. 2017, 50, 124002. [Google Scholar] [CrossRef]
- Ketir, W.; Bouguelia, A.; Trari, M. Visible light induced NO2-removal over CuCrO2 catalyst. Water. Air. Soil. Pollut. 2009, 199, 115–122. [Google Scholar] [CrossRef]
- Younsi, M.; Manaa, S. Synthesis and characterization of rich delafossite CuYO2+x: Application for solar energy conversion. Energy Procedia 2013, 36, 638–641. [Google Scholar] [CrossRef]
- Xiong, D.; Zhang, W.; Zeng, X.; Xu, Z.; Chen, W.; Cui, J.; Wang, M.; Sun, L.; Chen, Y.B. Enhanced performance of p-type dye-sensitized solar cells based on ultra-small Mg-doped CuCrO2 nanocrystals. Chem. Sustain. Chem. 2013, 6, 1432–1437. [Google Scholar] [CrossRef]
- Aakash Hossain, H.S.; Sarkar, S.; Bose, S.; Das, P. Synthesis, characterization, and application of delafossites as catalysts for degrading organic pollutants and degradation mechanisms: A detailed insight. Surf. Interf. 2023, 42, 103281. [Google Scholar] [CrossRef]
- Zheng, S.Y.; Jiang, G.S.; Su, J.R.; Zhu, C.F. The structural and electrical property of CuCr1−xNixO2 delafossite compounds. Mater. Lett. 2006, 60, 3871–3873. [Google Scholar] [CrossRef]
- Kondrashev, I.D. The crystal structure and composition of crednerite, CuMnO2. Sov. Phys. Crystallogr. 1959, 3, 703–706. [Google Scholar]
- Benreguia, N.; Barnabe, A.; Trari, M. Preparation and characterization of the semiconductor CuMnO2 by sol-gel route. Mater. Sci. Semicond. Process. 2016, 56, 14–19. [Google Scholar] [CrossRef]
- Benreguia, N.; Abdi, A.; Mahroua, O.; Trari, M. Photoelectrochemical properties of the credneriteCuMnO2 and its application to hydrogen production and Mn+ reduction (Mn+ = Cd2+, Pd2+, Zn2+, Ni2+, and Ag+). J. Mater. Sci. Mater. Electron. 2021, 32, 10498–10509. [Google Scholar] [CrossRef]
- Bessekouad, Y.; Gabes, Y.; Bouguelia, A.; Trari, M. The physical and photo electrochemical characterization of the crednerite CuMnO2. J. Mater. Sci. 2007, 42, 6469–6476. [Google Scholar] [CrossRef]
- Amrute, A.P.; Łodziana, Z.; Mondelli, C.; Krumeich, F.; Perez-Ramirez, J. Solid-state chemistry of cuprous delafossites: Synthesis and stability aspects. Chem. Mater. 2013, 25, 4423–4435. [Google Scholar] [CrossRef]
- Ma, C.; Pan, J.; Chen, C.; Dong, Y.; Yao, F.; Wang, F.; Song, M. Investigation into the roles of interfacial H2O structure in catalytic oxidation of HCHO and CO over CuMnO2 catalysts. J. Environ. Sci. 2024, 137, 310–320. [Google Scholar] [CrossRef]
- Chen, Y.C.; Kuo, Y.H.; Vincent, K.S.; Hsiao, H.; Huang, C.Y. Enhancement of seebeck coefficient in CuGaO2 thin films by optimization of sol-gel processing parameters. Mater. Chem. Phys. 2025, 339, 130769. [Google Scholar] [CrossRef]
- He, H.; Chen, Y.; Wang, F.; Liu, X.; Guo, Y. Nitrite sensing behaviors of tailored bimetallic oxide CuMnO2 nanostructures. J. Mater. Sci. Mater. Electron. 2022, 33, 1140–1153. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, C.; Wang, Y.; Yu, W.; Zhang, S.; Zhang, B.; Li, X. Insights into atomic arrangement in CuMnO2 with tailored exposed crystal facets for effectively micropollutant oxidation via peroxymonosulfate activation. J. Cleaner Prod. 2024, 458, 142517. [Google Scholar] [CrossRef]
- Trari, M.; Töpfer, J.; Dordor, P.; Grenier, J.C.; Pouchard, M.; Doumerc, J.P. Preparation and physical properties of the solid solutions Cu1+xMn1−xO2 (0 ≤ x ≤ 0.2). J. Solid State Chem. 2005, 178, 2751–2758. [Google Scholar] [CrossRef]
- Xiong, D.; Gao, H.; Deng, Y.; Qi, Y.; Du, Z.; Zeng, X.; Li, H. Impact of Mg doping on the optical and electrical properties of p-type CuMnO2 ultrathin nanosheets. J. Mat. Sci. Mater. Electron. 2020, 31, 5452–5461. [Google Scholar] [CrossRef]
- Poienar, M.; Sfirloaga, P.; Martin, C.; Ursu, D.; Vlazan, P. Hydrothermal synthesis of crednerite CuMn1−xMxO2 (M = Mg, Al; x = 0–0.08): Structural characterization and magnetic properties. J. Mater. Sci. 2018, 53, 2389–2395. [Google Scholar] [CrossRef]
- Malaescu, I.; Lungu, A.; Marin, C.N.; Sfirloaga, P.; Vlazan, P.; Brindusoiu, S.; Poienar, M. Temperature dependence of the dynamic electrical properties of Cu1+xMn1-xO2 (x = 0 and 0.06) crednerite materials. Ceram. Int. 2018, 44, 11610–11616. [Google Scholar] [CrossRef]
- Malaescu, I.; Poienar, M.; Marin, C.N. Investigation of the Electrical Properties of Polycrystalline Crednerite CuMn1−xMgxO2 (x = 0–0.06) Type Materials in a Low-Frequency Field. Crystals 2025, 15, 184. [Google Scholar] [CrossRef]
- Ogale, S.B.; Talyansky, V.; Chen, C.H.; Ramesh, R.; Greene, R.L.; Venkatesan, T. Unusual Electric Field Effects in Nd0. 7Sr0.3MnO3, Phys. Rev. Lett. 1996, 77, 1159–1162. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials; Clarendon: Oxford, UK, 1979. [Google Scholar]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Poienar, M.; Banica, R.; Sfirloaga, P.; Ianasi, C.; Mihali, C.V.; Vlazan, P. Microwave-assisted hydrothermal synthesis and catalytic activity study of crednerite-type CuMnO2 materials. Ceram. Intern. 2018, 44, 6157–6161. [Google Scholar] [CrossRef]
- Carvajal, J.R. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Cond. Matter. 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Lungu, A.; Malaescu, I.; Marin, C.N.; Vlazan, P.; Sfirloaga, P. The electrical properties of manganese ferrite powders prepared by two different methods. Phys. B Cond. Matter. 2015, 462, 80–85. [Google Scholar] [CrossRef]
- ASTM D150-98; Standard Test Methods for AC Loss Characteristics and Permittivity (Dielectric Constant) of Solid Electrical Insulation. ASTM International: West Conshohocken, PA, USA, 2017.
- Damay, F.; Poienar, M.; Martin, C.; Maignan, A.; Rodriguez-Carvajal, J.; André, G.; Doumerc, J.P. Spin-lattice coupling induced phase transition in the S=2 frustrated antiferromagnet CuMnO2. Phys. Rev. B. 2009, 80, 094410–094417. [Google Scholar] [CrossRef]
- Poienar, M.; Martin, C.; Lebedev, O.I.; Maignan, A. Advantage of low-temperature hydrothermal synthesis to grow stoichiometric crednerite crystals. Solid State Sci. 2018, 80, 39–45. [Google Scholar] [CrossRef]
- Poienar, M.; Vecchini, C.; Andre, G.; Daoud-Aladine, A.; Margiolaki, I.; Maignan, A.; Lappas, A.; Chapon, L.; Hervieu, M.; Damay, F.; et al. Substitution effect on the inter -plane coupling in crednerite: The Cu1.04Mn0.96O2 case. Chem. Mat. 2011, 23, 85–94. [Google Scholar] [CrossRef]
- Ushakov, A.V.; Streltsov, S.V.; Khomskii, D.I. Orbital structure and magnetic ordering in stoichiometric and doped crednerite CuMnO2. Phys. Rev. B. 2014, 89, 024406. [Google Scholar] [CrossRef]
- Julien, C.M.; Massot, M.; Poinsignon, C. Lattice vibrations of manganese oxides Part I. Periodic structures. Spectrochim. Acta Part A 2004, 60, 689–700. [Google Scholar] [CrossRef]
- Gillot, B.; El Guendouzi, M.; Laarj, M. Particle size effects on the oxidation–reduction behavior of Mn3O4 hausmannite. Mater. Chem. Phys. 2001, 70, 54–60. [Google Scholar] [CrossRef]
- Liu, C.; Nan, J.; Zuo, X.; Xiao, X.; Shu, D. Synthesis and electrochemical characteristics of an orthorhombic LiMnO2 cathode material modified with poly(vinyl-pyrrolidone) for lithium ion batteries. Int. J. Electrochem. Sci. 2012, 7, 7152–7164. [Google Scholar] [CrossRef]
- Costa, M.M.; Pires Junior, G.F.M.; Sombra, A.S.B. Dielectric and impedance properties’ studies of the of lead doped (PbO)-Co2Y type hexaferrite (Ba2Co2Fe12O22 (Co2Y)). Mat. Chem. Phys. 2010, 123, 35–39. [Google Scholar] [CrossRef]
- Valente, M.A.; Peres, M.; Nico, C.; Monteiro, T.; Graça, M.P.F.; Sombra, A.S.B.; Silva, C.C. Morphological, structural, optical and dielectric properties of 91SiO2:4Li2O:4Nb2O5:1Dy2O3 (% mole) glass prepared by sol–gel. Opti. Mat. 2011, 33, 1964–1969. [Google Scholar] [CrossRef]
- Barsoukov, E.; Ross Macdonald, J. Impedance Spectroscopy Theory, Experiment and Applications, 2nd ed.; Wiley Interscience: New York, NY, USA, 2005. [Google Scholar]
- Lily, K.; Kumari, K.; Prasad, R.; Choudhary, N.P. Impedance spectroscopy of (Na0.5Bi0.5)(Zr0.25Ti0.75)O3 lead-free ceramic. J. Alloys Compd. 2008, 453, 325–331. [Google Scholar] [CrossRef]
- Debye, P. Polar Molecules; Chemical Catalog Company, Inc.: New York, NY, USA, 1929. [Google Scholar]
- Jonscher, A.K. Universal Relaxation Law, 1st ed.; Chelsea Dielectrics Press: London, UK, 1996; pp. 198–200. [Google Scholar]
- Funke, K. Jump relaxation in solid electrolytes. Prog. Solid State Chem. 1993, 22, 111–195. [Google Scholar] [CrossRef]
- Malaescu, I.; Sfirloaga, P.; Marin, C.N.; Bunoiu, M.O.; Vlazan, P. Experimental Investigations on the Electrical Conductivity and Complex Dielectric Permittivity of ZnxMn1−xFe2O4 (x = 0 and 0.4) Ferrites in a Low-Frequency Field. Crystals 2024, 14, 437. [Google Scholar] [CrossRef]
- Iqbal, M.J.; Yaqub, N.; Sepiol, B.; Ismail, B. A study of the influence of crystallite size on the electrical and magnetic properties of CuFe2O4. Mat. Research Bull. 2011, 46, 1837–1842. [Google Scholar] [CrossRef]
- Davis, E.A.; Mott, N.F. Conduction in non-crystalline systems. Philos. Mag. 1970, 22, 903–922. [Google Scholar] [CrossRef]
- Efros, A.L.; Shklovskii, B.I. Coulomb gap and low temperature conductivity of disordered systems. J. Phys. C Solid State Phys. 1975, 8, L49–L51. [Google Scholar] [CrossRef]
- Plugaru, R.; Sandu, T.; Plugaru, N. First principles study and variable range hopping conductivity in disordered Al/Ti/Mn-doped ZnO. Results in Phys. 2012, 2, 190–197. [Google Scholar] [CrossRef]
- Lalanne, M.; Barnabé, A.; Mathieu, F.; Tailhades, P. Synthesis and thermostructural studies of a CuFe(1-x)Cr(x)O(2) delafossite solid solution with. Inorg. Chem. 2009, 48, 6065–6071. [Google Scholar] [CrossRef]
- Dyre, J.C.; Schroder, T.B. Universality of ac conduction in disordered solids. Rev. Mod. Phys. 2000, 72, 873–892. [Google Scholar] [CrossRef]
- Lalanne, M.; Demont, P.; Barnabe, A. Ac conductivity and dielectric properties of CuFe1−xCrxO2:Mg delafossite. J. Phys. D Appl. Phys. 2011, 44, 185401. [Google Scholar] [CrossRef]
- Okuda, T.; Jufuku, N.; Hidaka, S.; Terada, N. Magnetic, transport, and thermoelectric properties of the delafossite oxides CuCr1−xMgxO2 (0 < x < 0.04). Phys. Rev. B. 2005, 72, 144403. [Google Scholar]
- Nagarajan, R.; Draeseke, A.D.; Sleight, A.W.; Tate, J. p-type conductivity in CuCr1−xMgxO2 films and powders. J. Appl. Phys. 2001, 89, 8022–8025. [Google Scholar] [CrossRef]
- Pike, G.E. AC conductivity of scandium oxide and a new hopping model for conductivity. Phys. Rev. B. 1972, 6, 1572–1580. [Google Scholar] [CrossRef]
- Elliott, S.R. A theory of a.c. conduction in chalcogenide glasses. Philos. Mag. B. 1977, 36, 1291–1304. [Google Scholar] [CrossRef]

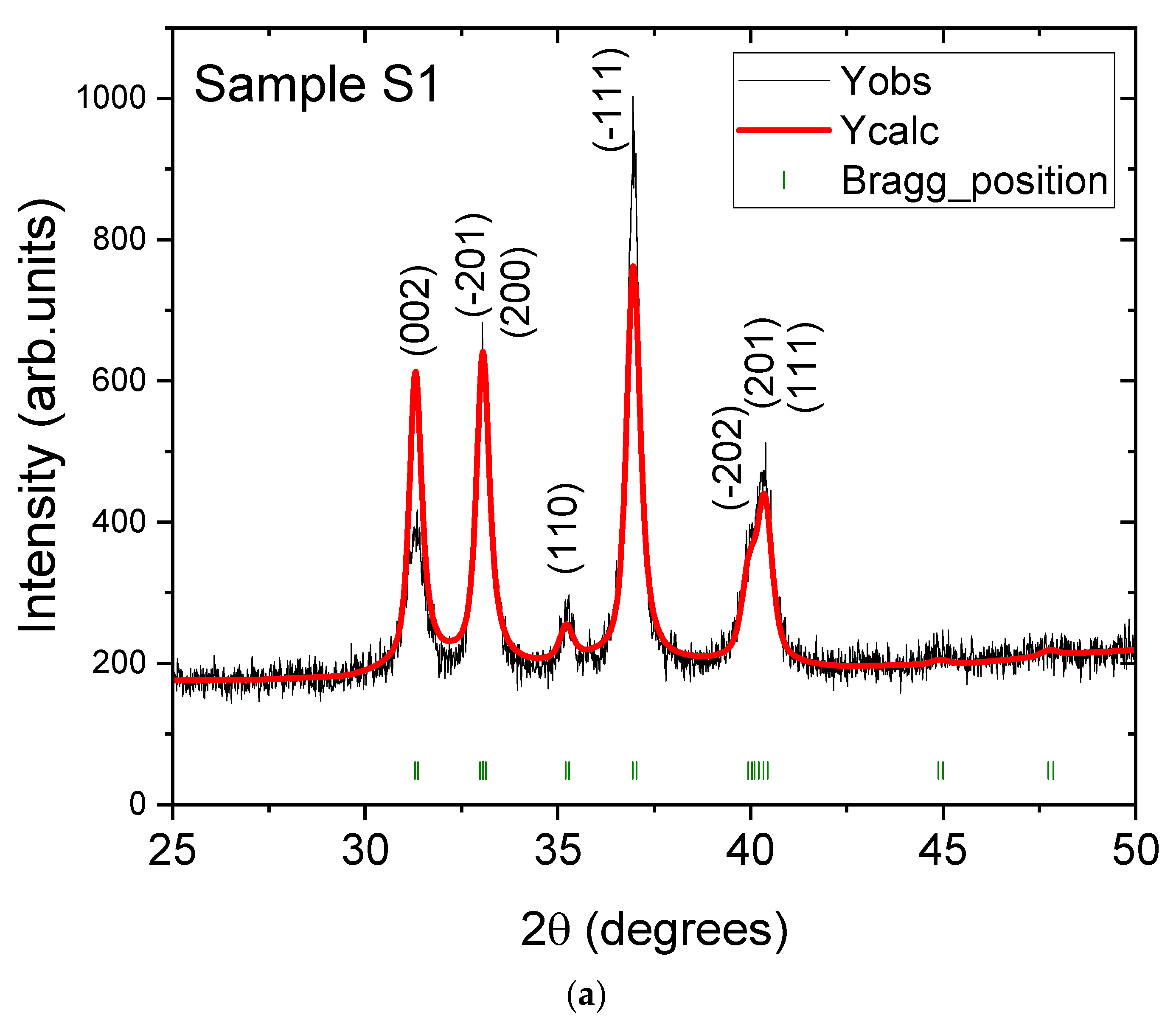
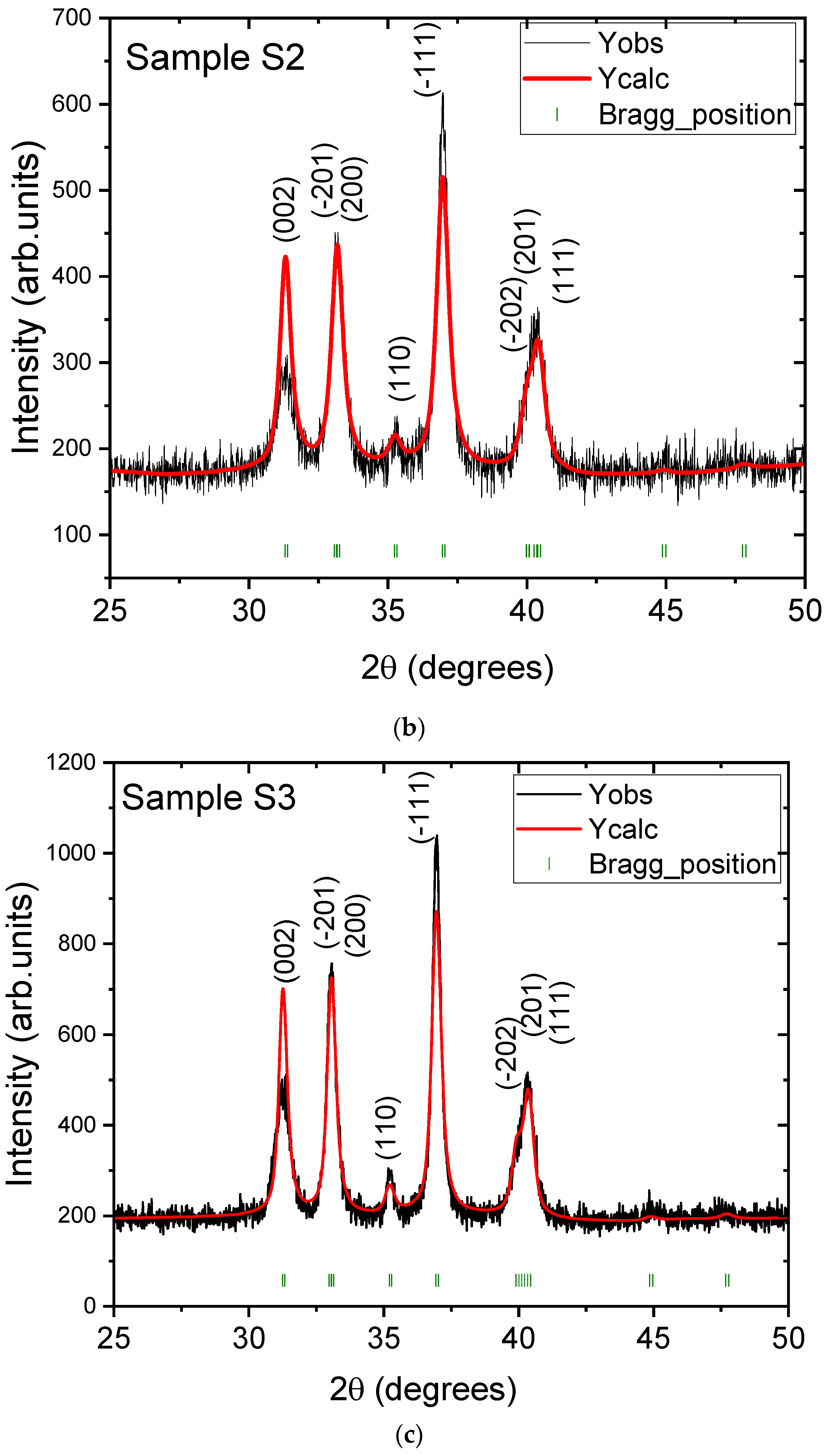
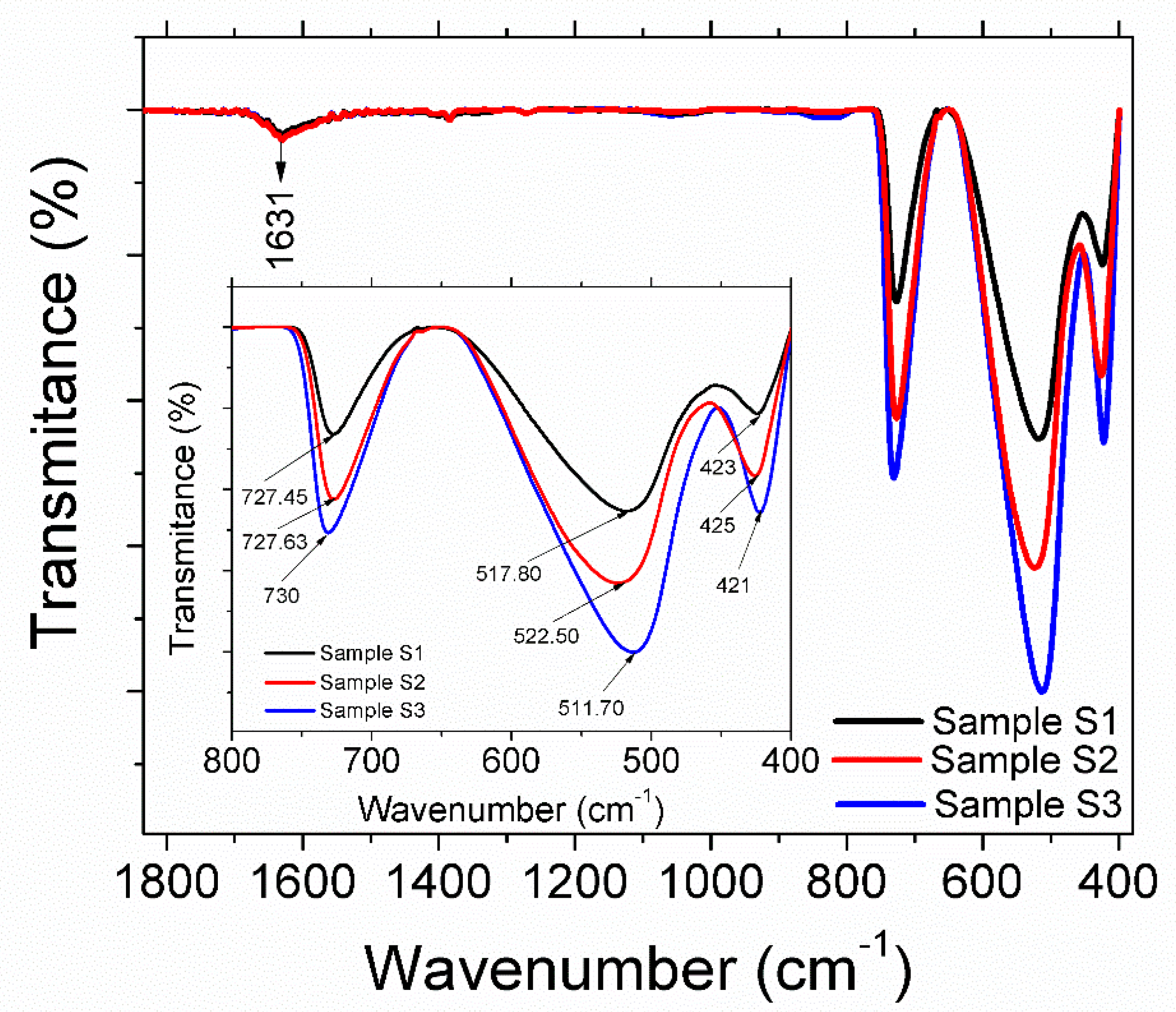

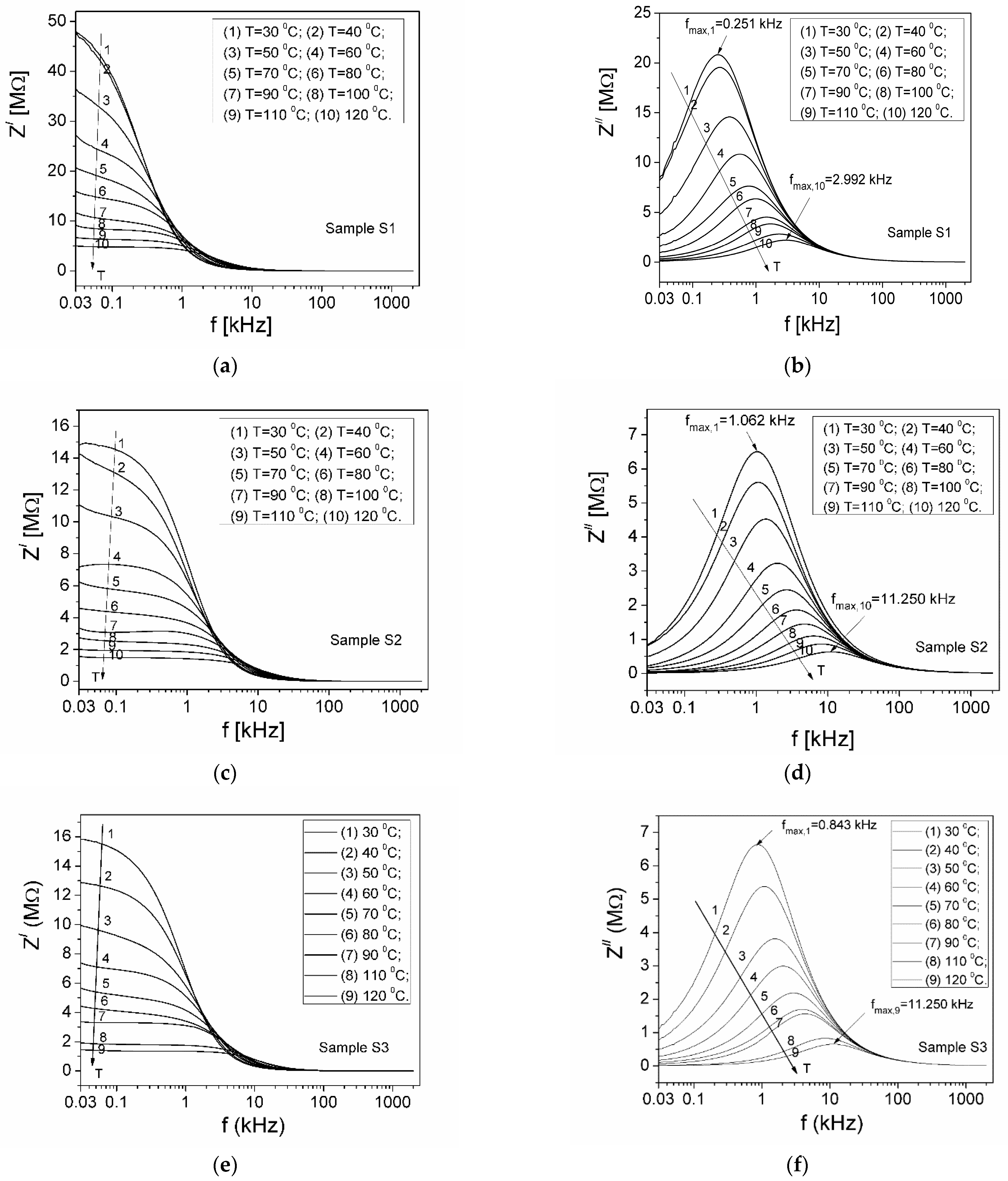
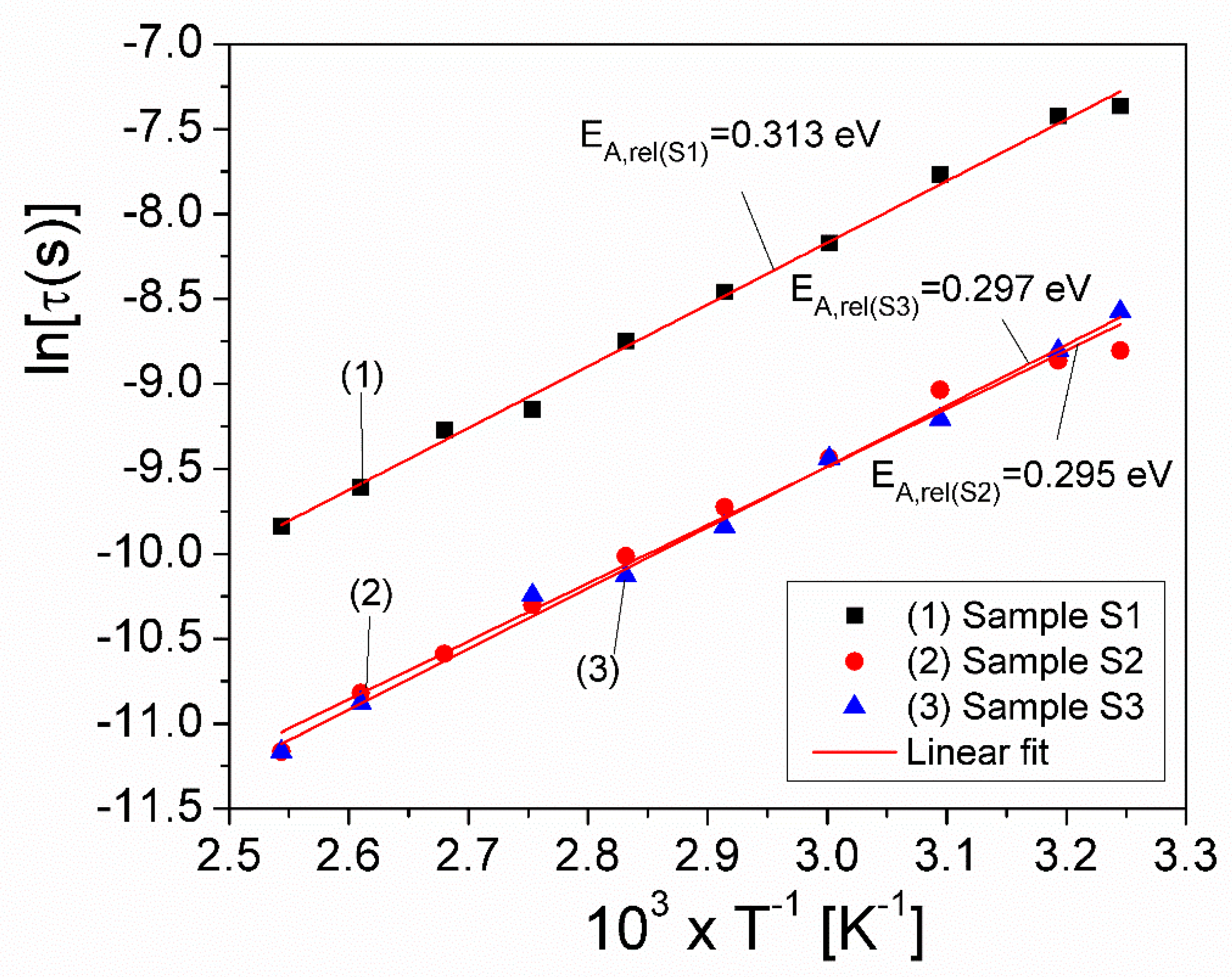
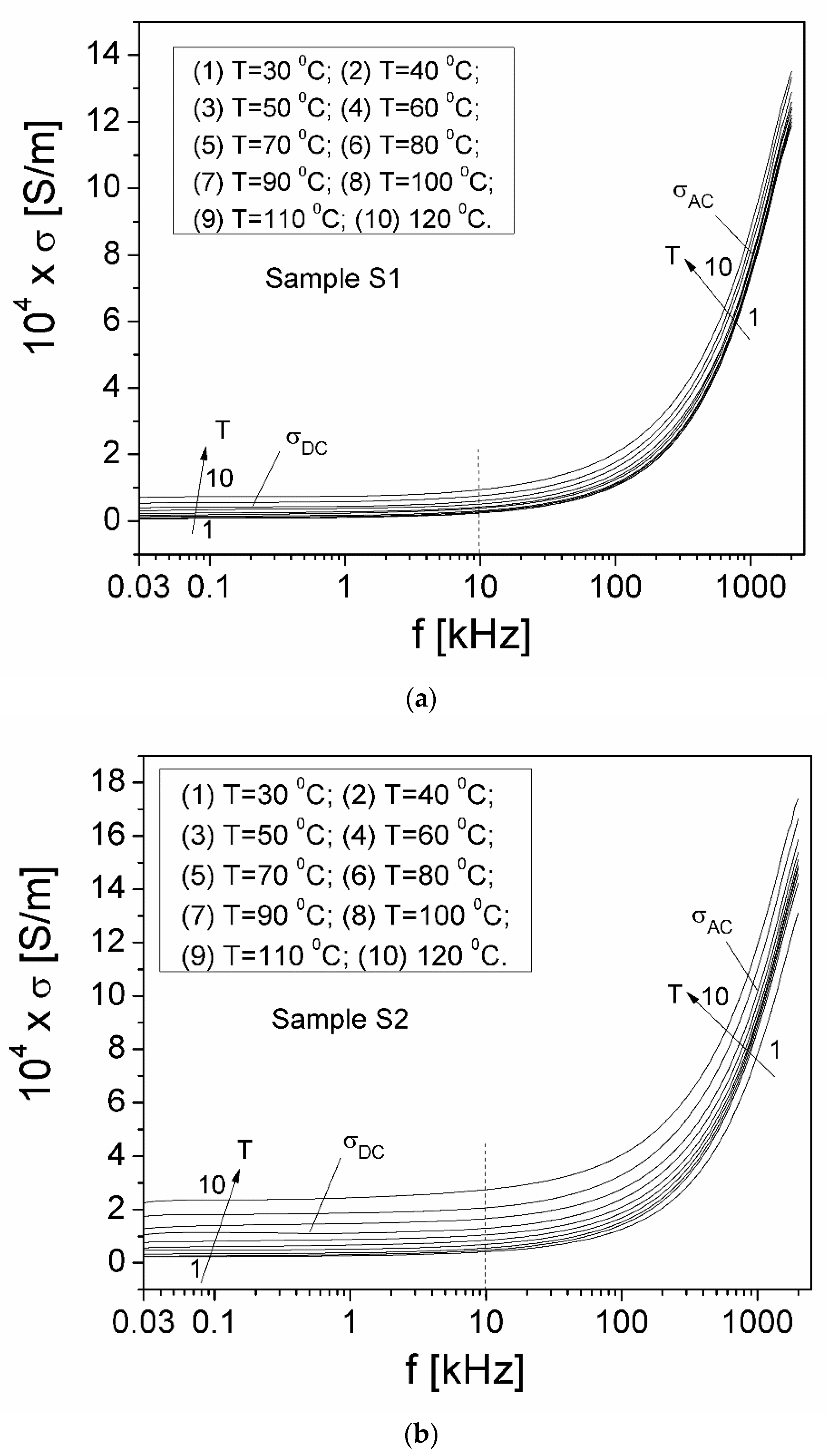
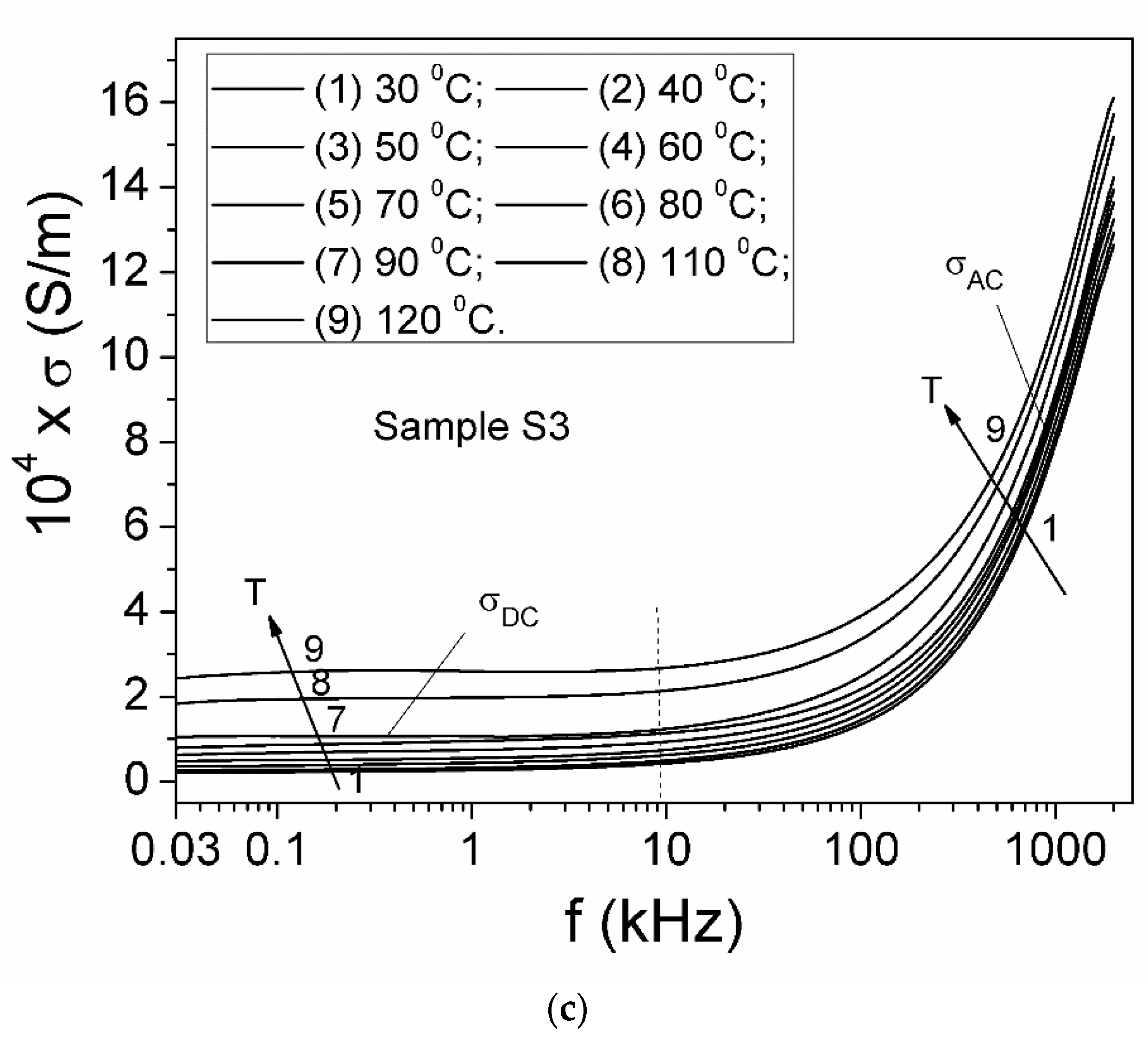
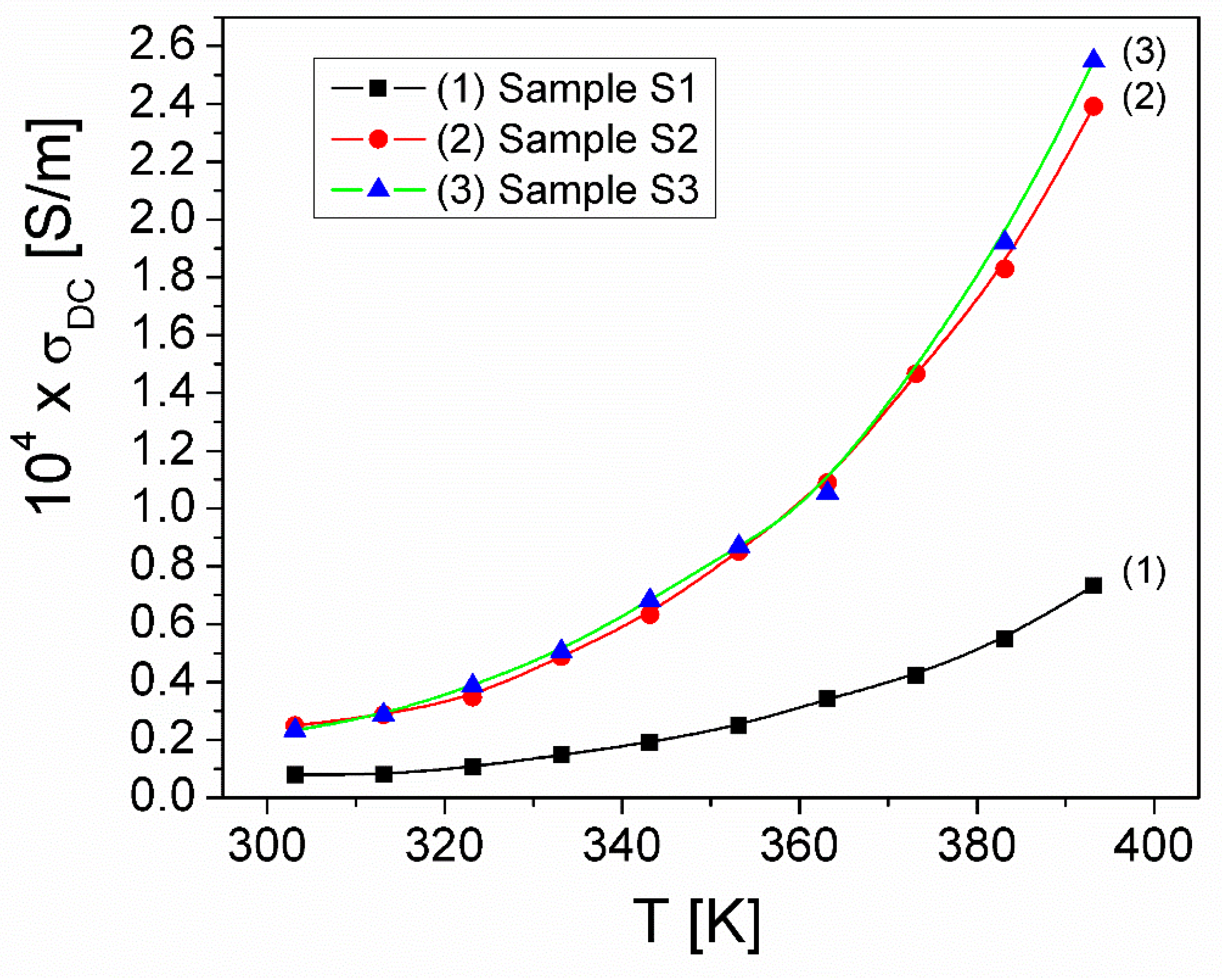



| Samples | Sample S1 | Sample S2 | Sample S3 |
|---|---|---|---|
| a (Å) | 5.56331(1) | 5.58146(8) | 5.58113(6) |
| b (Å) | 2.88611(5) | 2.88623(4) | 2.88616(3) |
| c (Å) | 5.88602(2) | 5.88560(9) | 5.89400(7) |
| β (deg) | 104.054(2) | 103.956(9) | 103.988(7) |
| Volume (Å3) | 91.679(3) | 92.014(2) | 92.125(2) |
| Crystallite size (nm) | 13.8 | 18.5 | 19.5 |
| Samples | Parameters | Arhenius Law | VRH Model | ES-VRH Model |
|---|---|---|---|---|
| Equation y = A + Bx | ln(σDC) = ln(σ0) — (EA,cond/k)·(T)−1 | ln(σDC)= ln(σ0M) — (T0M)1/4 ·(T)−1/4 | ln(σDC)= ln(σ0E-S) — (T0E-S)1/2 ·(T)−1/2 | |
| S1 | r2 | 0.99261 | 0.99569 | 0.99482 |
| Intercept (A) | −1.34565 | 26.831 | 8.04332 | |
| Slope (B) | −3248.1149 | −162.07472 | −349.54649 | |
| S2 | r2 | 0.99452 | 0.99731 | 0.99654 |
| Intercept (A) | −0.14884 | 27.99917 | 9.23323 | |
| Slope (B) | −3246.2966 | −161.96251 | −349.31997 | |
| S3 | r2 | 0.99027 | 0.99723 | 0.99670 |
| Intercept (A) | −0.31403 | 28.65122 | 9.57888 | |
| Slope (B) | −3173.86645 | −161.8811 | −355.24135 |
| T [K] | kT [eV] | Sample S1 | Sample S2 | Sample S3 | |||
|---|---|---|---|---|---|---|---|
| Rh[nm] | Wh[eV] | Rh[nm] | Wh[eV] | Rh[nm] | Wh[eV] | ||
| 303 | 0.0261 | 19.82 | 18.94 | 19.80 | 18.93 | 19.79 | 18.92 |
| 323 | 0.0278 | 0.110 | 0.126 | 0.110 | 0.125 | 0.110 | 0.125 |
| 343 | 0.0296 | 19.50 | 18.69 | 19.49 | 18.67 | 19.48 | 18.66 |
| 363 | 0.0313 | 0.115 | 0.131 | 0.115 | 0.131 | 0.115 | 0.131 |
| 383 | 0.0330 | 19.21 | 18.57 | 19.20 | 18.55 | 19.19 | 18.54 |
| 393 | 0.0339 | 0.121 | 0.134 | 0.120 | 0.133 | 0.120 | 0.133 |
| Sample S1 | Sample S2 | Sample S3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T [K] | n | 109 × A0 (S/msn) | 10−4 × ωh (rad/s) | n | 109 × A0 (S/msn) | 10−4 × ωh (rad/s) | n | 109 × A0 (S/msn) | 10−4 × ωh (rad/s) |
| 303 | 0.877 | 1.51 | 1.729 | 0.867 | 1.93 | 5.500 | 0.844 | 3.99 | 2.905 |
| 313 | 0.862 | 1.53 | 2.049 | 0.834 | 2.56 | 7.099 | 0.810 | 5.03 | 4.316 |
| 323 | 0.842 | 1.75 | 3.096 | 0.801 | 3.16 | 11.096 | 0.774 | 7.14 | 6.657 |
| 333 | 0.822 | 1.91 | 5.369 | 0.776 | 4.76 | 14.715 | 0.733 | 10.77 | 10.242 |
| 343 | 0.803 | 2.61 | 6.481 | 0.744 | 7.98 | 17.358 | 0.701 | 15.03 | 16.447 |
| 353 | 0.790 | 3.25 | 8.208 | 0.714 | 13.11 | 21.838 | 0.680 | 21.51 | 20.132 |
| 363 | 0.760 | 5.19 | 10.567 | 0.674 | 25.27 | 24.650 | 0.654 | 35.16 | 20.693 |
| 373 | 0.733 | 8.41 | 11.208 | 0.640 | 45.40 | 30.397 | - | - | - |
| 383 | 0.714 | 11.64 | 13.974 | 0.595 | 99.34 | 30.728 | 0.570 | 141.1 | 31.495 |
| 393 | 0.678 | 21.62 | 16.088 | 0.544 | 238.8 | 32.785 | 0.536 | 250.4 | 40.871 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marin, C.N.; Poienar, M.; Lungu, A.; Casut, C.; Sfirloaga, P.; Malaescu, I. Study of the Electrical Conduction Mechanism in Low-Frequency Field for CuMnO2 Crednerite-Type Materials Obtained by Microwave-Assisted Hydrothermal Synthesis. Crystals 2025, 15, 497. https://doi.org/10.3390/cryst15060497
Marin CN, Poienar M, Lungu A, Casut C, Sfirloaga P, Malaescu I. Study of the Electrical Conduction Mechanism in Low-Frequency Field for CuMnO2 Crednerite-Type Materials Obtained by Microwave-Assisted Hydrothermal Synthesis. Crystals. 2025; 15(6):497. https://doi.org/10.3390/cryst15060497
Chicago/Turabian StyleMarin, Catalin N., Maria Poienar, Antoanetta Lungu, Cristian Casut, Paula Sfirloaga, and Iosif Malaescu. 2025. "Study of the Electrical Conduction Mechanism in Low-Frequency Field for CuMnO2 Crednerite-Type Materials Obtained by Microwave-Assisted Hydrothermal Synthesis" Crystals 15, no. 6: 497. https://doi.org/10.3390/cryst15060497
APA StyleMarin, C. N., Poienar, M., Lungu, A., Casut, C., Sfirloaga, P., & Malaescu, I. (2025). Study of the Electrical Conduction Mechanism in Low-Frequency Field for CuMnO2 Crednerite-Type Materials Obtained by Microwave-Assisted Hydrothermal Synthesis. Crystals, 15(6), 497. https://doi.org/10.3390/cryst15060497







