Abstract
Various types of strain, as well as chemical pressure induced by dopants, can effectively tailor the performance of perovskite thin films, including their optical, electrical or photoelectrochemical properties. The control of these functional properties through such engineering techniques is key to fulfilling the application-specific requirements of ferroelectric devices in various fields. Numerous models and experimental data have been published on this subject, especially on ferrite-based ferroelectric materials. Within this paper, the mechanisms of tuning ferroelectric intrinsic properties, such as polarization and ferroelectric domain configurations, through epitaxial strain and doping, as well as the role of these techniques in influencing functional properties such as dielectric and photoelectrochemical ones, are presented. This review examines the significant improvements in dielectric properties and photoelectrochemical efficiency achieved by the strategical control of key functionalities including dielectric losses, domain structures, charge separation and surface reactions in strained/doped ferroelectric thin films, highlighting the advancements and research progress made in this field in recent years.
Keywords:
ferroelectric; strain engineering; doping; dielectric; photoelectrochemical; phase field; ab initio 1. Introduction
Ferroelectric materials, characterized by spontaneous polarization arising from their non-centrosymmetric crystal structures, have become indispensable in various modern technologies and hold promise for new and exciting applications, from energy storage and memory devices to photocatalysis and optoelectronics. Although, in their pristine state, ferroelectrics often suffer from different limitations like low polarization, high leakage currents or wide bandgaps, their functional properties are intimately coupled to those of the material lattice. Therefore, various forms of strain engineering have emerged as powerful strategies to tailor these properties, enabling the control of ferroelectric phases, domain configurations and other intrinsic properties.
With the advancement of thin-film fabrication techniques, the precise control of the lattice strain state has become possible through epitaxial strain (via substrates or superlattices), interphase engineering or chemical pressure induced by dopants. Concurrently, the large increase in computational power and accessibility has enabled the use of ab initio methods in studies revealing the atomic-scale mechanisms behind these techniques and their effects, such as strain- and doping-induced polarization amplification, bandgap tuning and stabilization of novel phases and domain structures. Bridging the gap between the two approaches, phase-field modeling has risen as a critical mesoscale tool in predicting strain-driven domain dynamics and phase changes, topological structures and functional enhancements.
This review synthesizes recent advances in the strain and doping engineering of ferroelectric perovskite thin films, focusing on the mechanisms behind dielectric and photoelectrochemical property enhancements in ferrite-based perovskite materials, thanks to the plethora of intrinsic properties they exhibit. Ferroelectric perovskite materials, characterized by spontaneous polarization and the resulting depolarization electric field, arising from symmetry breaking and electrostatic conditions, offer the possibility to fine-tune different functional properties for a wide range of applications. For example, within the electric fields present in ferroelectrics, positive and negative charges (holes and electrons) will separate and drift in opposite directions, similar to a classical p-n junction, opening the way to alternative approaches. Thus, many studies on perovskite materials have been centered on ferroelectric polarization and domain control within thin films for functionalities such as energy storage, data storage, nanoelectronics or sensing [1,2,3,4], as well as on the interaction of ferroelectric polarization with light, leading to photocatalytic, photovoltaic or other photoelectric applications [5,6,7,8,9,10]. These fields have increasingly leveraged machine learning (ML) to accelerate material discovery, optimize modeling techniques, and develop predictive frameworks [11,12,13,14,15,16,17]. While ML-driven advances are beyond the scope of this review, we highlight key references for readers interested in exploring these rapidly evolving approaches. The quest for renewable energy has triggered an avalanche of research studies involving ferroelectric perovskite materials, dedicated to their photovoltaic and photoelectrochemical properties [5,6,7,8,9,18]. Despite the fact that above-bandgap photovoltages have been generated in perovskite thin films, such as BiFeO3 (BFO), from both photovoltaic and photocatalytic points of view, the performances in terms of conversion efficiency are low with respect to those of other material systems [19,20]. To benefit from the advantage of the intrinsic electric field induced by reversible spontaneous polarization, ferroelectric perovskites must be tailored by different means to control internal occurring effects such as internal screening, charge separation and transport, electronic conductivity of ferroelectric domain walls, high leakage and dielectric losses, as well as optical bandgap and, especially for photocatalytic (PC) applications, chemical stability [9,21,22,23].
Direct solar energy-to-green hydrogen conversion through photoelectrochemical (PEC) reactions using ferroelectric perovskites has been studied, owning to its superior charge separation and transport characteristics, but led to low overall conversion efficiencies. For an effective conversion of solar light in PEC reactions, some aspects must be taken into account when designing a photoelectrode [24,25]: (1) an appropriate bandgap for light absorption and the creation of electron (e−)/hole (h+) pairs; (2) charge separation and charge transport efficiency toward the photoelectrode’s surface; (3) surface reduction/oxidation reactions occurring due to migrating charges at the interface between the liquid and the photoelectrode (anode/cathode). Ideally, all the photoinduced charge carriers would reach the surface of the photoelectrodes and be consumed in the redox reactions, but effects such as the electron–hole pair recombination pose major problems for reaching higher efficiencies in the PEC approach.
As mentioned above, strain engineering and doping engineering of ferroelectric perovskite thin films are appropriate tools for enhancing the overall efficiencies/functionalities of these materials compared with other material classes. From this point of view, the ferroelectric perovskite ABO3 class represented by lead titanate zirconate Pb(Zr1–xTix)O3 (PZT), comprises the perfect materials to be studied under structural or chemical doping forms of constrains. The current interest towards ferrite-based perovskite materials such as BiFeO3, LaFeO3 (LFO) and AlFeO3 has been triggered since the first reports of BiFeO3 having a substantially higher spontaneous polarization in thin film form than in bulk form, as well as being able to generate photovoltages above the bandgap in thin films with engineered domains [18,19,26]. Moreover, the light absorption of ferrite perovskites is often extended in the visible region, in contrast to that of titanates [8,9,27,28]. Specifically, BiFeO3 and LaFeO3 were widely used as photoelectrodes in photoelectrochemical applications, namely, for the photodegradation of dyes and water photolysis. With a bandgap of about 2.5 eV and outstanding photocatalytic activity, BFO is also one of the few room-temperature multiferroic materials [21].
Due to the coexistence of both polar and magnetic orders at room temperature in BFO, which is of interest for possible applications in nonvolatile memory, spintronics, piezoelectric devices, etc., BFO is perhaps the most studied ferroelectric/multiferroic material [21]. A complicated phase diagram results from the interaction of its ferroic order parameter with the several structural degrees of freedom [21]. Therefore, BFO changes from the paraelectric orthorhombic (O) Pnma phase to the rhombohedral (R) R3c ferroelectric (FE) phase below the threshold temperature of Tc = 1100 K. The rhombohedral ground state is characterized by ionic displacements from the centrosymmetric positions along the [111]c direction and anti-phase octahedral tilts about the same axis. A G-type anti-ferromagnetic (AFM) ordering of Fe3+ ions is also present in BFO below the Néel temperature TN = 640 K [29]. However, in normal conditions, it is compromised by a low dielectric constant, a large dielectric loss and high leakage currents, critical problems that make BFO unsuitable for use in electronic and electromechanical devices. BFO shows a highly dispersive behavior with the applied field frequency and a low-frequency (kHz–MHz regime) reported dielectric constant value of several hundred, which in the radio frequency regime, drops to only 30 [21,30]. Moreover, this decrease is accompanied by a substantial increase in the dielectric losses, which is the hallmark of space charge contributions.
In this review, we first outline theoretical advancements, then follow with experimental ones, each addressing characteristic strain-engineering approaches with accent on ferrite-based materials, highlighting their roles in the development of the field. Although the review tries to distinguish between theoretical and experimental contributions, many of the advances discussed here were achieved through close collaboration between the two, often within the same study. Throughout this work, we discuss challenges, including strain relaxation and defect control, and emergent applications such as negative capacitance, flexible electronics and topological storage, as well as future development directions.
2. Ab Initio Studies
First-principles calculations have proven to be essential in studying the atomic-scale mechanisms governing ferroelectricity in perovskite oxides and related materials. These computational techniques allow researchers to predict and analyze structural, electronic, magnetic and optical properties with minimal empirical input, offering deep insights into the underlying physics governing material behavior [31]. Moreover, they can be used in predicting and explaining how doping and strain can help in tailoring functional properties by introducing changes in crystal symmetries, electronic structures and polarization dynamics. This section synthesizes recent ab initio insights into three strategies for engineering ferroelectric materials.
2.1. Doping-Induced Enhancement of Functional Properties
Within the impressive palette of stable perovskite compounds, a particular interest resides in transition metal (TM) doping, as well as rare in earth–TM combinations, which significantly enhance the piezoelectric properties of perovskites even when doping is in minute amounts. An interesting case study is that of KTa1−xNbxO3 (KTN) doped with Mn and Fe, which showed an enhanced piezoelectric response [32]. Owing to the very high miscibility of KNbO3 and KTaO3, high-quality crystals can be produced, with highly tunable polarization. More importantly, the roles of the two doping elements were identified: while Mn doping increased the local structural heterogeneity, which determined an enhancement of the piezoelectric coefficient beyond 1000 pC/cm2, Fe doping further stabilized the polarization. Density functional perturbation theory (DFPT) calculations performed using the Quantum ESPRESSO software package [33] on KTN supercells (illustrated in Figure 1) described the dynamic evolution of phase structures upon applying an electric field, as revealed by Raman spectroscopy.
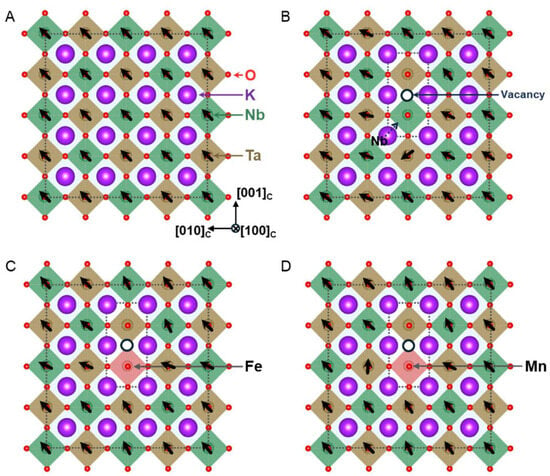
Figure 1.
Dipole moment orientations in the KTN octahedra within (100)C sections containing defect dipoles. (A) Pristine KTN lattice, (B) KTN lattice with an oxygen vacancy (VO-KTN), (C) Fe-doped lattice, and (D) Mn-doped lattice. Reproduced from [32] under CC-BY license.
Barium titanate (BaTiO3 or BTO) represents an alternative to the Pb-containing, more environmentally unfriendly PZT. Recently, it was shown that an enhanced hybridization between titanium and nitrogen in doped BTO could induce a large ferroelectric polarization of 70 μC/cm−2, which was about 2.8 times larger than that obtained in pristine BTO [34]. At the same time, the Curie temperature increased by ~810 K. First-principles calculations implemented using the Vienna Ab initio Simulation Package (VASP) [35,36] at the GGA-PBE level confirmed the preference of the nitrogen substitution at the apical site and consistently explained the modification of the c/a ratio and polarization depending on the N atomic fraction at the anionic site. D-block metal substitutions in BTO represent another approach for inducing and tuning the multi-ferroic properties.
Compounds of the BaXO3 (X = Cr, Mn, Co, Ni) type were investigated by density functional theory (DFT) calculations using the Cambridge Serial Total Energy Package (CASTEP) code [37], at the GGA-PBE level [38]. This study showed that besides adjusting the electronic properties, as the bandgaps ranged from 0.5 eV (X = Mn) to 1.04 eV (X = Ni), a precise control of the spin polarization could be achieved. In addition, the presence of spin–orbit coupling can extend the application of these compounds to spintronic devices. Going further, lanthanide-based perovskites exhibit exceptional-stability band structures, particularly well suited for spintronic applications. One prominent candidate is BaNpO3 perovskite, which has been investigated in the context of doping with Ca, Mg and Cr [39]. The resulting compounds of the BaxX1−xNpO3 type were investigated through a similar DFT-based procedure, and their electronic and optical properties were determined. They demonstrated a high versatility, ranging from photovoltaics to electromagnetic shielding and optical filtering applications. On the other hand, a DFT- and experiment-based study on Sr-doped BaTiO3 revealed the role of Sr in stabilizing the cubic phase [40]. This, in turn, led to a reduction in the bandgap and Curie temperature associated with the ferroelectric-paraelectric transition, at the same time impacting the piezoelectric performance. In other applications, like solar cell technology, photoelectrocatalysis and other visible-range optoelectronic devices, a reduction in the bandgap is usually desired.
SrTiO3 (STO) is one such promising semiconductor for photocatalysis, which exhibits quantum paraelectric behavior. However, in epitaxially thin films, Sr vacancy-induced tetragonality can potentiate ferroelectricity [41]. Here, it was shown that under high laser fluence conditions (2.5 J cm−2), a polarization of ~7.5 μC/cm2 could be achieved. Furthermore, first-principles calculations have shown the impact of doping by chalcogen elements (S, Se, Te) with respect to decreasing the bandgap, therefore producing an enhancement of the response in the optical spectrum [42]. Using the full-potential linearly augmented plane wave (FP-LAPW) method at the GGA-PBE level, implemented through the Wien2k code [43], a significant reduction in the bandgap was revealed, with a direct impact on absorption in the visible range.
As discussed in the introduction, another high-interest case is that of multiferroic BiFeO3, with many studies focusing on the influence of strain and chemical doping on its electric, magnetic and optical properties. A-site doping with rare earths was shown to cause phase changes and enhancements in both magnetic and electric properties [44,45,46,47,48]. For example, La doping was shown to simultaneously increase the ferroelectric polarization and decrease the bandgap [44,47]. Similarly, Nd doping led to a high-power conversion efficiency and decreased the bandgap [45]. B-site doping has also been extensively investigated, with candidates such as Mn, Mg, Co, Ni, Cu and Zn [46,48,49,50,51,52]. Low-cost, solution-processed BiFe1-xCoxO3 thin films have shown a tunable bandgap, depending on Co concentration, indicating potential as photoactive materials [52]. Moreover, Y and transition metal co-doping was proven to significantly increase the photocatalytic activity, especially in the case of Mg [46]. Studies also explored the possibility of N doping and predicted enhanced magnetic properties [48,53].
However, it is important to mention that for various doped BFO systems, the use of hybrid functionals instead of standard DFT functionals, such as GGA-PBE, was proven necessary, in order to correctly describe the electronic structure [54]. For example, alkali or alkaline earth metal substitutions (p doping) in the GGA-PBE approximation led to an over stabilization of the unoccupied iron states and even predicted partially filled bands at the Fermi level instead of acceptor states. Without prior knowledge of this effect, correct conclusions cannot be drawn, and the standard DFT analysis can lose even its qualitative predictive power. This actually hints at a more fundamental problem, the fact that the approximations used in density functional theory (DFT) that enable its low computational cost come with a critical tradeoff: they often yield poor accuracy for studying highly correlated systems or excitation properties, as DFT is fundamentally a ground-state theory. When such properties are of interest, researchers turn to high-precision high-computational-cost methods, such as the quasiparticle approximation (GW or the single-step G0W0) [55,56,57,58] or time-dependent DFT (TD-DFT) [59,60,61]. These resource-intensive approaches frequently produce results that closely align with the experimental data, offering key insights into optical or ultrafast phenomena. While these advanced techniques fall outside the scope of this review, references are provided as a starting point for readers interested in a deeper exploration of these topics.
2.2. Strain-Induced Enhancement of Dielectric, Ferroelectric and Photoelectrochemical Properties
Similar to chemical doping, strain can also enhance the polarization in established ferroelectric materials and induce ferroelectricity in materials that are normally paraelectric [62]. It is known that in the case of oxygen electrocatalysis, strain can improve the activity compared to that achieved for the corresponding unstrained materials by changing the bandgaps and also altering the defect chemistry. In ABO3 perovskites, the B-O bond length strongly influences the electronic structure. For example, it is known that compressive strain in LaNiO3/LaAlO3 superlattices can induce eg symmetry breaking [63]. Strain, alongside d-band filling and oxidation state, was shown to have a strong impact on the electronic structure and reactivity of LaBO3 and SrBO3 (B = Sc, Ti, V, Cr, Mn, Fe, Co, Ni and Cu) perovskites. In particular, a fine-tuning of the reactivity is possible based on strain, as revealed by DFT calculations implemented in DACAPO code [64]. In some cases, lattice deformations can be responsible for the experimentally observed metallic behavior, like in LaTiO3 grown on SrTiO3 substrates [65].
Much interest has also been shown for the effects of strain on the crystal structure and properties of multiferroic BFO [66,67,68,69,70,71,72,73,74]. Since the ab-initio reports that BiFeO3 (BFO) exhibits a substantially larger spontaneous polarization in thin film form than in bulk, the ferroelectric community has seen a significant increase in the number of research studies pertaining to the synthesis and properties of BFO thin films [26,75]. The predicted value of about 150 μC/cm2 in a super-tetragonal (T) crystal structure remains the highest spontaneous polarization of any single-phase ferroelectric material. In BFO thin films obtained under specific conditions, a comparable structure was also achieved experimentally at 90 K, and its spontaneous polarization was calculated through ab initio methods to be 143.5 μC/cm2; however, at room temperature, tetragonality was found to decrease to ∼1.01, with a corresponding measured polarization of only 102 μC/cm2 [76].
These results triggered studies to prove that it is possible to obtain a spontaneous polarization with gigantic values in systems with different structural features, including a low tetragonality ratio. Tensile strain was found to cause structural instabilities and induce large shear deformations in (001) BiFeO3 thin films, while stabilizing the monoclinic (Cc space group) and orthorhombic phases (Ima2 space group) [69,72]. This was found to increase the polarization and cause strong electronic changes. Compressive strain was later used to stabilize an intermediate S′ polymorph and tetragonal-like and super-tetragonal phases, with large increases in polarization, thanks to the added effect of Fe ion displacements, and opened the way to bandgap tuning [66,67,68,74]. Moreover, compressive strain was found to favor the formation of Bi and Bi-O pair vacancies [70,71]. Recent DFT studies took into account the effects of thermal strain induced into films through different thermal expansion properties of the substrates [77]. Other studies predicted large photostriction near the R-T phase boundary under varying epitaxial strain [73]. From a theoretical perspective, Jiang et al. investigated ferroelectric nitrides under compressive epitaxial strain and predicted the formation of bent domain structures that reduce the energy barriers for switching [78]. These strain-induced configurations could enhance the dielectric susceptibility by facilitating more responsive domain wall motion.
Defect engineering controlled by strain is another way to improve the ferroelectric properties. By tensile strain, the formation energy of oxygen vacancies can be lowered, as observed in the case of double-perovskite BiSmFe2O6−δ epitaxial thin films [79]. In this study, using DFT+U calculations implemented in VASP, four oxygen vacancy types were identified, and the formation energies were determined as a function of tensile strain. The Hubbard U term is usually required to get optimized volumes closer to the experimental values but may also lead to an overestimation of the saturation polarization. Considering the BaTiO3 and SrTiO3 systems, a detailed analysis encompassing multiple functionals, e.g., LDA, PBE, PBESol and HSE, has shown that PBE+U is the most balanced option to describe perovskite oxide ferroelectrics [80].
Other classes of perovskite materials, like XGeO3 (X = Sr, Ca), confirmed the general trend, as they also present an important enhancement of their ferroelectric properties by increasing the strain [81]. Chemical expansion can occur in the presence of oxygen vacancies in manganite and titanate perovskites resulting in volume change, which is shown to be linked to Hubbard repulsion in the AMnO3 and ATiO3 (A = Ca, Sr, Ba) systems [82]. Here, using DFT calculations implemented in VASP, the Hubbard term was shown to impact the ionic displacements, as indicated in Figure 2. Furthermore, the interplay between polarization, strain, and defect pairs in Fe-doped SrMnO3−δ showed that polarity and ferroelectricity can be adjusted in nonpolar perovskite oxides [83]. This analysis was performed in the DFT+U framework of Quantum Espresso.
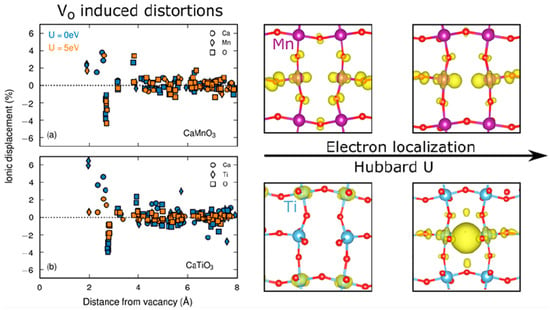
Figure 2.
Ionic displacements as a function of distance from an oxygen vacancy observed in (a) calcium manganate and (b) calcium titanate, under different Hubbard U corrections, along with examples of their density of states. Reproduced from [82] under CC-BY license.
2.3. Freestanding Structures and 2D Materials
More exotic structures have also been analyzed by first-principles calculations. Lately, ferroelectricity has been experimentally observed in a number of two-dimensional (2D) materials: CuInP2Se6 [84], group III2-VI3 materials like In2Se3 [85,86], MX-type materials (M = Ge, Sn; X = S, Se, Te), e.g., SnS [87], SnSe [88], SnTe [89], and other 2D materials, like MoTe2 [90] and NiI2 [91]. The major advantage of 2D materials relies on the fact that they eliminate the restrictions found in the case of epitaxially grown ferroelectric thin films, such as substrate–film lattice matching and the precise control of the experimental parameters. The breakthrough of the deterministic transfer of 2D materials has led to their integration with different materials in mixed-dimensional van der Waals heterostructures [92]. Moreover, by means of high-throughput calculations, 2D ferroelectric materials can be identified, which may have in-plane, out-of-plane and coupled in-plane–out-of-plane polarization. One example is VAgP2Se6, which shows a three-state switchable polarization that is strongly coupled to the magnetic excitation spectrum [93].
A similar case is that of the investigation of mechanical bending-induced ferroelectric phase transition in ultrathin perovskite nanobelts [94], such as those presented in Figure 3. Upon applying mechanical stress, it was revealed that PbTiO3 (PTO) and BaTiO3 nanobelts could exhibit axial polarization. Two-dimensional ferroelectric vortex patterns were identified in ferroelectric twisted freestanding BTO layers, due to the reciprocal strain gradients induced by the layers [95].
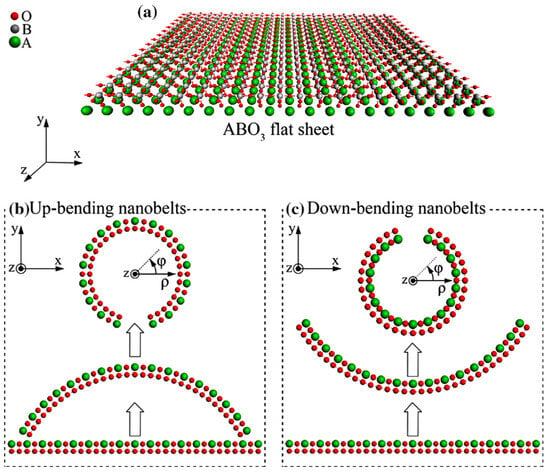
Figure 3.
(a) Planar, (b) up and (c) down bent ABO3 nanobelts. Reprinted from [94], copyright (2014), with permission from Elsevier.
BTO single-crystal membranes were also subjected to 180° folding without fracture, being under a very large induced strain of up to 10% [96]. This accomplishment led the way to new types of heterostructures obtained by combining freestanding complex oxides with 2D materials, for potential interesting electronic devices such as two-dimensional transistors [97,98,99].
Layered structures that combine ferroelectric perovskite oxides and two-dimensional semiconductors are employed in the development of high-performance transistors [99], where a monolayer of MoS2 is stacked on a BaTiO3 thin film, as depicted in Figure 4. A robust hysteresis in the current–voltage I-V curve was obtained, which is indicative of the influence of the ferroelectric substrate on the active transport layer, in comparison to other substrate materials, like silicon and hexagonal boron nitride (hBN) [84]. As perovskite materials are known electrocatalysts for both hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) [100], layered structures based on ferroelectric perovskite oxides and two-dimensional semiconductors are also seen as promising candidates to be used as photoelectrode materials for solar-driven water splitting.
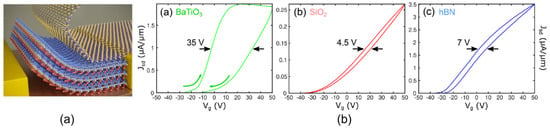
Figure 4.
(a) Transistor structure with a MoS2 active layer placed on a BTO ferroelectric substrate. (b) I–V hysteresis curves for different substrates (BTO, Si, hBN) outlining the role of the ferroelectric material. Reprinted from [99] under CC-BY 4.0 license.
3. Phase-Field Simulations
Although ab initio calculations are widely used for their precision in predicting and explaining fundamental properties, their high computational cost hinders the exploration of mesoscale systems. Here, phase-field simulations have relatively recently become an important tool for investigating microstructures in various material research fields, being an efficient and precise method that can be built upon experimental and first-principles data. As the name suggests, they are centered around the time evolution of a phase field, usually a conserved or non-conserved order parameter, that changes continuously across interfaces as described by the Cahn–Hilliard and Ginzburg–Landau (Allen-Cahn) equations. Starting as a tool for investigating crystal growth and solidification [101,102] and then crack propagation [103], they were readily applied to modelling ferroelectric thin films and their domain structures [104]. In recent years, this method has become a crucial tool in studying and predicting property optimizations, domain structure engineering and dynamics.
3.1. Freestanding Ferroelectric Membranes
Lots of phase-field studies have been focusing on freestanding structures. Dong et al. have shown that freestanding BTO single-crystal membranes could undergo an 180° folding without fracture, being under a very large induced strain of up to 10% [96]. This is accommodated in the lattice through continuous dipole rotation between the a and c domains under the effects of the flexoelectric effect, as observed in high-resolution scanning transmission electron microscopy (HR-STEM) images and phase-field simulations. Similar studies on BFO and PTO membranes have found the former to be able to endure a cyclic 180° folding and strains of up to 5.42% through a continuous rhombohedral–tetragonal transition, and the latter uniaxial strains of up to 6.4% [105,106]. Ferroelectric STO membranes have also been obtained, as presented in Figure 5, with in-plane 180° domain walls explained through phase-field simulations [107]. Bilayer freestanding ferroelectric La0.7Sr0.3MnO3/BaTiO3 heterostructures were successfully obtained and shown to self-assemble into nanosprings with large scalabilities of up to 500% [108] and to even present multiferroic properties [109]. Using this elasticity, Dong et al. created and studied periodically wrinkled BTO membranes [110], further confirming the role of continuous dipole rotation through atomistic simulations. Such freestanding ferroelectrics have been also investigated for use in THz high-data-rate wireless communication [111] and energy storage [112].
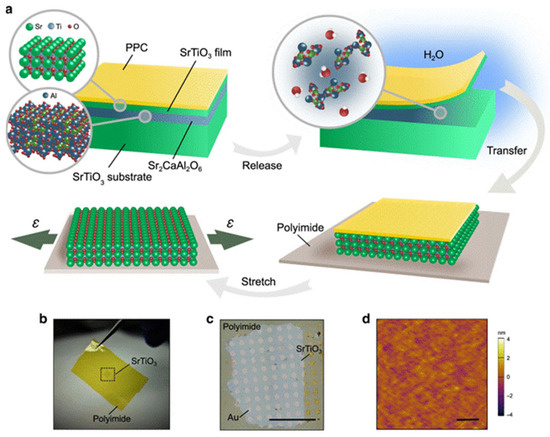
Figure 5.
(a) Schematic illustrating the lift-off and transfer process for SrTiO3 membranes onto polyimide sheets. By dissolving the sacrificial Sr2CaAl2O6 layer from the as-grown heterostructure, SrTiO3 films can be released and transferred onto a polyimide sheet with a layer of polypropylene carbonate (PPC) as the supporting material. The oxide/polymer bilayer structure can be stretched after PPC is thermally decomposed in O2. Optical images of the transferred millimeter-scale freestanding SrTiO3 membranes are shown in (b,c), with an ordered array of gold optical markers. The scale bar is 1 mm. (d) Detailed atomic force microscopy topographic images reveal the crack-free surface of SrTiO3 transferred onto the polyimide sheet. The scale bar is 1 µm. Reprinted from [107] under CC-BY license.
3.2. Topological Structures
Another critical use of phase-field modeling in ferroelectrics was to help in investigating topological structures formed in complex domain structures. Flux closure domains were first experimentally observed in STEM images of BFO thin films deposited on TbScO3 and were explained with the help of phase-field modeling based on the electrostatic energy of the system [113]. Soon after, topological domain configurations were observed experimentally in PZT thin films deposited on STO [114]. Here, the polarization structures were attributed to the combined effect of epitaxial strain, leading to the formation of 180° out-of-plane domains, and large depolarization fields caused by the latter.
While studying PTO/STO multilayers grown on tensile strain-inducing GdScO3, Tang et al. found huge strain gradients of up to 109 m−1 in periodic arrays of flux closures, with periods depending on the PTO layer thickness [115]. Later, long-range vortex–antivortex arrays were obtained in PTO/STO superlattices, as shown in Figure 6, and proven to be the ground state of the system for a range of sublattice periods through phase-field simulations [116]. Growing the superlattice on STO led to the first observation of three-dimensional polar skyrmions, and second-principles calculations were used to model the microscopic polarization structure and calculate the characteristic skyrmion number [117]. Tensile strain and poor screening of polarization were shown through experimental investigations and phase-field modeling to lead to the formation of large curvature layers of up to 107 m−1 in PTO/SRO and optically excited PTO/STO superlattices. Moreover, subterahertz collective dynamic modes were observed in such superstructures through both experiments and modelling, with dynamic phase-field modeling predicting the tunability of the vortexon mode by electric fields at room temperature [118]. Other structures such as merons formed in thin PTO films deposited on SmScO3 substrates, with phase-field simulations showing that they can be synthesized through careful manipulation of strain and electric boundary conditions [119]. Incommensurate spin crystals were later proved to also form in ferroelectrics [120], with possible Dzyaloshinskii–Moriya interaction (DMi) electric equivalents, such as oxygen octahedral tilting trilinear interactions with different possible cationic modes, previously explored through DFT calculations [121]. Recently, new strain states have been observed in twisted bilayer BTO membranes, leading to a highly correlated topological pattern with vortices and antivortices, which can be tuned by controlling the twisting angle [95].
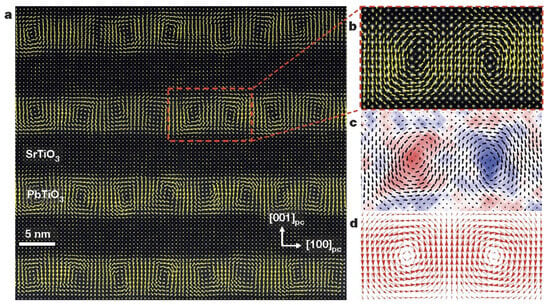
Figure 6.
(a) Cross-sectional HR-STEM image with an overlay of the polar displacement vectors (PPD, indicated by yellow arrows) for a (SrTiO3)10/(PbTiO3)10 superlattice, showing that an array of vortex–antivortex pairs is present in each PbTiO3 layer. (b) Magnified image of a single vortex–antivortex pair, showing the full density of the data points and the continuous rotation of the polarization state within such vortex–antivortex pairs. (c) The curl of the polar displacement (∇ × PPD) [010] for the same vortex–antivortex pair reveals the alternating rotation directions of the structures (no-vorticity (curl = 0) in white, clockwise (negative) rotation in blue and anticlockwise (positive) rotation in red). (d) Polarization vectors from a phase-field simulation of the same (SrTiO3)10/(PbTiO3)10 superlattice, which predicted vortex–antivortex pairs that closely matched the experimental observations. Reprinted from [116], copyright 2016, reproduced with permission from SNCSC.
3.3. Chemical, Defect and Epitaxial Strain Engineering for Enchanced Functional Properties
Several methods for preserving a large strain throughout thicker films have been developed such as chemical/defect engineering [18,122,123,124,125], interphase engineering [126,127], vertically arranged networks (VANs) [128,129], superlattices [115,130], or even freestanding films where the strain is induced mechanically [96,106]. Although thoroughly investigated in DFT simulations, chemical/defect engineering is still barely explored in phase-field simulations, with only a few studies published [131,132]. Most importantly, a random field theory-enhanced phase-field model was used to model relaxor ferroelectrics and their chemical disorder [133]. This was able to reproduce their behaviors, such as domain miniaturization, reduce their polarization and increase piezoelectricity, which was previously unexplained. The pinning effect of dislocations on ferroelectric domains and its influence on polarization–electric field (P-E) loops was also investigated by several studies [134,135,136,137,138] that found that P-E loops can become asymmetric, tend to shrink with smaller domains or higher grain misorientation and tilt or disappear with conductive grain boundaries. Accumulation of oxygen vacancies at the interface was also shown to lead to an increase in polarization in ultra-thin films through combined results from STEM analysis and phase-field calculations [139].
However, the primary method for introducing strain in thin films involves the use of lattice-mismatched substrates, and this was studied at length in phase-field simulations. The in-plane induced strain, which is often isotropic, arises from the difference between the lattice parameters of the film and those of the substrate. Commonly referred to as epitaxial strain, this effect has been extensively studied for its impact on phase stabilization, domain structures and the functional properties of well-known ferroelectric materials, including PbTiO3 [104,140], BaTiO3 [141,142], PbZrxTi1–xO3 [143,144,145] and BiFeO3 [146,147]. A few examples of domain structures are presented in Figure 7.
Notably, epitaxial strain has also been shown to induce a ferroelectric-like behavior in nominally non-ferroelectric perovskites, such as SrTiO₃ [148,149]. Similarly, binary oxides were also investigated by first principles calculations and proved to become ferroelectric at large-enough interfacial strains [150]. They are of great interest for computing applications, thanks to their larger bandgaps and good integration with silicon technology. Phase-field simulations were recently used to evaluate the potential of ZrO2 and HfO2 phase mixtures for negative capacitance applications [151,152] and to explain the low-temperature crystallization of ferroelectric Hf0.5Zr0.5O2 under an electric field [153]. By introducing a high epitaxial strain of up to +6.4%, ferromagnetic EuO was proven to become multiferroic in (EuO)2/(BaO)2 superlattices, with a ferroelectric transition being found at around 100 K [130].
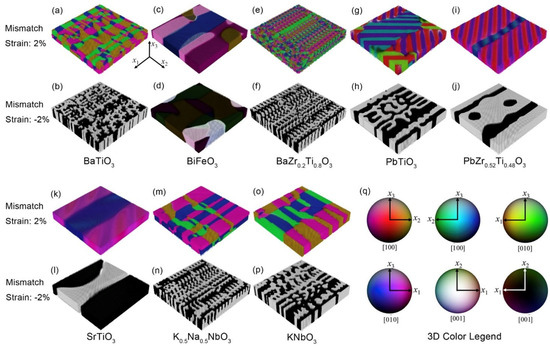
Figure 7.
Domain structures of (a,b) BaTiO3, (c,d) BiFeO3, (e,f) BaZr0.2Ti0.8O3, (g,h) PbTiO3, (i,j) PbZr0.52Ti0.48O3, (k,l) SrTiO3, (m,n) K0.5Na0.5NbO3, and (o,p) KNbO3 thin films under mismatch strains of 2% and −2%, respectively. (q) 3D color legend representing the polarization directions for different colors, as projected from different viewpoints. Generally, black and white colors represent domains with stronger out-of-plane polarization components, while other colors represent domains with stronger in-plane polarization components. Reprinted from [154], copyright 2020, with permission from Elsevier.
Application-specific studies were also carried out in the Ginzburg–Landau framework, with, for example, tensile stress being proven to significantly improve dischargeable energy densities and charge–discharge efficiencies in ferroelectric thin-film capacitors [154]. Huo et al. predicted, using a modified Landau–Devonshire-type potential and density functional theory, a large dielectric tunability of the tetragonal K0.5Na0.5NbO3 structure and then verified it experimentally [155]. High-frequency dielectric permittivity was shown to be spatially inhomogeneous and reach the highest value in 90° domain wall ferroelectrics, with tensile and compressive strain causing a reduction and an increase in permittivity, respectively [156].
In the anisotropic epitaxial strain case, often seen when using orthorhombic substrates, studies have found more complex effects, with new domain orientations and structures arising, compared to the isotropic case: 7 were observed as opposed to 3 for PTO [157], and 16 as opposed to 7 for BTO [158]. The opposite effect, that of domain selection, has also been studied, as BiFeO3 films grown on miscut substrates form only two of the possible four orientations, and this has been explained based on the introduction of a shear strain component [159]. Anisotropic strains play a major role in the engineering of complex domain structures and can even lead to the formation of polarization closure domains, as it was explained in the Section 3.2 [113].
4. Experimental Considerations on the Theoretical Approaches
There are several problems regarding the presented DTF and phase-field simulation approaches associated with using induced strain and chemical doping for the enhancement of functional properties in perovskite ferroelectrics: the limited availability of substrates with different lattice constants, as shown in Figure 8, the relaxation of the strain with increasing film thickness, as well as the homogeneity variability in the dopant distribution and deposition methods instabilities. Regarding the first problem, multiple groups started to incorporate thin buffer layers in order to tune the substrate lattice constant [160,161]. The second problem is even larger, as films continuously relax the induced strain through dislocations until reaching the fully relaxed state at a critical thickness. The relaxation of thin films has been described through the People–Bean model [162] and was previously implemented in phase-field simulations on ferroelectric thin films in order to correctly represent the domain structures of films with thicknesses over the critical limit [163]. Taking all the presented results into account, the phase-field method has become an important tool in studying and predicting property optimizations and domain structures. However, there are supplementary experimental factors, such as the deposition process, that need to be considered in order to fulfill the predicted functional properties enhancements obtained through means such as epitaxial strain in real ferroelectric perovskite thin films, and as such, experimental/modelling bi-directional verification of the results is required.
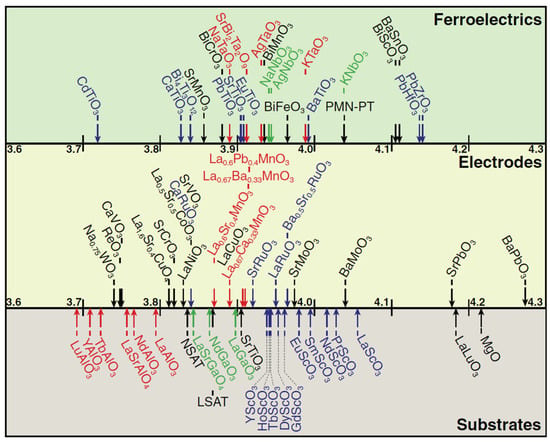
Figure 8.
List of commercially available substrate materials (bottom section) and select lists of perovskite electrode materials (middle section) and ferroelectric, incipient ferroelectric, and anti-ferroelectric materials. Reprinted from [164], copyright 2016, with permission from IOP Publishing.
One important feature of ferroelectric thin films is related to the control of ferroelectric domains and domain walls for dielectric/ferroelectric properties tuning, while another important fact to consider is the precise control of the film’s deposition parameters imposed by the deposition technique. As seen from phase-field simulations, domain structures play a critical role in the development of multiple fields. It is thus important to analyze the effects of domain walls (DWs) as well, as they significantly influence the macroscopic dielectric response of ferroelectric thin films. Their motion, interaction, and stability are intimately linked to material properties such as dielectric loss, polarization switching behavior and the shape of polarization–electric field (P-E) hysteresis loops. Thanks to its profound effects on ferroelectric materials, strain engineering has also emerged as a powerful tool for controlling domain wall dynamics and, thereby, tuning dielectric properties. Recent studies have demonstrated that strain not only modifies the domain structure but also alters the mobility and configuration of domain walls, influencing the dielectric response. For example, Lu et al. showed that in uniaxial ferroelectrics, electromechanical coupling at domain walls is highly sensitive to the applied mechanical boundary conditions [165], which could significantly modulate the local dielectric response and switching behavior. Moreover, combining epitaxial strain and compositional grading was found to allow for the deterministic control of highly mobile ferroelastic domain walls, leading to an enhanced piezoresponse [166]. Similarly, nanoscale mixed-phase ensembles were induced through the combined effect of epitaxial strain and chemical pressure and shown to create a high dielectric permittivity and a low loss structure in BFO [3], which will later be described in more detail. Moving in the opposite direction led to studies comparing the switching dynamics in clamped and freestanding films while attempting to tune BFO for ultra-low power memory and logic devices, with a ~40% reduction in the switching voltage and a consequent ~60% improvement in the switching speed obtained in the latter [167], thanks to the removal of the elastic constraints imposed by the substrate.
Regarding domain wall dynamics, cooperative dipole fluctuations near 180° walls in BTO were shown to provide a significant extrinsic contribution to dielectric permittivity and loss, with distinct frequency- and amplitude-dependent behaviors that influenced the material’s functional responses [168]. Moreover, studies on domain walls in the terahertz range found a lowering of the dielectric permittivity due to unfulfilled dipoles in the domain walls [169]. As the effect can be controlled through poling, this finding could open the way for domain wall dielectric switching memory. Strong enhancements of dielectric and piezoelectric properties were also induced through increased densities of charged domain walls in lead-free ferroelectrics [170]. Similarly, tuning of the dielectric properties after deposition was reported through thermal adjustments of insulating domain wall density and is suspected to work under mechanical strain also [171]. PTO/SRO superlattices with dense domain structures presented a temperature-dependent capacitance enhancement, expected to arise from the contribution of domain wall motion [172].
Even disregarding the used deposition technique, factors like stoichiometric transfer problems, especially for complex-chemical-composition materials, defect occurrence due to different reasons (lattice misfit, process gas and pressure, etc.) or other factors can reduce the impact of the induced strain or dopant on the desired properties. As an example of complex-stoichiometry perovskite thin films, reports on (1 − x)Ba(Ti0.8Zr0.2)TiO3 − x(Ba0.7Ca0.3)TiO3 (BCZT) solid-solution thin films under epitaxial strain and its impact upon relaxation with thickness over the dielectric properties have been made [4,173].
Chemical doping and strain engineering are also the two primary methods for controlling the phase stability and transition temperatures of ferrite-based perovskite materials, especially BFO-based materials. Both methods seek to enhance BFO dielectric and electromechanical activity by inducing a mixed state of the coexisting phases through various methods (mechanical pressure or chemical pressure). Polar displacements and oxygen octahedral tilts, two degrees of freedom that coexist throughout a broad temperature range in BFO, can react differently to changes in environmental parameters or chemical replacements, resulting in a variety of phases. Therefore, BFO is extremely sensitive to the application of external pressure. At lower pressures, low-symmetry (monoclinic) phases are stable at room temperature; however, at pressure values of 10 GPa, the high-temperature phase (O Pnma) appears at room temperature [174]. Given that the stress created within the plane of development in epitaxial films can reach several GPa [175], this is significant. In thin films, strain may be applied in a controlled way, and strain engineering is currently being employed to adjust the functional characteristics of these films [3,18]. Because of imposed strain, the crystallographic structure of epitaxial thin films frequently differs from that of the bulk material in thin film form. Depending on the film thickness and, consequently, the degree of strain relaxation, BFO films with thicknesses ranging from 50 nm to 1000 nm produced on STO (001) displayed monoclinic symmetry with varying lattice parameters [176].
As mentioned earlier, chemical substitutions are another method of tuning BFO-based materials’ dielectric or photoelectrochemical properties. Low dielectric loss (tanδ < 0.01) and very high in-plane dielectric permittivity (ε′ ≈ 2500) in BiFeO3 films by Y-doping, alongside imposed structural strain on SrTiO3(001) substrates, have been reported on films obtained by the pulsed laser deposition method [3], as shown in Figure 9 and Figure 10.
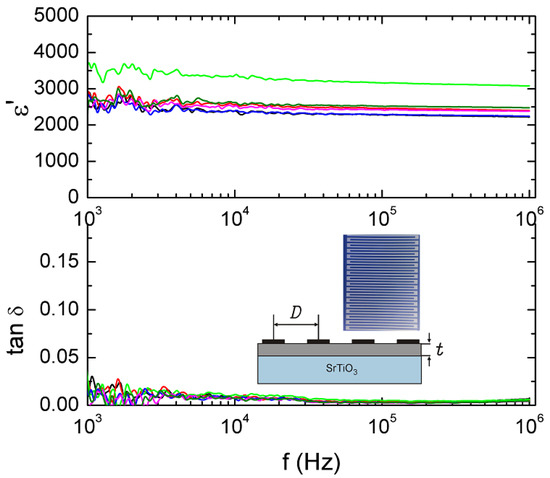
Figure 9.
Dielectric constant and loss tangent in the 1 kHz–1 MHz frequency range for Y-doped BFO thin films. Reprinted from [3], under CC-BY license.
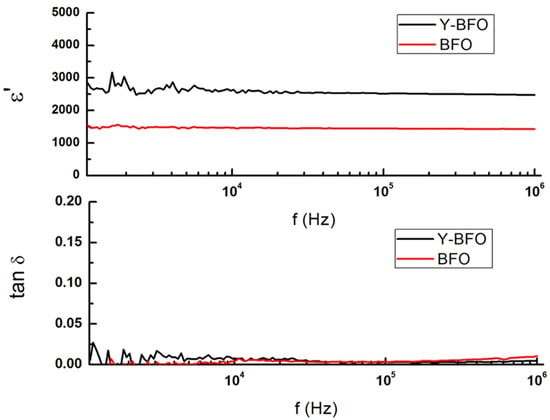
Figure 10.
Dielectric constant and loss tangent values comparison of Y-BFO and BFO samples. Reprinted from [3], under CC-BY license.
These experimental findings demonstrate that through the creation of mixed states at the nanoscale level, the dielectric limitations can be overcome in high-quality epitaxial films. The appearance of nanostripe domains with alternating compressive and tensile strain were proven by geometric phase analysis and high-resolution transmission electron microscopy, as shown in Figure 11.
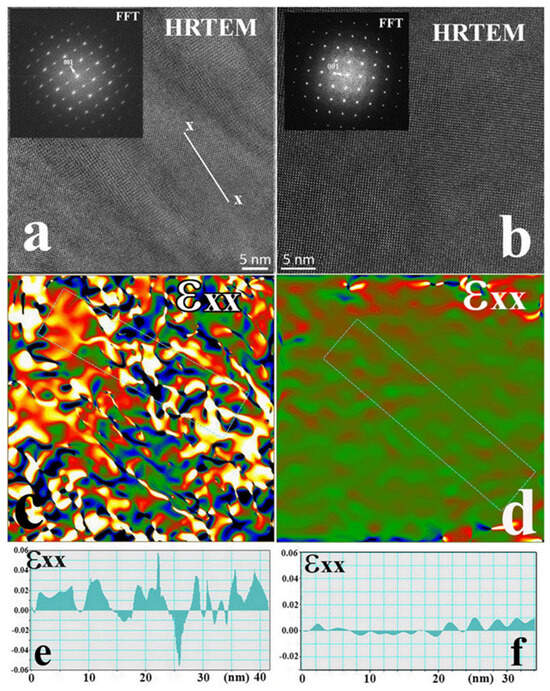
Figure 11.
Comparative analysis of Y-BFO–BFO films: HRTEM and FFT (a,b), stress/strain GPA maps (c,d), and line profiles of the strains (e,f). Reprinted from [3], under CC-BY license.
The effects of strain and Y-doping on BFO films, namely, the emergence of a stripe-like nanodomain structure with monoclinic symmetry, have been examined above. Nanostripe-like domain patterns have also been found in BFO films produced on various substrates [113] and in other ferroelectric systems [177]. The large observed dielectric response occurs due to this unusual nanostructure.
As mentioned above, the light-absorption property of ferrite perovskites is extended in the visible region, in contrast to that of titanates [8,9,27,28]. For BFO materials, due to the bandgap of about 2.5 eV and outstanding photocatalytic activity, both HER and OER properties have been documented; polycrystalline BFO in the form of nanowires and nanocubes produces solely O2 when exposed to UV light, whereas mixing BFO nanoparticles with SrTiO3 can result in the generation of H2 upon exposure to visible light [178]. While spontaneous polarization has a much smaller impact on photocatalytic activity in bulk BFO due to oxygen vacancies that cause high dielectric losses, the ferroelectric properties of BFO nanostructures can enhance electron–hole separation and photocatalytic activity [8,179,180]. By both chemical doping and induced epitaxial strain, enhanced photoelectrochemical activity of Y-doped BiFeO3 (Y-BFO) epitaxial thin films deposited on Nb:SrTiO3 substrates by pulsed laser deposition (PLD) has been observed [18] and is presented in Figure 12.
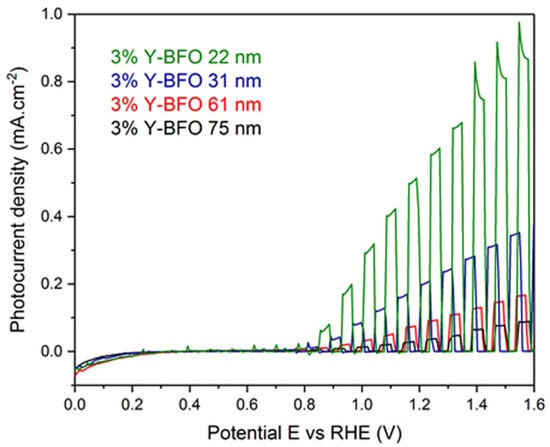
Figure 12.
PEC potentiodynamic measurements for Y-BFO thin films with different thicknesses performed at different E(V) vs. RHE. Reprinted from [18], under CC-BY license.
In the same study, a strong dependence of the photocurrent density values on the induced epitaxial strain for the Y-BFO films was noticed, as shown in Figure 13.
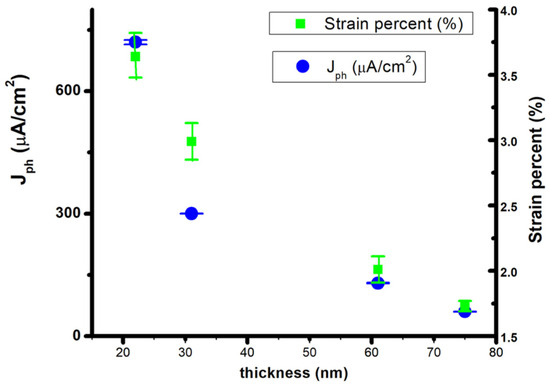
Figure 13.
The photocurrent density Jph values in Y-BFO films with different induced strain levels. Reprinted from [18], under CC-BY license.
The combined effects of Y-doping and induced strain led to a higher photocurrent density compared with that obtained for BFO thin films, accompanied by a photoanodic characteristic. The peculiar nanostripe-like domains rolling throughout the film’s thickness can induce band bending towards the film–electrolyte interface due to their high built-in potential and mobility towards external stimuli.
However, the relatively low efficiencies of both dielectric and PEC activities of ferroelectric perovskite materials have to be further enhanced. In the case of photoelectrochemical activity, photocurrent densities have to increase in the mA/cm2 range by supplementary means such as oxygen vacancy generation, heterojunction building, 2D-based material inclusion and others. Some of the present strategies to enhance the functional properties of perovskite materials, derived both from theoretical and experimental results, can be synthesized as follows:
- -
- Strain control beyond the substrate’s influence. The role played by freestanding thin films or heterostructures, as well as interface layers, in overcoming this problem will be very important, as the range of applications for nanodevices is increasing. Different other forms of induced strain have the potential to be used, such as thermal strain.
- -
- Improvements in the control, stability and regulation of polarization in ferroelectric perovskite thin films. Of particular interest for PEC applications, this task is still challenging, due to the fact that any external applied electric field can have detrimental effects on the chemical properties of the sample in in situ PEC systems. Further studies are needed to clarify the real effects of ferroelectric polarization on the whole range of photoelectrochemical processes.
- -
- New materials or heterostructure architectures that can increase PEC performances through stronger polarization or the harvesting of a wider range of external stimuli. Here, freestanding thin films, stand-alone or associated with 2D materials, could have an important role.
- -
- Improvements of the deposition/processing techniques in terms of control of the stoichiometric growth/chemical doping or induced nanostructured features both on the thin film’s surface and in bulk.
5. Conclusions
The findings reported in this review prove that strain engineering and chemical doping can be used for ferroelectric perovskites to both stabilize new phases and non-equilibrium domain configurations and enhance their functional response through increased ferroelectric polarization, dielectric constant and domain wall activity, decreased dielectric loss and altered hysteresis loops.
Taken together, these recent advances highlight the central role of strain and chemical doping in obtaining application- specific engineered materials. As the ability to precisely manipulate strain at the nanoscale level improves, especially through techniques like compositional grading, functionalized substrates, strain gradient architectures or even freestanding structures, the new and improved dielectric and ferroelectric performance of these materials becomes key in next-generation ferroelectric perovskite-based devices. Developments towards various applications were presented, with a central focus on ferroelectric perovskite thin films for dielectric and photoelectrochemical water splitting. Major problems and chalanges that need to be adressed were outlined along the way, along with possible future directions.
Author Contributions
Conceptualization, N.D.S.; investigation, N.D.S., G.A.N. and I.-M.G.; writing—original draft preparation, N.D.S., G.A.N. and I.-M.G.; writing—review and editing, N.D.S., G.A.N. and I.-M.G.; supervision, N.D.S.; funding acquisition, N.D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by UEFISCDI through the PN-III-P4-PCE-2021-1906 PCE97/2022 projects.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sharma, P.; Zhang, Q.; Sando, D.; Lei, C.H.; Liu, Y.; Li, J.; Nagarajan, V.; Seidel, J. Nonvolatile Ferroelectric Domain Wall Memory. Sci. Adv. 2017, 3, e1700512. [Google Scholar] [CrossRef] [PubMed]
- Catalan, G.; Seidel, J.; Ramesh, R.; Scott, J.F. Domain Wall Nanoelectronics. Rev. Mod. Phys. 2012, 84, 119–156. [Google Scholar] [CrossRef]
- Scarisoreanu, N.D.; Craciun, F.; Birjega, R.; Ion, V.; Teodorescu, V.S.; Ghica, C.; Negrea, R.; Dinescu, M. Joining Chemical Pressure and Epitaxial Strain to Yield Y-Doped BiFeO3 Thin Films with High Dielectric Response. Sci. Rep. 2016, 6, 25535. [Google Scholar] [CrossRef]
- Scarisoreanu, N.D.; Craciun, F.; Moldovan, A.; Ion, V.; Birjega, R.; Ghica, C.; Negrea, R.F.; Dinescu, M. High Permittivity (1 − x)Ba(Zr0.2 Ti0.8)O3−x (Ba0.7 Ca0.3)TiO3 (x = 0.45) Epitaxial Thin Films with Nanoscale Phase Fluctuations. ACS Appl. Mater. Interfaces 2015, 7, 23984–23992. [Google Scholar] [CrossRef]
- Han, X.; Ji, Y.; Yang, Y. Ferroelectric Photovoltaic Materials and Devices. Adv. Funct. Mater. 2022, 32, 2109625. [Google Scholar] [CrossRef]
- Zhang, K.; Li, H.; Mu, H.; Li, Y.; Wang, P.; Wang, Y.; Chen, T.; Yuan, J.; Chen, W.; Yu, W.; et al. Spatially Resolved Light-Induced Ferroelectric Polarization in A-In2Se3/Te Heterojunctions. Adv. Mater. 2024, 36, 2405233. [Google Scholar] [CrossRef]
- Yang, L.; Xiong, Y.; Guo, W.; Zhou, M.; Song, K.; Xiao, P.; Cao, G. Manipulation of Charge Transport in Ferroelectric-Semiconductor Hybrid for Photoelectrochemical Applications. Nano Energy 2018, 44, 63–72. [Google Scholar] [CrossRef]
- Andrei, F.; Ion, V.; Birjega, R.; Ghitiu, I.; Zamfir, M.; Moldovan, A.; Teodorescu, V.S.; Dinescu, M.; Marcu, I.-C.; Scarisoreanu, N.D. Strain Engineering of Epitaxial Perovskite-Type LaFeO3/BiFeO3 Heterostructures for Photoelectrochemical Water Splitting. Surf. Interfaces 2025, 62, 106234. [Google Scholar] [CrossRef]
- Andrei, F.; Ion, V.; Bîrjega, R.; Dinescu, M.; Enea, N.; Pantelica, D.; Mihai, M.D.; Maraloiu, V.-A.; Teodorescu, V.S.; Marcu, I.-C.; et al. Thickness-Dependent Photoelectrochemical Water Splitting Properties of Self-Assembled Nanostructured LaFeO3 Perovskite Thin Films. Nanomaterials 2021, 11, 1371. [Google Scholar] [CrossRef]
- Ion, V.; Teodorescu, V.; Birjega, R.; Dinescu, M.; Mitterbauer, C.; Alexandrou, I.; Ghitiu, I.; Craciun, F.; Scarisoreanu, N.D. Lead-Free Perovskite Thin Films with Tailored Pockels-Kerr Effects for Photonics. ACS Appl. Mater. Interfaces 2023, 15, 38039–38048. [Google Scholar] [CrossRef]
- Tao, Q.; Xu, P.; Li, M.; Lu, W. Machine Learning for Perovskite Materials Design and Discovery. NPJ Comput. Mater. 2021, 7, 23. [Google Scholar] [CrossRef]
- Frey, R.; Grosso, B.F.; Fandré, P.; Mächler, B.; Spaldin, N.A.; Mansouri Tehrani, A. Accelerated Search for New Ferroelectric Materials. Phys. Rev. Res. 2023, 5, 023122. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Hou, C.; Ni, J. Interpretable Machine Learning to Discover Perovskites with High Spontaneous Polarization. J. Phys. Chem. C 2023, 127, 23897–23905. [Google Scholar] [CrossRef]
- Nagai, R.; Akashi, R.; Sugino, O. Completing Density Functional Theory by Machine Learning Hidden Messages from Molecules. NPJ Comput. Mater. 2020, 6, 43. [Google Scholar] [CrossRef]
- del Rio, B.G.; Phan, B.; Ramprasad, R. A Deep Learning Framework to Emulate Density Functional Theory. NPJ Comput. Mater. 2023, 9, 158. [Google Scholar] [CrossRef]
- Alhada-Lahbabi, K.; Deleruyelle, D.; Gautier, B. Machine Learning Surrogate Model for Acceleration of Ferroelectric Phase-Field Modeling. ACS Appl. Electron. Mater. 2023, 5, 3894–3907. [Google Scholar] [CrossRef]
- Mai, H.; Le, T.C.; Chen, D.; Winkler, D.A.; Caruso, R.A. Machine Learning for Electrocatalyst and Photocatalyst Design and Discovery. Chem. Rev. 2022, 122, 13478–13515. [Google Scholar] [CrossRef]
- Haydous, F.; Scarisoreanu, N.D.; Birjega, R.; Ion, V.; Lippert, T.; Dumitrescu, N.; Moldovan, A.; Andrei, A.; Teodorescu, V.S.; Ghica, C.; et al. Rolling Dopant and Strain in Y-Doped BiFeO3 Epitaxial Thin Films for Photoelectrochemical Water Splitting. Sci. Rep. 2018, 8, 15826. [Google Scholar] [CrossRef]
- Seidel, J.; Fu, D.; Yang, S.-Y.; Alarcón-Lladó, E.; Wu, J.; Ramesh, R.; Ager, J.W. Efficient Photovoltaic Current Generation at Ferroelectric Domain Walls. Phys. Rev. Lett. 2011, 107, 126805. [Google Scholar] [CrossRef]
- Huang, H. Ferroelectric Photovoltaics. Nat. Photonics 2010, 4, 134–135. [Google Scholar] [CrossRef]
- Catalan, G.; Scott, J.F. Physics and Applications of Bismuth Ferrite. Adv. Mater. 2009, 21, 2463–2485. [Google Scholar] [CrossRef]
- Tijare, S.N.; Joshi, M.V.; Padole, P.S.; Mangrulkar, P.A.; Rayalu, S.S.; Labhsetwar, N.K. Photocatalytic Hydrogen Generation through Water Splitting on Nano-Crystalline LaFeO3 Perovskite. Int. J. Hydrogen Energy 2012, 37, 10451–10456. [Google Scholar] [CrossRef]
- Liu, Z.K.; Li, X.; Zhang, Q.M. Maximizing the Number of Coexisting Phases near Invariant Critical Points for Giant Electrocaloric and Electromechanical Responses in Ferroelectrics. Appl. Phys. Lett. 2012, 101, 082904. [Google Scholar] [CrossRef]
- Bard, A.J. Photoelectrochemistry. Science (1979) 1980, 207, 139–144. [Google Scholar] [CrossRef]
- Kim, T.W.; Choi, K.-S. Nanoporous BiVO4 Photoanodes with Dual-Layer Oxygen Evolution Catalysts for Solar Water Splitting. Science (1979) 2014, 343, 990–994. [Google Scholar] [CrossRef]
- Wang, J.; Neaton, J.B.; Zheng, H.; Nagarajan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathan, V.; Schlom, D.G.; Waghmare, U.V.; et al. Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures. Science (1979) 2003, 299, 1719–1722. [Google Scholar] [CrossRef]
- Tang, P.; Chen, H.; Cao, F.; Pan, G. Magnetically Recoverable and Visible-Light-Driven Nanocrystalline YFeO3 Photocatalysts. Catal. Sci. Technol. 2011, 1, 1145. [Google Scholar] [CrossRef]
- Ramachandran, B.; Ramachandra Rao, M.S. Chemical Pressure Effect on Optical Properties in Multiferroic Bulk BiFeO3. J. Appl. Phys. 2012, 112, 073516. [Google Scholar] [CrossRef]
- Fischer, P.; Polomska, M.; Sosnowska, I.; Szymanski, M. Temperature Dependence of the Crystal and Magnetic Structures of BiFeO3. J. Phys. C Solid. State Phys. 1980, 13, 1931–1940. [Google Scholar] [CrossRef]
- Kamba, S.; Nuzhnyy, D.; Savinov, M.; Šebek, J.; Petzelt, J.; Prokleška, J.; Haumont, R.; Kreisel, J. Infrared and Terahertz Studies of Polar Phonons and Magnetodielectric Effect in Multiferroic BiFeO3 Ceramics. Phys. Rev. B 2007, 75, 024403. [Google Scholar] [CrossRef]
- Lacerda, L.H.d.S.; Ribeiro, R.A.P.; de Lázaro, S.R. DFT Approaches for Smart Materials with Ferroelectric Properties. In Functional Properties of Advanced Engineering Materials and Biomolecules; Springer: Cham, Switzerland, 2021; pp. 317–334. [Google Scholar]
- Tan, P.; Huang, X.; Wang, Y.; Xing, B.; Zhang, J.; Hu, C.; Meng, X.; Xu, X.; Li, D.; Wang, X.; et al. Deciphering the Atomistic Mechanism Underlying Highly Tunable Piezoelectric Properties in Perovskite Ferroelectrics via Transition Metal Doping. Nat. Commun. 2024, 15, 10619. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Gong, F.; Ma, X.; Pan, S.; Wei, X.-K.; Kuo, C.; Yoshida, S.; Ku, Y.-C.; Wang, S.; Yang, Z.; et al. Large Enhancement of Ferroelectric Properties of Perovskite Oxides via Nitrogen Incorporation. Sci. Adv. 2025, 11, eads8830. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Kristallogr Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Eno, E.A.; Etiese, D.; Pathmanathan, K.; Agwamba, E.C.; Chukwu, U.G.; Magu, T.O.; Ikeuba, A.I.; Adeyinka, A.S.; Louis, H. Ab-Initio Study of Structural, Electronic, Phonon, X-Ray Spectroscopy, and the Optoelectronic Properties of D-Block Metals (Cr, Mn, Co, and Ni) Substitution of Barium Oxide Based-Perovskites. Chem. Phys. Impact 2023, 7, 100321. [Google Scholar] [CrossRef]
- Islam, M.Z.; Hasan, M.; Rahman, M.F.; Rhaman, M.M. Enhanced Optoelectronic Properties of Ca, Mg, Cr-Doped Half Metallic BaNpO3. SSRN Electron. J. 2023. [Google Scholar] [CrossRef]
- Kacimi-Naciri, H.; Rguiti, M.; Mabrouk, A.; Courtois, C.; Ben Achour, M.A.; Lorgouilloux, Y.; Amrousse, R.; Faska, N.; Bachar, A. DFT-Based and Experimental Study on Sr-Doped BaTiO3: Impacts on Piezoelectric and Ferroelectric Performance. Ceram. Int. 2025, in press. [Google Scholar] [CrossRef]
- Kang, K.T.; Seo, H.I.; Kwon, O.; Lee, K.; Bae, J.-S.; Chu, M.-W.; Chae, S.C.; Kim, Y.; Choi, W.S. Ferroelectricity in SrTiO3 Epitaxial Thin Films via Sr-Vacancy-Induced Tetragonality. Appl. Surf. Sci. 2020, 499, 143930. [Google Scholar] [CrossRef]
- Ou-khouya, A.; Ait Brahim, I.; Ez-Zahraouy, H.; Houba, A.; Mes-Adi, H.; Tahiri, M. First-Principles Calculations to Investigate Impact of Doping by Chalcogen Elements on the Electronic, Structural, and Optical Properties of SrTiO3 Compounds. Chem. Phys. 2024, 581, 112253. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo Program for Calculating the Properties of Solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Aguilar, E.; Hmŏk, H.; Siqueiros, J.M. Effect of La Doping on the Ferroelectric and Optical Properties of BiFeO3: A Theoretical-Experimental Study. Mater. Res. Express 2019, 6, 085098. [Google Scholar] [CrossRef]
- Peng, Y.-T.; Chiou, S.-H.; Hsiao, C.-H.; Ouyang, C.; Tu, C.-S. Remarkably Enhanced Photovoltaic Effects and First-Principles Calculations in Neodymium Doped BiFeO3. Sci. Rep. 2017, 7, 45164. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, L.; Liu, P.; Chen, F.; Chen, R. Tunable Photocatalytic and Magnetic Properties in Y and Transition Metals (TM = Mn, Co, Ni, Cu, Zn) Co-Doped BiFeO3: DFT + U Study*. Ferroelectrics 2023, 615, 212–222. [Google Scholar] [CrossRef]
- Ghosh, A.; Trujillo, D.P.; Choi, H.; Nakhmanson, S.M.; Alpay, S.P.; Zhu, J.-X. Electronic and Magnetic Properties of Lanthanum and Strontium Doped Bismuth Ferrite: A First-Principles Study. Sci. Rep. 2019, 9, 194. [Google Scholar] [CrossRef] [PubMed]
- Tan, Q.; Wang, Q.; Liu, Y. Magnetic Properties and Spontaneous Polarization of La-, Mn- and N-Doped Tetragonal BiFeO3: A First-Principles Study. Materials 2018, 11, 985. [Google Scholar] [CrossRef]
- Yang, R.; Lin, S.; Fang, X.; Gao, X.; Zeng, M.; Liu, J. First-Principles Study on the Magnetic Properties in Mg Doped BiFeO3 with and without Oxygen Vacancies. J. Appl. Phys. 2013, 114, 233912. [Google Scholar] [CrossRef]
- Ahmed, T.; Chen, A.; Yarotski, D.A.; Trugman, S.A.; Jia, Q.; Zhu, J.-X. Magnetic, Electronic, and Optical Properties of Double Perovskite Bi2FeMnO6. APL Mater. 2017, 5, 035601. [Google Scholar] [CrossRef]
- Ghosh, A.; Ahmed, T.; Yarotski, D.A.; Nakhmanson, S.M.; Zhu, J.-X. Oxygen Vacancy Effects on Double Perovskite Bi2FeMnO6: A First-Principles Study. EPL (Europhys. Lett.) 2016, 116, 57002. [Google Scholar] [CrossRef]
- Machado, P.; Scigaj, M.; Gazquez, J.; Rueda, E.; Sánchez-Díaz, A.; Fina, I.; Gibert-Roca, M.; Puig, T.; Obradors, X.; Campoy-Quiles, M.; et al. Band Gap Tuning of Solution-Processed Ferroelectric Perovskite BiFe1– xCoxO3 Thin Films. Chem. Mater. 2019, 31, 947–954. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.J.; Tan, Q.H.; Liu, Y.K. Enhanced Ferromagnetism in N-Doped BiFeO3: A First-Principles Prediction. J. Alloys Compd. 2015, 644, 30–39. [Google Scholar] [CrossRef]
- Gebhardt, J.; Rappe, A.M. Accuracy and Transferability of Ab. Initio Electronic Band Structure Calculations for Doped BiFeO3. J. Phys. Conf. Ser. 2017, 921, 012009. [Google Scholar] [CrossRef]
- Rodrigues Pela, R.; Vona, C.; Lubeck, S.; Alex, B.; Gonzalez Oliva, I.; Draxl, C. Critical Assessment of G0W0 Calculations for 2D Materials: The Example of Monolayer MoS2. NPJ Comput. Mater. 2024, 10, 77. [Google Scholar] [CrossRef]
- Umadevi, D.; Watson, G.W. Quasiparticle GW Calculations on Lead-Free Hybrid Germanium Iodide Perovskite CH3NH3GeI3 for Photovoltaic Applications. ACS Omega 2019, 4, 5661–5669. [Google Scholar] [CrossRef]
- Kim, S.-J.; Lebègue, S.; Ringe, S.; Kim, H. GW Quasiparticle Energies and Bandgaps of Two-Dimensional Materials Immersed in Water. J. Phys. Chem. Lett. 2022, 13, 7574–7582. [Google Scholar] [CrossRef]
- Biswas, T.; Jain, M. Quasiparticle Band Structure and Optical Properties of Hexagonal-YMnO3. J. Appl. Phys. 2016, 120, 155102. [Google Scholar] [CrossRef]
- Herring, C.J.; Montemore, M.M. Recent Advances in Real-Time Time-Dependent Density Functional Theory Simulations of Plasmonic Nanostructures and Plasmonic Photocatalysis. ACS Nanosci. Au 2023, 3, 269–279. [Google Scholar] [CrossRef]
- Lin, C.; Rohilla, J.; Kuo, H.; Chen, C.; Mark Chang, T.; Sone, M.; Ingole, P.P.; Lo, Y.; Hsu, Y. Density-Functional Theory Studies on Photocatalysis and Photoelectrocatalysis: Challenges and Opportunities. Solar RRL 2024, 8, 2300948. [Google Scholar] [CrossRef]
- Chen, W.; Wang, T.; Yu, C.-C.; Jing, Y.; Li, X.; Xiong, W. Small Polaron-Induced Ultrafast Ferroelectric Restoration in BiFeO3. Phys. Rev. X 2025, 15, 021046. [Google Scholar] [CrossRef]
- Hwang, J.; Feng, Z.; Charles, N.; Wang, X.R.; Lee, D.; Stoerzinger, K.A.; Muy, S.; Rao, R.R.; Lee, D.; Jacobs, R.; et al. Tuning Perovskite Oxides by Strain: Electronic Structure, Properties, and Functions in (Electro)Catalysis and Ferroelectricity. Mater. Today 2019, 31, 100–118. [Google Scholar] [CrossRef]
- Freeland, J.W.; Liu, J.; Kareev, M.; Gray, B.; Kim, J.W.; Ryan, P.; Pentcheva, R.; Chakhalian, J. Orbital Control in Strained Ultra-Thin LaNiO3 /LaAlO3 Superlattices. EPL (Europhys. Lett.) 2011, 96, 57004. [Google Scholar] [CrossRef]
- Akhade, S.A.; Kitchin, J.R. Effects of Strain, d-Band Filling, and Oxidation State on the Surface Electronic Structure and Reactivity of 3 d Perovskite Surfaces. J. Chem. Phys. 2012, 137, 084703. [Google Scholar] [CrossRef]
- Wong, F.J.; Baek, S.-H.; Chopdekar, R.V.; Mehta, V.V.; Jang, H.-W.; Eom, C.-B.; Suzuki, Y. Metallicity in LaTiO3 Thin Films Induced by Lattice Deformation. Phys. Rev. B 2010, 81, 161101. [Google Scholar] [CrossRef]
- Zhang, J.X.; He, Q.; Trassin, M.; Luo, W.; Yi, D.; Rossell, M.D.; Yu, P.; You, L.; Wang, C.H.; Kuo, C.Y.; et al. Microscopic Origin of the Giant Ferroelectric Polarization in Tetragonal-like BiFeO3. Phys. Rev. Lett. 2011, 107, 147602. [Google Scholar] [CrossRef]
- Dong, H.; Chen, C.; Wang, S.; Duan, W.; Li, J. Elastic Properties of Tetragonal BiFeO3 from First-Principles Calculations. Appl. Phys. Lett. 2013, 102, 182905. [Google Scholar] [CrossRef]
- Wei, L.; Ge, D.; Guan, L.; Guo, J.; Liu, B. Bandgap Tailoring of Tetragonal BiFeO3 with Different Magnetic Orders Calculated by First–Principles Calculations. Mater. Res. Express 2019, 6, 045907. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, J.; Sullivan, M.B.; Huan, A.; Singh, D.J.; Ong, K.P. Structural Instability of Epitaxial (001) BiFeO3 Thin Films under Tensile Strain. Sci. Rep. 2014, 4, 4631. [Google Scholar] [CrossRef]
- Xia, L.; Tybell, T.; Selbach, S.M. Bi Vacancy Formation in BiFeO3 Epitaxial Thin Films under Compressive (001)-Strain from First Principles. J. Mater. Chem. C Mater. 2019, 7, 4870–4878. [Google Scholar] [CrossRef]
- Xia, L.; Tybell, T.; Selbach, S.M. First Principles Study of Bismuth Vacancy Formation in (111)-Strained BiFeO3. Materials 2024, 17, 5397. [Google Scholar] [CrossRef]
- Dupé, B.; Prosandeev, S.; Geneste, G.; Dkhil, B.; Bellaiche, L. BiFeO3 Films under Tensile Epitaxial Strain from First Principles. Phys. Rev. Lett. 2011, 106, 237601. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Dansou, C.; Paillard, C.; He, J.; Xiang, H.; Bellaiche, L. Large Photostriction near the Phase Boundary in BiFeO3 under Varying Epitaxial Strain. Phys. Rev. B 2024, 109, 184111. [Google Scholar] [CrossRef]
- Dixit, H.; Beekman, C.; Schlepütz, C.M.; Siemons, W.; Yang, Y.; Senabulya, N.; Clarke, R.; Chi, M.; Christen, H.M.; Cooper, V.R. Understanding Strain-Induced Phase Transformations in BiFeO3 Thin Films. Adv. Sci. 2015, 2, 1500041. [Google Scholar] [CrossRef]
- Ricinschi, D.; Okuyama, M. Ab Initio Study of the Giant Spontaneous Polarization of BiFeO3: Carrier Doping Effects. Ferroelectrics 2007, 355, 101–107. [Google Scholar] [CrossRef]
- Ricinschi, D.; Yun, K.-Y.; Okuyama, M. A Mechanism for the 150 ΜC Cm−2 Polarization of BiFeO3 Films Based on First-Principles Calculations and New Structural Data. J. Phys. Condens. Matter 2006, 18, L97–L105. [Google Scholar] [CrossRef] [PubMed]
- Ritz, E.T.; Benedek, N.A. Strain Game Revisited for Complex Oxide Thin Films: Substrate-Film Thermal Expansion Mismatch in PbTiO3. Phys. Rev. Mater. 2020, 4, 084410. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, Z.; Paillard, C.; Xiang, H.; Bellaiche, L. Strain-Induced Bent Domains in Ferroelectric Nitrides. Phys. Rev. B 2024, 110, 054101. [Google Scholar] [CrossRef]
- Tu, J.; Fang, Y.-W.; Lu, Y.; Li, H.; Xi, G.; Ding, J.; Liu, X.; Liu, X.; Yang, Q.; Tian, J.; et al. Strain-Controlled Oxygen Vacancy for Robust Ferroelectric BiSmFe2O6−δ Double-Perovskite Epitaxial Thin Films. Appl. Phys. Rev. 2024, 11, 011413. [Google Scholar] [CrossRef]
- Watanabe, Y. DFT + U Accurate for Strain Effect and Overall Properties of Perovskite Oxide Ferroelectrics and Polaron. J. Appl. Phys. 2024, 135, 224103. [Google Scholar] [CrossRef]
- Waqdim, A.; Agouri, M.; Ouali, M.; Abbassi, A.; Taj, S.; Manaut, B.; El Idrissi, M. Ab Initio Insight into the Physical Properties of New Ferroelectric Perovskite Oxide Materials XGeO3 (X = Sr, Ca). Rev. Mex. De Física 2024, 70, 051603-1. [Google Scholar] [CrossRef]
- Marthinsen, A.; Grande, T.; Selbach, S.M. Microscopic Link between Electron Localization and Chemical Expansion in AMnO3 and ATiO3 Perovskites (A = Ca, Sr, Ba). J. Phys. Chem. C 2020, 124, 12922–12932. [Google Scholar] [CrossRef]
- Ricca, C.; Aschauer, U. Interplay between Polarization, Strain, and Defect Pairs in Fe-Doped SrMnO3−δ. Phys. Rev. Res. 2021, 3, 033237. [Google Scholar] [CrossRef]
- Brehm, J.A.; Neumayer, S.M.; Tao, L.; O’Hara, A.; Chyasnavichus, M.; Susner, M.A.; McGuire, M.A.; Kalinin, S.V.; Jesse, S.; Ganesh, P.; et al. Tunable Quadruple-Well Ferroelectric van Der Waals Crystals. Nat. Mater. 2020, 19, 43–48. [Google Scholar] [CrossRef]
- Ding, W.; Zhu, J.; Wang, Z.; Gao, Y.; Xiao, D.; Gu, Y.; Zhang, Z.; Zhu, W. Prediction of Intrinsic Two-Dimensional Ferroelectrics in In2Se3 and Other III2-VI3 van Der Waals Materials. Nat. Commun. 2017, 8, 14956. [Google Scholar] [CrossRef] [PubMed]
- Xue, F.; Hu, W.; Lee, K.; Lu, L.; Zhang, J.; Tang, H.; Han, A.; Hsu, W.; Tu, S.; Chang, W.; et al. Room-Temperature Ferroelectricity in Hexagonally Layered A-In2 Se3 Nanoflakes down to the Monolayer Limit. Adv. Funct. Mater. 2018, 28, 1803738. [Google Scholar] [CrossRef]
- Higashitarumizu, N.; Kawamoto, H.; Lee, C.-J.; Lin, B.-H.; Chu, F.-H.; Yonemori, I.; Nishimura, T.; Wakabayashi, K.; Chang, W.-H.; Nagashio, K. Purely In-Plane Ferroelectricity in Monolayer SnS at Room Temperature. Nat. Commun. 2020, 11, 2428. [Google Scholar] [CrossRef]
- Orlova, N.N.; Timonina, A.V.; Kolesnikov, N.N.; Deviatov, E.V. Switching Ferroelectricity in SnSe across Phase Transition. EPL (Europhys. Lett.) 2021, 135, 37002. [Google Scholar] [CrossRef]
- Chang, K.; Liu, J.; Lin, H.; Wang, N.; Zhao, K.; Zhang, A.; Jin, F.; Zhong, Y.; Hu, X.; Duan, W.; et al. Discovery of Robust In-Plane Ferroelectricity in Atomic-Thick SnTe. Science (1979) 2016, 353, 274–278. [Google Scholar] [CrossRef]
- Yuan, S.; Luo, X.; Chan, H.L.; Xiao, C.; Dai, Y.; Xie, M.; Hao, J. Room-Temperature Ferroelectricity in MoTe2 down to the Atomic Monolayer Limit. Nat. Commun. 2019, 10, 1775. [Google Scholar] [CrossRef]
- Song, Q.; Occhialini, C.A.; Ergeçen, E.; Ilyas, B.; Amoroso, D.; Barone, P.; Kapeghian, J.; Watanabe, K.; Taniguchi, T.; Botana, A.S.; et al. Evidence for a Single-Layer van Der Waals Multiferroic. Nature 2022, 602, 601–605. [Google Scholar] [CrossRef]
- Jariwala, D.; Marks, T.J.; Hersam, M.C. Mixed-Dimensional van Der Waals Heterostructures. Nat. Mater. 2017, 16, 170–181. [Google Scholar] [CrossRef] [PubMed]
- Kruse, M.; Petralanda, U.; Gjerding, M.N.; Jacobsen, K.W.; Thygesen, K.S.; Olsen, T. Two-Dimensional Ferroelectrics from High Throughput Computational Screening. NPJ Comput. Mater. 2023, 9, 45. [Google Scholar] [CrossRef]
- Li, H.F.; Zhang, G.H.; Zheng, Y.; Wang, B.; Chen, W.J. Ab Initio Study on Mechanical-Bending-Induced Ferroelectric Phase Transition in Ultrathin Perovskite Nanobelts. Acta Mater. 2014, 76, 472–481. [Google Scholar] [CrossRef]
- Sánchez-Santolino, G.; Rouco, V.; Puebla, S.; Aramberri, H.; Zamora, V.; Cabero, M.; Cuellar, F.A.; Munuera, C.; Mompean, F.; Garcia-Hernandez, M.; et al. A 2D Ferroelectric Vortex Pattern in Twisted BaTiO3 Freestanding Layers. Nature 2024, 626, 529–534. [Google Scholar] [CrossRef]
- Dong, G.; Li, S.; Yao, M.; Zhou, Z.; Zhang, Y.-Q.; Han, X.; Luo, Z.; Yao, J.; Peng, B.; Hu, Z.; et al. Super-Elastic Ferroelectric Single-Crystal Membrane with Continuous Electric Dipole Rotation. Science (1979) 2019, 366, 475–479. [Google Scholar] [CrossRef]
- Huang, J.-K.; Wan, Y.; Shi, J.; Zhang, J.; Wang, Z.; Wang, W.; Yang, N.; Liu, Y.; Lin, C.-H.; Guan, X.; et al. High-κ Perovskite Membranes as Insulators for Two-Dimensional Transistors. Nature 2022, 605, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.J.; Han, K.; Huang, K.; Ye, C.; Wen, W.; Zhu, R.; Zhu, R.; Xu, J.; Yu, T.; Gao, P.; et al. Van Der Waals Integration of High-κ Perovskite Oxides and Two-Dimensional Semiconductors. Nat. Electron. 2022, 5, 233–240. [Google Scholar] [CrossRef]
- Puebla, S.; Pucher, T.; Rouco, V.; Sanchez-Santolino, G.; Xie, Y.; Zamora, V.; Cuellar, F.A.; Mompean, F.J.; Leon, C.; Island, J.O.; et al. Combining Freestanding Ferroelectric Perovskite Oxides with Two-Dimensional Semiconductors for High Performance Transistors. Nano Lett. 2022, 22, 7457–7466. [Google Scholar] [CrossRef]
- Deeksha; Kour, P.; Ahmed, I.; Sunny; Sharma, S.K.; Yadav, K.; Mishra, Y.K. Transition Metal-based Perovskite Oxides: Emerging Electrocatalysts for Oxygen Evolution Reaction. ChemCatChem 2023, 15, e202300040. [Google Scholar] [CrossRef]
- Collins, J.B.; Levine, H. Diffuse Interface Model of Diffusion-Limited Crystal Growth. Phys. Rev. B 1985, 31, 6119–6122. [Google Scholar] [CrossRef]
- Chen, L.-Q.; Yang, W. Computer Simulation of the Domain Dynamics of a Quenched System with a Large Number of Nonconserved Order Parameters: The Grain-Growth Kinetics. Phys. Rev. B 1994, 50, 15752–15756. [Google Scholar] [CrossRef] [PubMed]
- Aranson, I.S.; Kalatsky, V.A.; Vinokur, V.M. Continuum Field Description of Crack Propagation. Phys. Rev. Lett. 2000, 85, 118–121. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.L.; Hu, S.Y.; Liu, Z.K.; Chen, L.Q. Phase-Field Model of Domain Structures in Ferroelectric Thin Films. Appl. Phys. Lett. 2001, 78, 3878–3880. [Google Scholar] [CrossRef]
- Peng, B.; Peng, R.-C.; Zhang, Y.-Q.; Dong, G.; Zhou, Z.; Zhou, Y.; Li, T.; Liu, Z.; Luo, Z.; Wang, S.; et al. Phase Transition Enhanced Superior Elasticity in Freestanding Single-Crystalline Multiferroic BiFeO3 Membranes. Sci. Adv. 2020, 6, eaba5847. [Google Scholar] [CrossRef]
- Han, L.; Fang, Y.; Zhao, Y.; Zang, Y.; Gu, Z.; Nie, Y.; Pan, X. Giant Uniaxial Strain Ferroelectric Domain Tuning in Freestanding PbTiO3 Films. Adv. Mater. Interfaces 2020, 7, 1901604. [Google Scholar] [CrossRef]
- Xu, R.; Huang, J.; Barnard, E.S.; Hong, S.S.; Singh, P.; Wong, E.K.; Jansen, T.; Harbola, V.; Xiao, J.; Wang, B.Y.; et al. Strain-Induced Room-Temperature Ferroelectricity in SrTiO3 Membranes. Nat. Commun. 2020, 11, 3141. [Google Scholar] [CrossRef]
- Dong, G.; Hu, Y.; Guo, C.; Wu, H.; Liu, H.; Peng, R.; Xian, D.; Mao, Q.; Dong, Y.; Zhao, Y.; et al. Self-Assembled Epitaxial Ferroelectric Oxide Nanospring with Super-Scalability. Adv. Mater. 2022, 34, 2108419. [Google Scholar] [CrossRef]
- Kang, K.T.; Corey, Z.J.; Hwang, J.; Sharma, Y.; Paudel, B.; Roy, P.; Collins, L.; Wang, X.; Lee, J.W.; Oh, Y.S.; et al. Heterogeneous Integration of Freestanding Bilayer Oxide Membrane for Multiferroicity. Adv. Sci. 2023, 10, 2207481. [Google Scholar] [CrossRef]
- Dong, G.; Li, S.; Li, T.; Wu, H.; Nan, T.; Wang, X.; Liu, H.; Cheng, Y.; Zhou, Y.; Qu, W.; et al. Periodic Wrinkle-Patterned Single-Crystalline Ferroelectric Oxide Membranes with Enhanced Piezoelectricity. Adv. Mater. 2020, 32, 2004477. [Google Scholar] [CrossRef]
- Chen, T.; Wang, B.; Zhu, Y.; Zhuang, S.; Chen, L.-Q.; Hu, J.-M. Analytical Model and Dynamical Phase-Field Simulation of Terahertz Transmission across Ferroelectrics. Phys. Rev. B 2024, 109, 094305. [Google Scholar] [CrossRef]
- Guo, C.; Yang, H.; Dong, S.; Tang, S.; Wang, J.; Wang, X.; Huang, H. Advancing Energy-Storage Performance in Freestanding Ferroelectric Thin Films: Insights from Phase-Field Simulations. Adv. Electron. Mater. 2024, 10, 2400001. [Google Scholar] [CrossRef]
- Nelson, C.T.; Winchester, B.; Zhang, Y.; Kim, S.-J.; Melville, A.; Adamo, C.; Folkman, C.M.; Baek, S.-H.; Eom, C.-B.; Schlom, D.G.; et al. Spontaneous Vortex Nanodomain Arrays at Ferroelectric Heterointerfaces. Nano Lett. 2011, 11, 828–834. [Google Scholar] [CrossRef] [PubMed]
- Jia, C.-L.; Urban, K.W.; Alexe, M.; Hesse, D.; Vrejoiu, I. Direct Observation of Continuous Electric Dipole Rotation in Flux-Closure Domains in Ferroelectric Pb(Zr, Ti)O3. Science (1979) 2011, 331, 1420–1423. [Google Scholar] [CrossRef]
- Tang, Y.L.; Zhu, Y.L.; Ma, X.L.; Borisevich, A.Y.; Morozovska, A.N.; Eliseev, E.A.; Wang, W.Y.; Wang, Y.J.; Xu, Y.B.; Zhang, Z.D.; et al. Observation of a periodic array of flux-closure quadrants in strained ferroelectric PbTiO3 films. Science 2015, 348, 547–551. [Google Scholar] [CrossRef]
- Yadav, A.K.; Nelson, C.T.; Hsu, S.L.; Hong, Z.; Clarkson, J.D.; Schlepütz, C.M.; Damodaran, A.R.; Shafer, P.; Arenholz, E.; Dedon, L.R.; et al. Observation of Polar Vortices in Oxide Superlattices. Nature 2016, 530, 198–201. [Google Scholar] [CrossRef]
- Das, S.; Tang, Y.L.; Hong, Z.; Gonçalves, M.A.P.; McCarter, M.R.; Klewe, C.; Nguyen, K.X.; Gómez-Ortiz, F.; Shafer, P.; Arenholz, E.; et al. Observation of Room-Temperature Polar Skyrmions. Nature 2019, 568, 368–372. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Stoica, V.A.; Paściak, M.; Zhu, Y.; Yuan, Y.; Yang, T.; McCarter, M.R.; Das, S.; Yadav, A.K.; Park, S.; et al. Subterahertz Collective Dynamics of Polar Vortices. Nature 2021, 592, 376–380. [Google Scholar] [CrossRef]
- Wang, Y.J.; Feng, Y.P.; Zhu, Y.L.; Tang, Y.L.; Yang, L.X.; Zou, M.J.; Geng, W.R.; Han, M.J.; Guo, X.W.; Wu, B.; et al. Polar Meron Lattice in Strained Oxide Ferroelectrics. Nat. Mater. 2020, 19, 881–886. [Google Scholar] [CrossRef]
- Rusu, D.; Peters, J.J.P.; Hase, T.P.A.; Gott, J.A.; Nisbet, G.A.A.; Strempfer, J.; Haskel, D.; Seddon, S.D.; Beanland, R.; Sanchez, A.M.; et al. Ferroelectric Incommensurate Spin Crystals. Nature 2022, 602, 240–244. [Google Scholar] [CrossRef]
- Zhao, H.J.; Chen, P.; Prosandeev, S.; Artyukhin, S.; Bellaiche, L. Dzyaloshinskii–Moriya-like Interaction in Ferroelectrics and Antiferroelectrics. Nat. Mater. 2021, 20, 341–345. [Google Scholar] [CrossRef]
- Cao, C.; Lu, Z.; Wang, L.; Li, L.; Deng, D.; Liao, D.; Mo, C. Ce-Doped BiFeO3 as a Photocatalyst to Enhance Photo-Fenton Degradation of Tetracycline. J. Photochem. Photobiol. A Chem. 2024, 446, 115161. [Google Scholar] [CrossRef]
- Zhang, N.; Chen, D.; Niu, F.; Wang, S.; Qin, L.; Huang, Y. Enhanced Visible Light Photocatalytic Activity of Gd-Doped BiFeO3 Nanoparticles and Mechanism Insight. Sci. Rep. 2016, 6, 26467. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Kang, Y.; Liu, J.; Yao, T.; Qiu, J.; Du, P.; Huang, B.; Hu, W.; Liang, Y.; Xie, T.; et al. Gradient Tungsten-Doped Bi3TiNbO9 Ferroelectric Photocatalysts with Additional Built-in Electric Field for Efficient Overall Water Splitting. Nat. Commun. 2023, 14, 7948. [Google Scholar] [CrossRef]
- Billah, A.; Anju, A.N.; Hirose, F.; Ahmmad, B. Visible-Light-Driven Oxygen Evolution by a BaTiO3 Based Ferroelectric Photocatalyst via Water Splitting. J. Mater. Chem. A Mater. 2024, 12, 15885–15892. [Google Scholar] [CrossRef]
- Zhang, Z.; Dai, Y.; Li, Z.; Lu, L.; Zhang, X.; Fu, K.; Xu, X.; Tian, W.; Jia, C.; Jiang, Y. Growth Modulation of Super-Tetragonal PbTiO3 Thin Films with Self-Assembled Nanocolumn Structures. Adv. Electron. Mater. 2021, 7, 2100547. [Google Scholar] [CrossRef]
- Enriquez, E.; Li, Q.; Bowlan, P.; Lu, P.; Zhang, B.; Li, L.; Wang, H.; Taylor, A.J.; Yarotski, D.; Prasankumar, R.P.; et al. Induced Ferroelectric Phases in SrTiO3 by a Nanocomposite Approach. Nanoscale 2020, 12, 18193–18199. [Google Scholar] [CrossRef] [PubMed]
- Harrington, S.A.; Zhai, J.; Denev, S.; Gopalan, V.; Wang, H.; Bi, Z.; Redfern, S.A.T.; Baek, S.-H.; Bark, C.W.; Eom, C.-B.; et al. Thick Lead-Free Ferroelectric Films with High Curie Temperatures through Nanocomposite-Induced Strain. Nat. Nanotechnol. 2011, 6, 491–495. [Google Scholar] [CrossRef]
- Li, W.; Zhang, W.; Wang, L.; Gu, J.; Chen, A.; Zhao, R.; Liang, Y.; Guo, H.; Tang, R.; Wang, C.; et al. Vertical Interface Induced Dielectric Relaxation in Nanocomposite (BaTiO3)1−x:(Sm2O3)x Thin Films. Sci. Rep. 2015, 5, 11335. [Google Scholar] [CrossRef]
- Goian, V.; Held, R.; Bousquet, E.; Yuan, Y.; Melville, A.; Zhou, H.; Gopalan, V.; Ghosez, P.; Spaldin, N.A.; Schlom, D.G.; et al. Making EuO Multiferroic by Epitaxial Strain Engineering. Commun. Mater. 2020, 1, 74. [Google Scholar] [CrossRef]
- Song, Y.; Xu, K.; Wang, J.; Huang, H. Thickness-Dependent Dielectric Properties in Doped Relaxor Films by the Phase-Field Model. ACS Appl. Electron. Mater. 2024, 6, 6477–6483. [Google Scholar] [CrossRef]
- Fedeli, P.; Kamlah, M.; Frangi, A. Phase-Field Modeling of Domain Evolution in Ferroelectric Materials in the Presence of Defects. Smart Mater. Struct. 2019, 28, 035021. [Google Scholar] [CrossRef]
- Wang, S.; Yi, M.; Xu, B.-X. A Phase-Field Model of Relaxor Ferroelectrics Based on Random Field Theory. Int. J. Solids Struct. 2016, 83, 142–153. [Google Scholar] [CrossRef]
- Wu, H.H.; Wang, J.; Cao, S.G.; Zhang, T.Y. Effect of Dislocation Walls on the Polarization Switching of a Ferroelectric Single Crystal. Appl. Phys. Lett. 2013, 102, 232904. [Google Scholar] [CrossRef]
- Li, Y.L.; Hu, S.Y.; Choudhury, S.; Baskes, M.I.; Saxena, A.; Lookman, T.; Jia, Q.X.; Schlom, D.G.; Chen, L.Q. Influence of Interfacial Dislocations on Hysteresis Loops of Ferroelectric Films. J. Appl. Phys. 2008, 104, 104110. [Google Scholar] [CrossRef]
- Wu, H.H.; Wang, J.; Cao, S.G.; Chen, L.Q.; Zhang, T.Y. Micro-/Macro-Responses of a Ferroelectric Single Crystal with Domain Pinning and Depinning by Dislocations. J. Appl. Phys. 2013, 114, 164108. [Google Scholar] [CrossRef]
- Wang, J.; Shu, W.; Fang, H.; Kamlah, M. Phase Field Simulations of the Poling Process and Nonlinear Behavior of Ferroelectric Polycrystals with Semiconducting Grain Boundaries. Smart Mater. Struct. 2014, 23, 095016. [Google Scholar] [CrossRef]
- Vidyasagar, A.; Tan, W.L.; Kochmann, D.M. Predicting the Effective Response of Bulk Polycrystalline Ferroelectric Ceramics via Improved Spectral Phase Field Methods. J. Mech. Phys. Solids 2017, 106, 133–151. [Google Scholar] [CrossRef]
- Li, L.; Cheng, X.; Blum, T.; Huyan, H.; Zhang, Y.; Heikes, C.; Yan, X.; Gadre, C.; Aoki, T.; Xu, M.; et al. Observation of Strong Polarization Enhancement in Ferroelectric Tunnel Junctions. Nano Lett. 2019, 19, 6812–6818. [Google Scholar] [CrossRef]
- Li, Y.L.; Hu, S.Y.; Liu, Z.K.; Chen, L.Q. Effect of Substrate Constraint on the Stability and Evolution of Ferroelectric Domain Structures in Thin Films. Acta Mater. 2002, 50, 395–411. [Google Scholar] [CrossRef]
- Li, Y.L.; Chen, L.Q. Temperature-Strain Phase Diagram for BaTiO3 Thin Films. Appl. Phys. Lett. 2006, 88, 072905. [Google Scholar] [CrossRef]
- Li, Y.L.; Cross, L.E.; Chen, L.Q. A Phenomenological Thermodynamic Potential for BaTiO3 Single Crystals. J. Appl. Phys. 2005, 98, 064101. [Google Scholar] [CrossRef]
- Li, Y.L.; Choudhury, S.; Liu, Z.K.; Chen, L.Q. Effect of External Mechanical Constraints on the Phase Diagram of Epitaxial PbZr1−xTixO3 Thin Films—Thermodynamic Calculations and Phase-Field Simulations. Appl. Phys. Lett. 2003, 83, 1608–1610. [Google Scholar] [CrossRef]
- Li, Y.L.; Hu, S.Y.; Chen, L.Q. Ferroelectric Domain Morphologies of (001) PbZr1−xTixO3 Epitaxial Thin Films. J. Appl. Phys. 2005, 97, 034112. [Google Scholar] [CrossRef]
- Karthik, J.; Martin, L.W. Pyroelectric Properties of Polydomain Epitaxial Pb(Zr1−x,Tix)O3 Thin Films. Phys. Rev. B 2011, 84, 024102. [Google Scholar] [CrossRef]
- Zhang, J.X.; Li, Y.L.; Wang, Y.; Liu, Z.K.; Chen, L.Q.; Chu, Y.H.; Zavaliche, F.; Ramesh, R. Effect of Substrate-Induced Strains on the Spontaneous Polarization of Epitaxial BiFeO3 Thin Films. J. Appl. Phys. 2007, 101, 114105. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, F.; Chen, Z.; Liu, J.-M.; Chen, L.-Q. Presence of a Purely Tetragonal Phase in Ultrathin BiFeO3 Films: Thermodynamics and Phase-Field Simulations. Acta Mater. 2020, 183, 110–117. [Google Scholar] [CrossRef]
- Vasudevarao, A.; Kumar, A.; Tian, L.; Haeni, J.H.; Li, Y.L.; Eklund, C.-J.; Jia, Q.X.; Uecker, R.; Reiche, P.; Rabe, K.M.; et al. Multiferroic Domain Dynamics in Strained Strontium Titanate. Phys. Rev. Lett. 2006, 97, 257602. [Google Scholar] [CrossRef]
- Li, Y.L.; Choudhury, S.; Haeni, J.H.; Biegalski, M.D.; Vasudevarao, A.; Sharan, A.; Ma, H.Z.; Levy, J.; Gopalan, V.; Trolier-McKinstry, S.; et al. Phase Transitions and Domain Structures in Strained Pseudocubic (100) SrTiO3 Thin Films. Phys. Rev. B 2006, 73, 184112. [Google Scholar] [CrossRef]
- Bousquet, E.; Spaldin, N.A.; Ghosez, P. Strain-Induced Ferroelectricity in Simple Rocksalt Binary Oxides. Phys. Rev. Lett. 2010, 104, 037601. [Google Scholar] [CrossRef]
- Kumar, P.; Hoffmann, M.; Nonaka, A.; Salahuddin, S.; Yao, Z. 3D Ferroelectric Phase Field Simulations of Polycrystalline Multi-Phase Hafnia and Zirconia Based Ultra-Thin Films. Adv. Electron. Mater. 2024, 10, 2400085. [Google Scholar] [CrossRef]
- Kim, T.; Kim, G.; Lee, Y.K.; Ko, D.H.; Hwang, J.; Lee, S.; Shin, H.; Jeong, Y.; Jung, S.; Jeon, S. The Opportunity of Negative Capacitance Behavior in Flash Memory for High-Density and Energy-Efficient In-Memory Computing Applications. Adv. Funct. Mater. 2023, 33, 2208525. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, X.; Wang, J.; Huang, H. Electric-Field-Induced Crystallization of Hf0.5Zr0.5O2 Thin Film Based on Phase-Field Modeling. NPJ Quantum Mater. 2024, 9, 44. [Google Scholar] [CrossRef]
- Wang, J.-J.; Su, Y.-J.; Wang, B.; Ouyang, J.; Ren, Y.-H.; Chen, L.-Q. Strain Engineering of Dischargeable Energy Density of Ferroelectric Thin-Film Capacitors. Nano Energy 2020, 72, 104665. [Google Scholar] [CrossRef]
- Hao, L.; Yang, Y.; Huan, Y.; Cheng, H.; Zhao, Y.-Y.; Wang, Y.; Yan, J.; Ren, W.; Ouyang, J. Achieving a High Dielectric Tunability in Strain-Engineered Tetragonal K0.5Na0.5NbO3 Films. NPJ Comput. Mater. 2021, 7, 62. [Google Scholar] [CrossRef]
- Chu, P.; Chen, D.P.; Wang, Y.L.; Xie, Y.L.; Yan, Z.B.; Wan, J.G.; Liu, J.-M.; Li, J.Y. Kinetics of 90° Domain Wall Motions and High Frequency Mesoscopic Dielectric Response in Strained Ferroelectrics: A Phase-Field Simulation. Sci. Rep. 2014, 4, 5007. [Google Scholar] [CrossRef]
- Sheng, G.; Zhang, J.X.; Li, Y.L.; Choudhury, S.; Jia, Q.X.; Liu, Z.K.; Chen, L.Q. Domain Stability of PbTiO3 Thin Films under Anisotropic Misfit Strains: Phase-Field Simulations. J. Appl. Phys. 2008, 104, 054105. [Google Scholar] [CrossRef]
- Sheng, G.; Zhang, J.X.; Li, Y.L.; Choudhury, S.; Jia, Q.X.; Liu, Z.K.; Chen, L.Q. Misfit Strain–Misfit Strain Diagram of Epitaxial BaTiO3 Thin Films: Thermodynamic Calculations and Phase-Field Simulations. Appl. Phys. Lett. 2008, 93, 232904. [Google Scholar] [CrossRef]
- Winchester, B.; Wu, P.; Chen, L.Q. Phase-Field Simulation of Domain Structures in Epitaxial BiFeO3 Films on Vicinal Substrates. Appl. Phys. Lett. 2011, 99, 052903. [Google Scholar] [CrossRef]
- Lu, D.; Hikita, Y.; Baek, D.J.; Merz, T.A.; Sato, H.; Kim, B.; Yajima, T.; Bell, C.; Vailionis, A.; Kourkoutis, L.F.; et al. Strain Tuning in Complex Oxide Epitaxial Films Using an Ultrathin Strontium Aluminate Buffer Layer. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2018, 12, 1700339. [Google Scholar] [CrossRef]
- Deng, X.; Chen, C.; Chen, D.; Cai, X.; Yin, X.; Xu, C.; Sun, F.; Li, C.; Li, Y.; Xu, H.; et al. Strain Engineering of Epitaxial Oxide Heterostructures beyond Substrate Limitations. Matter 2021, 4, 1323–1334. [Google Scholar] [CrossRef]
- People, R.; Bean, J.C. Calculation of Critical Layer Thickness versus Lattice Mismatch for GexSi1−x/Si Strained-Layer Heterostructures. Appl. Phys. Lett. 1985, 47, 322–324. [Google Scholar] [CrossRef]
- Wang, J.-J.; Wang, Y.; Ihlefeld, J.F.; Hopkins, P.E.; Chen, L.-Q. Tunable Thermal Conductivity via Domain Structure Engineering in Ferroelectric Thin Films: A Phase-Field Simulation. Acta Mater. 2016, 111, 220–231. [Google Scholar] [CrossRef]
- Damodaran, A.R.; Agar, J.C.; Pandya, S.; Chen, Z.; Dedon, L.; Xu, R.; Apgar, B.; Saremi, S.; Martin, L.W. New Modalities of Strain-Control of Ferroelectric Thin Films. J. Phys. Condens. Matter 2016, 28, 263001. [Google Scholar] [CrossRef]
- Lu, H.; Tan, Y.; Richarz, L.; He, J.; Wang, B.; Meier, D.; Chen, L.; Gruverman, A. Electromechanics of Domain Walls in Uniaxial Ferroelectrics. Adv. Funct. Mater. 2023, 33, 2213684. [Google Scholar] [CrossRef]
- Agar, J.C.; Damodaran, A.R.; Okatan, M.B.; Kacher, J.; Gammer, C.; Vasudevan, R.K.; Pandya, S.; Dedon, L.R.; Mangalam, R.V.K.; Velarde, G.A.; et al. Highly Mobile Ferroelastic Domain Walls in Compositionally Graded Ferroelectric Thin Films. Nat. Mater. 2016, 15, 549–556. [Google Scholar] [CrossRef] [PubMed]
- Shi, Q.; Parsonnet, E.; Cheng, X.; Fedorova, N.; Peng, R.-C.; Fernandez, A.; Qualls, A.; Huang, X.; Chang, X.; Zhang, H.; et al. The Role of Lattice Dynamics in Ferroelectric Switching. Nat. Commun. 2022, 13, 1110. [Google Scholar] [CrossRef]
- Gurung, A.; Ishtiyaq, M.F.; Alpay, S.P.; Mangeri, J.; Nakhmanson, S. Extrinsic Dielectric Response Due to Domain Wall Motion in Ferroelectric BaTiO3. Comput. Mater. Today 2025, 5, 100016. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Z.; Yue, Y.; Chen, T.; Yan, Z.; Jiang, Q.; Yang, B.; Eriksson, M.; Tang, J.; Zhang, D.; et al. Terahertz Reading of Ferroelectric Domain Wall Dielectric Switching. ACS Appl. Mater. Interfaces 2021, 13, 12622–12628. [Google Scholar] [CrossRef]
- Sluka, T.; Tagantsev, A.K.; Damjanovic, D.; Gureev, M.; Setter, N. Enhanced Electromechanical Response of Ferroelectrics Due to Charged Domain Walls. Nat. Commun. 2012, 3, 748. [Google Scholar] [CrossRef]
- Zhou, L.; Puntigam, L.; Lunkenheimer, P.; Bourret, E.; Yan, Z.; Kézsmárki, I.; Meier, D.; Krohns, S.; Schultheiß, J.; Evans, D.M. Post-Synthesis Tuning of Dielectric Constant via Ferroelectric Domain Wall Engineering. Matter 2024, 7, 2996–3006. [Google Scholar] [CrossRef]
- Hadjimichael, M.; Li, Y.; Yedra, L.; Dkhil, B.; Zubko, P. Domain Structure and Dielectric Properties of Metal-Ferroelectric Superlattices with Asymmetric Interfaces. Phys. Rev. Mater. 2020, 4, 094415. [Google Scholar] [CrossRef]
- Ion, V.; Craciun, F.; Scarisoreanu, N.D.; Moldovan, A.; Andrei, A.; Birjega, R.; Ghica, C.; Di Pietrantonio, F.; Cannata, D.; Benetti, M.; et al. Impact of Thickness Variation on Structural, Dielectric and Piezoelectric Properties of (Ba, Ca)(Ti, Zr)O3 Epitaxial Thin Films. Sci. Rep. 2018, 8, 2056. [Google Scholar] [CrossRef] [PubMed]
- Guennou, M.; Bouvier, P.; Chen, G.S.; Dkhil, B.; Haumont, R.; Garbarino, G.; Kreisel, J. Multiple High-Pressure Phase Transitions in BiFeO3. Phys. Rev. B 2011, 84, 174107. [Google Scholar] [CrossRef]
- Yang, Y.; Infante, I.C.; Dkhil, B.; Bellaiche, L. Strain Effects on Multiferroic BiFeO3 Films. Comptes Rendus Phys. 2015, 16, 193–203. [Google Scholar] [CrossRef]
- Saito, K.; Ulyanenkov, A.; Grossmann, V.; Ress, H.; Bruegemann, L.; Ohta, H.; Kurosawa, T.; Ueki, S.; Funakubo, H. Structural Characterization of BiFeO3 Thin Films by Reciprocal Space Mapping. Jpn. J. Appl. Phys. 2006, 45, 7311. [Google Scholar] [CrossRef]
- Yao, J.; Yang, Y.; Ge, W.; Li, J.; Viehland, D. Domain Evolution in PbMg1/3Nb2/3O3-60at%PbTiO3 with Temperature and Electric Field. J. Am. Ceram. Soc. 2011, 94, 2479–2482. [Google Scholar] [CrossRef]
- Luo, J.; Maggard, P.A. Hydrothermal Synthesis and Photocatalytic Activities of SrTiO3-Coated Fe2O3 and BiFeO3. Adv. Mater. 2006, 18, 514–517. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Influence of Strain and Oxygen Vacancies on the Magnetoelectric Properties of Multiferroic Bismuth Ferrite. Phys. Rev. B 2005, 71, 224103. [Google Scholar] [CrossRef]
- Song, J.; Kim, T.L.; Lee, J.; Cho, S.Y.; Cha, J.; Jeong, S.Y.; An, H.; Kim, W.S.; Jung, Y.-S.; Park, J.; et al. Domain-Engineered BiFeO3 Thin-Film Photoanodes for Highly Enhanced Ferroelectric Solar Water Splitting. Nano Res. 2018, 11, 642–655. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).