Anisotropy in the Creep–Fatigue Behaviors of a Directionally Solidified Ni-Based Superalloy: Damage Mechanisms and Life Assessment
Abstract
1. Introduction
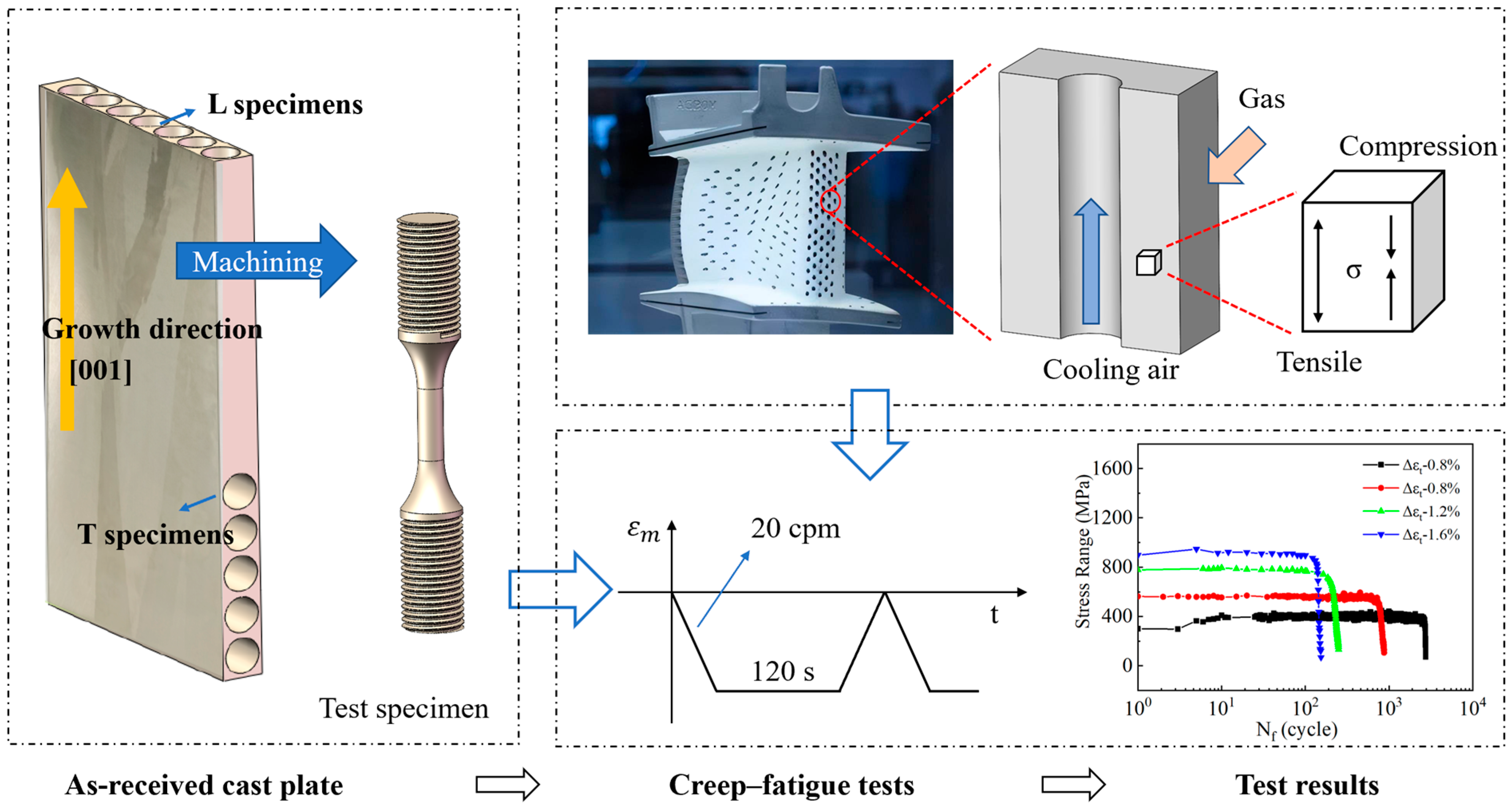
2. Materials and Methods
2.1. Materials and Heat Treatment
2.2. Creep–Fatigue Testing
2.3. Microstructural Characterization
3. Results
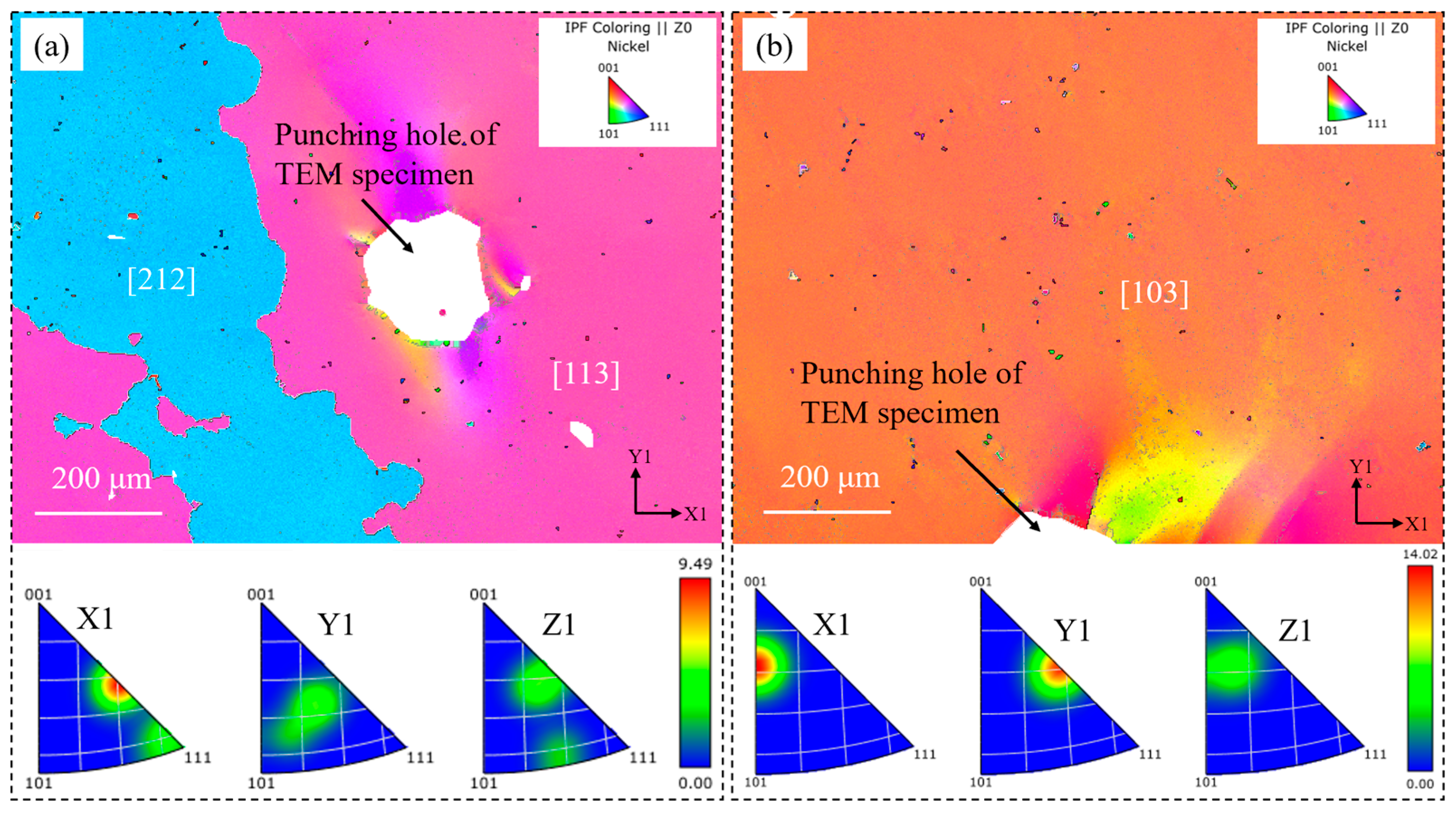
3.1. Original Microstructure
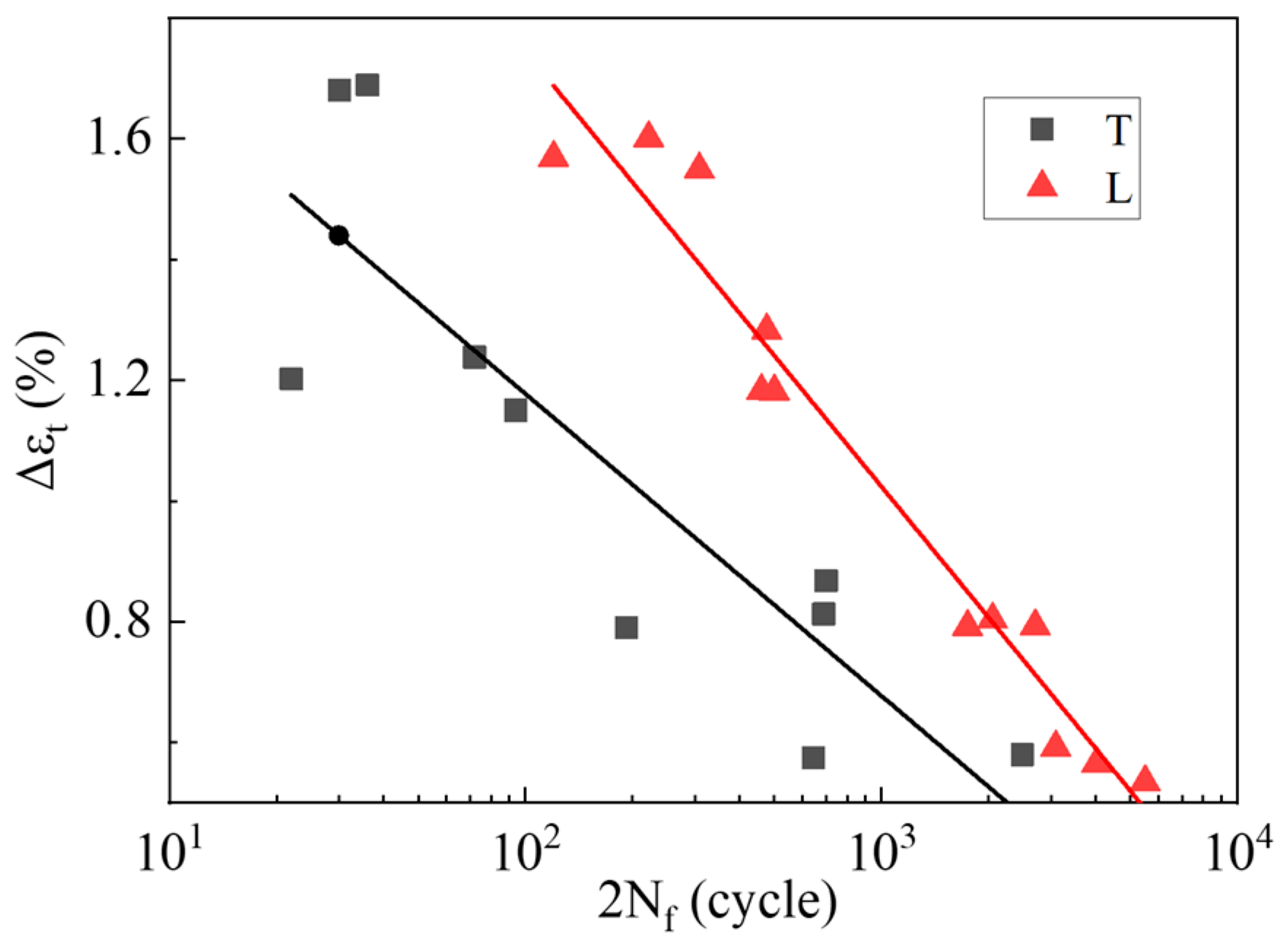
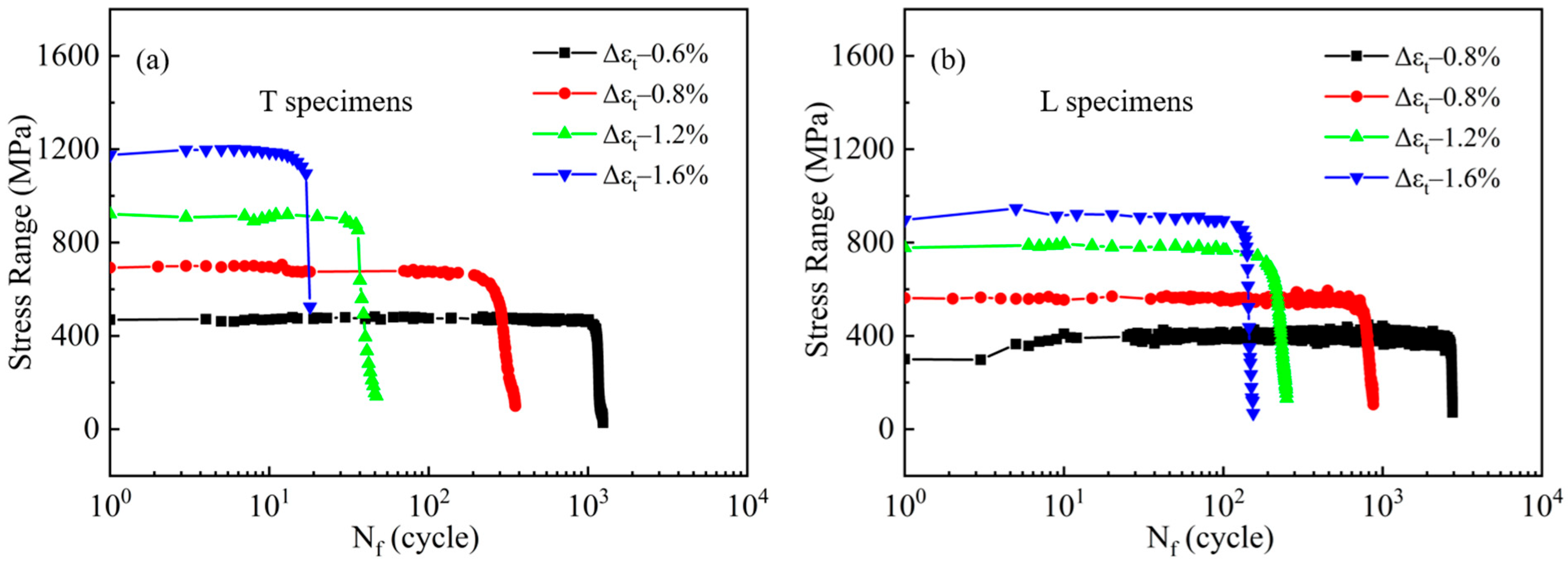
3.2. Creep–Fatigue Properties
3.3. Fracture Morphology
4. Discussion
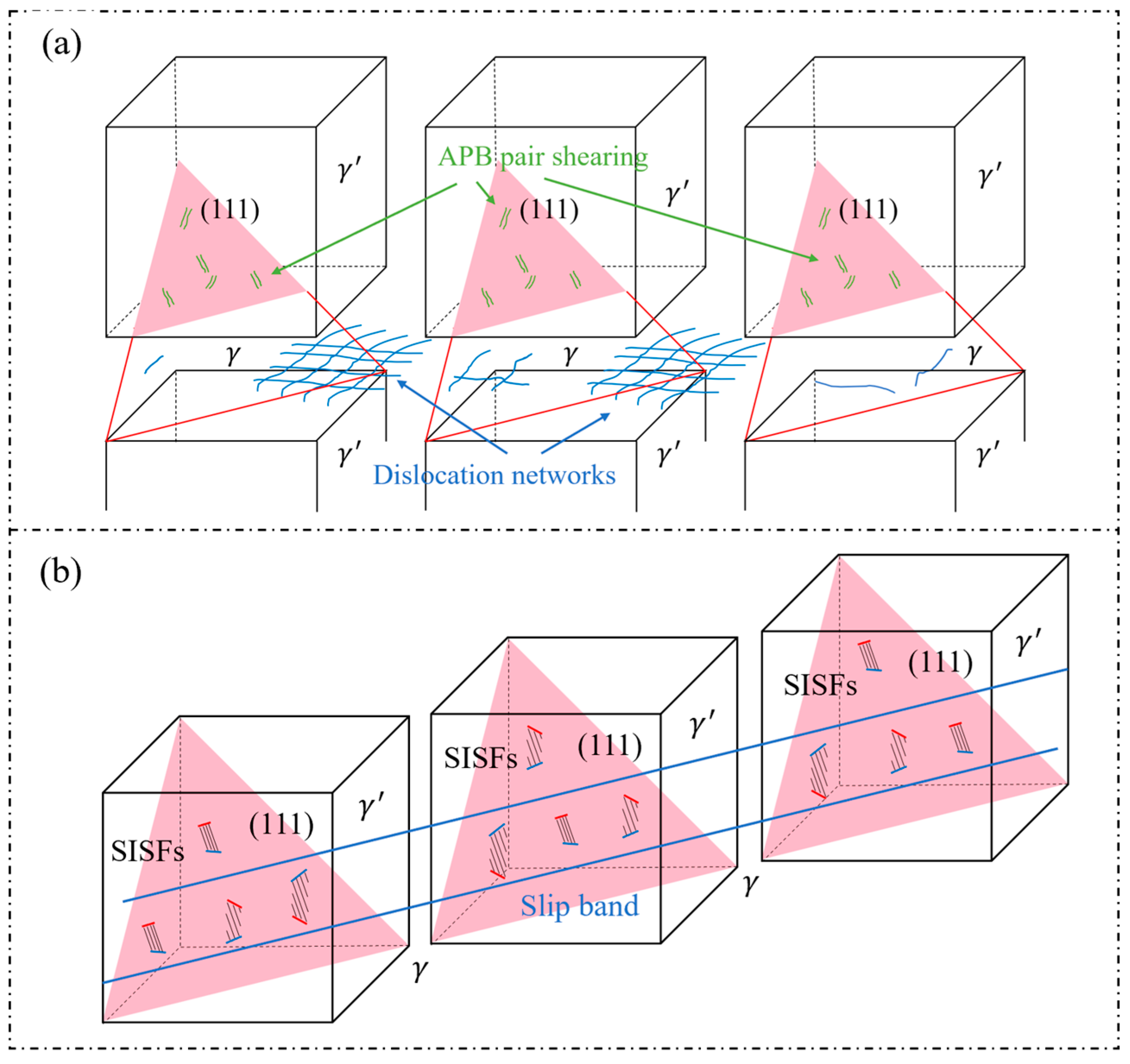
4.1. Damage Mechanisms
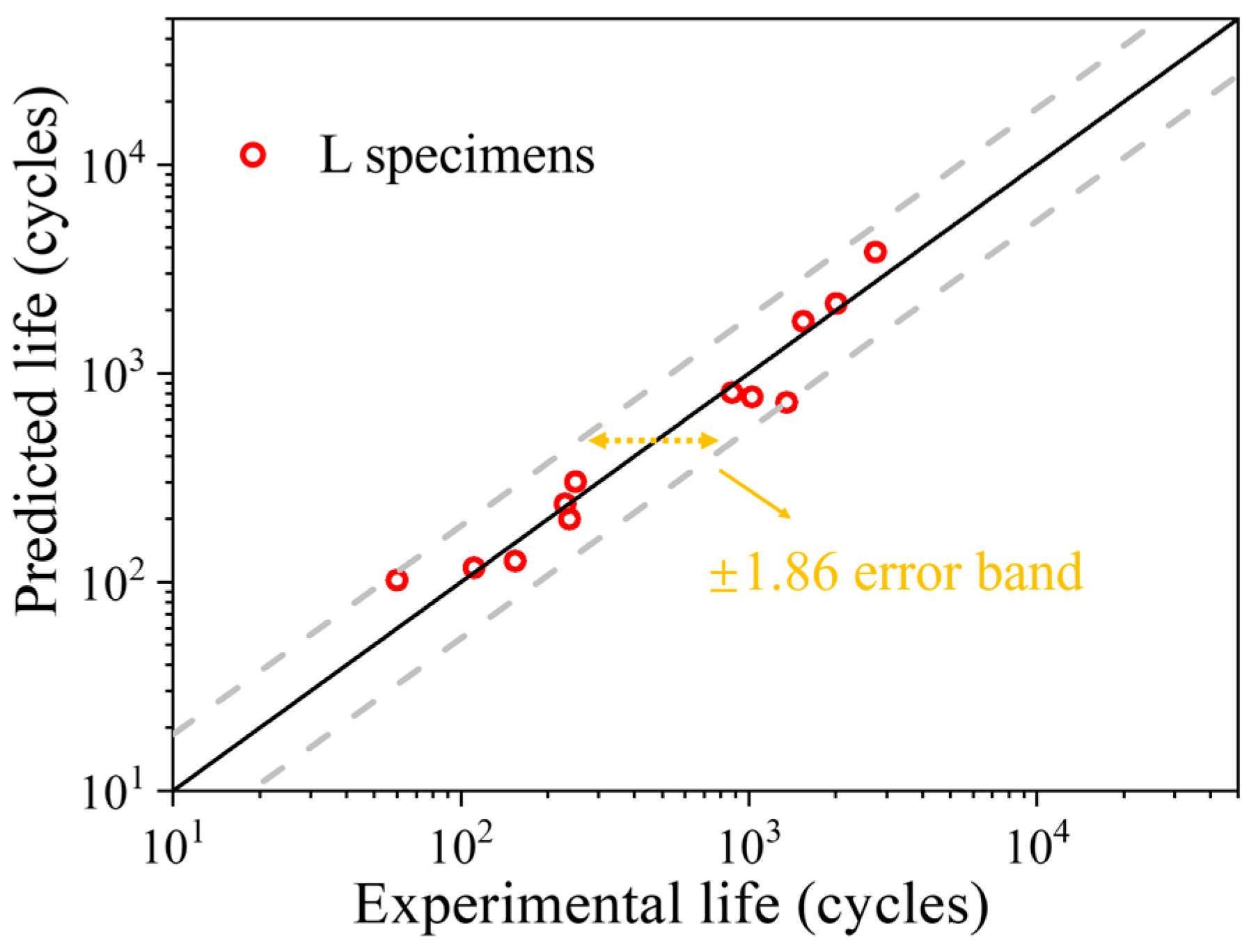
4.2. Life Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| APB | Antiphase boundary |
| SISFs | Superlattice intrinsic stacking faults |
| T | Transverse |
| L | Longitudinal |
| OM | Optical microscope |
| SEM | Scanning electron microscope |
| EDS | Energy-dispersive spectroscopy |
| TEM | Transmission electron microscope |
| EBSD | Electron Backscatter Diffraction |
| MSFCs | Microstructural small fatigue cracks |
| SADE | Stress-assisted dynamic embrittlement |
| CDM | Continuum damage mechanics |
References
- Sun, D.B.; Ma, G.L.; Wan, Z.H.; Gao, J.H. Study on creep-fatigue interaction mechanism and life prediction of aero-engine turbine blade. Eng. Failure Anal. 2023, 154, 107715. [Google Scholar] [CrossRef]
- Abu, A.O.; Eshati, S.; Laskaridis, P.; Singh, R. Aero-engine turbine blade life assessment using the Neu/Sehitoglu damage model. Int. J. Fatigue 2014, 61, 160–169. [Google Scholar] [CrossRef]
- Sajjadi, S.A.; Nategh, S. A high temperature deformation mechanism map for the high performance Ni-base superalloy GTD-111. J. Mater. Sci. Eng. A 2001, 307, 158–164. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Hu, L.J.; Yang, Z.Y.; Niu, S.X.; Bao, H.Z.; Jin, Q.C.; Renqing, D.J.; Jiang, R.S. A Contribution to the Study of the Integrity Surface of the IC10 Ni3Al-Based Alloy After Creep-Feed Grinding with a Focus on High-Temperature Fatigue Life. Metals 2024, 14, 1440. [Google Scholar] [CrossRef]
- Kang, D.S.; Lee, H.; Yun, D.W.; Jeong, H.W.; Yoo, Y.S.; Seo, S.M. Microstructural mechanism of local dynamic recrystallization around cavity during tertiary creep in directionally solidified superalloy CM247LC. Mater. Charact. 2023, 198, 112727. [Google Scholar] [CrossRef]
- Ding, X.; Huang, D.W.; Guo, Z.X.; Zhang, X.J.; Shen, C.Y.; Luan, X.; Wangyin, Z.R. Fracture failure analysis of DZ125 directionally solidified superalloy under combined high and low cycle fatigue. Eng. Fract. Mech. 2024, 310, 110459. [Google Scholar] [CrossRef]
- An, W.R.; Utada, S.; Antonov, S.; Lu, S.; He, S.L.; Lu, F.; Zheng, W.W.; Li, L.F.; Cormier, J.; Feng, Q. Microstructural evolution and creep mechanism of a directionally solidified superalloy DZ125 under thermal cycling creep. J. Alloys Compd. 2023, 947, 169533. [Google Scholar] [CrossRef]
- Rai, R.K.; Sahu, J.K.; Das, S.K.; Paulose, N.; Fernando, C. Creep-fatigue deformation micromechanisms of a directionally solidified nickel-base superalloy at 850 °C. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 51–62. [Google Scholar] [CrossRef]
- Shi, D.Q.; Dong, C.L.; Yang, X.G.; Sun, Y.T.; Wang, J.K.; Liu, J.L. Creep and fatigue lifetime analysis of directionally solidified superalloy and its brazed joints based on continuum damage mechanics at elevated temperature. Mater. Des. 2013, 45, 643–652. [Google Scholar] [CrossRef]
- Li, K.S.; Wang, R.Z.; Yuan, G.J.; Zhu, S.P.; Zhang, X.C.; Tu, S.T.; Miura, H. A crystal plasticity-based approach for creep-fatigue life prediction and damage evaluation in a nickel-based superalloy. Int. J. Fatigue 2021, 143, 106031. [Google Scholar] [CrossRef]
- Kumar, C.; Kumar, P. Creep-fatigue damage evolution in a nickel-based superalloy: An experiment-inspired modeling approach for life prediction. Int. J. Fatigue 2025, 195, 108872. [Google Scholar] [CrossRef]
- Cheng, L.Y.; Wang, R.Z.; Wang, J.; Zhu, S.P.; Zhao, P.C.; Miura, H.; Zhang, X.C.; Tu, S.T. Cycle-dependent creep-fatigue deformation and life predictions in a nickel-based superalloy at elevated temperature. Int. J. Mech. Sci. 2021, 206, 106628. [Google Scholar] [CrossRef]
- Sun, D.B.; Wan, Z.H. Experimental study and creep-fatigue life prediction of turbine blade material DZ125 considering the nonholding effect and coupling effect of stress and high temperature. J. Pressure Vessel Technol. 2024, 146, 031702. [Google Scholar] [CrossRef]
- Hu, J.H.; Zhao, G.L.; Li, S.L.; Qi, H.Y.; Yang, X.G.; Shi, D.Q. Damage evolution and life modeling of hot corrosion environment on creep-fatigue of a directionally solidified nickel-based superalloy. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1512–1526. [Google Scholar] [CrossRef]
- Wang, R.Z.; Zhu, S.P.; Wang, J.; Zhang, X.C.; Tu, S.T.; Zhang, C.C. High temperature fatigue and creep-fatigue behaviors in a Ni-based superalloy: Damage mechanisms and life assessment. Int. J. Fatigue 2019, 118, 8–21. [Google Scholar] [CrossRef]
- Ding, B.; Ren, W.; Peng, J.C.; Zhong, Y.B.; Li, F.; Yu, J.B.; Ren, Z.M. Revealing the creep-fatigue deformation mechanism for a directionally-solidified Ni-based superalloy DZ445 at 900 °C. Mater. Res. Express 2018, 5, 076513. [Google Scholar] [CrossRef]
- Ding, B.; Ren, W.L.; Deng, K.; Li, H.T.; Liang, Y.C. An abnormal increase of fatigue life with dwell time during creep-fatigue deformation for directionally solidified Ni-based superalloy DZ445. High Temp. Mater. Processes 2018, 37, 277–284. [Google Scholar] [CrossRef]
- Hu, X.A.; Zhang, Q.; Jiang, Y.; Rao, G.F.; Miao, G.L.; He, W.F.; Nie, X.F. The effect of cyclic loading on the creep fatigue life and creep strength of a DS superalloy: Damage mechanism and life modeling. Int. J. Fatigue 2020, 134, 105452. [Google Scholar] [CrossRef]
- Long, A.P.; Xiong, J.Y.; Wei, B.; Zhang, G.X.; Feng, G.J.; Guo, J.Z.; Liu, R.T. Creep Mechanism and Microstructure Evolution of a Directionally Solidified Ni-Based Superalloy with Different Orientations at 850 °C. Materials 2025, 18, 1540. [Google Scholar] [CrossRef]
- Chen, J.B.; Chen, J.Y.; Wang, Q.J.; Wu, Y.D.; Li, Q.; Xiao, C.B.; Li, S.L.; Wang, Y.D.; Hui, X.D. Enhanced creep resistance induced by minor Ti additions to a second generation nickel-based single crystal superalloy. Acta Mater. 2022, 232, 117938. [Google Scholar] [CrossRef]
- Wei, B.S.; Lin, Y.; Huang, Z.W.; Huang, L.; Zhou, K.C.; Zhang, L.F.; Zhang, L.J. A novel Re-free Ni-based single-crystal superalloy with enhanced creep resistance and microstructure stability. Acta Mater. 2022, 240, 118336. [Google Scholar] [CrossRef]
- Stinville, J.C.; Suave, L.M.; Mauget, F.; Marcin, L.; Villechaise, P.; Pollock, T.M.; Cormier, J. Damage nucleation during transverse creep of a directionally solidified Ni-based superalloy. Mater. Sci. Eng. A 2022, 858, 144089. [Google Scholar] [CrossRef]
- Li, Q.Y.; Tian, S.G.; Yu, H.C.; Tian, N.; Su, Y.; Li, Y. Effects of carbides and its evolution on creep properties of a directionally solidified nickel-based superalloy. Mater. Sci. Eng. A 2015, 633, 20–27. [Google Scholar] [CrossRef]
- Gdoutos, E.E. Fracture Mechanics: An Introduction, 3rd ed.; Springer Nature: Cham, Switzerland, 2020; Volume 263, pp. 15–63. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the royal society of London. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Zheng, H.W.; Muraishi, S. Two ways to estimate precipitate elastic fields through Eshelby inclusion theory. Results Mater. 2024, 21, 100544. [Google Scholar] [CrossRef]
- Rodriguez, P.; Rao, K.B.S. Nucleation and growth of cracks and cavities under creep-fatigue interaction. Prog. Mater. Sci. 1993, 37, 403–480. [Google Scholar] [CrossRef]
- Rao, K.B.S.; Meurer, H.P.; Schuster, H. Creep-fatigue interaction of Inconel 617 at 950 °C in simulated nuclear reactor helium. J. Mater. Sci. Eng. A 1988, 104, 37–51. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998; pp. 132–162. Available online: https://books.google.com.hk/books?id=j4w6frFAiQcC&printsec=frontcover&hl=zh-CN#v=onepage&q&f=false (accessed on 5 April 2025).
- Pineau, A.; Antolovich, S.D. High temperature fatigue of nickel-base superalloys–A review with special emphasis on deformation modes and oxidation. Eng. Failure Anal. 2009, 16, 2668–2697. [Google Scholar] [CrossRef]
- Jiang, R.; Song, Y.D.; Reed, P.A. Fatigue crack growth mechanisms in powder metallurgy Ni-based superalloys—A review. Int. J. Fatigue 2020, 141, 105887. [Google Scholar] [CrossRef]
- Muller, F.M.; Fang, C.Z.; Basoalto, H.C.; Williams, S.; Bowen, P. Modelling and predictions of time-dependent local stress distributions around cracks under dwell loading in a nickel-based superalloy at high temperatures. Int. J. Fatigue 2022, 163, 107038. [Google Scholar] [CrossRef]
- Chan, K.S. A grain boundary fracture model for predicting dynamic embrittlement and oxidation-induced cracking in superalloys. Metall. Mater. Trans. A 2015, 46, 2491–2505. [Google Scholar] [CrossRef]
- Liu, L.; Meng, J.; Liu, J.L.; Zhang, H.F.; Sun, X.D.; Zhou, Y.Z. Effects of crystal orientations on the low-cycle fatigue of a single-crystal nickel-based superalloy at 980 °C. Acta Metall. Sin. 2019, 32, 381–390. [Google Scholar] [CrossRef]
- Suzuki, S.Y.; Sakaguchi, M.; Inoue, H. Temperature dependent fatigue crack propagation in a single crystal Ni-base superalloy affected by primary and secondary orientations. Mater. Sci. Eng. A 2018, 724, 559–565. [Google Scholar] [CrossRef]
- Wollgramm, P.; Bürger, D.; Parsa, A.B.; Neuking, K.; Eggeler, G. The effect of stress, temperature and loading direction on the creep behaviour of Ni-base single crystal superalloy miniature tensile specimens. Mater. High Temp. 2016, 33, 346–360. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Needleman, A.; Van der Giessen, E. Discrete dislocation modeling of fatigue crack propagation. Acta Mater. 2002, 50, 831–846. [Google Scholar] [CrossRef]
- Reddy, G.P.; Robertson, C.; Déprés, C.; Fivel, M. Effect of grain disorientation on early fatigue crack propagation in face-centred-cubic polycrystals: A three-dimensional dislocation dynamics investigation. Acta Mater. 2013, 61, 5300–5310. [Google Scholar] [CrossRef]
- Cheng, Z.X.; Wang, H.; Liu, G.R. Fatigue crack propagation in carbon steel using RVE based model. Eng. Fract. Mech. 2021, 258, 108050. [Google Scholar] [CrossRef]
- Ma, L.; Xiao, S.F.; Deng, H.Q.; Hu, W.Y. Molecular dynamics simulation of fatigue crack propagation in bcc iron under cyclic loading. Int. J. Fatigue 2014, 68, 253–259. [Google Scholar] [CrossRef]
- Gillis, P.P. Manson-coffin fatigue. Acta Metall. 1966, 14, 1673–1676. [Google Scholar] [CrossRef]
- Koul, A.K.; Castillo, R.; Willett, K. Creep life predictions in nickel-based superalloys. Mater. Sci. Eng. 1984, 66, 213–226. [Google Scholar] [CrossRef]
- Sandström, R. Basic Modeling and Theory of Creep of Metallic Materials, 1st ed.; Springer Nature: Cham, Switzerland, 2024; pp. 185–203. [Google Scholar] [CrossRef]
- Salehnasab, B. Low cycle fatigue behavior and life prediction of a directionally solidified alloy. J. Des. Fatigue 2024, 2, 1–10. [Google Scholar] [CrossRef]
- Dinesh, K.; Dash, B.B.; Kannan, R.; Paulose, N.; Reddy, G.P.; Krishnaswamy, H.; Sankaran, S. Effect of temperature on fatigue behavior and deformation mechanisms of nickel-based superalloy SU-263. Int. J. Fatigue 2025, 192, 108721. [Google Scholar] [CrossRef]
- Chaboche, J.L. Continuum damage mechanics: Part I—General concepts. J. Appl. Mech. 1988, 55, 59–64. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials, 1st ed.; Cambridge University Press: Cambridge, UK, 1994; pp. 346–450. Available online: https://books.google.com.hk/books?id=YfHTNHfjqXoC&printsec=frontcover&hl=zh-CN#v=onepage&q&f=false (accessed on 5 April 2025).
- Chaboche, J.L. Continuous damage mechanics—A tool to describe phenomena before crack initiation. Nucl. Eng. Des. 1981, 64, 233–247. [Google Scholar] [CrossRef]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Rabotnov, Y.N. Kinetics of creep and creep rupture. In Proceedings of the Irreversible Aspects of Continuum Mechanics and Transfer of Physical Characteristics in Moving Fluids, Symposia, Vienna, Austria, 22–28 June 1966. [Google Scholar] [CrossRef]
- Berti, G.A.; Monti, M. Thermo-mechanical fatigue life assessment of hot forging die steel. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 1025–1034. [Google Scholar] [CrossRef]
- Yu, H.C.; Wu, X.R. Material Data Manual for Aero-Engine Design, 1st ed.; Aviation Industry Press: Beijing, China, 2010; Volume 4, pp. 338–344. Available online: https://scholar.google.com/scholar?cluster=14401761704590689732&hl=zh-CN&as_sdt=2005&sciodt=0,5 (accessed on 26 April 2025).









| Specimen Orientation | /2 (%) | /2 (%) | /2 (%) | (MPa) | (MPa) | (Cycles) |
|---|---|---|---|---|---|---|
| L | 0.296 | 0.227 | 0.069 | 219 | 305 | 1544 |
| 0.283 | 0.224 | 0.058 | 219 | 313 | 2010 | |
| 0.267 | 0.228 | 0.040 | 196 | 295 | 2750 | |
| 0.396 | 0.289 | 0.107 | 278 | 377 | 873 | |
| 0.402 | 0.289 | 0.113 | 275 | 358 | 1025 | |
| 0.396 | 0.269 | 0.127 | 257 | 337 | 1351 | |
| 0.591 | 0.363 | 0.228 | 376 | 453 | 230 | |
| 0.641 | 0.376 | 0.265 | 374 | 436 | 238 | |
| 0.591 | 0.409 | 0.182 | 382 | 479 | 250 | |
| 0.785 | 0.443 | 0.342 | 518 | 602 | 60 | |
| 0.801 | 0.454 | 0.346 | 455 | 537 | 111 | |
| 0.775 | 0.452 | 0.323 | 457 | 541 | 154 | |
| T | 0.287 | 0.219 | 0.068 | 254 | 360 | 323 |
| 0.290 | 0.227 | 0.062 | 234 | 340 | 1243 | |
| 0.300 | 0.226 | 0.075 | 285 | 393 | 210 | |
| 0.395 | 0.262 | 0.133 | 360 | 456 | 96 | |
| 0.406 | 0.289 | 0.118 | 320 | 418 | 344 | |
| 0.434 | 0.308 | 0.126 | 326 | 406 | 350 | |
| 0.599 | 0.362 | 0.237 | 454 | 491 | 47 | |
| 0.601 | 0.292 | 0.309 | 499 | 546 | 11 | |
| 0.619 | 0.370 | 0.249 | 476 | 529 | 36 | |
| 0.840 | 0.434 | 0.407 | 544 | 600 | 15 | |
| 0.844 | 0.400 | 0.445 | 595 | 630 | 18 |
| r | A (MPa) | m | β | M (MPa) |
|---|---|---|---|---|
| 6.423 | 410.8 | 17.357 | 2.866 | 150.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, A.; Liu, X.; Xiao, L.; Zhang, G.; Xiong, J.; Feng, G.; Guo, J.; Liu, R. Anisotropy in the Creep–Fatigue Behaviors of a Directionally Solidified Ni-Based Superalloy: Damage Mechanisms and Life Assessment. Crystals 2025, 15, 429. https://doi.org/10.3390/cryst15050429
Long A, Liu X, Xiao L, Zhang G, Xiong J, Feng G, Guo J, Liu R. Anisotropy in the Creep–Fatigue Behaviors of a Directionally Solidified Ni-Based Superalloy: Damage Mechanisms and Life Assessment. Crystals. 2025; 15(5):429. https://doi.org/10.3390/cryst15050429
Chicago/Turabian StyleLong, Anping, Xiaoshan Liu, Lei Xiao, Gaoxiang Zhang, Jiangying Xiong, Ganjiang Feng, Jianzheng Guo, and Rutie Liu. 2025. "Anisotropy in the Creep–Fatigue Behaviors of a Directionally Solidified Ni-Based Superalloy: Damage Mechanisms and Life Assessment" Crystals 15, no. 5: 429. https://doi.org/10.3390/cryst15050429
APA StyleLong, A., Liu, X., Xiao, L., Zhang, G., Xiong, J., Feng, G., Guo, J., & Liu, R. (2025). Anisotropy in the Creep–Fatigue Behaviors of a Directionally Solidified Ni-Based Superalloy: Damage Mechanisms and Life Assessment. Crystals, 15(5), 429. https://doi.org/10.3390/cryst15050429






