Sm3+-Doped Bismuth(III) Oxosilicate (Bi4Si3O12:Sm3+): A Study of Crystal Structure and Mulliken Charges
Abstract
1. Introduction
2. Computational Methods
2.1. Setting Up a Structural Model
2.2. Parameter Setup for Calculations
3. Results and Discussion
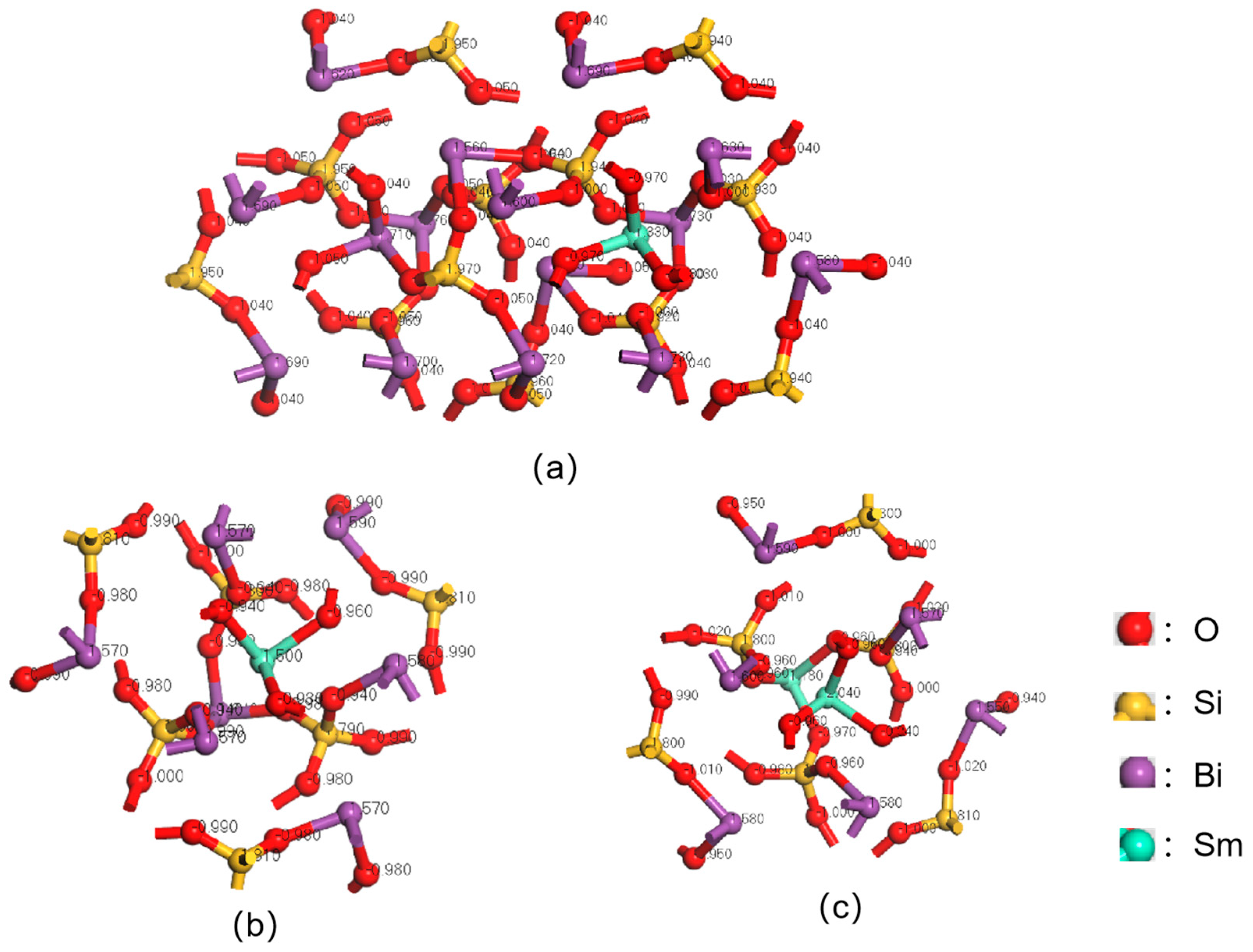
3.1. Mulliken Charge Calculation for Sm3+ Doping Level of 1/12
3.2. Mulliken Charge Calculation for Sm3+ Doping Level of 1/6
3.3. Mulliken Charge Calculation for Sm3+ Doping Level of 1/3
3.4. Mulliken Charge Analysis of Sm3+-Doped BSO Crystals
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodnyi, P.A. Physical Processes in Inorganic Scintillators; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Akande, S.; Bouhali, O. First-principles studies of defect behaviour in bismuth germanate. Sci. Rep. 2022, 12, 15728. [Google Scholar] [CrossRef] [PubMed]
- Akchurin, N.; Bedeschi, F.; Cardini, A.; Cascella, M.; Ciapetti, G.; De Pedis, D.; Fasoli, M.; Ferrari, R.; Franchino, S.; Fraternali, M.; et al. A comparison of BGO and BSO crystals used in the dual-readout mode. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 640, 91–98. [Google Scholar] [CrossRef]
- Wan, Q.; Zhang, X.; Wang, F. The elastic anisotropy electronic and optical properties of Bi4Si3O12, Bi2SiO5, Bi12SiO20 and Bi2Si3O9 crytals from first-principles calculations. Chem. Phys. Lett. 2023, 814, 140323. [Google Scholar] [CrossRef]
- Fischer, P.; Waldner, F. Comparison of neutron diffraction and EPR results on the cubic crystal structures of piezoelectric Bi4Y3O12 (Y = Ge, Si). Solid State Commun. 1982, 44, 657–661. [Google Scholar] [CrossRef]
- Xiao, X.; Xu, J.; Wei, H.; Chu, Y.; Yang, B.; Zhang, X. Optical and scintillation properties of Bi4Si3O12:RE (RE=Eu3+, Sm3+, Ho3+, Tb3+) single crystals. J. Rare Earths 2019, 37, 260–264. [Google Scholar] [CrossRef]
- Lira, A.C.; Martín-Rodríguez, E.; Martínez-Martínez, R.; Camarillo, I.; Muñoz, G.H.; Garcia-Solé, J.; Caldiño, U. Spectroscopy of the Bi4Si3O12: Er3+ glass for optical amplification and laser application. Opt. Mater. 2010, 32, 1266–1273. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, J.Y.; Zhang, T.T. Synthesis and Luminescence properties of Eu3+-droped Bi4Si3O12. J. Inorg. Mater. 2011, 26, 1341–1344. [Google Scholar] [CrossRef]
- Senguttuvan, N.; Kidokoro, N.; Ootsuka, K.; Ishii, M.; Kobayashi, M.; Taira, T.; Kurimura, S. Crystal growth and optical properties of Bi4Si3O12: Nd. J. Cryst. Growth 2001, 229, 188–192. [Google Scholar] [CrossRef]
- Lalic, M.V.; Souza, S.O. The first-principles study of electronic and optical properties of BGO and BSO scintillators. Opt. Mater. 2008, 30, 1189–1192. [Google Scholar] [CrossRef]
- Xiao, X.; Huang, Y.; Zhang, Y.; Si, J.; Liang, S.; Xu, Q.; Shen, H. Research on optical properties of Eu3+ doped bismuth silicate crystals based on first principles. Jpn. J. Appl. Phys. 2024, 63, 092002. [Google Scholar] [CrossRef]
- Guo, K.; Man, Z.Y.; Chen, H.H.; Guo, X.; Zhao, J.T. Effects of rare-earth substitution on the stability and electronic structure of REZnOSb (RE=La–Nd, Sm–Gd) investigated via first-principles calculations. Chem. Phys. 2011, 380, 54–60. [Google Scholar] [CrossRef]
- Yue, S.; Zhang, H. First principles study on magnetic and electronic properties with rare-earth atoms doped SWCNTs. Front. Phys. 2012, 7, 353–359. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, J.; Yang, H.; Fang, Z.; Fan, X.; Kuang, F.; Ye, H.; Fang, Y. Effect of uniaxial strain on electronic structure of intrinsic and N-doped 4H-SiC. Acta Phys. Chim. Sinica 2025, 42, 179–185. [Google Scholar]
- Zhang, Y.; Xiao, X.; Huang, Y.; Si, J.; Liang, S.; Xu, Q.; Shen, H. Eu3+-doped bismuth silicate crystal structure and Mulliken charge analysis. Cryst. Struct. Commun. 2024, 80, 815–820. [Google Scholar] [CrossRef] [PubMed]
- Nordheim, L. Zur elektronentheorie der metalle. I. Ann. Der Phys. 1931, 401, 607–640. [Google Scholar] [CrossRef]
- Brik, M. First-principles calculations of electronic, optical and elastic properties of ZnAl2S4 and ZnGa2O4. J. Phys. Chem. Solids 2010, 71, 1435–1442. [Google Scholar] [CrossRef]
- Liu, B.X.; Lai, W.S.; Zhang, Z.J. Solid-state crystal-to-amorphous transition in metal-metal multilayers and its thermodynamic and atomistic modelling. Adv. Phys. 2001, 50, 367–429. [Google Scholar] [CrossRef]
- Mulliken, R. Electronic population analysis on LCAO-MO molecular wave functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, X.; Zhang, Y.; Si, J.; Liang, S.; Xu, Q.; Shen, H. Study on the Optical Properties of Sm3+ Doped Bismuth Silicate Crystals Based on First Principles. Mater. Res. Express 2024, 11, 115902. [Google Scholar] [CrossRef]
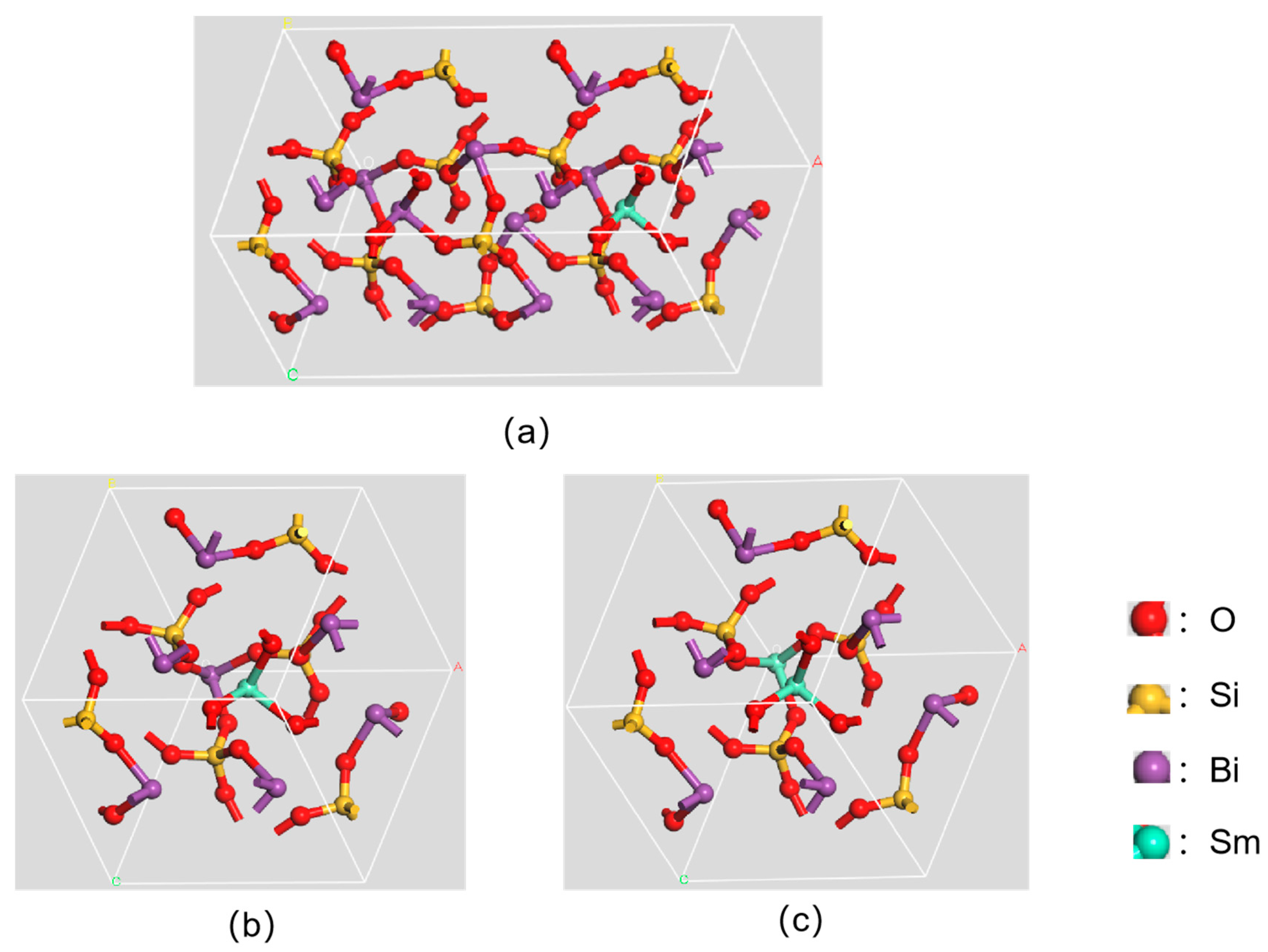
| Proportion | Chemical Formula | a/Å | b/Å | c/Å | /° | /° | |
|---|---|---|---|---|---|---|---|
| 1/12 | Bi15SmSi12O48 | 17.885734 | 8.937319 | 8.940963 | 109.47279 | 109.54748 | 109.54261 |
| 1/6 | Bi7SmSi6O24 | 9.7811 | 9.7902 | 9.7937 | 109.3735 | 109.5783 | 109.4024 |
| 1/3 | Bi6Sm2Si6O24 | 9.7763 | 9.758 | 9.7597 | 108.8562 | 108.9487 | 108.9563 |
| Atom | s | p | d | f | Total | Charge/e |
|---|---|---|---|---|---|---|
| O1 | 1.87 | 5.17 | — | — | 7.05 | −1.05 |
| O2 | 1.87 | 5.16 | — | — | 7.04 | −1.04 |
| O3 | 1.87 | 5.17 | — | — | 7.04 | −1.04 |
| O4 | 1.88 | 5.17 | — | — | 7.05 | −1.05 |
| O5 | 1.88 | 5.17 | — | — | 7.04 | −1.04 |
| O6 | 1.87 | 5.18 | — | — | 7.05 | −1.05 |
| O7 | 1.88 | 5.15 | — | — | 7.03 | −1.03 |
| O8 | 1.88 | 5.16 | — | — | 7.04 | −1.04 |
| O9 | 1.87 | 5.16 | — | — | 7.03 | −1.03 |
| O10 | 1.86 | 5.11 | — | — | 6.87 | −0.97 |
| O11 | 1.86 | 5.14 | — | — | 7.00 | −1.00 |
| O12 | 1.86 | 5.12 | — | — | 6.97 | −0.97 |
| O13 | 1.86 | 5.13 | — | — | 7.00 | −1.00 |
| O14 | 1.86 | 5.12 | — | — | 6.98 | −0.98 |
| Si1 | 0.69 | 1.35 | — | — | 2.04 | 1.96 |
| Si2 | 0.69 | 1.36 | — | — | 2.04 | 1.96 |
| Si3 | 0.68 | 1.36 | — | — | 2.05 | 1.95 |
| Si4 | 0.69 | 1.37 | — | — | 2.05 | 1.95 |
| Si5 | 0.70 | 1.37 | — | — | 2.07 | 1.93 |
| Si6 | 0.70 | 1.36 | — | — | 2.06 | 1.94 |
| Si7 | 0.69 | 1.37 | — | — | 2.06 | 1.94 |
| Si8 | 0.69 | 1.36 | — | — | 2.06 | 1.94 |
| Si9 | 0.70 | 1.37 | — | — | 2.08 | 1.92 |
| Si10 | 0.68 | 1.35 | — | — | 2.03 | 1.97 |
| Sm | 2.24 | 6.03 | 1.04 | 5.37 | 14.67 | 1.33 |
| Bi1 | 1.89 | 1.50 | — | — | 3.38 | 1.62 |
| Bi2 | 1.74 | 1.50 | — | — | 3.24 | 1.76 |
| Bi3 | 1.80 | 1.51 | — | — | 3.31 | 1.69 |
| Bi4 | 1.93 | 1.50 | — | — | 3.42 | 1.58 |
| Bi5 | 1.91 | 1.50 | — | — | 3.41 | 1.57 |
| Bi6 | 1.79 | 1.50 | — | — | 3.29 | 1.71 |
| Bi7 | 1.95 | 1.50 | — | — | 3.44 | 1.56 |
| Bi8 | 1.80 | 1.50 | — | — | 3.30 | 1.70 |
| Bi9 | 1.82 | 1.50 | — | — | 3.31 | 1.69 |
| Bi10 | 1.77 | 1.50 | — | — | 3.27 | 1.73 |
| Bi11 | 1.78 | 1.49 | — | — | 3.28 | 1.72 |
| Bi12 | 1.82 | 1.49 | — | — | 3.31 | 1.69 |
| Bi13 | 1.90 | 1.50 | — | — | 3.40 | 1.60 |
| Bi14 | 1.87 | 1.51 | — | — | 3.37 | 1.63 |
| Bi15 | 1.76 | 1.51 | — | — | 3.27 | 1.73 |
| Atom | s | p | d | f | Total | Charge/e |
|---|---|---|---|---|---|---|
| O1 | 1.89 | 5.10 | — | — | 6.99 | −0.99 |
| O2 | 1.90 | 5.07 | — | — | 6.98 | −0.98 |
| O3 | 1.90 | 5.09 | — | — | 6.99 | −0.99 |
| O4 | 1.90 | 5.08 | — | — | 6.98 | −0.98 |
| O5 | 1.89 | 5.09 | — | — | 6.98 | −0.98 |
| O6 | 1.89 | 5.06 | — | — | 6.96 | −0.96 |
| O7 | 1.89 | 5.05 | — | — | 6.94 | −0.94 |
| O8 | 1.89 | 5.04 | — | — | 6.93 | −0.93 |
| O9 | 1.90 | 5.10 | — | — | 7.00 | −1.00 |
| O10 | 1.89 | 5.04 | — | — | 6.94 | −0.94 |
| O11 | 1.89 | 5.09 | — | — | 6.99 | −0.99 |
| O12 | 1.90 | 5.11 | — | — | 7.00 | −1.00 |
| Si1 | 0.81 | 1.39 | — | — | 2.20 | 1.80 |
| Si2 | 0.80 | 1.39 | — | — | 2.19 | 1.81 |
| Si3 | 0.82 | 1.39 | — | — | 2.21 | 1.79 |
| Sm | 2.24 | 6.02 | 0.83 | 5.41 | 14.50 | 1.50 |
| Bi1 | 1.92 | 1.51 | — | — | 3.43 | 1.57 |
| Bi2 | 1.85 | 1.51 | — | — | 3.36 | 1.64 |
| Bi3 | 1.91 | 1.50 | — | — | 3.41 | 1.59 |
| Bi4 | 1.90 | 1.52 | — | — | 3.42 | 1.58 |
| Bi5 | 1.91 | 1.53 | — | — | 3.43 | 1.57 |
| Atom | s | p | d | f | Total | Charge/e |
|---|---|---|---|---|---|---|
| O1 | 1.89 | 5.08 | — | — | 6.97 | −0.97 |
| O2 | 1.89 | 5.06 | — | — | 6.95 | −0.95 |
| O3 | 1.90 | 5.07 | — | — | 6.98 | −0.98 |
| O4 | 1.89 | 5.12 | — | — | 7.01 | −1.01 |
| O5 | 1.89 | 5.07 | — | — | 6.96 | −0.96 |
| O6 | 1.89 | 5.05 | — | — | 6.95 | −0.95 |
| O7 | 1.90 | 5.11 | — | — | 7.00 | −1.00 |
| O8 | 1.90 | 5.12 | — | — | 7.02 | −1.02 |
| O9 | 1.89 | 5.05 | — | — | 6.94 | −0.94 |
| O10 | 1.90 | 5.10 | — | — | 7.01 | −1.01 |
| O11 | 1.89 | 5.06 | — | — | 6.96 | −0.96 |
| O12 | 1.90 | 5.13 | — | — | 7.02 | −1.02 |
| O13 | 1.90 | 5.09 | — | — | 6.99 | −0.99 |
| Si1 | 0.82 | 1.38 | — | — | 2.20 | 1.80 |
| Si2 | 0.82 | 1.39 | — | — | 2.21 | 1.79 |
| Si3 | 0.81 | 1.39 | — | — | 2.20 | 1.80 |
| Si4 | 0.81 | 1.38 | — | — | 2.19 | 1.81 |
| Sm1 | 2.22 | 6.11 | 0.81 | 5.67 | 14.82 | 1.18 |
| Sm2 | 2.22 | 6.11 | 0.80 | 4.82 | 13.96 | 2.04 |
| Bi1 | 1.90 | 1.51 | — | — | 3.41 | 1.59 |
| Bi2 | 1.91 | 1.51 | — | — | 3.42 | 1.58 |
| Bi3 | 1.92 | 1.53 | — | — | 3.45 | 1.55 |
| Bi4 | 1.89 | 1.51 | — | — | 3.40 | 1.60 |
| Bi5 | 1.91 | 1.52 | — | — | 3.43 | 1.57 |
| Bi6 | 1.90 | 1.52 | — | — | 3.42 | 1.58 |
| Proportion | Atom | Average Charge/e |
|---|---|---|
| 1/12 | O | −1.02 |
| Si | 1.95 | |
| Bi | 1.67 | |
| Sm | 1.33 | |
| 1/6 | O | −0.97 |
| Si | 1.80 | |
| Bi | 1.59 | |
| Sm | 1.50 | |
| 1/3 | O | −0.98 |
| Si | 1.80 | |
| Bi | 1.58 | |
| Sm | 1.61 |
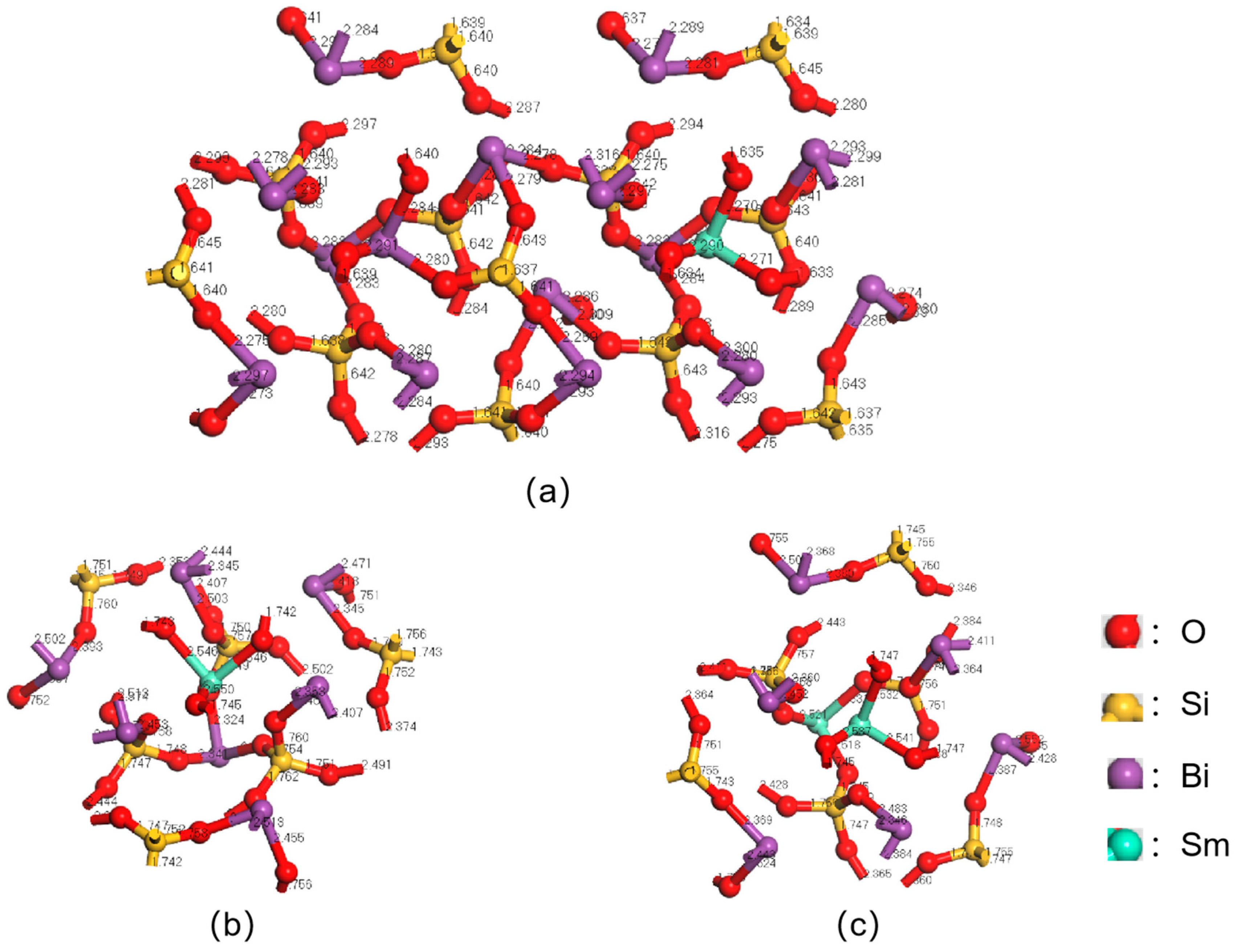
| Proportion | Bond | Length/Å |
|---|---|---|
| 1/12 | Sm-O | 2.28 |
| Bi1-O | 2.29 | |
| Bi2-O | 2.29 | |
| Bi3-O | 2.29 | |
| Bi4-O | 2.28 | |
| Bi5-O | 2.28 | |
| Bi6-O | 2.29 | |
| Bi7-O | 2.28 | |
| Bi8-O | 2.28 | |
| Bi9-O | 2.28 | |
| Bi10-O | 2.29 | |
| Bi11-O | 2.29 | |
| Bi12-O | 2.28 | |
| Bi13-O | 2.30 | |
| Bi14-O | 2.30 | |
| Bi15-O | 2.29 | |
| 1/6 | Sm-O | 2.55 |
| Bi1-O | 2.43 | |
| Bi2-O | 2.34 | |
| Bi3-O | 2.41 | |
| Bi4-O | 2.39 | |
| Bi5-O | 2.43 | |
| 1/3 | Sm1-O | 2.52 |
| Sm2-O | 2.54 | |
| Bi1-O | 2.42 | |
| Bi2-O | 2.45 | |
| Bi3-O | 2.46 | |
| Bi4-O | 2.39 | |
| Bi5-O | 2.43 | |
| Bi6-O | 2.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xiao, X.; Huang, Y.; Si, J.; Liang, S.; Xu, Q.; Zhang, H.; Ma, L.; Yang, C.; Ma, T.; et al. Sm3+-Doped Bismuth(III) Oxosilicate (Bi4Si3O12:Sm3+): A Study of Crystal Structure and Mulliken Charges. Crystals 2025, 15, 423. https://doi.org/10.3390/cryst15050423
Zhang Y, Xiao X, Huang Y, Si J, Liang S, Xu Q, Zhang H, Ma L, Yang C, Ma T, et al. Sm3+-Doped Bismuth(III) Oxosilicate (Bi4Si3O12:Sm3+): A Study of Crystal Structure and Mulliken Charges. Crystals. 2025; 15(5):423. https://doi.org/10.3390/cryst15050423
Chicago/Turabian StyleZhang, Yan, Xuefeng Xiao, Yan Huang, Jiashun Si, Shuaijie Liang, Qingyan Xu, Huan Zhang, Lingling Ma, Cui Yang, Tianyong Ma, and et al. 2025. "Sm3+-Doped Bismuth(III) Oxosilicate (Bi4Si3O12:Sm3+): A Study of Crystal Structure and Mulliken Charges" Crystals 15, no. 5: 423. https://doi.org/10.3390/cryst15050423
APA StyleZhang, Y., Xiao, X., Huang, Y., Si, J., Liang, S., Xu, Q., Zhang, H., Ma, L., Yang, C., Ma, T., Zhang, X., Xu, J., Tian, T., & Shen, H. (2025). Sm3+-Doped Bismuth(III) Oxosilicate (Bi4Si3O12:Sm3+): A Study of Crystal Structure and Mulliken Charges. Crystals, 15(5), 423. https://doi.org/10.3390/cryst15050423







