A First-Principles Study of Sn Dimer Adsorbed on MgO Surface

Abstract

A detailed characterization of metal clusters bound at the surface of crystalline metal oxide supports is crucial for identifying their structure–property relationships relevant to practical applications. Theoretical investigations based on first-principles calculations have proven to be helpful in characterizing supported metal clusters. In this work, the adsorption of an Sn dimer on the regular and defective (100) surfaces of MgO crystal was studied by means of density functional theory (DFT) calculations. The investigated defects included ${\mathrm{F}}_{\mathrm{s}}^0$, ${\mathrm{F}}_{\mathrm{s}}^{+}$, and ${\mathrm{F}}_{\mathrm{s}}^{2+}$ oxygen vacancies on MgO(100). From the results of the calculations, it is clear that the adsorption of Sn₂ at the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers is stronger than that occurring on the defect-free MgO(100) surface. While the triplet spin multiplicity of a free Sn dimer tends to be preserved upon its adsorption at the ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center, spin quenching is favored for the dimer adsorbed at the regular O²⁻ and defective ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers. The topological analysis of the electron density for the adsorbed dimer was carried out within the quantum theory of atoms in molecules (QTAIM). The calculated values of QTAIM parameters for the Sn-Sn bond of the adsorbed dimer do not differ radically from the corresponding values for the dimer in the gas phase.

1. Introduction

Metal nanoparticles dispersed on crystalline metal oxide supports are of great fundamental and practical interest in material science and catalysis [1,2,3]. Recently, oxide-supported single-atom and single-cluster catalysts have drawn considerable attention owing to their unique electronic structure and excellent performance in important industrial reactions [4,5,6]. For such catalysts, their active sites consist of single metal atoms or groups of metal atoms forming a cluster with a well-defined structure on the oxide support and maintaining a well-dispersed state under reaction conditions. However, the isolated metal atoms and clusters deposited on supports tend to sinter to larger nanoparticles that lose their catalytic activity and selectivity. In such cases, various surface defects are introduced into oxide supports to anchor the isolated metal atoms and clusters and, consequently, to suppress their sintering [5]. In fact, the kind of oxide support and its surface irregularities may change the catalytic reactivity and sintering rates of supported metal clusters to a great extent [7,8,9]. Therefore, a detailed description of the adsorption of metal atoms and clusters at various regular and defective surface centers of oxide supports is crucial for understanding and tailoring the reactivity and growth of supported metal nanoparticles. A microscopic view on such surface phenomena can be relatively easily gained from theoretical investigations based on first-principles calculations [10].

Tin often acts as a promoter for platinum-based catalysts for selective hydrogenation of unsaturated hydrocarbons [11] and unsaturated aldehydes [12], as well as for selective dehydrogenation of alkanes [13,14,15]. The Sn promoter is added to modify Pt active sites, so as to increase their activity, selectivity, and long-term stability. Aside from combining Pt with Sn, the bimetallic clusters are deposited on the surface of a crystalline metal oxide support that plays a critical role in controlling the dispersion of the clusters, thus influencing their catalytic performance [16]. As a matter of fact, the role of the support has been considered important as much as the Pt-Sn nanoparticles alone [17]. Specifically, the support and its surface properties have a profound effect on the nucleation, growth, and stability of Pt-Sn clusters under reaction conditions [15,18,19]. Among a variety of crystalline metal oxide supports, magnesium oxide is viewed as the prototype of such supports due to its strong ionic character, wide electronic gap, simple rock salt structure, and facility of synthesis [20]. Accordingly, MgO has been used in many fundamental studies of supported metallic catalysts, including those containing Pt [21,22], Sn [23,24], and Pt-Sn nanoparticles [25,26,27]. Although MgO essentially provides a chemically relatively inert support, it is not only a structural skeleton across which metal nanoparticles are dispersed but rather can largely determine the geometric and electronic properties of these nanoparticles [28,29,30,31]. Moreover, the presence of point defects on the surface of an MgO support may additionally exert considerable influence on the properties of the adsorbed metal nanoparticles [32,33]. Among various point defects occurring on the MgO(100) surface, which is more stable in terms of its surface energy than other faces of MgO crystal [34,35], the main part of such defects is due to oxygen vacancies and these can be relatively easily generated using well-known experimental techniques [36]. It has been observed that neutral oxygen vacancies (labelled as ${\mathrm{F}}_{\mathrm{s}}^0$) on MgO(100) are the preferential adsorption center for nanoparticles of many transition and noble metals [37,38]. Singly and doubly charged oxygen vacancies (${\mathrm{F}}_{\mathrm{s}}^{+}$ and ${\mathrm{F}}_{\mathrm{s}}^{2+}$) have also been deduced from experimental measurements on MgO(100) [36,39,40] but the concentration of ${\mathrm{F}}_{\mathrm{s}}^{2+}$ is likely to be small due to its low stability [41]. The ${\mathrm{F}}_{\mathrm{s}}^0$ center possesses two excess electrons that are largely localized in the cavity of the vacancy, while a single electron is trapped at the paramagnetic ${\mathrm{F}}_{\mathrm{s}}^{+}$ center [41]. The ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center is associated with a missing O²⁻ anion on the MgO(100) surface.

In this study, the adsorption of the Sn dimer (Sn₂) at the regular five-coordinated anionic O²⁻ center (labelled as O_5c) and at three point defects (${\mathrm{F}}_{\mathrm{s}}^0$, ${\mathrm{F}}_{\mathrm{s}}^{+}$, and ${\mathrm{F}}_{\mathrm{s}}^{2+}$) on MgO(100) was studied using computational first-principles methods. So far, only the defect-free MgO(100) surface has been taken into consideration in a single computational study of small Sn clusters deposited on the MgO support [24]. Furthermore, the present study is an extension of our previous theoretical work on atomic Sn adsorption on MgO(100) with defects [23]. Here, the structural, energetic, and electronic characterization of Sn₂ on MgO(100) is obtained within the framework of the density functional theory (DFT) [42], while the topological analysis of electron density distribution for the adsorbed dimer is carried out using Bader’s quantum theory of atoms in molecules (QTAIM) [43]. Being the simplest Sn cluster, the dimer represents an economical computational model to estimate the interaction between small Sn clusters and individual regular and defective adsorption centers. Interactions of support with mono- and bimetallic clusters are one of the factors controlling the performance of MgO-supported Pt-Sn catalysts. Specifically, the interaction between Sn clusters and the support affects the length of their surface diffusion, which in turn plays an important role in cluster sintering and alloying with Pt. Thus, results of first-principles calculations for the adsorption of Sn₂ on the regular and defective centers of MgO(100) may have implications for catalysis by MgO-supported Pt-Sn nanoparticles.

2. Methods

First-principles calculations were conducted within the framework of the generalized gradient DFT formalism, employing the exchange-correlation functional proposed by Perdew, Burke, and Ernzerhof (PBE) [44]. This functional was combined with its respective Grimme’s D3 semi-empirical correction for long-range dispersion effects [45] with rational damping according to Becke and Johnson (BJ) [46]. It should be underlined that the performance of a specific density functional in producing reliable results generally depends on the chemical system under study. Thus, the selection of a specific density functional should be always made with great caution. The dispersion-corrected PBE-D functional was adopted here to calculate exchange-correlation energy because there is some rationale behind the choice of this functional. PBE-D was successful in predicting various properties of MgO [47,48]. Moreover, this functional was previously used to investigate the adsorption of metallic clusters on MgO(100) [49,50], as well as Sn clusters on different supports [51,52].

The regular and defective (100) surfaces of MgO crystal were modeled within the framework of an embedded cluster method. The application of such a method to reproducing MgO surfaces is widely accepted and regarded as an alternative to periodic boundary conditions [53,54]. The embedded cluster method applied here to the regular MgO(100) surface features finite-sized clusters (Mg₁₃O₁₃ and Mg₃₀O₃₀) treated quantum-chemically and embedded in a large array of point charges. The Mg₁₃O₁₃ and Mg₃₀O₃₀ clusters combined with an embedding scheme were successfully used in many previous studies of surface phenomena for MgO(100) [38,55,56,57,58]. The Mg₁₃O₁₃ cluster was formed by the surface Mg₄O₉ layer and the subsurface Mg₉O₄ layer, while the Mg₃₀O₃₀ cluster was cut out from four layers of an ideal MgO crystal: Mg₁₂O₁₃, Mg₁₃O₁₂, Mg₄O₅, and a single Mg atom, passing from the surface layer to the deepest layer, respectively (Figure 1). Each cluster was embedded in a 15 × 15 × 8 grid of point charges following the Evjen embedding scheme [59] to minimize effects coming from the presence of cluster borders and to approximate the Madelung field of the extended surface at the adsorption centers on the clusters. The point charges were at the positions of ions in an ideal MgO crystal lattice. Positive point charges immediately surrounding the clusters were replaced by effective core potentials (ECPs) corresponding to Mg²⁺ to provide a representation of the finite size of the cations and to avoid the artificial over-polarization of the O atoms at the cluster borders. The Los Alamos National Laboratory (LANL2) ECPs [60] were used for 16 cations surrounding the Mg₁₃O₁₃ cluster and for 32 cations neighboring on the Mg₃₀O₃₀ cluster (Figure 1). The Mg and O atoms in the surface layer of the clusters were described by the 6-31G(d) and 6-31+G(d) basis sets, respectively [61,62]. The 6-31G basis set [61] was assigned to the atoms of the second layer, while the 3-21G basis set [63] was employed for all atoms in the third and fourth layer of Mg₃₀O₃₀. The choice of these basis sets was adopted from previous studies of adsorption on MgO(100) [23,38,55,56,57,58] and the PBE-D energies calculated using these basis sets show discrepancies of up to 0.1–0.2 eV relative to energies obtained from more extended basis sets (see Section S1 in Supplementary Materials). The Mg₃₀O₃₀ and Mg₁₃O₁₃ clusters in combination with the embedding scheme described above are termed from now on as Model 1 and Model 2, respectively.

In order to model the defective MgO(100) surfaces, the central oxygen atom or anion was removed from the surface layer of the Mg₃₀O₃₀ and Mg₁₃O₁₃ clusters belonging to Model 1 and Model 2. To be precise, the removal of O, O⁻, or O²⁻ produced an ${\mathrm{F}}_{\mathrm{s}}^0$, ${\mathrm{F}}_{\mathrm{s}}^{+}$, or ${\mathrm{F}}_{\mathrm{s}}^{2+}$ vacancy, respectively. Thus, the ${\mathrm{F}}_{\mathrm{s}}^0$ defect was a cavity holding two electrons, while no excess electrons were trapped at the ${\mathrm{F}}_{\mathrm{s}}^{2+}$ defect. The Mg₃₀O₂₉ and Mg₁₃O₁₂ clusters formed in this way inherited all basis sets from their parent clusters of Model 1 and Model 2.

The Sn atoms in the dimer were described by the LANL08d basis set [64]. It was reported that this basis set, combined with a hybrid density functional, is able to predict fundamental properties of an isolated Sn₂ molecule with reasonable accuracy [65], so it is likely that this basis set may also perform well for the Sn dimers investigated here.

The geometry optimizations of Sn₂ on the embedded clusters representing the regular and defective centers on MgO(100) were carried out for a large set of initial positions of the dimer on these clusters. No symmetry restraints were imposed in the course of the geometry optimizations. The coordinates of Sn₂ and of the surface atoms belonging to each adsorption center were allowed to vary subject to energy minimization, while Mg and O atoms being more distant from the adsorption center, the Mg²⁺ ions treated with the ECPs, as well as the grid of point charges were held fixed in the positions taken from the ideal MgO crystal lattice exhibiting an Mg-O distance of 2.106 Å. During the geometry optimizations, a variety of possible electronic spin multiplicities (2S + 1, where S is the total electron spin angular momentum) were taken into account for the dimer at each individual adsorption center. Singlet, triplet, and quintet states (2S + 1 = 1, 3, 5, respectively) were considered for Sn₂ at the O_5c, ${\mathrm{F}}_{\mathrm{s}}^0$, and ${\mathrm{F}}_{\mathrm{s}}^{2+}$ adsorption centers, whereas doublet, quartet and sextet states (2S + 1 = 2, 4, 6, respectively) were designated for Sn₂ at the ${\mathrm{F}}_{\mathrm{s}}^{+}$ defect.

The energetic effect of Sn₂ adsorption on the regular and defective centers of MgO(100) was characterized by its respective adsorption energy (E_ads). For the adsorbed dimer in any electronic spin state, its E_ads energy was defined by the following formula:

E_ads = E_tot(Sn₂/MgO) − E_tot(Sn₂)_isolated − E_tot(MgO)_isolated

(1)

where E_tot(Sn₂/MgO) signifies the total energy of the whole system containing the Sn dimer at a given adsorption center, E_tot(Sn₂)_isolated denotes the total energy of a free Sn dimer in its ground state, and E_tot(MgO)_isolated refers to the total energy of an isolated embedded MgO cluster in its relaxed geometry and its ground state. According to this definition, a negative E_ads value indicates that adsorption is an energetically favorable process.

The strength of the interaction between the adsorbed dimer and the surface was estimated by the adhesion energy (E_adh) formulated as follows:

E_adh = E_tot(Sn₂/MgO) − E_tot(Sn₂)_interacting − E_tot(MgO)_interacting

(2)

where the total energies of Sn₂ and an embedded MgO cluster in their interacting geometries taken from Sn₂/MgO were considered. The total energy of Sn₂ in its spin multiplicity inherited from the Sn₂/MgO system was calculated, while the embedded MgO cluster showed the lowest possible spin multiplicity. The basis-set superposition error correction [66] was included in E_adh. The more negative the value of E_adh is yielded, the stronger the interaction between the adsorbed dimer and the surface is found.

Finally, a tendency of single Sn atoms to form a dimer on the regular and defective MgO(100) surfaces was analyzed in terms of two energetic quantities [67]:

$$E_{\dim }^{\mathrm{gas}}=E_{\mathrm{t}\mathrm{o}\mathrm{t}}({\mathrm{S}\mathrm{n}}_2/\mathrm{M}\mathrm{g}\mathrm{O})-E_{\mathrm{t}\mathrm{o}\mathrm{t}}(\mathrm{S}\mathrm{n}/\mathrm{M}\mathrm{g}\mathrm{O})-E_{\mathrm{t}\mathrm{o}\mathrm{t}}(\mathrm{S}\mathrm{n}{)}_{\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}}$$

(3)

$$E_{\dim }^{\mathrm{ads}}=E_{\mathrm{t}\mathrm{o}\mathrm{t}}({\mathrm{S}\mathrm{n}}_2/\mathrm{M}\mathrm{g}\mathrm{O})+E_{\mathrm{t}\mathrm{o}\mathrm{t}}(\mathrm{M}\mathrm{g}\mathrm{O}{)}_{\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}}-E_{\mathrm{t}\mathrm{o}\mathrm{t}}(\mathrm{S}\mathrm{n}/\mathrm{M}\mathrm{g}\mathrm{O})-E_{\mathrm{t}\mathrm{o}\mathrm{t}}(\mathrm{S}\mathrm{n}/\mathrm{M}\mathrm{g}\mathrm{O}{)}_{\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}}$$

(4)

The former signifies the dimerization energy of a free Sn atom (that is, a gas-phase one) to another Sn atom already bound at a given adsorption center (Sn/MgO), while the latter roughly estimates the dimerization energy between two already adsorbed Sn atoms, one of which has been always bound at the O_5c center [(Sn/MgO)_regular]. To obtain these dimerization energies, the adsorption of a single Sn atom on the regular and defective MgO(100) surfaces was studied using PBE-D in combination with Model 1 and Model 2. According to the convention adopted in Equations (3) and (4), the more and more negative values of $E_{\dim }^{\mathrm{gas}}$ and $E_{\dim }^{\mathrm{ads}}$ signal the growing tendency of single Sn atoms to dimerize.

For the isolated molecule of Sn₂, its binding energy (E_bind) was calculated as the difference between the total energy of Sn₂ showing its optimized bond length and the double total energy of a free Sn atom in its ground state.

E_bind = E_tot(Sn₂)_isolated − 2E_tot(Sn)_isolated

(5)

The E_bind energy of Sn₂ was corrected for the basis-set superposition error.

Geometry optimizations and single-point energy calculations were carried out using the Gaussian 16 C.01 program [68]. Orbital composition analysis was conducted with the Multiwfn 3.8 program [69] using a method proposed by Becke [70,71]. The QTAIM implementation available in AIMAll 19.10.12 [72] was used with the default parameters of the program.

3. Results and Discussion

First, the lowest-energy structures of the Sn dimer adsorbed on the regular and defective MgO(100) surfaces were identified in a series of geometry optimizations starting from configurations in which the dimer was initially distant from the surface and showed the original bond length taken from a free Sn₂ molecule (2.823 Å). The results of the search for the lowest-energy structures are depicted in Figure 2. These structures are characterized in terms of several geometric and energetic parameters listed in

Table 1. Geometric and energetic parameters for the adsorption of Sn₂ at the regular and defective centers of MgO(100). The results derived from Model 1 and Model 2 of MgO(100) are shown without and in parentheses, respectively. Distances are given in Å, energies are in eV.

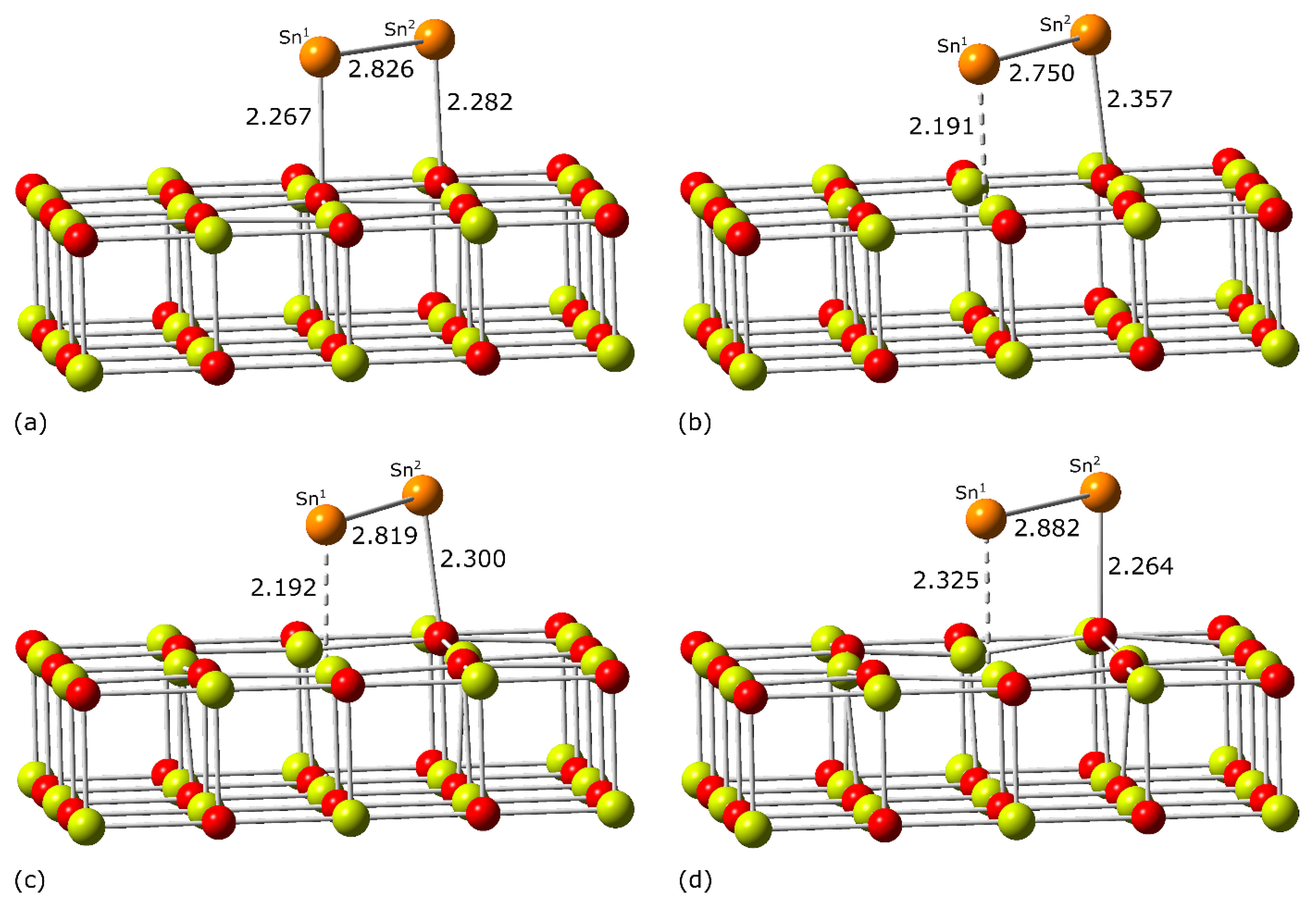
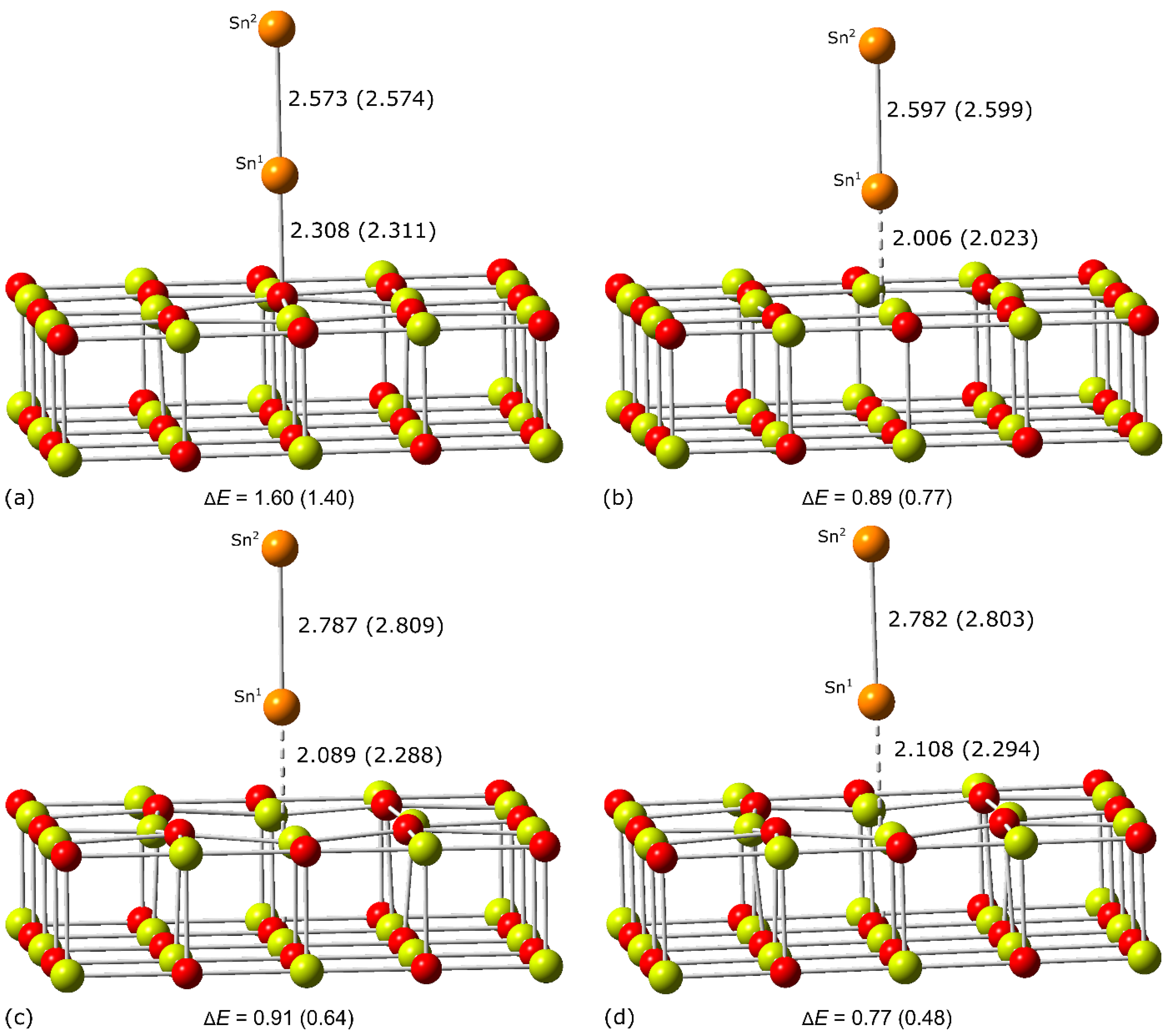
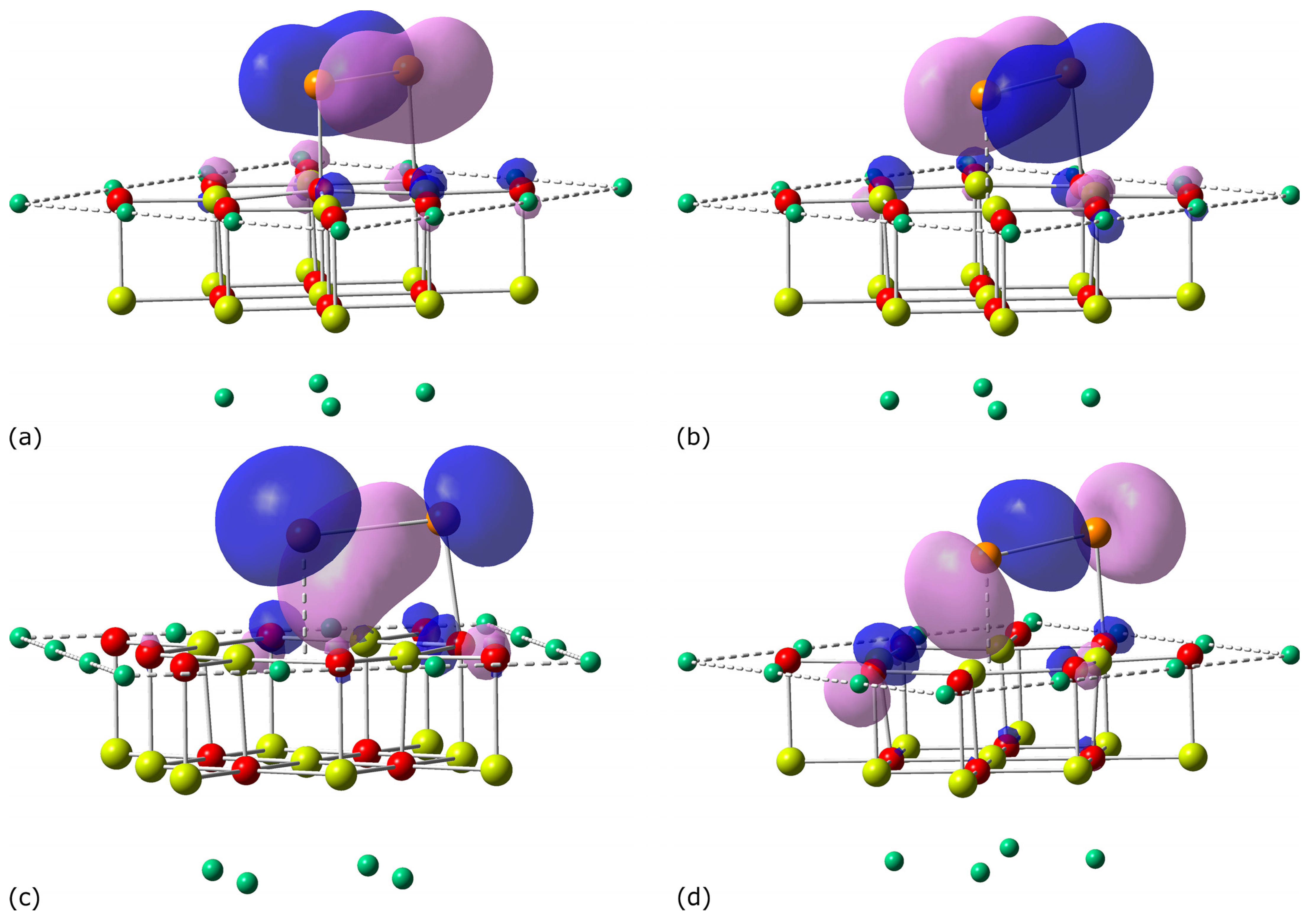
Adsorption Center	2S + 1	Distance			ΔE	Eads	Eadh
		Sn1-Surface a	Sn2-Surface b	Sn1-Sn2
O5c	1	2.267 (2.233)	2.282 (2.355)	2.826 (2.808)	0.00 (0.00)	−2.86 (−2.85)	−3.46 (−3.44)
	3	2.318 (2.259)	2.802 (2.954)	2.879 (2.857)	0.92 (0.85)	−1.93 (−2.01)	−1.80 (−1.88)
	5	2.242 (2.195)	2.887 (3.256)	3.074 (3.053)	1.83 (1.71)	−1.03 (−1.15)	−1.96 (−2.10)
${\mathrm{F}}_{\mathrm{s}}^0$	1	2.191 (2.195)	2.357 (2.447)	2.750 (2.724)	0.00 (0.00)	−4.24 (−4.28)	−4.80 (−4.84)
	3	2.193 (2.195)	2.332 (2.426)	3.014 (2.970)	0.96 (1.03)	−3.28 (−3.25)	−3.18 (−3.11)
	5	2.171 (2.170)	3.129 (3.413)	3.115 (3.062)	2.09 (2.07)	−2.15 (−2.21)	−3.04 (−3.04)
${\mathrm{F}}_{\mathrm{s}}^{+}$	2	2.192 (2.169)	2.300 (2.390)	2.819 (2.796)	0.00 (0.00)	−3.08 (−2.92)	−3.55 (−3.41)
	4	2.108 (2.039)	2.305 (2.434)	3.023 (2.987)	0.82 (0.94)	−2.26 (−1.98)	−2.17 (−1.85)
	6	2.315 (2.294)	3.062 (3.342)	3.229 (3.118)	2.27 (2.27)	−0.81 (−0.64)	−1.65 (−1.45)
${\mathrm{F}}_{\mathrm{s}}^{2+}$	1	2.327 (2.118)	2.273 (2.364)	2.893 (2.869)	0.11 (0.17)	−2.30 (−2.28)	−2.96 (−2.95)
	3	2.325 (2.105)	2.264 (2.366)	2.882 (2.865)	0.00 (0.00)	−2.41 (−2.45)	−2.40 (−2.39)
	5	2.244 (2.244)	2.299 (2.345)	3.163 (3.121)	0.90 (0.98)	−1.51 (−1.47)	−2.45 (−2.37)

^a This distance is defined as Sn¹-O for the regular adsorption center, while a height above the surface layer of MgO is taken for the defective centers. ^b This distance is defined as Sn²-O for all centers.

.

On the defect-free MgO(100) surface, the most stable adsorption configuration of Sn₂ is when its bond axis is positioned practically parallel to this surface. The Sn atoms of the adsorbed dimer sit on top of two neighboring oxygen anions that are located 2.938 Å away from one another. This O-O distance is quite close to the bond length of a free Sn₂ molecule, and consequently, the Sn-Sn bond length remains essentially unchanged upon adsorption. The occupation of two neighboring O_5c centers by the Sn dimer is actually expected from the preference of single Sn atoms for adsorbing at the O_5c centers on the defect-free MgO(100) surface [23]. The Sn-O distances of the adsorbed dimer are very similar to the Sn-O distance calculated for the Sn atom adsorption at the O_5c center (

Table 2. Geometric, energetic, and electronic parameters for the adsorption of an Sn atom at the regular and defective centers of MgO(100). The results derived from Model 1 and Model 2 of MgO(100) are shown without and in parentheses, respectively. Distances are given in Å, energies are in eV, whereas charge and spin distributions are in e.

Adsorption Center	2S + 1	Sn-Surface a	ΔE	Eads	Eadh	q(Sn)	Nspin(Sn)
O5c	1	2.270 (2.235)	0.17 (0.18)	−1.64 (−1.83)	−2.80 (−3.00)	−0.114 (−0.131)	0.000 (0.000)
	3	2.276 (2.241)	0.00 (0.00)	−1.81 (−2.01)	−1.86 (−2.05)	−0.117 (−0.135)	1.694 (1.691)
${\mathrm{F}}_{\mathrm{s}}^0$	1	2.229 (2.230)	0.14 (0.14)	−2.82 (−2.94)	−3.85 (−3.96)	−1.369 (−1.381)	0.000 (0.000)
	3	2.244 (2.246)	0.00 (0.00)	−2.96 (−3.08)	−2.86 (−2.98)	−1.371 (−1.384)	1.639 (1.657)
${\mathrm{F}}_{\mathrm{s}}^{+}$	2	2.204 (2.344)	0.13 (0.22)	−1.98 (−1.93)	−2.96 (−2.93)	−0.719 (−0.671)	0.837 (0.866)
	4	2.188 (2.152)	0.00 (0.00)	−2.11 (−2.15)	−2.00 (−2.05)	−0.697 (−0.699)	2.300 (2.332)
${\mathrm{F}}_{\mathrm{s}}^{2+}$	1	2.080 (2.300)	0.14 (0.20)	−1.26 (−1.29)	−2.41 (−2.42)	−0.087 (−0.056)	0.000 (0.000)
	3	2.326 (2.316)	0.00 (0.00)	−1.40 (−1.49)	−1.32 (−1.42)	−0.031 (−0.021)	1.542 (1.573)

^a This distance is defined as Sn¹-O for the regular adsorption center, while a height above the surface layer of MgO is taken for the defective centers.

). Furthermore, our lowest-energy structure of Sn₂ on the regular MgO(100) surface compares well with the result of previous periodic DFT calculations with a plane–wave basis set [24]. A range of spin multiplicities from the singlet to the quintet state were considered here for the Sn dimer on MgO(100). The corresponding results are appended to Table 1. Interestingly, the most stable adsorption configuration of the dimer on the regular MgO(100) surface is associated with the singlet spin state although both a free Sn₂ molecule and a single Sn atom adsorbed at the O_5c center hold a triplet multiplicity in their ground states [23,73]. The adsorption configurations of the dimer in higher spin multiplicities are characterized by positive values of their energies relative to the energy of the most stable structure (ΔE). The destabilizing effect becomes stronger with the growing number of unpaired electrons. For the triplet and quintet multiplicities, the dimer still binds to the O_5c centers but its bond axis is tilted toward MgO(100), with one Sn atom being significantly more distant from the surface. This results in a weaker interaction of Sn₂ with the surface, as evidenced by the less negative values of E_adh. Higher spin multiplicities also lead to an Sn-Sn bond lengthening in the adsorbed dimer. The negative values of E_ads indicate that the adsorption of Sn₂ on the regular MgO(100) surface is an energetically favorable process, regardless of the spin multiplicity. It should be stressed that Model 1 and Model 2 produce identical trends in the structural and energetic parameters describing the adsorption of Sn₂ on the defect-free MgO(100) surface.

The adsorption of Sn₂ at the defective centers leads to the most stable configurations in which one Sn atom sits on top of the oxygen vacancy, while the other Sn atom binds to one of the oxygen anions in the neighborhood of this vacancy (Figure 2). The bond axis of the dimer is tilted toward the cavity of the ${\mathrm{F}}_{\mathrm{s}}^0$, ${\mathrm{F}}_{\mathrm{s}}^{+}$, and ${\mathrm{F}}_{\mathrm{s}}^{2+}$ defects, while the Sn atom bound to one of the surrounding oxygen anions is regularly moved upward above the surface. In the case of ${\mathrm{F}}_{\mathrm{s}}^{2+}$, the Mg²⁺ and O²⁻ ions surrounding the defect are clearly rumpled. Specifically, the oxygen anion involved in the Sn₂ adsorption is moved upward by 0.232 Å, and, therefore, the resulting Sn-O distance amounts to merely 2.264 Å (Figure 2). The most stable adsorption configurations of Sn₂ at the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers are associated with spin quenching in the adsorbed dimer although the ${\mathrm{F}}_{\mathrm{s}}^{+}$ defect as such is paramagnetic and an unpaired electron still exists for the Sn dimer adsorbed at this defect. By contrast, the most stable adsorption configuration of the Sn dimer at the ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center preserves the triplet spin multiplicity typical of a free Sn₂ molecule. On the other hand, the singlet state of the dimer adsorbed at the ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center lies very close in energy to the triplet one (Table 1). As with the Sn₂ adsorption at the O_5c center, the adsorption of the dimer in higher spin states at the defective centers is accompanied by an elongation in the Sn-Sn bond length and a weakening in the interaction between the adsorbed dimer and the defects. The calculated values of E_ads reveal that the favorable energetic effect of Sn₂ adsorption decreases regularly with the growing formal charge of oxygen vacancies. The favorable E_ads effect for the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers is larger in magnitude than E_ads for Sn₂ at O_5c. In this regard, the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers contrast with ${\mathrm{F}}_{\mathrm{s}}^{2+}$ at which the Sn dimer shows a less negative E_ads energy than Sn₂ at O_5c. In other words, the Sn dimer prefers to bind to the O_5c center rather than to the doubly charged oxygen vacancy. This trend mimics the one observed for the adsorption of single Sn atoms at the regular and defective centers on the MgO(100) surface (Table 2) [23]. According to the values of ΔE in Table 1, the propensity of Sn₂ at ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ to change its spin states is essentially similar to that found for the Sn dimer at the O_5c center. The results obtained from Model 1 and Model 2 compare well for the energetic parameters of Sn₂ adsorption on the defective MgO(100) surfaces. A mismatch between these models in the geometric parameters of Sn₂ adsorption usually do not exceed 0.1 Å but the adverse effect of small cluster size in Model 2 is evident for higher spin states and for the ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center where the rumpling of cluster boundaries occurs.

It is instructive to compare the E_ads energy of Sn₂ on the MgO(100) surfaces to the corresponding energetic effects for the dimers of other metals. The most stable adsorption configuration of Sn₂ at the O_5c center is associated with much more favorable E_ads energy (−2.86 eV) than the adsorption of such noble metal dimers as Pd₂ (−1.66 eV [74]) or Au₂ (−1.49 eV [67]) on the regular MgO(100) surface. Similarly, the most stable adsorption configurations of Sn₂ at the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers produce a slightly greater gain in E_ads than Au₂ adsorption at these defects on MgO(100) [67].

To our knowledge, no experimental observations of the structure of Sn dimers on MgO supports have been reported so far but experimental insights into the structure of MgO-supported dimers of certain noble metals are available. It was deduced from low-temperature scanning tunneling microscopy (STM) measurements that Pd dimers tend to lie flat on the MgO(100) surface [75], while Au dimers can actually exist as flat lying dimers as well as in an upright orientation with respect to the surface [76]. It is interesting to establish whether such an upright adsorption configuration is possible for the Sn dimer at the centers investigated in this work. As a matter of fact, stable adsorption configurations with the upright orientation of Sn-Sn bond axis with respect to the MgO(100) surface have been found for all the centers except the paramagnetic ${\mathrm{F}}_{\mathrm{s}}^{+}$ one. These configurations are presented in Figure 3. Their stability is decreased (ΔE > 0) but their spin states are in agreement with the corresponding spin multiplicities of the preferred adsorption configurations. To be precise, the upright orientation of Sn₂ at the O_5c and ${\mathrm{F}}_{\mathrm{s}}^0$ centers is associated with maximal spin pairing, along with the marked shortening of Sn-Sn bond, while the ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center allows the dimer to preserve its triplet spin state and then a potential transition to the low spin state requires only a small portion of energy (0.14 eV).

An important factor determining the properties of supported metal clusters is the amount of electron charge acquired by the clusters. For example, the rational design of efficient Pt-Sn/TiO₂ catalysts benefits from the substantial charge transfer from Sn to the support that prevents the agglomeration of Sn atoms into larger clusters [77]. For the Sn dimer adsorbed on the regular and defective MgO(100) surfaces, the electron charge (q) acquired by the dimer was calculated as a sum of partial charges accumulated on two Sn atoms. Bader’s analysis of the electron density was used to determine these partial charges, as well as the electronic spin population (N_spin) of each Sn atom in the dimer. The calculated values of q(Sn₂) and N_spin(Sn) for the most stable adsorption configurations are presented in

Table 3. Charge and spin distributions for the Sn dimer adsorbed at the regular and defective centers of MgO(100). The results derived from Model 1 and Model 2 of MgO(100) are shown without and in parentheses, respectively. All values are given in e.

Adsorption Center	2S + 1	q(Sn2)	Nspin(Sn1)	Nspin(Sn2)
O5c	1	−0.242 (−0.299)	0.000 (0.000)	0.000 (0.000)
	3	−0.167 (−0.207)	0.639 (0.575)	1.001 (1.095)
	5	−0.149 (−0.194)	1.457 (1.393)	1.982 (2.151)
${\mathrm{F}}_{\mathrm{s}}^0$	1	−1.462 (−1.508)	0.000 (0.000)	0.000 (0.000)
	3	−1.470 (−1.515)	0.809 (0.825)	0.845 (0.871)
	5	−1.437 (−1.486)	1.537 (1.558)	1.834 (1.929)
${\mathrm{F}}_{\mathrm{s}}^{+}$	2	−0.753 (−0.779)	0.473 (0.483)	0.323 (0.313)
	4	−0.768 (−0.806)	1.499 (1.537)	0.961 (0.938)
	6	−0.688 (−0.698)	2.071 (2.082)	2.041 (2.144)
${\mathrm{F}}_{\mathrm{s}}^{2+}$	1	−0.032 (−0.077)	0.000 (0.000)	0.000 (0.000)
	3	−0.025 (−0.075)	1.126 (1.169)	0.430 (0.369)
	5	−0.054 (−0.064)	1.890 (1.894)	1.297 (1.345)

. The q(Sn₂) values clearly indicate that the dimer adsorbed at the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers behaves as a strong electron acceptor. The significant amount of two extra electrons largely localized in the cavity of ${\mathrm{F}}_{\mathrm{s}}^0$ can be easily transferred and, as a result, the adsorbed dimer acquires an ancillary charge of ca. 1.5 e. Half this amount of electron charge is accumulated by Sn₂ at the ${\mathrm{F}}_{\mathrm{s}}^{+}$ center, whereas at ${\mathrm{F}}_{\mathrm{s}}^{2+}$, the dimer remains practically neutral. This effect of oxygen vacancies on q is common to the adsorption of Sn₂ and a single Sn atom (Table 2). Our calculations produce a small negative charge for the Sn dimer at the O_5c center, which is in contradiction to the result of a previous theoretical study [24]. The periodic DFT calculations with a plane–wave basis set predicted a loss of a small amount of electron charge for the Sn dimer adsorbed on the defect-free MgO(100) surface [24]. The N_spin values listed in Table 3 prove that significant spin populations reside on the atoms of the Sn dimer in higher spin states upon adsorption on MgO(100).

It is interesting to examine how the defective centers affect the highest occupied molecular orbital (HOMO) for the adsorbed dimer. The HOMO is essential for describing the reactivity of chemical systems [78], including metal atoms and clusters adsorbed on MgO(100) [29,37,58]. The contours of the HOMO for the lowest-energy structures of Sn₂ adsorbed on the regular and defective MgO(100) surfaces are plotted in Figure 4. While the shapes of the HOMO for Sn₂ at the O_5c and ${\mathrm{F}}_{\mathrm{s}}^0$ centers look almost identical, the presence of charged oxygen vacancies noticeably influences the shape of the HOMO for the dimer adsorbed at the ${\mathrm{F}}_{\mathrm{s}}^{+}$ or ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center. The orbital composition analysis of the HOMOs in Figure 4 reveals that these orbitals contain leading contributions from atomic orbitals of both Sn atoms, regardless of the surface center adsorbing the dimer. The contributions from the Sn atoms add up to at least 64% and this percentage total reaches a maximum of 74% at the upper end of the following sequence Sn₂/${\mathrm{F}}_{\mathrm{s}}^{2+}$ < Sn₂/${\mathrm{F}}_{\mathrm{s}}^{+}$ < Sn₂/${\mathrm{F}}_{\mathrm{s}}^0$ < Sn₂/O_5c. The Sn atoms of the dimer adsorbed at O_5c, ${\mathrm{F}}_{\mathrm{s}}^0$ or ${\mathrm{F}}_{\mathrm{s}}^{+}$ provide almost exclusively their p-type atomic orbitals to form the HOMO whereas the HOMO of Sn₂/${\mathrm{F}}_{\mathrm{s}}^{2+}$ also exhibits minor contributions from the s- and d-type orbitals of the Sn atoms (these contributions amount to 8% in total).

Next, we discuss the tendency of Sn atoms to dimerize on the regular and defective MgO(100) surfaces. The calculated values of $E_{\dim }^{\mathrm{gas}}$ and $E_{\dim }^{\mathrm{ads}}$ are collected in

Table 4. Dimerization energies for the Sn dimer adsorbed at the regular and defective centers of MgO(100). The results derived from Model 1 and Model 2 of MgO(100) are shown without and in parentheses, respectively. All values are given in eV.

Adsorption Center	2S + 1	${\mathit{E}}_{\mathbf{dim}}^{\mathbf{gas}}$	${\mathit{E}}_{\mathbf{dim}}^{\mathbf{ads}}$
O5c	1	−3.63 (−3.43)	−1.81 (−1.42)
	3	−2.70 (−2.58)	−0.89 (−0.57)
	5	−1.80 (−1.72)	0.02 (0.29)
${\mathrm{F}}_{\mathrm{s}}^0$	1	−3.87 (−3.78)	−1.86 (−1.77)
	3	−2.91 (−2.76)	−0.90 (−0.74)
	5	−1.78 (−1.71)	0.23 (0.30)
${\mathrm{F}}_{\mathrm{s}}^{+}$	2	−3.55 (−3.35)	−1.54 (−1.34)
	4	−2.73 (−2.41)	−0.72 (−0.40)
	6	−1.28 (−1.08)	0.73 (0.93)
${\mathrm{F}}_{\mathrm{s}}^{2+}$	1	−3.48 (−3.37)	−1.47 (−1.36)
	3	−3.60 (−3.54)	−1.59 (−1.53)
	5	−2.70 (−2.56)	−0.69 (−0.55)

. From the negative values of $E_{\dim }^{\mathrm{gas}}$, it can be deduced that the Sn dimer can be easily formed through the binding of a gas-phase Sn atom to another Sn atom already adsorbed at any of the investigated centers on MgO(100) and leading to any of the investigated spin states. According to $E_{\dim }^{\mathrm{gas}}$, the kind of oxygen vacancy has a minor influence on the energetic effect of dimerization process. The $E_{\dim }^{\mathrm{gas}}$ values are more negative than the E_bind energy of a free Sn₂ molecule (

Table 5. Bond length, binding energy, and selected QTAIM parameters at the bond critical point for an isolated Sn dimer. The bond length is given in Å, the energy is in eV, while the QTAIM parameters are in a.u.

2S + 1	Bond Length	Ebind	ρb	∇2ρb	Gb/ρb	Hb/ρb	δ
1	2.830	−2.41	0.0547	0.0050	0.1511	−0.3405	2.05
3	2.823	−2.58	0.0553	0.0054	0.1516	−0.3432	2.05
5	2.996	−1.63	0.0350	0.0201	0.1994	−0.2427	1.35

), which results from an additional energy gain due to the binding of one gas-phase Sn atom to the MgO(100) surface. The values of $E_{\dim }^{\mathrm{ads}}$ indicate that the formation of Sn₂ at any of the investigated centers on MgO(100), as a result of combining two already adsorbed Sn atoms, one of which is adsorbed at the O_5c center by definition, is associated with an energy gain ($E_{\dim }^{\mathrm{ads}}$ < 0) unless the dimer is in the highest spin state. On the one hand, such dimerization of two already adsorbed Sn atoms is energetically less favorable than the dimerization through the capture of one gas-phase Sn atom and combining with another already adsorbed Sn atom. On the other hand, the $E_{\dim }^{\mathrm{ads}}$ energies for the most stable adsorption configurations of Sn₂ are below −1.5 eV and such energy gains should be sufficient for an Sn atom to overcome diffusion barriers while moving across the MgO(100) surface to collide with another adsorbed Sn atom. Furthermore, the $E_{\dim }^{\mathrm{ads}}$ energies for the most stable adsorption configurations of Sn₂ are less negative than the E_bind energy of a free Sn₂ molecule. This suggests that the Sn-Sn bond in the supported dimer is weaker than in a free Sn₂ molecule. In other words, the MgO(100) surface exerts a certain effect on the Sn-Sn bond of the dimer deposited on this surface. The values of $E_{\dim }^{\mathrm{ads}}$ for the preferred configurations of Sn₂ adsorbed at the ${\mathrm{F}}_{\mathrm{s}}^0$, ${\mathrm{F}}_{\mathrm{s}}^{+}$, and ${\mathrm{F}}_{\mathrm{s}}^{2+}$ centers do not differ much from the $E_{\dim }^{\mathrm{ads}}$ value for the O_5c center. Thus, these defective centers seem not to have a special role in promoting the dimerization, as compared to the regular O_5c center on MgO(100).

Finally, the QTAIM topological analysis of the electron density was performed to characterize the properties of the Sn-Sn bond in the dimer adsorbed at the regular and defective centers on MgO(100). This analysis detected a bond path connecting the Sn atoms of each dimer adsorbed at the investigated centers and in all considered spin multiplicities. The bond critical point associated with this bond path was characterized in terms of such parameters as the electron density (ρ_b), its Laplacian (∇²ρ_b), the amount of kinetic energy (G_b/ρ_b), and the amount of total energy (H_b/ρ_b). Additionally, the electron delocalization index (δ) between the Sn atoms of the adsorbed dimer was evaluated within the framework of the QTAIM. The calculated values of the aforementioned parameters for the most stable adsorption configurations are collected in

Table 6. Selected QTAIM parameters at the bond critical point of the Sn-Sn bond in the Sn dimer adsorbed at the regular and defective centers of MgO(100). The results derived from Model 1 and Model 2 of MgO(100) are shown without and in parentheses, respectively. All values are given in a.u.

Adsorption Center	2S + 1	ρb	∇2ρb	Gb/ρb	Hb/ρb	δ
O5c	1	0.0532 (0.0543)	0.0088 (0.0099)	0.1511 (0.1498)	−0.3320 (−0.3363)	1.61 (1.65)
	3	0.0505 (0.0518)	0.0050 (0.0055)	0.1484 (0.1476)	−0.3180 (−0.3251)	1.47 (1.51)
	5	0.0320 (0.0330)	(0.0167) (0.0163)	0.1930 (0.1877)	−0.2203 (−0.2279)	0.95 (0.94)
${\mathrm{F}}_{\mathrm{s}}^0$	1	0.0550 (0.0566)	0.0238 (0.0269)	0.1717 (0.1710)	−0.3446 (−0.3519)	1.77 (1.86)
	3	0.0414 (0.0434)	0.0056 (0.0067)	0.1501 (0.1513)	−0.2651 (−0.2779)	1.10 (1.19)
	5	0.0323 (0.0347)	0.0128 (0.0133)	0.1724 (0.1702)	−0.2156 (−0.2327)	0.94 (1.01)
${\mathrm{F}}_{\mathrm{s}}^{+}$	2	0.0527 (0.0543)	0.0115 (0.0133)	0.1585 (0.1593)	−0.3326 (−0.3402)	1.51 (1.58)
	4	0.0393 (0.0424)	0.0070 (0.0050)	0.1506 (0.1448)	−0.2584 (−0.2753)	0.96 (1.04)
	6	0.0250 (0.0293)	0.0155 (0.0169)	0.2026 (0.1983)	−0.1695 (−0.2037)	0.74 (0.84)
${\mathrm{F}}_{\mathrm{s}}^{2+}$	1	0.0501 (0.0514)	0.0026 (0.0037)	0.1448 (0.1468)	−0.3180 (−0.3259)	1.30 (1.33)
	3	0.0503 (0.0521)	0.0036 (0.0032)	0.1461 (0.1457)	−0.3202 (−0.3285)	1.30 (1.32)
	5	0.0293 (0.0310)	0.0131 (0.0144)	0.1838 (0.1871)	−0.1993 (−0.2099)	0.73 (0.79)

. As can be seen in this table, the bond critical point between the Sn atoms of the adsorbed dimer is described by a relatively low value of ρ_b and a positive yet very low ∇²ρ_b value. The value of G_b/ρ_b is much smaller than unity, while H_b/ρ_b adopts a negative value, which signals a high degree of covalency. Such QTAIM characteristics are indicative of a typical metal–metal bond [79]. The elongation of the Sn-Sn bond in the adsorbed dimer in higher spin states is associated with the decreased values of ρ_b. As evidenced by the values of δ, the average number of electrons delocalized between the Sn atoms of the dimer adsorbed in the highest considered spin states is reduced significantly, which may suggest a weakening of the Sn-Sn bond. The QTAIM properties of the Sn-Sn bond in the most stable adsorption configurations depend to a small extent on the kind of the investigated adsorption center. Comparing these results with the corresponding QTAIM properties of a free Sn₂ molecule (Table 5) reveals that the Sn-Sn bond does not change drastically while the dimer adsorbs on MgO(100). This is in line with the previous finding coming from the comparison of $E_{\dim }^{\mathrm{ads}}$ and E_bind.

4. Conclusions

The adsorption of an Sn dimer at the O_5c, ${\mathrm{F}}_{\mathrm{s}}^0$, ${\mathrm{F}}_{\mathrm{s}}^{+}$ and ${\mathrm{F}}_{\mathrm{s}}^{2+}$ centers of MgO(100) has been explored at the atomic level by means of first-principles DFT calculations. The characterization of Sn₂ at the surface oxygen vacancies has been reported here for the first time. When the Sn dimer adsorbs at the defective centers, one of its Sn atoms sits atop the cavity of a defect, while another Sn atom binds to one of the oxygen anions neighboring on this cavity. The E_ads energy of Sn₂ adsorption at the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers is more favorable than the adsorption at the regular O_5c center. At these defective centers the Sn dimer is adsorbed with a greater energy gain than the dimers of other metals, e.g., Au₂. A strong interaction between Sn₂ and the O_5c, ${\mathrm{F}}_{\mathrm{s}}^0$, and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers gives rise to spin pairing while the triplet spin multiplicity of a free Sn dimer tends to be preserved upon its adsorption at the ${\mathrm{F}}_{\mathrm{s}}^{2+}$ center. The dimer adsorbed at the ${\mathrm{F}}_{\mathrm{s}}^0$ and ${\mathrm{F}}_{\mathrm{s}}^{+}$ centers acquires a significant amount of ancillary electron charge, in contrast to ${\mathrm{F}}_{\mathrm{s}}^{2+}$, where Sn₂ remains practically neutral. The calculated $E_{\dim }^{\mathrm{ads}}$ energy indicates a possibility that two already adsorbed Sn atoms may actually dimerize at all four centers considered in this study. The QTAIM analysis reveals that the features of the Sn-Sn bond do not change drastically while the dimer adsorbs on MgO(100) and preserves its electronic spin state.