First-Principles Study on the Migration and Release Properties of Xe on the Surface of Uranium Mononitride
Abstract
1. Introduction
2. Method
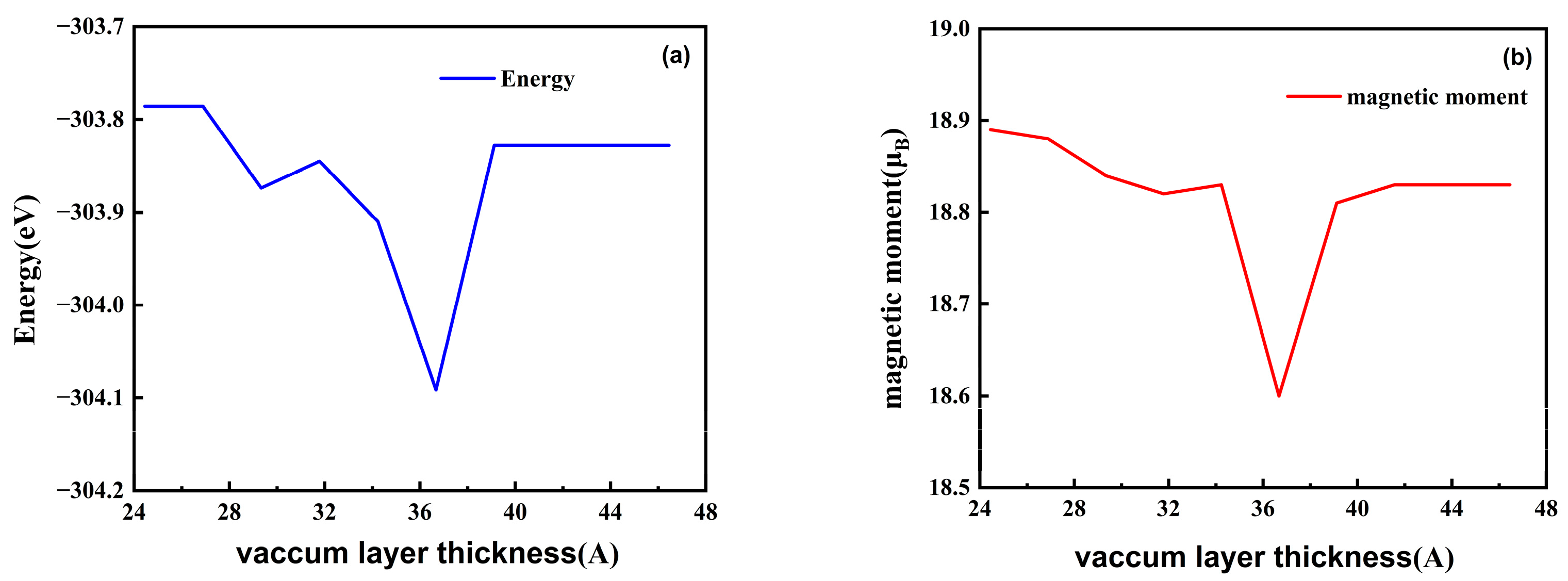
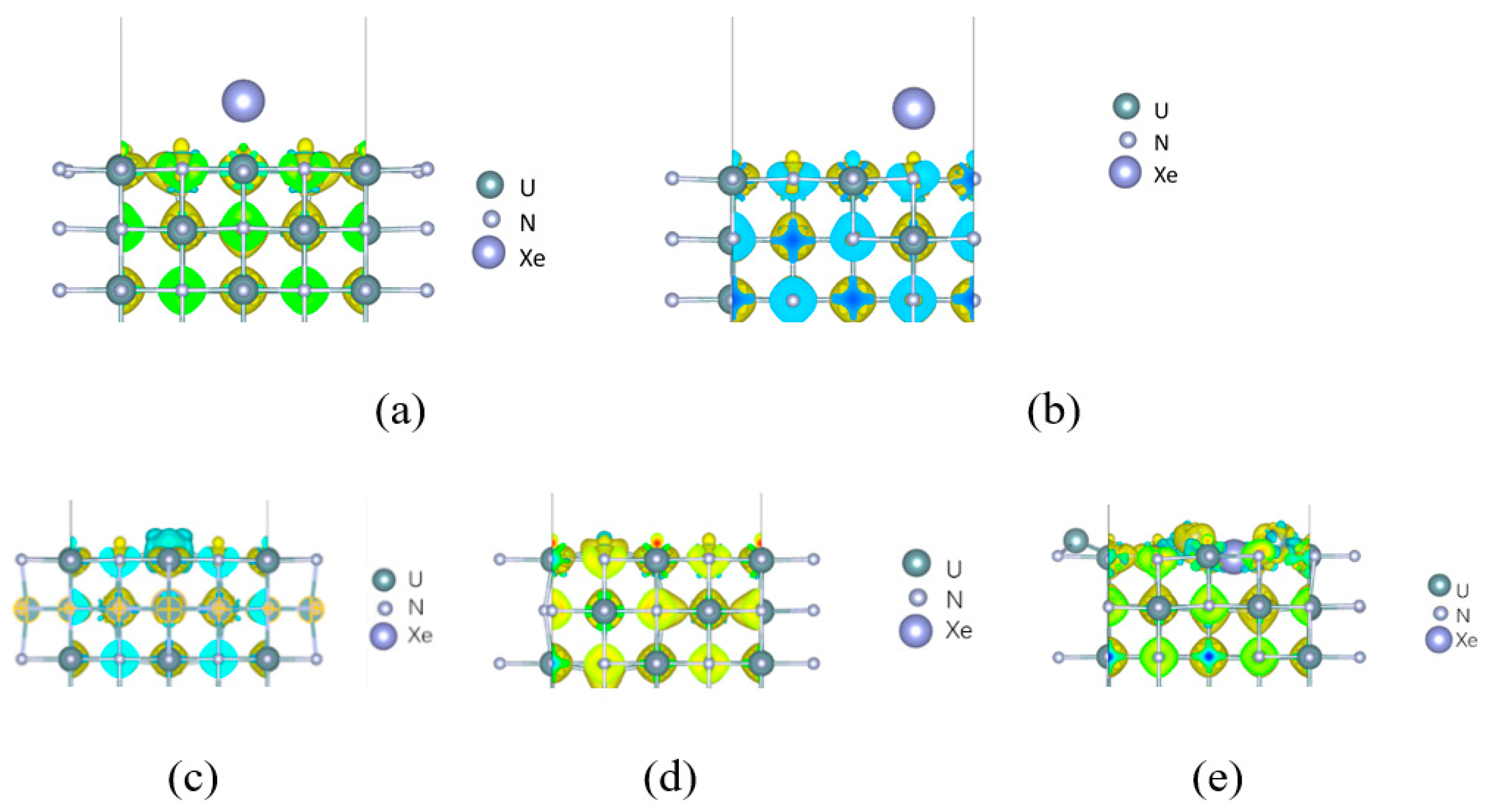
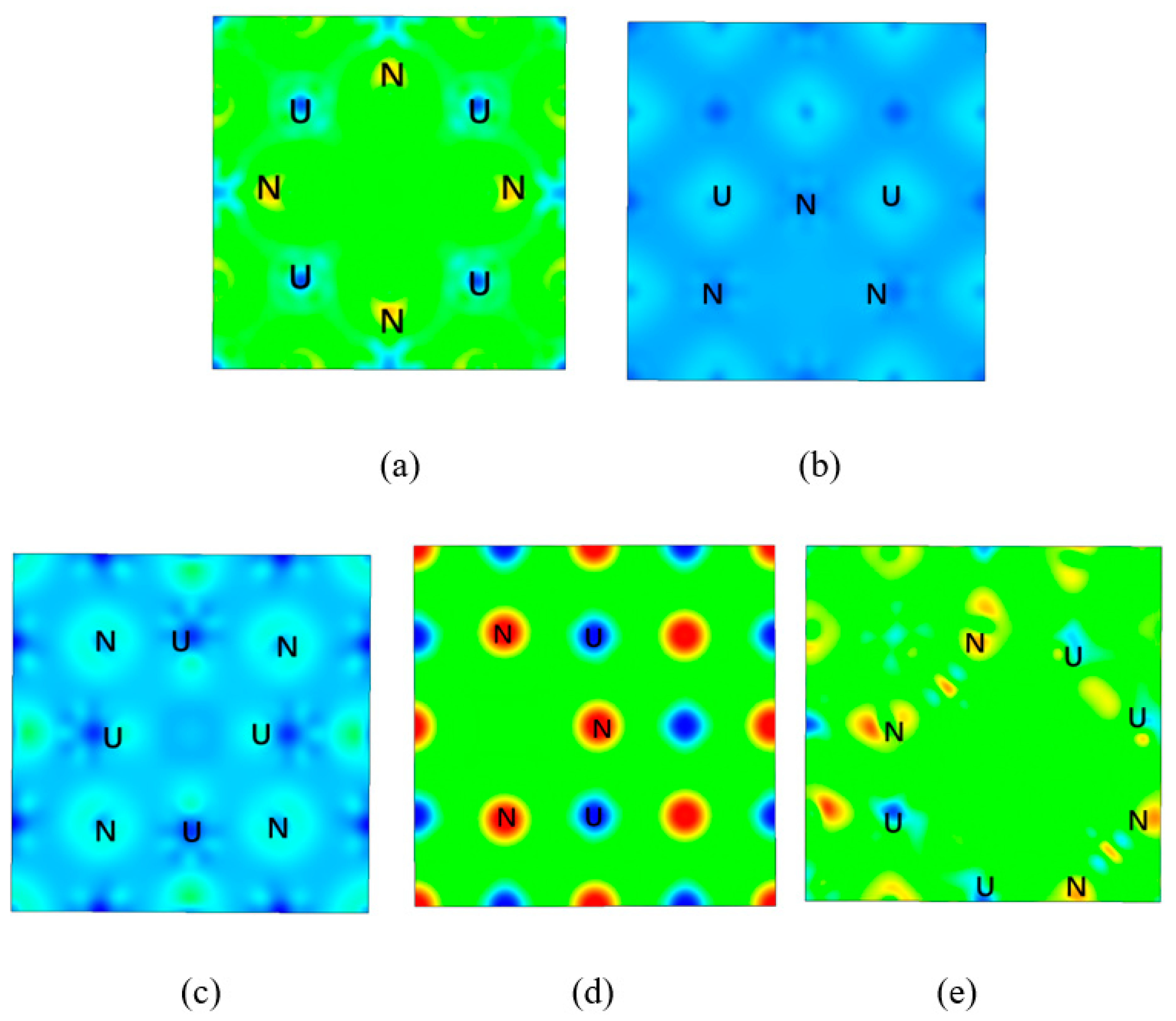
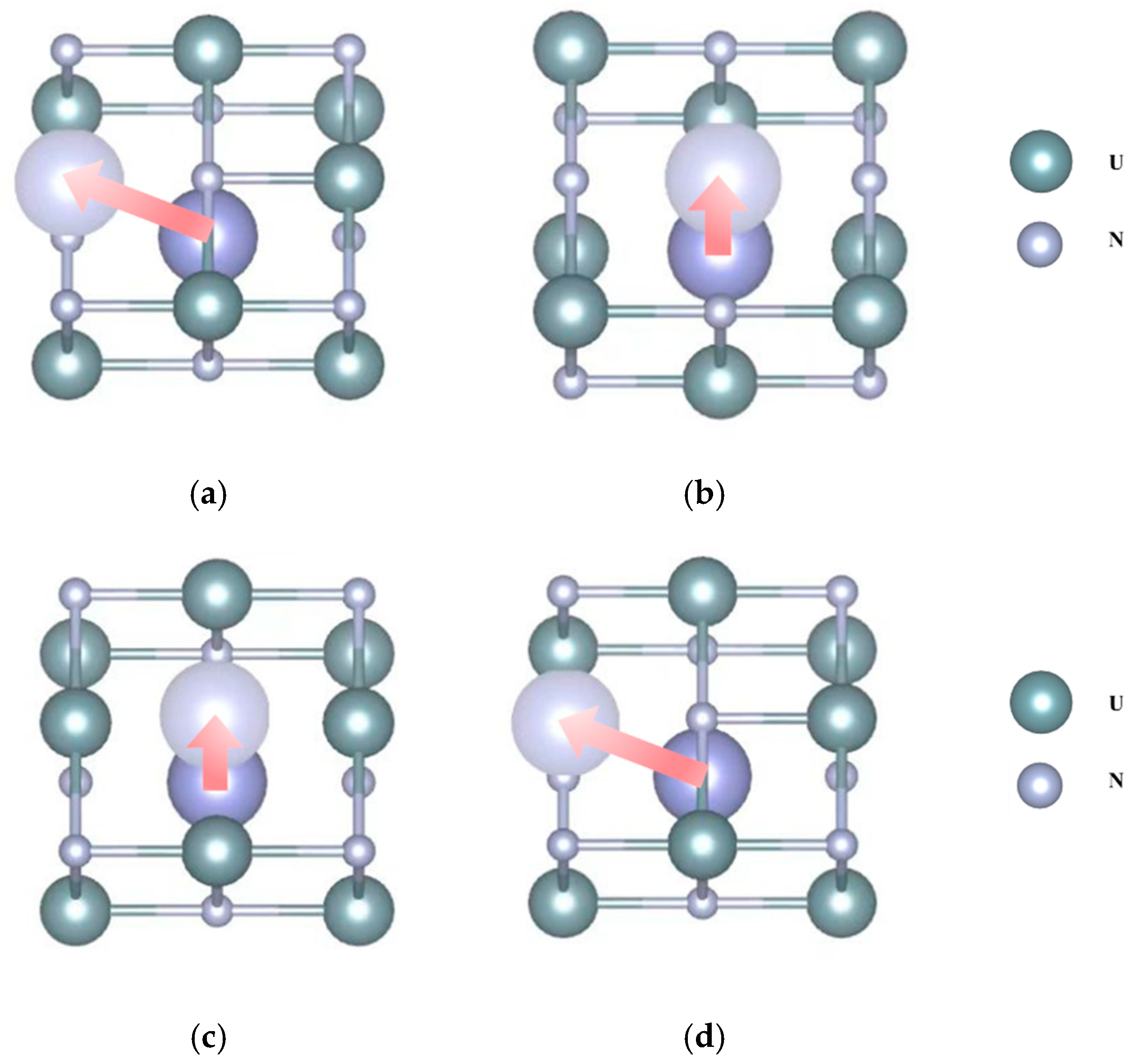
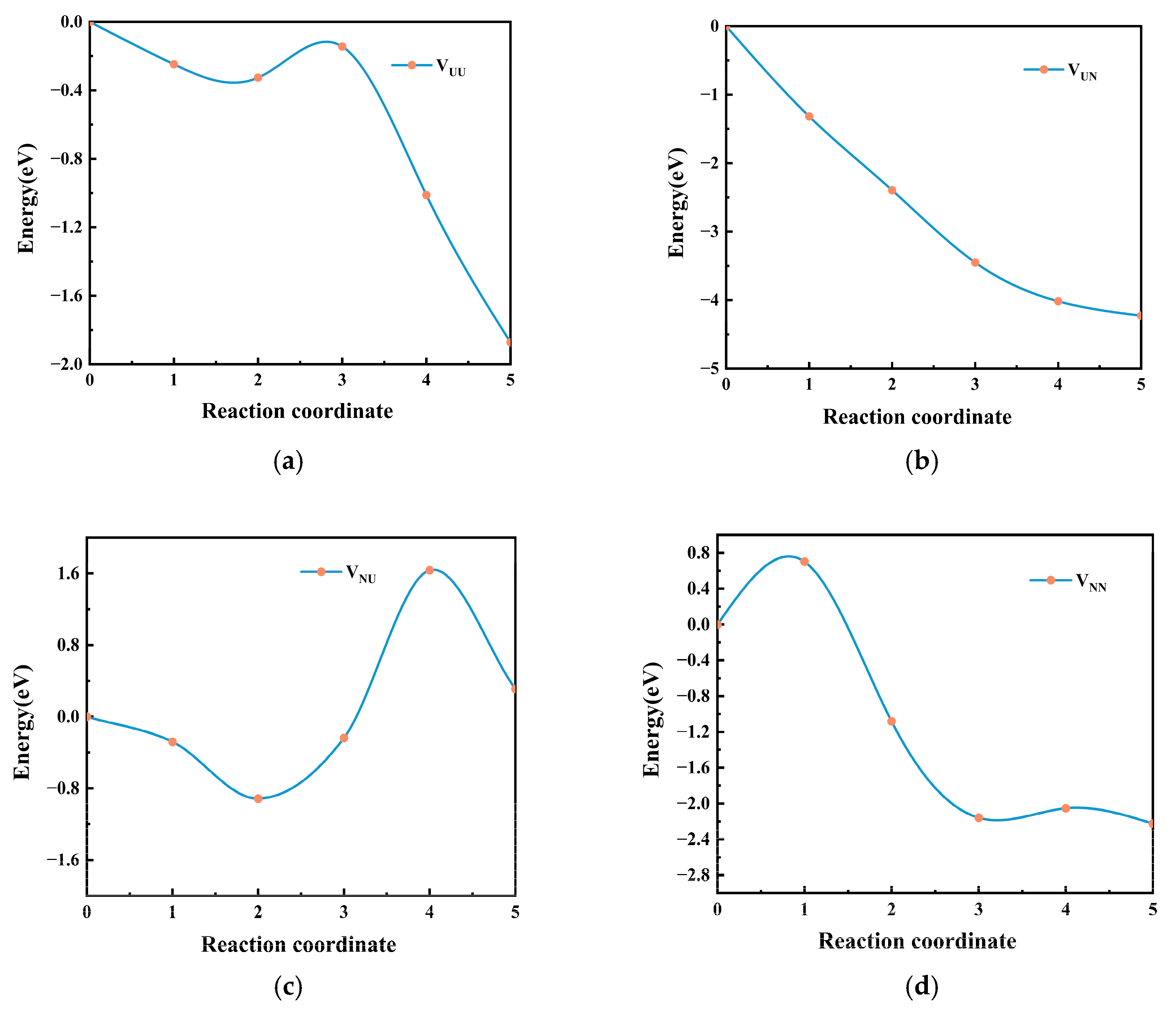
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watkins, J.K.; Gonzales, A.; Wagner, A.R.; Sooby, E.S.; Jaques, B.J. Challenges and opportunities to alloyed and composite fuel architectures to mitigate high uranium density fuel oxidation: Uranium mononitride. J. Nucl. Mater. 2021, 553, 153048. [Google Scholar] [CrossRef]
- Mishchenko, Y.; Johnson, K.D.; Jädernäs, D.; Wallenius, J.; Lopes, D.A. Uranium nitride advanced fuel: An evaluation of the oxidation resistance of coated and doped grains. J. Nucl. Mater. 2021, 556, 153249. [Google Scholar] [CrossRef]
- Gong, B.; Yao, T.; Lei, P.; Cai, L.; Metzger, K.E.; Lahoda, E.J.; Boylan, F.A.; Mohamad, A.; Harp, J.; Nelson, A.T.; et al. U3Si2 and UO2 composites densified by spark plasma sintering for accident-tolerant fuels. J. Nucl. Mater. 2020, 534, 152147. [Google Scholar] [CrossRef]
- Watkins, J.K.; Butt, D.P.; Jaques, B.J. Microstructural degradation of UN and UN-UO2 composites in hydrothermal oxidation conditions. J. Nucl. Mater. 2019, 518, 30–40. [Google Scholar] [CrossRef]
- Tonks, M.; Andersson, D.; Devanathan, R.; Dubourg, R.; El-Azab, A.; Freyss, M.; Iglesias, F.; Kulacsy, K.; Pastore, G.; Phillpot, S.R.; et al. Unit mechanisms of fission gas release: Current understanding and future needs. J. Nucl. Mater. 2018, 504, 300–317. [Google Scholar] [CrossRef]
- Liu, R.; Zhou, W.; Prudil, A.; Chan, P.K. Multiphysics modeling of UO2-SiC composite fuel performance with enhanced thermal and mechanical properties. Appl. Therm. Eng. 2016, 107, 86–100. [Google Scholar] [CrossRef]
- Guo, J.; Lai, H.; Zhou, W.; Wei, J. Fission Gas Behaviors and Relevant Phenomena in Different Nuclear Fuels: A Review of Models and Experiments. Front. Energy Res. 2022, 10, 766865. [Google Scholar] [CrossRef]
- Amato, I.; Colombo, R.L.; Grappiolo, G.C. Grain boundary grooving in uranium dioxide. Solid State Commun. 1966, 4, 237–239. [Google Scholar] [CrossRef]
- Reynolds, G.L. The surface self-diffusion of uranium dioxide. J. Nucl. Mater. 1967, 24, 69–73. [Google Scholar] [CrossRef]
- Henney, J.; Jones, J.W.S. Surface-diffusion studies on UO2 and MgO. J. Mater. Sci. 1968, 3, 158–164. [Google Scholar] [CrossRef]
- Maiya, P.S. Surface diffusion, surface free energy, and grain-boundary free energy of uranium dioxide. J. Nucl. Mater. 1971, 40, 57–65. [Google Scholar] [CrossRef]
- Marlowe, M.O.; Kaznoff, A.I. Tracer study of the surface diffusivity of UO2. J. Nucl. Mater. 1968, 25, 328–333. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Olander, D.R. Tracer surface diffusion on uranium dioxide. Surf. Sci. 1984, 136, 82–102. [Google Scholar] [CrossRef]
- Robertson, W.M. Surface diffusion of oxides (A review). J. Nucl. Mater. 1969, 30, 36–49. [Google Scholar] [CrossRef]
- Olander, D.R. Interpretation of tracer surface diffusion experiments on UO2—roles of gas and solid transport processes. J. Nucl. Mater. 1981, 96, 243–254. [Google Scholar] [CrossRef]
- Auskern, A.B.; Belle, J. Uranium ion self diffusion in UO2. J. Nucl. Mater. 1961, 3, 311–319. [Google Scholar] [CrossRef]
- Claisse, A.; Schuler, T.; Lopes, D.A.; Olsson, P. Transport properties in dilute UN(X) solid solutions (X = Xe, Kr). Phys. Rev. B 2016, 94, 174302. [Google Scholar] [CrossRef]
- Muntaha, A.; Chatterjee, S.; Blondel, S.; Aagesen, L.; Andersson, D.; Wirth, B.D.; Tonks, M.R. Impact of grain boundary and surface diffusion on predicted fission gas bubble behavior and release in UO2 fuel. J. Nucl. Mater. 2024, 594, 155032. [Google Scholar] [CrossRef]
- Feng, B.; Kazimi, M.S.; Forget, B. Feasibility of Breeding in Hard Spectrum Boiling Water Reactors with Oxide and Nitride Fuels. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2011. [Google Scholar]
- Deforest, D.L. Transient Fission Gas Behavior in Uranium Nitride Fuel Under Proposed Space Applications. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 1991. [Google Scholar]
- Klipfel, M.; Uffelen, P.V. Ab initio modelling of volatile fission products in uranium mononitride. J. Nucl. Mater. 2012, 422, 137–142. [Google Scholar] [CrossRef]
- Nie, J.L.; Ao, L.; Zu, X.T.; Huang, H.; Liu, K.Z. First-principles study of oxygen adsorption and diffusion on the UN(001) surface. Phys. Scr. 2015, 90, 125801. [Google Scholar] [CrossRef]
- Bocharov, D.; Gryaznov, D.; Zhukovskii, Y.; Kotomin, E. DFT calculations of point defects on UN(001) surface. Surf. Sci. 2011, 605, 396–400. [Google Scholar] [CrossRef]
- Andersson, D.A.; Uberuaga, B.P.; Nerikar, P.V.; Unal, C.; Stanek, C.R. U and Xe transport in UO2±x: Density functional theory calculations. Phys. Rev. B—Condens. Matter Mater. Phys. 2011, 84, 054105. [Google Scholar] [CrossRef]
- Ono, T.; Hirose, K. Real-space density-functional calculations for transport properties of nanostructures. J. Comput. Theor. Nanosci. 2007, 4, 840–859. [Google Scholar] [CrossRef]
- Ono, T.; Heide, M.; Atodiresei, N.; Baumeister, P.; Tsukamoto, S.; Blügel, S. Real-space electronic structure calculations with full-potential all-electron precision for transition metals. Phys. Rev. B 2010, 82, 205115. [Google Scholar] [CrossRef]
- Iwata, J.I. First-principles calculations for extremely large systems by parallel computations based on the order-N3 real-space density-functional theory. J. Comput. Theor. Nanosci. 2009, 6, 2514–2520. [Google Scholar] [CrossRef]
- Wang, Y.C.; Jiang, H. Local screened Coulomb correction approach to strongly correlated d-electron systems. J. Chem. Phys. 2019, 150, 154116. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B Condens. Matter 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, B.; Zhang, Q.; Liu, H.; Song, H. Theoretical insights into the hydroxyl-promoted H2 releasing reaction after H2O splitting on Pu-oxide surfaces. J. Nucl. Mater. 2023, 585, 154642. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, B.; Zhang, Q.; Liu, H.; Song, H. The reaction mechanism of CO2 on PuO2 and α-Pu2O3 surfaces. J. Nucl. Mater. 2025, 603, 155451. [Google Scholar] [CrossRef]
- South, C.J.; Roy, L.E. Insights into the thermal decomposition of plutonium(IV) oxalate—A DFT study of the intermediate structures. J. Nucl. Mater. 2021, 549, 152864. [Google Scholar] [CrossRef]
- Andersson, D.; Wang, G.; Yang, P.; Beeler, B. KCl-UCl3 molten salts investigated by Ab Initio Molecular Dynamics (AIMD) simulations: A comparative study with three dispersion models. J. Nucl. Mater. 2024, 599, 155226. [Google Scholar] [CrossRef]
- Duemmler, K.; Andersson, D.; Beeler, B. First-principles investigation of the thermophysical properties of NaCl, PuCl3, and NaCl-PuCl3 Molten salts. J. Nucl. Mater. 2024, 591, 154902. [Google Scholar] [CrossRef]
- Andersson, D.A.; Beeler, B.W. Ab initio molecular dynamics (AIMD) simulations of NaCl, UCl3 and NaCl-UCl3 molten salts. J. Nucl. Mater. 2022, 568, 153836. [Google Scholar] [CrossRef]
- Yang, L.; Kaltsoyannis, N. Incorporation of Kr and Xe in Uranium Mononitride: A Density Functional Theory Study. J. Phys. Chem. C 2021, 125, 26999–27008. [Google Scholar] [CrossRef]
- Liu, F.; Ding, X.; Sun, J. High local oxygen coverage causes initial oxidation of UN(001) surface, J. Nucl. Mater. 2023, 574, 154171. [Google Scholar] [CrossRef]
- Fathurrahman, F.; Kasai, H. Density functional study of hydrazine N-N bond cleaving on 3d metal surfaces. Surf. Sci. 2015, 641, 191–197. [Google Scholar] [CrossRef]
- Chen, C.; Niu, J.; Huang, H.; Zhu, D.; Nie, J.-F.; Yuan, G. Basal-plane stacking fault energies of biodegradable Zn-based alloys: A first-principles study of alloying effects. Mater. Lett. 2022, 309, 131413. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Y.; Liu, Y.; Wang, Z.; Wärnå, J.; Xu, Z.; Zhang, P. Investigating the solution and diffusion properties of hydrogen in α-Uranium by first-principles calculations. Prog. Nucl. Energy 2020, 122, 103268. [Google Scholar] [CrossRef]
- Yoon, K.S.; Hwang, C.O.; Won, T. Determination of the KMC parameters for indium diffusion in silicon substrates via an ab-initio calculation. J. Korean Phys. Soc. 2007, 50, 1651–1655. [Google Scholar] [CrossRef]
- Yoon, K.S.; Won, T. Ab-initio study with transition state theory (TST) for the calculation of the barrier height of migration energy of neutral indium in silicon. Solid State Phenom. 2007, 124-126, 1681–1684. [Google Scholar] [CrossRef]
- Mei, Z.G.; Liang, L.; Yacout, A.M. First-principles study of fission gas incorporation and migration in zirconium nitride. Comput. Mater. Sci. 2017, 133, 175–184. [Google Scholar] [CrossRef]
| Functions | Lattice Constants (Å) | Magnetic Moment (μB) |
|---|---|---|
| PW91 | 4.87 | 1.17 |
| PBE | 4.868 | 1.25 |
| Model | This Work | Reference [23] |
|---|---|---|
| Surface U vacancy | 1.273 | 1.44 |
| Surface N vacancy | 3.753 | 3.70 |
| Subsurface U vacancy | 2.756 | 3.09 |
| Subsurface N vacancy | 4.413 | 4.33 |
| Models | Incorporation Energies (eV) |
|---|---|
| Xe occupies a surface U atom vacancy | 1.19 |
| Xe occupies a surface N atom vacancy | 4.10 |
| Xe occupies an interstitial site between the surface and subsurface layers | 8.63 |
| Xe occupies a subsurface U atom vacancy | 7.78 |
| Xe occupies a subsurface N atom vacancy | 12.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rui, T.; Lan, Y.; Ma, Z.; Lu, L.; Wang, Y.; Yu, Y.; Deng, M.; Lan, T.; Zhao, Z.; Wang, J.; et al. First-Principles Study on the Migration and Release Properties of Xe on the Surface of Uranium Mononitride. Crystals 2025, 15, 409. https://doi.org/10.3390/cryst15050409
Rui T, Lan Y, Ma Z, Lu L, Wang Y, Yu Y, Deng M, Lan T, Zhao Z, Wang J, et al. First-Principles Study on the Migration and Release Properties of Xe on the Surface of Uranium Mononitride. Crystals. 2025; 15(5):409. https://doi.org/10.3390/cryst15050409
Chicago/Turabian StyleRui, Tianhao, Yulin Lan, Zhuangzhuang Ma, Linyuan Lu, Yunhao Wang, Yang Yu, Mingxuan Deng, Tianxing Lan, Zhekang Zhao, Junjie Wang, and et al. 2025. "First-Principles Study on the Migration and Release Properties of Xe on the Surface of Uranium Mononitride" Crystals 15, no. 5: 409. https://doi.org/10.3390/cryst15050409
APA StyleRui, T., Lan, Y., Ma, Z., Lu, L., Wang, Y., Yu, Y., Deng, M., Lan, T., Zhao, Z., Wang, J., Li, C., & Zhang, H. (2025). First-Principles Study on the Migration and Release Properties of Xe on the Surface of Uranium Mononitride. Crystals, 15(5), 409. https://doi.org/10.3390/cryst15050409







