Understanding the Deformation and Fracture Behavior of β−HMX Crystal and Its Polymer−Bonded Explosives with Void Defects on the Atomic Scale

Abstract

The effect of the void defect on β−HMX−based polymer−bonded explosives (PBXs) for a comprehensive understanding of the deformation and fracture process is lacking. In this paper, the atomic scale model of the β−HMX crystal and its PBX is built using LAMMPS software to investigate the mechanical response under dynamic tensile conditions. The void defect considers both regular and stochastic distributions. The simulation concerns the deformation and fracture process with respect to the void size, void number, void spacing, and the stochastic characteristics. The tensile stress–strain relationship is obtained, and the fracture morphology is simulated well. The crack propagation is discussed in detail. Further, the fracture mode is compared between the single crystal and PBX. In addition, the characteristic defect parameter combines both the damage area and the void spacing, and it is used to predict the crack occurrence and propagation for the single crystal. However, for PBX, the interface between the crystal and binder determines the fracture process instead of the characteristic defect parameter.

1. Introduction

β−HMX−based (beta−1,3,5,7−tetranitro−1,3,5,7−tetraazacyclooctane) polymer−bonded explosives (PBXs), as highly particle−filled energetic composite materials, are mainly composed of β−HMX crystals and a small amount of polymer binder. In past decades, as the application of β−HMX−based PBXs increased, the mechanical behavior of PBXs was the focus. A great number of efforts to understand its deformation, damage, and fracture under different load conditions have been conducted [1,2,3]. However, it is still a great challenge to quantify the damage evolution in view of the microstructure scale. The reason for this is that, on the one hand, the differences in mechanical properties between explosive crystals and polymer binders are obvious, and the morphology of these materials is extremely complex to describe [4,5]. On the other hand, in the process of β−HMX crystal synthesis and explosive manufacturing, the formation of void defects is inevitable [6,7]. The characteristics of void defects show the stochastic distribution of the size and position. The stochastic initial void defects affect the degradation of the mechanical properties of crystals and the interface between the components, which greatly contributes to the damage evolution [8,9].

In early works, researchers designed different tests to study the mechanical response of PBXs at different scales [10,11,12]. Lots of evidence points to the hypothesis that under quasi−static loading conditions, the main failure mode under tension is interface debonding, while the main failure mode under compression is transgranular fracture [13,14]. Furthermore, to understand the strain rate effect, the dynamic mechanical response attracts much attention. By using split−Hopkinson pressure bar testing, the deformation, damage, and fracture are studied [15,16]. Picart et al. studied the dynamic response of PBXs in the medium− and high−strain−rate range using the split−Hopkinson pressure bar test [17]. Parab et al. used the high−speed X-ray phase contrast imaging technique to obtain the microstructure evolution of HMX−based PBXs under dynamic loading [18]. These results show that the strength of PBXs increases as the strain rate increases, and that the fracture mode under dynamic loading conditions is still similar to that under quasi−static loading conditions.

The aforementioned efforts provide a good basic knowledge of the fracturing of PBXs. However, for a further understanding of the microstructure of PBX, the initial void defects play an important role on the damage evolution, and it is important to study the effect of the defects [19,20]. Duart et al. designed a machined void in an HMX single crystal and measured the dynamic evolution of the morphology of the void under weak shock. The mechanical response was further analyzed [21]. The following work of Drake et al. focused on the effect of the initial crack. The result showed the process of crack propagation, and the fracture under the gas gun’s impact [22].

Due to the temporal and spatial resolution limitations of measurement, the in situ observation of the damage evolution is still difficult. In recent years, multi−scale simulations have provided some knowledge on how the initial void defects affect the mechanical response [23,24,25]. Manner et al. applied an X-ray scanning technique to rebuild the 3D geometrical microstructure of HMX−based PBXs, and developed the computational model, including the explosive crystal, polymer binder, and the interface of the two materials based on the scanning images [10]. Kang et al. developed the modified Voronoi method to build the virtual microstructure of HMX−based PBXs and discussed the effects of the initial defects on the mechanical properties [26]. Kim et al. used the mesoscale simulation method to analyze the mechanical–thermal–chemistry coupled response of PBXs under shock [27]. In these works, the constitutive material model of HMX crystal was usually simplified as the elastic model or the elastic–plastic model. However, the real mechanical response of explosive crystals is complex. Zecevic et al. used the crystal plasticity finite element method to analyze the deformation of β−HMX under dynamic loading, which described the twin growth well [28].

Also, this is an important way to study the mechanical responses of materials on the atomic scale [29,30]. Some works have focused on the response of the explosive crystals in this field, since the crystals are the main component [31,32]. Lafourcade et al. applied molecular dynamics to calibrate the plasticity critical shear stresses of explosive crystal, and it helped us to understand the plasticity slide process of explosive crystal under impact [33]. A series of works by Long et al. were conducted to study the tensile mechanical properties of the interface between explosive crystals and polymer binders [34,35]. To understand the effects of the defects, Eason designed a cylindrical pore in the oriented single explosive crystal, and the collapse of the pore under impact was simulated [36]. The stronger penetration produces more molecular rotation during and after collapse, along with a greater amount of energy convection to material away from the initial collapse zone. Li et al. analyzed the effects of the defect shape and size on the shock compression of HMX crystal using large−scale molecular dynamics [37]. These works explained the response of explosive crystals by considering the defects.

In this paper, the molecular dynamics modeling framework is developed to understand the initial void defect’s effects on the mechanical response of β−HMX crystals and its polymer−bonded explosives using LAMMPS software. The model considers the characteristics of the size, number, and distribution of the defects, and a Smith force field is used. The remaining paper consists of three parts. The first part mainly describes the force field, computational model, and the principle of the void defect generation. The second part revolves around the initial void defect’s effects on the mechanical behavior of the β−HMX crystal, referring to different void defect characteristics. The third part focuses on the initial void defect’s effect on the mechanical behavior of the β−HMX−based PBX.

2. Methods and Models

2.1. Force Field

A force field is critical to determine the interaction among the atoms. Essentially, a force field is defined as a potential energy function, referring to bonding energy and non−bonding energy. Bonding energy includes the energy produced by bond stretching, bond bending, and dihedral angle torsion, while non−bonding energy includes the interaction energy of Van Der Waals, electrostatic interaction, and hydrogen bonding.

A Smith force field is used in this work; its potential has been widely used in thermal and mechanical property simulations [38,39,40,41], and many studies have demonstrated its accuracy and effectiveness for the prediction of the crystal structure, equation of state, elastic constant, and thermal conductivity of β−HMX crystals [42]. In addition to that, Li et al. calculated the lattice constant, thermal expansion coefficient, and elastic modulus of β−HMX using this potential, which indicates that the force field is constructed correctly [43]. The total energy of a Smith force field can be written as shown in Equation (1):

$$E_{HMX}=E_{vdwl}+E_{Coul}+E_{bond}+E_{angle}+E_{dihedral}+E_{improper}$$

(1)

where $E_{vdwl}$, $E_{Coul}$, $E_{bond}$, $E_{angle}$, $E_{dihedral}$, and $E_{improper}$ represent the Van Der Waals interaction energy, electrostatic interaction energy, bond energy, angular energy, dihedral angular energy, and special bond energy, respectively.

The Van Der Waals interaction energy $E_{vdwl}$ is used to describe the interaction among molecules and atoms, and it can be calculated using Equation (2):

$$E_{vdwl}={\displaystyle \frac{A}{R^{12}}}-{\displaystyle \frac{B}{R^6}}$$

(2)

where A and B are constant parameters, representing the attractive and repulsive forces between molecules, respectively, and R is the distance between molecules. When the distance is large, the interaction means that the attractive force, on the contrary, is the repulsive force.

Electrostatic interaction energy $E_{Coul}$ describes the interaction between charged particles. The Coulomb potential function is widely used for the calculation of electrostatic interactions, which can be obtained using Equation (3):

$$E_{Coul}={\displaystyle \frac{1}{4\pi \epsilon }}\times {\displaystyle \frac{q_i{q}_j}{r_{ij}}}$$

(3)

where $\epsilon$ is the dielectric constant parameter, $q_i$ and $q_j$ are the charges of the particles, and $r_{ij}$ is the distance between the particles.

The bond energy $E_{bond}$ depends on the type and length of the bond, and it can be calculated using Equation (4):

$$E_{bond}={\displaystyle \frac{k_{bond}}{2}}\times {\left(r_{bond}-r_{eq}\right)}^2$$

(4)

where $k_{bond}$ is the bond elastic constant, $r_{bond}$ is the current bond length, and $r_{eq}$ is the equilibrium bond length.

The angular energy $E_{angle}$ depends on the type and value of the angle, and it can be calculated using Equation (5):

$$E_{angle}={\displaystyle \frac{k_{angle}}{2}}\times {\left({\theta }_{angle}-{\theta }_{eq}\right)}^2$$

(5)

where $k_{angle}$ is the angular elastic constant, ${\theta }_{angle}$ is the current angle, and ${\theta }_{eq}$ is the equilibrium angle.

The dihedral angle energy $E_{dihedral}$ depends on the type and value of the dihedral angle, and it can be calculated using Equation (6):

$$E_{dihedral}=k_{dihedral}\left[1+\cos \left(n{\phi }_{dihedral}-\delta \right)\right]$$

(6)

where $k_{dihedral}$ is the dihedral angular energy constant, $n$ is a multinominal number, ${\phi }_{dihedral}$ is the current dihedral angular value, and $\delta$ is a relative shift.

The special bond energy $E_{improper}$ refers to preventing molecules from flipping over to another mirror phase, and it can be calculated using Equation (7):

$$E_{improper}=k_{improper}{\left({\phi }_{improper}-{\phi }_{eq}\right)}^2$$

(7)

where $k_{improper}$ is the special term constant, ${\phi }_{improper}$ is the current special angle, and ${\phi }_{eq}$ is the equilibrium special angle.

For the polymer binder F2311, a COMPASS force field is widely used [44,45]. Its parameters were optimized by Sun et al. to describe the additives in PBXs, including various fluoropolymers [46]. Its potential energy can be calculated using Equation (8):

$$\begin{gathered} E_{F2311}={\sum }_b\left[{k_2\left(b-b_0\right)}^2+{k_3\left(b-b_0\right)}^3+{k_4\left(b-b_0\right)}^4\right]+{\sum }_{\theta }\left[{k_2\left(\theta -{\theta }_0\right)}^2+{k_3\left(\theta -{\theta }_0\right)}^3+{k_4\left(\theta -{\theta }_0\right)}^4\right]+ \\ {\sum }_{b,b^{\prime }}\left[{k_{b,b^{\prime }}\left(b-b_0\right)\left(b^{\prime }-b_0^{\prime }\right)}^2\right]+{\sum }_{b,\theta }\left[{k_{b,\theta }\left(b-b_0\right)\left(\theta -{\theta }_0\right)}^2\right]+{\sum }_{i,j}{\displaystyle \frac{q_i{q}_j}{r_{ij}}}+{\sum }_{i,j}{\epsilon }_{ij}\left[{2\left({\displaystyle \frac{r_{ij}^0}{r_{ij}}}\right)}^9-{3\left({\displaystyle \frac{r_{ij}^0}{r_{ij}}}\right)}^6\right] \end{gathered}$$

(8)

where the terms in the equation correspond to the bond energy, the angular energy, the chemical bond coupling energy, the bond length–bond angle coupling energy, the electrostatic interaction energy, and the Van Der Waals interaction energy, respectively.

The interface between explosive crystals and polymer binders must be considered for PBXs. Long et al. established a library of interaction potential functions, referring to different kinds of explosive crystals and polymer binders based on first principles calculation, which is used in this work [34]. A series of interface mechanical behaviors are obtained using this potential, and the tensile barrier and tensile stress are gained [34,47]. Furthermore, the total energy of the β−HMX−based PBX can be written as in Equation (9):

$$E_{total}=E_{HMX}+E_{F2311}+E_{interface}$$

(9)

The mechanical behavior of the interface is simulated in this paper, and it should be stressed that considering that there is no atom bond at the interface, but only the Van Der Waals interaction exists, in the process of dynamic stretching, the breaking and formation of bonds are not considered. The attractive interaction between interfaces is described by the Morse potential, and the repulsive interaction between all the interfaces is described by the exponential potential. Furthermore, the interface energy can be written as in Equation (10):

$$E_{interface}={\sum }_{ij}{\phi }_{ij}\left(r_{ij}\right)$$

(10)

where $ij$ denotes the atom pair across interfaces, $r_{ij}$ is the pair distance, and ${\phi }_{ij}$ is the pair interaction. Due to there being no bond between the interfaces, the pair potential function can be used.

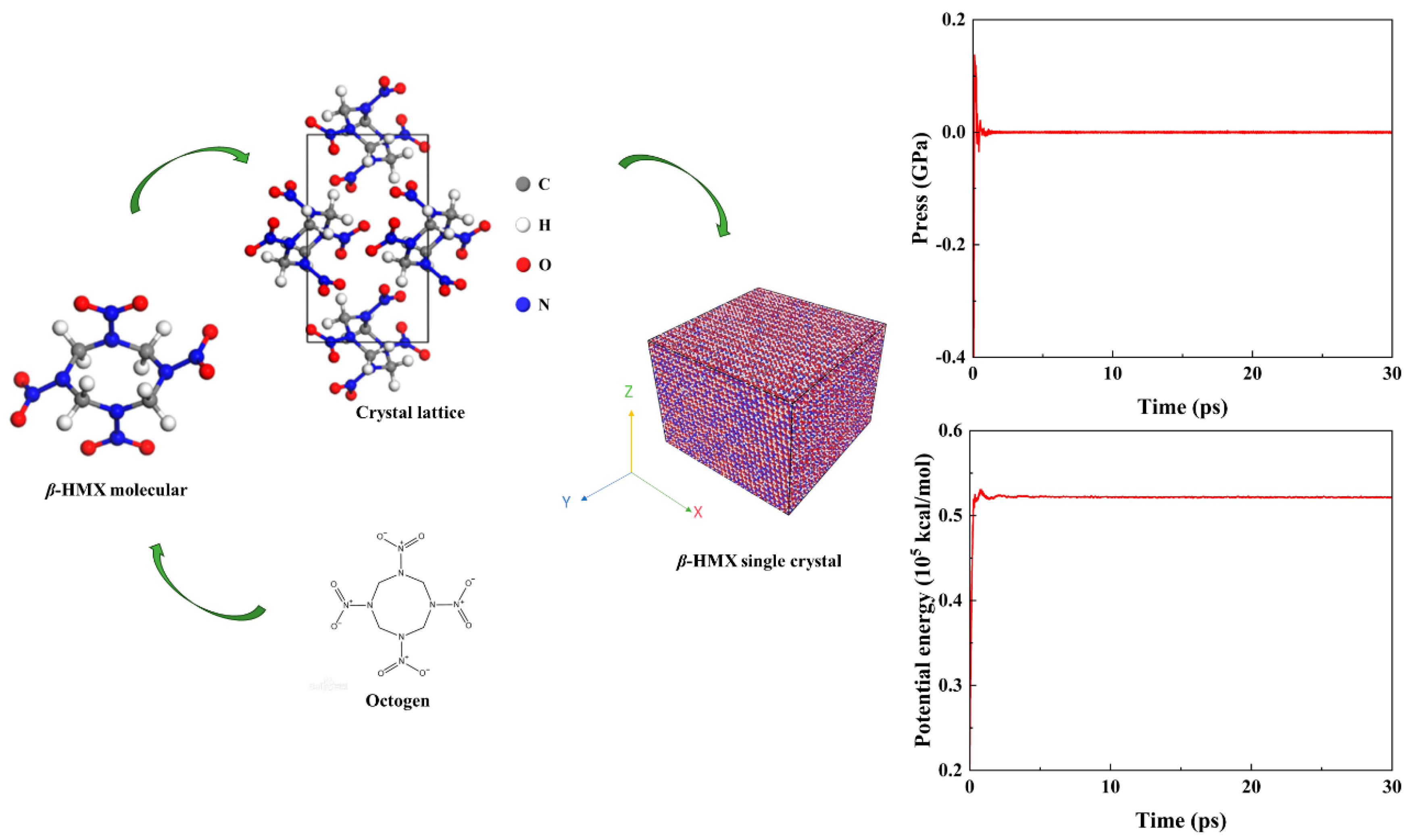
2.2. The β−HMX Single−Crystal Model

HMX has four different crystal structures α, β, γ, and δ, where type β is the most stable under room temperature and pressure. According to the crystal structure database, β−HMX crystal is the P21/c space group, and has five independent lattice constants, as shown in

Table 1. Lattice constants of β−HMX crystal [48].

Lattice Constant Parameter	a/Å	b/Å	c/Å	α	β	γ
Value	6.54	11.05	8.7	90°	124.3°	90°

[48].

In this work, a β−HMX single−crystal model is built, which contains 21,600 β−HMX molecules. In the box, X × Y × Z is 200 Å × 200 Å × 150 Å, as Figure 1 shown. It should be mentioned that the molecular always deviates from the equilibrium state in the initial arrangement, which brings high energy and strong interaction in the whole system. The relaxation must be conducted to reduce the system energy and force the conjugate gradient method, and the system can be in the equilibrium state. In this work, the relaxation condition is that the temperature is 300 K, and the relaxation time is 30 ps under the NVT ensemble. In addition, the force convergence tolerance is set to 10⁻⁸ kcal/mol/Å. Figure 1 shows how to build a stable β−HMX single−crystal model. According to the energy and stress of the system at the time, after the relaxation time 30 ps, the whole system reaches a low energy and stress, which means that the β−HMX single−crystal model is in the most stable state. Furthermore, it can be used in the following simulation.

To further verify the β−HMX single−crystal model, the aforementioned size of the box and number of molecules is used. The density and the Young’s modulus are estimated via molecular dynamic simulation.

Table 2. The Young’s modulus and density of β−HMX single crystal from test and simulation.

Parameter	Experiment	Simulation
Young’s modulus/GPa	17.48 [49]	14.50
Density/(g·cm3)	1.904 [50]	1.829

shows the results of two material parameters between a test and simulation. The density calculated is 1.829 g/cm³, while the density measured is 1.904 g/cm³ [49]. The discrepancy is only around 4%. For the Young’s modulus, the discrepancy between the test 17.48 GPa and simulation 14.50 GPa is around 17% [50]. Thus, the simulation can match the test well. It is demonstrated that a Smith force field can be used to predict the mechanical response of a β−HMX single crystal.

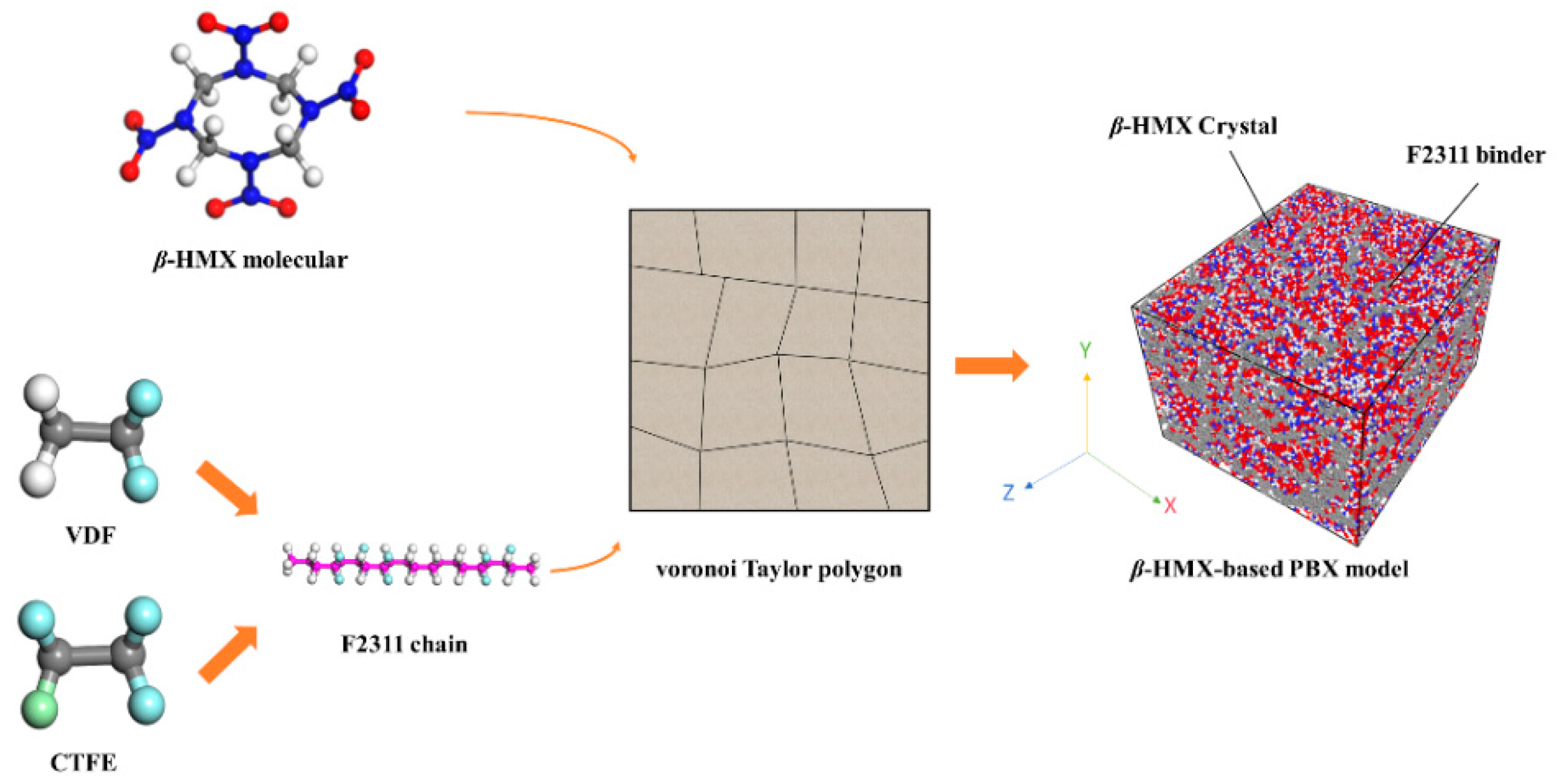
2.3. The β−HMX−Based PBX Model

To build the β−HMX−based PBX model, a three−dimensional Taylor polygon structure is created using the Voronoi method. An F2311 binder molecular with a thickness of around 10 Å is filled at the boundary of the polygon, and the polygon is stochastically filled with β−HMX crystals. Furthermore, the β−HMX−based PBX model is obtained as shown in Figure 2. The size of the model X × Y × Z is 200 Å × 200 Å × 100 Å. The density of the model is 1.825 g/cm³, which has a 1.3% discrepancy compared to the real HMX−based PBX [51].

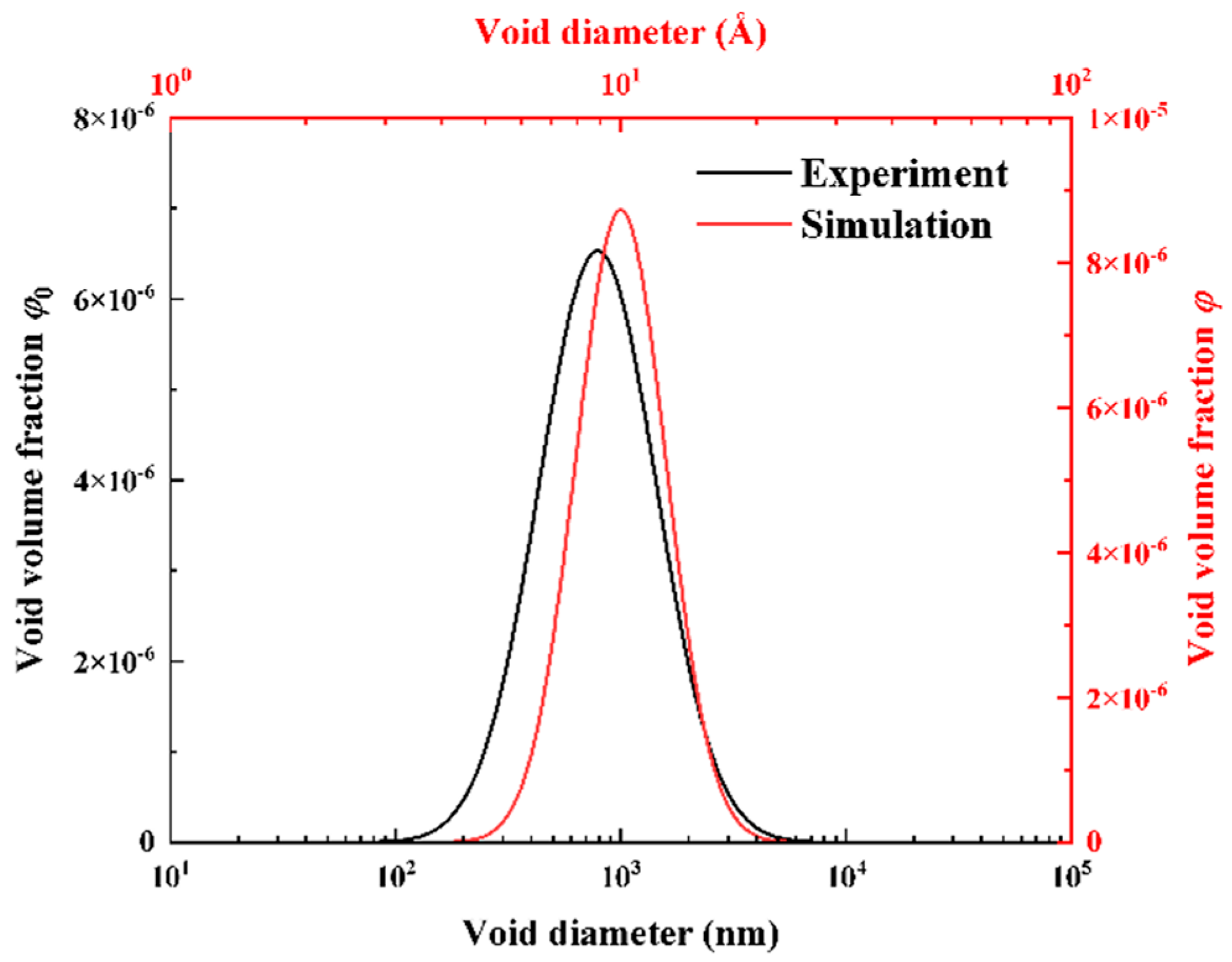
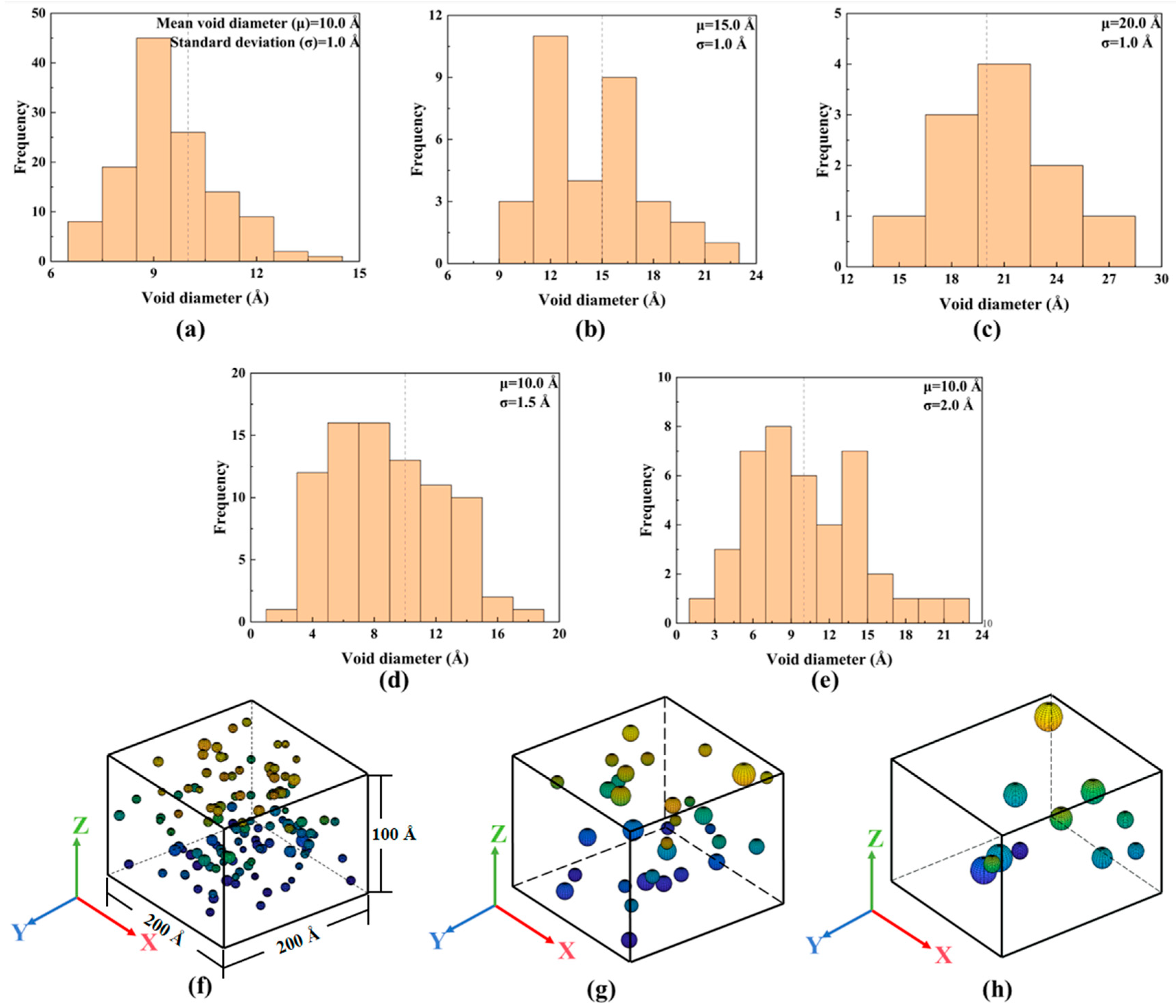
2.4. The Stochastic Void Defect Model

The real void defect follows stochastic distribution. Based on the ultra−small−angle neutron scattering technique, the void distribution inside the HMX−based PBX is obtained [52]. The experimental result shows that it approximately follows a normal distribution. Furthermore, the void volume fraction ${\phi }_0$ follows Equation (11):

$${\phi }_0=aexp\left[-{\displaystyle \frac{{\left(lg\left(x_v\right)-lg\left(\mu \right)\right)}^2}{2{\lg \left(\sigma \right)}^2}}\right]$$

(11)

where $x_v$ represents the void size, $\mu$ represents the mean, $\sigma$ represents the standard deviation, and $a$ represents the parameter.

Figure 3 shows the real void distribution, where the average value of the void size is 790 nm, and the porosity is around 1%. Considering the size of the molecular dynamic simulation, the scaling must be used to take the place of the real size, but it keeps the normal distribution. First, the average value of the void size is selected, and the Monte Carlo method is used to produce different void sizes with some variance. Afterwards, these voids are assigned to the spatial location in the box under uniform distribution, and the porosity of the model is controlled at around 1.0%. Finally, the virtual void distribution is obtained, and it is similar to in the real case.

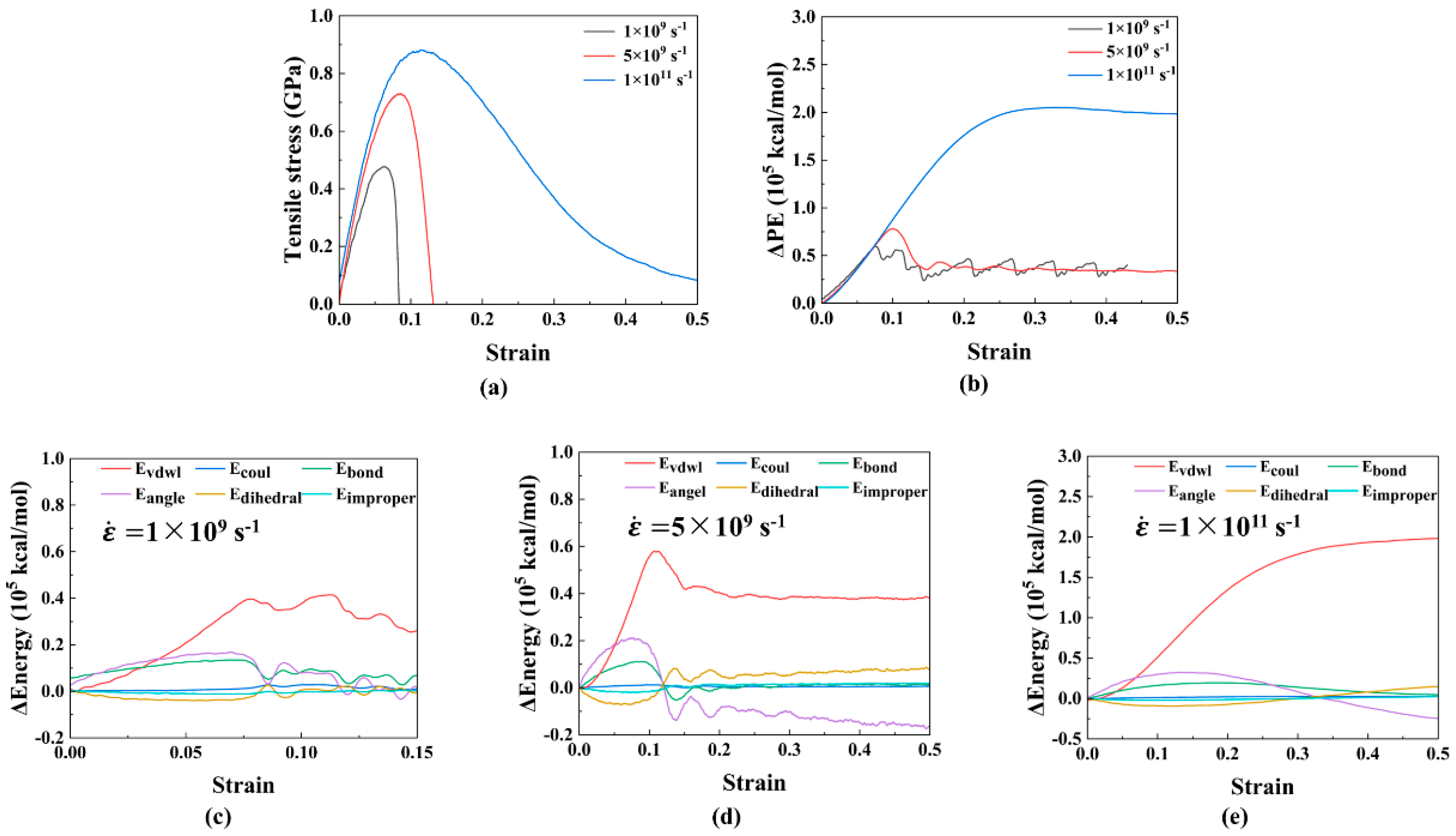
2.5. The Simulation Conditions

To understand the effects of the void defect on the mechanical response of the β−HMX crystal and its PBX, different types of void defects are designed. Firstly, for the regular void distribution, a single void is located in the center of the model, whose diameter is 40 Å, 50 Å, and 60 Å, respectively, corresponding to a porosity of 0.6%, 1.1%, and 2.0%. On the condition of the porosity being 0.6%, the number of voids are designed as two and four, respectively, and the void is assigned along the X axis in the middle of the model. Furthermore, the effect of the number on the void can be analyzed. The details can be found in Figure 4 and

Table 3. The design of the porosity and void diameter.

Void Number	Void Diameter/Å	Porosity in Crystal	Porosity in PBX
1	40.0	0.6%	1.1%
1	50.0	1.1%	2.0%
1	60.0	2.0%	4.0%
2	32.0	0.6%	1.1%
4	25.0	0.6%	1.1%

. In addition, the effect of the distance between the voids is discussed. For the cases of both the two voids and the four voids, the distance between the voids is set as 40 Å, 60 Å, 80 Å, and 100 Å, respectively.

For the stochastic void distribution, since the void size follows the normal distribution, the effect of the mean and standard deviation is considered. In this work, the mean of the void diameter changes from 10 Å to 20 Å, and the standard deviation changes from 1.0 Å to 2.0 Å. In all cases, the porosity is controlled as 1%. The models with stochastic voids are shown in Figure 5.

Moreover, the tensile force is along the Z axis, and the strain rate is 1 × 10⁹ s⁻¹, 5 × 10⁹ s⁻¹ and 1 × 10¹¹ s⁻¹, respectively. A periodic boundary is used in the model, and the whole system is an isothermal and isobaric ensemble. The timestep Δt = 0.1 fs, the total number of CPU cores is 96, and the simulation time is 50 ps. All calculations were performed using LAMMPS software.

3. The Initial Void Defect’s Effect on the Mechanical Behavior of the β−HMX Crystal

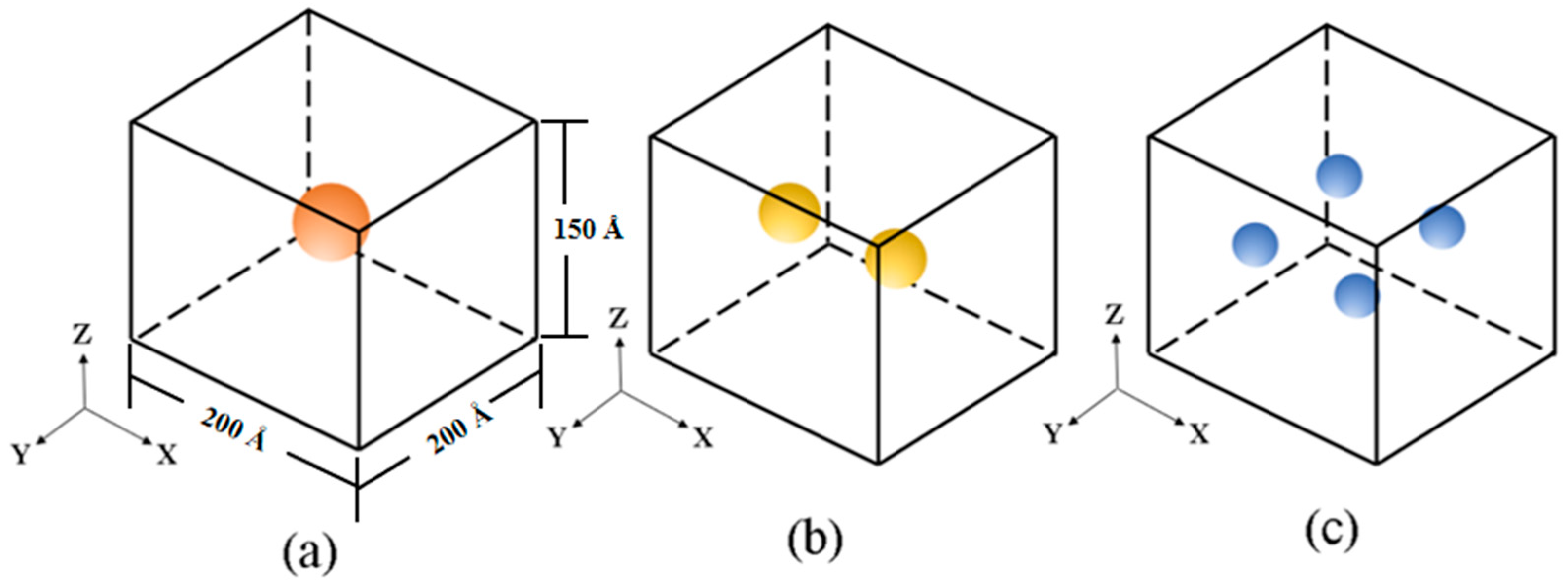
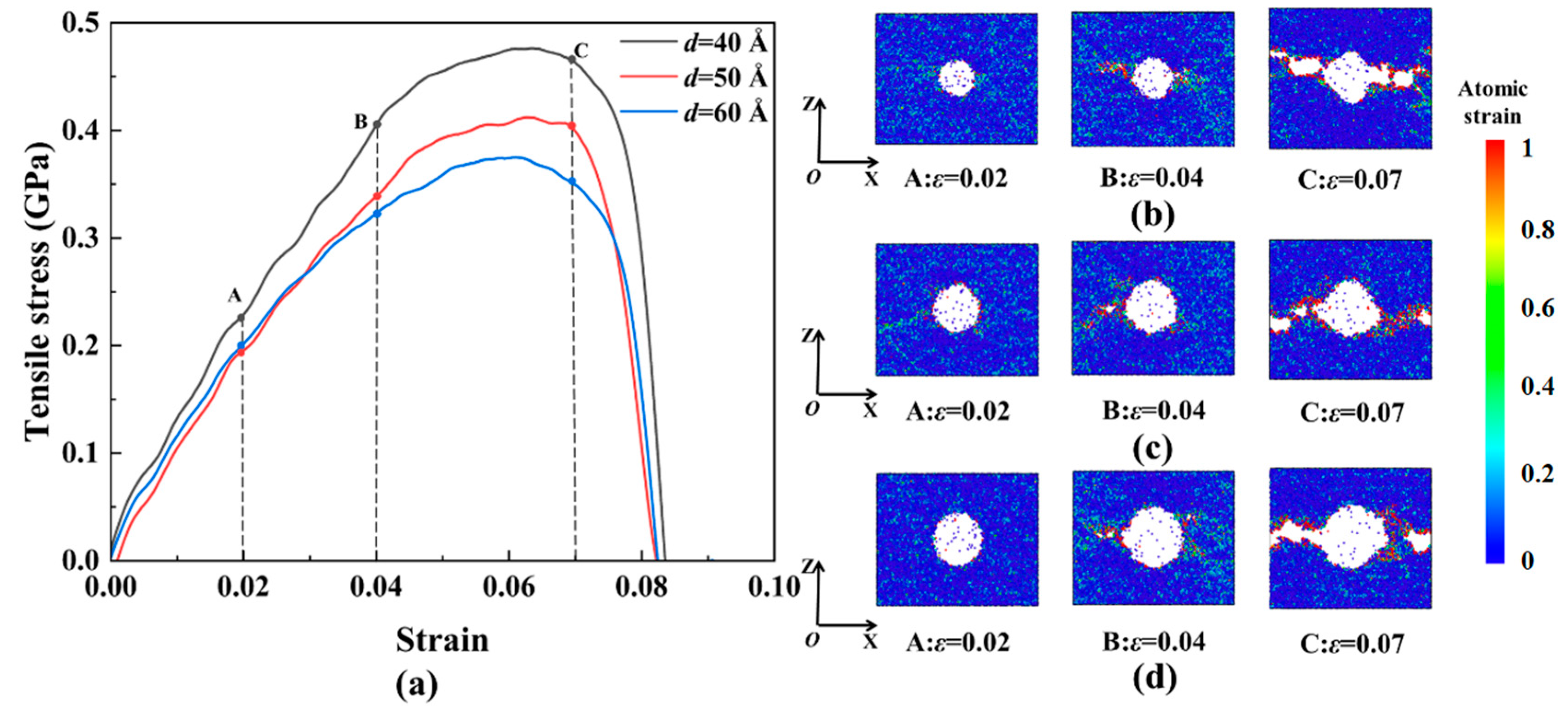
3.1. The Regular Void Defect’s Effect

Firstly, the porosity effect on the mechanical response of the β−HMX single crystal is analyzed. Figure 6a shows the stress–strain relationship, with different void diameters under the tensile strain rate 1 × 10⁹ s⁻¹. When the porosity is increased from 0.6% to 2%, the tensile strength obviously decreases from 0.48 GPa to 0.37 GPa. High porosity corresponds to a big void size, and it means high initial damage, which reduce the resistance capability and the binding energy. Figure 6b–d show the atomic strain evolution with the strain for different void sizes. At the initial stage of the deformation, when the strain is as small as 0.02, it is found that the crack nucleation is around the void, according to the atomic strain. As the strain increases to 0.04, the crack grows along the vertical direction of the load. When the void size is 60 Å, some visible fracture around the void is presented, and it means that the resistance loading capability reduces. Until the strain is up to 0.07, the crack propagates, and the fracture of the crystal soon occurs.

Secondly, the effect of the void distance on the mechanical response with two voids in the β−HMX single crystal is analyzed. Figure 7a shows the stress–strain relationship with different void distances under the tensile strain rate 1 × 10⁹ s⁻¹. When the void distance increases from 40 Å to 80 Å, the tensile stress increases from 0.40 GPa to 0.45 GPa. It should be noted that the change in the tensile strength is not obvious until the distance increases to 80 Å, and it means that a critical distance between 60 Å and 80 Å exists to influence the deformation. Figure 7b–d show the atomic strain distribution as the deformation. It can be found that when the void distance is small, the crack growth of each void interacts, and the cracks can penetrate each other. Furthermore, the fracture occurs. As the void distance increases, the interaction between the voids becomes weak, and finally the crack growth and propagation of each void interfere with each other.

In addition, the effect of the void distance on the mechanical response with four voids in the β−HMX single crystal is also analyzed. Figure 8a shows the stress–strain relationship with different void distances under the tensile strain rate 1 × 10⁹ s⁻¹. As is the case with two voids, a critical void distance also exists. When the void distance increases up to 100 Å, the interaction among the voids is not obvious. Moreover, compared with the single void, on the condition that the porosity is 0.6%, the tensile strength reduces to 0.37 GPa for the void distance 40 Å. Even when the void distance is 100 Å, the tensile strength also reduces to 0.42 GPa. This means that a high void number easily causes the degradation of mechanical properties. Figure 8b–e show the atomic strain evolution, which demonstrates the interaction among the voids.

In order to better understand the cracks’ propagation inside the material, Figure 9a–d shows the 3D defect evolution distribution with a 20 Å void. It can be observed that the cracks begin to form around the void when the ε = 0.02, and as the strain increases to 0.04, the crack grows along the vertical direction of the load. Until the strain is up to 0.06, the crack propagates, and the fracture of the crystal soon occurs. In addition, the fracture section is also analyzed and the lower separated part of the material is shown in Figure 9e— the surface is particularly rough. Figure 9f provides a top view of the fracture section; there is a circular region without atomic strain in the middle of the model, which is due to the cracks forming around the void. The direction of crack growth is random, and this leads to the fracture section, which is rough.

For the strain rate 5 × 10⁹ s⁻¹ and 1 × 10¹¹ s⁻¹, when the diameter of a single void is 40 Å, the mechanical response of the β−HMX single crystal is similar to in the case of 1 × 10⁹ s⁻¹. Figure 10a shows the tensile stress–strain curves at different strain rates with a single void. The strain rate effect is obvious. When the strain rate increases from 1 × 10⁹ s⁻¹ to 1 × 10¹¹ s⁻¹, the tensile strength increases from 0.48 GPa to 0.88 GPa. Figure 9b shows the potential energy curves under different strain rates. Higher potential energy corresponds to higher tensile stress strength, which means that the crack formation requires more energy dissipation. Furthermore, the components of the potential energy are analyzed in Figure 10c–e. It is found that the Van Der Waals energy is the primary energy, while the bond energy and angle energy are secondary. Essentially, the fracture of the β−HMX single crystal results from the weakening of intermolecular interactions as the distance increases. However, the effect of the atoms in the molecule is not important, and furthermore, intramolecular bond breaking does not occur. In other words, the tensile fracture is a physical process rather than a chemical process.

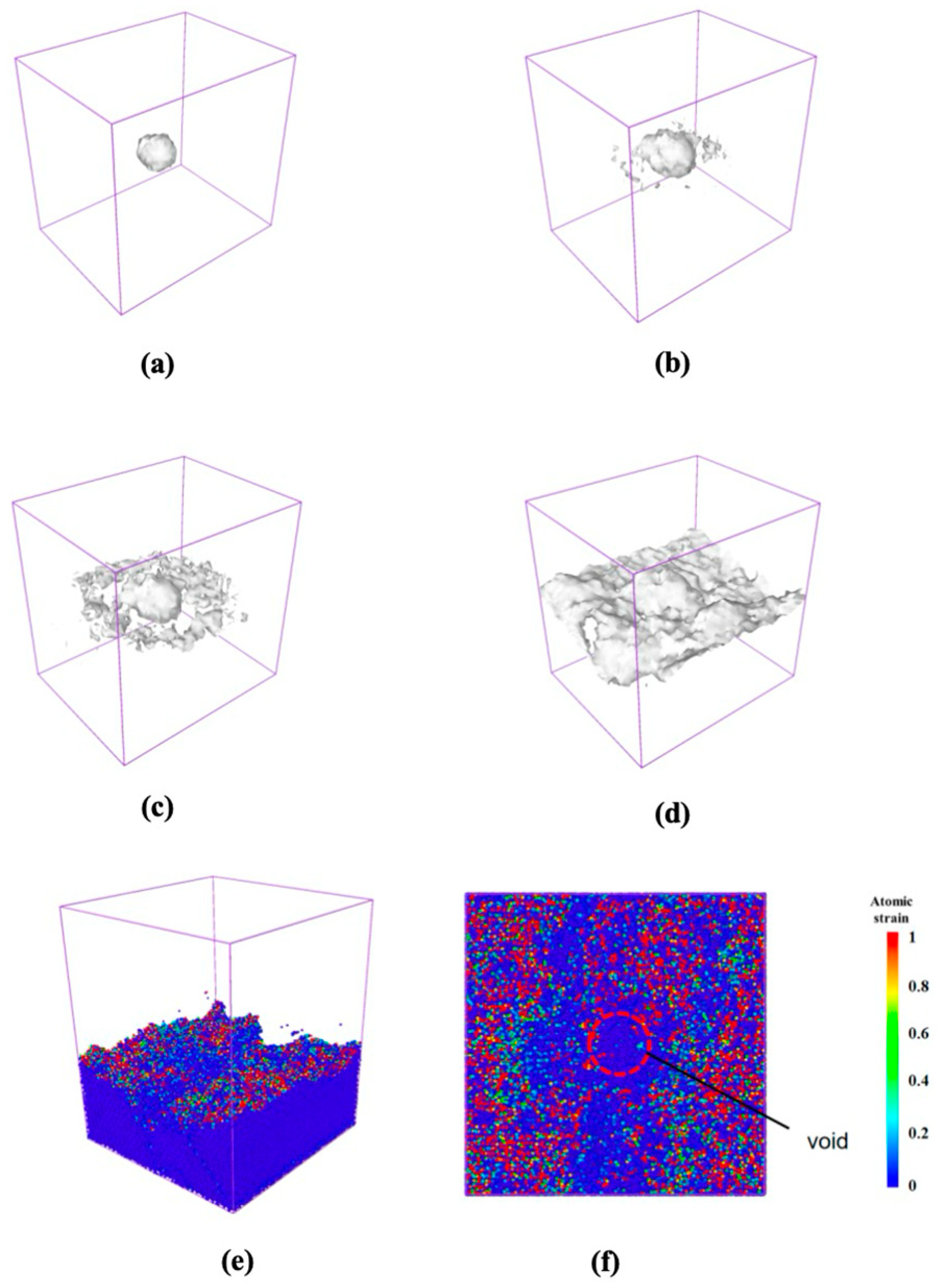
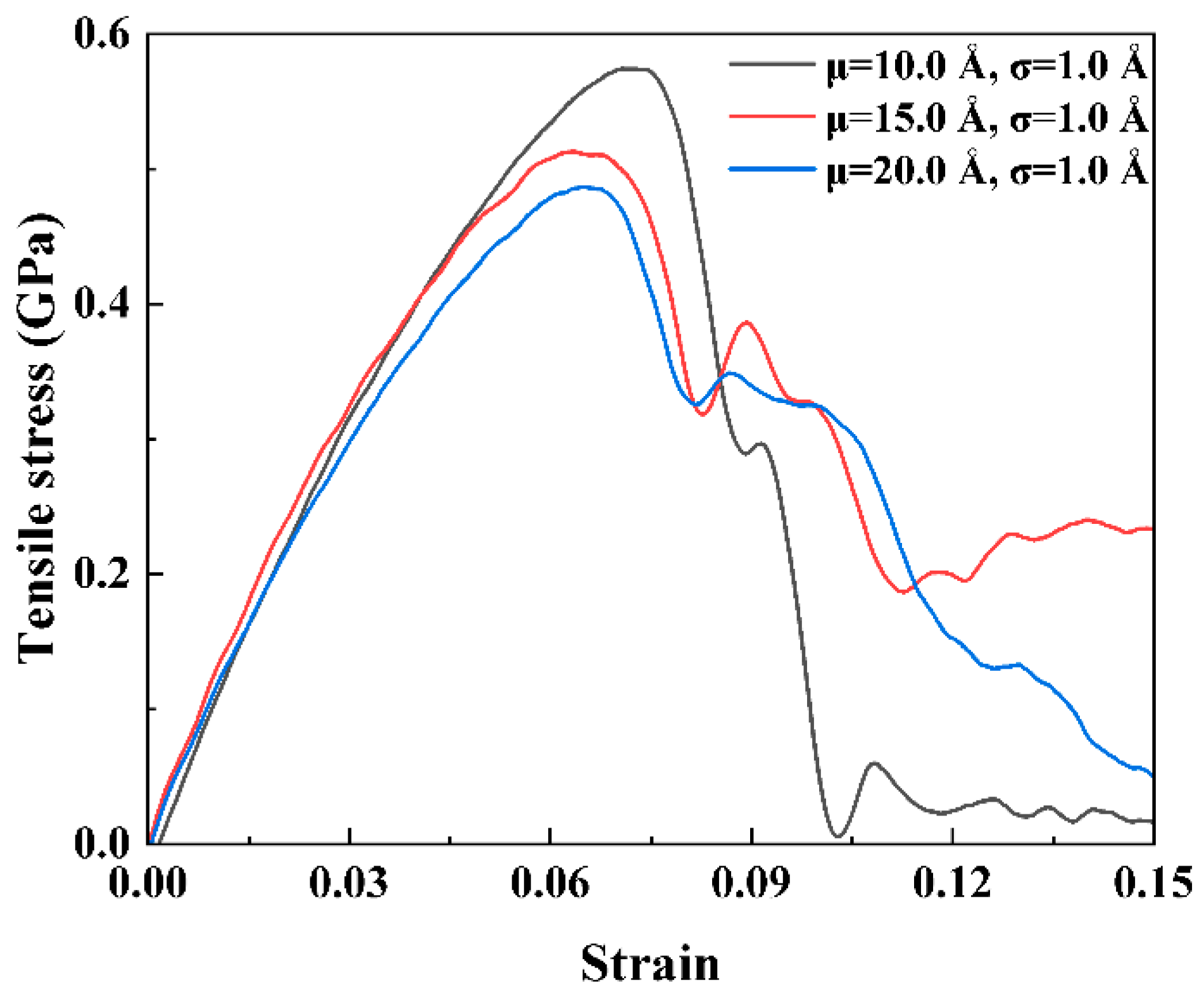
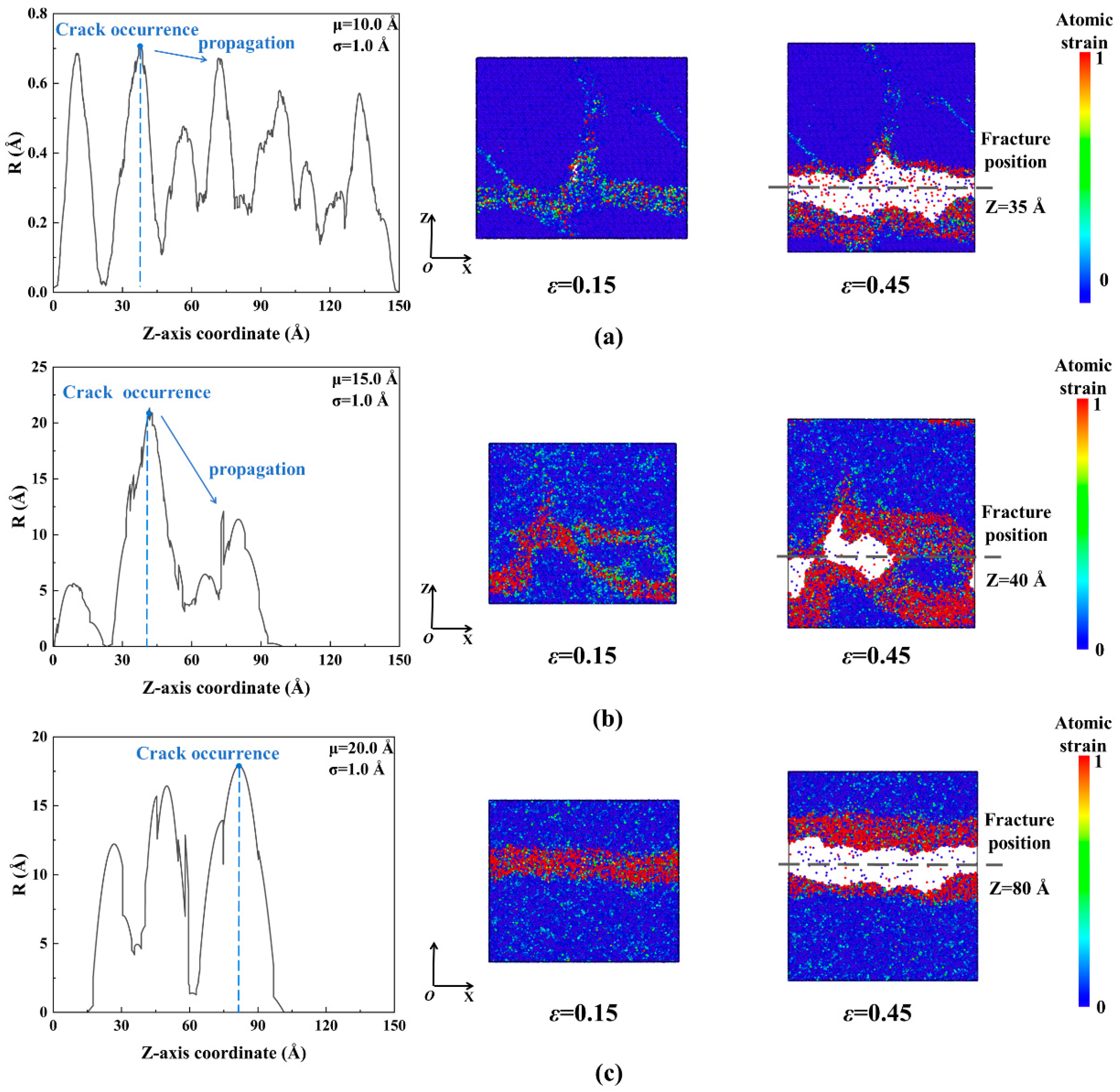
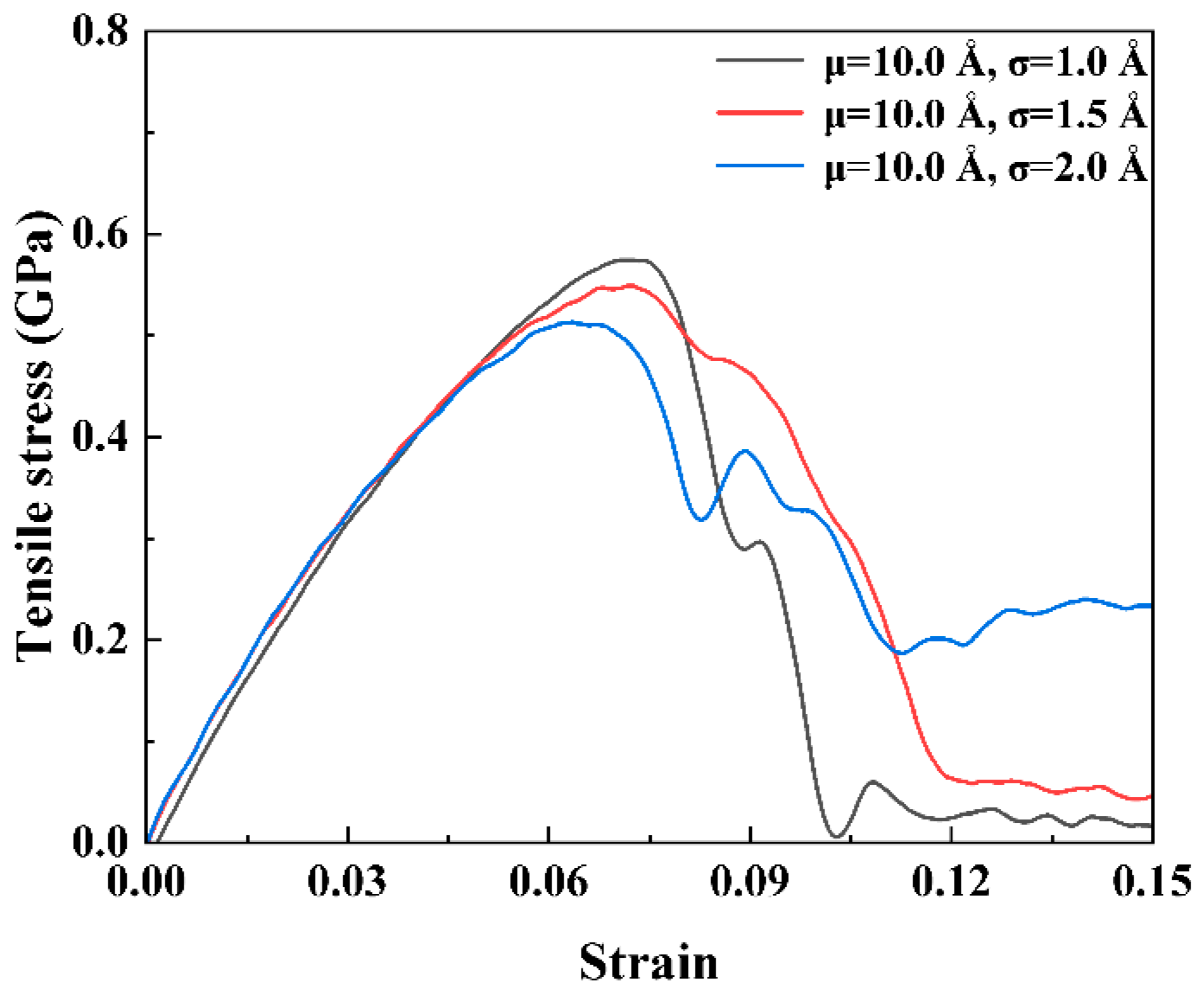
3.2. The Stochastic Void Defect’s Effect

Figure 11 shows the stress–strain relationship with different stochastic void distributions under the strain rate 1 × 10⁹ s⁻¹. When the mean of the void diameter increases from 10.0 Å to 20.0 Å, the strength decreases from around 0.58 GPa to 0.49 GPa. With the same standard deviation 1.0 Å, an increasing mean represents that there are more voids with a bigger void diameter. Furthermore, it means higher initial damage, which reduces the strength.

To understand the fracture behavior of the β−HMX single crystal with stochastic voids, the characteristic defect parameter is defined as in Equation (12):

$$R={\displaystyle \frac{{\sum }_{i=1}^n{D}_i}{\sum l}}$$

(12)

where $R$ is the characteristic defect parameter of each layer, $D_i$ is the defect area of the void in each layer, and $l$ is the void spacing. The parameter combines the effects of the void size and spacing, based on the results of the β−HMX single crystal with regular voids.

Figure 12 shows the distribution of the characteristic defect parameters and the crack propagation process with different stochastic void distributions. The simulation results indicate that the crack always occurs at the maximum of the characteristic defect parameter, and that the crack propagates towards a local peak of the parameter. When the mean and standard deviation of the void diameter are 10 Å and 1.00 Å, the crack occurs at the highest value of the parameter Z = 35 Å, and furthermore, it propagates towards the local peak value at Z = 70 Å. It is similar in the case of the mean of the void diameter 15 Å. Essentially, a bigger void area represents a higher initial damage level, which reduces the material strength. The crack nucleation and occurrence start around the voids. Moreover, the interaction among the voids influences the crack propagation direction. Considering that the voids are in the 3D space, it is possible that the crack deflects along the Z axis. When the mean of the diameter increases to 20 Å, the crack occurs and propagates at the maximum Z = 80 Å, and the effect of the local peak of the parameter is not obvious. It is plausible that the initial void area plays a more important role than the interaction among the voids.

Also, the effect of the standard deviation is discussed. Figure 13 shows the stress–strain relationship with different standard deviations under the tensile strain rate 1 × 10⁹ s⁻¹. With the same mean, the tensile strength slightly reduces from around 0.58 GPa to 0.51 GPa, as does the standard deviation from 1.0 Å to 2.0 Å. This is because the high standard deviation probably produces a big void diameter, which can be seen in Figure 5.

Furthermore, the characteristic defect parameter with different standard deviations is calculated, and the distribution is shown in Figure 14. It is demonstrated again that the crack occurs at the maximum of the parameter, and that the following crack propagation will be towards a local peak of the parameter.

4. The Initial Void Defect’s Effect on the Mechanical Behavior of the β−HMX−Based PBX

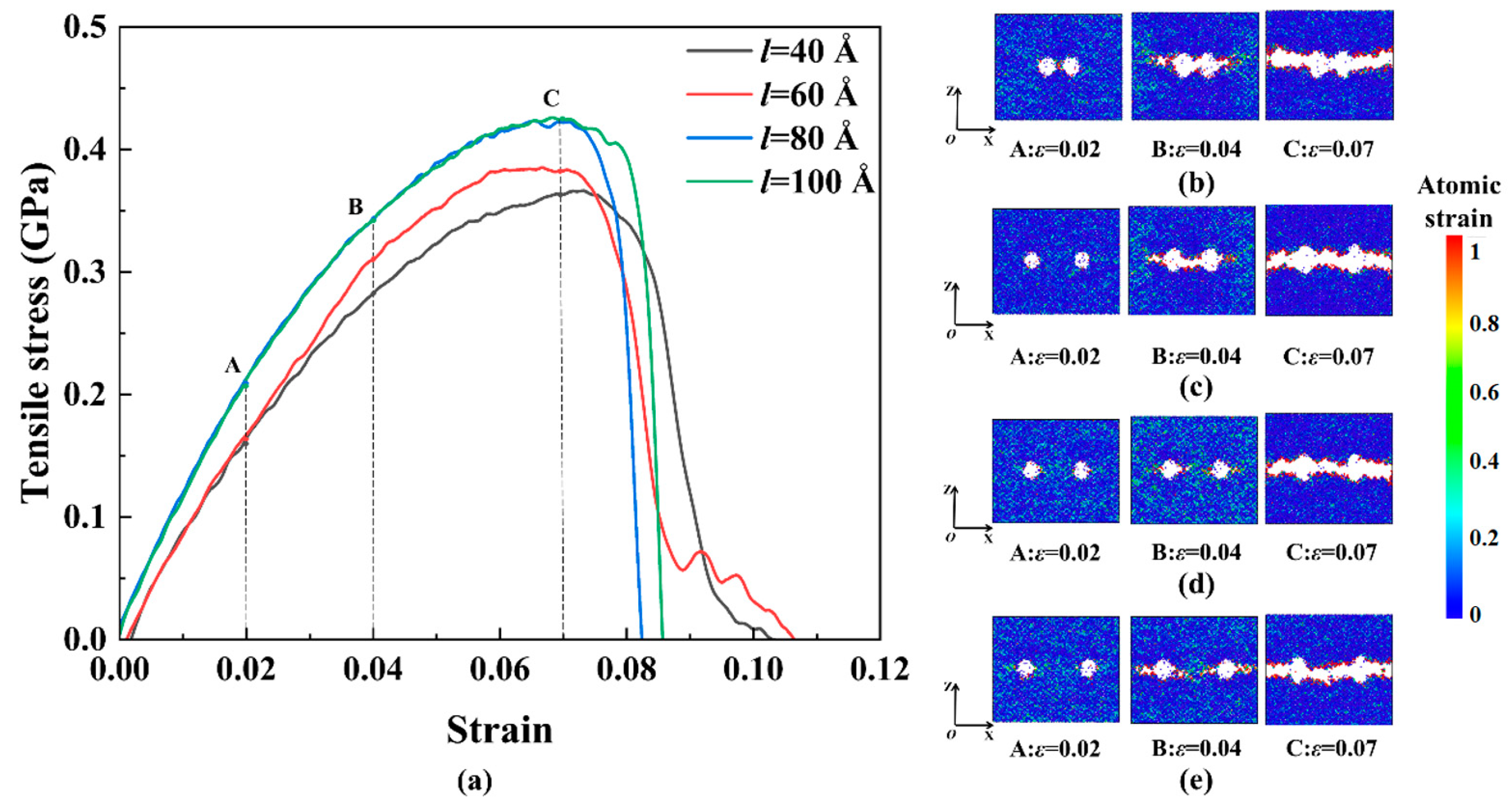
4.1. The Regular Void Defect’s Effect

Similarly to the β−HMX crystal, the porosity effect on the mechanical properties of the β−HMX−based PBX with a single void is analyzed. Figure 15a shows the stress–strain relationship with different porosities under the strain rate 5 × 10⁹ s⁻¹. When the porosity increases from 1.1% to 4.0%, the tensile strength decreases from 0.43 GPa to 0.39 GPa. Figure 15b–d show the fracture process in the case of the void diameter from 40 Å to 60 Å. The crack nucleation and growth start from the initial void, while the crack propagation is mainly along the interface between the crystal and the binder, which is vertical to the load direction. This phenomenon matches the experimental observations [53].

The effect of void spacing on the mechanical response with two voids in the β−HMX−based PBX is analyzed. Figure 16a shows the stress–strain relationship with different void spacings under the tensile strain rate 5 × 10⁹ s⁻¹. Different from the case of the β−HMX single crystal, the effect of void spacing is not obvious. When the void spacing changes from 30 Å to 60 Å, the tensile strength changes a bit. This is probably because the mechanical response of the β−HMX−based PBX mainly depends on the interface between the crystal and the binder. As Figure 16b–e show, the initial void exists in the crystal and the binder, which brings in the defect. In the early deformation stage, the defect results in crack nucleation and growth around the voids. It should be mentioned that the strength of the crystal is much higher than that of the interface. Furthermore, the crack propagation is along the interface around the void. Although the interaction between the voids is weak, as the distance increases, the fracture occurs at another interface, not the interface where the void is located.

In addition, the effect of the void distance on the mechanical response with four voids in the β−HMX−based PBX is also analyzed. Figure 17 shows the stress–strain relationship and the fracture process. This result also demonstrates that in the case of four voids, the effect of distance is also not obvious. In other words, under tension, the initial defect cannot strongly reduce the strength of the crystal, and furthermore, the interface is the weak point for determining the fracture behavior. Some observations show that the intergranular fracture is central, even if several defects exist in PBXs [14].

4.2. The Stochastic Void Defect’s Effect

Also, the stochastic void defect’s effect on PBX is analyzed. The details of the parameters can be found in Section 2.4. Figure 18a shows the tensile stress–strain relationship with different stochastic void distributions under the strain rate 5 × 10⁹ s⁻¹. When the mean of the diameter increases from 10.0 Å to 20.0 Å and the standard deviation increases from 1.0 Å to 2.0 Å, the tensile stress–strain relationship is similar, and the tensile strength does not change significantly. Furthermore, the characteristic defect parameter is analyzed. Compared with the single crystal, the crack occurrence and propagation does not depend on the parameter, but the fracture occurs at the interface between the crystal and the binder, as Figure 18b–d show. As mentioned above, the stochastic defect can reduce the mechanical properties of the single crystal, which are still higher than those of the interface. In addition, the interaction of the stochastic defect is not strong enough. For PBXs, the tensile mechanical response mainly depends on the interface strength instead of the inside defect. It should be stressed that these stochastic defects probably play an important role in the response under complex load conditions, and also that it they are critical for hotspot formation [54].

5. Conclusions

In this study, a molecular dynamics model of the β−HMX single crystal and its PBX with different void distributions is built. The deformation and fracture process under tensile conditions are analyzed. The following conclusions are drawn:

(1)

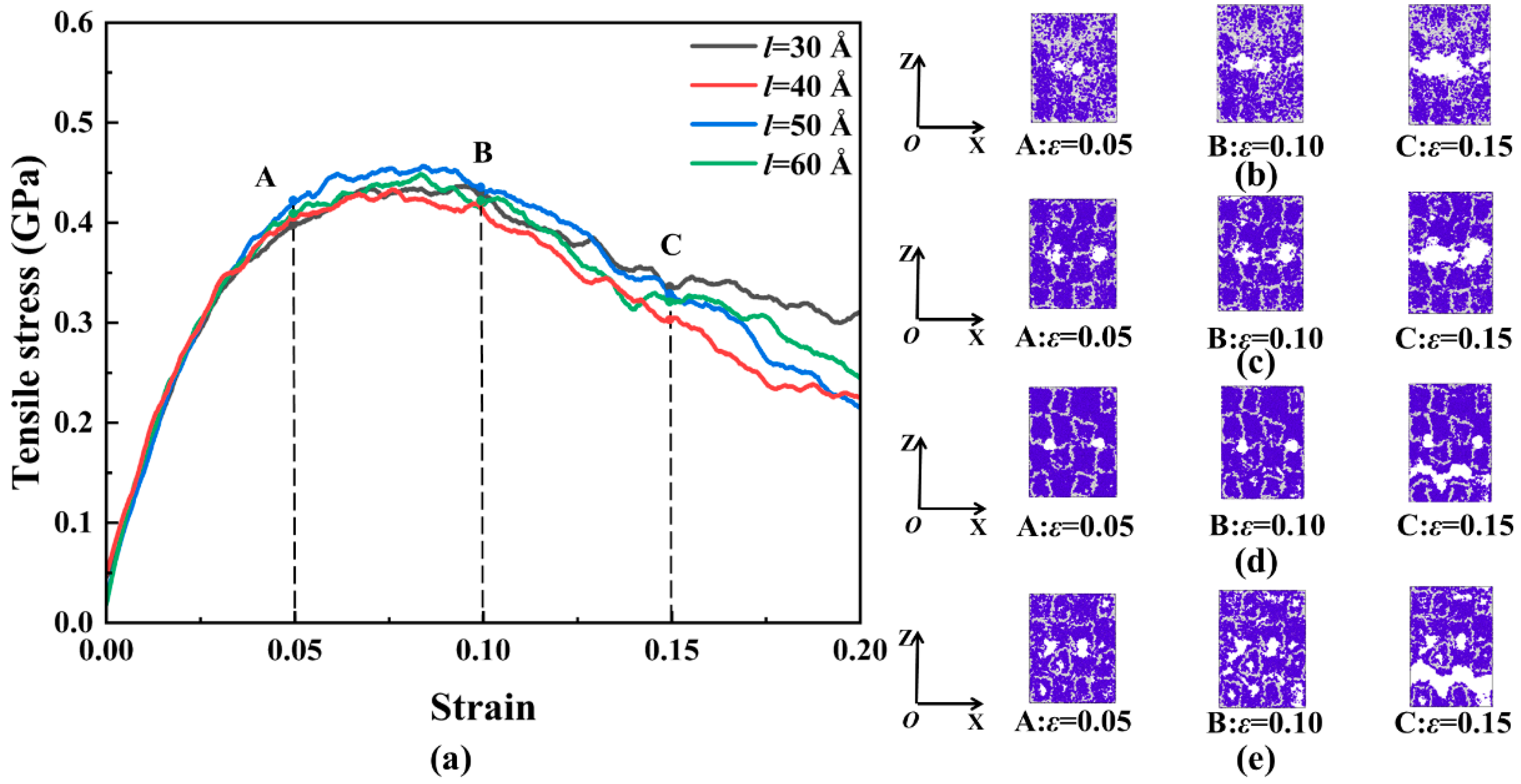
The effect of different regular void distributions on the β−HMX single crystal is obtained. The tensile strength depends on the initial damage. It decreases as the void size increases. There is critical spacing between the voids to strength the interaction of these defects, which can reduce the tensile strength significantly. The fracture process mainly depends on the Van Der Waals force;

(2)

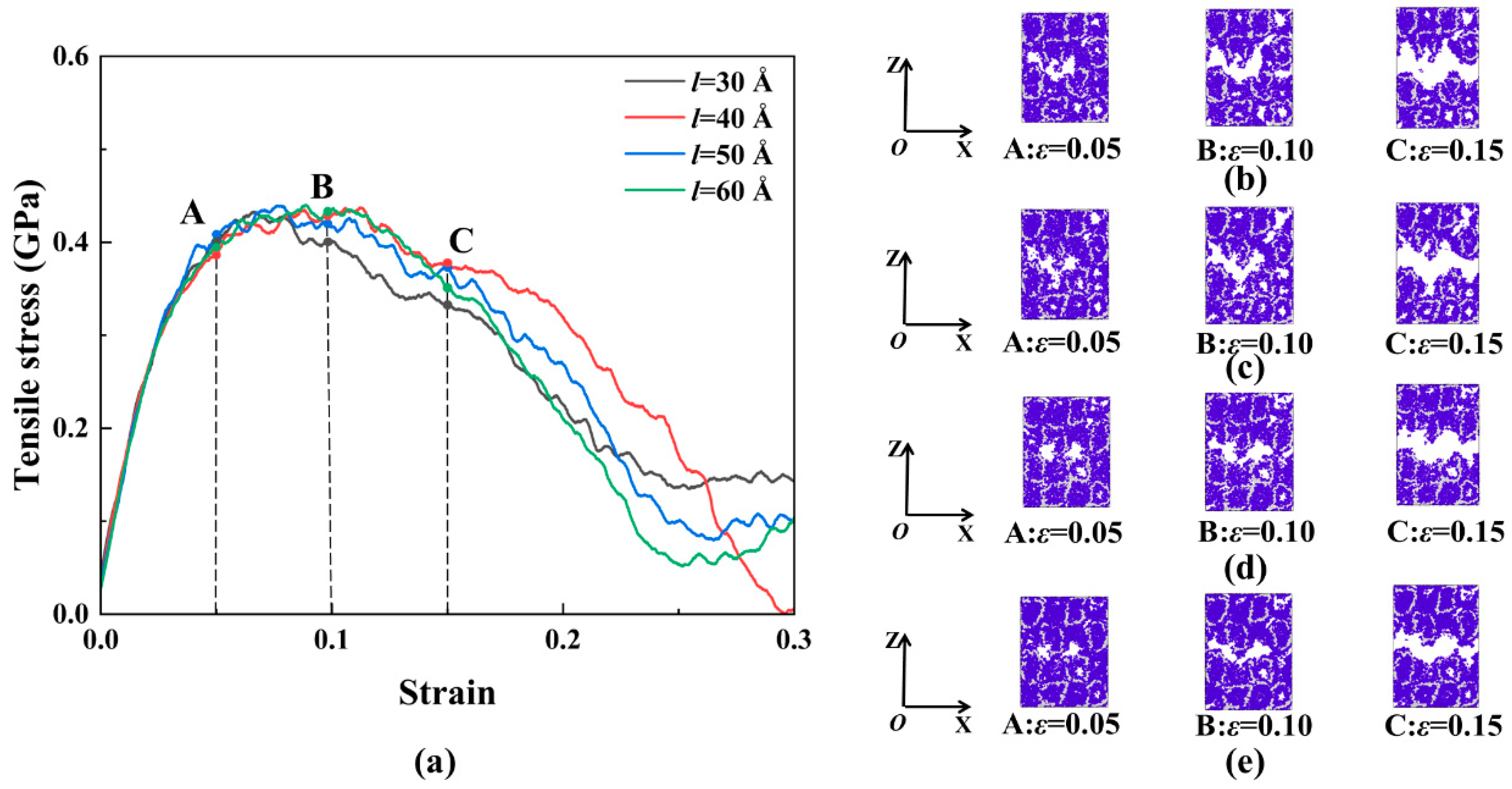
The effect of different regular void distributions on the β−HMX crystal’s PBX is obtained. Compared with the single crystal, the initial damage also plays an important role in the mechanical properties. Although there is similar critical spacing, the effect is not obvious. The fracture mechanism changes as the void spacing increases, and when the void spacing is large, the failure starts at the interface of PBX instead of at the defect.

(3)

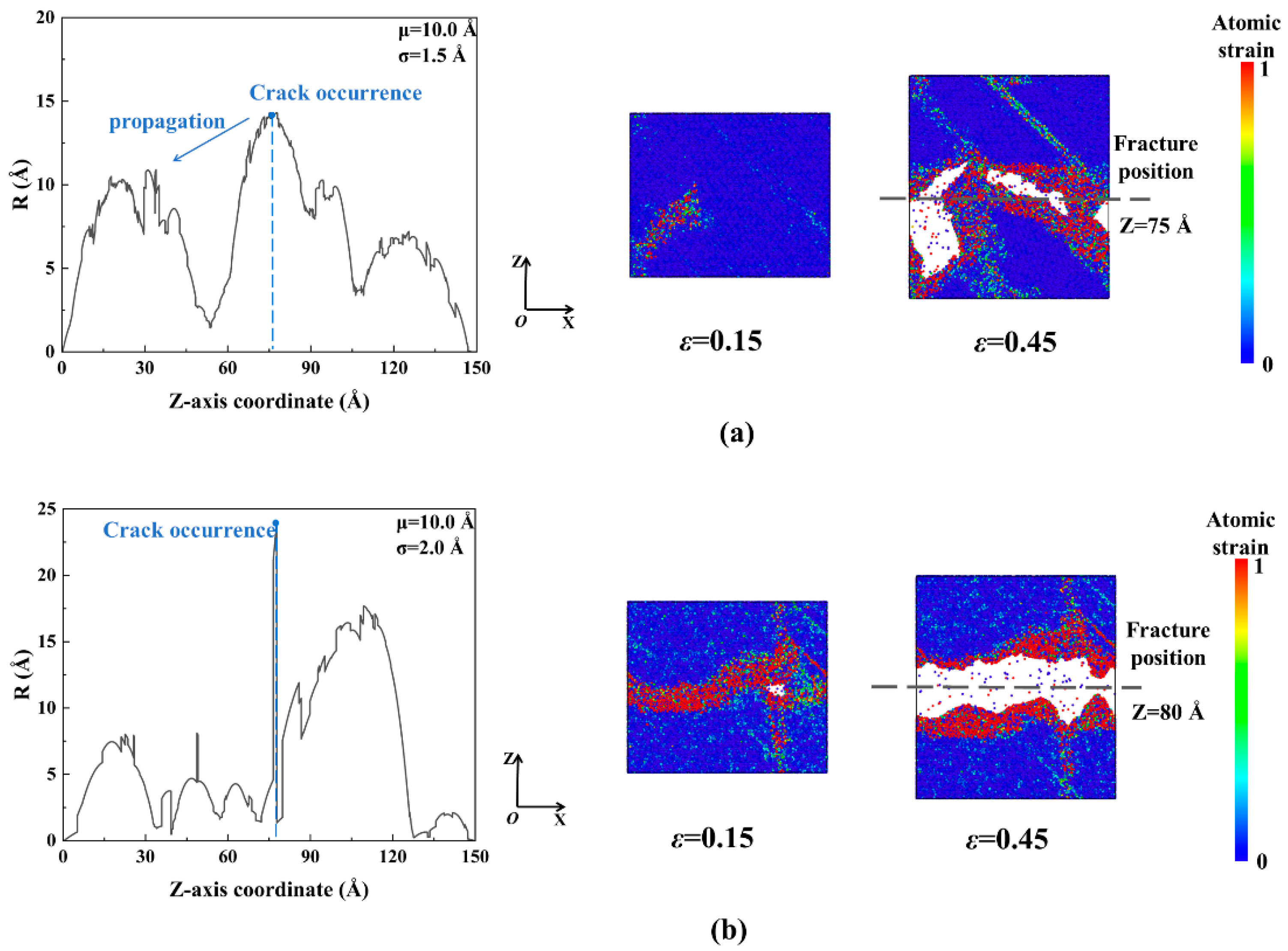
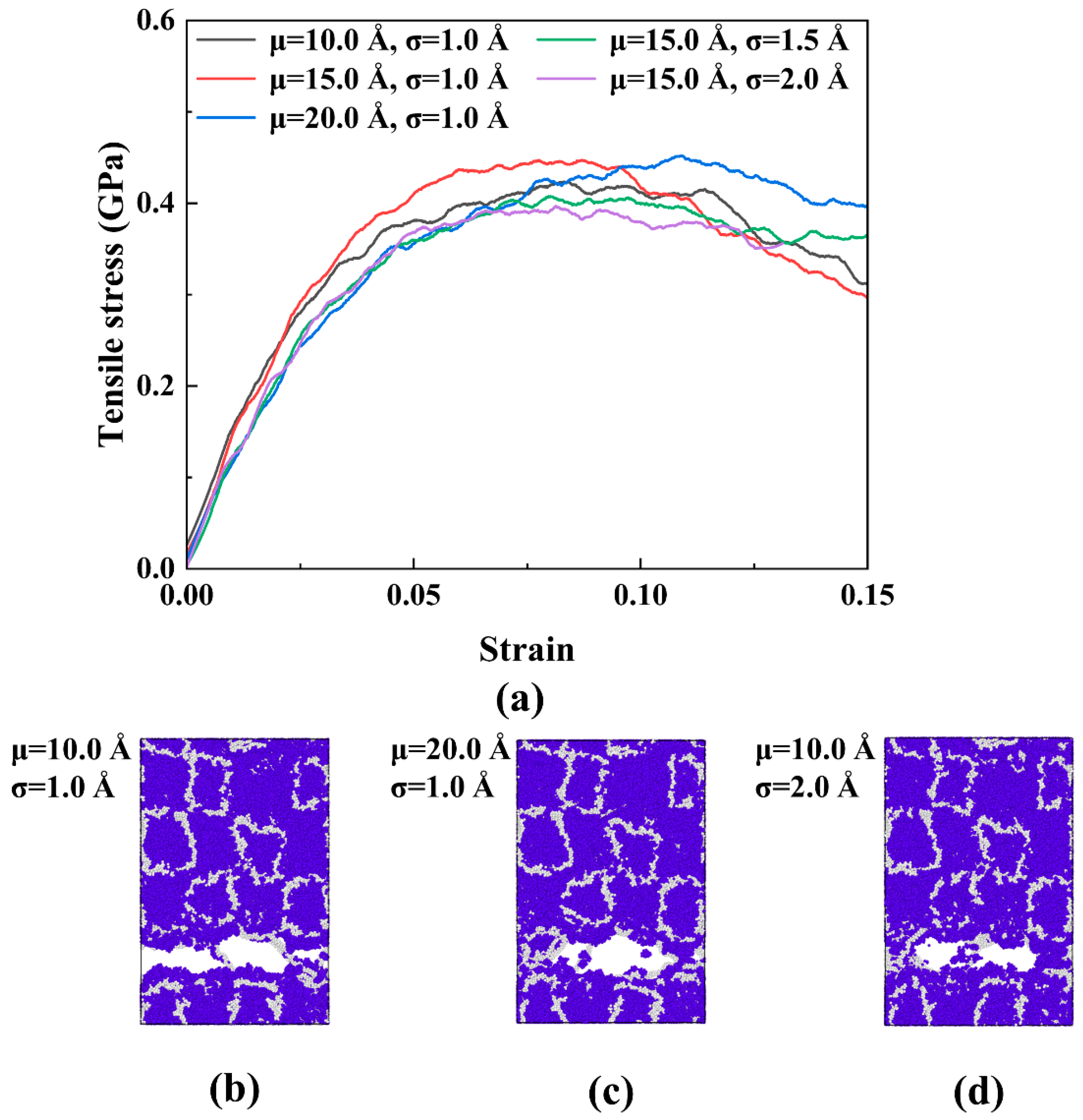
The effect of different stochastic void distributions on the single crystal and its PBX is obtained. Further, the proposed characteristic defect parameter considers the effect of the damage area and the interaction of the defects. It can predict the crack occurrence and propagation of the β−HMX single crystal well. For PBX, the interface determines the deformation and fracture process instead of the characteristic defect parameter.

In this paper, the deformation and fracture behavior with void defects under tensile conditions are obtained. However, the mechanism of void collapse and the chemical reaction under impact are not clear, and this will be our next research target.