On the Molecular Kinetics of Protein Crystal Nucleation and the Causes of Its Slowness: Peculiarities of the Protein–Protein Association

Abstract

The rate of nucleation of crystals is the subject of extensive research, since it—together with the nucleation time—determines the number of crystals growing; in turn, their number is related to their size. Experimental studies show that, for biomolecular crystals, despite the required unusually high supersaturations, the nucleation process is distinctly slow. This slowness arises from the inherent peculiarity of the nucleation of such crystals. Therefore, a prerequisite for management of the crystallization process towards the desired outcome is the molecular level understanding of the nucleation mechanism. In this paper, analyzing the mechanisms behind the nucleation process of protein crystals, it is argued that the highly inhomogeneous molecule surface is the main reason for the slow crystal nucleation: only a few small patches on their surface are capable of forming crystalline bonds. Therefore, the partner proteins must not only be brought to encounter one another but must also find each other’s binding site. In turn, this requirement imposes a severe steric restriction on the association of protein molecules, which, however, is alleviated by a rotational-diffusional reorientation. This is why particular attention is paid to this aspect of the protein crystal nucleation process.

1. Introduction

Due to their pharmaceutical application, proteins in crystalline form have attracted considerable interest [1]. On the other hand, relatively large and well-diffracted crystals are required for X-ray studies of the molecular structures of newly expressed proteins. Of course, only spontaneous crystallization can be used in this case, the prerequisite for which is the formation of crystalline embryos, the so-called nuclei.

Starting the crystallization process, the nucleation stage predetermines important characteristics of the produced crystals. Often of interest is the number of crystals grown, which affects important characteristics of the crystalline product. Therefore, the rate of the nucleation of protein crystals, which is determined by the molecular kinetics of this process, is considered in this paper.

Since the nucleation of crystals cannot be observed at the molecular level, there are different conceptions of its mechanism. First, we first present the understanding of kinetics of crystal nucleation according to classical nucleation theory (CNT). Although it was originally developed to explain the nucleation of crystals from small molecules, it is also often used to explain the nucleation of protein crystals. The reason for this is that, by enabling quantitative estimates and predictions concerning the results of many experimental studies, CNT provides a general framework for the fundamental analysis of nucleation processes.

But the assumption of CNT for simultaneous condensation and ordering during a single nucleation process, i.e., the mechanism of this process, is frequently contested, for instance, in the so-called two-stage nucleation mechanism (TSNM) [2,3]. In contrast, the basic (thermodynamic) postulate of CNT, that for crystal nucleation to occur it is imperative to overcome an energy barrier, ΔG*, which happens through interphase fluctuations, remains indisputable. On this basis, the rate J of crystal nucleation (measured in number of nuclei formed per unit time per unit volume) was calculated in the framework of CNT [4]:

$$J=A\exp \left(-{\displaystyle \frac{\Delta G*}{k_{\mathrm{B}}T}}\right)={c_1\nu *}^{+}Z\exp \left(-{\displaystyle \frac{\Delta G*}{k_{\mathrm{B}}T}}\right),$$

(1)

where A is a pre-exponential factor, which remains unknown in Volmer’s statistical-thermodynamic derivation [4], but was calculated by Becker and Döring [5] and by Zel’dovich [6]. ΔG* is the energy barrier for the formation of the critical nucleus under isothermal and isobaric conditions, k_B is the Boltzmann constant, and T is the absolute temperature. c₁ (molecules per cm³) is the concentration of the monomers, ν*⁺ is the attachment probability (frequency) of a molecule to the critical nucleus, and Z is the Zel’dovich factor.

The thermodynamic energy barrier, ΔG*, is the dominant factor in the crystal nucleation rate expressed by Equation (1), while the effect of the pre-exponential factor, A, is significantly weaker. Therefore, traditionally, when studying the rate of crystal nucleation, attention has been focused on ΔG* (e.g., see [7,8,9]), while less attention has been paid to the kinetic pre-exponential factor, A. (Also, TSNM focuses on the thermodynamic factor).

The barrier ΔG* (which must be surmounted for nucleation to occur) depends strongly on the supersaturation, Δμ:

$${\displaystyle \frac{\Delta G*}{k_{\mathrm{B}}T}}={\displaystyle \frac{B}{\Delta {\mu }^2}},$$

(2)

where B is a constant thermodynamic parameter.

The logarithm of J from Equation (1), in combination with Equation (2),

$$\mathrm{l}\mathrm{n}J=\mathrm{l}\mathrm{n}A-B/\Delta {\mu }^2,$$

(3)

is used for calculating ΔG* from experimental data (e.g., see [7,8,10]).

In Equation (1), $\exp \left(-{\displaystyle \frac{\Delta G*}{k_{\mathrm{B}}T}}\right)$ is a dimensionless multiplying factor that shows how A decreases to the actual J when $\Delta G*\gg k_{\mathrm{B}}T$. But, although purely mathematically, J becomes equal to A when $\Delta G*=0$, physically, the disappearance of the energy barrier means the occurrence of a fundamentally different kind of phase separation, the so-called spinodal decomposition. The latter is a spontaneous phase separation into two different phases, which does not require nucleation events: nucleation occurs when a homogenous phase becomes metastable, meaning that it remains at a local minimum while another biphasic system becomes lower in free energy. In contrast, spinodal decomposition occurs when a homogenous phase becomes thermodynamically unstable, i.e., it is at the maximum in free energy. Importantly, a phase change due to nucleation begins at discrete points, whereas in spinodal decomposition, the two distinct phases start growing in any location throughout the volume of the system.

The pre-exponential kinetic factor, $A={c_1\nu *}^{+}Z$ in Equation (1), has the same dimensions as J, but according to CNT it does not depend on the supersaturation. However, using Equation (1), A can be calculated. For instance, to substantiate his claim that the CNT overestimates the crystal nucleation rate by 10 orders of magnitude, Vekilov [2] calculated A for the case of lysozyme crystal nucleation. Based on experimental data for the velocities of propagation of steps on lysozyme crystal faces, he estimated the attachment rate of protein molecules to kink sites to be ≈ 300 s⁻¹ and placed this value for ν*⁺ into Equation (1). However, since the critical nuclei are too small to have faces with kinks on them, there is a significant difference between molecule joining to kink sites and joining to critical nuclei (incidentally, Vekilov also wrote “This estimate of ν*⁺ should be viewed as approximate since the configuration of molecules in a kink on the smooth crystal face during crystal growth may be significantly different than the molecular configuration on the rough surface of a near-critical cluster”).

In fact, the similarity between the two processes is restricted to the circumstance that, in both cases, protein molecules must have the same suitable spatial orientation. However, because, before joining to the kink site, protein molecules diffuse on the crystal face [11,12,13], attachment to the kink site can be easier than to the critical nucleus. The reason for this is that the protein molecules can be stirred to the required spatial orientation for the following reasons.

-

First, once on the crystal face, the globular protein molecules begin to roll on it, like balls on a floor. Thus, only those protein molecules that reorient themselves towards the crystal face, in such a way as to be attached firmly enough, remain adsorbed—the rest are returned to the solution.

-

Second, according to the BCF model (the theory of Burton, Cabrera, and Frank [14]), diffusing on a crystal face, molecules reach the steps on it, and moving along these steps they reach the kink sites, where they embed themselves. Although there is no direct experimental evidence, it is very likely that this mechanism also works in protein crystal growth. The reason for this is that, roaming arbitrarily on the crystal face, protein molecules will fall much more often onto the relatively long steps rather than hit the point like-kink sites directly. And if this is indeed the case, the interaction with the step riser will reorient the protein molecule in the second appropriate for bonding direction.

-

Directed in the correct spatial orientation, the protein molecules can move to kink sites, where they are integrated.

Evidently, this plausible scenario would lead to a significant increase in the attachment frequency to the kink sites. In contrast, on the extremely small critical nuclei, there are neither faces nor steps. Therefore, the attachment frequency to critical nuclei, ν*⁺, should differ from the attachment frequency to the kink site.

The aim of this paper is to calculate the value of ν*⁺ for protein crystal nucleation in solutions. This is done quantitatively by elucidating the molecular-kinetic mechanism by which crystalline bonds between globular proteins are created. Focusing on the way in which protein molecules start to arrange in a crystalline structure, either simultaneously with their condensation (according to CNT) or after a preliminary condensation step (according to TSNM), it was shown that the low ν*⁺ cannot be attributed to fewer hits between biomolecules. Rather, the reason for the slow nucleation of protein crystals is the fact that only several small patches on the highly inhomogeneous molecule surfaces are capable to form crystalline bonds. And in order to confirm this assumption in a convincing way, the probability of forming complexes of two protein molecules (with which the nucleation begins) and the probability of attachment of a molecule to the critical nucleus were calculated. Also, considering the case of protein crystal growth by direct embedding of molecules from the solution into the kink sites, the probability of such attaching has been revised.

Brief Outline of TSNM

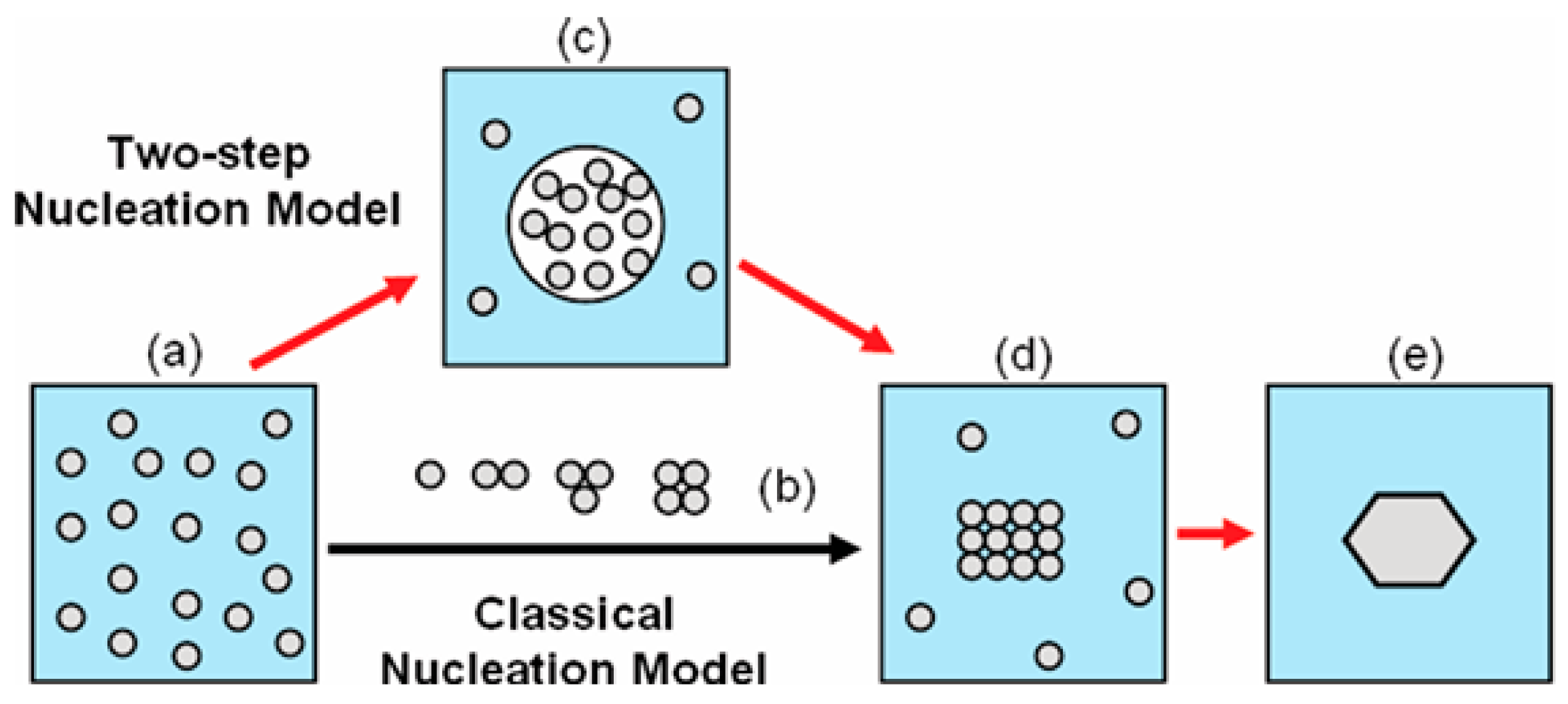
Although CNT is followed by many systems, in other cases it fails to correctly predict nucleation rates, and the deviations can be of many orders of magnitude, e.g., [15,16]. Importantly, such experimental results prompted the development of competing theories for crystal nucleation, the most common deviation from CNT being the TSNM [17,18,19,20]. TSNM assumes nucleation initiation via an intermediate condensed liquid droplets appearing in bulk solution [15,21,22], and afterwards-crystal nuclei are formed inside such highly concentrated droplets (Figure 1).

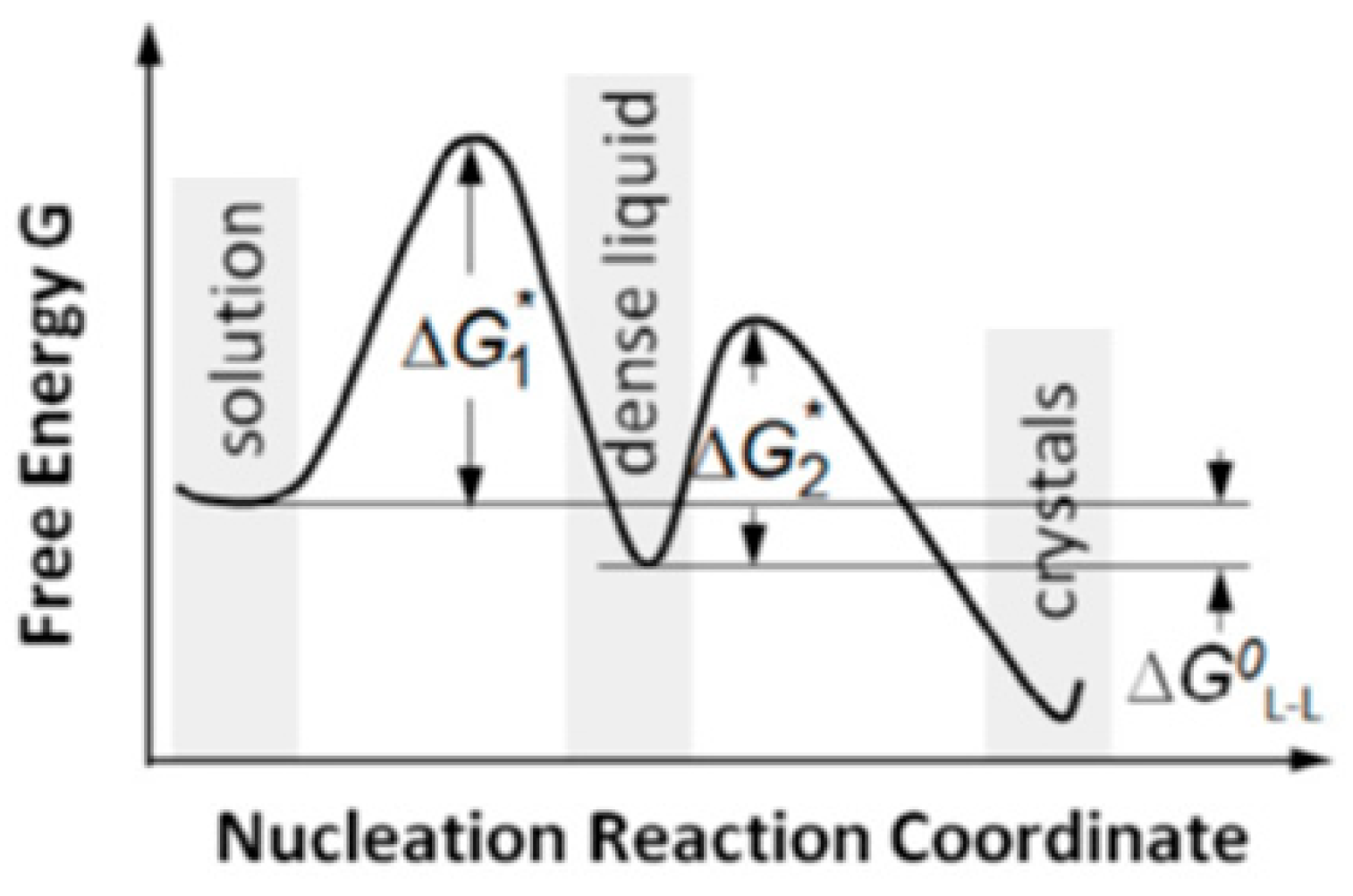
And being only densified, the droplets preserves some similarity to the mother phase, which lowers the phase-transition energy barrier. Therefore, the crystal nucleation per se occurs at a lower energy barrier–significantly lower than the one needed for direct transition mother-phase-to-crystal occurring via the CNT mechanism. So, the single, relatively high energy barrier for crystal nucleation, which surmounting is required by CNT, is split into two lower barriers (see Figure 2), which are surmounted easier.

TSNM also predicts rate J of crystal nucleation [23]:

$$J={\displaystyle \frac{U_{2}exp\left(-\frac{E_2}{k_{B}T}\right)}{1+\frac{U_1}{U_0}exp\left(-\frac{\Delta G^{\prime }}{k_{B}T}\right)}}$$

(4)

where U₂ is rate of transformation of the precursor into a ordered crystal nucleus, U₁ is dissociation rate of the crystal precursor, and U₀ is temperature-dependent and protein-concentration-dependent rate of formation of liquid-like clusters in the supersaturated dilute solution; E₂ is the free-energy change needed for formation of an ordered cluster, $\Delta G^{\prime }$ being the free-energy change needed for the formation of the intermediate phase.

Kashchiev [24] has shown that CNT can provide a general conceptual and mathematical framework for describing the process of two-step nucleation, and to compare TSNM with CNT. And a comparison of TSNM with experimental data was provided by Vekilov [2].

2. Comparison of CNT with Experiments

Experimentally, various methods have been used for observing crystal nucleation onset and for measuring the rate of protein crystal nucleation. First, as a non-invasive technique, scattering of light [25,26,27,28] finds wide application. Also, different techniques for measuring induction times for crystal nucleation, i.e., the times when the first crystal(s) are detected, e.g., see [29,30], etc. have been used. However, these techniques are indirect. The only quasi-direct method for measuring crystals nucleation rates is the so-called ‘double-pulse method’, DPT [9,15,31,32,33,34]. (Originally, the nucleation/growth separation method was used by Tamann [31] who studied glass crystallization. Afterwards, Scheludko and Todorova [32] adapted this method for electro-crystallization studies, calling it ‘double pulse technique’, DPT.) According to DPT, visible crystals are counted, and J is determined from data for number densities N of nucleated/grown crystals, relative to nucleating times, t. Often the experimental points lie on sigmoid curves, e.g., Figure 3. In such cases, stationery nucleation rates are determined from the linear parts of N vs. t curves.

In this paper, the data from Figure 3, are used to reaffirm that CNT also applies to the nucleation of protein crystals: It is seen that supersaturation change from 3.22 (in which the curve has a clearly expressed rectilinear part) to 3.69, i.e., for an increase of B/Δμ² of only about 15%, J increases from about 1 nucleus.s⁻¹ to nearly 75 nuclei.s⁻¹. (Note that supersaturation 3.69 was the upper limit for DPT measurements, since a further supersaturation increase led to uncountable numbers of crystals.) In accordance with CNT, this result can be explained with the lower ΔG*, which is due to the increase of Δμ² (see Equation (2)).

Importantly, experimental studies have shown that the kinetics of the formation of crystal nuclei from proteins differs significantly from the kinetics of nucleation of crystals from small-molecule substances: Unusually high supersaturations are needed for protein crystal nucleation-typically, c/c_e = 800% and even more. And despite the high supersaturations, the protein crystal nucleation is distinctly slow. For instance, applying dimensionless supersaturations Δμ/k_BT between 2.1 and 3.7, Galkin and Vekilov [15] measured J for nucleation of hen-egg-white lysozyme (HEWL) crystals between 0.01 and 0.5 nuclei cm⁻³ s⁻¹. Similar results for HEWL crystal nucleation, J ≈ 0.03 to 0.10 nuclei cm⁻² s⁻¹, were obtained in my group for nucleation on bare glass, hexamethyl-disilazane and poly-L-lysine templates at dimensionless supersaturations Δμ/k_BT from 2.0 up to 2.5 (but under lower concentration than Galkin and Vekilov [15] have used). Also, for ferritin crystal nucleation on the same templates, Tsekova et al. [36] measured J to be from 0.008 till 0.820 nuclei cm⁻² s⁻¹, with Δμ/k_BT between 2 and 4.

Besides, experimental studies have shown that despite the unusually high supersaturations required for the nucleation of biomolecular crystals, the energy barriers ΔG* for nucleation of lysozyme [9], insulin [10], as well as for ferritin [36] are of the same order of magnitude (10⁻¹³ erg) as the values calculated for crystals constituted by small molecules. Therefore, the slower nucleation of biomolecular crystals should be attributed to a smaller pre-exponential factor $A={c_1\nu *}^{+}Z$ in Equation (1).

Based on these experimental results, the idea arose, as early as 2007, that the reason for the slow kinetics of protein crystal nucleation is rooted in the highly inhomogeneous surfaces of protein molecules [37]. Considering the case of simultaneous condensation and structuring during the nucleation of protein crystals, i.e., from CNT point of view, it was argued that a collision between two protein molecules leading to the formation of the crystalline bond between them requires not only their sufficiently close approach, but also their suitable spatial orientation. As already noted, the reason is that only several small patches on the protein molecule surface are capable to form crystalline bonds [37]. In turn, the need to meet the right patches imposes a severe steric restriction for the association of protein molecules, slowing down the process below reasonable values. However, performing computer Brownian dynamic simulations (BDS) of protein–protein molecule association (and approximating the protein molecule by hard spheres of equal radius of 18 Å, which is the typical of some small proteins), Northrup and Erickson proved that rotational diffusion mitigates the steric restriction for forming protein couples [38]. On this basis, it was inferred [37] that the rotational diffusional reorientation of a protein molecule toward meeting of the right patches also facilitates its joining to the critical nucleus. The results of the study of Northrup and Erickson [38] are used in this paper to quantitatively consider: (1) why protein crystals nucleation is that slow, and (2) what is the effect of rotational diffusion on the probability of attachment of protein molecules to critical nuclei.

3. Why Do Protein Crystals Nucleate Much More Slowly than Crystals of Small Molecules?

As already mentioned, the highly inhomogeneous surfaces of protein molecules slows down the process of protein critical nucleation. And since $Z\approx 0.01$ in Equation (1) should be approximately the same for biomolecular and small-molecule crystal nucleation, and c₁ can be varied in both cases, the slower nucleation of biomolecular crystals should be attributed to a smaller ν*⁺. That’s why the answer to the question put above lies in the way the crystalline bond between two protein molecules occurs.

First, by analyzing the molecular-kinetic mechanism of crystal bond formation, it can be shown that the low ν*⁺ can hardly be attributed to fewer hits between biomolecules. Especially for unstirred solutions, in which diffusion is the sole mechanism for the transport of molecules, this is not the case. Although the translational diffusion coefficient, D_t, for proteins (which is 10⁻⁶ to 5 × 10⁻⁷ cm²/s) is more than one order of magnitude smaller than the one for small molecules and inorganic crystals, the smaller D_t is compensated by the small distances between the protein molecules in solutions under crystallization conditions; the reason for this is that such solutions are highly concentrated. According to Rosenberger et al. [39,40], the intermolecular distances can be comparable to their diameter, 2R, where R is the radius of the protein molecule; evidently, at such a short distance, the diffusing protein molecules move quickly enough.

To estimate the time, τ, needed to move a protein molecule via translational diffusion at the distance 2R, let us place the mean-square particle displacement $\overline{x^2}={4R}^2$. And since $\overline{x^2}$ is:

$$\overline{x^2}=2D_{\mathrm{t}}t,$$

(5)

with

$$D_{\mathrm{t}}={\displaystyle \frac{k_{\mathrm{B}}T}{6\mathrm{\pi }\eta R}},$$

(6)

where η is the dynamic (or shear) viscosity, the result is:

$$\tau ={\displaystyle \frac{12\mathrm{\pi }\eta R^3}{k_{\mathrm{B}}T}}.$$

(7)

Thus, for a protein molecule with radius R = 10 nm, and with water viscosity η ~ 0.01 poise [41], τ = 9.2 × 10⁻⁶ s.

Since, in the volume of the solution (recall that Equation (1) is for homogeneous crystal nucleation), each protein molecule is surrounded (on all sides) by other protein molecules, any movement of a protein molecule at a distance 2R results in its collision with other protein molecules from the overcrowded surrounding. This leads to a very large number of collisions every second: about 1.1 × 10⁵ collisions per protein molecule per sec. Thus, an enormously large number of collisions of protein molecules in one cubic centimeter of solution is happening every second, and if every collision were successful, i.e., leading to the formation of intermolecular bonds, an extremely rapid formation of paired protein molecules should be expected. This would also mean rapid crystal bond formation.

However, this is not the real situation. Generating random collisions of hard spheres, Northrup and Erickson [38] found that the probability of an effective collision leading to the formation of protein pairs is negligibly small: two protein molecules (of radius 18 Å) collide in a suitable position for their bonding space orientation with a probability of 2 × 10⁻⁷. This gives about 2 × 10⁻² successful collisions per protein molecule per sec, which is very slow. This is the main reason to assume that the slow nucleation of protein crystals is due to the highly inhomogeneous surface of the protein molecules. However, the probability of attachment of protein molecules to the critical nucleus approaches the one that corresponds to the measured rates of protein crystal nucleation because the molecules perform rotational diffusion. Why?

In water solutions, the large protein molecules are subject to incessant collisions with water molecules. And while some of the energy arising from the collision of water molecules with a protein molecule is transferred to its translational kinetic energy, another energy part is transferred to torque [41]. In plane words, due to the varied speeds, number, and directions of impact of water molecules colliding with a protein molecule, the latter not only performs translational diffusion but also a fluctuating torque generates on it. And due to the equipartition theorem, larger particles rotate more slowly than smaller objects do.

Especially important for the present consideration is the different behavior of large biomolecules and small molecules when they collide in water environments. In such environments, in contrast to small molecules, two biomolecules remain trapped close to each other after their first collision. So, being not completely separated, the biomolecules undergo many (on average, nine [38]) additional collisions per encounter, and during the time intervals between the collisions, they can perform rotational diffusional reorientation towards a correct match.

Probability of Forming Complexes of Two Protein Molecules

The data from the computer BDS conducted by Northrup and Erickson [38] allow a quantitative assessment of the effect of rotational diffusion of protein molecules on the rate of their association (and thus permits the evaluation of the attachment probability of a molecule to the critical nucleus). Northrup and Erickson viewed the formation of a complex of two protein molecules as a stepwise process. First, proteins encounter in an orientationally non-specific fashion. Then, rotational movements begin, which lead to the formation of inter-molecular contacts.

An important factor that increases the efficiency of rotational diffusion is the possibility of partial overlapping of contacting patches to become completely overlapped. Even if only a part of the binding interactions is formed, the probability that molecules separate is decreased, and a partially formed bond obtains a chance to be transformed into a proper one. Northrup and Erickson [38] consider two possibilities for how, due to rotational diffusion, partial overlap of patches can become a stable bond.

-

First, the probability of forming only one contact (from a maximum possible four) between two colliding molecules is 3 × 10⁻⁴ [38]. But, although most of such complexes separate eventually, the BDS shows that about 1% of them survive (i.e., their probability of survival becomes 3 × 10⁻⁶). In the time between the following collisions there is also the possibility for rotation to bring another pair of contact points close to each other, which leads to a state with two contacts. This state is a key point in the pathway leading, with high probability, to completion of the final complex [38].

-

Second, the BDS rate constant for the state with two contacts is 4 × 10⁶ M⁻¹ s⁻¹, which is 400 times greater than the geometric rate constant (see Table 1 in [38]) and is very close to the measurements for most protein rates of protein–protein bond formations; the latter are also in the order of 10⁶ M⁻¹ s⁻¹ [38]. Northrup and Erickson attributed this bonding enhancement to multiple collisions and rotational reorientation in-between encounters. Here, we must recall that the upper limit of the diffusion-limited association of spheres, with every contact between them regardless of their orientation in space being successful, is given by the Smoluchowski rate constant for a second-order reaction, k₂ = 8πDr = 7 × 10⁹ M⁻¹ s⁻¹ [42]. Thus, by dividing the rate for the formation of two contacts by the Smoluchowski rate constant, we obtain the probability of dimer formation due to rotational diffusion of hard spheres (of equal radius 18 Å) as p⁺ ≈ 5.7 × 10⁻⁴. This probability is larger than the probability of transforming the state of one contact to the state with two contacts. Therefore, the preferred way of creating a stable bond between two protein molecules should be via the formation of two contacts.

However, despite the effect of rotational diffusion, the formation of pairs of protein molecules is a relatively rare event, i.e., it is a slow process. Moreover, since protein molecules are not exactly spheres, but have surface protrusions that increase their hydrodynamic radii (i.e., increase the frictional drag coefficient in the denominator in Equation (8); see below), the rate of the rotational reorientation of a protein molecule is decreased (for the rotational diffusion of protein molecules having nearly flat shapes, see Discussion).

Importantly, it must be emphasized that the results of Northrup and Erickson [38] refer to biochemical protein–protein associations and apply only to molecule pairing, i.e., only to the very beginning of the nucleation process. The probability of association of a protein molecule to the critical nucleus is larger (see Section 4).

4. Probability of Direct Attachment of Protein Molecules to Kink Sites and to Critical Nuclei

For spheres, the Stokes–Einstein–Debye relation gives the coefficient of rotational diffusion, D_r (in units of radians²/s), as:

$$D_{\mathrm{r}}={\displaystyle \frac{k_{\mathrm{B}}T}{8\mathrm{\pi }\eta R^3}}.$$

(8)

Thus, since D_r is related to the radius of the sphere in power three, small differences in R will have a large impact on D_r. Therefore, when a crystal becomes large enough, so large that it does not rotate any more, only the incoming protein molecule adjusts rotationally to it. This is exactly the case of protein crystal growing by the direct embedding of molecules from the solution into the kink sites. And it is easy to show that, in this case, the probability, p_k⁺, of embedding molecules in the kink sites of a growing crystal is many times greater than the probability of association of two protein molecules, p⁺.

In fact, the probability of meeting the bonding patches of two molecules in the appropriate spatial orientation (p⁺) is tantamount to the probability of the simultaneous appearance of these patches in the same place in space. This means that p⁺ is the product of the attachment probabilities (p_k⁺) of the two individual molecules. Hence, p_k⁺ is equal to the square root of p⁺:

$${\mathrm{p}}_{\mathrm{k}}^{+}=({\mathrm{p}}^{+}{)}^{1/2}.$$

(9)

Thus, using the value of p⁺ ≈ 5.7 × 10⁻⁴ calculated in the section titled Probability of Forming Complexes of Two Protein Molecules, the probability of a protein molecules attaching directly from the solution into the kink sites is p_k⁺ ≈ 2.4 × 10⁻² (about 42 times larger than p⁺).

Hence, since the critical nucleus rotates slower than the individual protein molecules (see Equation (8)), the probability of attachment of a molecule to the critical nucleus is between 5.7 × 10⁻⁴ and 2.4 × 10⁻², but closer to the lower limit (the reason for this is that particles with a linear scale of about 1 μm do not rotate [41]). Because larger nuclei rotate more slowly, ν*⁺ is larger for them.

In conclusion, importantly, because the size of the critical nucleus depends on Δμ, ν*⁺ also depends on Δμ, which is the fundamental difference from the CNT for the nucleation of crystal constituted by small molecules.

5. Time Scale of Rotational Reorientation of Biomolecules

To further clarify the role of the rotational reorientation of biomolecules in the nucleation (and growth) of protein crystals, we begin with the simplest case, this one of a sphere rotating around a fixed axis. Viewed from above this axis, the sphere is seen as a circle (Figure 4), and a point at the rotating sphere periphery moves to consecutive positions characterized by angles θ from 0 through 360 degrees, before having a complete rotation, i.e., reaching the starting position at 0 degrees. Obviously, rotating over sufficiently long periods of time, the point has had the entire range of angles, θ, between the starting θ_o and θ_o + 2π. Therefore, at large enough times, the sum of all probabilities for possible 2π (radians) angles is equal to 1, meaning that, since the probability is evenly distributed through each angle, there is necessarily a point at some angle θ along the circle, whose probability is ${\mathrm{p}}_{\mathrm{\theta }}\approx {\displaystyle \frac{1}{2\pi }}$.

In analogy to the translational diffusion, the mean-square angular deviation $\overline{{\theta }^2}$ in time t is:

$$\overline{{\theta }^2}=2D_{\mathrm{r}}t.$$

(10)

Thus, using Equation (8), we have:

$$\overline{{\theta }^2}={\displaystyle \frac{k_{\mathrm{B}}T}{8\mathrm{\pi }\eta R^3}}t.$$

(11)

To calculate the time, τ_r, that is needed for the vector 0A in Figure 4 to visit all points of the circle, i.e., to make a complete circumference of 2π, we use the expression $\overline{{\theta }^2}=(2\pi {)}^2$:

$${\tau }_{\mathrm{r}}={\displaystyle \frac{32{\pi }^3\eta R^3}{k_{\mathrm{B}}T}}.$$

(12)

Hence, for a protein molecule with radius R = 10 nm, τ_r = 2.4 × 10⁻⁴ s.

However, a complete circumference on 2π is superfluous: the bonding patches on the protein molecule surfaces are not points but occupy at least 10% of the protein surface [38]. Importantly, partial overlaps can occur beforehand. As already seen, even if the bonding patches overlap only partially, there is a chance that this overlap will become a complete overlap (and of course, the larger the patch, the more probable the crystalline bond formation). Therefore, recalling that the protein molecules undergo, on average, nine additional collisions, the above calculated τ_r value seems feasible; each collision between water and protein molecules lasts for the order of 10⁻¹² s, but in each individual collision the momentum of the protein molecule hardly changes. Such change results only from collisions with a great number of water molecules, and on a much longer timescale of about 10⁻⁶ s and greater. Then, an erratic trajectory of the molecule in the configuration space of the physical system is observed [41]. In conclusion, the calculated time, τ_r, which is needed for a complete circumference on 2π is only the upper time limit for bonding between patches to occur. But, since the bonding patches on the protein molecule surfaces differ in size, non-universally valid τ_r can be derived.

However, the complication is that, although not completely excluded (especially for small rotations), rotation around one fixed axis is rather an exception; rotation around more axes prevails by far. And roughly, the situation is equivalent to rotating πR circles about a fixed axis and simultaneously rotating each of these axis. This means that the number of positions to be visited increases πR times, i.e., that the desired angular positions on the sphere are reached more rarely. And again, the sizes of the bonding patches on the surfaces of the protein molecules are important for the creation of stable crystalline bonds (of course, the strength of the intermolecular interaction also plays a role). This raises the question of what these patches are.

6. What Is Known About the Bonding Patches on the Surfaces of Protein Molecules

Unfortunately, even the most advanced instrumental techniques used currently for visualization of the mechanism of protein crystal nucleation on a molecular scale, such as liquid-cell transition electron microscopy and atomic electron tomography, do not permit observation of the protein bonding patches. Instead, information delivered from X-ray diffraction studies regarding crystalline intermolecular contacts, formed in already grown protein crystals, has been used to reveal the bond selection preferences. Statistically reliable information was extracted from data available in the Protein Data Bank (PDB) for protein molecule structures (e.g., see [43,44,45,46,47,48,49,50]) and was used to reveal the patches in crystal lattice contacts. It was concluded that, in contrast to the physiological protein–protein bonds, which result from strong hydrophobic interactions via contacting areas occupying relatively large portions on the protein molecule surface, the crystal lattice contacts are selected in such a way as to avoid hydrophobic interactions and are smaller in size; the protein crystal lattice contacts are hydrophilic and polar (polar interaction means hydrogen bonds and salt bridges). For instance, for cutinase crystals, Jelsch et al. [48] found that, on average, ~70% of the interfacial residues of protein complexes are hydrophilic, including ~37% charged residues, i.e., hydrophilic interfaces are clearly of larger importance for protein assembly. Also, multiple van der Waals attractive forces, which include interactions between the partial electric charges of polar amino acid residues, are acting.

Dasgupta et al. [43] have shown that only a highly limited number of discrete patches situated over the protein molecule surfaces are prone to binding to partner protein molecules. Careful examination of the contacts in the protein crystal lattice has shown that the most common in them are arginine and glutamine residues; although lysine and glutamate residues (i.e., the carboxylate anion of glutamic acid) are situated almost exclusively on the surface of the proteins, they are the least likely residues to be found in crystal lattice contacts. Referring to larger than most databases taken from the PDB for previous studies with similar aims, Ansari and Helms [51] found a general agreement with previous studies concerning the protein–protein interfaces and the protein–protein interactions.

7. Discussions

Frequently, protein molecules that make up crystals are drawn as small circles (for example, see Figure 1) or small spheres with homogeneous surfaces. However, such sketches are somewhat misleading. As already noted, reality is completely different: the inhomogeneity of the surfaces of protein molecules (e.g., see Figure 5) determines the mechanism of their binding into crystal lattices. Although not accounted, either by CNT or by modern TSNM, this peculiarity of the protein crystal nucleation explain some deviations of measured nucleation rates from CNT predictions.

In this paper, accounting for the inhomogeneity of the surfaces of protein molecules, the reason for the slow nucleation rate of protein crystals has been revised. In doing so, the physical reasons for the slowness of nucleation are clarified. As a result of the reconsideration of the mechanism of the formation of protein crystal nuclei, quantitative values were calculated for (1) the number of collisions per protein molecule per sec, and how many of the strokes were successful; (2) for the probability of forming complexes of two protein molecules; (3) for the probability of the attachment of protein molecules to critical nuclei; (4) for the probability of direct attachment of protein molecules to kink sites. The study flags up the important fact that, to form crystalline bonds, the meeting protein molecules need to reorient to a suitable spatial position. Therefore, the time it takes for protein molecules to reorient themselves to locations that are suitable for the formation of crystalline bonds has been estimated.

In this paper, we have been looking at the rotation of near-spherical protein molecules. With them, rotation around each axis is equally likely and can be conservative. However, this is not the case with protein molecules, which deviate strongly from the spherical shape; in this case, the picture is substantially more complicated. For instance, according to the tennis racket theorem, rotation of a flat noncircular object (like a tennis racket) around its first and third principal axes is stable, whereas rotation around its second principal axis (which is an axis in the flat noncircular protein molecule that is perpendicular to the protrusion of the molecule) is unstable, i.e., non-conservative.

Importantly, this consideration applies not only to CNT but also to TSNM, according to which the rate determining, i.e., the slower stage of the process, is nucleus structuring [2], i.e., the creation of crystal bonds between protein molecules.

8. Conclusions

The comparatively slow nucleation of protein crystals has been explained in a quantitative way from a new perspective. It has been shown that the reason for this slowness is the highly inhomogeneous surfaces of the protein molecules, which have a limited number of small patches that can form crystalline bonds.

It is to be hoped that increasing knowledge regarding what happens at a molecular level during the nucleation of protein crystals brings us closer to the ability to control the rate of this process.