Abstract
In this study, first-principles calculations in conjunction with the particle swarm optimization (PSO) algorithm structure search method were employed to investigate the stable phases of Ca-Pt intermetallic compounds under various pressure conditions. The previously reported CaPt5 phase and the hitherto unreported phases Ca3Pt and Ca2Pt were successfully predicted, perfecting the known phase diagram for Ca-Pt intermetallic compounds. Furthermore, the pressure-induced phase transition in Ca2Pt has been identified. The structure of Ca2Pt undergoes a phase transition from Cmmm to C2/m and then to Cm at pressures ranging from 25 to 75 GPa. Electronic properties analyses revealed stable metallic bonds between the Ca and Pt atoms in the Ca-Pt intermetallic compounds. Simultaneously, the anionic character of the Pt atoms and the localization of electrons within the intermetallic compounds were observed. Analysis of the mechanical properties showed that Ca3Pt and CaPt5 exhibited different degrees of anisotropy. The CaPt5 structure exhibits significant transverse isotropy, whereas the Ca3Pt structure exhibits pronounced anisotropic behavior. The results of this study provide theoretical support for further research on Ca-Pt intermetallic compounds and the expansion of Pt oxidation states.
1. Introduction
Novel materials exhibiting unique electrical and mechanical characteristics have emerged as prominent areas of investigation in materials science [1,2,3]. Identifying such materials holds the potential to not only enhance existing technologies but also pave the way for new revolutionary applications. An enormous number of new materials can theoretically be synthesized. However, the practical application of these materials is constrained by their thermodynamic and kinetic stabilities. Many of these novel structures are prone to decomposition into simpler monomers or known compounds, which significantly reduces the number of new materials that can be synthesized. Despite the disparity between the number of new materials synthesized experimentally and those theoretically predicted, the pool of novel yet-to-be-explored materials remains substantial. In recent years, with the advent and refinement of density functional theory (DFT), robust software suites such as VASP, CASTEP, ABINIT, PWSCF, SIESTA, Gaussian, Quantum Espresso, and WIEN2K have been developed [4,5,6,7,8,9,10,11,12,13,14,15]. Owing to their exceptional efficiency and precision in performing first-principles calculations, these tools have become the cornerstones of material theory research. Building upon these methodologies, crystal structure prediction software such as CALYPSO and USPEX have been developed [16,17]. These tools can be used to predict the crystal structures of compounds at various stoichiometric ratios. Using these software packages has significantly enhanced the efficiency of exploring novel material systems.
The arrangement of electrons in the atomic electron shell is pivotal for elucidating the chemical behavior of elements, including aspects such as reactivity and periodic trends [18,19,20]. Transition metals exhibit distinct properties that distinguish them from other elements in the periodic table. Owing to the presence of multiple unpaired electrons in their electronic configurations, these metals are prone to variable valencies, facilitating the formation of complexes. Consequently, under specific conditions, the chemical repertoire of platinum-group metals can be significantly expanded, enabling the synthesis of a diverse array of compounds, including halides and others [21,22]. Expansion of the 5d orbital in platinum-group metals allows electron donation, enabling these metals to adopt +2 and +4 valence states within their compounds [21,22]. According to the Miedema rule [23] and the findings of Zintl [24], metals with either small disparities in electron charge density or substantial differences in electronegativity have a higher propensity to form intermetallic compounds. Consequently, it is theoretically feasible for less electronegative alkali and alkaline earth metals to form stable intermetallic compounds with more electronegative platinum group metals. The exceptional contraction of the 6s shell in Pt distinguishes it from a transition metal with unique and unconventional properties [25,26,27]. These characteristics imply that Pt exists in a negative oxidation state. The Cs-Pt structures with diverse electronic properties were identified by structural searches conducted at 10 GPa [28]. Additionally, platinum can assume a negative oxidation state under ambient pressure conditions, as demonstrated by the synthesis of Cs2Pt and Cs9Pt4H, which achieved the anionization of platinum (Pt2−) [29,30]. Numerous studies have reported that Pt can form intermetallic compounds with alkali metals such as Na [31] and Li [32,33]. The valence states of the Pt atoms within these compounds can be altered by manipulating the stoichiometric ratio of Pt to the alkali metals.
Pressure, a pivotal thermodynamic parameter, profoundly impacts the physical and chemical properties of materials. The electronic structure of elements can be dramatically modified under pressure, which can significantly alter the electronic configurations and chemical bonding and give rise to new phases that may not be stable under ambient conditions [34,35,36,37,38]. Consequently, the application of high pressure has emerged as the primary technique for synthesizing compounds with nontraditional stoichiometric ratios and exceptional physical properties [39,40,41]. Structural prediction methods employing the density functional theory indicate that pressure can extend the maximum achievable valence state of an atom, thereby revealing new chemical properties [42,43]. Concurrently, the pressure-induced s→d electron transfer endows group I and II elements with transition metal-like characteristics, enhancing their propensity to form alloys with other transition metals. Experimental and theoretical evidence has confirmed that high-pressure conditions can promote the alloying of alkali metals (K and Na) with iron (Fe) [44,45]. Yang et al. discovered that the alkali metal Li and the transition metal Au can form stable intermetallic compounds under various pressure conditions [42]. The authors further demonstrated the ability to manipulate the negative oxidation state of Au by adjusting the Li content of the compounds. Building on the aforementioned research, an AuLi8 compound with a NaCl-like structure was designed [46]. Subsequently, the superconducting properties of AuLi8 were investigated. It was observed that the crystal structure underwent a phase transition under pressure, which led to alterations in its physical and chemical properties. Recently, an increasing number of scholars have focused on studying pressure-driven phase transitions of crystal structures and have effectively established their phase transition sequences [47,48,49,50]. Throughout this process, the benefits of high pressure have been illustrated for optimizing the high-temperature superconducting characteristics of materials [51,52,53,54,55], facilitating the transition to metallic conductivity in nonmetallic substances [52,53,54,55,56], and altering their optical characteristics [37].
The considerable electronegativity differential (0.7 to 1.58) separating Pt from alkali and alkaline earth metals implies a theoretical capacity for the generation of stable intermetallic compounds. The synthesis of intermetallic compounds involving Pt and alkali metals (e.g., Cs-Pt [28], Na-Pt [31], and Li-Pt [32,33]) has also been explored. However, research on intermetallic compounds derived from Pt and alkaline earth metals, including their synthesis and properties, remains limited. The electronegativity disparity between Pt and the alkaline earth metal Ca, amounting to 1.28, is a mere 0.02, which is greater than that observed between Pt and the alkali metal Li, which is 1.26. This slight difference suggests that the formation of stable Ca-Pt intermetallic compounds is theoretically plausible under suitable conditions. Previous studies have made predictions for the Ca-Pt system under normal pressure [57]. This study introduces a structural prediction method that combines a particle swarm optimization algorithm with first-principles calculations. The method described above was employed to extensively investigate stable Ca-Pt intermetallic compounds across the pressure range of 0–75 GPa. This was the first use of this computational approach to discover such compounds. This investigation successfully identified previously unreported Ca3Pt and Ca2Pt intermetallic compounds and delineated the phase transition pathway of Ca2Pt with increasing pressure. Ca and Pt atoms are connected through metallic bonds in the Ca-Pt intermetallic compounds. In addition, a negative oxidation state of the Pt atoms and electron localization were observed. The mechanical properties of these compounds were investigated, revealing that Ca3Pt and CaPt5 exhibited varying degrees of anisotropy under atmospheric conditions.
2. Calculation Methods
The fusion of crystal structure predictions with first-principle calculations has initiated a new paradigm for identifying and investigating novel materials. The validity of this approach has been confirmed by its application in several material systems, as evidenced in the literature [28,31,42]. The stability and electronic properties of the crystal structure are closely linked to both pressure and stoichiometric ratio. Using the CALYPSO program, we predicted the crystal structures of the CaxPty (x = 1, y = 1–6 or x = 1–6, y = 1) intermetallic compounds at four target pressures (0 GPa, 25 GPa, 50 GPa, and 75 GPa). Following the structural prediction, we optimized and calculated the electronic and mechanical properties of the identified low-energy structures. The structure prediction methodology incorporates a tiered optimization approach, incrementally increasing accuracy. K-point grids with progressively finer resolutions are used. The minimum k-point spacing is set to 0.8 Å for the low-accuracy tier, 0.6 Å for the medium-accuracy tier, and 0.3 Å for the high-accuracy tier, respectively. The energy convergence criteria are correspondingly tightened, with values of 3 × 10−2 eV, 1 × 10−3 eV, and 1 × 10−6 eV, respectively, for each tier of the optimization process. A systematic approach was adopted for structural prediction, encompassing 45 sets of calculations based on varying pressures and stoichiometric ratios. Each set underwent a rigorous 30-generation search process, with 30 structures produced per generation. The initial generation comprised random structures, whereas the PSO algorithm was employed to generate 18 structures in each subsequent generation, complemented by an additional 12 random structures. This process resulted in 9900 generated structures, and 29,700 crystal structure optimizations were performed. Structural predictions were performed under a defined pressure at a temperature of 0 K. The thermal stability of the predicted structures was quantified by their enthalpy of formation (ΔH), as depicted in Equation (1), to assess their relative stability.
The lowest energy and most stable configurations were chosen for analysis across varying pressures and stoichiometric ratios. These structures were then computationally characterized, including structural relaxation, electronic structure, and mechanical property calculations, all of which were performed using the VASP (6.3.0) software suite. The VASP-based first-principles calculations describe the interactions between electrons using a projector-augmented wave (PAW) approach. The Perdew (Burke) Ernzerhof functional within the generalized gradient approximation (GGA) was employed as the exchange-correlation functional. For the valence electron configurations of Ca and Pt, the PAW pseudopotentials were 4s2 and 5d96s1, respectively. The plane-wave cutoff energy was set to 250 eV. The convergence criteria for total energy and Hellmann–Feynman force calculations were set at 10−6 eV and −10−3 meV/Å, respectively. In addition, the Monkhorst–Pack k-point grid was optimized with a minimum spacing of 0.25 Å. Phonons were calculated using VASP to evaluate the kinetic stability of the crystal structure. Ab initio molecular dynamics (AIMD) simulations were conducted on the structure within the canonical ensemble (NVT) framework to assess the thermal stability at 1000 K, 1250 K, 1500 K, 1750 K, and 2000 K. For the thermal stability assessment of the crystal structure, the time step was set to 1 fs, with a total simulation duration of 30 ps. COHP was computed using Lobster (5.1.1) [58] software for electronic structure analysis, and charge transfer analysis was performed using Bader (1.05) [59] software. The processed energy bands and density of states were obtained using the VASPKIT (1.4.1) [60] software package. The mechanical properties of the crystal structures were examined using the Voigt–Reuss–Hill approximation. This method involves the calculation of the stiffness constant Cij by imposing a series of minute strains on the crystal structure, ranging from −0.015% to 0.015% in increments of 0.005%.
3. Results and Discussion
3.1. Convex Hull
A convex hull diagram was constructed based on Equation (1) through a systematic series of structural predictions using CALYPSO (6.0) and VASP. The phases within the convex hull of the enthalpy of formation are deemed stable and, in principle, experimentally synthesizable. In contrast, the phases above this convex hull are considered substable or unstable and susceptible to decomposition into other compounds or monomers. Nevertheless, the thermodynamically stable phase Ca2Pt was not found [61]. Due to the differences in all algorithms and parameters of structural search, the results of this paper are different from those in reference [57].
As shown in Figure 1a, a previously documented CaPt5 structure with P6/mmm symmetry was replicated, thereby confirming the reliability of the method. Furthermore, this study unearthed the Ca3Pt and Ca2Pt structures. The Ca3Pt structure was thermodynamically stable at ambient pressure, whereas the Ca2Pt structure could only maintain its thermodynamic stability at pressures exceeding 5 GPa.

Figure 1.
(a) Thermodynamic stability of Ca-Pt intermetallic compounds relative to monomeric Ca and Pt at specific pressures. The thermodynamically stable phase is represented by an opaque symbol on the convex envelope. The solid circle represents the thermodynamically stable phase, and the hollow circle represents the thermodynamically metastable phase. (b) Stabilization pressure of Ca-Pt intermetallic compounds.
At 0 GPa, alongside the stable CaPt5 and Ca3Pt phases, the formation enthalpies for the four structures CaPt4, CaPt3, CaPt2, and Ca2Pt are all negative, and they lie 0.019, 0.18, 0.24, and 0.33 eV above the convex hull, respectively. This indicates that these phases can potentially be synthesized under suitable temperature and pressure conditions. Upon applying a pressure of 25 GPa, the CaPt5 and Ca3Pt phases, which are stable at atmospheric pressure, were positioned above the convex hull and were no longer thermodynamically stable. In contrast, a novel Ca2Pt phase with Cmmm symmetry is identified. Furthermore, the enthalpies of formation of the Pt-rich structures, namely CaPt5, CaPt4, and CaPt3, are only slightly higher than those of the convex hull. This indicates that these structures are substable phases that can potentially be synthesized under specific conditions. At 50 GPa, the Ca2Pt structure remained thermodynamically stable. Meanwhile, the Ca-rich structure (Ca4Pt) shifted closer to the convex hull, effectively reducing the difficulty of its synthesis. When the pressure continued to rise, the enthalpy of formation of Ca4Pt structure showed a trend away from the convex hull line. Therefore, under 50 GPa, high pressure is beneficial to the synthesis of Ca4Pt compounds. Driven by pressure, the Ca2Pt structure underwent a phase transition from Cmmm to C2/m (Figure 1b). As the pressure further increased to 75 GPa, the Ca2Pt phase remained stable, but the structures with other stoichiometric ratios exhibited a trend of moving away from the convex hull in terms of formation enthalpy. This suggests that Ca2Pt has a substantial pressure stability window. Driven by the pressure, the Ca2Pt structure underwent a phase transition from C2/m to Cm. Under this pressure, only the enthalpy of formation of the Ca4Pt structure remains negative, making it the only Ca-rich structure that can be synthesized under specific conditions.
3.2. Structural Characteristics and Stability
To ascertain the predicted characteristics and stability of the structure, it has been optimized and a comprehensive structural diagram was prepared, as shown in Figure 2. The CaPt5 phase, characterized by the P6/mmm symmetry, adopts a rhombohedral cell structure with equal lengths of 5.4 Å on the a and b-axes and 4.4 Å on the c-axis. The lattice vector angles are α = β = 90° and γ = 120°. In this structure, the Ca atoms are located at the midpoint along the c-axis, and the Pt atoms are distributed in two distinct positions within the cell. One Pt atom resided at the midpoint of the 110-face edge, centered on the face. The other is positioned at the intersection of cell vectors a–b, forming an equidistant distribution bounded by Ca atoms along the c-axis. The Pt atoms within the crystal cell exhibit a uniform interatomic spacing of 2.7 Å, with the shortest distance being 3.1 Å between Ca and Pt atoms. At ambient pressure, the Ca3Pt phase maintained a symmetry of P4/mmm (Figure 2b) and assumed a rhombohedral structure analogous to that of the CaPt5 phase at the same pressure level. The a and b-axes’ lengths are 5.08 Å, and the c-axis’s length is 5.89 Å. The lattice vector angles are α = β = 91.3° and γ = 61.5°. The Ca atoms were evenly distributed along the diagonal body of the cell vector a + b − c, with an interatomic spacing of 3.66 Å. The Pt atoms were located at face-centered positions on the 110 faces of the cell, and the minimum distance between these atoms and the Ca atoms was 2.9 Å.
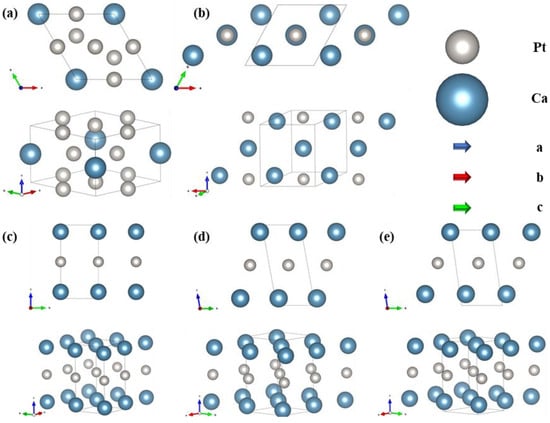
Figure 2.
Crystal structures of Ca-Pt intermetallic compounds stabilized at specific pressures, Ca atoms and Pt atoms are represented by blue and gray spheres, respectively. (a) CaPt5 (P6/mmm) at 0 GPa, (b) Ca3Pt (P4/mmm) at 0 GPa, (c) Ca2Pt (Cmmm) at 25 GPa, (d) Ca2Pt (C2/m) at 50 GPa, (e) Ca2Pt (Cm) at 75 GPa.
Under pressure, the Ca2Pt structure underwent a phase transition. The stabilized forms of Ca2Pt at 25, 50, and 75 GPa are presented in Figure 2c–e, respectively. At 25 GPa, Ca2Pt adopted Cmmm symmetry, with all atoms situated at the cell vertices. This arrangement yielded an equidistant distribution of Pt atoms at the midpoint of the c-axis and Ca atoms at the c-axis terminals. Upon increasing the pressure to 50 GPa, the symmetry of Ca2Pt transitioned from Cmmm to C2/m. The atoms within the unit cell moved from the boundary positions to the interior sites, resulting in a notable modification of the interatomic angles and a minor adjustment in the lengths of the lattice vectors. This leads to a decrease in the cell volume from 41.2 Å3 to 37.1 Å3, corresponding to a 9.9% volume reduction under the applied pressure. When the pressure was further increased to 75 GPa, the lengths of the cell vectors were uniformly reduced with no significant change in their angles. Furthermore, the atomic positions within the cell were adjusted, resulting in a change in the structural symmetry of Cm. The detailed parameter variations are listed in Table S1.
Two distinct methods were employed to rigorously evaluate the kinetic and thermal stabilities of the predicted structures: phonon spectroscopy and kinetic thermal bath simulations. These techniques provide insights into structural stability from varying angles. The results are illustrated in Figure 3a,b; additional data are available in Figure S1.

Figure 3.
Phonon spectra and molecular dynamics time and temperature versus time curves of CaPt5 and Ca3Pt intermetallic compounds. (a) Phonon spectrum of CaPt5, (b) phonon spectrum of Ca3Pt, the blue line is phonon dispersion, and the red line is the baseline. (c) temperature of CaPt5, (d) energy of CaPt5, (e) energy of Ca3Pt, (f) temperature of Ca3Pt.
The calculated stable structure displays no imaginary phonon modes, indicating that it is dynamically stable in its equilibrium configuration. To further evaluate the thermal stability of the predicted structures, molecular dynamics simulations were performed under thermal bath conditions over a range of temperatures. The thermal stabilities of the Ca3Pt and CaPt5 structures at 1000–2000 K under atmospheric pressure are depicted in Figure 3c–f. The figure illustrates that the temperature and energy performances of both the Ca3Pt and CaPt5 structures are consistent over a range of temperatures. The structures exhibited slight fluctuations around their respective temperatures and specific energy values, indicating dependable thermal stability within the studied temperature range. Simultaneously, the radial distribution functions (RDF) and coordination numbers (n) of the structures were analyzed (Figure S2). The coordination numbers of the Ca atoms in Ca3Pt and CaPt5 were determined to be 12 and 10, respectively, at various temperatures. The radial distribution functions and coordination numbers exhibited substantial overlap in the temperature range of 1000–2000 K, indicating that the atomic distribution within the crystal cell underwent minimal alteration. This consistency corroborates the thermal stability of the structures within the investigated temperature range.
3.3. Electronic Properties
The properties of atoms are profoundly influenced by their electronic structure, which in turn exerts a decisive impact on the physical and chemical properties of compounds. The density of states (DOS), projected density of states (PDOS), and energy band structures of the ground-state configurations of Ca3Pt and CaPt5 were calculated. Both Ca3Pt and CaPt5 intermetallic compounds have several bands that cross the Fermi level, which is characteristic of metallic behavior (Figure 4a,b). Similarly, the energy bands that cross the Fermi level exhibit a relatively steep trend, and a large energy gradient results in higher electron velocities. However, the reasons for this phenomenon are different. Below and at the Fermi level, the electronic states of the CaPt5 structure are primarily attributed to the 5d orbitals of the Pt atoms, whereas the electronic states of the Ca3Pt structure are jointly contributed by both Ca and Pt atoms. Furthermore, the contributions from various orbitals of the Ca atoms were balanced, as shown in Figure 4c.
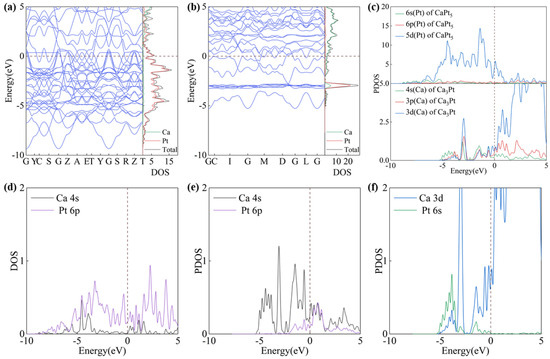
Figure 4.
Plots of energy band structure and projected density of states of CaPt5 and Ca3Pt. (a) Energy band structure of CaPt5, (b) energy band structure of Ca3Pt, (c) projected density of states of CaPt5 and Ca3Pt, (d) projected density of states of CaPt5, (e,f) projected density of states of Ca3Pt.
The Ca0Pt structure was synthesized based on the Ca3Pt structure by retaining the Pt atom occupancy and removing all Ca atoms to examine the electronic interactions within the Ca-Pt intermetallic crystal structure. A comparison of the PDOS diagrams for Ca and Pt atoms in both the Ca3Pt and Ca0Pt structures (as shown in Figures S3–S5) can characterize the interaction in the electronic structure. In the CaPt3 structure, the electrons occupying different orbitals of the Ca atoms migrated to lower energy levels, thereby increasing their reactivity (Figure S4). Simultaneously, the electrons on different orbitals of the Pt atoms transitioned from a delocalized state to a localized state, manifesting as isolated orbitals (Figure S5). In contrast, electrons occupying different orbitals of the Ca atoms maintained their delocalized characteristics.
Analysis of the projected state densities (Figure 4d–f and Figures S6 and S7) indicated that the DOS of the CaPt5 and Ca3Pt structures exhibited peak overlaps at specific energy levels, suggesting weak interactions between the Ca and Pt atoms. This overlap implies the potential for Ca-Pt bonding, which is inferred to be metallic. This hypothesis is further validated in the subsequent sections. In the bonding electrons of the CaPt5 structure, the main contributions originate from the d orbitals of the Ca atoms and the s and p orbitals of the Pt atoms. The overlap of the state density peaks is primarily distributed in the energy range of −5 to 0 eV. In the Ca3Pt structure, the projected densities of states of the s, p, and d orbitals of the Ca and Pt atoms show different degrees of peak overlap. The bonding electrons are primarily localized in the s orbitals of the Ca atoms and in the s and p orbitals of the Pt atoms.
Their atomic numbers are shown in Figure 5a,b. We calculated the COHP and its integral value below the Fermi energy level (ICOHP) for the Ca3Pt and CaPt5 structures to elucidate further the bonding strength and type between the Ca and Pt atoms using LOBSTER (5.1.1) software. COHP partitions the energy band structure into orbital pairwise interactions, functioning as a “bond-weighted” density of states between adjacent atoms. This illustrates the contributions of the bonding and antibonding states to the energy-band structure. Bonding states are indicated by COHP values less than zero, whereas antibonding states are indicated by COHP values greater than zero. The ICOHP is based on the integration of a COHP within a specific energy window. A value below the Fermi energy level of the ICOHP can be interpreted as the number of bonding electrons between the pairs of atoms, which provides insight into the bonding strength, as shown in Figure 5c,d. In the CaPt5 and Ca3Pt structures, the COHP values for the Ca and Pt atoms are negative below the Fermi level, suggesting the formation of bonding states between these atoms. As can be seen from the figures, the bonding strengths between the Ca and Pt atoms are not the same because of the differences in the coordination and spacing of the atoms.

Figure 5.
(a) Atomic numbering of CaPt5 structure, (b) atomic numbering of Ca3Pt structure, (c) -COHP and its integrals for the CaPt5 structure, (d) -COHP and its integrals for the Ca3Pt structure, (e) ELF of CaPt5, (f) ELF of Ca3Pt, (g) charge gain/loss of each atom in the CaPt5 structure, (h) charge gain/loss of each atom in the Ca3Pt structure.
ELF is an efficacious and straightforward tool for characterizing chemical bonds in stable compounds. ELF maps the electron probability density within a crystal. The different colors represent distinct levels of electron localization. Typically, ELF values exceeding 0.5 indicate the presence of covalent bonds, inner-shell electrons, or lone pairs, whereas values below 0.5 are associated with ionic or metallic bonds. ELF calculations were performed on the stabilized Ca3Pt and CaPt5 structures at atmospheric pressure. The ELF diagrams were constructed using planes that contained the maximum number of atoms in the unit cell, as depicted in Figure 5e,f. The ELF of CaPt5 revealed a distribution of Pt atoms encircling the Ca atoms, with ELF values between the different Ca and Pt atoms notably below 0.5. This pattern signifies the evident ionic bonding characteristics and confirms that the chemical bonding between Ca and Pt in this structure is metallic. In Ca3Pt structures, the atoms are positioned in a staggered arrangement on the crystal faces. The ELF values between the atoms were less than 0.1, indicating metallic bonding. Furthermore, the Pt atoms in both the Ca3Pt and CaPt5 structures underwent different degrees of electron gain, and their oxidation states were negative (Figure 5g,h).
3.4. Mechanical Properties
The Young’s modulus for the material faces was calculated from the elastic constants to evaluate the mechanical properties of the Ca-Pt intermetallic compounds. To ensure the accuracy of the calculation method, Young’s modulus was calculated using the stress-strain and energy-strain methods, as shown in Figure S8. The results from these distinct methods are plotted in polar diagrams, with the results of the strain-energy method represented by lines and those of the stress-strain method represented by points. The data points for the mechanical parameters of the material aligned with or closely approximated the lines in the plots, thereby corroborating the reliability of the calculation methods.
Figure 6 depicts the relationship between Young’s modulus and the measurement angle. As shown in the figure, the circular distribution of the data points indicates a weak correlation between Young’s modulus and angle, indicating that the structure exhibits isotropic behavior in the plane. Figure 6a reveals that the CaPt5 structure is characterized by transverse isotropy, with Young’s modulus that spans from 171 to 258 GPa. The CaPt5 structure exhibits isotropic behavior within the 001 plane, maintaining a constant Young’s modulus of 171 GPa across all angles. The Young’s modulus of CaPt5 demonstrates a clear directionality in the 010 and 100 planes. It reaches its peak value of 258 GPa when aligned with the principal axis of the lattice, specifically along the c-axis at angles θ = 90° or 270° within the 010 and 100 planes. The Ca3Pt structure is anisotropic, with Young’s modulus ranging from 14 to 67 GPa. The three planes (001, 010, and 100) exhibit pronounced anisotropy, with Young’s modulus in the 100 planes exhibiting the same trend as the CaPt5 structure’s 010 and 100 planes. The maximum value of Young’s modulus in the Ca3Pt structure occurs along the principal axis of the lattice (0°, 90°, 180°, 270°). In the 001 plane, the principal axis no longer aligns with the direction of the maximum Young’s modulus.

Figure 6.
Young’s modulus: (a) CaPt5, (b) Ca3Pt.
4. Conclusions
This work represents the first comprehensive search for stable Ca-Pt intermetallic compounds across a wide pressure range of 0–75 GPa. Novel phases Ca3Pt and Ca2Pt were predicted, and their kinetic and thermal stabilities were confirmed using phonon spectroscopy and AIMD simulations. Furthermore, the Ca2Pt structure underwent a symmetrical transition from Cmmm to C2/m to Cm as the pressure was increased from 25 GPa to 75 GPa. The metallic bonding properties between the Ca and Pt atoms in the intermetallic compounds were clarified by COHP, Bader charge, and ELF analyses. Anionization and electron localization of Pt atoms in the compounds were demonstrated. Analysis of the mechanical properties revealed that Ca3Pt exhibits pronounced anisotropic behavior, whereas CaPt5 demonstrates significant transverse isotropy. These results indicate that the electronic and mechanical properties of the compounds could be altered by adjusting the stoichiometric ratio. Additionally, the symmetry of Ca-Pt intermetallic compounds can be engineered to suit diverse application requirements by varying the pressure conditions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15030263/s1, Table S1: The calculated lattice parameters for the selected stable Ca-Pt structures; Figure S1: Phonon spectrum of Ca2Pt under different pressures. (a) 25 GPa, (b) 50 GPa, (c) 75 GPa; Figure S2: Radial distribution function and coordination number of CaPt5 and Ca3Pt structures at different temperatures. (a) RDF of CaPt5, (b) n of CaPt5, (c) RDF of Ca3Pt, (d) n of Ca3Pt; Figure S3: Total density of states (TDOS) for Ca atoms and Pt atoms in Ca3Pt and comparative structures. (a) TDOS of Ca, (b) TDOS of Pt; Figure S4: Projected density of states (PDOS) for Ca atoms in Ca3Pt and comparative structures. (a) PDOS of 4s, (b) PDOS of 3p, (c) PDOS of 3d; Figure S5: Projected density of states (PDOS) for Pt atoms in Ca3Pt and comparative structures. (a) PDOS of 6s, (b) PDOS of 6p, (c) PDOS of 5d; Figure S6: Projected density of states (PDOS) for Pt atoms and Ca atoms in CaPt5. (a) PDOS of Pt_6s and Ca_3d, (b) PDOS of Pt_5p and Ca 3_d; Figure S7: Projected density of states(PDOS) for Pt atoms and Ca atoms in Ca3Pt. (a) PDOS of Pt_6s and Ca_4s, (b) PDOS of Pt_5d and Ca_4s, (c) PDOS of Pt_6s and Ca_3p, (d) PDOS of Pt_6p and Ca_3p, (e) PDOS of Pt_5d and Ca_3p, (f) PDOS of Pt_6p and Ca_3d, (g) PDOS of Pt_5d and Ca_3d; Figure S8: Young’s modulus calculated using different methods. (a) Young’s modulus for the (001) plane, (b) Young’s modulus for the (010) plane, (c) Young’s modulus for the (100) plane.
Author Contributions
D.Y. conceived the idea, supervised the progress of the project, and revised the manuscript. Y.W. carried out first-principles structural prediction calculations and wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in the article are included in the main text and its Supporting Information.
Acknowledgments
The authors are grateful to Lingxin Kong at Kunming University of Science and Technology for his instruction and invaluable suggestion.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yaghi, O.M.; O’Keeffe, M.; Kanatzidis, M. Design of solids from molecular building blocks: Golden opportunities for solid state chemistry. J. Solid State Chem. 2000, 152, 1–2. [Google Scholar] [CrossRef]
- Cava, R.J.; DiSalvo, F.J.; Brus, L.E.; Dunbar, K.R.; Gorman, C.B.; Haile, S.M.; Interrante, L.V.; Musfeldt, J.L.; Navrotsky, A.; Nuzzo, R.G.; et al. Future directions in solid state chemistry: Report of the NSF-sponsored workshop. Prog. Solid State Chem. 2002, 30, 1–101. [Google Scholar] [CrossRef]
- Chamorro, J.R.; McQueen, T.M. Progress toward solid state synthesis by design. Acc. Chem. Res. 2018, 51, 2918–2925. [Google Scholar] [CrossRef]
- Orio, M.; Pantazis, D.A.; Neese, F. Density functional theory. Photosynth. Res. 2009, 102, 443–453. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding density functional theory (DFT) and completing it in practice. AIP Adv. 2014, 4, 127104. [Google Scholar] [CrossRef]
- Obot, I.B.; Macdonald, D.D.; Gasem, Z.M. Density functional theory (DFT) as a powerful tool for designing new organic corrosion inhibitors. Part 1: An overview. Corros. Sci. 2015, 99, 1–30. [Google Scholar] [CrossRef]
- Kohn, W.; Becke, A.D.; Parr, R.G. Density functional theory of electronic structure. J. Phys. Chem. 1996, 100, 12974–12980. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Crocombette, J.P. Theoretical study of point defects in crystalline zircon. Phys. Chem. Miner. 1999, 27, 138–143. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, C.; Chen, L.; Duan, J.; Li, F.; Liu, W. Different reaction mechanisms of SO4•− and •OH with organic compound interpreted at molecular orbital level in Co (II)/peroxymonosulfate catalytic activation system. Water Res. 2023, 229, 119392. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+ lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Glass, C.W.; Oganov, A.R.; Hansen, N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Commun. 2006, 175, 713–720. [Google Scholar] [CrossRef]
- Eickerling, G.; Reiher, M. The shell structure of atoms. J. Chem. Theory Comput. 2008, 4, 286–296. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Smits, O.R.; Pyykkö, P. The periodic table and the physics that drives it. Nat. Rev. Chem. 2020, 4, 359–380. [Google Scholar] [CrossRef]
- Miao, M.; Sun, Y.; Zurek, E.; Lin, H. Chemistry under high pressure. Nat. Rev. Chem. 2020, 4, 508–527. [Google Scholar] [CrossRef]
- Schweizer, A.E.; Kerr, G.T. Thermal decomposition of hexachloroplatinic acid. Inorg. Chem. 1978, 17, 2326–2327. [Google Scholar] [CrossRef]
- Arnold, W.; Eric, S.P.; John, A.R.; Emory, E.T. Handbook of Organic Compounds. Nature 1956, 177, 639–640. [Google Scholar]
- Miedema, A.R.; De Boer, F.R.; De Chatel, P.F. Empirical description of the role of electronegativity in alloy formation. J. Phys. F Met. Phys. 1973, 3, 1558. [Google Scholar] [CrossRef]
- Corbett, J.D. Polyatomic Zintl anions of the post-transition elements. Chem. Rev. 1985, 85, 383–397. [Google Scholar] [CrossRef]
- Pyykko, P.; Desclaux, J.P. Relativity and the periodic system of elements. Acc. Chem. Res. 1979, 12, 276–281. [Google Scholar] [CrossRef]
- Desclaux, J.P. Relativistic Dirac-Fock expectation values for atoms with Z = 1 to Z = 120. At. Data Nucl. Data Tables 1973, 12, 311–406. [Google Scholar] [CrossRef]
- Andersen, T.; Haugen, H.K.; Hotop, H. Binding energies in atomic negative ions: III. J. Phys. Chem. Ref. Data 1999, 28, 1511–1533. [Google Scholar] [CrossRef]
- Arrieta, R.; Brgoch, J. Forming Platinide Phases under Pressure in the Cs–Pt System. J. Phys. Chem. C 2022, 126, 2062–2069. [Google Scholar] [CrossRef]
- Smetana, V.; Mudring, A.V. Cesium platinide hydride 4Cs2Pt CsH: An intermetallic double salt featuring metal anions. Angew. Chem. Int. Ed. 2016, 55, 14838–14841. [Google Scholar] [CrossRef]
- Karpov, A.; Nuss, J.; Wedig, U.; Jansen, M. Cs2Pt: A Platinide (-ii) Exhibiting Complete Charge Separation. Angew. Chem. Int. Ed. 2003, 42, 4818–4821. [Google Scholar] [CrossRef]
- Mao, J.; Wang, Y.; Li, K.; Chen, Y.-C. Pressure-Enriched Chemistry of Pt: Prediction and Synthesis of Dense Sodium Platinides. J. Phys. Chem. C 2021, 125, 11791–11798. [Google Scholar] [CrossRef]
- Bronger, W.; Nacken, B.; Ploog, K. Zur synthese und struktur von Li2Pt und LiPt. J. Less Common Met. 1975, 43, 143–146. [Google Scholar] [CrossRef]
- Nash, C.P.; Boyden, F.M.; Whittig, L.D. Intermetallic compounds of alkali metals with platinum. A novel preparation of a colloidal platinum hydrogenation catalyst. J. Am. Chem. Soc. 1960, 82, 6203–6204. [Google Scholar] [CrossRef]
- McMillan, P.F. High pressure synthesis of solids. Curr. Opin. Solid State Mater. Sci. 1999, 4, 171–178. [Google Scholar] [CrossRef]
- Badding, J.V. High-pressure synthesis, characterization, and tuning of solid state materials. Annu. Rev. Mater. Sci. 1998, 28, 631–658. [Google Scholar] [CrossRef]
- Prewitt, C.T.; Downs, R.T. High-pressure crystal chemistry. Rev. Mineral. 1998, 37, 284–318. [Google Scholar]
- Li, Y.H. Crystal structure, electronic structure, the density of states, optical properties, and superconducting transition temperature of ZrBeSi crystal under pressure. Phys. Status Solidi 2023, 260, 2300196. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, L.; Feng, L.; Tuo, H.-H.; Zhang, Y.; Wei, Q.; Li, P.-F. Pressure-induced phase transition and electronic structure evolution in layered semimetal HfTe2. Chin. Phys. B 2023, 32, 086101. [Google Scholar] [CrossRef]
- Miao, M.; Brgoch, J.; Krishnapriyan, A.; Goldman, A.; Kurzman, J.A.; Seshadri, R. On the stereochemical inertness of the auride lone pair: Ab initio studies of AAu (A = K, Rb, Cs). Inorg. Chem. 2013, 52, 8183–8189. [Google Scholar] [CrossRef]
- Brgoch, J.; Hermus, M. Pressure-Stabilized Ir3−in a Superconducting Potassium Iridide. J. Phys. Chem. C 2016, 120, 20033–20039. [Google Scholar] [CrossRef]
- Zhong, X.; Li, X.; Yang, L.; Wang, D.; Qu, X.; Liu, H. Predicted Stable Structures of the Li–Ag System at High Pressures. J. Phys. Chem. Lett. 2021, 12, 1671–1675. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Y.; Peng, F.; Bergara, A.; Ma, Y. Gold as a 6p-element in dense lithium aurides. J. Am. Chem. Soc. 2016, 138, 4046–4052. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, S.; Guan, W.; Yang, G.; Ma, Y. Gold with +4 and +6 oxidation states in AuF4 and AuF6. J. Am. Chem. Soc. 2018, 140, 9545–9550. [Google Scholar] [CrossRef]
- Lee, K.K.M.; Jeanloz, R. High-pressure alloying of potassium and iron: Radioactivity in the Earth’s core? Geophys. Res. Lett. 2003, 30, 2212. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Zhu, C.; Liu, H.; Tse, J.S.; Ma, Y. Prediction of host–guest Na–Fe intermetallics at high pressures. Inorg. Chem. 2016, 55, 7026–7032. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, Y.; Ding, S.; Bergara, A.; Li, F.; Liu, Y.; Zhou, X.-F.; Yang, G. Superconductivity in Li8Au electride. Phys. Rev. B 2023, 107, L100501. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, S.; Li, H.; Wang, H.; Liu, G.; Ma, J.; Xu, H.; Liu, H.; Ma, Y. Coexistence of superconductivity and electride states in Ca2H with an antifluorite-type motif under compression. J. Mater. Chem. A 2023, 11, 21345–21353. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, T.; Li, D. Emerging d−d orbital coupling between non-d-block main-group elements Mg and I at high pressure. IScience 2023, 26, 106113. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, X.; Wan, B.; Zhang, Z.; Shen, W.; Zhang, Y.; Fang, C.; Chen, L.; Wang, Q.; He, J.; et al. A pressure-induced high-pressure metallic GeTe phase. J. Chem. Phys. 2023, 158, 134711. [Google Scholar] [CrossRef]
- Zhang, A.; Cui, Y.; Yue, J.; Li, J.; Pan, Y.; Chen, X.; Liu, Y.; Cui, T. Pressure-induced enhancement of thermoelectric performance of CoP3 by the structural phase transition. Acta Mater. 2023, 248, 118773. [Google Scholar] [CrossRef]
- He, X.-L.; Zhang, P.; Ma, Y.; Li, H.; Zhong, X.; Wang, Y.; Liu, H.; Ma, Y. Potential high-temperature superconductivity in the substitutional alloy of (Y, Sr) H11 under high pressure. Phys. Rev. B 2023, 107, 134509. [Google Scholar] [CrossRef]
- Rahman, S.; Wang, L.; Saqib, H.; Errandonea, D.; Yang, L.; Zhao, Y.; Zhuang, Y.; Gao, G.; Wang, L.; Tian, Y. Metallization and superconductivity with Tc > 12 K in transition metal dichalcogenide HfS2 under pressure. Mater. Today Phys. 2023, 34, 101091. [Google Scholar] [CrossRef]
- Wei, X.; Hao, X.; Bergara, A.; Zurek, E.; Liang, X.; Wang, L.; Song, X.; Li, P.; Wang, L.; Gao, G.; et al. Designing ternary superconducting hydrides with A15-type structure at moderate pressures. Mater. Today Phys. 2023, 34, 101086. [Google Scholar] [CrossRef]
- Pei, C.; Zhang, J.; Wang, Q.; Zhao, Y.; Gao, L.; Gong, C.; Tian, S.; Luo, R.; Li, M.; Yang, W.; et al. Pressure-induced superconductivity at 32 K in MoB2. Natl. Sci. Rev. 2023, 10, nwad034. [Google Scholar] [CrossRef]
- Dai, G.; Jia, Y.; Gao, B.; Peng, Y.; Zhao, J.; Ma, Y.; Chen, C.; Zhu, J.; Li, Q.; Yu, R. Pressure-induced superconductivity in the nonsymmorphic topological insulator KHgAs. NPG Asia Mater. 2023, 15, 52. [Google Scholar] [CrossRef]
- Shan, P.F.; Han, X.; Li, X.; Liu, Z.Y.; Yang, P.T.; Wang, B.S.; Wang, J.F.; Liu, H.Y.; Shi, Y.G.; Sun, J.P.; et al. Pressure-induced metallic state in a van der Waals cluster Mott insulator Nb3Cl8. Mater. Today Phys. 2023, 38, 101267. [Google Scholar] [CrossRef]
- Yan, D.; Kong, L.; Xu, B.; Yang, B. One−Step Synthesis Strategy for a Platinum−Based Alloy Catalyst Designed via Crystal−Structure Prediction. Molecules 2024, 29, 5634. [Google Scholar] [CrossRef]
- Nelson, R.; Ertural, C.; Geogre, J.; Deringer, V.L.; Hautier, G. LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory. J. Comput. Chem. 2020, 41, 1931–1940. [Google Scholar] [CrossRef]
- Henkelman, G.; Andri, A.; Hannes, J. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Wood, E.A.; Compton, V.B. Laves-phase compounds of alkaline earths and noble metals. Acta Crystallogr. 1958, 11, 429–433. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).