Unraveling the Determinant Mechanisms in Flow-Mediated Crystal Growth and Phase Behaviors
Abstract
1. Introduction
2. Materials and Methods
2.1. HXPFC-s2 Formalism
2.1.1. Free Energy Functional and Advected XPFC Equation
2.1.2. Navier–Stokes Momentum Coupling
2.2. HXPFC-s2 Dimensionless Form
2.3. Significant Dimensionless Numbers
2.4. Numerical Methods
2.5. Simulation Setup
3. Results
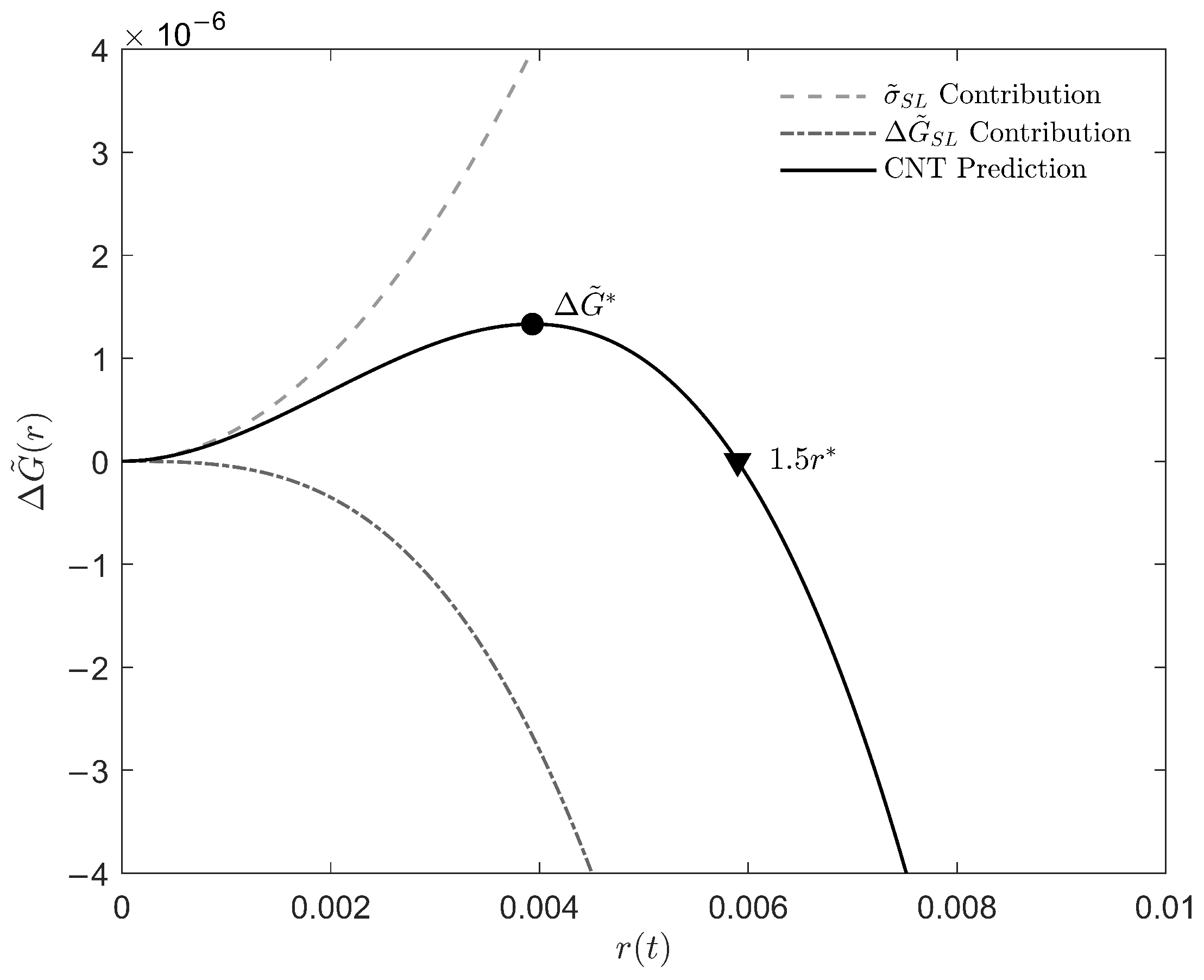
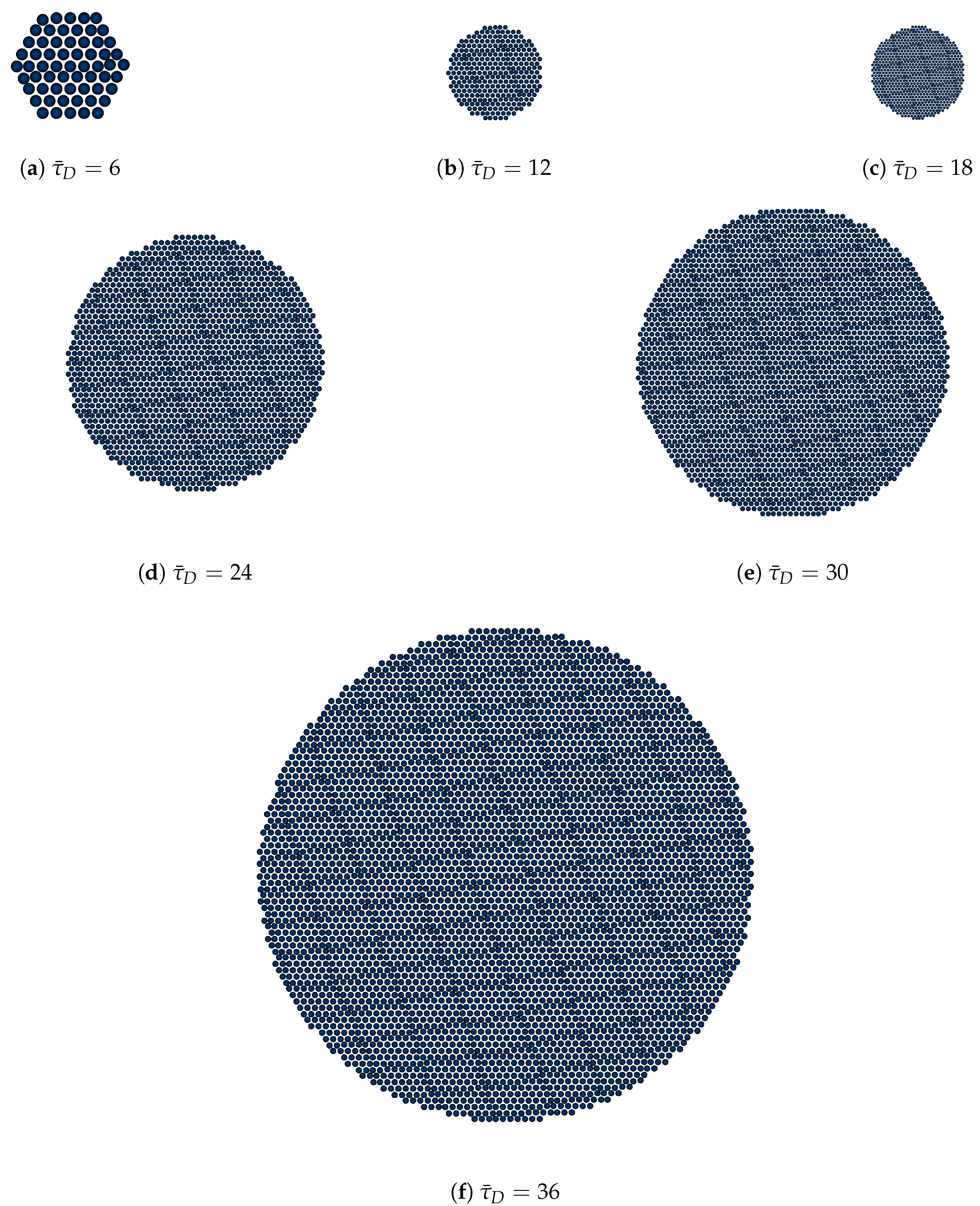
3.1. Effective Temperature-Dependent Crystal Growth
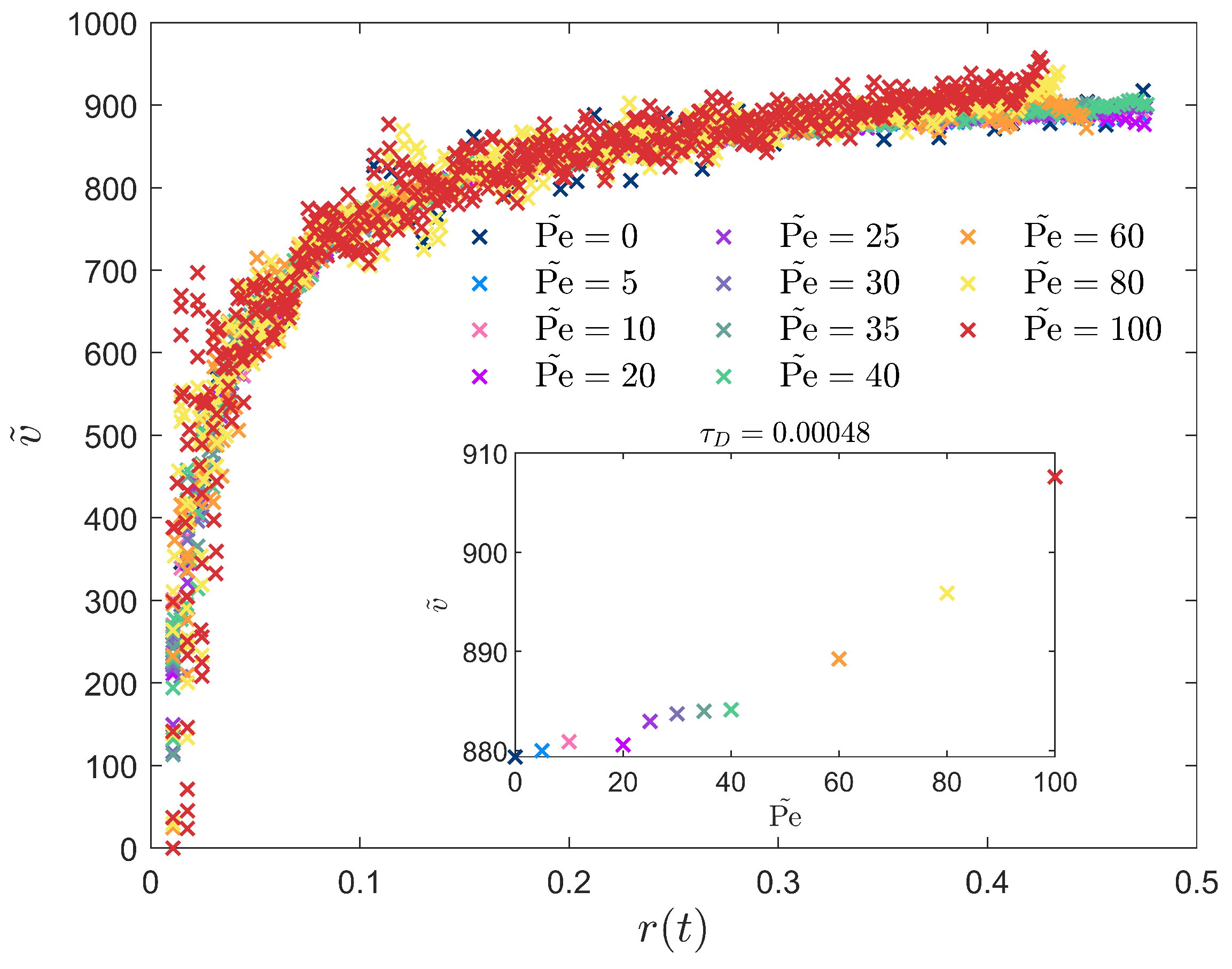
3.2. Peclet-Dependent Crystal Growth
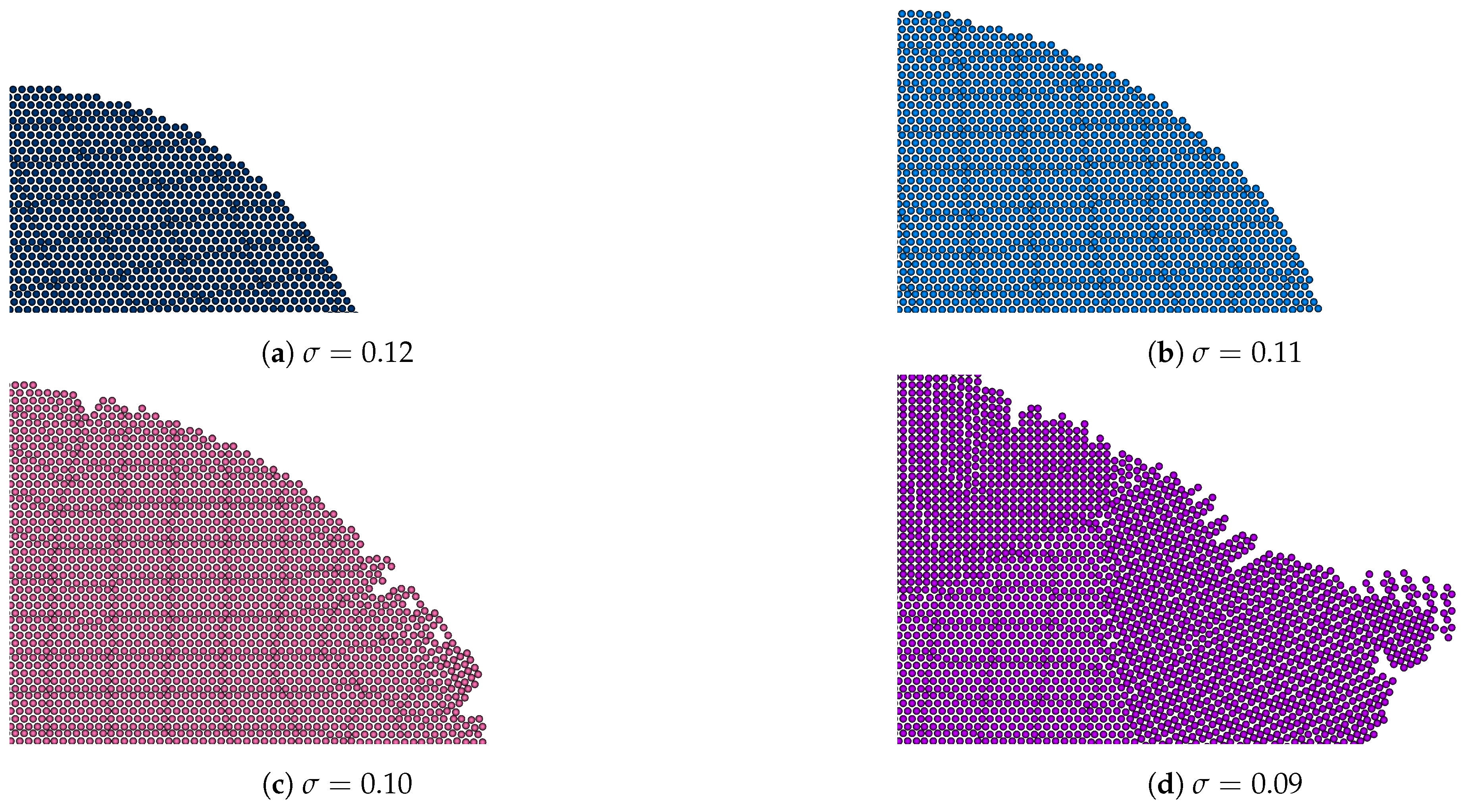
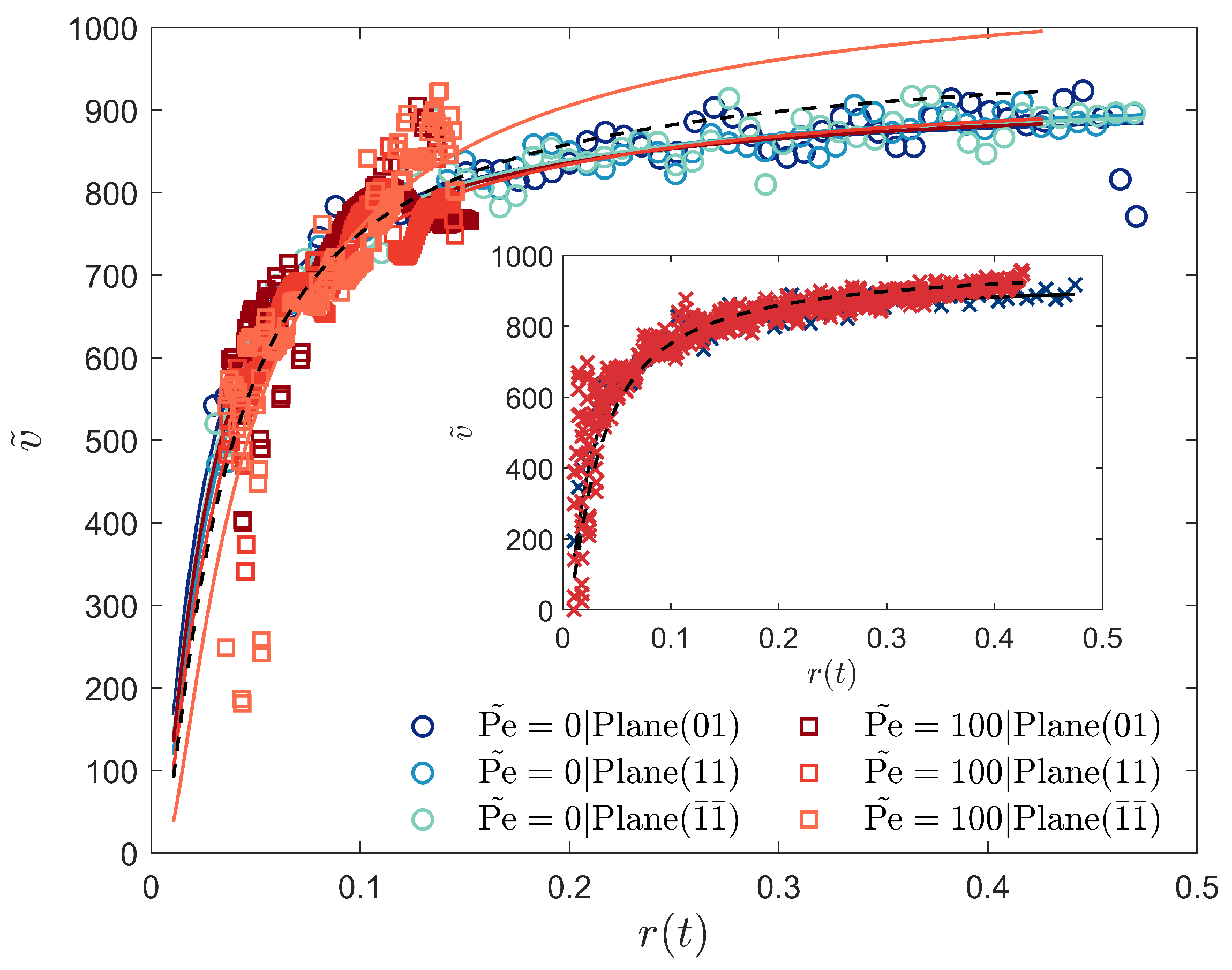
3.3. Crystal Plane Growth Dependence
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HXPFC-s2 | Hydrodynamic Structural Phase Field Crystal semi-two-way Coupled |
| PFC | Phase Field Crystal |
| XPFC | Structural Phase Field Crystal |
| DCF | Direct Correlation Function |
| DDFT | Dynamic Density Functional Theory |
| HNC | Hypernetted Chain |
| MSA | Mean Spherical Approximation |
| RPA | Random Phase Approximation |
Appendix A. General HXPFC Formalism Derivation
Appendix A.1. Free Energy Functional
Appendix A.2. Advected PFC Equation
Appendix A.3. Navier–Stokes Coupling
Appendix B. Dimensionless HXPFC-s2 Form Derivation
Appendix B.1. Convective Timescale
Appendix B.2. Diffusive Timescale
Appendix C. Derivation of Theoretical Growth Rate Equation
References
- Yang, H.; Wang, H.; Wang, K.; Liu, D.; Zhao, L.; Chen, D.; Zhu, W.; Zhang, J.; Zhang, C. Recent Progress of Film Fabrication Process for Carbon-Based All-Inorganic Perovskite Solar Cells. Crystals 2023, 13, 679. [Google Scholar] [CrossRef]
- Soto-Montero, T.; Soltanpoor, W.; Morales-Masis, M. Pressing challenges of halide perovskite thin film growth. APL Mater. 2020, 8, 110903. [Google Scholar] [CrossRef]
- Li, Z.; Klein, T.R.; Kim, D.H.; Yang, M.; Berry, J.J.; Van Hest, M.F.A.M.; Zhu, K. Scalable fabrication of perovskite solar cells. Nat. Rev. Mater. 2018, 3, 18017. [Google Scholar] [CrossRef]
- Weerasinghe, H.C.; Macadam, N.; Kim, J.E.; Sutherland, L.J.; Angmo, D.; Ng, L.W.T.; Scully, A.D.; Glenn, F.; Chantler, R.; Chang, N.L.; et al. The first demonstration of entirely roll-to-roll fabricated perovskite solar cell modules under ambient room conditions. Nat. Commun. 2024, 15, 1656. [Google Scholar] [CrossRef]
- Guo, Q.; Gong, X.; Shen, Z.; Hao, X.; Zhang, J. Numerical Simulation on Preparing Uniform and Stable Perovskite Wet Film in Slot-Die Coating Process. ACS Omega 2023, 8, 19547–19555. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Y. Research on Single Crystal Preparation via Dynamic Liquid Phase Method. Crystals 2023, 13, 1150. [Google Scholar] [CrossRef]
- Małysiak, A.; Orda, S.; Drzazga, M. Influence of Supersaturation, Temperature and Rotational Speed on Induction Time of Calcium Sulfate Crystallization. Crystals 2021, 11, 1236. [Google Scholar] [CrossRef]
- Mura, F.; Zaccone, A. Effects of shear flow on phase nucleation and crystallization. Phys. Rev. E 2016, 93, 042803. [Google Scholar] [CrossRef]
- Elder, K.R.; Katakowski, M.; Haataja, M.; Grant, M. Modeling Elasticity in Crystal Growth. Phys. Rev. Lett. 2002, 88, 245701. [Google Scholar] [CrossRef] [PubMed]
- Elder, K.R.; Grant, M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals. Phys. Rev. E 2004, 70, 051605. [Google Scholar] [CrossRef]
- Ramakrishnan, T.V.; Yussouff, M. First-principles order-parameter theory of freezing. Phys. Rev. B 1979, 19, 2775–2794. [Google Scholar] [CrossRef]
- Elder, K.R.; Provatas, N.; Berry, J.; Stefanovic, P.; Grant, M. Phase-field crystal modeling and classical density functional theory of freezing. Phys. Rev. B 2007, 75, 064107. [Google Scholar] [CrossRef]
- Gao, N.; Zhao, Y.; Xia, W.; Liu, Z.; Lu, X. Phase-Field Crystal Studies on Grain Boundary Migration, Dislocation Behaviors, and Topological Transition under Tension of Square Polycrystals. Crystals 2023, 13, 777. [Google Scholar] [CrossRef]
- Hirvonen, P.; Ervasti, M.M.; Fan, Z.; Jalalvand, M.; Seymour, M.; Vaez Allaei, S.M.; Provatas, N.; Harju, A.; Elder, K.R.; Ala-Nissila, T. Multiscale modeling of polycrystalline graphene: A comparison of structure and defect energies of realistic samples from phase field crystal models. Phys. Rev. B 2016, 94, 035414. [Google Scholar] [CrossRef]
- Ankudinov, V.; Galenko, P.K. Noise-Induced Defects in Honeycomb Lattice Structure: A Phase-Field Crystal Study. Crystals 2023, 14, 38. [Google Scholar] [CrossRef]
- Podmaniczky, F.; Gránásy, L. Nucleation and Post-Nucleation Growth in Diffusion-Controlled and Hydrodynamic Theory of Solidification. Crystals 2021, 11, 437. [Google Scholar] [CrossRef]
- Praetorius, S.; Voigt, A. A Phase Field Crystal Approach for Particles in a Flowing Solvent. Macromol. Theory Simul. 2011, 20, 541–547. [Google Scholar] [CrossRef]
- Praetorius, S.; Voigt, A. A Navier-Stokes phase-field crystal model for colloidal suspensions. J. Chem. Phys. 2015, 142, 154904. [Google Scholar] [CrossRef]
- Heinonen, V.; Achim, C.; Kosterlitz, J.; Ying, S.C.; Lowengrub, J.; Ala-Nissila, T. Consistent Hydrodynamics for Phase Field Crystals. Phys. Rev. Lett. 2016, 116, 024303. [Google Scholar] [CrossRef]
- Podmaniczky, F.; Gránásy, L. Molecular scale hydrodynamic theory of crystal nucleation and polycrystalline growth. J. Cryst. Growth 2022, 597, 126854. [Google Scholar] [CrossRef]
- Dean, D.S. Langevin equation for the density of a system of interacting Langevin processes. J. Phys. A Math. Gen. 1996, 29, L613–L617. [Google Scholar] [CrossRef]
- Marconi, U.M.B.; Tarazona, P. Dynamic density functional theory of fluids. J. Chem. Phys. 1999, 110, 8032–8044. [Google Scholar] [CrossRef]
- Van Teeffelen, S.; Backofen, R.; Voigt, A.; Löwen, H. Derivation of the phase-field-crystal model for colloidal solidification. Phys. Rev. E 2009, 79, 051404. [Google Scholar] [CrossRef]
- Emmerich, H.; Löwen, H.; Wittkowski, R.; Gruhn, T.; Tóth, G.I.; Tegze, G.; Gránásy, L. Phase-field-crystal models for condensed matter dynamics on atomic length and diffusive time scales: An overview. Adv. Phys. 2012, 61, 665–743. [Google Scholar] [CrossRef]
- Greenwood, M.; Provatas, N.; Rottler, J. Free Energy Functionals for Efficient Phase Field Crystal Modeling of Structural Phase Transformations. Phys. Rev. Lett. 2010, 105, 045702. [Google Scholar] [CrossRef]
- Greenwood, M.; Rottler, J.; Provatas, N. Phase-field-crystal methodology for modeling of structural transformations. Phys. Rev. E 2011, 83, 031601. [Google Scholar] [CrossRef] [PubMed]
- Cavaterra, C.; Grasselli, M.; Mehmood, M.A.; Voso, R. Analysis of a Navier–Stokes phase-field crystal system. Nonlinear Anal. Real World Appl. 2025, 83, 104263. [Google Scholar] [CrossRef]
- An, J.; Zhang, J.; Yang, X. A novel second-order time accurate fully discrete finite element scheme with decoupling structure for the hydrodynamically-coupled phase field crystal model. Comput. Math. Appl. 2022, 113, 70–85. [Google Scholar] [CrossRef]
- Yang, X.; He, X. Numerical approximations of flow coupled binary phase field crystal system: Fully discrete finite element scheme with second-order temporal accuracy and decoupling structure. J. Comput. Phys. 2022, 467, 111448. [Google Scholar] [CrossRef]
- Yang, J.; Kim, J. Consistent energy-stable method for the hydrodynamics coupled PFC model. Int. J. Mech. Sci. 2023, 241, 107952. [Google Scholar] [CrossRef]
- Rauscher, M. DDFT for Brownian particles and hydrodynamics. J. Phys. Condens. Matter 2010, 22, 364109. [Google Scholar] [CrossRef] [PubMed]
- Archer, A.J. Dynamical density functional theory for molecular and colloidal fluids: A microscopic approach to fluid mechanics. J. Chem. Phys. 2009, 130, 014509. [Google Scholar] [CrossRef] [PubMed]
- Willis, L.W.; Rao, R.R.; Liu, L.L. Towards a multiscale computational framework for simulating flow-mediated crystallization based on phase-field crystal formalisms. In Proceedings of the 16th World Congress on Computational Mechanics and 4th Pan American Congress on Computational Mechanics, Vancouver, BC, Canada, 21–26 July 2024. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, J.; Wang, Z.; Li, J.; Guo, C.; Guo, Y.; Yang, Y. Existence and forming mechanism of metastable phase in crystallization. Comput. Mater. Sci. 2016, 122, 167–176. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods: For Physics, Chemistry and the Natural Sciences, study ed., 2. ed., 6. print ed.; Number 13 in Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids: With Applications to Soft Matter, 4th ed.; Elsevier/AP: Amstersdam, The Netherlands, 2013. [Google Scholar]
- Liu, Z.; Zhu, Y.; Clausen, J.R.; Lechman, J.B.; Rao, R.R.; Aidun, C.K. Multiscale method based on coupled lattice-Boltzmann and Langevin-dynamics for direct simulation of nanoscale particle/polymer suspensions in complex flows. Int. J. Numer. Methods Fluids 2019, 91, 228–246. [Google Scholar] [CrossRef]
- Rasaiah, J.C.; Card, D.N.; Valleau, J.P. Calculations on the “Restricted Primitive Model” for 1–1 Electrolyte Solutions. J. Chem. Phys. 1972, 56, 248–255. [Google Scholar] [CrossRef]
- Solana, J.R. Perturbation Theories for the Thermodynamic Properties of Fluids and Solids; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Te Vrugt, M.; Löwen, H.; Wittkowski, R. Classical dynamical density functional theory: From fundamentals to applications. Adv. Phys. 2020, 69, 121–247. [Google Scholar] [CrossRef]
- Lovett, R.; Mou, C.Y.; Buff, F.P. The structure of the liquid–vapor interface. J. Chem. Phys. 1976, 65, 570–572. [Google Scholar] [CrossRef]
- Henderson, D.; Boda, D. Mean spherical approximation for the Yukawa fluid radial distribution function. Mol. Phys. 2011, 109, 1009–1013. [Google Scholar] [CrossRef]
- Kundu, M.; Howard, M.P. Dynamic density functional theory for drying colloidal suspensions: Comparison of hard-sphere free-energy functionals. J. Chem. Phys. 2022, 157, 184904. [Google Scholar] [CrossRef] [PubMed]
- Taira, K.; Colonius, T. The immersed boundary method: A projection approach. J. Comput. Phys. 2007, 225, 2118–2137. [Google Scholar] [CrossRef]
- Tanaka, H.; Araki, T. Simulation Method of Colloidal Suspensions with Hydrodynamic Interactions: Fluid Particle Dynamics. Phys. Rev. Lett. 2000, 85, 1338–1341. [Google Scholar] [CrossRef] [PubMed]
- Sanz, E.; Vega, C.; Espinosa, J.R.; Caballero-Bernal, R.; Abascal, J.L.F.; Valeriani, C. Homogeneous Ice Nucleation at Moderate Supercooling from Molecular Simulation. J. Am. Chem. Soc. 2013, 135, 15008–15017. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics 2: Specific Techniques for Different Flow Categories; Scientific Computation, Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; Software, Environments, Tools; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Strikwerda, J.C. Finite Difference Schemes and Partial Differential Equations, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2004. [Google Scholar]
- Qu, G.; Zhao, X.; Newbloom, G.M.; Zhang, F.; Mohammadi, E.; Strzalka, J.W.; Pozzo, L.D.; Mei, J.; Diao, Y. Understanding Interfacial Alignment in Solution Coated Conjugated Polymer Thin Films. ACS Appl. Mater. Interfaces 2017, 9, 27863–27874. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, V.; Haward, S.J.; Shen, A.Q. Effects of Shearing and Extensional Flows on the Alignment of Colloidal Rods. Macromolecules 2021, 54, 4176–4185. [Google Scholar] [CrossRef]
- Kristupas, T. peaks2-find peaks in 2D data without additional toolbox.
- Kelton, K.; Greer, A. Interpretation of Experimental Measurements of Transient Nucleation. In Rapidly Quenched Metals; Elsevier: Amsterdam, The Netherlands, 1985; pp. 223–226. [Google Scholar] [CrossRef]
- Kelton, K. Crystal Nucleation in Liquids and Glasses. In Solid State Physics; Elsevier: Amsterdam, The Netherlands, 1991; Volume 45, pp. 75–177. [Google Scholar] [CrossRef]
- Kelton, K.; Greer, A. Transient nucleation effects in glass formation. J. Non-Cryst. Solids 1986, 79, 295–309. [Google Scholar] [CrossRef]
- Mermin, N.D. Crystalline Order in Two Dimensions. Phys. Rev. 1968, 176, 250–254. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Trout, B.L. Order parameter approach to understanding and quantifying the physico-chemical behavior of complex systems. In Handbook of Materials Modeling: Methods; Springer: Dordrecht, The Netherlands, 2005; pp. 1613–1626. [Google Scholar]
- Athreya, B.P.; Goldenfeld, N.; Dantzig, J.A.; Greenwood, M.; Provatas, N. Adaptive mesh computation of polycrystalline pattern formation using a renormalization-group reduction of the phase-field crystal model. Phys. Rev. E 2007, 76, 056706. [Google Scholar] [CrossRef]
- Wu, Y.L.; Derks, D.; Van Blaaderen, A.; Imhof, A. Melting and crystallization of colloidal hard-sphere suspensions under shear. Proc. Natl. Acad. Sci. USA 2009, 106, 10564–10569. [Google Scholar] [CrossRef]
- Li, W.; Peng, Y.; Still, T.; Yodh, A.G.; Han, Y. Nucleation kinetics and virtual melting in shear-induced structural transitions. Rep. Prog. Phys. 2025, 88, 010501. [Google Scholar] [CrossRef] [PubMed]
- Stefan-Kharicha, M.; Kharicha, A.; Zaidat, K.; Reiss, G.; Eßl, W.; Goodwin, F.; Wu, M.; Ludwig, A.; Mugrauer, C. Impact of hydrodynamics on growth and morphology of faceted crystals. J. Cryst. Growth 2020, 541, 125667. [Google Scholar] [CrossRef]
- Stefan-Kharicha, M.; Kharicha, A.; Zaidat, K.; Reiss, G.; Eßl, W.; Goodwin, F.; Wu, M.; Ludwig, A.; Mugrauer, C. Hydrodynamically driven facet kinetics in crystal growth. J. Cryst. Growth 2022, 584, 126557. [Google Scholar] [CrossRef]
- Qazi, S.J.S.; Rennie, A.R.; Tucker, I.; Penfold, J.; Grillo, I. Alignment of Dispersions of Plate-Like Colloidal Particles of Ni(OH)2 Induced by Elongational Flow. J. Phys. Chem. B 2011, 115, 3271–3280. [Google Scholar] [CrossRef]



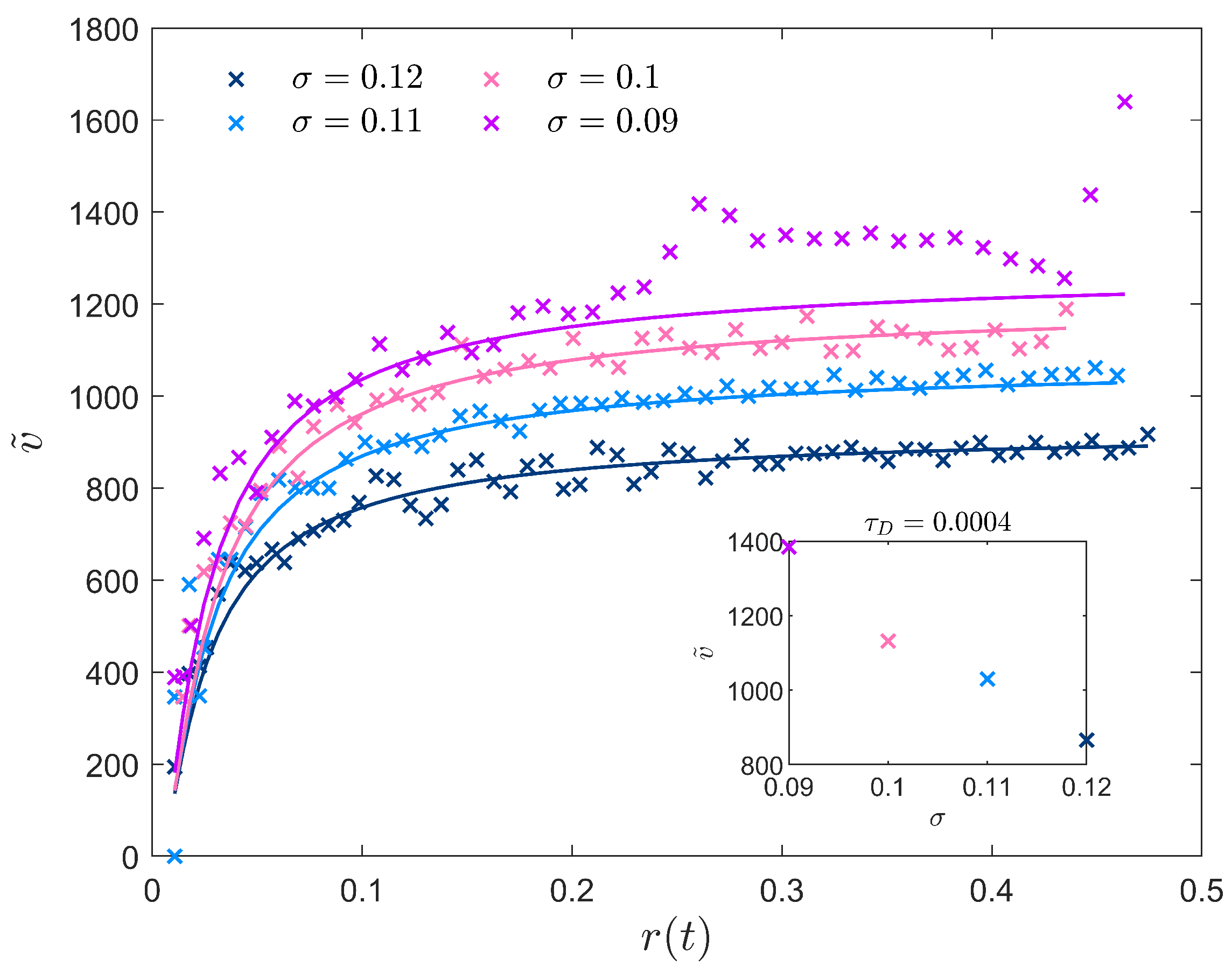
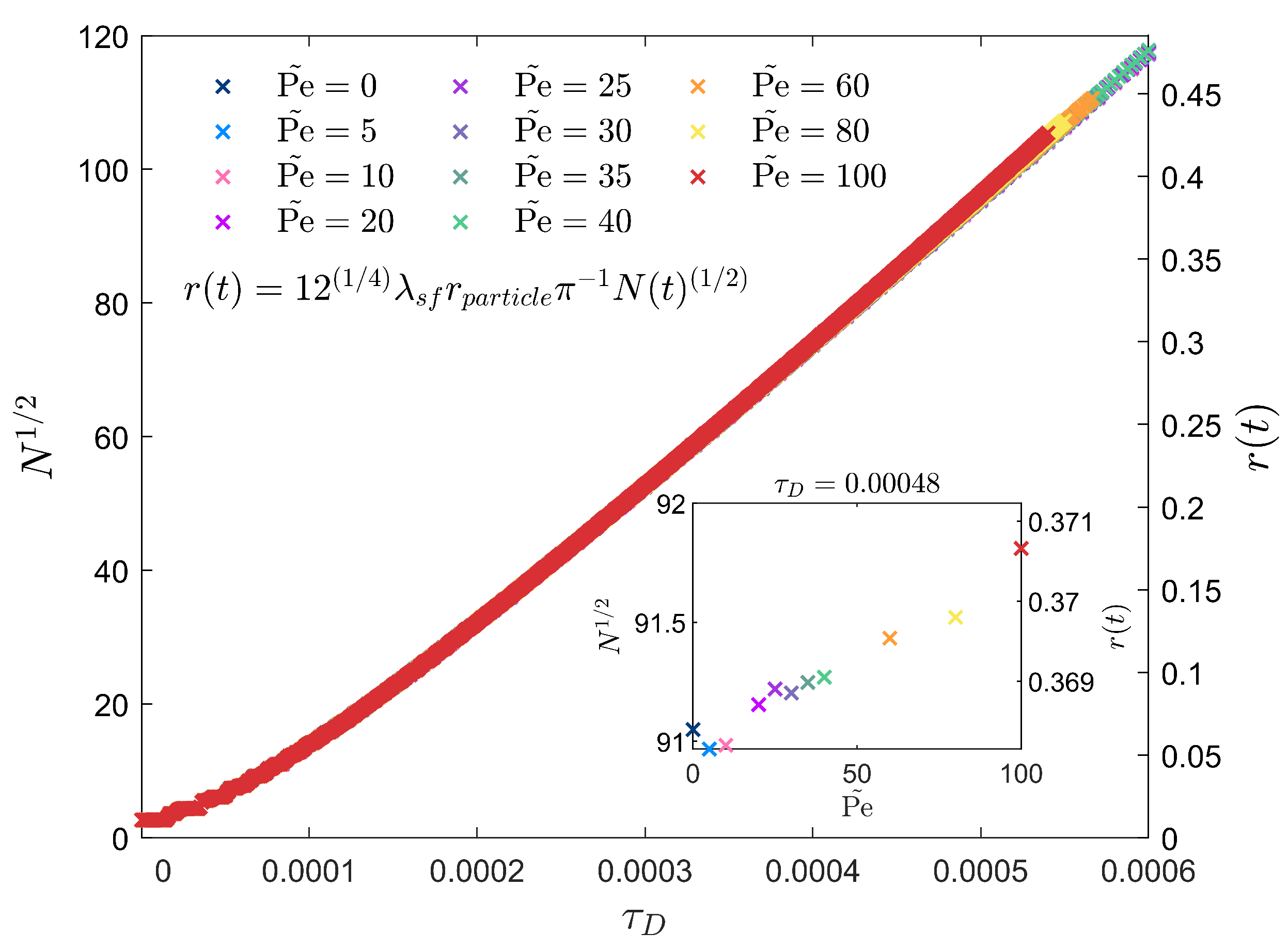
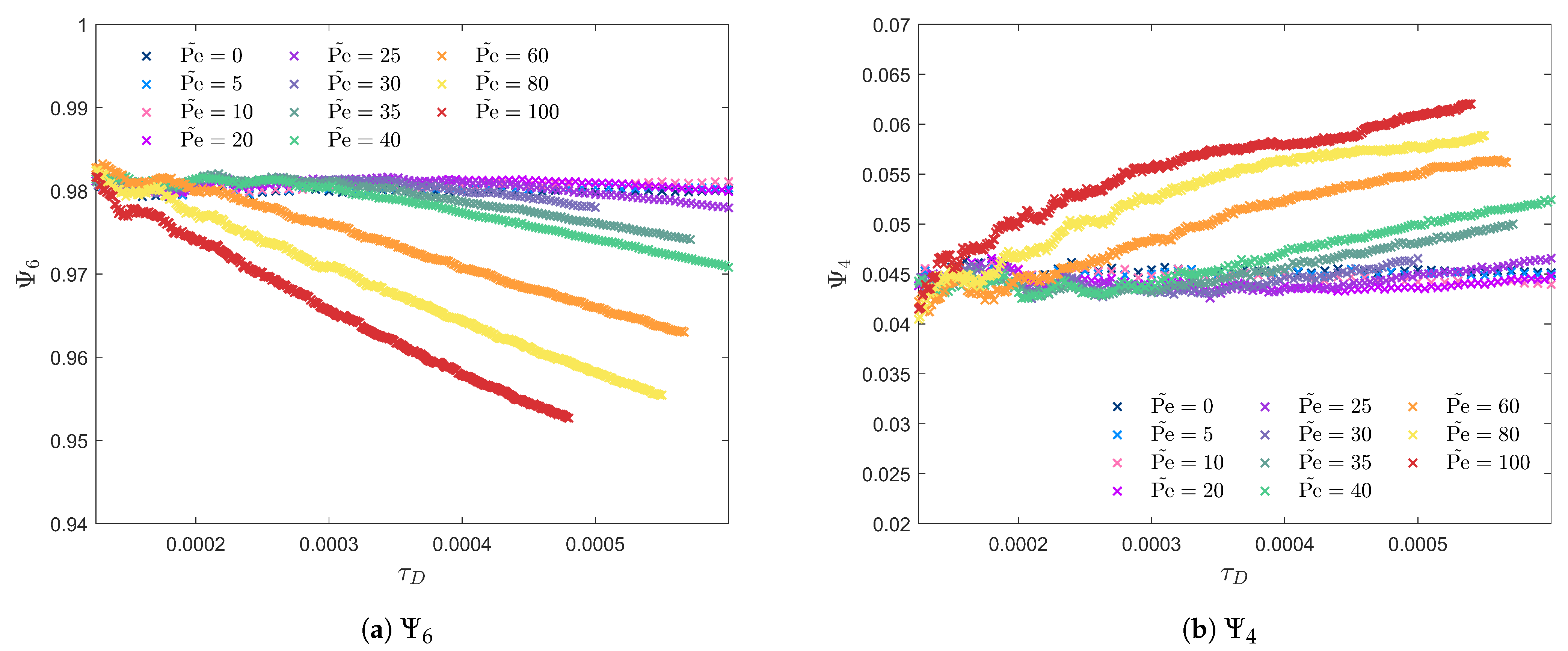

| Parameter | Description |
|---|---|
| Order-parameter, representing density fluctuations | |
| Kinematic Viscosity | |
| Dimensionless Kinematic Viscosity Field | |
| Reference liquid kinematic viscosity | |
| Dynamic viscosity | |
| Reference liquid number density | |
| Average liquid order-parameter 1 | |
| Effective temperature 1 | |
| m | Atomic mass |
| M | Interface mobility |
| Optional thermal noise | |
| Interplanar spacing 2 | |
| Atomic density within plane 2 | |
| Interfacial properties 2 | |
| Number of planes in planar family 2 | |
| Pressure normalized by | |
| Dimensionless free energy, normalized by | |
| Dimensionless chemical potential, normalized by |
| Parameter Definition | Analogy |
|---|---|
| − 1 | |
| − 1 | |
| Analogous to Peclet Number | |
| Analogous to Euler Number 2 | |
| Analogous to Schmidt Number | |
| Analogous to Deborah Number 2 | |
| Dimensionless Convective Timescale | |
| Dimensionless Diffusive Timescale |
| Parameter | Value |
|---|---|
| 1 | |
| 4 | |
| 4 | |
| 1 | |
| 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Willis, L.C.; Janicki, T.D.; Rao, R.R.; Liu, Z.L. Unraveling the Determinant Mechanisms in Flow-Mediated Crystal Growth and Phase Behaviors. Crystals 2025, 15, 157. https://doi.org/10.3390/cryst15020157
Willis LC, Janicki TD, Rao RR, Liu ZL. Unraveling the Determinant Mechanisms in Flow-Mediated Crystal Growth and Phase Behaviors. Crystals. 2025; 15(2):157. https://doi.org/10.3390/cryst15020157
Chicago/Turabian StyleWillis, L. Connor, Tesia D. Janicki, Rekha R. Rao, and Z. Leonardo Liu. 2025. "Unraveling the Determinant Mechanisms in Flow-Mediated Crystal Growth and Phase Behaviors" Crystals 15, no. 2: 157. https://doi.org/10.3390/cryst15020157
APA StyleWillis, L. C., Janicki, T. D., Rao, R. R., & Liu, Z. L. (2025). Unraveling the Determinant Mechanisms in Flow-Mediated Crystal Growth and Phase Behaviors. Crystals, 15(2), 157. https://doi.org/10.3390/cryst15020157






