Defect Pinning and Critical Current of Magnetic Vortex Cluster in Mesoscopic Type-1.5 Superconductors
Abstract
1. Introduction
2. Theoretical Formalism
3. Finite Element Method and Numerical Computations
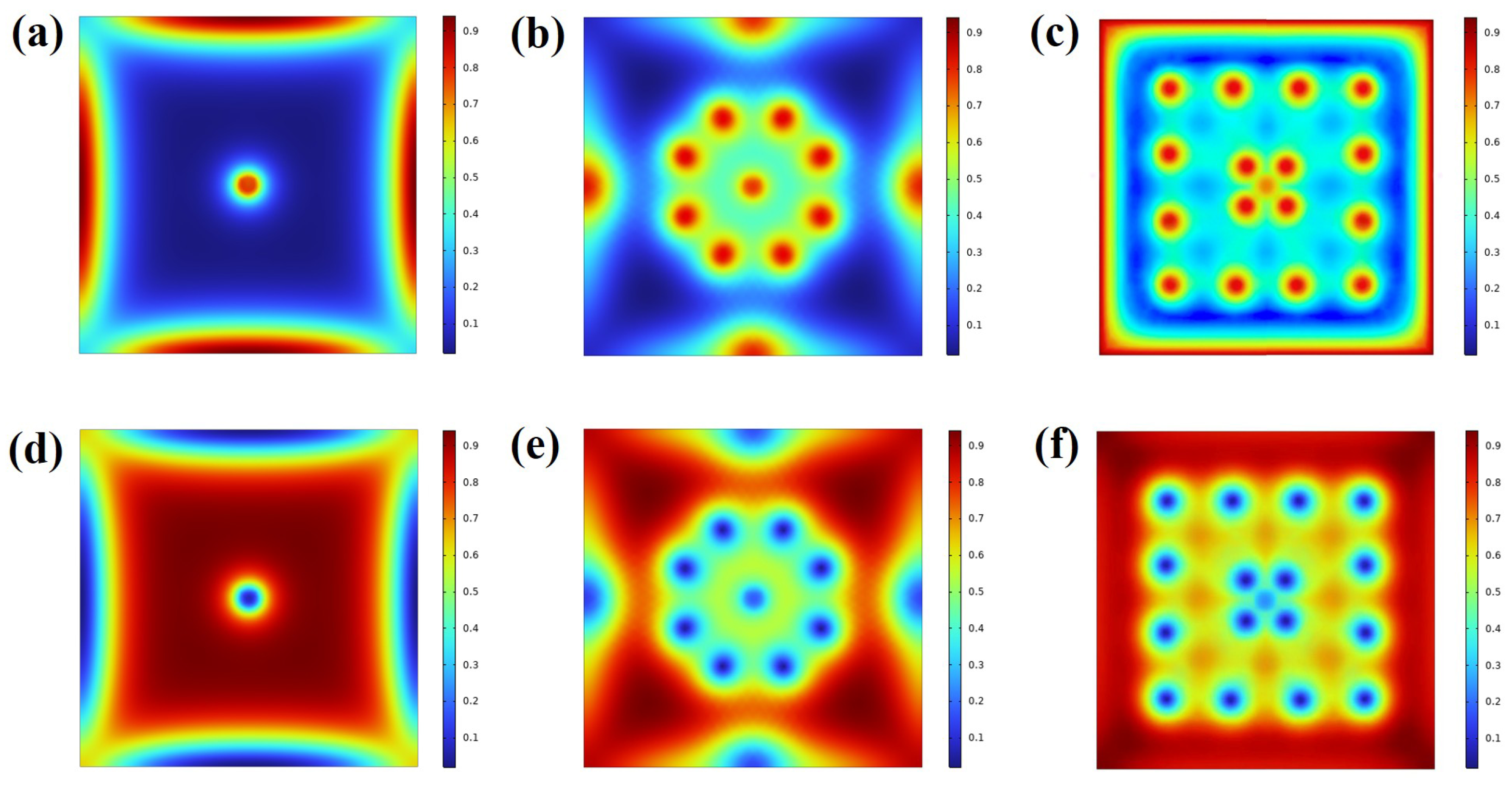
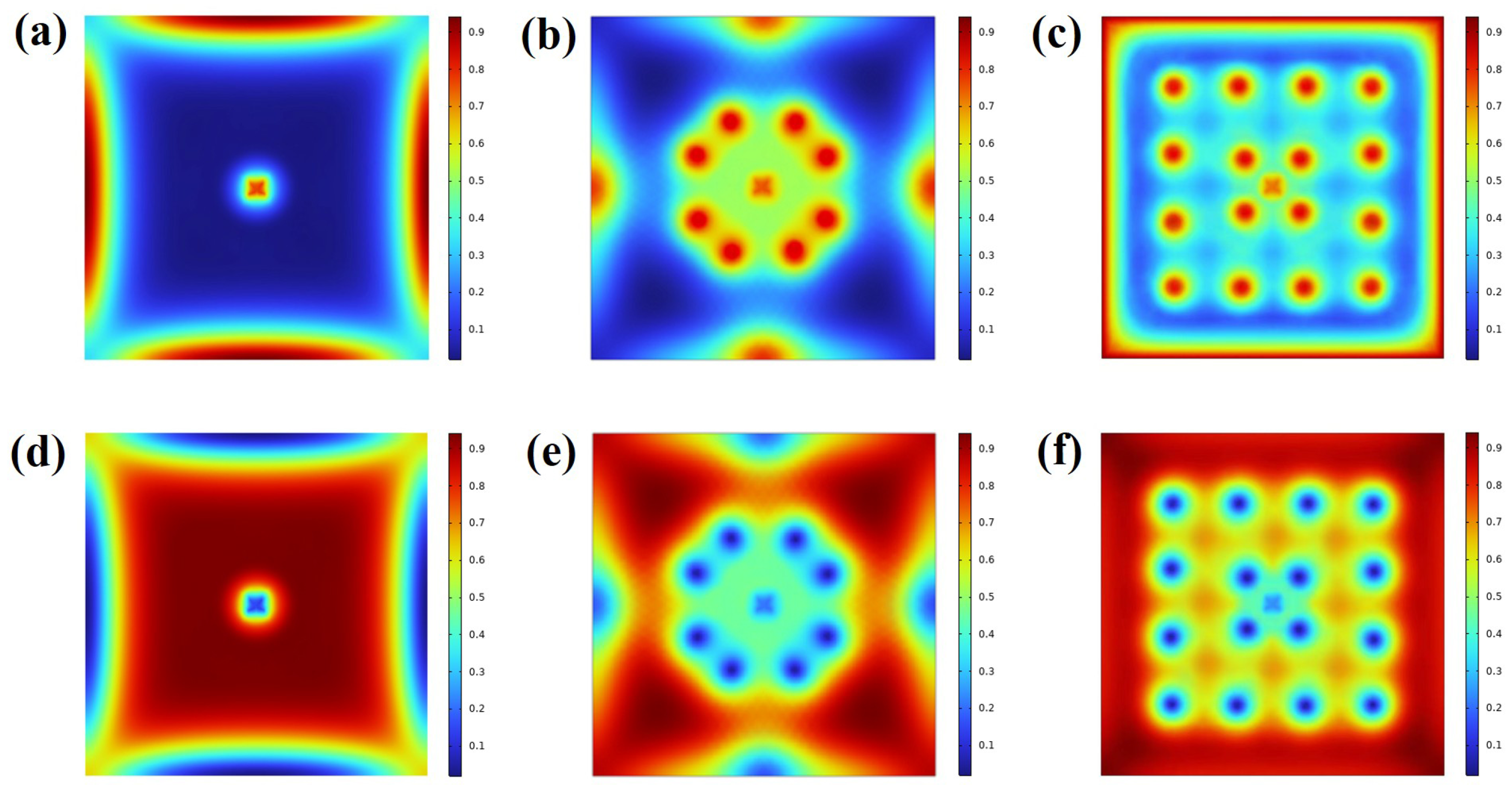
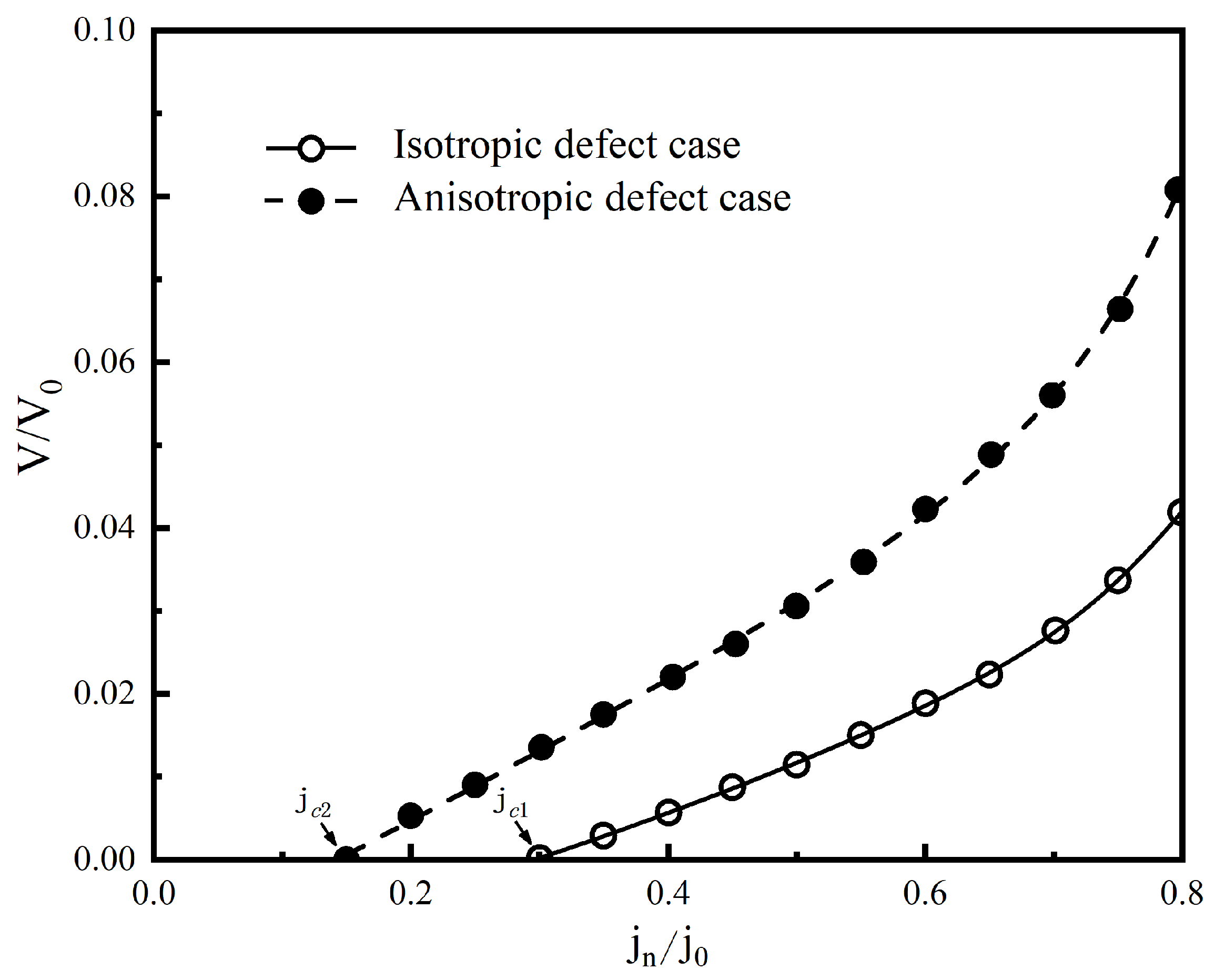
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63. [Google Scholar] [CrossRef] [PubMed]
- Zehetmayer, M. A review of two-band superconductivity: Materials and effects on the thermodynamic and reversible mixed-state properties. Supercond. Sci. Technol. 2013, 26, 043001. [Google Scholar] [CrossRef]
- Salamone, T.; Hugdal, H.G.; Jacobsen, S.H.; Amundsen, M. High magnetic field superconductivity in a two-band superconductor. Phys. Rev. B 2023, 107, 174516. [Google Scholar] [CrossRef]
- Tanaka, Y. Soliton in two-band superconductor. Phys. Rev. Lett. 2002, 88, 017002. [Google Scholar] [CrossRef]
- Babaev, E. Vortices with fractional flux in two-gap superconductors and in extended Faddeev model. Phys. Rev. Lett. 2002, 89, 067001. [Google Scholar] [CrossRef]
- Babaev, E.; Speight, M. Semi-Meissner state and neither type-I nor type-II superconductivity in multicomponent superconductors. Phys. Rev. B 2005, 72, 180502. [Google Scholar] [CrossRef]
- Carlström, J.; Garaud, J.; Babaev, E. Length scales, collective modes, and type-1.5 regimes in three-band superconductors. Phys. Rev. B 2011, 84, 134518. [Google Scholar] [CrossRef]
- Moshchalkov, V.; Menghini, M.; Nishio, T.; Chen, Q.H.; Silhanek, A.V.; Dao, V.H.; Chibotaru, L.F.; Zhigadlo, N.D.; Karpinski, J. Type-1.5 superconductivity. Phys. Rev. Lett. 2009, 102, 117001. [Google Scholar] [CrossRef]
- Hicks, C.W.; Kirtley, J.R.; Lippman, T.M.; Koshnick, N.C.; Huber, M.E.; Maeno, Y.; Yuhasz, W.M.; Maple, M.B.; Moler, K.A. Limits on superconductivity-related magnetization in Sr2RuO4 and PrOs4Sb12 from scanning SQUID microscopy. Phys. Rev. B 2010, 81, 214501. [Google Scholar] [CrossRef]
- Ray, S.J.; Gibbs, A.S.; Bending, S.J.; Curran, P.J.; Babaev, E.; Baines, C.; Mackenzie, A.P.; Lee, S.L. Muon-spin rotation measurements of the vortex state in Sr2RuO4: Type-1.5 superconductivity, vortex clustering, and a crossover from a triangular to a square vortex lattice. Phys. Rev. B 2014, 89, 094504. [Google Scholar] [CrossRef]
- Kawasaki, I.; Watanabe, I.; Amitsuka, H.; Kunimori, K.; Tanida, H.; Onuki, Y. Superconducting properties of noncentrosymmetric superconductor LaPt3Si studied by muon spin spectroscopy. J. Phys. Soc. Jpn. 2013, 82, 084713. [Google Scholar] [CrossRef]
- Fujisawa, T.; Yamaguchi, A.; Motoyama, G.; Kawakatsu, D.; Sumiyama, A.; Takeuchi, T.; Settai, R.; Onuki, Y. Magnetization measurements of non-centrosymmetric superconductor LaPt3Si: Construction of low temperature magnetometers with the SQUID and Hall sensor. Jpn. J. Appl. Phys. 2015, 54, 048001. [Google Scholar] [CrossRef]
- Cadorim, L.R.; Toledo, L.V.; Ortiz, W.A.; Berger, J.; Sardella, E. Closed vortex state in three-dimensional mesoscopic superconducting films under an applied transport current. Phys. Rev. B 2023, 107, 094515. [Google Scholar] [CrossRef]
- Cadorim, L.R.; Sardella, E.; Domínguez, D.; Berger, J. Stability limits of flux states in two-band superconductor rings. Phys. Rev. B 2024, 110, 144513. [Google Scholar] [CrossRef]
- Benites, T.N.S.; Presotto, A.; Ortega, J.B.; Sardella, E.; Zadorosny, R. Influence of surface defects on the vortex penetration and arrangement at mesoscopic superconducting samples. J. Phys. Conf. Ser. 2024, 2726, 012004. [Google Scholar] [CrossRef]
- Gokhfeld, D.M.; Maksimova, A.N.; Kashurnikov, V.A.; Moroz, A.N. Optimizing trapped field in superconductors with perforations. Phys. C 2022, 600, 1354106. [Google Scholar] [CrossRef]
- Moroz, A.; Rudnev, I.; Stepanenko, A.; Maksimova, A.; Kashurnikov, V. Features of vortex dynamics in a HTS with disordered pinning lattice. J. Supercond. Nov. Magn. 2024, 37, 339. [Google Scholar] [CrossRef]
- Maksimova, A.N.; Gokhfeld, D.M.; Moroz, A.N.; Kashurnikov, V.A. Relaxation of the trapped magnetic flux in a mesoscopic HTS with artificial pinning in the form of submicron holes. Chin. J. Phys. 2024, 88, 493. [Google Scholar] [CrossRef]
- Maksimova, A.N.; Moroz, A.N.; Rudnev, I.A.; Pokrovskii, S.V.; Kashurnikov, V.A. Critical current of a layered high-temperature superconductor with tilted irradiation defects. Phys. Scr. 2024, 99, 105938. [Google Scholar] [CrossRef]
- Yerin, Y.S.; Omelyanchouk, A.N. Coherent current states in a two-band superconductor. Low Temp. Phys. 2007, 33, 401. [Google Scholar] [CrossRef]
- Silva, R.M.; Milošević, M.V.; Domínguez, D.; Peeters, F.M.; Aguiar, J.A. Distinct magnetic signatures of fractional vortex configurations in multiband superconductors. Appl. Phys. Lett. 2014, 105, 232601. [Google Scholar] [CrossRef]
- Maiti, S.; Sigrist, M.; Chubukov, A. Spontaneous currents in a superconductor with s + is symmetry. Phys. Rev. B 2015, 91, 161102. [Google Scholar] [CrossRef]
- Garaud, J.; Silaev, M.; Babaev, E. Thermoelectric signatures of time-reversal symmetry breaking states in multiband superconductors. Phys. Rev. Lett. 2016, 116, 097002. [Google Scholar] [CrossRef] [PubMed]
- Vadimov, V.L.; Silaev, M.A. Polarization of the spontaneous magnetic field and magnetic fluctuations in s + is anisotropic multiband superconductors. Phys. Rev. B 2018, 98, 104504. [Google Scholar] [CrossRef]
- Lin, S.Z.; Maiti, S.; Chubukov, A. Distinguishing between s + id and s + is pairing symmetries in multiband superconductors through spontaneous magnetization pattern induced by a defect. Phys. Rev. B 2016, 94, 064519. [Google Scholar] [CrossRef]
- Sørensen, M.P.; Pedersenand, N.F.; Ögren, M. The dynamics of magnetic vortices in type II superconductors with pinning sites studied by the time dependent Ginzburg-Landau model. Phys. C 2017, 533, 40. [Google Scholar]
- Schmid, A. A time dependent Ginzburg-Landau equation and its application to the problem of resistivity in the mixed state. Phys. Kondens. Mater. 1966, 5, 302. [Google Scholar] [CrossRef]
- Gor’kov, L.P.; Éliashberg, G.M. Generlization of the Ginzburg-Landau equations for non-stationaryproblems in the case of alloys with paramagnetic impurities. Zh. Eksp. Teor. Fiz. 1968, 54, 612. [Google Scholar]
- Aguirre, C.A.; Joya, M.R.; Barba-Ortega, J. On the vortex matter in a two-band superconducting meso-prism. Phys. C 2021, 585, 1353867. [Google Scholar] [CrossRef]
- Du, S.Z.; Zhong, Y.N.; Yao, S.W.; Peng, L.; Shi, T.T.; Sang, L.N.; Liu, X.L.; Lin, J. The dynamics of current-driven vortex in two-band superconductor with s + d wave pairing. Phys. Lett. A 2022, 443, 128206. [Google Scholar] [CrossRef]
- Garaud, J.; Silaev, M.; Babaev, E. Microscopically derived multi-component Ginzburg-Landau theories for s + is superconducting state. Phys. C 2017, 533, 63. [Google Scholar] [CrossRef]
- Yao, S.W.; Peng, L.; Lin, J.; Chen, J.; Cai, C.B.; Zhou, Y. Properties of vortex configurations in two-band mesoscopic superconductors with Josphson coupling: The Ginzburg-Landau theory. J. Low. Temp. Phys. 2021, 202, 329. [Google Scholar] [CrossRef]
- Ryu, Y.G.; Mun, G.I.; Kwon, Y.N.; Kim, S.H.; Hong, S. Motion of magnetic vortices in type-II superconductor with randomly distributed pinning centers. Phys. C 2022, 602, 1354125. [Google Scholar] [CrossRef]
- Ryu, Y.G.; Om, J.H.; Kim, J.H.; Ro, G.I.; Mun, G.I.; Hong, S. The influence of surface defects on motion of magnetic vortices in mesoscopic type-II superconductor with randomly distributed pinning centers. J. Supercond. Nov. Magn. 2024, 37, 527. [Google Scholar] [CrossRef]
- Polo, A.S.M.; da Silva, R.M.; Vagov, A.; Shanenko, A.A.; Toro, C.E.D.; Aguiar, J.A. Nonequilibrium interband phase textures induced by vortex splitting in two-band superconductors. Phys. Rev. B 2017, 96, 054517. [Google Scholar] [CrossRef]
- Schuller, I.K.; Gray, K.E. Time-dependent Ginzburg-Landau: From single particle to collective behavior. J. Supercond. Nov. Magn. 2006, 19, 3. [Google Scholar] [CrossRef]
- COMSOL, Comsol Multiphysics Modeling Guide. 2012. Available online: https://www.comsol.com (accessed on 15 October 2024).
- Du, Q.; Gunzburger, M.D.; Peterson, J.S. Solving the Ginzburg-Landau equations by finite-element methods. Phys. Rev. B 1992, 46, 9027. [Google Scholar] [CrossRef]
- Alstrøm, T.S.; Sørensen, M.P.; Pedersen, N.F.; Madsen, S. Magnetic flux lines in complex geometry type-II superconductors studied by the time dependent Ginzburg-Landau equation. Acta. Appl. Math. 2011, 115, 63. [Google Scholar]
- Oripov, B.; Anlage, S.M. Time-dependent Ginzburg-Landau treatment of rf magnetic vortices in superconductors: Vortex semiloops in a spatially nonuniform magnetic field. Phys. Rev. E 2020, 101, 033306. [Google Scholar] [CrossRef] [PubMed]
- Li, J.C.; Huang, Y.Q. Time-Domain Finite Element Methods for Maxwell’s Equations in Metamaterials; Springer: Heidelberg, NY, USA, 2013. [Google Scholar]
- Tinkham, M. Introduction to Superconductivity; McGraw-Hill Inc: New York, NY, USA, 1996. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Han, T.; Li, J.; Zhang, J.; Huang, H. Defect Pinning and Critical Current of Magnetic Vortex Cluster in Mesoscopic Type-1.5 Superconductors. Crystals 2025, 15, 133. https://doi.org/10.3390/cryst15020133
Wang G, Han T, Li J, Zhang J, Huang H. Defect Pinning and Critical Current of Magnetic Vortex Cluster in Mesoscopic Type-1.5 Superconductors. Crystals. 2025; 15(2):133. https://doi.org/10.3390/cryst15020133
Chicago/Turabian StyleWang, Guo, Tianyi Han, Jie Li, Jiangning Zhang, and Hai Huang. 2025. "Defect Pinning and Critical Current of Magnetic Vortex Cluster in Mesoscopic Type-1.5 Superconductors" Crystals 15, no. 2: 133. https://doi.org/10.3390/cryst15020133
APA StyleWang, G., Han, T., Li, J., Zhang, J., & Huang, H. (2025). Defect Pinning and Critical Current of Magnetic Vortex Cluster in Mesoscopic Type-1.5 Superconductors. Crystals, 15(2), 133. https://doi.org/10.3390/cryst15020133





