3D Study of Microstructural Influences on Retained Austenite Transformation in Q&P 1180 Steel
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
Potential Bias in the Data
5. Conclusions
- Over 90% of RA grains had transformed after application of 8.4% tensile strain.
- While small RA grains transform first (according to [37]), these grains are statistically replaced by the remnants of partially transformed larger RA grains—and, as observed in this study, more commonly from the remnants of larger grain with lower maximum Schmid factor and lower shear affinity factor. These observations also indicate that RA grains with high maximum Schmid factor and SAF are more likely to both transform and to fully transform.
- The shear affinity factor, defined in terms of resolved stress onto the habit planes, rather than the slip planes, was introduced as a potential better indicator of likelihood of transformation than the regular Schmid factor. However, the statistics do not indicate a better correlation with the likelihood of transformation.
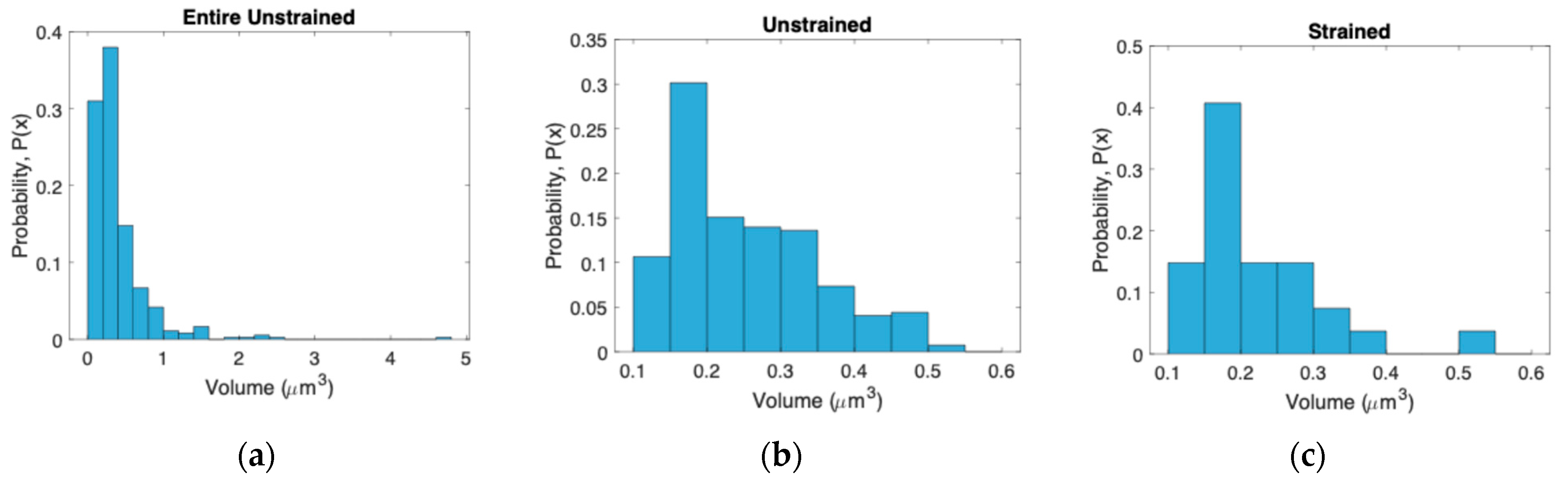
- The size distribution across the range of smaller grains (<0.51 μm3) remained approximately constant between the unstrained and the strained samples.
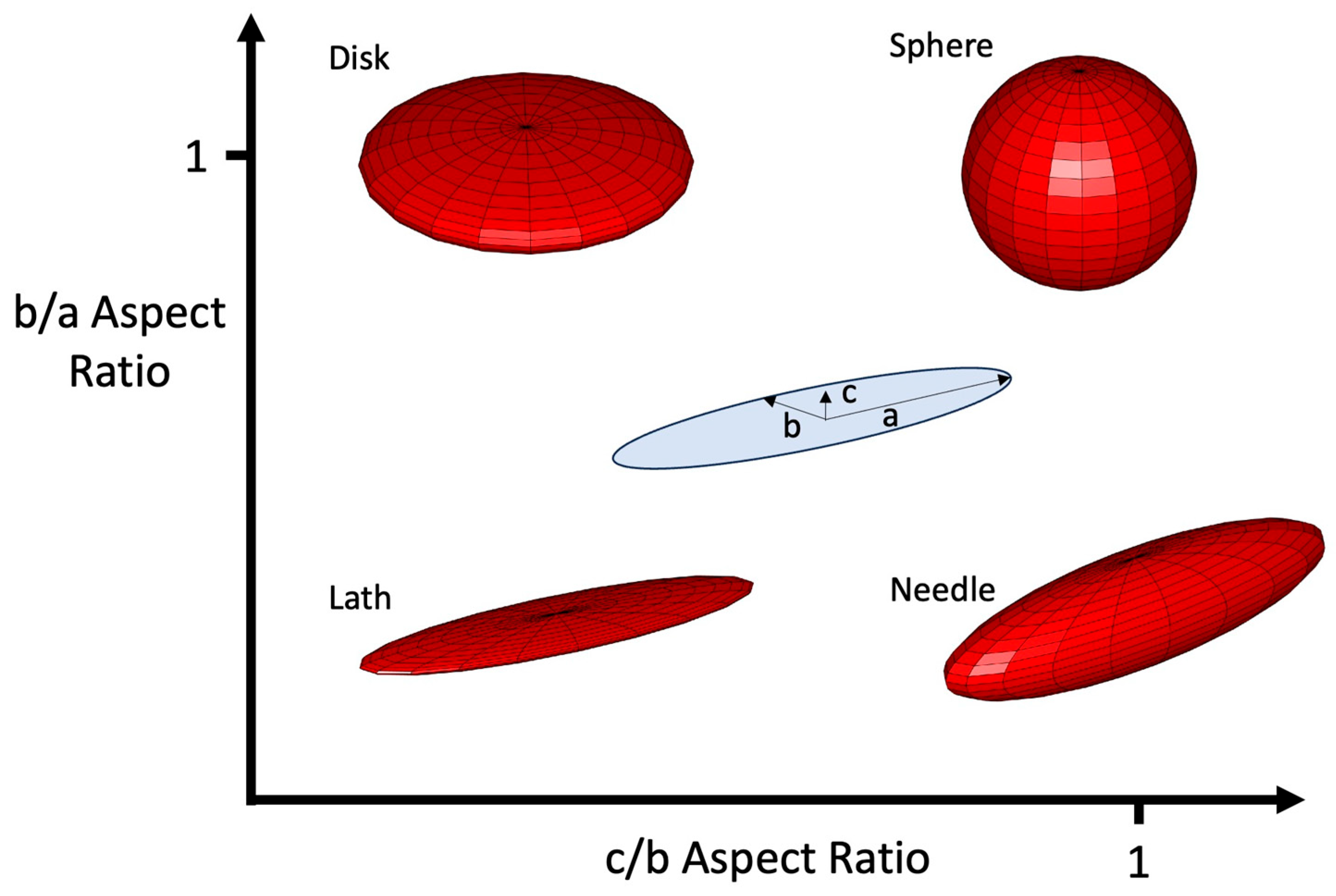
- Similarly, the fractions of spherical (or ‘globular’) and disk-shaped small grains remained relatively constant; but the relative ratio of lath- and needle-shaped grains changed significantly, with a marked upward trend in the needle-shaped grain population.
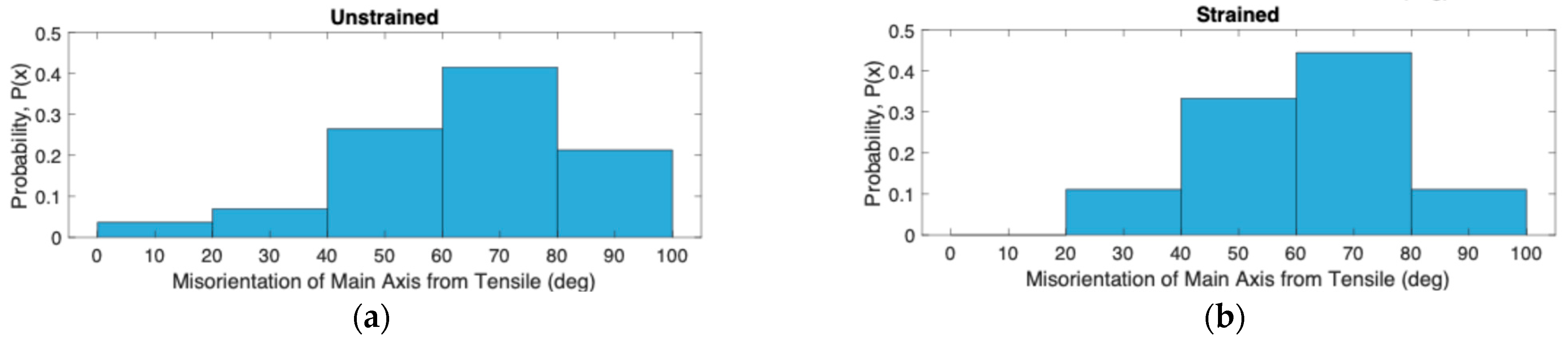
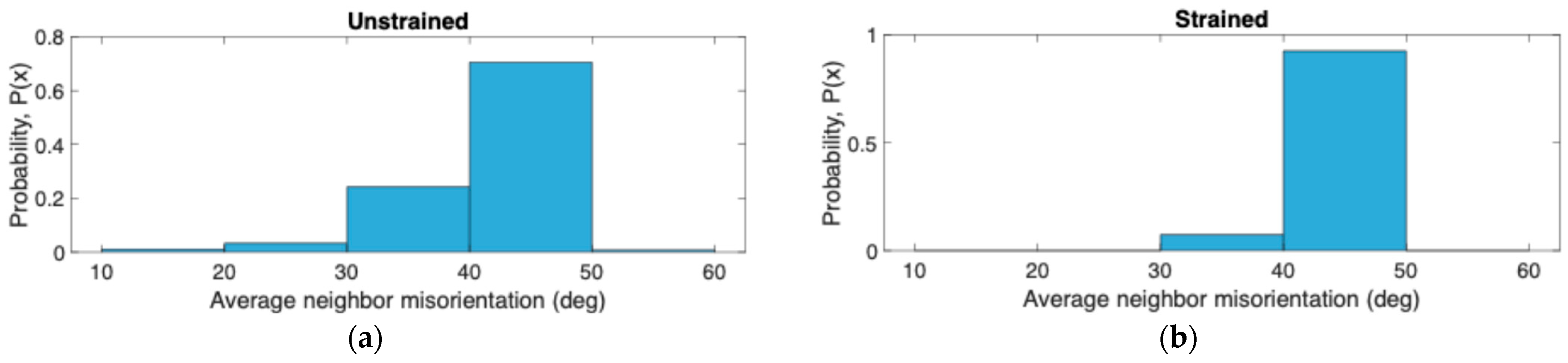
- The distribution of misorientation of the major axis of the best-fit ellipse from the tensile direction remained constant after straining, and the average misorient from neighbors of RA grains was most commonly in the range of 40–50° before and after straining, potentially indicating that this misorientation metric is not a significant contributor to the propensity to transform.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RA | Retained austenite |
| TRIP | Transformation-induced plasticity |
| EBSD | Electron backscatter diffraction |
| Q&P | Quenched and partitioned |
| 3GAHSS | Third generation advanced high-strength steels |
| K-S | Kurdjumov–Sachs |
| SAF | Shear affinity factor |
| OR | Orientation relationships |
| SEM | Scanning electron microscopy |
| FIB-SEM | Focused ion beam—scanning electron microscope |
| IPF | Inverse pole figure |
References
- Edmonds, D.V.; He, K.; Rizzo, F.C.; De Cooman, B.C.; Matlock, D.K.; Speer, J.G. Quenching and partitioning martensite—A novel steel heat treatment. Mater. Sci. Eng. A-Struct. 2006, 438, 25–34. [Google Scholar] [CrossRef]
- Speer, J.G.; Matlock, D.K.; Wang, L.; Edmonds, D.V. Quenched and Partitioned Steels. Ref. Modul. Mater. Sci. Mater. Eng. 2014, 1, 217–225. [Google Scholar]
- Santofimia, M.J.; Zhao, L.; Sietsma, J. Overview of Mechanisms Involved During the Quenching and Partitioning Process in Steels. Metall. Mater. Trans. A 2011, 42, 3620–3626. [Google Scholar] [CrossRef]
- Diego-Calderon, I.d.; Sabirov, I.; Molina-Aldareguia, J.M.; Fojer, C.; Thiessen, R.; Petrov, R.H. Microstructural design in quenched and partitioned (Q&P) steels to improve their fracture properties. Mater. Sci. Eng. A 2016, 657, 136–146. [Google Scholar] [CrossRef]
- Chiang, J.; Boyd, J.D.; Pilkey, A.K. Effect of microstructure on retained austenite stability and tensile behaviour in an aluminum-alloyed TRIP steel. Mater. Sci. Eng. A-Struct. 2015, 638, 132–142. [Google Scholar] [CrossRef]
- Shen, Y.F.; Qiu, L.N.; Sun, X.; Zuo, L.; Liaw, P.K.; Raabe, D. Effects of retained austenite volume fraction, morphology, and carbon content on strength and ductility of nanostructured TRIP-assisted steels. Mater. Sci. Eng. A-Struct. 2015, 636, 551–564. [Google Scholar] [CrossRef]
- De Knijf, D.; Fojer, C.; Kestens, L.A.I.; Petrov, R. Factors influencing the austenite stability during tensile testing of Quenching and Partitioning steel determined via in-situ Electron Backscatter Diffraction. Mater. Sci. Eng. A-Struct. 2015, 638, 219–227. [Google Scholar] [CrossRef]
- Xiong, X.C.; Chen, B.; Huang, M.X.; Wang, J.F.; Wang, L. The effect of morphology on the stability of retained austenite in a quenched and partitioned steel. Scr. Mater. 2013, 68, 321–324. [Google Scholar] [CrossRef]
- Jimenez-Melero, E.; van Dijk, N.H.; Zhao, L.; Sietsma, J.; Offerman, S.E.; Wright, J.P.; van der Zwaag, S. Martensitic transformation of individual grains in low-alloyed TRIP steels. Scr. Mater. 2007, 56, 421–424. [Google Scholar] [CrossRef]
- Tirumalasetty, G.K.; van Huis, M.A.; Kwakernaak, C.; Sietsma, J.; Sloof, W.G.; Zandbergen, H.W. Deformation-induced austenite grain rotation and transformation in TRIP-assisted steel. Acta Mater. 2012, 60, 1311–1321. [Google Scholar] [CrossRef]
- Jacques, P.J.; Ladriere, J.; Delanny, F. On the influence of interactions between phases on the mechanical stability of retained austenite in transformation-induced plasticity multiphase steels. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2001, 32, 2759–2768. [Google Scholar] [CrossRef]
- Li, W.-S.; Gao, H.-Y.; Nakashima, H.; Hata, S.; Tian, W.-H. In-situ EBSD study of deformation behavior of retained austenite in a low-carbon quenching and partitioning steel via uniaxial tensile tests. Mater. Charact. 2016, 118, 431–437. [Google Scholar] [CrossRef]
- Wang, X.D.; Huang, B.X.; Rong, Y.H.; Wang, L. Microstructures and stability of retained austenite in TRIP steels. Mater. Sci. Eng. A-Struct. 2006, 438, 300–305. [Google Scholar] [CrossRef]
- Blonde, R.; Jimenez-Melero, E.; Zhao, L.; Wright, J.P.; Bruck, E.; van der Zwaag, S.; van Dijk, N.H. High-energy X-ray diffraction study on the temperature-dependent mechanical stability of retained austenite in low-alloyed TRIP steels. Acta Mater. 2012, 60, 565–577. [Google Scholar] [CrossRef]
- Chiang, J.; Lawrence, B.; Boyd, J.D.; Pilkey, A.K. Effect of microstructure on retained austenite stability and work hardening of TRIP steels. Mater. Sci. Eng. A-Struct. 2011, 528, 4516–4521. [Google Scholar] [CrossRef]
- Haidemenopoulos, G.N.; Constantinou, M.; Kamoutsi, H.; Krizan, D.; Bellas, I.; Koutsokeras, L.; Constantinides, G. Probing the Evolution of Retained Austenite in TRIP Steel During Strain-Induced Transformation: A Multitechnique Investigation. JOM 2018, 70, 924–928. [Google Scholar] [CrossRef]
- Burja, J.; Lindič, J.; Batič, B.Š.; Nagode, A. Temperature-Dependent Martensitic Transformation in Cold-Rolled AISI 304 Stainless Steel. Crystals 2025, 15, 652. [Google Scholar] [CrossRef]
- Russ, J.C.; DeHoff, R.T. Practical Stereology, 2nd ed.; Kluwer Academic/Plenum: New York, NY, USA, 2000; p. 381. [Google Scholar]
- Dehoff, R.T. Quantitative Serial Sectioning Analysis—Preview. J. Microsc. 1983, 131, 259–263. [Google Scholar] [CrossRef]
- Zaefferer, S.; Elhami, N.-N.; Konijnenberg, P. 18—Electron backscatter diffraction (EBSD) techniques for studying phase transformations in steels. In Phase Transformations in Steels; Pereloma, E., Edmonds, D.V., Eds.; Woodhead Publishing: Cambridge, UK, 2012; Volume 2, pp. 557–587. [Google Scholar]
- Groeber, M.A.; Haley, B.K.; Uchic, M.D.; Dimiduk, D.M.; Ghosh, S. 3D reconstruction and characterization of polycrystalline microstructures using a FIB-SEM system. Mater. Charact. 2006, 57, 259–273. [Google Scholar] [CrossRef]
- Sun, Z.; Tsai, S.-P.; Konijnenberg, P.; Wang, J.-Y.; Zaefferer, S. A large-volume 3D EBSD study on additively manufactured 316L stainless steel. Scr. Mater. 2024, 238, 115723. [Google Scholar] [CrossRef]
- Britton, T.B.; Jiang, J.; Guo, Y.; Vilalta-Clemente, A.; Wallis, D.; Hansen, L.N.; Winkelmann, A.; Wilkinson, A.J. Tutorial: Crystal orientations and EBSD—Or which way is up? Mater. Charact. 2016, 117, 113–126. [Google Scholar] [CrossRef]
- Marder, A.R.; Krauss, G. Morphology of Martensite in Iron-Carbon Alloys. ASM Trans. 1967, 60, 651–660. [Google Scholar]
- Marder, J.M.; Marder, A.R. Morphology of Iron-Nickel Massive Martensite. ASM Trans. 1969, 62, 1–10. [Google Scholar]
- Kral, M.V. Proeutectoid ferrite and cementite transformations in steels. In Phase Transformation in Steels: Fundamentals and Diffusion-Controlled Transformations; Pereloma, E.V., Edmonds, D.V., Eds.; Woodhead Publishing Series in Metals and Surface Engineering; Woodhead Publishing Ltd.: Cambridge, UK, 2012; Volume 1, pp. 225–275. [Google Scholar]
- Kelly, P.M.; Jostsons, A.; Blake, R.G. The Orientation Relationship between Lath Martensite and Austenite in Low-Carbon, Low-Alloy Steels. Acta Metall. Mater. 1990, 38, 1075–1081. [Google Scholar] [CrossRef]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Morito, S.; Saito, H.; Ogawa, T.; Furuhara, T.; Maki, T. Effect of austenite grain size on the morphology and crystallography of lath martensite in low carbon steels. ISIJ Int. 2005, 45, 91–94. [Google Scholar] [CrossRef]
- Morito, S.; Adachi, Y.; Ohba, T. Morphology and Crystallography of Sub-Blocks in Ultra-Low Carbon Lath Martensite Steel. Mater. Trans. 2009, 50, 1919–1923. [Google Scholar] [CrossRef]
- Kelly, P.M. Crystallography of Lath Martensite in Steels. Mater. Trans. JIM 1992, 33, 235–242. [Google Scholar] [CrossRef]
- Cramer, J.; Adams, D.; Miles, M.P.; Fullwood, D.T.; Homer, E.R.; Brown, T.; Mishra, R.K.; Sachdev, A. Effect of strain path on forming limits and retained austenite transformation in Q&P 1180 steel. Mater. Sci. Eng. A-Struct. 2018, 734, 192–199. [Google Scholar] [CrossRef]
- Brahme, A.; Alvi, M.H.; Saylor, D.; Fridy, J.; Rollett, A.D. 3D reconstruction of microstructure in a commercial purity aluminum. Scr. Mater. 2006, 55, 75–80. [Google Scholar] [CrossRef]
- Saylor, D.M.; Fridy, J.; El-Dasher, B.S.; Jung, K.Y.; Rollett, A.D. Statistically representative three-dimensional microstructures based on orthogonal observation sections. Metall. Mater. Trans. A 2004, 35, 1969–1979. [Google Scholar] [CrossRef]
- Rollett, A.D.; Campman, R.; Saylor, D. Three dimensional microstructures: Statistical analysis of second phase particles in AA7075-T651. Mater. Sci. Forum 2006, 519–521, 1–10. [Google Scholar] [CrossRef]
- Wang, S.Y.; Holm, E.A.; Suni, J.; Alvi, M.H.; Kalu, P.N.; Rollett, A.D. Modeling the recrystallized grain size in single phase materials. Acta Mater. 2011, 59, 3872–3882. [Google Scholar] [CrossRef]
- Adams, D.; Behling, M.; Miles, M.P.; Homer, E.R.; Sachdev, A.K.; White, E.V.; Fullwood, D.T. Characterization of the Factors Influencing Retained Austenite Stability in Q&P Steels via In-situ EBSD. Met. Trans. A 2023, 54, 1355–1363. [Google Scholar]



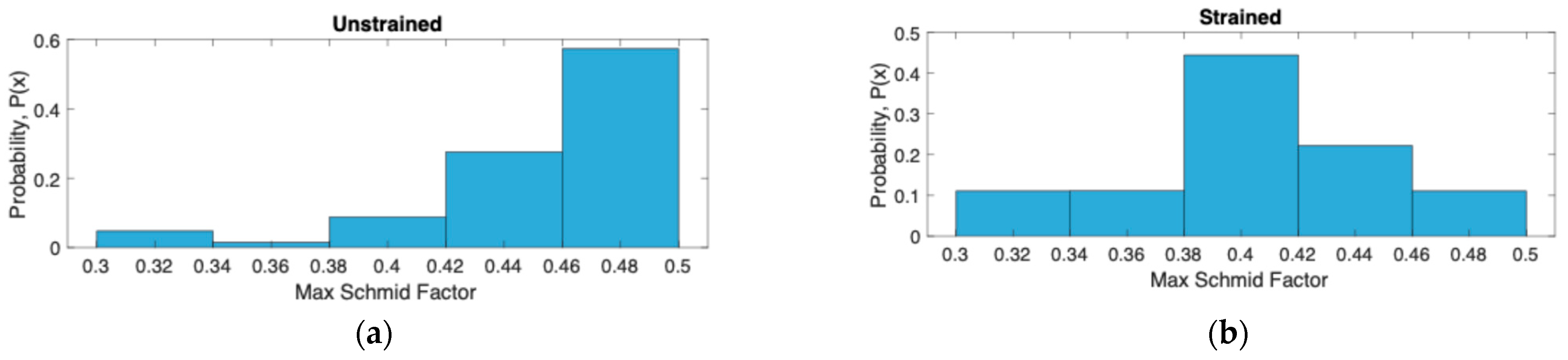
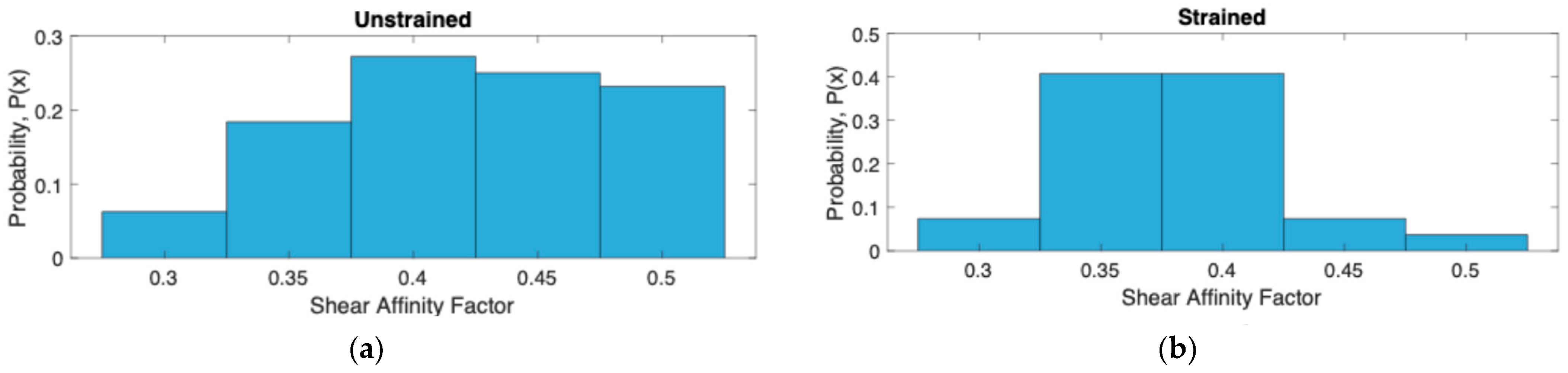

| RA Grain Attributes | p-Value |
|---|---|
| Volume of grain | 0.29 |
| Grain shape | 0.02 |
| Aspect ratio b/a | 0.66 |
| Aspect ratio c/a | 0.06 |
| Aspect ratio c/b | 0.004 |
| Misorientation of major axis from tensile direction | 0.40 |
| Average misorientation from neighboring grains | 0.04 |
| Maximum Schmid factor | 1 × 10−10 |
| Shear affinity factor | 6 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chelladurai, I.; White, E.V.; Miles, M.P.; Homer, E.R.; Sachdev, A.K.; Fullwood, D.T. 3D Study of Microstructural Influences on Retained Austenite Transformation in Q&P 1180 Steel. Crystals 2025, 15, 1015. https://doi.org/10.3390/cryst15121015
Chelladurai I, White EV, Miles MP, Homer ER, Sachdev AK, Fullwood DT. 3D Study of Microstructural Influences on Retained Austenite Transformation in Q&P 1180 Steel. Crystals. 2025; 15(12):1015. https://doi.org/10.3390/cryst15121015
Chicago/Turabian StyleChelladurai, Isaac, Emily V. White, Michael P. Miles, Eric R. Homer, Anil K. Sachdev, and David T. Fullwood. 2025. "3D Study of Microstructural Influences on Retained Austenite Transformation in Q&P 1180 Steel" Crystals 15, no. 12: 1015. https://doi.org/10.3390/cryst15121015
APA StyleChelladurai, I., White, E. V., Miles, M. P., Homer, E. R., Sachdev, A. K., & Fullwood, D. T. (2025). 3D Study of Microstructural Influences on Retained Austenite Transformation in Q&P 1180 Steel. Crystals, 15(12), 1015. https://doi.org/10.3390/cryst15121015






