BayCoN Plots and Systematic Errors in Single-Crystal Diffraction Experiments
Abstract
1. Introduction
2. Methods
3. The BayCoN Plots and Complementing Metrics
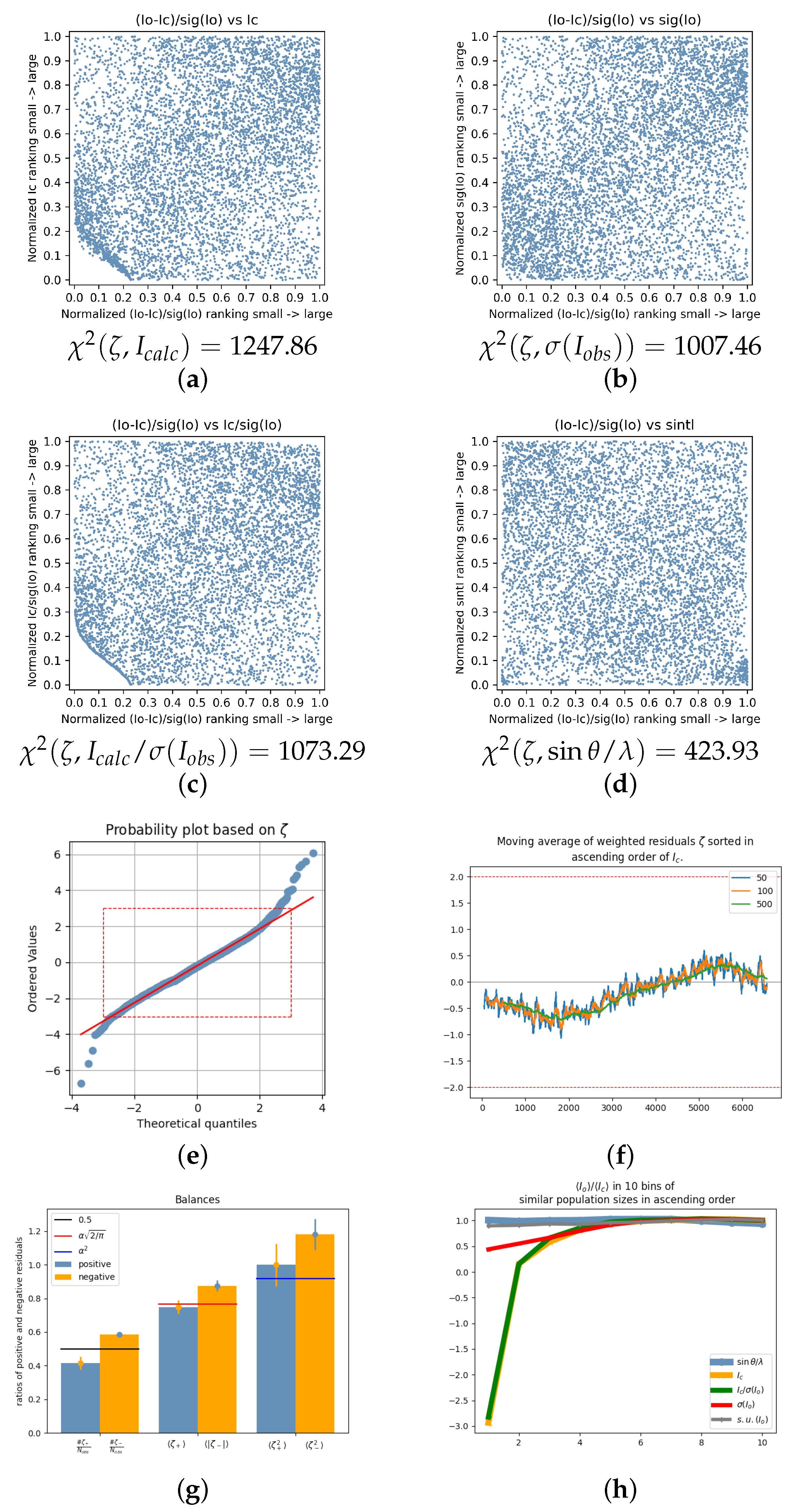
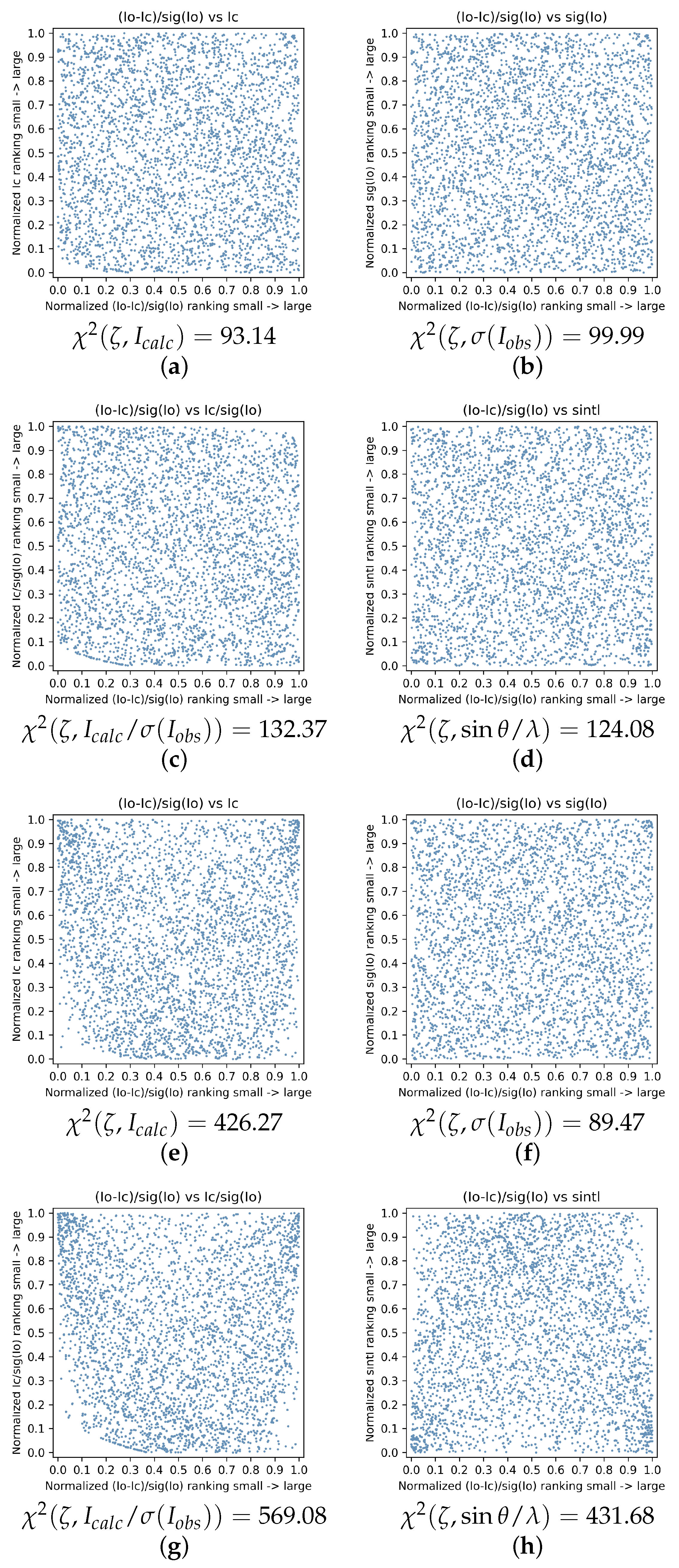
3.1. Construction of the BayCoN Plots
3.2. Limitations of the BayCoN Plots
3.3. Complementing Metrics
4. Test Data
4.1. Diffractometers
4.2. Weighting Scheme Parameters
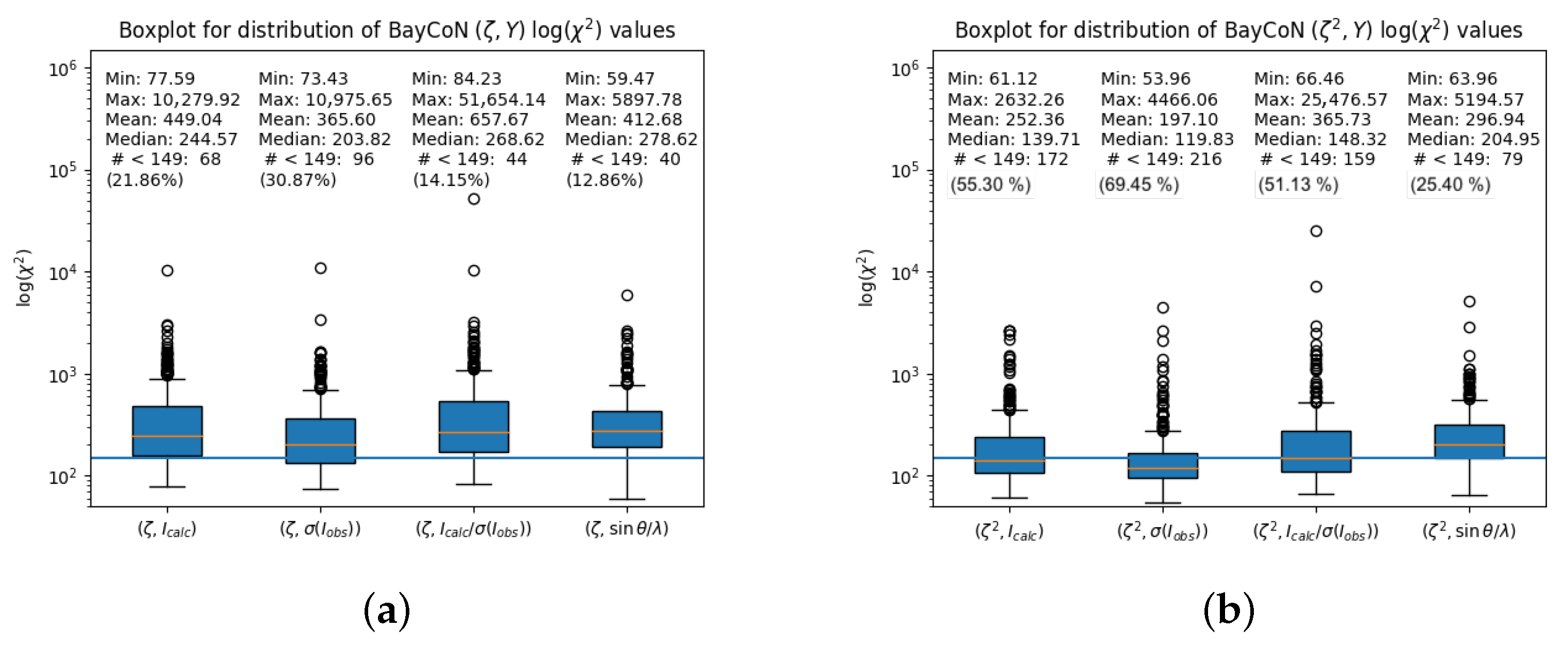
4.3. Distribution of Different Metrics for the Whole Sample
4.3.1. BayCoN Plot-Associated Values
4.3.2. Agreement Factor Ratio g and Other Values
5. Diagnosis of Systematic Errors—Application
5.1. Errors in the
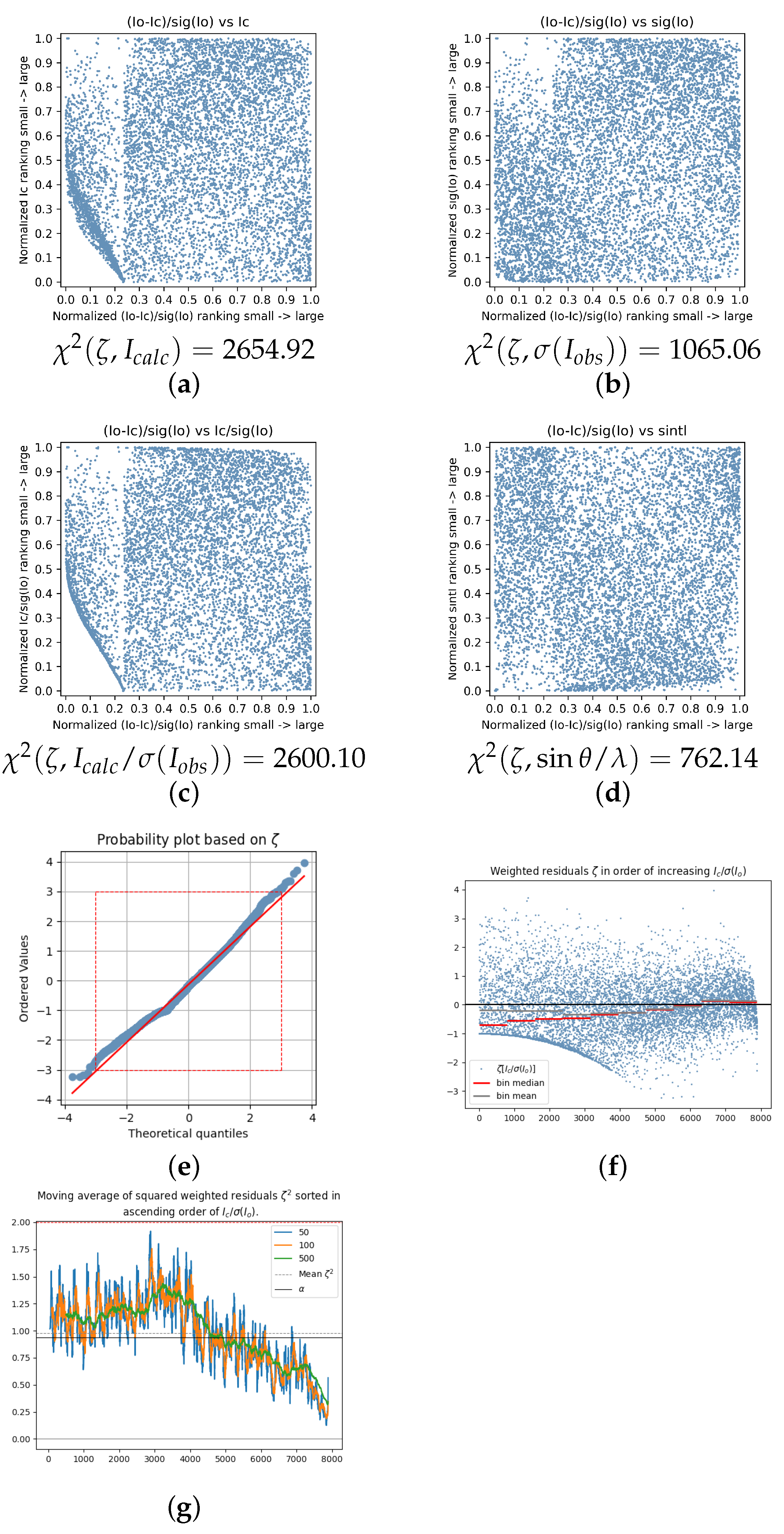
5.2. Significance Cut-Off
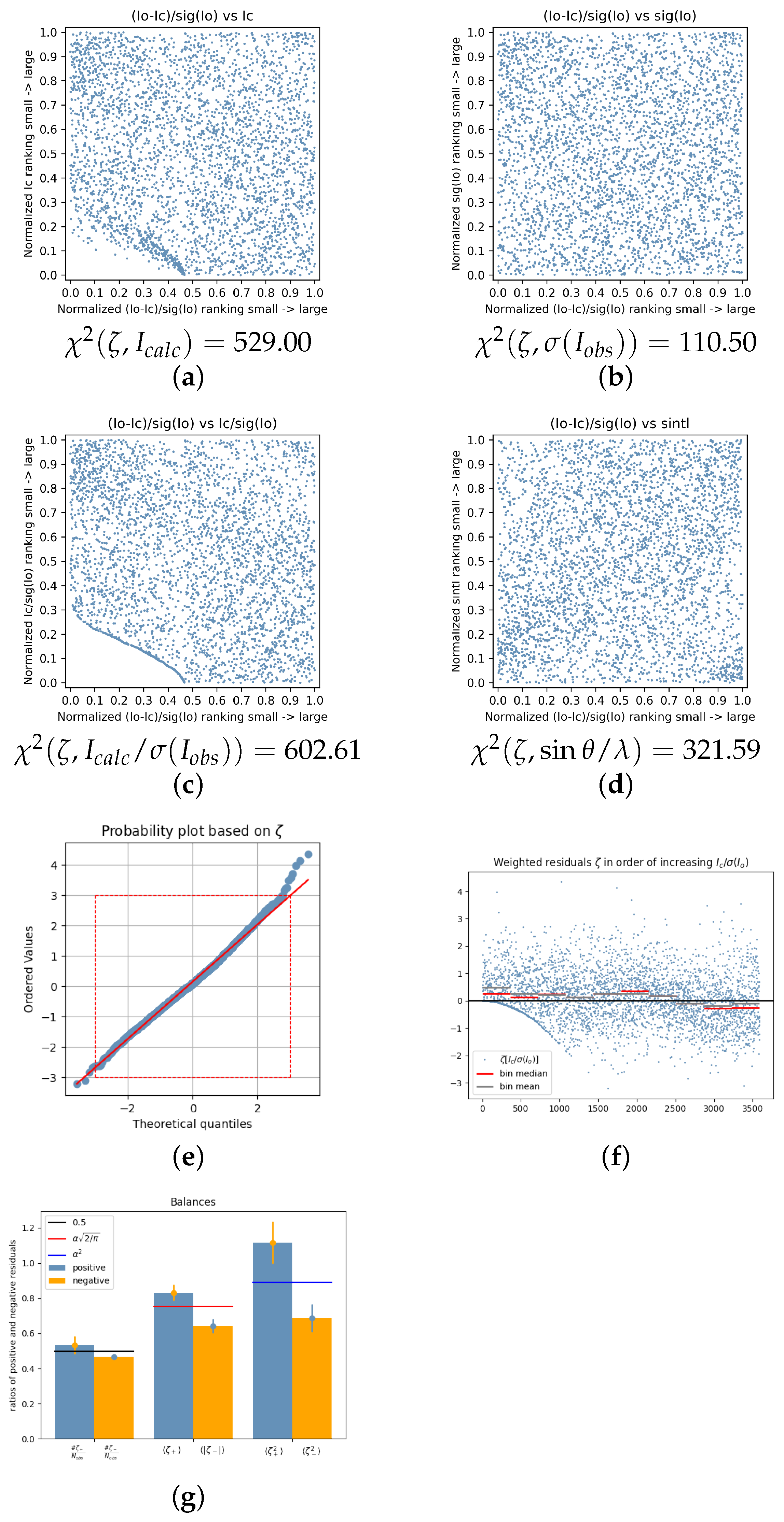
5.3. Intensity Cut-Off
5.4. Incomplete Absorption Correction Procedures
5.5. Weak Observed Intensities Stronger than Weak Calculated Intensities
| Radiation | Elements | Habitus | Mono | T | Diffractometer | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chromator | [K] | [mm] | [mm−1] | [mm−1] | ||||||||
| 2022_016 | ms | Cu K | S, O, N, C, H | needle | mirror | 100 | 0.04 | 0.10 | 4.00 | 2.38 | 9.54 | XtaLAB Synergy |
| 2020_011 | — | Cu K | Bi, S, N, C, H | needle | mirror | 100 | 0.12 | 2.11 | 4.51 | 17.34 | 78.14 | Agilent SuperNova |
| 2020_039 | — | Mo K | Cu, I, S, N, C, H | plate | graphite | 293 | 0.50 | 5.93 | 3.85 | 11.87 | 45.63 | Stoe IPDS 1 |
| 2020_119 | — | Mo K | Cu, S, F, O, N, C, H | plate | mirror | 100 | 0.40 | 0.46 | 5.71 | 1.15 | 6.58 | XtaLAB AFC12 |
| 2020_122 | ms | Mo K | Pb, O, C, H | prism | mirror | 120 | 0.25 | 3.60 | 1.54 | 14.45 | 22.21 | Bruker D8 |
| 2021_061 | ms | Mo K | Nb, Cl, O, H | block | mirror | 123 | 0.20 | 1.22 | 1.25 | 6.08 | 7.60 | Bruker Apex II CCD |
| 2021_081 | — | Mo K | Cu, Cl, S, F, O, N, C, H | block † | mirror ‡ | 98 | 0.47 | 0.75 | 4.70 | 1.59 | 7.48 | XtaLAB AFC12 |
| 2022_052 | — | Mo K | Cu, S | fragment | ? | 296 | 0.11 | 2.47 | 1.62 | 23.54 | 38.02 | Bruker D8 |
| 2022_083 | ms | Cu K | Zn, Cl, S, F, O, C, H | needle | mirror | 100 | 0.22 | 0.97 | 5.59 | 4.46 | 24.93 | XtalAB Synergy Dualflex |
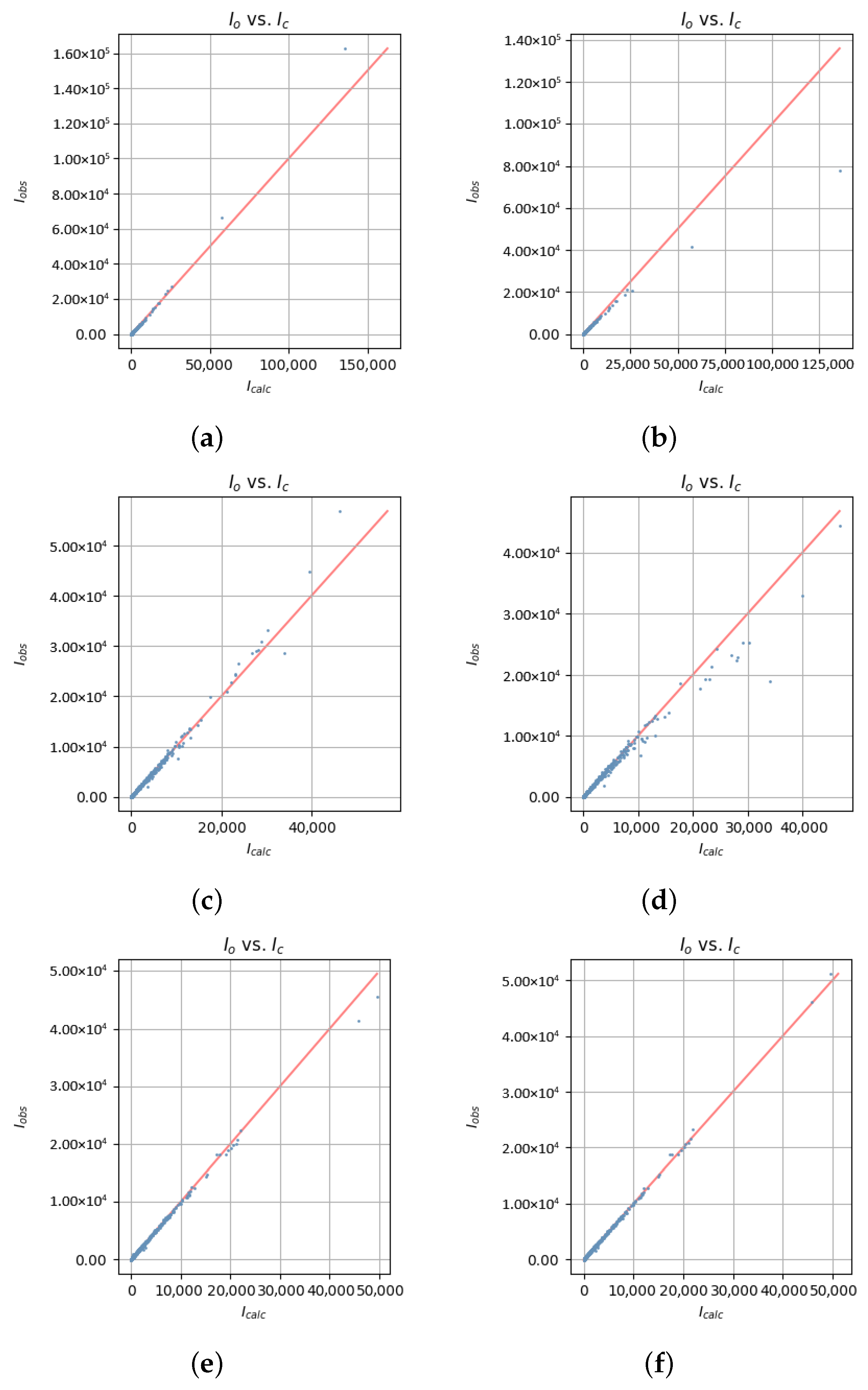
5.6. Weak Systematically Weaker than Weak
5.7. Uniform BayCoN Plots
| Radiation | Elements | Habitus | Monochromator | T | Diffractometer | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| [K] | [mm] | |||||||||
| 2021_042 | mf | Mo K | Co, F, N, C, H | prism | mirror | 183 | 0.18 | 4.50 | 3329 | Bruker D8 |
| 2020_012 | mf | Mo K | Cs, Br, F | block | — | 100 | 0.11 | 1.83 | 669 | Bruker D8 |
| 2020_081 | mf | Mo K | Pt, S, N, C, H | plate | mirror | 100 | 0.05 | 5.00 | 1556 | XtaLAB Synergy |
| 2020_117 | ff | Mo K | O, N, C, H | block | graphite | 170 | 0.35 | 1.75 | 1238 | XtaLAB mini |
| 2020_128 | mf | Mo K | Cl, S, O, N, C, H | plate | mirror | 100 | 0.32 | 5.33 | 1968 | Bruker Apex II |
| 2021_076 | — | Mo K | S, N, C, H | plate | — | 150 | 0.18 | 4.50 | 562 | XtaLAB Synergy |
| 2022_024 | mf | Ag K | P, O, N, C, H | prism | — | 298 | 0.12 | 1.33 | 608 | Bruker D8 |
| 2022_043 | ms | Mo K | Br, N, C, H | neelde | graphite | 200 | 0.12 | 3.00 | 1715 | Bruker Apex II |
| 2022_055 | ms | Cu K | F, O, N, C, H | column | — | 100 | 0.28 | 5.60 | 1309 | Bruker D8 |
5.8. Other Patterns
6. Discussion
7. Summary
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Construction of BayCoN Plots
References
- Henn, J.; Meindl, K. More About Systematic Errors in Charge Density Studies. Acta Crystallogr. Sect. A 2014, 70, 499–513. [Google Scholar] [CrossRef]
- Fournier, B.; Sokolow, J.; Coppens, P. Analysis of multicrystal pump–probe data sets. II. Scaling of ratio data sets. Acta Crystallogr. Sect. A 2016, 72, 250–260. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.E.; Thompson, A.L.; Watkin, D.J. The role of multiple observations in small-molecule single-crystal service X-ray structure determination. Acta Crystallogr. Sect. B 2019, 75, 657–673. [Google Scholar] [CrossRef]
- Korlyukov, A.A.; Nelyubina, Y.V. Quantum chemical methods in charge density studies from X-ray diffraction data. Russ. Chem. Rev. 2019, 88, 677–716. [Google Scholar] [CrossRef]
- Gajda, R.; Woźniak, K. Charge density studies of an inorganic-organic hybrid p-phenylenediammonium tetrachlorocuprate. Struct. Chem. 2017, 28, 1607–1622. [Google Scholar] [CrossRef]
- Henn, J. Metrics for crystallographic diffraction- and fit-data: A review of existing ones and the need for new ones. Crystallogr. Rev. 2019, 25, 83–156. [Google Scholar] [CrossRef]
- Domagala, S.; Nourd, P.; Diederichs, K.; Henn, J. Progress in detection of and correction for low-energy contamination. J. Appl. Crystallogr. 2023, 56, 1200–1220. [Google Scholar] [CrossRef] [PubMed]
- Henn, J. Two metrics for quantifying systematic errors in diffraction experiments: Systematic errors in the variance of the observed intensities and agreement factor gap. J. Appl. Crystallogr. 2025, 58, 1174–1184. [Google Scholar] [CrossRef]
- Dean, R.; Miller, C.N.; Zingales, S.K.; Padgett, C.W. 3-(4-Iodophenyl)-2,3-dihydro-1H-benzo[f]chromen-1-one. IUCrData 2020, 5, x200110. [Google Scholar] [CrossRef]
- Mamallan, K.; Gomathi, S.; Soundararajan, K.; Sethuraman, V. 2-[(5-Chloropyridin-2-ylimino)methyl]phenol. IUCrData 2020, 5, x200011. [Google Scholar] [CrossRef]
- Narvekar, K.U.; Srinivasan, B.R. Benzene-1,2-diaminium bis(4-methylbenzene-1-sulfonate). IUCrData 2020, 5, x200100. [Google Scholar] [CrossRef]
- Morris, L.L.; Alvarado, C.A.; Goncalves, J.M.; Singh, R.P.; Lovely, C.J.; Yousufuddin, M. [4-(4-Methoxyphenyl)-8-oxo-3-(phenylselanyl)spiro[4.5]deca-3,6,9-trien-2-yl]methylcyanamide. IUCrData 2020, 5, x200078. [Google Scholar] [CrossRef]
- Yoo, M.; Koh, D. (E)-1-(4-Fluoro-2-hydroxyphenyl)-3-(2,3,4-trimethoxyphenyl)prop-2-en-1-one. IUCrData 2020, 5, x200071. [Google Scholar] [CrossRef]
- Yoo, M.; Koh, D. Diethyl 4-(1H-imidazol-2-yl)-2,6-dimethyl-1,4-dihydropyridine-3,5-dicarboxylate. IUCrData 2020, 5, x200034. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. N′-(2-Hydroxy-3-methoxybenzylidene)pyrazine-2-carbohydrazide monohydrate. IUCrData 2020, 5, x191731. [Google Scholar] [CrossRef]
- Shraddha, K.N.; Devika, S.; Begum, N.S. 4-Chloro-2-[1-(4-ethylphenyl)-4,5-diphenyl-1H-imidazol-2-yl]phenol. IUCrData 2020, 5, x191690. [Google Scholar] [CrossRef]
- MacNeil, C.S.; Ogweno, A.O.; Ojwach, S.O.; Hayes, P.G. Dichloridobis[2-(pyridin-2-yl-κN)-1H-benzimidazole-κN3]nickel(II) monohydrate. IUCrData 2020, 5, x200040. [Google Scholar] [CrossRef]
- Giltzau, N.O.; Köckerling, M. Bis(1-dodecyl-4-aza-1-azoniabicyclo[2.2.2]octane)tetraisothiocyanatocobalt(II). IUCrData 2020, 5, x200023. [Google Scholar] [CrossRef] [PubMed]
- Stammler, H.G.; Imran, M. Bis(4-phenyl-2-sulfanylidene-2,3-dihydro-1,3-thiazol-3-ido-κ2S2,N)(4-phenyl-1,3-thiazole-2-thiolato-κS2)bismuth. IUCrData 2020, 5, x200067. [Google Scholar] [CrossRef] [PubMed]
- Malin, A.V.; Ivlev, S.I.; Ostvald, R.V.; Kraus, F. Redetermination of the crystal structure of caesium tetrafluoridobromate(III) from single-crystal X-ray diffraction data. IUCrData 2020, 5, x200114. [Google Scholar] [CrossRef]
- Lough, A.J.; Ho, A.; Tam, W. [(1R*,3S*,4S*)-3-(2-Hydroxybenzoyl)-1,2,3,4-tetrahydro-1,4-epoxynaphthalen-1-yl]methyl 4-nitrobenzoate. IUCrData 2020, 5, x200265. [Google Scholar] [CrossRef]
- Doboszewski, B.; Nazarenko, A.Y.; Soares, F.d.P. 1,3-Bis(2-oxopropyl)thymine. IUCrData 2020, 5, x200257. [Google Scholar] [CrossRef]
- Narvekar, K.U.; Srinivasan, B.R. 2-Aminoanilinium 4-methylbenzenesulfonate. IUCrData 2020, 5, x200230. [Google Scholar] [CrossRef]
- Weil, M.; Kremsmayr, T.; Mihovilovic, M.D. 6-[(tert-Butyldimethylsilyl)oxy]-3-ethenyl-7-methoxy-4-[(trimethylsilyl)ethynyl]naphtho[2,3-c]furan-1(3H)-one. IUCrData 2020, 5, x200224. [Google Scholar] [CrossRef]
- Manickam, R.; Jagadeesan, G.; Karunakaran, J.; Srinivasan, G. 1,4-Bis(4-methoxyphenyl)naphthalene. IUCrData 2020, 5, x200212. [Google Scholar] [CrossRef] [PubMed]
- Freitas, J.F.d.; Brown, S.; Oberndorfer, J.S.; Crundwell, G. 6-Nitro-2,3-bis(thiophen-2-yl)quinoxaline. IUCrData 2020, 5, x200203. [Google Scholar] [CrossRef]
- Muller II, J.E.; Osborn, L.R.; Traver, J.R.; Hillesheim, P.C.; Zeller, M.; Mirjafari, A. 2-(Octadecylsulfanyl)-1,3-thiazole. IUCrData 2020, 5, x200170. [Google Scholar] [CrossRef]
- Siegel, D.J.; Howarth, A.N.; Traver, J.R.; Hillesheim, P.C.; Zeller, M.; Mirjafari, A. 2,2′-[Methylenebis(sulfanediyl)]bis(pyridine 1-oxide). IUCrData 2020, 5, x200171. [Google Scholar] [CrossRef]
- Powell, G.L.; Rix, B.A. 5-Methyl-4-(5-methyl-3-oxo-2-phenyl-2,3-dihydro-1H-pyrazol-4-yl)-2-phenyl-1H-pyrazol-3(2H)-one. IUCrData 2020, 5, x200121. [Google Scholar] [CrossRef] [PubMed]
- Soundararajan, K.; Sethuraman, V.; Thanigaimani, K. (3S,5R,6S)-Diphenylmethyl 1-oxo-6-bromopenicillanate. IUCrData 2020, 5, x200143. [Google Scholar] [CrossRef] [PubMed]
- Kitada, A.; Funasako, Y.; Matsumoto, K.; Hagiwara, R.; Inokuchi, M.; Fukami, K.; Murase, K. Hydronium bis(trifluoromethanesulfonyl)amide–18-crown-6 (1/1). IUCrData 2020, 5, x200162. [Google Scholar] [CrossRef]
- Shahri, N.N.M.; Omar Ali, N.H.S.; Sheikh Abdul Hamid, M.H.; Mirza, A.H.; Usman, A.; Hoq, M.R.; Karim, M.R. N-[(E)-Quinolin-2-ylmethylidene]-1,2,4-triazol-4-amine hemihydrate. IUCrData 2020, 5, x200134. [Google Scholar] [CrossRef]
- Rincke, C.; Schmidt, H.; Voigt, W. Dicaesium tetramagnesium pentakis(carbonate) decahydrate, Cs2Mg4(CO3)5·10H2O. IUCrData 2020, 5, x200165. [Google Scholar] [CrossRef] [PubMed]
- Lesley, M.J.G.; Ozhan, K.; Sung, H.H.Y.; Williams, I.D. Trimethyl 4,4′,4″-(ethene-1,1,2-triyl)tribenzoate. IUCrData 2020, 5, x200417. [Google Scholar] [CrossRef] [PubMed]
- Bhat, R.; Shraddha, K.N.; Begum, N.S. 4-Amino-6-(piperidin-1-yl)pyrimidine-5-carbonitrile. IUCrData 2020, 5, x200385. [Google Scholar] [CrossRef] [PubMed]
- Narayan, E.; Fu, L.; Gribble, G.W.; Kaur, M.; Jasinski, J.P. 7-Chloro-3-(4-methylbenzenesulfonyl)pyrrolo[1,2-c]pyrimidine. IUCrData 2020, 5, x200382. [Google Scholar] [CrossRef]
- Detert, H.; Jochem, M.; Schollmeyer, D. 2,5-Bis[(E)-2-phenylethenyl]-3,6-bis(pyridin-2-yl)pyrazine. IUCrData 2020, 5, x200372. [Google Scholar] [CrossRef]
- Purdy, S.K.; Spasyuk, D.; Chitanda, J.M.; Reaney, M.J.T. [1–9-NαC]-Linusorb B3 (Cyclolinopeptide A) dimethyl sulfoxide monosolvate. IUCrData 2020, 5, x200318. [Google Scholar] [CrossRef]
- Tojiboev, A.; Nasrullaev, A.; Turgunov, K.; Elmuradov, B.; Tashkhodjaev, B. (E)-6-(Furan-2-ylmethylidene)-6,7,8,9-tetrahydropyrido[2,1-b]quinazoline-11-thione. IUCrData 2020, 5. [Google Scholar] [CrossRef]
- Lough, A.J.; Koh, S.; Tam, W. 12,15-Dimethyl-8-oxatetracyclo[8.8.0.02,7.011,16]octadeca-1(18),2,4,6,11(16),12,14-heptaen-10-ol. IUCrData 2020, 5, x200315. [Google Scholar] [CrossRef]
- Detert, H.; Jacobs, N.; Schollmeyer, D. The head-to-head photodimer of indenoindene. IUCrData 2020, 5, x200307. [Google Scholar] [CrossRef]
- Anzaldo-Olivares, B.; Arroyo, M.; Ramírez-Monroy, A.; Bernès, S. Tris(1H-benzimidazol-2-ylmethyl)amine methanol trisolvate. IUCrData 2020, 5, x200281. [Google Scholar] [CrossRef]
- Lough, A.J.; Pounder, A.; Wicks, C.; Tam, W. 1,2,3,5-Tetrahydronaphtho[2,1-c]oxepine. IUCrData 2020, 5, x200288. [Google Scholar] [CrossRef] [PubMed]
- Lough, A.J.; Pounder, A.; Tam, W. 12-Ethyl-6a,10a-dihydro-5H-6-oxachrysene. IUCrData 2020, 5, x200286. [Google Scholar] [CrossRef] [PubMed]
- Assoumatine, T.; Stoeckli-Evans, H. Poly[(μ4-5,7-dihydro-1H,3H-dithieno[3,4-b:3′,4′-e]pyrazine-κ4N:N′:S:S′)tetra-μ3-iodido-tetracopper]: A three-dimensional copper(I) coordination polymer. IUCrData 2020, 5, x200401. [Google Scholar] [CrossRef] [PubMed]
- Giltzau, N.O.; Köckerling, M. Bis(N-adamantyl-N′-ethylimidazolium) tetrabromidomanganate(II). IUCrData 2020, 5, x200261. [Google Scholar] [CrossRef]
- Crundwell, G.; Leeds, A. 2,3-Diethylbenzo[g]quinoxaline. IUCrData 2020, 5, x200454. [Google Scholar] [CrossRef]
- Manjula, V.; Venkateswaramoorthi, R.; Dharmaraja, J.; Selvanayagam, S. 2,6-Diphenyl-3-(prop-2-en-1-yl)piperidin-4-one. IUCrData 2020, 5, x200526. [Google Scholar] [CrossRef]
- Chadeayne, A.R.; Pham, D.N.K.; Golen, J.A.; Manke, D.R. 5-MeO-DALT: The freebase of N,N-diallyl-5-methoxytryptamine. IUCrData 2020, 5, x200498. [Google Scholar] [CrossRef]
- Feightner, K.; Powell, D.R.; Burba, C.M. 2,2,3,3,4,4,5,5-Octafluorohexane-1,6-diol. IUCrData 2020, 5, x200445. [Google Scholar] [CrossRef]
- Carmel Y., S.; Prasad, N.L.; Begum, N.S.; Suresh, H.P. 6-Methyl-4-[4-(trimethylsilyl)-1H-1,2,3-triazol-1-yl]methyl-2H-chromen-2-one. IUCrData 2020, 5, x200427. [Google Scholar] [CrossRef]
- Dalecky, L.M.; Juillerat, C.A.; Cody, J.A. Bis(3-methyl-1-propyl-1H-imidazol-3-ium) bis(4,6-disulfanidyl-4,6-disulfanylidene-1,2,3,5,4,6-tetrathiadiphosphinane-κ3S2,S4,S6)nickel. IUCrData 2020, 5, x200312. [Google Scholar] [CrossRef]
- Assoumatine, T.; Stoeckli-Evans, H. Poly[[μ4-3,4,8,10,11,13-hexahydro-1H,6H-bis([1,4]dithiocino)[6,7-b:6′,7′-e]pyrazine]di-μ-iodido-dicopper(I)]: A two-dimensional copper(I) coordination polymer. IUCrData 2020, 5, x200467. [Google Scholar] [CrossRef]
- Kodama, S.; Kondo, S.; Nomoto, A.; Ogawa, A. Tris(4,4′-di-tert-butyl-2,2′-bipyridine)(trans-4-tert-butylcyclohexanolato)deca-μ-oxido-heptaoxidoheptavanadium acetonitrile monosolvate including another unknown solvent molecule. IUCrData 2020, 5, x200449. [Google Scholar] [CrossRef]
- Srinivasan, B.R.; Bhargao, P.H.; Sudhadevi, P.K. Diaquatetrakis(μ-3-methoxybenzoato-κ2O1:O1′)dicopper(II). IUCrData 2020, 5, x200448. [Google Scholar] [CrossRef]
- Geng, X.; Wen, B.; Fan, C. Crystal structure of the Al8Cr5-type intermetallic Al7.85Cr5.16. IUCrData 2020, 5, x200422. [Google Scholar] [CrossRef]
- Pérez-Benítez, A.; Bernès, S. Redetermination of diammonium trivanadate, (NH4)2V3O8. IUCrData 2020, 5, x200488. [Google Scholar] [CrossRef] [PubMed]
- Alanazi, S.A.; Abdel-Wahab, B.F.; Hegazy, A.S.; Kariuki, B.M.; El-Hiti, G.A. 2-[3-(4-Chlorophenyl)-5-(4-fluorophenyl)-4,5-dihydro-1H-pyrazol-1-yl]-5-[(4-fluorophenyl)diazenyl]-4-methylthiazole. IUCrData 2020, 5, x200700. [Google Scholar] [CrossRef] [PubMed]
- Morales-Collazo, O.; Lynch, V.M.; Brennecke, J.F. 6,7-Dihydro-5H-pyrrolo[1,2-a]imidazole. IUCrData 2020, 5, x200681. [Google Scholar] [CrossRef]
- Cyr, N.; Zeller, M.; Hillesheim, P.C.; Mirjafari, A. 2,3-Dimethyl-1H-imidazol-3-ium benzenesulfonate–1,2-dimethyl-1H-imidazole co-crystal. IUCrData 2020, 5, x200689. [Google Scholar] [CrossRef] [PubMed]
- Anderson, G.; Mirjafari, A.; Zeller, M.; Hillesheim, P.C. 2,3-Dimethyl-1H-imidazol-3-ium chloride. IUCrData 2020, 5, x200660. [Google Scholar] [CrossRef]
- Yu, M.; Wang, L.; Wang, L.; Wu, Z. 2-(2-Ethoxy-2-oxoacetamido)benzoic acid. IUCrData 2020, 5, x200603. [Google Scholar] [CrossRef]
- AaminaNaaz, Y.; Rajkumar, K.; Thirumurugan, S.; Anbalagan, K.; SubbiahPandi, A. Tris(ethane-1,2-diamine-κ2N,N′)zinc(II) tetrachloridozincate(II). IUCrData 2020, 5, x200618. [Google Scholar] [CrossRef]
- Uzorka, B.; LaDuca, R.L. catena-Poly[[[aquacopper(II)]-μ-(biphenyl-2,2′-dicarboxylato)-μ-[N,N′-bis(pyridin-4-yl)urea]] 1.25-hydrate]. IUCrData 2020, 5, x200589. [Google Scholar] [CrossRef]
- Schödel, F.; Lerner, H.W.; Bolte, M. [1,3-Bis(2,6-diisopropylphenyl)-1,3-dihydro-2H-imidazol-2-ylidene]triiodoborane benzene hemisolvate. IUCrData 2020, 5, x200863. [Google Scholar] [CrossRef]
- Arunkumar, D.; Samshuddin, S.; Ansar, M.; Mague, J.T.; Ramli, Y. 4-[(E)-3-(4-Methylphenyl)-3-oxoprop-1-en-1-yl]benzonitrile. IUCrData 2020, 5, x200800. [Google Scholar] [CrossRef]
- Amaro Hernández, A.G.; Rodríguez Tzompantzi, T.; Dávila García, Á.; Meza-León, R.L.; Bernès, S. Ethyl (3S)-3-[(3aR,5R,6S,6aR)-6-hydroxy-2,2-dimethyltetrahydrofuro[4,5-d][1,3]dioxol-5-yl]-3-(3S)-3-[(3aR,5R,6S,6aR)-6-hydroxy-2,2-dimethyltetrahydrofuro[4,5-d][1,3]dioxol-5-yl]-5-oxoisoxazolidin-2-ylpropanoate chloroform monosolvate. IUCrData 2020, 5, x200788. [Google Scholar] [CrossRef] [PubMed]
- Yoo, M.; Koh, D. (E)-3-4,6-Dimethoxy-2-[(E)-4-methoxystyryl]-3-methylphenyl-1-(2-hydroxy-5-methoxyphenyl)prop-2-en-1-one. IUCrData 2020, 5, x200792. [Google Scholar] [CrossRef]
- Encarnacion-Thomas, E.; Sommer, R.D.; Mallia, A.; Sloop, J. (E)-2-(3,5-Dimethoxybenzylidene)indan-1-one. IUCrData 2020, 5, x200759. [Google Scholar] [CrossRef] [PubMed]
- Peppel, T.; Wulf, C.; Spannenberg, A. 1-Benzyl-3-methylimidazolium bromide. IUCrData 2020, 5, x200768. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Gao, J.; Long, S. Tetrakis[μ2-5-nitro-2-(phenylsulfanyl)benzoato-κ2O:O′]bis[(acetonitrile-κN)copper(II)]. IUCrData 2020, 5, x200801. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, B.R.; Harmalkar, S.S.; D’Souza, L.R.; Dhuri, S.N. Di-μ-aqua-bis[aqua(2,2′-bipyridine)(4-nitrobenzoato)cobalt(II)] bis(4-nitrobenzoate). IUCrData 2020, 5, x200796. [Google Scholar] [CrossRef]
- Wu, M.F.; Chen, L.Y.; Li, Y. 3-(2,2-Dioxo-3,4-dihydrobenzo[e][1,2,3]oxathiazin-4-yl)-3-fluoro-1-phenylindolin-2-one. IUCrData 2020, 5, x201028. [Google Scholar] [CrossRef]
- Detert, H.; Kluge, L.; Schollmeyer, D. Methyl 3,3,6,6-tetramethyl-1,8-dioxo-4,5,7,9-tetrahydro-2H-xanthene-9-carboxylate. IUCrData 2020, 5, x201018. [Google Scholar] [CrossRef]
- Shraddha, K.N.; Begum, N.S. 2-[1-(4-tert-Butylphenyl)-4,5-diphenyl-1H-imidazol-2-yl]-4,6-dichlorophenol. IUCrData 2020, 5, x200870. [Google Scholar] [CrossRef]
- Outahar, F.; Moumou, M.; Rakib, E.M.; Hannioui, A.; Saadi, M.; El Ammari, L. Ethyl 10α-hydroxy-4,9-dimethyl-14-oxo-3,8,15-trioxatetracyclo[10.3.0.02,4.07,9]pentadecane-13-spiro-5′-pyrazole-3′-carboxylate. IUCrData 2020, 5, x200945. [Google Scholar] [CrossRef] [PubMed]
- Mayorova, O.A.; Grinev, V.S.; Yegorova, A.Y. (Z)-5-(4-Bromophenyl)-3-[(3,5-dichlorophenyl)amino]methylidenefuran-2(3H)-one. IUCrData 2020, 5, x200937. [Google Scholar] [CrossRef]
- Devika, S.; Begum, N.S.; Manjappa, K.B.; Yang, D.Y. (2-Hydroxyphenyl)(4,2′:4′,4″-terpyridin-6′-yl)methanone. IUCrData 2020, 5, x200857. [Google Scholar] [CrossRef]
- Linkova, E.I.; Grinev, V.S.; Mayorova, O.A.; Yegorova, A.Y. 7a-Phenyltetrahydropyrrolo[2,1-b]oxazol-5(6H)-one. IUCrData 2020, 5, x200919. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Li, Y.L.; Zhou, J.; Sun, H.S.; Zhang, Q.Y.; Shi, X.H.; Zhang, Z.Y.; Ling, T. Diethyl 3,3′-[(3-fluorophenyl)methylene]bis(1H-indole-2-carboxylate). IUCrData 2020, 5, x200912. [Google Scholar] [CrossRef]
- Siddiqui, M.J.; Nesterov, V.V.; Steidle, M.T.; Smucker, B.W. trans-Diamminebis(1,2-dicyanoethene-1,2-dithiolato)platinum(IV). IUCrData 2020, 5, x200980. [Google Scholar] [CrossRef]
- Hoffman, J.L.; Akhigbe, J.E.; Reinheimer, E.W.; Smucker, B.W. Poly[[[μ-trans-1,2-bis(pyridin-4-yl)ethene-κ2N:N′]-μ-iodido-copper(I)]–trans-1,2-bis(pyridin-4-yl)ethene (1/0.25)]. IUCrData 2020, 5, x200998. [Google Scholar] [CrossRef] [PubMed]
- Corfield, P.W.R.; Stavola, T.J. Poly[diethylammonium [tetra-μ2-cyanido-κ8C:N-tricuprate(I)]], a two-dimensional network solid. IUCrData 2020, 5, x200968. [Google Scholar] [CrossRef]
- Marolf, D.M.; Brehm, K.L.; Lynch, V.M.; Powell, G.L. 1,1,2,2,2,3,3,3-Octacarbonyl-1,1,2,3-tetrakis(1,3,5-triaza-7-phosphatricyclo[3.3.1.13,7]decane-κP)-triangulo-triosmium(0). IUCrData 2020, 5, x200935. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, B.; Fontenot, P.; Donahue, J.P. Tris[N,N-bis(3,5-di-tert-butylbenzyl)dithiocarbamato-κ2S,S′]-μ3-sulfido-tris-μ2-disulfido-triangulo-trimolybdenum(IV) iodide. IUCrData 2020, 5, x200939. [Google Scholar] [CrossRef]
- Lin, Z.; Li, J. [5,10,15,20-Tetrakis(pentafluorophenyl)porphyrinato]zinc(II) benzene disolvate. IUCrData 2020, 5, x200877. [Google Scholar] [CrossRef]
- Ibragimov, A. Bis(3,5-dinitrobenzoato-κO)bis(ethane-1,2-diamine-κ2N,N′)cadmium(II). IUCrData 2020, 5, x200843. [Google Scholar] [CrossRef]
- Deubner, H.L.; Ivlev, S.I.; Kraus, F. Rerefinement of the crystal structure of trichloridosulfonium(IV) hexachloridouranate(V), (SCl3)[UCl6]. IUCrData 2020, 5, x200960. [Google Scholar] [CrossRef] [PubMed]
- Uppu, S.N.; Agu, O.A.; Deere, C.J.; Fronczek, F.R. N-(4-Ethoxy-2,5-dinitrophenyl)acetamide. IUCrData 2020, 5, x201121. [Google Scholar] [CrossRef]
- Detert, H.; Schollmeyer, D. rac-12-Selena-13,14-diazatricyclo[9.3.0.02,4]tetradeca-11,13-diene. IUCrData 2020, 5, x201081. [Google Scholar] [CrossRef] [PubMed]
- Shripanavar, C.S.; Butcher, R.J. (Z)-N′-[(E)-4-Methoxybenzylidene]-2-(methoxyimino)-2-2-[(2-methylphenoxy)methyl]phenylacetohydrazide. IUCrData 2020, 5, x201060. [Google Scholar] [CrossRef]
- Camargo-Cortés, E.B.; Acosta, M.; Martínez, J.C.; Pineda, L.W. Tetraaquabis(2,3-dihydro-1,4-benzodioxine-2-carboxylato)calcium(II). IUCrData 2020, 5, x201092. [Google Scholar] [CrossRef]
- Braun, J.D.; Uppal, G.; Herbert, D.E. [2,2′-Bis(diphenylphosphanyl)-1,1′-binaphthyl-κ2P,P′]dichloridoplatinum(II) acetonitrile trisolvate. IUCrData 2020, 5, x201048. [Google Scholar] [CrossRef]
- Schollmeyer, D.; Heidrich, M.; Detert, H. rac-(E,trans)-4-Bromo-10,10-dimethyl-9,11-dioxabicyclo[6.3.0]undec-4-ene. IUCrData 2020, 5, x201302. [Google Scholar] [CrossRef] [PubMed]
- Mizuhata, Y.; Iwai, K.; Tokitoh, N. 2,2-Bis[3,5-bis(dimethylamino)phenyl]-1,1,1,3,3,3-hexamethyltrisilane. IUCrData 2020, 5, x201299. [Google Scholar] [CrossRef] [PubMed]
- Whalen, A.C.; Hernandez Brito, C.; Choi, K.H.; Warner, E.J.T.; Thole, D.A.; Gau, M.R.; Carroll, P.J.; Anstey, M.R. 10-Phenyl-10H-phenoxazine-4,6-diol tetrahydrofuran monosolvate. IUCrData 2020, 5, x201276. [Google Scholar] [CrossRef]
- Mallard, H.H.; Kennedy, N.D.; Rudman, N.A.; Greenwood, A.M.; Nicoleau, J.; Angle, C.E.; Torquato, N.A.; Gau, M.R.; Carroll, P.J.; Anstey, M.R. 2,2′-Oxybis[1,3-bis(4-methoxyphenyl)-2,3-dihydro-1H-benzo[d][1,3,2]diazaborole]. IUCrData 2020, 5, x201248. [Google Scholar] [CrossRef]
- Cai, C.; Lin, B.; Wu, W.; Zhu, Q. (3Z,5E)-2-Amino-4,6-bis(pyridin-3-yl)hepta-1,3,5-triene-1,1,3-tricarbonitrile. IUCrData 2020, 5, x201246. [Google Scholar] [CrossRef] [PubMed]
- Chakkarapani, N.; Murugan, S.; Ibrahim, A.R.; Kavitha, S.J.; Hemamalini, M.; Rajakannan, V. 2,6-Diamino-4-chloropyrimidine–succinic acid (2/1). IUCrData 2020, 5, x201239. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, B.; Jia, Z. 6-(3,4-Difluorophenyl)-7,8,13,14-tetrahydrodibenzo[c,k]phenanthridine. IUCrData 2020, 5, x201241. [Google Scholar] [CrossRef]
- Guerrero-Luna, G.; Reyes Melchor, J.; Bernès, S.; Hernández-Linares, M.G. Diosgenin-3,6-dione: Second polymorph in space group P212121. IUCrData 2020, 5, x201200. [Google Scholar] [CrossRef]
- Lynch, W.E.; Whitlock, C.R.; Padgett, C.W. Ethyl 1H-indole-2-carboxylate. IUCrData 2020, 5, x201205. [Google Scholar] [CrossRef]
- Chen, L.; Hu, J.; Wu, L.L.; Sun, H.S. 11,11-Diphenyl-11H-indeno[1,2-b]quinoxaline. IUCrData 2020, 5, x201213. [Google Scholar] [CrossRef]
- Sung, J. 3-(2-Methoxyphenyl)-2,3-dihydro-1H-benzo[f]chromen-1-one. IUCrData 2020, 5, x201209. [Google Scholar] [CrossRef]
- Adrian, R.A.; Arman, H.D. Chlorido(4′-chloro-2,2′:6′,2″-terpyridine-κ3N,N′,N″)(trifluoromethanesulfonato-κO)zinc(II) acetonitrile monosolvate. IUCrData 2020, 5, x201292. [Google Scholar] [CrossRef] [PubMed]
- Setifi, Z.; Setifi, F.; Dege, N.; Al-Douh, M.H.; Glidewell, C. Bis[tris(pyridin-2-yl)amine]iron(II) tris(dicyanomethylidene)methanediide. IUCrData 2020, 5, x201278. [Google Scholar] [CrossRef]
- Wang, S.; Han, H.; Han, Y. Diaquabis(4-ferrocenyl-1,1,1-trifluoro-4-oxobutan-2-olato)cobalt(II). IUCrData 2020, 5, x201240. [Google Scholar] [CrossRef]
- Zometa Paniagua, D.F.; Powell, G.L.; Powell, C.B.; Reinheimer, E.W. Bis(μ4-adamantane-1,3-dicarboxylato-1κO1:2κO1′:3κO3:4κO3′)octacarbonyl-1κ2C,2κ2C,3κ2C,4κ2C-tetrakis[tris(4-methylphenyl)phosphane]-1κP,2κP,3κP,4κP-tetraosmium(I)(2 Os–Os). IUCrData 2020, 5, x201204. [Google Scholar] [CrossRef] [PubMed]
- Miecznikowski, J.R.; Jasinski, J.P.; Flaherty, N.F.; Mircovich, E.E.; Smolinsky, A.N.; Bertolotti, N.R. trans-Diaquabis(N,N,N′-trimethylethylenediamine)nickel(II) dichloride. IUCrData 2020, 5, x201182. [Google Scholar] [CrossRef] [PubMed]
- Frerichs, N.; Schmidtmann, M.; Beckhaus, R. Tetrakis(dicyclohexylamido)zirconium(IV). IUCrData 2020, 5, x201145. [Google Scholar] [CrossRef]
- Eckhardt, T.; Wagner, C.; Imming, P.; Seidel, R.W. Re-refinement of sodium ammonium sulfate dihydrate at 170K. IUCrData 2020, 5, x201275. [Google Scholar] [CrossRef] [PubMed]
- Dallasta Pedroso, S.; Caracelli, I.; Zukerman-Schpector, J.; Soto-Monsalve, M.; De Almeida Santos, R.H.; Correia, C.R.D.; Llanes Garcia, A.L.; Tiekink, E.R.T. Ethyl 3,4-bis(acetyloxy)-2-(4-methoxyphenyl)pyrrolidine-1-carboxylate. IUCrData 2020, 5, x201228. [Google Scholar] [CrossRef] [PubMed]
- Böhme, U.; Fels, S. 6-[(2-Hydroxy-5-methylanilino)methylidene]-4-nitrocyclohexa-2,4-dien-1-one. IUCrData 2020, 5, x201384. [Google Scholar] [CrossRef]
- Tiouabi, M.; Tabacchi, R.; Stoeckli-Evans, H. (8-Hydroxy-6-methoxy-1-oxo-1H-isochromen-3-yl)methyl formate: A supramolecular framework. IUCrData 2020, 5, x201391. [Google Scholar] [CrossRef]
- Kotha, S.; Ansari, S.; Cheekatla, S.R. 7-Methoxypentacyclo[5.4.0.02,6.03,10.05,9]undecane-8,11-dione. IUCrData 2020, 5, x201380. [Google Scholar] [CrossRef] [PubMed]
- Padgett, C.W.; Sheriff, K.; Lynch, W.E. Pyridine-4-carboxamidoxime N-oxide. IUCrData 2020, 5, x201335. [Google Scholar] [CrossRef]
- Kelley, S.P.; Mossine, V.V.; Mawhinney, T.P. 4-(Dimethylamino)benzohydrazide. IUCrData 2020, 5, x201310. [Google Scholar] [CrossRef]
- Adrian, R.A.; Hernandez, D.R.; Arman, H.D. catena-Poly[[[bis(acetonitrile-κN)(4,4′-dimethoxy-2,2′-bipyridine-κ2N,N′)copper(II)]-μ-trifluoromethanesulfonato-κ2O:O′] trifluoromethanesulfonate]. IUCrData 2020, 5, x201407. [Google Scholar] [CrossRef]
- Diop, A.; Diop, T.; Kama, A.B.; Diop, C.A.K.; Tumanov, N. catena-Poly[[chloridotris(1,3-thiazolidine-2-thione-κS)cadmium(II)]-μ-chlorido]. IUCrData 2020, 5, x201423. [Google Scholar] [CrossRef]
- Adrian, R.A.; Canales, D.; Arman, H.D. (4′-Chloro-2,2′:6′,2″-terpyridine-κ3N,N′,N″)bis(nitrato-κO)zinc(II). IUCrData 2020, 5, x201344. [Google Scholar] [CrossRef]
- Samolová, E.; Fábry, J. Rerefinement of poly[diaquabis(μ3-2-methylpropanoato-κ4O:O,O′:O′)bis(μ3-2-methylpropanoato-κ3O:O:O)(μ2-2-methylpropanoato-κ3O:O,O′)(2-methylpropanoato-κ2O,O′)trilead(II)]. IUCrData 2020, 5, x201311. [Google Scholar] [CrossRef] [PubMed]
- Geng, X.; Wen, B.; Fan, C. Crystal structure of Al2.95Cr0.59, a phase closely related to the η-phase in the binary Al–Cr system. IUCrData 2020, 5, x201412. [Google Scholar] [CrossRef]
- Sammeta, V.R.; Rasapalli, S.; Chadeayne, A.R.; Golen, J.A.; Manke, D.R. The hydrochloride salt of 4-hydroxy-N,N-di-n-propyltryptamine (4-HO-DPT). IUCrData 2020, 5, x201546. [Google Scholar] [CrossRef]
- Kotha, S.; Gupta, N.K.; Ansari, S. (E)-3-Thia-1,5(1,3)-dibenzenacycloundecaphan-8-ene-6,11-dione 3,3-dioxide. IUCrData 2020, 5, x201464. [Google Scholar] [CrossRef]
- Harish Chinthal, C.; Kavitha, C.N.; Yathirajan, H.S.; Foro, S.; Glidewell, C. 1-(3,5-Dinitrobenzoyl)-4-(2-methoxyphenyl)piperazine. IUCrData 2020, 5, x201523. [Google Scholar] [CrossRef] [PubMed]
- Eigner, V. Crystal structure of 2-[(naphthalen-2-yl)methyl]isothiouronium bromide. IUCrData 2020, 5, x201511. [Google Scholar] [CrossRef]
- Ehweiner, M.A.; Belaj, F.; Mösch-Zanetti, N.C. 2H-[1,3]Thiazolo[5,4,3-ij]quinolin-3-ium chloride monohydrate. IUCrData 2020, 5, x201465. [Google Scholar] [CrossRef] [PubMed]
- Böhme, U.; Bitto, F. (3,5-Dimethyl-1H-pyrazol-1-yl)trimethylsilane. IUCrData 2020, 5, x201444. [Google Scholar] [CrossRef]
- Srinivasan, B.R.; Parsekar, N.U.; Narvekar, K.U. catena-Poly[barium(II)-μ2-(dimethylsulfoxide)-κ2O:O-bis(μ2-2,4,6-trinitrophenolato-κ4O2,O1:O1,O6)]. IUCrData 2020, 5, x201498. [Google Scholar] [CrossRef]
- Liang, B.B.; Xiong, H.G.; Hong, W.Y.; Yao, H.G. cis-1-Butyl-3-[2-(phenylsulfanyl)ethyl]-4-imidazolin-2-yl-κ2C2,S′dichloridoplatinum(II). IUCrData 2020, 5, x201433. [Google Scholar] [CrossRef]
- Bendia, S.; Ouari, K.; Ait Ali, M.; Firdousi, L.e.; Nazarenko, A.Y. 1,7,7-Trimethyl-3-(naphthalen-2-ylcarbonyl)bicyclo[2.2.1]heptan-2-one. IUCrData 2020, 5, x201662. [Google Scholar] [CrossRef]
- Nazarenko, A.Y. Naphthalen-1-ylmethanol. IUCrData 2020, 5, x201646. [Google Scholar] [CrossRef] [PubMed]
- Doboszewski, B.; Nazarenko, A.Y. 1,2-O-Isopropylidene-β-d-lyxo-furanose. IUCrData 2020, 5, x201630. [Google Scholar] [CrossRef] [PubMed]
- Nagayama, N.; Taniguchi, N.; Matsumoto, M.; Takeshita, K.; Ishii, T. Ethyl α-l-sorboside. IUCrData 2020, 5, x201625. [Google Scholar] [CrossRef]
- Detert, H.; Schollmeyer, D. 5,12-Diselena-3,4,13,14-tetraazatricyclo[9.3.0.02,6]tetradeca-3,13-diene. IUCrData 2020, 5, x201585. [Google Scholar] [CrossRef] [PubMed]
- Majer, T.; Schollmeyer, D.; Koch, P.; Gross, H. (2S,3′S,3a’R,5′R,7a’R)-5′-[(E)-5-(Furan-3-yl)-2-methylpent-1-en-1-yl]-3-hydroxy-3′,4,7′-trimethyl-1′,2′,3′,3a’,5′,7a’-hexahydro-5H-spiro[furan-2,4′-inden]-5-one. IUCrData 2020, 5, x201578. [Google Scholar] [CrossRef]
- Sha, F.; Johnson, A.R. 4-Fluoro-2-([(2R)-1-hydroxy-1,1,3-triphenylpropan-2-yl]iminomethyl)phenol. IUCrData 2020, 5, x201580. [Google Scholar] [CrossRef]
- Show, V.L.; Fok, E.Y.; Johnson, A.R. 2-([(2S)-1-Hydroxy-1,1,3-triphenylpropan-2-yl]iminomethyl)-4,6-bis(4-methylphenyl)phenol. IUCrData 2020, 5, x201576. [Google Scholar] [CrossRef]
- Papa, V.; Spannenberg, A.; Beller, M.; Junge, K. Bis(benzo[h]quinolin-10-olato-κ2N,O)bromidomanganese(III). IUCrData 2020, 5, x201570. [Google Scholar] [CrossRef]
- Yoo, M.; Koh, D. 1-[5-(3,5-Dimethoxyphenyl)-3-(2-methoxyphenyl)-4,5-dihydro-1H-pyrazol-1-yl]ethanone. IUCrData 2021, 6, x210096. [Google Scholar] [CrossRef]
- Detert, H.; Schollmeyer, D. rac-11-Selena-12,13-diazabicyclo[10.3.0]pentadeca-10a(13a),12-dien-1-ol. IUCrData 2021, 6, x210069. [Google Scholar] [CrossRef]
- Chen, L.; Hu, J.; Sun, H.S. 7,8-Dimethyl-11H-indeno[1,2-b]quinoxalin-11-one. IUCrData 2021, 6, x210018. [Google Scholar] [CrossRef]
- Ovalle, M.A.; Romero, J.A.; Aguirre, G. N-[2-(3,4-Dimethoxyphenyl)-2-(phenylsulfanyl)ethyl]-2-(2-fluorophenyl)acetamide. IUCrData 2021, 6, x201663. [Google Scholar] [CrossRef]
- Ha, K. Di-μ2-chlorido-bischlorido[2,4,6-tris(pyridin-2-yl)-1,3,5-triazine-κ3N2,N1,N6]nickel(II). IUCrData 2021, 6, x210093. [Google Scholar] [CrossRef] [PubMed]
- Ha, K. (Nitrato-κO)(2,2′:6′,2″-terpyridine-κ3N,N′,N″)palladium(II) nitrate. IUCrData 2021, 6, x210085. [Google Scholar] [CrossRef]
- Ha, K. catena-Poly[[(2,2′-bipyridine-κ2N,N′)manganese(II)]-di-μ-bromido]. IUCrData 2021, 6, x210083. [Google Scholar] [CrossRef]
- Ha, K. 4,4′-Dibromo-2,2′-[cyclohexane-1,2-diylbis(nitrilomethanylylidene)]diphenolato-κ4O,N,N′,O′nickel(II). IUCrData 2021, 6, x210084. [Google Scholar] [CrossRef]
- Ravisankar, V.; Ramesh, V.; Krishnamohan, M.; Gunasekaran, B.; Girisun, T.C.S. Bis(benzo-15-crown-5-κ5O)barium tetrakis(isothiocyanato-κN)cobaltate(II). IUCrData 2021, 6, x210024. [Google Scholar] [CrossRef]
- Saha, A.; Padgett, C.W.; LeMagueres, P.; Moncur, K.; Onajobi, G. Di-μ-benzoato-di-μ-ethanolato-tetrakis[μ3-5-(hydroxymethyl)-2-methyl-4-(oxidomethyl)pyridin-1-ium-3-olato]tetrakis[μ3-5-(hydroxymethyl)-2-methyl-4-(oxidomethyl)pyridin-3-olato]di-μ3-oxido-heptamanganese(II,III) ethanol octasolvate. IUCrData 2021, 6, x201643. [Google Scholar] [CrossRef] [PubMed]
- Vinotha, G.; Sundar, T.V.; Sharmila, N. 13-Benzyl-4,11-dihydroxy-1,8-diphenyl-2,9-dithia-13-azadispiro[4.1.4.3]tetradecan-6-one. IUCrData 2021, 6, x210210. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.L.; Zhou, J.; Jiang, H.; Sun, H.S.; Li, R.Z.; Liu, S.L.; Zhang, X.D. Dimethyl 3,3′-[(4-nitrophenyl)methylene]bis(1H-indole-2-carboxylate) ethanol hemisolvate. IUCrData 2021, 6, x210057. [Google Scholar] [CrossRef]
- Andreev, S.; Schollmeyer, D.; Koch, P. 1-3-[(7-Fluoro-9H-pyrimido[4,5-b]indol-4-yl)(methyl)amino]piperidin-1-ylpropan-1-one. IUCrData 2021, 6, x210159. [Google Scholar] [CrossRef] [PubMed]
- Kotha, S.; Fatma, A.; Ansari, S. 2,3-Dihydro-1H-cyclopenta[b]naphthalene-4,9-dione. IUCrData 2021, 6, x210167. [Google Scholar] [CrossRef]
- Kanagawa, M.; Akagi, K.; Okuno, T. 9-[(Z)-2-(4,4,5,5-Tetramethyl-1,3,2-dioxaborolan-2-yl)ethenyl]-9H-carbazole. IUCrData 2021, 6, x210142. [Google Scholar] [CrossRef] [PubMed]
- Pham, D.N.K.; Chadeayne, A.R.; Golen, J.A.; Manke, D.R. Bufotenidinium iodide. IUCrData 2021, 6, x210123. [Google Scholar] [CrossRef]
- Huang, H.; Wu, Z. 2-(2,4-Dinitrophenyl)-1-(pyridin-4-yl)ethanol monohydrate. IUCrData 2021, 6, x201640. [Google Scholar] [CrossRef] [PubMed]
- Al-Sudani, A.R.H.; Abdulridha, M.Q.; Kariuki, B.M. Di-μ-chlorido-bis(chlorido8-[2-(dimethylamino)ethylamino]quinolinecadmium) ethanol monosolvate. IUCrData 2021, 6, x210150. [Google Scholar] [CrossRef]
- Ha, K. Bis[2,3-bis(pyridin-2-yl)pyrazine-κ2N2,N3]palladium(II) dinitrate acetonitrile monosolvate. IUCrData 2021, 6, x210153. [Google Scholar] [CrossRef]
- Ha, K. Dichlorido(pyridine-κN)[2,3,5,6-tetrakis(pyridin-2-yl)pyrazine-κ3N2,N1,N6]nickel(II). IUCrData 2021, 6, x210094. [Google Scholar] [CrossRef]
- El-Hiti, G.A.; Abdel-Wahab, B.F.; Baashen, M.A.; Yousif, E.; Hegazy, A.S.; Kariuki, B.M. 2-(Naphthalen-2-yloxy)-N′-[2-(naphthalen-2-yloxy)acetyl]acetohydrazide monohydrate. IUCrData 2021, 6, x210314. [Google Scholar] [CrossRef]
- Shirmila, D.A.; Jonathan, D.R.; Priya, M.K.; Hemalatha, J.; Usha, G. (2E)-2-(3,4-Dimethoxybenzylidene)-3,4-dihydronaphthalen-1(2H)-one. IUCrData 2021, 6, x210309. [Google Scholar] [CrossRef]
- Reed, C.R.; Garner, R.N.; Brennessel, W.W. (4-Aminopyridine-κN1)(2,2′-bipyridine-κ2N,N′)(2,2′:6′,2″-terpyridine-κ3N,N′,N″)ruthenium(II) bis(hexafluoridophosphate) unknown solvate. IUCrData 2021, 6. [Google Scholar] [CrossRef]
- Schröder, F.; Köckerling, M. Hexaaquadodeca-μ2-iodido-octahedro-hexatantalum diiodide tetrahydrate. IUCrData 2021, 6, x210304. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, V.; Holzmann, G.; Schollmeyer, D.; Detert, H. [2,5-Bis(dipropylamino)-4-(hydroxymethyl)phenyl]methanol. IUCrData 2021, 6, x210443. [Google Scholar] [CrossRef] [PubMed]
- Yan, D. 9-[3-(9H-Carbazol-9-yl)-5-iodophenyl]-9H-carbazole. IUCrData 2021, 6, x210428. [Google Scholar] [CrossRef] [PubMed]
- Anderson, G.I.; Bellia, S.; Zeller, M.; Hillesheim, P.C.; Mirjafari, A. Quinine dihydrochloride hemihydrate. IUCrData 2021, 6, x210406. [Google Scholar] [CrossRef]
- Noland, W.E.; Herzig, R.J.; Fox, R.J.; Tritch, K.J. 3,5-Dibromo-4-carbamoylbenzoic acid 2-propanol monosolvate. IUCrData 2021, 6, x210391. [Google Scholar] [CrossRef]
- Sathya, U.; Nirmal Ram, J.S.; Gomathi, S.; Ramu, S.; Jegan Jennifer, S.; Ibrahim, A.R. 4-(2,3-Dichlorophenyl)piperazin-1-ium picrate. IUCrData 2021, 6, x210379. [Google Scholar] [CrossRef]
- Khanum, G.; Fatima, A.; Sharma, P.; Srivastava, S.K.; Butcher, R.J. Ethyl 2-amino-4-methylthiophene-3-carboxylate. IUCrData 2021, 6, x210351. [Google Scholar] [CrossRef]
- El-Hiti, G.A.; Abdel-Wahab, B.F.; Yousif, E.; Hegazy, A.S.; Kariuki, B.M. 2-(2,4-Dichlorophenoxy)-N′-[2-(2,4-dichlorophenoxy)acetyl]acetohydrazide. IUCrData 2021, 6, x210318. [Google Scholar] [CrossRef]
- Samoľová, E.; Dehno Khalaji, A.; Eigner, V. 4-(Diphenylmethoxy)-3-ethoxybenzaldehyde. IUCrData 2021, 6, x210356. [Google Scholar] [CrossRef]
- Samoľová, E.; Dehno Khalaji, A.; Eigner, V. 4-Bromo-2-[(2-[(2-hydroxyethyl)amino]ethylimino)methyl]phenol. IUCrData 2021, 6, x210335. [Google Scholar] [CrossRef]
- Kotha, S.; Gupta, N.K.; Ansari, S. 5-[(1,3-Dimethyl-5-oxo-2-sulfanylideneimidazolidin-4-ylidene)amino]-2-methylisoindoline-1,3-dione. IUCrData 2021, 6, x210322. [Google Scholar] [CrossRef]
- Ichimaru, Y.; Kato, K.; Kurosaki, H.; Fujioka, H.; Sakai, M.; Yamaguchi, Y.; Wanchun, J.; Sugiura, K.; Imai, M.; Koike, T. Aqua(1,4,7,10-tetraazacyclododecane)zinc(II) bis(perchlorate). IUCrData 2021, 6, x210397. [Google Scholar] [CrossRef]
- Yang, X.; Long, S. Methyl 2-(3-chloro-2-methylanilino)pyridine-3-carboxylate. IUCrData 2021, 6, x210539. [Google Scholar] [CrossRef]
- Sivapriya, S.; Priyanka, S.; Gopalakrishnan, M.; Manikandan, H.; Selvanayagam, S. Ethyl 2-cyano-2-(Z)-2-[2,2-dicyano-1-(4-methylphenyl)ethyl]cyclohexylideneacetate. IUCrData 2021, 6, x210500. [Google Scholar] [CrossRef] [PubMed]
- Mamadrakhimov, A.; Mutalliyev, L.; Abdullaev, S.; Khodjaniyazov, K.; Izotova, L.; Aisa, H.A. 8-Hydroxy-6-methoxy-7-(3-methylbut-2-enyloxy)coumarin (capensine). IUCrData 2021, 6, x210451. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Li, J. Bis(1-methylimidazole)[meso-α,α,α,α-tetrakis(o-nicotinamidophenyl)porphinato]iron(II)–1-methylimidazole–tetrahydrofuran (1/1/1.5). IUCrData 2021, 6. [Google Scholar] [CrossRef] [PubMed]
- Sathya, U.; Nirmal Ram, J.S.; Gomathi, S.; Jegan Jennifer, S.; Abdul Razak, I. catena-Poly[[bis(1H-indole-5-carboxylato-κ2O,O′)zinc(II)]-μ-4,4′-azobipyridine-κ2N1:N1′]. IUCrData 2021, 6, x210522. [Google Scholar] [CrossRef]
- Bowen, C.L.; Wile, B.M. Dioxidomolybdenum(VI) complex featuring a 2,4-difluoro-substituted amine bis(phenolate) ligand. IUCrData 2021, 6, x210516. [Google Scholar] [CrossRef]
- Menia, D.; Höfer, T.; Wurst, K.; Bildstein, B. (Cobaltoceniumylamido)pyridinium hexafluoridophosphate. IUCrData 2021, 6, x210460. [Google Scholar] [CrossRef]
- Abou, A.; Bamba, F.; Marrot, J.; Yaya, S.; Coustard, J.M. 8-Methyl-3-methylsulfanyl-8a,8b-dihydro-5H-1-oxa-2,4-diazaacenaphthylene. IUCrData 2021, 6, x210674. [Google Scholar] [CrossRef]
- Schollmeyer, D.; Sadovski, O.; Detert, H. Diethyl [(2,5-diiodo-4-methylphenyl)methyl]phosphonate. IUCrData 2021, 6, x210654. [Google Scholar] [CrossRef]
- Yoo, M.; Koh, D. 3-(4-Methylphenyl)-4H-chromen-4-one. IUCrData 2021, 6, x210590. [Google Scholar] [CrossRef] [PubMed]
- Myers, S.; Johnson, P.; Benedict, J.B. N-[6-(Dimethylamino)-9-phenyl-3H-telluroxanthen-3-ylidene]-N-methylmethanaminium hexafluorophosphate monoclinic polymorph. IUCrData 2021, 6, x210545. [Google Scholar] [CrossRef]
- Howarth, A.; Barbosa, T.J.; Zeller, M.; Hillesheim, P.C. Pyridinium 3-nitrobenzoate–3-nitrobenzoic acid (1/1). IUCrData 2021, 6, x210581. [Google Scholar] [CrossRef]
- Wang, S.; Liu, G.; Wu, Z. 1,1′-(Ethane-1,2-diyl)bis(4-(E)-2-[4-(dimethylamino)phenyl]ethenylpyridin-1-ium) dibromide ethanol 0.67-solvate. IUCrData 2021, 6, x210396. [Google Scholar] [CrossRef] [PubMed]
- Peppel, T.; Köckerling, M. (S)-Alanine ethyl ester tetracyanidoborate, (C5H12NO)[B(CN)4]. IUCrData 2021, 6, x210562. [Google Scholar] [CrossRef]
- Gao, J.; Long, S. Ethyl 4-oxo-1,4-dihydropyridine-3-carboxylate. IUCrData 2021, 6, x210555. [Google Scholar] [CrossRef] [PubMed]
- Polito-Lucas, J.A.; Núñez-Ávila, J.A.; Bernès, S.; Pérez-Benítez, A. Tetraammonium bis(metforminium) di-μ6-oxido-tetra-μ3-oxido-tetradeca-μ2-oxido-octaoxidodecavanadium(V) hexahydrate. IUCrData 2021, 6, x210634. [Google Scholar] [CrossRef]
- Liebing, P.; Merzweiler, K. cyclo-Tetrakis(μ-2,4,6-trimethylphenyl-κC1:κC1)bis(trimethylphosphane)-1κP,3κP-tetracopper(I). IUCrData 2021, 6, x210594. [Google Scholar] [CrossRef]
- Rood, J.A.; Subedi, C.B.; Risell, J.P.; Astashkin, A.V.; Rajaseelan, E. [(1,2,5,6-η)-Cycloocta-1,5-diene](1-ethyl-3-isopropyl-1,3-imidazol-2-ylidene)(triphenylphosphane)rhodium(I) tetrafluoridoborate. IUCrData 2021, 6, x210597. [Google Scholar] [CrossRef]
- Khelfa, S.; Touil, M.; Setifi, Z.; Setifi, F.; Al-Douh, M.H.; Glidewell, C. catena-Poly[[bis(quinolin-8-amine-κ2N,N′)cadmium(II)]-μ-cyanido-κ2N:C-[dicyanidonickel(II)]-μ-cyanido-κ2C:N]. IUCrData 2021, 6, x210568. [Google Scholar] [CrossRef] [PubMed]
- Bernès, S.; Hernández-Linares, M.G. N,N′-Dicyclohexyl-N-(phthaloylglycyl)urea. IUCrData 2021, 6, x210697. [Google Scholar] [CrossRef] [PubMed]
- Thiruvalluvar, A.A.; Kusanur, R.; Sridharan, M. tert-Butyl 3-amino-5-bromo-1H-indazole-1-carboxylate. IUCrData 2021, 6, x210694. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Fu, T.; Xu, Z. Bis(ethanol-κO)bis(1-ferrocenyl-4,4,4-trifluorobutane-1,3-dionato-κ2O,O′)nickel(II). IUCrData 2021, 6, x210693. [Google Scholar] [CrossRef]
- Salerno, E.V.; Kadel, L.R.; Eichhorn, D.M. Ethanol(nitrato)[tris(4-cyano-3-phenyl-1H-pyrazol-1-yl)hydroborato]nickel(II). IUCrData 2021, 6, x210690. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, B.; Sun, Q. Bis(pyridine-2-carboxylato-κ2N,O)copper(II)]–benzene-1,3,5-tricarboxylic acid–water (1/2/2). IUCrData 2021, 6, x210672. [Google Scholar] [CrossRef]
- Ivlev, S.I.; Kraus, F. Barium bis[tetrafluoridobromate(III)]. IUCrData 2021, 6, x210735. [Google Scholar] [CrossRef]
- Schröder, F.; Köckerling, M. Hexaaquadodeca-μ2-chlorido-octahedro-hexaniobium diiodide. IUCrData 2021, 6, x210696. [Google Scholar] [CrossRef]
- Bruekers, J.; Elemans, J.; Nolte, R.; Tinnemans, P. 1,1′-Methylenebis(4-tert-butylpyridinium) dichloride hemihydrate. IUCrData 2021, 6, x210768. [Google Scholar] [CrossRef] [PubMed]
- Harakas, G.N.; Whittlesey, B.R. Poly[octacarbonylheptakis(tetrahydrofuran)diironmanganesedisodium(2 Mn—Fe)]. IUCrData 2021, 6, x210845. [Google Scholar] [CrossRef]
- Newman, E.B.; Astashkin, A.V.; Albert, D.R.; Rajaseelan, E. (4-Benzyl-1-methyl-1,2,4-triazol-5-ylidene)[(1,2,5,6-η)-cycloocta-1,5-diene](triphenylphosphane-κP)iridium(I) tetrafluoridoborate. IUCrData 2021, 6, x210836. [Google Scholar] [CrossRef] [PubMed]
- Peppel, T.; Köckerling, M. 1-Butyl-3-methylimidazolium tribromido(triphenylphosphane-κP)nickelate(II) butan-1-ol hemisolvate. IUCrData 2021, 6, x210818. [Google Scholar] [CrossRef]
- Rushlow, J.; Astashkin, A.V.; Albert, D.R.; Rajaseelan, E. (Chlorido/bromido)[(1,2,5,6-η)-cycloocta-1,5-diene](4-isopropyl-1-methyl-1,2,4-triazol-5-ylidene)rhodium(I). IUCrData 2021, 6, x210811. [Google Scholar] [CrossRef]
- Johnston, D.H.; King, C.; Seitz, A.; Sethi, M. Bis(2,4-dioxopentan-3-ido-κ2O,O′)dioxidomolybdenum(VI): A redetermination. IUCrData 2021, 6, x210778. [Google Scholar] [CrossRef] [PubMed]
- Diop, A.; Diop, T.; Diop, C.A.K.; Tumanov, N.; Ennio, Z.; Sidibé, M. (3E)-4-[(Naphthalen-1-yl)amino]pent-3-en-2-one hemihydrate. IUCrData 2021, 6, x210989. [Google Scholar] [CrossRef]
- Sung, J. Ethyl 2-[(E)-(2,4-dimethoxy-6-[2-(4-methoxyphenyl)ethenyl]benzylideneamino)oxy]acetate. IUCrData 2021, 6, x210950. [Google Scholar] [CrossRef]
- Schmidt, A.C.; Iovkova, L.; Hiersemann, M. (2R,4S,5S)-5-Methoxy-4-methyl-3-oxohept-6-en-2-yl benzoate. IUCrData 2021, 6, x210951. [Google Scholar] [CrossRef]
- Guo, H.; Du, W.; Zhou, H. (E)-Benzyl 2-4-[ethyl(2-hydroxyethyl)amino]benzylidenehydrazinecarbodithioate. IUCrData 2021, 6, x210901. [Google Scholar] [CrossRef]
- Yaffa, L.; Pouye, S.F.; Ndoye, D.; Diallo, W.; Diop, M.; Sidibe, M.; Diop, C.A.K. Tetraammonium μ-ethylenediaminetetraacetato-1κ3O,N,O′:2κ3O″,N′,O‴-bis[trioxidotungstate(VI)] tetrahydrate. IUCrData 2021, 6, x210982. [Google Scholar] [CrossRef]
- Hu, Q.; Wen, B.; Fan, C. The structure of the aluminium-abundant γ-brass-type Al8.6Mn4.4. IUCrData 2021, 6, x210988. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Wen, B.; Fan, C. Crystal structure of the Al20Mn5.37Ni1.31 phase in the Al–Mn–Ni system. IUCrData 2021, 6, x210981. [Google Scholar] [CrossRef] [PubMed]
- Olszewski, A.; Wzgarda-Raj, K. Pyrazine-2(1H)-thione. IUCrData 2021, 6, x211102. [Google Scholar] [CrossRef]
- Taeufer, T.; Spannenberg, A.; Pospech, J. 1-[(Methylsulfonyl)oxy]pyridin-1-ium methanesulfonate. IUCrData 2021, 6, x211026. [Google Scholar] [CrossRef]
- Hickstein, D.D.; Reinheimer, E.W.; Johnson, A.R.; O’Leary, D.J. Dimethyl 4,5-dichlorophthalate. IUCrData 2021, 6, x211043. [Google Scholar] [CrossRef]
- Patel, D.G.; Cox, J.M.; Bender, B.M.; Benedict, J.B. 3′,5′-Dichloro-N,N-diphenyl-[1,1′-biphenyl]-4-amine. IUCrData 2021, 6, x211016. [Google Scholar] [CrossRef] [PubMed]
- Hajjar, C.; Ovens, J.S.; Bryce, D.L. 1,3,5-Trifluoro-2,4,6-triiodobenzene–piperazine (2/1). IUCrData 2021, 6, x211044. [Google Scholar] [CrossRef]
- Adrian, R.A.; Duarte, J.J.; Arman, H.D. Di-μ-chlorido-bis[(2,2′:6′,2″-terpyridine-κ3N,N′,N″)copper(II)] bis(trifluoromethanesulfonate). IUCrData 2021, 6, x211096. [Google Scholar] [CrossRef]
- Menia, D.; Wurst, K.; Bildstein, B. Bis(μ-cobaltoceniumselenolate-1:2κ2Se:Se)bis[bis(cobaltoceniumselenolate-κSe)mercury(II)] tetrakis(hexafluoridophosphate) acetonitrile disolvate. IUCrData 2021, 6, x211083. [Google Scholar] [CrossRef]
- Adrian, R.A.; Ibarra, S.J.; Arman, H.D. Bis(isonicotinamide-κN)silver(I) trifluoromethanesulfonate acetonitrile disolvate. IUCrData 2021, 6, x211073. [Google Scholar] [CrossRef] [PubMed]
- Kodama, S.; Bunno, K.; Nomoto, A.; Ogawa, A. trans-Bis[8-(benzylsulfanyl)quinoline-κ2N,S]dichloridocobalt(II). IUCrData 2021, 6, x210992. [Google Scholar] [CrossRef] [PubMed]
- Meenatchi, C.S.; Athimoolam, S.; Suresh, J.; Rubina, S.R.; Kumar, R.R.; Bhandari, S.R. (E)-5-(4-Chlorobenzylidene)-1-phenyl-4,5,6,7-tetrahydro-1H-indazol-4-one: Crystal structure and Hirshfeld surface analysis. IUCrData 2021, 6, x211195. [Google Scholar] [CrossRef] [PubMed]
- Butcher, R.J.; Purdy, A.P. Tetramethylammonium (Z)-N′-cyanocarbamimidate. IUCrData 2021, 6, x211098. [Google Scholar] [CrossRef]
- Ishida, H. Bis[2-(2-hydroxyphenyl)-1H-benzimidazol-3-ium] chloranilate. IUCrData 2021, 6, x211150. [Google Scholar] [CrossRef]
- Adrian, R.A.; Lagemann, B.J.; Arman, H.D. [1,2-Bis(diphenylphosphanyl)ethane-κ2P,P]chlorido(isonicotinamide-κN)palladium(II) nitrate acetonitrile monosolvate. IUCrData 2021, 6, x211171. [Google Scholar] [CrossRef]
- Castaldi, K.T.; Astashkin, A.V.; Albert, D.R.; Rajaseelan, E. (4-Butyl-1-methyl-1,2,4-triazol-5-ylidene)[(1,2,5,6-η)-cycloocta-1,5-diene](triphenylphosphane)iridium(I) tetrafluoridoborate. IUCrData 2021, 6, x211142. [Google Scholar] [CrossRef]
- Lozinšek, M. Nitrosonium tetrafluoridoborate, NOBF4. IUCrData 2021, 6, x211215. [Google Scholar] [CrossRef]
- Matsumoto, M.; Nagayama, N.; Hirose, R.; Takeshita, K.; Ishii, T. Methyl α-l-sorboside monohydrate. IUCrData 2021, 6, x211325. [Google Scholar] [CrossRef]
- Fait, M.J.G.; Spannenberg, A.; Kondratenko, E.V.; Linke, D. 1,3-Thiazole-4-carbonitrile. IUCrData 2021, 6, x211332. [Google Scholar] [CrossRef]
- Kotha, S.; Ansari, S.; Gupta, N.K. rac-(2aS,2a1R,3aR,3a1S,5aS,6aR)-2a-Allyl-2,4-dichloro-2a,2a1,3a1,5a,6,6a-hexahydro-3aH-3-oxadicyclopenta[cd,gh]pentalen-3a-ol. IUCrData 2021, 6, x211260. [Google Scholar] [CrossRef]
- Pacifico, J.; Stoeckli-Evans, H. (μ-2,2′,2″,2‴-[Pyrazine-2,3,5,6-tetrayltetrakis(methylene)]tetrakis(sulfanediyl)tetraacetato)bis[aquanickel(II)] heptahydrate. IUCrData 2021, 6, x211295. [Google Scholar] [CrossRef]
- Davis, W.L.; Muller, A. Dichlorido(η6-p-cymene)[tris(4-methoxyphenyl)phosphane]ruthenium(II). IUCrData 2021, 6, x211259. [Google Scholar] [CrossRef] [PubMed]
- Hatayama, Y.; Akagi, K.; Okuno, T. N-Phenyl-N-[(E)-2-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan-2-yl)ethenyl]aniline. IUCrData 2022, 7, x220083. [Google Scholar] [CrossRef] [PubMed]
- Mossine, V.V.; Kelley, S.P.; Mawhinney, T.P. β-d-Galactopyranosyl-(1→4)–2-amino-2-deoxy-α-d-glucopyranose hydrochloride monohydrate (lactosamine). IUCrData 2022, 7, x220061. [Google Scholar] [CrossRef]
- Corfield, P.W.R. [Sulfonylbis(bromomethylene)]dibenzene. IUCrData 2022, 7, x211351. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Han, Z.B. Bis(dimethylamine-κN)bis[4-(1,2,4-triazol-1-yl)benzoato-κO]copper(II). IUCrData 2022, 7, x220046. [Google Scholar] [CrossRef]
- Hu, Q.; Wen, B.; Fan, C. The Al61.49Mn11.35Ni4 phase in the Al–Mn–Ni system. IUCrData 2022, 7, x220038. [Google Scholar] [CrossRef]
- Hines III, J.E.; Deere, C.J.; Fronczek, F.R.; Uppu, R.M. N-(4-Hydroxy-2-nitrophenyl)acetamide. IUCrData 2022, 7, x220201. [Google Scholar] [CrossRef]
- Chachlaki, E.; Choquesillo-Lazarte, D.; Demadis, K.D. 5-Phenyl-3-(2-phosphonoethyl)-1,2,3-triazol-1-ium chloride. IUCrData 2022, 7, x220189. [Google Scholar] [CrossRef]
- Surya Prakash Rao, H.; M, P.; Muthukumaran, J. Ethyl 10-cyano-7-hydroxy-6-oxo-3-phenyl-8,9,10,10a-tetrahydro-6H-benzo[c]chromene-10-carboxylate. IUCrData 2022, 7, x220199. [Google Scholar] [CrossRef]
- Schollmeyer, D.; Detert, H. 13,13′-Bi(dibenzo[a,i]fluorenylidene). IUCrData 2022, 7, x220169. [Google Scholar] [CrossRef]
- Moussa Slimane, N.; Benarous, N.; Bougueria, H.; Cherouana, A. 2-Hydroxybenzenaminium acetate. IUCrData 2022, 7, x220112. [Google Scholar] [CrossRef]
- Koehne, S.; Mirmelli, B.; Mague, J.T.; Donahue, J.P. Bis[1,2-bis(4-chlorophenyl)ethylene-1,2-dithiolato(1–)]nickel(II). IUCrData 2022, 7, x220148. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Nesterov, V.V.; Smucker, B.W. trans-Bis(4-aminopyridine-κN)bis(quinoxaline-2,3-dithiolato-κ2S,S′)platinum(IV) dimethyl sulfoxide monosolvate. IUCrData 2022, 7, x220101. [Google Scholar] [CrossRef] [PubMed]
- Pacifico, J.; Stoeckli-Evans, H. Poly[dipotassium [(μ6-2,2′,2″,2‴-[pyrazine-2,3,5,6-tetrayltetrakis(methylene)]tetrakis(sulfanediyl)tetraacetato)disilver(I)] 5.2-hydrate]. IUCrData 2022, 7, x220077. [Google Scholar] [CrossRef]
- Song, J.; Jiang, X.; Wang, Z.; Pei, J.; Li, H. 4-Chloro-5-(dimethylamino)-2-[(5-phenyl-1,3,4-oxadiazol-2-yl)methyl]pyridazin-3(2H)-one. IUCrData 2022, 7, x220342. [Google Scholar] [CrossRef]
- Abdallah, A.E.M.; Elgemeie, G.H.; Jones, P.G. 3-(Benzo[d]thiazol-2-yl)-2H-chromen-2-one. IUCrData 2022, 7, x220332. [Google Scholar] [CrossRef] [PubMed]
- Meenatchi, C.S.; Athimoolam, S.; Suresh, J.; Priya, R.V.; Rubina, S.R.; Bhandari, S.R. (E)-5-(4-Methylbenzylidene)-1-phenyl-4,5,6,7-tetrahydro-1H-indazol-4-one. IUCrData 2022, 7, x220283. [Google Scholar] [CrossRef]
- Angevine, D.J.; Benedict, J.B. 1,2-Bis(pyridin-4-yl)ethene–4-hydroxy-3-methoxybenzoic acid (1/1). IUCrData 2022, 7, x220304. [Google Scholar] [CrossRef]
- Hines III, J.E.; Deere, C.J.; Vaddi, P.; Kondati, R.R.; Fronczek, F.R.; Uppu, R.M. N-(4-Methoxy-2-nitrophenyl)acetamide. IUCrData 2022, 7, x220277. [Google Scholar] [CrossRef]
- Lambrecht, S.; Villinger, A.; Jopp, S. 1-(Methyl-α-d-glucopyranosid-6-yl)-3-vinylimidazolium iodide dimethylformamide monosolvate. IUCrData 2022, 7, x220265. [Google Scholar] [CrossRef] [PubMed]
- Welton, C.E.; Nesterov, V.N.; Smucker, B.W. 1-(2-Methylphenyl)-4,4′-bipyridin-1-ium tetrafluoridoborate. IUCrData 2022, 7, x220248. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.G. N′-[(E)-1-(5-Chloro-2-oxidophenyl)ethylidene]-4-methoxybenzohydrazidato-κ3O,N′,O′(1H-imidazole-κN3)nickel(II). IUCrData 2022, 7, x220295. [Google Scholar] [CrossRef]
- Chachlaki, E.; Choquesillo-Lazarte, D.; Demadis, K.D. catena-Poly[oxidanium [trisμ-[amino(iminio)methyl]phosphonatozincate(II)]]. IUCrData 2022, 7, x220247. [Google Scholar] [CrossRef]
- Aquino, A.J.; Gerrior, D.; Cameron, T.S.; Robertson, K.N.; Aquino, M.A. Tetra-μ-acetato-κ8O:O′-bis[(3-chloropyridine-κN)ruthenium(II,III)](Ru—Ru) hexafluoridophosphate 1,2-dichloroethane monosolvate. IUCrData 2022, 7, x220249. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, J. ([2.2.2]Cryptand)potassium (4-methylbenzenethiolato)[5,10,15,20-tetrakis(4-chlorophenyl)porphyrinato]manganate(II) tetrahydrofuran disolvate. IUCrData 2022, 7, x220241. [Google Scholar] [CrossRef]
- Ghallab, R.; Bougueria, H.; Merazig, H. 4-Amidinopyridinium hexachloridostannate(IV) dihydrate. IUCrData 2022, 7, x220195. [Google Scholar] [CrossRef] [PubMed]
- Ghallab, R.; Bougueria, H.; Merazig, H. Bis(2-amino-3,5-dichloropyridinium) hexachloridostannate(IV) dihydrate. IUCrData 2022, 7, x220191. [Google Scholar] [CrossRef]
- Obidova, N.; Ashurov, J.; Izotova, L.; Ibragimov, B. 2-Hydroxyethylammonium [2-(2,6-dichloroanilino)phenyl]acetate monohydrate. IUCrData 2022, 7, x220441. [Google Scholar] [CrossRef]
- Azzam, R.A.; Elgemeie, G.H.; Gad, N.M.; Jones, P.G. 4-Amino-5-(4-bromobenzoyl)-3-(benzo[d]thiazol-2-yl)-2-[(2′,3′,4′,6′-tetra-O-acetyl-β-d-galactopyranosyl)sulfanyl]thiophene. IUCrData 2022, 7, x220412. [Google Scholar] [CrossRef]
- Bosch, E.; Bowling, N.P. 5-[4-(Dimethylamino)phenyl]ethynylpyrimidine–1,2,3,5-tetrafluoro-4,6-diiodobenzene (1/2). IUCrData 2022, 7, x220380. [Google Scholar] [CrossRef]
- Pineda, L.W.; Ferllini, N.; Cabezas, J.A. 1-(Phenylsulfonyl)-1H-indole-2-carbaldehyde. IUCrData 2022, 7, x220401. [Google Scholar] [CrossRef]
- Naeem, M.; Chadeayne, A.R.; Golen, J.A.; Manke, D.R. Bis(oxotremorine) fumarate bis(fumaric acid). IUCrData 2022, 7, x220364. [Google Scholar] [CrossRef]
- Cao, H.; Wang, J.; Li, J. Nitrato(5,10,15,20-tetraphenylporphinato)manganese(III)–benzene–n-hexane (2/1/1). IUCrData 2022, 7, x220386. [Google Scholar] [CrossRef]
- Deng, M.; Yin, Y.; Wang, S.S.; Qi, X.Y.; Zhu, A.X. Poly[bis[μ2-4,4′-bis(imidazol-1-ylmethyl)biphenyl-κ2N:N′]dichloridonickel(II)]. IUCrData 2022, 7, x220377. [Google Scholar] [CrossRef] [PubMed]
- Neal, H.C.; Nesterov, V.V.; Smucker, B.W. 1,1′-Methylenebis4-[(E)-2-(pyridin-4-yl)ethenyl]pyridinium dibromide dihydrate. IUCrData 2022, 7, x220525. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.A.; Nesterov, V.V.; Smucker, B.W. 1,1′-Methylenebis(4,4′-bipyridin-1-ium) dibromide. IUCrData 2022, 7, x220526. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.J.; Koser, G.; Chen, Y.; Zeller, M.; Iacino, R.; Selzer, N. (Phenyliodosyl)benzene tosylate dihydrate. IUCrData 2022, 7, x220522. [Google Scholar] [CrossRef]
- Angevine, D.J.; Benedict, J.B. 4,4’-(Ethene-1,2-diyl)dipyridinium bis(2-hydroxy-3-methoxybenzoate). IUCrData 2022, 7, x220510. [Google Scholar] [CrossRef]
- Bruekers, J.P.J.; Elemans, J.A.A.W.; Nolte, R.J.M.; Tinnemans, P. Bis(3-methyl-1-propyl-1,3-dihydro-1H-imidazol-2-ylidene)silver(I) chlorido(5,10,15,20-tetraphenylporphinato)cadmate(II). IUCrData 2022, 7, x220489. [Google Scholar] [CrossRef] [PubMed]
- Franklin, D.; Lee, A.; Fronczek, F.R.; Junk, T. [1,4]Ditellurino[2,3-b:5,6-b′]dipyrazine. IUCrData 2022, 7, x220622. [Google Scholar] [CrossRef]
- Guerrab, W.; El Moutaouakil Ala Allah, A.; Alsubari, A.; Mague, J.T.; Ramli, Y. 3-Isobutyl-5,5-diphenylimidazolidine-2,4-dione. IUCrData 2022, 7, x220598. [Google Scholar] [CrossRef]
- Brihi, O.; Medjani, M.; Bougueria, H.; Djedouani, A.; Francois, M.; Fleutot, S.; Boudjada, A. 2,6-Dibromo-4-methylaniline. IUCrData 2022, 7, x220577. [Google Scholar] [CrossRef]
- Zaoui, Y.; Assila, H.; Mague, J.T.; Alsubari, A.; Taoufik, J.; Ramli, Y.; Ansar, M. Ethyl 2-[4-(4-methoxybenzyl)-3-methyl-6-oxopyridazin-1-yl]acetate. IUCrData 2022, 7, x220582. [Google Scholar] [CrossRef]
- Pérez-Benítez, A.; Ariza-Ramírez, J.L.; Fortis-Valera, M.; Arroyo-Carmona, R.E.; Martínez de la Luz, M.I.; Ramírez-Contreras, D.; Bernès, S. Bis[amino(iminiumyl)methyl]urea tetrakis2-[(dimethylamino)(iminiumyl)methyl]guanidine di-μ6-oxido-tetra-μ3-oxido-tetradeca-μ2-oxido-octaoxidodecavanadium(V) tetrahydrate. IUCrData 2022, 7, x220627. [Google Scholar] [CrossRef]
- Schröder, F.; Köckerling, M. Tetraaquadodekakis-μ2-chlorido-diiodido-octahedro-hexaniobium(12 Nb—Nb) tetrahydrofuran octasolvate. IUCrData 2022, 7, x220618. [Google Scholar] [CrossRef]
- Corfield, P.W.R. trans-Carbonylchloridobis(triethylphosphane-κP)platinum(II) tetrafluoridoborate. IUCrData 2022, 7, x220607. [Google Scholar] [CrossRef]
- Missioui, M.; Guerrab, W.; Alsubari, A.; Mague, J.T.; Ramli, Y. 2-Azido-N-(4-methylphenyl)acetamide. IUCrData 2022, 7, x220621. [Google Scholar] [CrossRef] [PubMed]
- Abad, N.; Missioui, M.; Alsubari, A.; Mague, J.T.; Essassi, E.M.; Ramli, Y. Crystal structure of ethyl 2-4-[(2-oxo-3-phenyl-1,2-dihydroquinoxalin-1-yl)methyl]-1H-1,2,3-triazol-1-ylacetate. IUCrData 2022, 7. [Google Scholar] [CrossRef] [PubMed]
- Rushlow, J.; Astashkin, A.V.; Albert, D.R.; Rajaseelan, E. [(1,2,5,6-η)-Cycloocta-1,5-diene](4-isopropyl-1-methyl-1,2,4-triazol-5-ylidene)(tricyclohexylphosphane-κP)iridium(I) tetrafluoridoborate dichloromethane monosolvate. IUCrData 2022, 7, x220685. [Google Scholar] [CrossRef]
- Moris, S.; Galdámez, A. Rerefinement of the crystal structure of SnTe0.73(2)Se0.27(2) from single-crystal X-ray diffraction data. IUCrData 2022, 7, x220729. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, C.; Wen, B.; Zhang, L. Natural djurleite with refined composition Cu61.39S32 revealing disorder of some Cu sites. IUCrData 2022, 7, x220694. [Google Scholar] [CrossRef] [PubMed]
- Shank, N.; Stadler, A.L.; Barrett, S.P.; Padgett, C.W. 1-(Hex-5-en-1-yl)-4-[3-methyl-2,3-dihydro-1,3-benzothiazol-2-ylidene]methylquinolin-1-ium iodide monohydrate. IUCrData 2022, 7, x220797. [Google Scholar] [CrossRef] [PubMed]
- Newell, B.D.; McMillen, C.D.; Lee, J.P. N-(2,3,5,6-Tetrafluoropyridin-4-yl)formamide. IUCrData 2022, 7, x220804. [Google Scholar] [CrossRef] [PubMed]
- Ichimaru, Y.; Kato, K.; Kurihara, M.; Jin, W.; Koike, T.; Kurosaki, H. Bis(nitrato-κO)(1,4,8,11-tetraazacyclotetradecane-κ4N)zinc(II) methanol monosolvate. IUCrData 2022, 7, x220854. [Google Scholar] [CrossRef]
- Harakas, G.N.; Demmin, M.E. Tetracarbonyldi-μ-chlorido-dichloridobis(η5-cyclopentadienyl)diirondigallium(2 Fe—Ga). IUCrData 2022, 7, x220832. [Google Scholar] [CrossRef]
- Shevlin, M.R.; Stumbo, E.E.; McMillen, C.D.; Pienkos, J.A. Bis[3,5-difluoro-2-(pyridin-2-yl)phenyl](4,4′-dimethoxy-2,2′-bipyridine)iridium(III) hexafluoridophosphate. IUCrData 2022, 7, x220830. [Google Scholar] [CrossRef]
- Ren, J.Y.; Huang, R.; Yin, Z.; Cao, L.H. Poly[bis(μ2-N,N-dimethylformamide-κ2O:O)bis(μ4-thiophene-2,5-dicarboxylato-κ4O:O′:O″:O‴)dicobalt(II)]. IUCrData 2022, 7, x220775. [Google Scholar] [CrossRef]
- Potgieter, K.; Malan, F.P.; Alimi, O.A.; Meijboom, R. Bis[(4-methylphenyl)diphenylphosphine-κP](nitrito-κ2O,O′)silver(I). IUCrData 2022, 7, x220771. [Google Scholar] [CrossRef]
- Potgieter, K.; Malan, F.P.; Meijboom, R. catena-Poly[[(benzyldiphenylphosphine-κP)silver(I)]-μ-nitrato-κ2O:O′-[(benzyldiphenylphosphine-κP)silver(I)]-μ-nitrato-κ4O,O′:O′,O″]. IUCrData 2022, 7, x220772. [Google Scholar] [CrossRef]
- Okuno, T.; Doi, I. 10-[(4-Nitrophenyl)ethynyl]-10H-phenothiazine. IUCrData 2022, 7, x220942. [Google Scholar] [CrossRef]
- Koh, D. (E)-1-(2-Hydroxy-4,6-dimethoxyphenyl)-3-(naphthalen-1-yl)prop-2-en-1-one. IUCrData 2022, 7, x220932. [Google Scholar] [CrossRef]
- Martínez-de la Luz, I.; López-Velázquez, D.; Bernès, S.; Varela Caselis, J.L. Bis(4-hydroxyphenyl) 1,4-phenylenebiscarbamate. IUCrData 2022, 7, x220919. [Google Scholar] [CrossRef]
- Archana, S.D.; Nagma Banu, H.A.; Kalluraya, B.; Yathirajan, H.S.; Balerao, R.; Butcher, R.J. 3-Methyl-5-(4-methylphenoxy)-1-phenyl-1H-pyrazole-4-carbaldehyde. IUCrData 2022, 7, x220924. [Google Scholar] [CrossRef] [PubMed]
- Priyanka, P.; Jayanna, B.K.; Kiran Kumar, H.; Yathirajan, H.S.; Divakara, T.R.; Foro, S.; Butcher, R.J. Isopropyl 4-aminobenzoate. IUCrData 2022, 7, x220904. [Google Scholar] [CrossRef]
- Sung, J. 3-(2,3-Dimethoxyphenyl)-2,3-dihydro-1H-benzo[f]chromen-1-one. IUCrData 2022, 7, x220885. [Google Scholar] [CrossRef]
- Blackwelder, L.A.; Kelley, A.R.; Balaich, G.J.; Jefferies, L.R. 2,2′-(1E,1′E)-[Ethane-1,2-diylbis(azanylylidene)]bis(methanylylidene)bis(4-iodophenol). IUCrData 2022, 7, x220895. [Google Scholar] [CrossRef]
- Shimazaki, R.; Sadakiyo, M. Ethidium heptafluorobutyrate. IUCrData 2022, 7, x220884. [Google Scholar] [CrossRef] [PubMed]
- Bellia, S.; Anderson, G.; Zeller, M.; Mirjafari, A.; Hillesheim, P.C. 1-Methyl-5-nitroimidazolium chloride. IUCrData 2022, 7, x220878. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Li, J. μ-Oxido-bis[(5,10,15,20-tetraphenylporphyrinato-κ4N,N′,N″,N‴)manganese(III)]. IUCrData 2022, 7, x220869. [Google Scholar] [CrossRef]
- Saini, A.; Dhanwant, K.; Thirumoorthi, R. 1-Hydroxy-4-methylpyridinium chloride. IUCrData 2022, 7, x221023. [Google Scholar] [CrossRef]
- Archana, S.D.; Nagma Banu, H.A.; Kalluraya, B.; Yathirajan, H.S.; Balerao, R.; Butcher, R.J. 5-(4-Fluorophenyl)-1-[4-(4-methylphenyl)thiazol-2-yl]-3-[4-(prop-2-ynyloxy)phenyl]-4,5-dihydro-1H-pyrazole. IUCrData 2022, 7, x221003. [Google Scholar] [CrossRef] [PubMed]
- Campos Fernandez, C.; Procupez-Schtirbu, R.; Soto-Tellini, V.H.; Salazar, J.C.; Jancik, V. (1S,3R)-N-(3S,10S,12S,13R,17R)-12-Hydroxy-17-[(R)-5-hydroxypentan-2-yl]-10,13-dimethylhexadecahydro-1H-cyclopenta[a]phenanthren-3-yladamantane-1-carboxamide 0.25-hydrate. IUCrData 2022, 7, x220947. [Google Scholar] [CrossRef]
- Shimazaki, R.; Sadakiyo, M. Ethidium tetraphenylborate acetonitrile disolvate. IUCrData 2022, 7, x220951. [Google Scholar] [CrossRef] [PubMed]
- Vinaya; Basavaraju, Y.B.; Nagma Banu, H.A.; Kalluraya, B.; Yathirajan, H.S.; Balerao, R.; Butcher, R.J. 3-(3-Nitrophenyl)-1-[4-(prop-2-ynyloxy)phenyl]prop-2-en-1-one. IUCrData 2022, 7, x220957. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-García, J.J.; Flores-Alamo, M.; Nuñez-Gordillo, A.; Klimova, E.I. 4,5-Diferrocenyl-1,2-dithiole-3-thione. IUCrData 2022, 7, x221011. [Google Scholar] [CrossRef]
- Khan, S.S.; Howlader, M.B.H.; Miyatake, R.; Sheikh, M.C.; Zangrando, E. Diethyl 4,4′-[octane-1,8-diylbis(oxy)]dibenzoate. IUCrData 2022, 7, x221080. [Google Scholar] [CrossRef]
- Archana, S.D.; Nagma Banu, H.A.; Kalluraya, B.; Yathirajan, H.S.; Balerao, R.; Butcher, R.J. 5-(4-Methoxyphenyl)-1-[4-(4-methoxyphenyl)thiazol-2-yl]-3-[4-(prop-2-ynyloxy)phenyl]-4,5-dihydro-1H-pyrazole. IUCrData 2022, 7, x221047. [Google Scholar] [CrossRef]
- Butcher, R.J.; Purdy, A.P. 2,5,8,11-Tetramethyl-2,5,8,11-tetraazadodecane-2,11-diium bis[hydroxytris(pentafluorophenyl)borate] benzene 2.5-solvate. IUCrData 2022, 7, x221049. [Google Scholar] [CrossRef]
- Mohamed-Ezzat, R.A.; Kariuki, B.M.; Azzam, R.A. Morpholin-4-ium [5-cyano-6-(4-methylphenyl)-4-(morpholin-4-yl)pyrimidin-2-yl](phenylsulfonyl)amide. IUCrData 2022, 7, x221033. [Google Scholar] [CrossRef]
- Adrian, R.A.; Ibarra, S.J.; Arman, H.D. Bis(4′-chloro-2,2′:6′,2″-terpyridine-κ3N,N′,N″)zinc(II) bis(trifluoromethanesulfonate). IUCrData 2022, 7, x221096. [Google Scholar] [CrossRef]
- Malan, F.P.; Potgieter, K.; Meijboom, R. Bis[(4-methylphenyl)diphenylphosphane-κP](nitrato-κ2O,O′)silver(I). IUCrData 2022, 7, x221045. [Google Scholar] [CrossRef]
- Halz, J.H.; Heiser, C.; Merzweiler, K. Bis(acetylacetonato-κ2O,O′)(N,N,N′,N′-tetramethylethylenediamine-κ2N,N′)magnesium(II). IUCrData 2022, 7, x221035. [Google Scholar] [CrossRef]
- Lutz, M.; Kroon-Batenburg, L. Accurate intensity integration in the twinned γ-form of o-nitroaniline. IUCrData 2022, 7, x221059. [Google Scholar] [CrossRef]
- Butcher, R.J.; Purdy, A.P. 2-Ethyl-4-methyl-1H-imidazol-3-ium bromide. IUCrData 2022, 7, x221172. [Google Scholar] [CrossRef] [PubMed]
- Saadallah, Y.; Setifi, Z.; Geiger, D.K.; Al-Douh, M.H.; Satour, A.; Setifi, F. trans-Bis(2,2′-dipyridylamine-κ2N,N′)bis(1,1,3,3-tetracyano-2-ethoxypropenido-κN)copper(II). IUCrData 2022, 7, x221180. [Google Scholar] [CrossRef]
- Graaff, S.d.; Elma, A.; Schmidtmann, M.; Beckhaus, R. (Carbazol-9-ido-κN)dichlorido(η5:η1-2,3,4,5-tetramethylpentafulvene)tantalum(V). IUCrData 2022, 7, x221201. [Google Scholar] [CrossRef]
- Malan, F.P.; Potgieter, K.; Meijboom, R. (Nitrito-κ2O,O′)bis[tris(4-methylphenyl)phosphane-κP]silver(I). IUCrData 2022, 7, x221148. [Google Scholar] [CrossRef]
- Potgieter, K.; Malan, F.P.; Alimi, O.A.; Meijboom, R. Tris(benzyldiphenylphosphane-κP)(nitrato-κO)silver(I). IUCrData 2022, 7, x221147. [Google Scholar] [CrossRef] [PubMed]
- Adrian, R.A.; Rios, J.J.; Arman, H.D. Dichlorido(4,4′-dimethyl-2,2′-bipyridine-κ2N,N′)zinc(II) acetonitrile monosolvate. IUCrData 2022, 7, x221149. [Google Scholar] [CrossRef]
- Adrian, R.A.; Gutierrez, M.C.; Arman, H.D. Diacetonitrile(2,2′-bipyridine-κ2N,N′)palladium(II) bis(trifluoromethanesulfonate). IUCrData 2022, 7, x221151. [Google Scholar] [CrossRef]
- Fang, C.; Wang, Z.; Cong, Z.; Li, S.; Li, F. [SP-4-2]-(Acetonitrile-κN)chlorido[2-(4,6-diphenylpyridin-2-yl)phenyl-κ2C1,N]platinum(II). Corrigendum. IUCrData 2020, 5, x200155. [Google Scholar] [CrossRef]
- Naveen, S.; Al-Maqtari, H.M.; Jamalis, J.; Sirat, H.M.; Lokanath, N.K.; Abdoh, M. (E)-3-(3-Methylthiophen-2-yl)-1-p-tolylprop-2-en-1-one. Corrigendum. IUCrData 2021, 6, x211077. [Google Scholar] [CrossRef]
- Patel, N.V.; Golab, J.T.; Kaduk, J.A. Diammonium potassium citrate, (NH4)2KC6H5O7. IUCrData 2020, 5, x200612. [Google Scholar] [CrossRef] [PubMed]
- Peña Hueso, A.; Esparza Ruiz, A.; Flores Parra, A. Bis(2-aminobenzimidazolium) sulfate monohydrate. IUCrData 2022, 7, x220172. [Google Scholar] [CrossRef]
- Freitas, J.F.d.; Brown, S.; Oberndorfer, J.S.; Crundwell, G. 5-Nitro-2,3-bis(thiophen-2-yl)quinoxaline. IUCrData 2020, 5, x200196. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, F.; Li, P.; Xu, M.; Xu, G.; Li, W.; Wang, F. 2,4,6-Triphenyl-N-(3E)-3-[(2,4,6-triphenylphenyl)imino]butan-2-ylideneaniline. IUCrData 2020, 5, x200531. [Google Scholar] [CrossRef] [PubMed]
- Sarr, B.; Mbaye, A.; Touré, A.; Diop, C.A.K.; Sidibé, M.; Michaud, F. Dipropylammonium 4-aminobenzenesulfonate. IUCrData 2020, 5, x200659. [Google Scholar] [CrossRef] [PubMed]
- Flores-Alamo, M.; Perez-Ortiz, F.J.; Arevalo, A.; Garcia, J.J. [1,2-Bis(diisopropylphosphanyl)ethane-κ2P,P′](2-fluoro-N-[(2-fluorophenyl)azanidyl]carbonylanilinido-κ2N,N′)nickel(II). IUCrData 2020, 5, x200649. [Google Scholar] [CrossRef]
- Lee, K.S.; Turner, L.; Powell, C.B.; Reinheimer, E.W. (S)-2-[(4-Fluorophenyl)formamido]-3-phenylpropanoic acid. IUCrData 2020, 5, x200897. [Google Scholar] [CrossRef]
- Araújo, R.S.A.d.; Zondegoumba, E.N.T.; Tankoua, W.L.D.; Nyassé, B.; Mendonça-Junior, F.J.B.; De Simone, C.A. 1-Hydroxy-3,4-dimethoxy-10-methylacridin-9-one. IUCrData 2020, 5, x201005. [Google Scholar] [CrossRef]
- Prapakaran, T.; Murugavel, R. 4,4′-Methylenebis[N-(2-hydroxy-3-methoxybenzylidene)-2,6-diisopropylaniline]. IUCrData 2022, 7, x220793. [Google Scholar] [CrossRef]
- Neviani, V.; Lutz, M.; Oosterheert, W.; Gros, P.; Kroon-Batenburg, L. Crystal structure of the second extracellular domain of human tetraspanin CD9: Twinning and diffuse scattering. IUCrData 2022, 7, x220852. [Google Scholar] [CrossRef]
- Henn, J. Bias caused by a popular weighting scheme. J. Appl. Crystallogr. 2025, 58, 283–289. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Keve, E.T. Normal probability plot analysis of error in measured and derived quantities and standard deviations. Acta Crystallogr. Sect. A 1971, 27, 157–165. [Google Scholar] [CrossRef]
- Porȩba, T.; Macchi, P.; Ernst, M. Pitfalls in the location of guest molecules in metal-organic frameworks. Nat. Commun. 2022, 13, 5288. [Google Scholar] [CrossRef]
- Wang, B.; Wang, P.; Xie, L.H.; Lin, R.B.; Lv, J.; Li, J.R.; Chen, B. A stable zirconium based metal-organic framework for specific recognition of representative polychlorinated dibenzo-p-dioxin molecules. Nat. Commun. 2019, 10, 3861. [Google Scholar] [CrossRef] [PubMed]
- Henn, J. Incomplete Absorption Correction Results in an Increased Positive Mean Value of Weighted Residuals. Crystals 2025, 15, 898. [Google Scholar] [CrossRef]
- Krause, L.; Herbst-Irmer, R.; Sheldrick, G.M.; Stalke, D. Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination. J. Appl. Crystallogr. 2015, 48, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Harmening, T.; van Wüllen, L.; Eckert, H.; Rodewald, U.C.; Pöttgen, R. Sc4Pt7Si2—An Intergrowth Structure of ScPtSi and ScPt Related Slabs. J. Inorg. Gen. Chem. 2010, 636, 972–976. [Google Scholar] [CrossRef]
- Farrugia, L.J. Sodium tungstate dihydrate: A redetermination. Acta Crystallogr. Sect. E Struct. Rep. Online 2007, 63, i142. [Google Scholar] [CrossRef]
- Rohrmoser, B.; Eickerling, G.; Presnitz, M.; Scherer, W.; Eyert, V.; Hoffmann, R.D.; Rodewald, U.C.; Vogt, C.; Poettgen, R. Experimental electron density of the complex carbides Sc3 [Fe (C2) 2] and Sc3 [Co (C2) 2]. J. Am. Chem. Soc. 2007, 129, 9356–9365. [Google Scholar] [CrossRef] [PubMed]
- Azhakar, R.; Ghadwal, R.S.; Roesky, H.W.; Hey, J.; Krause, L.; Stalke, D. Mixed valence η 6-arene cobalt (i) and cobalt (ii) compound. Dalton Trans. 2013, 42, 10277–10281. [Google Scholar] [CrossRef]
- Krause, L.; Herbst-Irmer, R.; Stalke, D. An empirical correction for the influence of low-energy contamination. J. Appl. Crystallogr. 2015, 48, 1907–1913. [Google Scholar] [CrossRef]
- Henn, J.; Meindl, K. Two common sources of systematic errors in charge density studies. Int. J. Mater. Chem. Phys. 2015, 1, 417–430. [Google Scholar]
- Kabsch, W. Integration, scaling, space-group assignment and post-refinement. Acta Crystallogr. Sect. D 2010, 66, 133–144. [Google Scholar] [CrossRef]
- Evans, P.R.; Murshudov, G.N. How good are my data and what is the resolution? Acta Crystallogr. Sect. D 2013, 69, 1204–1214. [Google Scholar] [CrossRef]
- Borek, D.; Minor, W.; Otwinowski, Z. Measurement errors and their consequences in protein crystallography. Acta Crystallogr. Sect. D 2003, 59, 2031–2038. [Google Scholar] [CrossRef]


| Data Set | g | a | b | Reference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Equation (5)) | (Equation (6)) | Equation (3) | [mm−1] | |||||||||
| Flawed (Section 5.1): | ||||||||||||
| 2021_088 | 1.4539 | 0.1163 | 0.0150 | 0.0500 | 1497.03 | 308.92 | 1859.74 | 1083.76 | 2.02 | 4.86 | 0.77 | [226] |
| 2020_031 | 6.3721 | 0.9506 | 0.0551 | 0.0000 | 283.91 | 82.66 | 294.14 | 182.52 | 1.66 | 2.09 | 0.08 | [37] |
| 2020_064 | 4.7502 | 0.8280 | 0.1189 | 68.6175 | 968.90 | 742.32 | 1263.96 | 812.27 | 14.92 | 18.88 | 2.89 | [65] |
| 2022_045 | 1.9121 | 0.8852 | 0.0523 | 0.0000 | 2302.77 | 1386.49 | 2450.53 | 2255.98 | 1.28 | 3.15 | 0.82 | [276] |
| Significance cut-off (Section 5.2): | ||||||||||||
| 2020_018 | 11.3657 | 0.9967 | 0.1238 | 3.8143 | 2654.92 | 1065.06 | 2600.10 | 762.14 | −7.01 | −12.28 | 0.08 | [25] |
| 2020_054 | 5.2586 | 0.9794 | 0.0445 | 0.6409 | 313.61 | 185.62 | 303.19 | 297.39 | 3.99 | 1.23 | 0.29 | [58] |
| 2020_073 | 7.9499 | 0.8915 | 0.0577 | 2.4014 | 271.59 | 236.57 | 264.65 | 246.80 | 4.01 | 0.16 | 0.09 | [74] |
| 2020_080 | 3.1707 | 0.5385 | 0.0600 | 0.0000 | 653.51 | 259.82 | 712.50 | 399.29 | 18.36 | 3.29 | 0.09 | [80] |
| 2021_012 | 3.7749 | 0.8062 | 0.0500 | 2.0000 | 1629.58 | 183.40 | 1694.25 | 249.57 | 5.70 | 0.86 | 0.10 | [151] |
| 2021_018 | 2.5073 | 0.0762 | 0.0253 | 3.3741 | 894.57 | 748.71 | 685.71 | 268.24 | 2.45 | −13.25 | 1.63 | [157] |
| 2021_044 | 8.3321 | 0.9321 | 0.0494 | 24.3530 | 1744.65 | 1047.59 | 1778.95 | 730.88 | 4.74 | 4.15 | 4.12 | [183] |
| 2022_010 | 12.4101 | 0.9831 | 0.0953 | 14.3038 | 1812.42 | 735.26 | 1998.22 | 571.72 | 1.69 | −2.29 | 0.07 | [242] |
| Intensity cut-off (Section 5.3): | ||||||||||||
| 2020_029 | 7.7116 | 0.9861 | 0.1087 | 0.0972 | 305.27 | 171.15 | 390.66 | 155.30 | 2.54 | 1.14 | 0.08 | [35] |
| 2020_046 | 2.8304 | 0.8679 | 0.0517 | 6.1123 | 529.00 | 110.50 | 602.61 | 321.59 | 8.35 | 9.14 | 0.15 | [51] |
| 2020_074 | 5.5571 | 0.9617 | 0.1532 | 0.0304 | 866.30 | 455.34 | 2109.38 | 214.12 | 2.42 | 2.97 | 0.27 | [75] |
| 2020_092 | 1.6338 | 0.0171 | 0.0506 | 0.0000 | 1236.17 | 312.76 | 1689.98 | 617.73 | 6.65 | 19.82 | 0.09 | [91] |
| 2022_046 | 3.9830 | 0.8582 | 0.0359 | 173.2937 | 2016.80 | 1635.85 | 1811.10 | 283.84 | 0.33 | −16.22 | 2.72 | [277] |
| 2022_054 | 2.3415 | 0.7791 | 0.0622 | 0.1317 | 358.89 | 457.24 | 321.17 | 166.91 | 0.67 | −1.88 | 1.51 | [284] |
| Weak too strong (Section 5.5): | ||||||||||||
| 2022_016 | 5.6240 | 0.8892 | 0.0479 | 1.2289 | 1406.00 | 1187.24 | 1480.05 | 390.85 | 4.40 | 16.01 | 2.38 | [248] |
| 2020_011 | 3.0415 | 0.7686 | 0.0178 | 1.2762 | 1080.84 | 1012.90 | 1126.10 | 1039.08 | 1.25 | 11.46 | 17.34 | [19] |
| 2020_039 | 3.3080 | 0.7887 | 0.0717 | 0.7287 | 246.52 | 180.38 | 379.19 | 163.09 | 2.21 | 5.33 | 11.87 | [45] |
| 2020_119 | 5.2589 | 0.9600 | 0.0600 | 2.9000 | 1060.86 | 637.64 | 1263.86 | 374.88 | 3.19 | 9.85 | 1.15 | [118] |
| 2020_122 | 1.8527 | 0.5512 | 0.0240 | 0.0000 | 998.50 | 1385.48 | 1332.03 | 377.17 | 1.72 | 16.28 | 14.45 | [121] |
| 2021_061 | 5.0337 | 0.6790 | 0.0050 | 1.1433 | 532.78 | 523.53 | 556.01 | 235.15 | 1.87 | 6.89 | 6.08 | [200] |
| 2021_081 | 4.2205 | 0.9551 | 0.0529 | 0.6752 | 1369.33 | 992.03 | 1323.52 | 226.74 | 2.32 | 4.20 | 1.59 | [219] |
| 2022_052 | 3.3012 | 0.8497 | 0.0431 | 226.7933 | 2915.09 | 397.42 | 2973.92 | 423.35 | 11.15 | 41.42 | 23.54 | [283] |
| 2022_083 | 7.3501 | 0.9543 | 0.0100 | 25.0000 | 999.02 | 658.24 | 1248.98 | 171.44 | 3.61 | 14.64 | 4.46 | [312] |
| Weak systematically weaker than weak (Section 5.6): | ||||||||||||
| 2020_003 | 4.8220 | 0.9015 | 0.0525 | 2.9966 | 1247.86 | 1007.46 | 1073.29 | 423.93 | −2.93 | −15.78 | 0.29 | [11] |
| 2020_008 | 3.5354 | 0.5087 | 0.0461 | 1.5828 | 783.62 | 728.95 | 701.61 | 175.21 | −0.12 | −10.91 | 0.19 | [16] |
| 2020_018 | 11.3657 | 0.9967 | 0.1238 | 3.8143 | 2654.92 | 1065.06 | 2600.10 | 762.14 | −7.01 | −12.28 | 0.08 | [25] |
| 2020_024 | 1.1999 | 0.3543 | 0.0349 | 0.0000 | 494.50 | 273.13 | 494.40 | 258.45 | −0.87 | −12.25 | 2.16 | [30] |
| 2021_009 | 2.4729 | 0.7696 | 0.0375 | 5.4623 | 1060.86 | 988.79 | 943.32 | 191.58 | −3.00 | −14.69 | 1.60 | [148] |
| 2021_018 | 2.5073 | 0.0762 | 0.0253 | 3.3741 | 894.57 | 748.71 | 685.71 | 268.24 | 2.45 | −13.25 | 1.63 | [157] |
| 2021_054 | 2.8780 | 0.8050 | 0.0239 | 0.6589 | 989.51 | 887.61 | 987.29 | 618.01 | −1.04 | −13.13 | 1.89 | [193] |
| 2021_058 | 5.0823 | 0.9649 | 0.0804 | 1.0693 | 1223.38 | 1231.21 | 871.45 | 254.50 | −0.19 | −10.54 | 0.66 | [197] |
| 2021_085 | 6.1444 | 0.9114 | 0.0578 | 3.7997 | 566.19 | 643.44 | 493.76 | 339.27 | −1.00 | −11.11 | 0.24 | [223] |
| 2022_012 | 3.6222 | 0.9330 | 0.0524 | 1.0724 | 1273.89 | 1358.52 | 1028.27 | 290.15 | −0.50 | −16.81 | 1.37 | [244] |
| 2022_046 | 3.9830 | 0.8582 | 0.0359 | 173.2937 | 2016.80 | 1635.85 | 1811.10 | 283.84 | 0.33 | −16.22 | 2.72 | [277] |
| 2022_050 | 2.6287 | 0.7725 | 0.0234 | 23.3944 | 1188.70 | 1210.66 | 891.84 | 357.53 | 0.70 | −15.28 | 3.98 | [281] |
| 2022_058 | 2.5887 | 0.5885 | 0.0194 | 21.8494 | 1611.50 | 1576.42 | 1641.98 | 1109.17 | 0.56 | −13.89 | 9.27 | [288] |
| Uniform BayCoN plots (Section 5.7): | ||||||||||||
| 2021_042 | 3.2288 | 0.8791 | 0.0512 | 0.4385 | 93.14 | 99.99 | 132.37 | 124.08 | 1.19 | 2.29 | 1.20 | [181] |
| 2020_012 | 1.9280 | 0.3890 | 0.0065 | 0.5686 | 144.90 | 109.33 | 142.21 | 127.26 | 1.37 | −1.96 | 16.75 | [20] |
| 2020_081 | 1.4835 | 0.3693 | 0.0154 | 0.3678 | 110.07 | 73.43 | 109.68 | 98.50 | 1.14 | −0.84 | 10.45 | [81] |
| 2020_117 | 4.7997 | 0.8482 | 0.0443 | 0.2172 | 99.32 | 77.02 | 109.98 | 133.08 | 1.58 | 1.16 | 0.12 | [116] |
| 2020_128 | 1.6161 | 0.4453 | 0.0260 | 0.8115 | 83.63 | 76.72 | 103.75 | 125.90 | 1.32 | 0.94 | 0.55 | [127] |
| 2021_076 | 3.9178 | 0.2439 | 0.0411 | 0.0767 | 97.07 | 85.33 | 98.50 | 105.97 | 1.24 | −0.52 | 0.49 | [214] |
| 2022_024 | 2.8324 | 0.8038 | 0.0321 | 0.6811 | 119.96 | 130.82 | 143.32 | 128.18 | 0.60 | −1.79 | 1.06 | [255] |
| 2022_043 | 1.3355 | 0.5733 | 0.0409 | 0.0000 | 111.41 | 140.57 | 146.17 | 115.38 | 0.79 | −1.93 | 9.62 | [274] |
| 2022_055 | 2.0678 | 0.7640 | 0.0317 | 0.0410 | 124.84 | 124.23 | 111.70 | 108.80 | 0.88 | −0.62 | 0.21 | [285] |
| Data Set | g | a | b | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Equation (5) | Equation (6) | Equation (3) | ||||||||
| Crystal 1 | Scandium platinate [341] | 3.1987 | 0.6444 | 0.0265 | 6.5030 | 1514.93 | 1407.27 | 1686.90 | 386.57 | 17.75 |
| Crystal 3 | Sodium tungstate [342] | 2.0825 | 0.4185 | 0.0103 | 1.1388 | 1745.17 | 1653.66 | 1775.41 | 769.16 | 25.13 |
| Crystal 4 | Scandium cobalt carbide [343] | 5.0227 | 0.8754 | 0.0174 | 0.0528 | 236.06 | 212.19 | 252.53 | 292.02 | 4.31 |
| Crystal 5 | Dibromoacridine derivative— | 4.6856 | 0.9371 | 0.0260 | 1.6275 | 168.63 | 149.10 | 177.20 | 292.21 | 4.78 |
| Crystal 6 | Inorganic cobalt complex [344] | 4.0642 | 0.9104 | 0.0270 | 2.4392 | 148.27 | 153.40 | 153.68 | 749.06 | 1.43 |
| Radiation | Elements | Habitus | Monochromator | T | Diffractometer | Reference | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [K] | [mm] | [mm−1] | [mm−1] | ||||||||||
| 2020_003 | — | Mo K | S, O, N, C, H | block | ? | 293 | 0.56 | 0.16 | 4.85 | 0.29 | 1.39 | Bruker D8 | [11] |
| 2020_008 | — | Mo K | Cl, O, N, C, H | block | ? | 297 | 0.45 | 0.08 | 1.29 | 0.19 | 0.24 | Bruker Smart Apex | [16] |
| 2020_018 | — | Mo K | O, C, H | block | Graphite | 296 | 0.20 | 0.02 | 1.33 | 0.08 | 0.11 | Bruker Kappa Apex | [25] |
| 2020_024 | — | Mo K | Br, S, O, N, C, H | block | Graphite | 293 | 0.30 | 0.65 | 1.50 | 2.16 | 3.25 | Bruker Kappa Apex | [30] |
| 2021_009 | — | Mo K | Ba, Co, S, O, N, C, H | block | ? | 296 | 0.20 | 0.32 | 1.33 | 1.60 | 2.13 | Bruker Apex | [148] |
| 2021_018 | — | Mo K | Cd, Cl, N, O, C, H | block | ? | 296 | 0.16 | 0.27 | 1.66 | 1.63 | 2.70 | Rig. Ox. Diff. SuperNova | [157] |
| 2021_054 | — | Mo K | Cd, Ni, N, C, H | block | Graphite | 123 | 0.15 | 0.29 | 2.34 | 1.89 | 4.41 | Rig. Ox. Diff. Excal. | [193] |
| 2021_058 | — | Mo K | Ni, O, N, C, B, H | block | Graphite | 150 | 0.59 | 0.39 | 1.85 | 0.66 | 1.22 | Bruker Apex | [197] |
| 2021_085 | — | Mo K | Cl, O, C, N, H | block | ? | 293 | 0.22 | 0.05 | 1.38 | 0.24 | 0.32 | Bruker Smart Apex | [223] |
| 2022_012 | — | Mo K | Ni, Cl, S, C, H | column | Graphite | 170 | 0.27 | 0.37 | 2.85 | 1.37 | 3.92 | Bruker D8 | [244] |
| 2022_046 | mf | Mo K | Nb, Cl, I, O, C, H | block | ? | 123 | 0.23 | 0.63 | 1.64 | 2.72 | 4.47 | Bruker Apex | [277] |
| 2022_050 | — | Mo K | Ir, Cl, P, F, C, N, H | plate | ? | 100 | 0.27 | 1.07 | 3.86 | 3.98 | 15.35 | Bruker Apex | [281] |
| 2022_058 | ms | Cu K | Ir, P, F, O, N, C, H | column | ? | 100 | 0.21 | 1.86 | 3.24 | 9.27 | 30.06 | Bruker D8 | [288] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henn, J. BayCoN Plots and Systematic Errors in Single-Crystal Diffraction Experiments. Crystals 2025, 15, 1014. https://doi.org/10.3390/cryst15121014
Henn J. BayCoN Plots and Systematic Errors in Single-Crystal Diffraction Experiments. Crystals. 2025; 15(12):1014. https://doi.org/10.3390/cryst15121014
Chicago/Turabian StyleHenn, Julian. 2025. "BayCoN Plots and Systematic Errors in Single-Crystal Diffraction Experiments" Crystals 15, no. 12: 1014. https://doi.org/10.3390/cryst15121014
APA StyleHenn, J. (2025). BayCoN Plots and Systematic Errors in Single-Crystal Diffraction Experiments. Crystals, 15(12), 1014. https://doi.org/10.3390/cryst15121014






