Particle Size-Dependent Mechanical Behaviors of Disordered Copper Nanoparticle Assemblies: A Molecular Dynamics Study
Abstract
1. Introduction
2. Material and Methodology
2.1. Granular Simulation for Constructing Disordered Assembly
2.2. Atomic Simulation for Uniaxial Compression
3. Results and Discussion
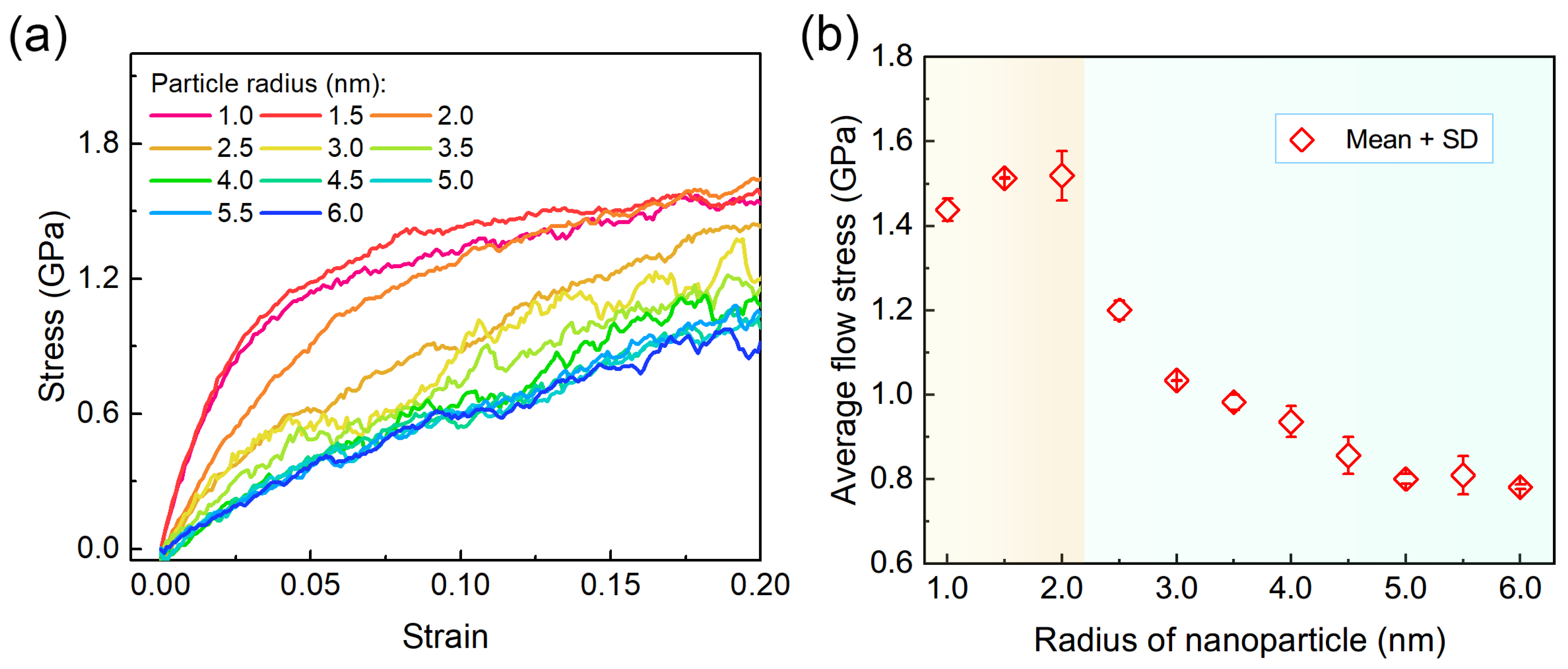
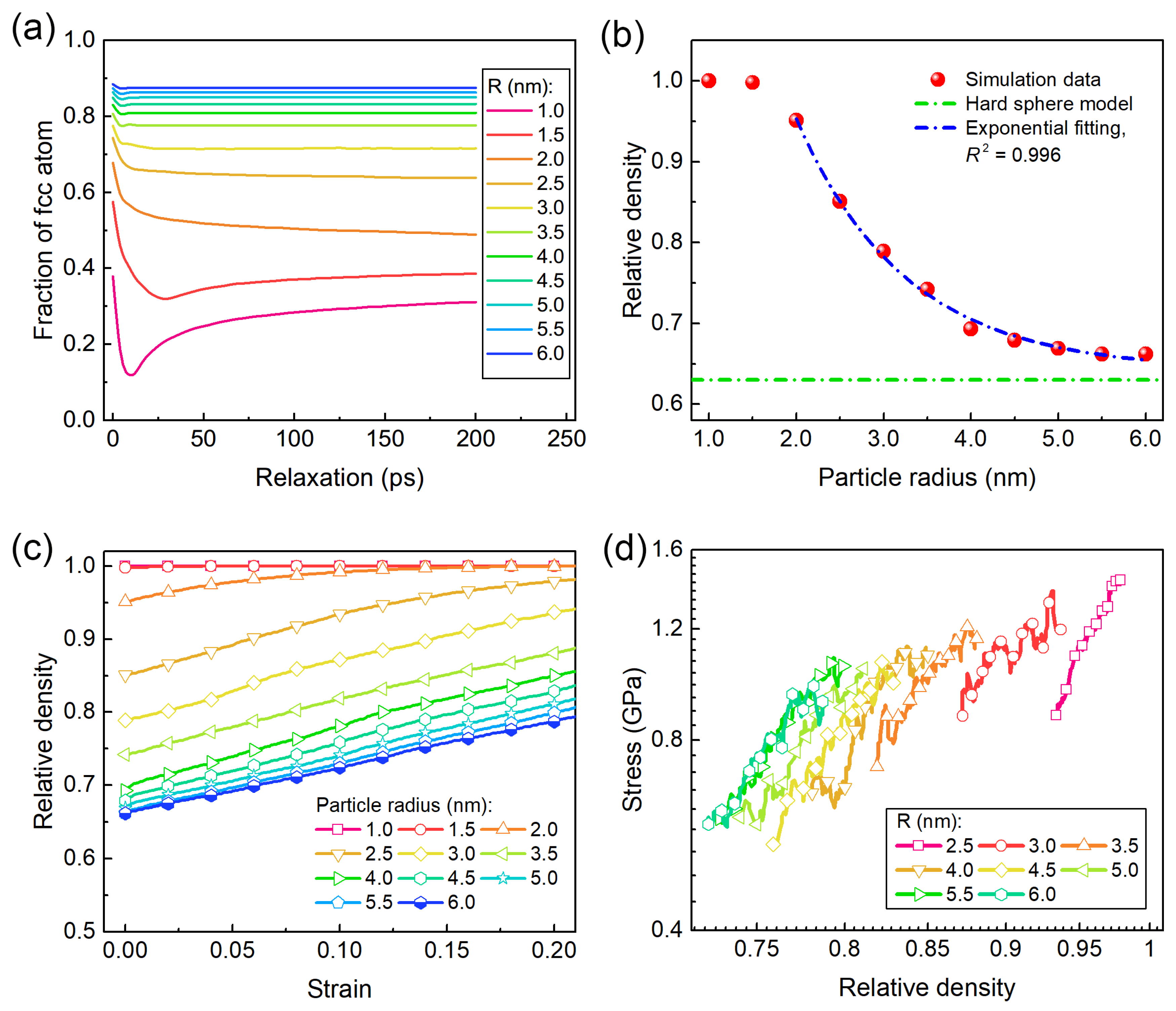
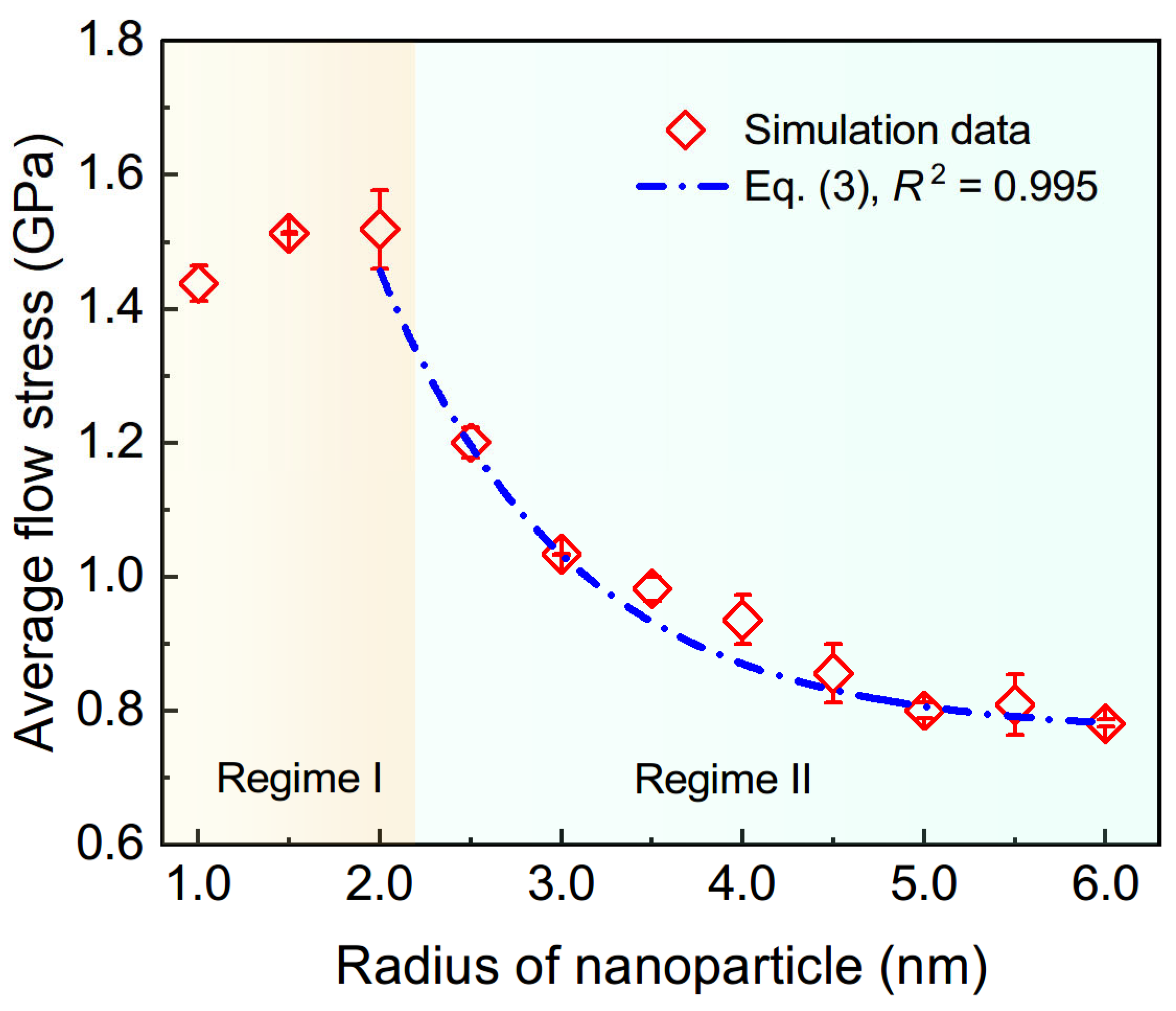
3.1. Overall Loading Responses and Particle Size-Dependent Strength
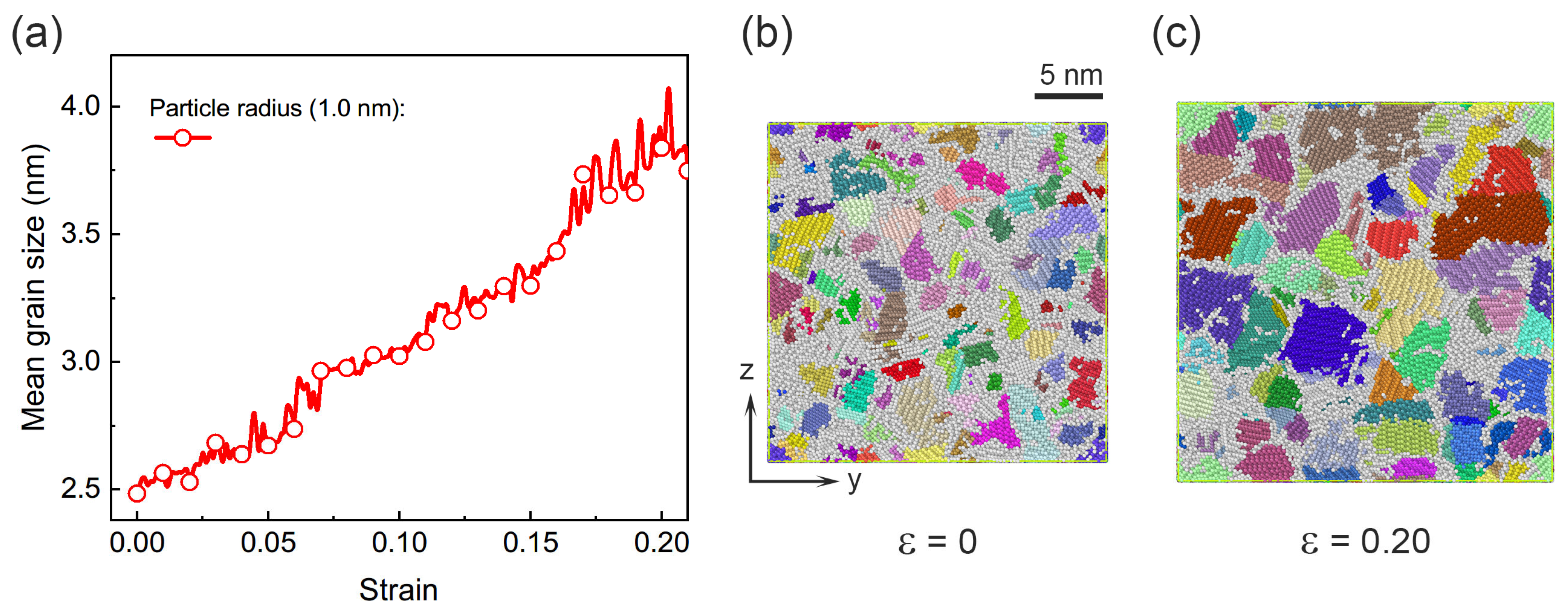
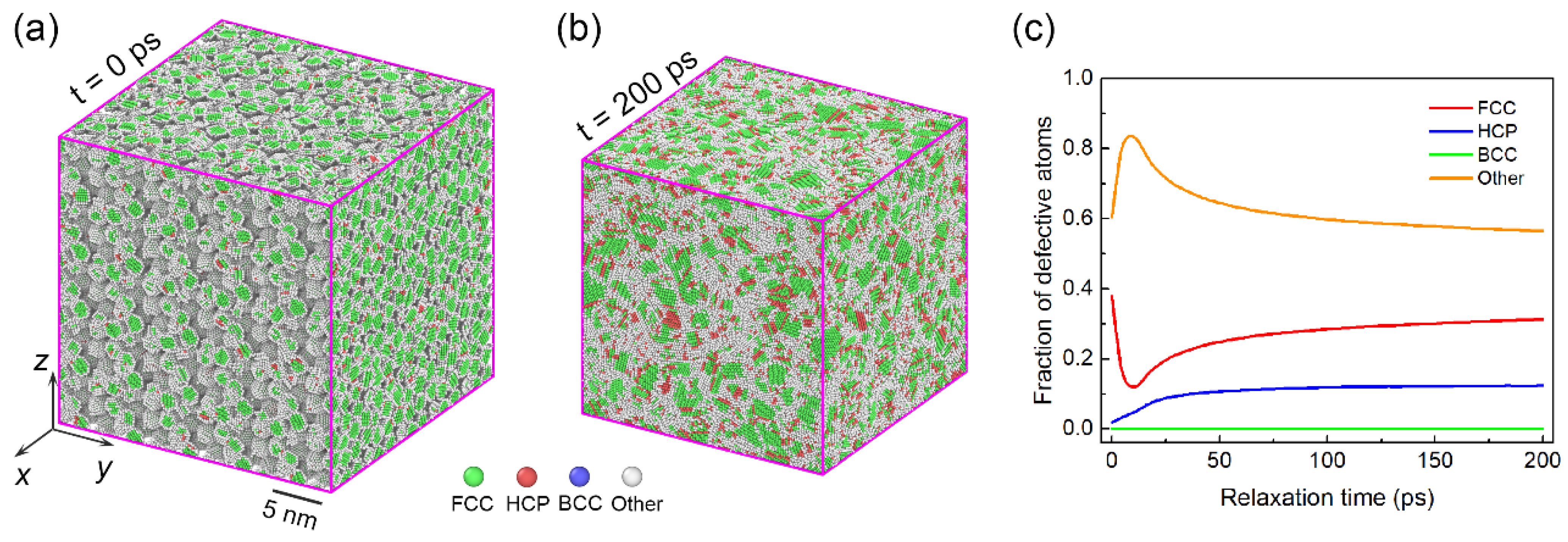
3.2. Deformation Mechanisms in Assemblies with Smaller Particle Size
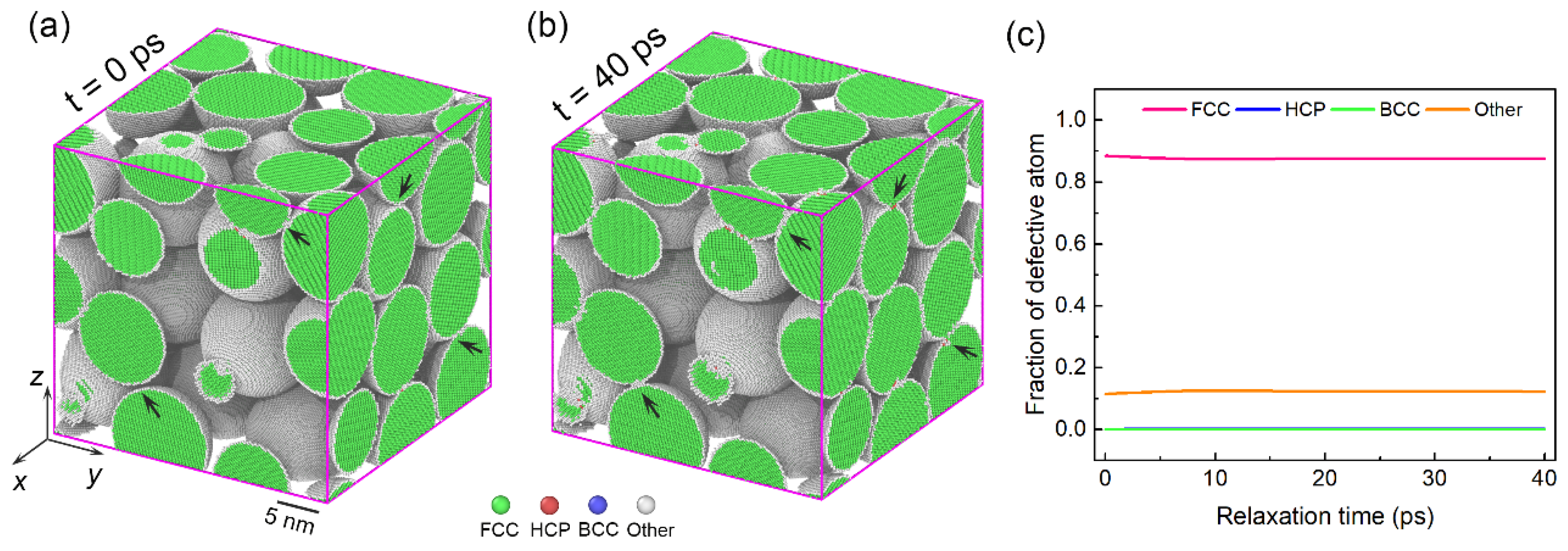
3.3. Deformation Mechanisms in Assemblies with Larger Particle Size
3.4. Scaling Laws of Particle Size-Dependent Mechanical Responses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Santos, P.J.; Gabrys, P.A.; Zornberg, L.Z.; Lee, M.S.; Macfarlane, R.J. Macroscopic materials assembled from nanoparticle superlattices. Nature 2021, 591, 586–591. [Google Scholar] [CrossRef]
- Zabet-Khosousi, A.; Dhirani, A. Charge transport in nanoparticle assemblies. Chem. Rev. 2008, 108, 4072–4124. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Kanjanaboos, P.; McBride, S.P.; Barry, E.; Lin, X.M.; Jaeger, H.M. Mechanical properties of self-assembled nanoparticle membranes: Stretching and bending. Faraday Discuss. 2015, 181, 325–338. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Yan, Y.; Chen, X.; Wang, T. Combining printing and nanoparticle assembly: Methodology and application of nanoparticle patterning. Innovation 2022, 3, 100253. [Google Scholar] [CrossRef]
- He, H.; Yang, T.; Liu, T.; Gao, Y.; Zhang, Z.; Yang, Z.; Liang, F. Soft-hard Janus nanoparticles triggered hierarchical conductors with large stretchability, high sensitivity, and superior mechanical properties. Adv. Mater. 2024, 36, 2312278. [Google Scholar]
- Du, L.; Liu, K.; Hu, D.; Backe, O.; Hu, X.; Ji, X.; Fan, J.; Poelma, R.H.; Colliander, M.H.; Zhang, G. Microstructural and mechanical anisotropy in pressure-assisted sintered copper nanoparticles. Acta Mater. 2025, 287, 120772. [Google Scholar] [CrossRef]
- Yan, X.; Du, L.; Gu, C.; Tian, T.; Gao, C.; Zhang, G.; Fan, J. Microscale mechanical properties in sintered copper nanoparticles. Mater. Sci. Eng. A 2025, 943, 148684. [Google Scholar] [CrossRef]
- Dong, T.; Wu, H.H.; Lin, M.C. Superlattice of octanethiol-protected copper nanoparticles. Langmuir 2006, 22, 6754–6756. [Google Scholar] [CrossRef]
- Zurcher, J.; Yu, K.; Schlottig, G.; Baum, M.; Taklo, M.M.V.; Wunderle, B.; Warszynski, P.; Brunschwilder, T. Nanoparticle assembly and sintering towards all-copper flip chip interconnects. In Proceedings of the 2015 IEEE 65th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 26–29 May 2015; IEEE: New York, NY, USA, 2015; pp. 1330–1337. [Google Scholar]
- Liu, L.; Choi, B.G.; Tung, S.O.; Hu, T.; Liu, Y.; Li, T.; Zhao, T.; Kotov, N.A. Low-current field-assisted assembly of copper nanoparticles for current collectors. Faraday Discuss. 2015, 181, 383–401. [Google Scholar]
- Lequieu, J.; Cordoba, A.; Hinckley, D.; de Pablo, J.J. Mechanical response of DNA-nanoparticle crystals to controlled deformation. ACS Cent. Sci. 2016, 2, 614–620. [Google Scholar]
- Srivastava, I.; Peters, B.L.; Lane, J.M.D.; Fan, H.; Grest, G.S.; Salerno, M.K. Mechanics of gold nanoparticle superlattices at high hydrostatic pressures. J. Phys. Chem. C 2019, 123, 16457–16466. [Google Scholar] [CrossRef]
- An, L.; Zhang, D.; Zhang, L.; Feng, G. Effect of nanoparticle size on the mechanical properties of nanoparticle assemblies. Nanoscale 2019, 11, 9563–9573. [Google Scholar] [CrossRef] [PubMed]
- Erbi, M.; Amara, H.; Gatti, R. Tuning elastic properties of metallic nanoparticles by shape controlling: From atomistic to continuous models. Small 2023, 19, 2302116. [Google Scholar] [CrossRef] [PubMed]
- Pizzagalli, L.; Godet, J.; Durinck, J.; Brochard, S.; Furstoss, J.; Valencia, F. Twinning and amorphization as plasticity mechanisms in ultra small tungsten nanoparticles. Comp. Mater. Sci. 2025, 258, 114077. [Google Scholar] [CrossRef]
- Yang, L.; Bian, J.J.; Wang, G.F. Impact of atomic-scale surface morphology on the size-dependency yield stress of gold nanoparticles. J. Phys. D: Appl. Phys. 2017, 50, 245302. [Google Scholar]
- Yan, J.; Yin, S.; Asta, M.; Ritchie, R.O.; Ding, J.; Yu, Q. Anomalous size effect on yield strength enabled by compositional heterogeneity in high-entropy alloy nanoparticles. Nat. Commun. 2022, 13, 2789. [Google Scholar] [CrossRef]
- Han, W.Z.; Huang, L.; Ogata, S.; Kimizuka, H.; Yang, Z.C.; Weinberger, C.; Li, Q.J.; Liu, B.Y.; Zhang, X.X.; Li, J.; et al. From ‘smaller is stronger’ to ‘size-independent strength plateau’: Towards measuring the ideal strength of iron. Adv. Mater. 2015, 27, 3385–3390. [Google Scholar]
- Greer, J.R.; Oliver, W.C.; Nix, W.D. Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients. Acta Mater. 2005, 53, 1821–1830. [Google Scholar] [CrossRef]
- Greer, J.R.; Nix, W.D. Size dependence of mechanical properties of gold at the submicron scale. Appl. Phys. A Mater. Sci. Process. 2005, 80, 1625–1629. [Google Scholar]
- Zhang, Z.; Hossain, Z.M. Geometric confinement governs toughness and strength in defective diamond nanowires. Phys. Rev. B 2020, 101, 014111. [Google Scholar] [CrossRef]
- Mao, R.; Pretti, E.; Mittal, J. Temperature-controlled reconfigurable nanoparticle binary superlattices. ACS Nano 2021, 15, 8466–8473. [Google Scholar] [CrossRef] [PubMed]
- Missoni, L.L.; Tagliazucchi, M. The phase behavior of nanoparticle superlattices in the presence of a solvent. ACS Nano 2020, 14, 5649–5658. [Google Scholar] [CrossRef] [PubMed]
- Shaik, A.H.; Chakraborty, J. Synthesis of monodisperse copper nanoparticles using a modified digestive ripening technique and formation of superlattices. RSC Adv. 2015, 5, 85974–85977. [Google Scholar] [CrossRef]
- Ouyang, T.; Akbari-Sharbaf, A.; Park, J.; Bauld, R.; Cottam, M.G.; Fanchini, G. Self-assembled metallic nanoparticle superlattices on large-area graphene thin films: Growth and evanescent waveguiding properties. RSC Adv. 2015, 5, 98814–98821. [Google Scholar] [CrossRef]
- Lu, L.; Shen, Y.; Chen, X.; Qian, L.; Lu, K. Ultrahigh strength and high electrical conductivity in copper. Science 2004, 304, 422–426. [Google Scholar] [CrossRef]
- Lu, L.; Chen, X.; Huang, X.; Lu, K. Revealing the maximum strength in nanotwinned copper. Science 2009, 323, 607. [Google Scholar] [CrossRef]
- Lu, C.; Pan, Y.; Fang, H.; Wu, B.; Wu, Y.; Chen, J.; He, Q.; Liu, Z. Weak size-dependent strength and extreme plastic deformation of single crystal Cu microparticles. J. Phys. Chem. C 2024, 128, 11419–11426. [Google Scholar] [CrossRef]
- Bian, J.J.; Wang, G.F. Atomistic deformation mechanisms in copper nanoparticles. J. Comput. Theor. Nanosci. 2013, 10, 2299–2303. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Plimpton, S.J. Aspherical particle models for molecular dynamics simulation. Comp. Phys. Commun. 2019, 243, 12–24. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique force. ASME J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Nosé, S.A. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
- Zhang, X.; Han, J.; Plombon, J.J.; Sutton, A.P.; Srolovitz, D.J.; Boland, J.J. Nanocrystalline copper films are never flat. Science 2017, 357, 398–400. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Hickman, J.; Gazit, N.; Rabkin, E.; Mishin, Y. Nickel nanoparticles set a new record of strength. Nat. Commun. 2018, 9, 4102. [Google Scholar] [CrossRef]
- Morante, S.; Rossi, G.C.; Testa, M. The stress tensor of a molecular system: An exercise in statistical mechanics. J. Chem. Phys. 2006, 125, 034101. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification method for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comp. Phys. Commun. 2007, 177, 518–523. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with Ovito-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192. [Google Scholar] [CrossRef]
- Schiotz, J.; Jacobsen, K.W. A maximum in the strength of nanocrystalline copper. Science 2002, 301, 1357–1359. [Google Scholar]
- Schiotz, J.; Di Tolla, F.D.; Jacobsen, K.W. Softening of nanocrystalline metals at very small grain sizes. Nature 1998, 391, 561–563. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Sun, X.; Xu, G.; Li, X.; Feng, X.; Gao, H. Mechanical properties and scaling laws of nanoporous gold. J. Appl. Phys. 2013, 113, 023505. [Google Scholar] [CrossRef]
- Bian, J.; Wang, G.; Feng, X. Atomistic calculation of surface energy of spherical copper surfaces. Acta Mech. Solida. Sin. 2012, 25, 557–561. [Google Scholar] [CrossRef]
- Wang, J.; Chen, S.; Cui, K.; Li, D.; Chen, D. Approach and coalescence of gold nanoparticles driven by surface thermodynamic fluctuations and atomic interaction forces. ACS Nano 2016, 10, 2893–2902. [Google Scholar] [CrossRef]
- Singh-Miller, N.E.; Marzari, N. Surface energies, work functions, and surface relaxations of low-index metallic surfaces from first principles. Phys. Rev. B 2009, 89, 235407. [Google Scholar] [CrossRef]
- Schweizer, P.; Sharma, A.; Petho, L.; Huszar, E.; Vogl, L.M.; Michler, J.; Maeder, X. Atomic scale volume and grain boundary diffusion elucidated by in situ STEM. Nat. Commun. 2023, 14, 7601. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiotz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, J.; Yang, L. Particle Size-Dependent Mechanical Behaviors of Disordered Copper Nanoparticle Assemblies: A Molecular Dynamics Study. Crystals 2025, 15, 1007. https://doi.org/10.3390/cryst15121007
Bian J, Yang L. Particle Size-Dependent Mechanical Behaviors of Disordered Copper Nanoparticle Assemblies: A Molecular Dynamics Study. Crystals. 2025; 15(12):1007. https://doi.org/10.3390/cryst15121007
Chicago/Turabian StyleBian, Jianjun, and Liang Yang. 2025. "Particle Size-Dependent Mechanical Behaviors of Disordered Copper Nanoparticle Assemblies: A Molecular Dynamics Study" Crystals 15, no. 12: 1007. https://doi.org/10.3390/cryst15121007
APA StyleBian, J., & Yang, L. (2025). Particle Size-Dependent Mechanical Behaviors of Disordered Copper Nanoparticle Assemblies: A Molecular Dynamics Study. Crystals, 15(12), 1007. https://doi.org/10.3390/cryst15121007




