A Comprehensive Review of Machine-Learning Approaches for Crystal Structure/Property Prediction
Abstract
1. Introduction
1.1. Importance of Crystal Structure/Property Prediction in Material Science
1.2. Traditional CSP/CPP Analyses and Their Limitations
1.3. ML in CSP/CPP Analyses
2. ML Algorithms for CSP/CPP Analyses
2.1. Supervised Learning
2.1.1. Linear Regression
2.1.2. k-Nearest Neighbor (k-NN) Algorithm and Naive Bayes (NB)
2.1.3. Support Vector Machine (SVM)
2.1.4. Decision Trees and Ensemble Methods
2.1.5. Artificial Neural Networks (ANNs)
2.2. Unsupervised Learning
2.2.1. Dimensionality Reduction: Principal Component Analysis (PCA) and Nonnegative Matrix Factorization (NMF)
2.2.2. Principal Component Regression (PCR)
3. ML Approaches for CSP/CPP Analyses
3.1. Background and Recent Trends in ML for CSP/CPP Analyses
3.2. Review of ML-Based Methods for CSP/CPP
3.3. Improving the Accuracy of ML Potentials for CSP and CPP
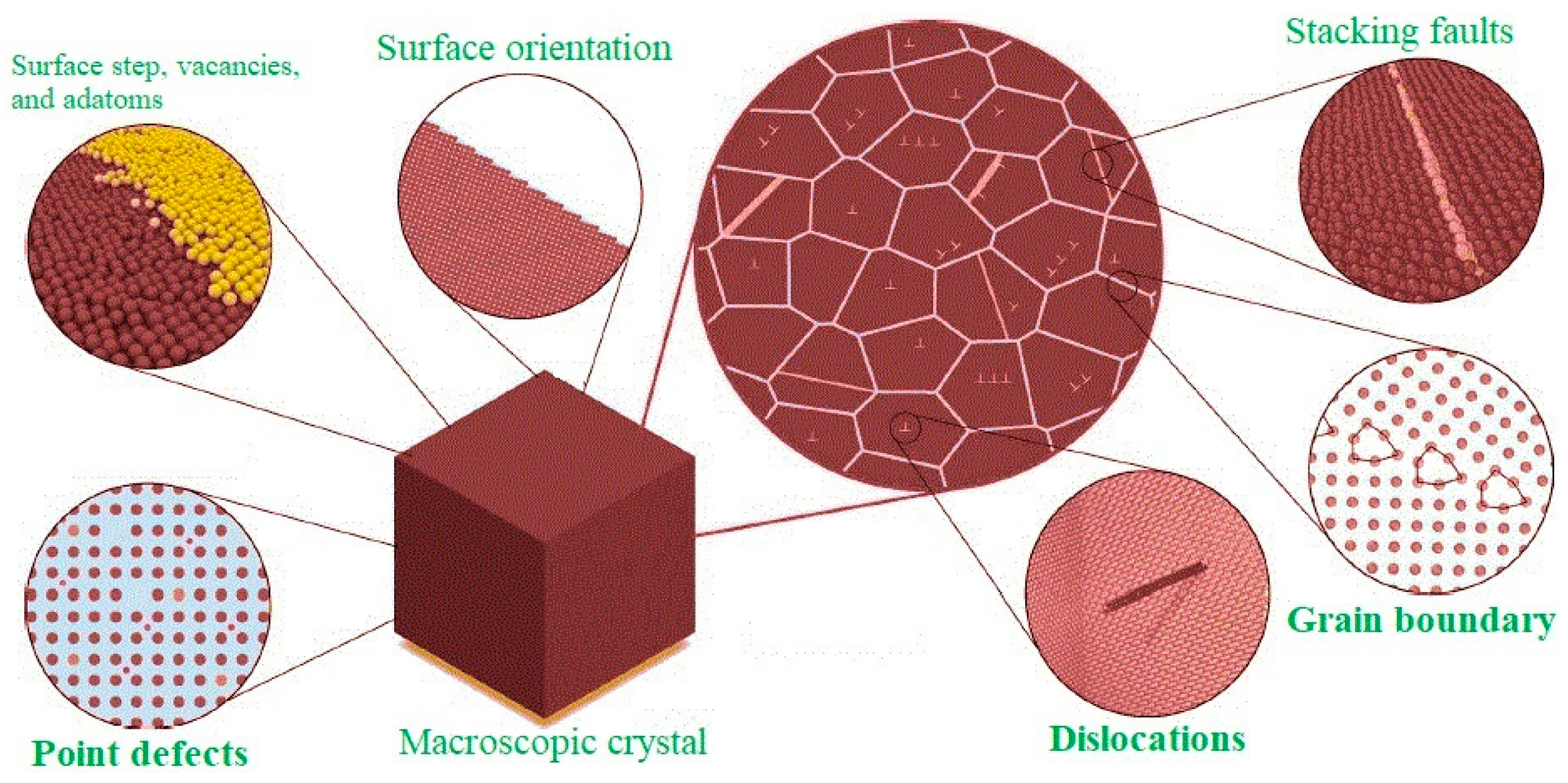
4. ML Approaches for Identification and Modeling of Crystal Defects
4.1. Fundamentals and Development of ML-Based Interatomic Potentials for Crystal Defect Analyses
4.2. Advanced Applications and Case Studies in ML-Based Crystal Defects Analyses
4.3. Improving the Accuracy of ML Potentials for Crystal Defects
5. Possible Future Research Opportunities
5.1. Future Directions in CSP Analysis with ML
5.2. Future Directions in CPP Analysis with ML
5.3. Future Directions in Crystal Defect Modeling and Analysis with ML
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, M.; Rao, S.; Yue, H.; Han, J.; Wang, J. Recent Advances in the Application of Machine Learning to Crystal Behavior and Crystallization Process Control. Cryst. Growth Des. 2024, 24, 5374–5396. [Google Scholar] [CrossRef]
- Oganov, A.R.; Pickard, C.J.; Zhu, Q.; Needs, R.J. Structure prediction drives materials discovery. Nat. Rev. Mater. 2019, 4, 331–348. [Google Scholar] [CrossRef]
- Oganov, A.R.; Lyakhov, A.O.; Valle, M. How Evolutionary Crystal Structure Prediction Works—And Why. Acc. Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef]
- Needs, R.J.; Pickard, C.J. Perspective: Role of structure prediction in materials discovery and design. APL Mater. 2016, 4, 053210. [Google Scholar] [CrossRef]
- Rosen, A.S.; Fung, V.; Huck, P.; O’Donnell, C.T.; Horton, M.K.; Truhlar, D.G.; Persson, K.A.; Notestein, J.M.; Snurr, R.Q. High-throughput predictions of metal–organic framework electronic properties: Theoretical challenges, graph neural networks, and data exploration. Npj Comput. Mater. 2022, 8, 112. [Google Scholar] [CrossRef]
- Kruglov, I.A.; Yanilkin, A.V.; Propad, Y.; Mazitov, A.B.; Rachitskii, P.; Oganov, A.R. Crystal structure prediction at finite temperatures. Npj Comput. Mater. 2023, 9, 197. [Google Scholar] [CrossRef]
- Wu, X.; Kang, F.; Duan, W.; Li, J. Density functional theory calculations: A powerful tool to simulate and design high-performance energy storage and conversion materials. Prog. Nat. Sci. Mater. Int. 2019, 29, 247–255. [Google Scholar] [CrossRef]
- Chen, C.; Ye, W.; Zuo, Y.; Zheng, C.; Ong, S.P. Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals. Chem. Mater. 2019, 31, 3564–3572. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Xu, P.; Wang, H.; Ren, L.; Tu, B.; Wang, W.; Fu, Z. Theoretical study on composition-dependent properties of ZnO·nAl2O3 spinels. Part I: Optical and dielectric. J. Am. Ceram. Soc. 2021, 104, 5099–5109. [Google Scholar] [CrossRef]
- Nyangiwe, N.N. Applications of density functional theory and machine learning in nanomaterials: A review. Next Mater. 2025, 8, 100683. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, X.; Zhang, X.; Huang, P.; Novoselov, K.S.; Shen, L. Modeling crystal defects using defect informed neural networks. Npj Comput. Mater. 2025, 11, 229. [Google Scholar] [CrossRef]
- Domingos, R.; Shaik, K.M.; Militzer, B. Prediction of novel high-pressure H2O-NaCl and carbon oxide compounds with a symmetry-driven structure search algorithm. Phys. Rev. B 2018, 98, 174107. [Google Scholar] [CrossRef]
- Lu, Z.; Zhu, B.; Shires, B.W.B.; Scanlon, D.O.; Pickard, C.J. Ab initio random structure searching for battery cathode materials. J. Chem. Phys. 2021, 154, 174111. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.H.; Ferreira, L.G.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Structure of phase III of solid hydrogen. Nat. Phys. 2007, 3, 473–476. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. High-Pressure Phases of Nitrogen. Phys. Rev. Lett. 2009, 102, 125702. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Dense Low-Coordination Phases of Lithium. Phys. Rev. Lett. 2009, 102, 146401. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Hickel, T.; Rogal, J.; Li, Y.; Neugebauer, J. Mechanism of collective interstitial ordering in Fe–C alloys. Nat. Mater. 2020, 19, 849–854. [Google Scholar] [CrossRef] [PubMed]
- Falls, Z.; Avery, P.; Wang, X.; Hilleke, K.P.; Zurek, E. The XtalOpt Evolutionary Algorithm for Crystal Structure Prediction. J. Phys. Chem. C 2021, 125, 1601–1620. [Google Scholar] [CrossRef]
- Cheng, G.; Gong, X.-G.; Yin, W.-J. Crystal structure prediction by combining graph network and optimization algorithm. Nat. Commun. 2022, 13, 1492. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Lv, J.; Xu, M.; Lin, S.; Shao, X.; Zhang, X.; Liu, Y.; Wang, Y.; Chen, Z.; Ma, Y. Direct-gap semiconducting tri-layer silicene with 29% photovoltaic efficiency. Nano Energy 2018, 51, 489–495. [Google Scholar] [CrossRef]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
- Wang, J.; Hanzawa, K.; Hiramatsu, H.; Kim, J.; Umezawa, N.; Iwanaka, K.; Tada, T.; Hosono, H. Exploration of Stable Strontium Phosphide-Based Electrides: Theoretical Structure Prediction and Experimental Validation. J. Am. Chem. Soc. 2017, 139, 15668–15680. [Google Scholar] [CrossRef]
- Kaappa, S.; del Río, E.G.; Jacobsen, K.W. Global optimization of atomic structures with gradient-enhanced Gaussian process regression. Phys. Rev. B 2021, 103, 174114. [Google Scholar] [CrossRef]
- Kaappa, S.; Larsen, C.; Jacobsen, K.W. Atomic Structure Optimization with Machine-Learning Enabled Interpolation between Chemical Elements. Phys. Rev. Lett. 2021, 127, 166001. [Google Scholar] [CrossRef]
- Bisbo, M.K.; Hammer, B. Global optimization of atomic structure enhanced by machine learning. Phys. Rev. B 2022, 105, 245404. [Google Scholar] [CrossRef]
- Wille, L.T. Searching potential energy surfaces by simulated annealing. Nature 1987, 325, 374. [Google Scholar] [CrossRef]
- Doll, K.; Schön, J.C.; Jansen, M. Structure prediction based on ab initio simulated annealing for boron nitride. Phys. Rev. B 2008, 78, 144110. [Google Scholar] [CrossRef]
- Timmermann, J.; Lee, Y.; Staacke, C.G.; Margraf, J.T.; Scheurer, C.; Reuter, K. Data-efficient iterative training of Gaussian approximation potentials: Application to surface structure determination of rutile IrO2 and RuO2. J. Chem. Phys. 2021, 155, 244107. [Google Scholar] [CrossRef]
- Fischer, C.C.; Tibbetts, K.J.; Morgan, D.; Ceder, G. Predicting crystal structure by merging data mining with quantum mechanics. Nat. Mater. 2006, 5, 641–646. [Google Scholar] [CrossRef]
- Gubernatis, J.E.; Lookman, T. Machine learning in materials design and discovery: Examples from the present and suggestions for the future. Phys. Rev. Mater. 2018, 2, 120301. [Google Scholar] [CrossRef]
- Curtarolo, S.; Setyawan, W.; Hart, G.L.W.; Jahnatek, M.; Chepulskii, R.V.; Taylor, R.H.; Wang, S.; Xue, J.; Yang, K.; Levy, O.; et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 2012, 58, 218–226. [Google Scholar] [CrossRef]
- Aslam, A.; Saeed, S.; Kanwal, S.; Tchier, F. Investigating hexagonal closed packed crystal lattice through QSPR modeling via linear regression analysis and Topsis. Phys. Scr. 2024, 99, 025201. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, A.; Sun, Z.; Xin, C.; Jin, G. Machine learning regression model for predicting the band gap of multi-elements nonlinear optical crystals. Comput. Mater. Sci. 2024, 242, 113109. [Google Scholar] [CrossRef]
- Kongsompong, S.; E-kobon, T.; Chumnanpuen, P. K-Nearest Neighbor and Random Forest-Based Prediction of Putative Tyrosinase Inhibitory Peptides of Abalone Haliotis diversicolor. Molecules 2021, 26, 3671. [Google Scholar] [CrossRef]
- Leitherer, A.; Ziletti, A.; Ghiringhelli, L.M. Robust recognition and exploratory analysis of crystal structures via Bayesian deep learning. Nat. Commun. 2021, 12, 6234. [Google Scholar] [CrossRef]
- Mobarak, M.H.; Mimona, M.A.; Islam, M.A.; Hossain, N.; Zohura, F.T.; Imtiaz, I.; Rimon, M.I.H. Scope of machine learning in materials research—A review. Appl. Surf. Sci. Adv. 2023, 18, 100523. [Google Scholar] [CrossRef]
- Horak, J.; Vrbka, J.; Suler, P. Support Vector Machine Methods and Artificial Neural Networks Used for the Development of Bankruptcy Prediction Models and their Comparison. J. Risk Financ. Manag. 2020, 13, 60. [Google Scholar] [CrossRef]
- Kutsukake, K. Review of machine learning applications for crystal growth research. J. Cryst. Growth 2024, 630, 127598. [Google Scholar] [CrossRef]
- Xiouras, C.; Cameli, F.; Quilló, G.L.; Kavousanakis, M.E.; Vlachos, D.G.; Stefanidis, G.D. Applications of Artificial Intelligence and Machine Learning Algorithms to Crystallization. Chem. Rev. 2022, 122, 13006–13042. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Tamaki, H.; Yokoyama, T.; Wakasugi, K.; Yotsuhashi, S.; Kusaba, M.; Oganov, A.R.; Yoshida, R. Shotgun crystal structure prediction using machine-learned formation energies. Npj Comput. Mater. 2024, 10, 298. [Google Scholar] [CrossRef]
- Li, L.; Shen, J.; Xiao, Q.; He, C.; Zheng, J.; Chu, C.; Chen, C. Stable crystal structure prediction using machine learning-based formation energy and empirical potential function. Chin. Chem. Lett. 2025, 36, 110421. [Google Scholar] [CrossRef]
- Liu, J.; Wang, A.; Gao, P.; Bai, R.; Liu, J.; Du, B.; Fang, C. Machine learning-based crystal structure prediction for high-entropy oxide ceramics. J. Am. Ceram. Soc. 2024, 107, 1361–1371. [Google Scholar] [CrossRef]
- Kusaba, M.; Liu, C.; Yoshida, R. Crystal structure prediction with machine learning-based element substitution. Comput. Mater. Sci. 2022, 211, 111496. [Google Scholar] [CrossRef]
- Dey, D.; Das, S.; Pal, A.; Dey, S.; Raul, C.K.; Mandal, P.; Chatterjee, A.; Chatterjee, S.; Ghosh, M. Improved machine learning framework for prediction of phases and crystal structures of high entropy alloys. J. Alloys Metall. Syst. 2025, 9, 100144. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Yuan, Y.; Wang, Y. CrySPAI: A New Crystal Structure Prediction Software Based on Artificial Intelligence. Inventions 2025, 10, 26. [Google Scholar] [CrossRef]
- Yamashita, T.; Shinichi, K.; Nobuya, S.; Hiori, K.; Kei, T.; Hikaru, S.; Takumi, S.; Futoshi, U.; Koji, T.; Takashi, M.; et al. CrySPY: A crystal structure prediction tool accelerated by machine learning. Sci. Technol. Adv. Mater. Methods 2021, 1, 87–97. [Google Scholar] [CrossRef]
- Jarin, S.; Yuan, Y.; Zhang, M.; Hu, M.; Rana, M.; Wang, S.; Knibbe, R. Predicting the Crystal Structure and Lattice Parameters of the Perovskite Materials via Different Machine Learning Models Based on Basic Atom Properties. Crystals 2022, 12, 1570. [Google Scholar] [CrossRef]
- Deng, B.; Zhong, P.; Jun, K.; Riebesell, J.; Han, K.; Bartel, C.J.; Ceder, G. CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat. Mach. Intell. 2023, 5, 1031–1041. [Google Scholar] [CrossRef]
- Merchant, A.; Batzner, S.; Schoenholz, S.S.; Aykol, M.; Cheon, G.; Cubuk, E.D. Scaling deep learning for materials discovery. Nature 2023, 624, 80–85. [Google Scholar] [CrossRef]
- Deringer, V.L.; Bartók, A.P.; Bernstein, N.; Wilkins, D.M.; Ceriotti, M.; Csányi, G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021, 121, 10073–10141. [Google Scholar] [CrossRef]
- Damewood, J.; Karaguesian, J.; Lunger, J.R.; Tan, A.R.; Xie, M.; Peng, J.; Gómez-Bombarelli, R. Representations of Materials for Machine Learning. Annu. Rev. Mater. Res. 2023, 53, 399–426. [Google Scholar] [CrossRef]
- Yeo, B.C.; Nam, H.; Nam, H.; Kim, M.-C.; Lee, H.W.; Kim, S.-C.; Won, S.O.; Kim, D.; Lee, K.-Y.; Lee, S.Y.; et al. High-throughput computational-experimental screening protocol for the discovery of bimetallic catalysts. Npj Comput. Mater. 2021, 7, 137. [Google Scholar] [CrossRef]
- Rittiruam, M.; Noppakhun, J.; Setasuban, S.; Aumnongpho, N.; Sriwattana, A.; Boonchuay, S.; Saelee, T.; Wangphon, C.; Ektarawong, A.; Chammingkwan, P.; et al. High-throughput materials screening algorithm based on first-principles density functional theory and artificial neural network for high-entropy alloys. Sci. Rep. 2022, 12, 16653. [Google Scholar] [CrossRef]
- Szymanski, N.J.; Rendy, B.; Fei, Y.; Kumar, R.E.; He, T.; Milsted, D.; McDermott, M.J.; Gallant, M.; Cubuk, E.D.; Merchant, A.; et al. An autonomous laboratory for the accelerated synthesis of novel materials. Nature 2023, 624, 86–91. [Google Scholar] [CrossRef]
- Chmiela, S.; Vassilev-Galindo, V.; Unke, O.T.; Kabylda, A.; Sauceda, H.E.; Tkatchenko, A.; Müller, K.-R. Accurate global machine learning force fields for molecules with hundreds of atoms. Sci. Adv. 2023, 9, eadf0873. [Google Scholar] [CrossRef]
- Sauceda, H.E.; Gálvez-González, L.E.; Chmiela, S.; Paz-Borbón, L.O.; Müller, K.-R.; Tkatchenko, A. BIGDML—Towards accurate quantum machine learning force fields for materials. Nat. Commun. 2022, 13, 3733. [Google Scholar] [CrossRef]
- Noh, J.; Gu, G.H.; Kim, S.; Jung, Y. Machine-enabled inverse design of inorganic solid materials: Promises and challenges. Chem. Sci. 2020, 11, 4871–4881. [Google Scholar] [CrossRef]
- Behler, J. Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 2015, 115, 1032–1050. [Google Scholar] [CrossRef]
- Hoffmann, J.; Maestrati, L.; Sawada, Y.; Tang, J.; Sellier, J.M.; Bengio, Y. Data-driven approach to encoding and decoding 3-d crystal structures. arXiv 2019, arXiv:1909.00949. [Google Scholar] [CrossRef]
- Schütt, K.T.; Sauceda, H.E.; Kindermans, P.J.; Tkatchenko, A.; Müller, K.R. SchNet—A deep learning architecture for molecules and materials. J. Chem. Phys. 2018, 148, 241722. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Choudhary, K.; DeCost, B. Atomistic Line Graph Neural Network for improved materials property predictions. Npj Comput. Mater. 2021, 7, 185. [Google Scholar] [CrossRef]
- Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 2011, 134, 074106. [Google Scholar] [CrossRef]
- Bartók, A.P.; De, S.; Poelking, C.; Bernstein, N.; Kermode, J.R.; Csányi, G.; Ceriotti, M. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 2017, 3, e1701816. [Google Scholar] [CrossRef]
- Batzner, S.; Musaelian, A.; Sun, L.; Geiger, M.; Mailoa, J.P.; Kornbluth, M.; Molinari, N.; Smidt, T.E.; Kozinsky, B. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 2022, 13, 2453. [Google Scholar] [CrossRef]
- Batatia, I.; Kovacs, D.P.; Simm, G.; Ortner, C.; Csányi, G. MACE: Higher order equivariant message passing neural networks for fast and accurate force fields. Adv. Neural Inf. Process. Syst. 2022, 35, 11423–11436. [Google Scholar]
- Gale, J.D.; LeBlanc, L.M.; Spackman, P.R.; Silvestri, A.; Raiteri, P. A Universal Force Field for Materials, Periodic GFN-FF: Implementation and Examination. J. Chem. Theory Comput. 2021, 17, 7827–7849. [Google Scholar] [CrossRef]
- Cole, D.J.; Horton, J.T.; Lauren, N.; Kurdekar, V. The Future of Force Fields in Computer-Aided Drug Design. Future Med. Chem. 2019, 11, 2359–2363. [Google Scholar] [CrossRef] [PubMed]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Jeong, W.; Hong, C.; Hwang, S.; Yoon, Y.; Han, S. Accelerated identification of equilibrium structures of multicomponent inorganic crystals using machine learning potentials. Npj Comput. Mater. 2022, 8, 108. [Google Scholar] [CrossRef]
- Tong, Q.; Xue, L.; Lv, J.; Wang, Y.; Ma, Y. Accelerating CALYPSO structure prediction by data-driven learning of a potential energy surface. Faraday Discuss. 2018, 211, 31–43. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. Model Compression and Acceleration for Deep Neural Networks: The Principles, Progress, and Challenges. IEEE Signal Process. Mag. 2018, 35, 126–136. [Google Scholar] [CrossRef]
- Zhang, Q.-s.; Zhu, S.-c. Visual interpretability for deep learning: A survey. Front. Inf. Technol. Electron. Eng. 2018, 19, 27–39. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Noh, J.; Kim, J.; Stein, H.S.; Sanchez-Lengeling, B.; Gregoire, J.M.; Aspuru-Guzik, A.; Jung, Y. Inverse Design of Solid-State Materials via a Continuous Representation. Matter 2019, 1, 1370–1384. [Google Scholar] [CrossRef]
- Ren, Z.; Tian, S.I.P.; Noh, J.; Oviedo, F.; Xing, G.; Li, J.; Liang, Q.; Zhu, R.; Aberle, A.G.; Sun, S.; et al. An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties. Matter 2022, 5, 314–335. [Google Scholar] [CrossRef]
- Nouira, A.; Sokolovska, N.; Crivello, J.-C. Crystalgan: Learning to discover crystallographic structures with generative adversarial networks. arXiv 2018, arXiv:1810.11203. [Google Scholar]
- Fung, V.; Zhang, J.; Hu, G.; Ganesh, P.; Sumpter, B.G. Inverse design of two-dimensional materials with invertible neural networks. Npj Comput. Mater. 2021, 7, 200. [Google Scholar] [CrossRef]
- Zeni, C.; Pinsler, R.; Zügner, D.; Fowler, A.; Horton, M.; Fu, X.; Shysheya, S.; Crabbé, J.; Sun, L.; Smith, J. Mattergen: A generative model for inorganic materials design. arXiv 2023, arXiv:2312.03687. [Google Scholar]
- Zhao, C.; Duan, Y.; Gao, J.; Liu, W.; Dong, H.; Dong, H.; Zhang, D.; Oganov, A.R. Unexpected stable phases of tungsten borides. Phys. Chem. Chem. Phys. 2018, 20, 24665–24670. [Google Scholar] [CrossRef]
- Li, C.-N.; Liang, H.-P.; Zhang, X.; Lin, Z.; Wei, S.-H. Graph deep learning accelerated efficient crystal structure search and feature extraction. Npj Comput. Mater. 2023, 9, 176. [Google Scholar] [CrossRef]
- Podryabinkin, E.V.; Tikhonov, E.V.; Shapeev, A.V.; Oganov, A.R. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys. Rev. B 2019, 99, 064114. [Google Scholar] [CrossRef]
- Tong, Q.; Gao, P.; Liu, H.; Xie, Y.; Lv, J.; Wang, Y.; Zhao, J. Combining Machine Learning Potential and Structure Prediction for Accelerated Materials Design and Discovery. J. Phys. Chem. Lett. 2020, 11, 8710–8720. [Google Scholar] [CrossRef]
- Mansouri Tehrani, A.; Oliynyk, A.O.; Parry, M.; Rizvi, Z.; Couper, S.; Lin, F.; Miyagi, L.; Sparks, T.D.; Brgoch, J. Machine Learning Directed Search for Ultraincompressible, Superhard Materials. J. Am. Chem. Soc. 2018, 140, 9844–9853. [Google Scholar] [CrossRef]
- Xue, D.; Balachandran, P.V.; Yuan, R.; Hu, T.; Qian, X.; Dougherty, E.R.; Lookman, T. Accelerated search for BaTiO3-based piezoelectrics with vertical morphotropic phase boundary using Bayesian learning. Proc. Natl. Acad. Sci. USA 2016, 113, 13301–13306. [Google Scholar] [CrossRef]
- Padhy, S.P.; Chaudhary, V.; Lim, Y.-F.; Zhu, R.; Thway, M.; Hippalgaonkar, K.; Ramanujan, R.V. Experimentally validated inverse design of multi-property Fe-Co-Ni alloys. iScience 2024, 27, 109723. [Google Scholar] [CrossRef]
- Balachandran, P.V.; Kowalski, B.; Sehirlioglu, A.; Lookman, T. Experimental search for high-temperature ferroelectric perovskites guided by two-step machine learning. Nat. Commun. 2018, 9, 1668. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. Npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Syed, T.A.; Ansari, K.B.; Banerjee, A.; Wood, D.A.; Khan, M.S.; Al Mesfer, M.K. Machine-learning predictions of caffeine co-crystal formation accompanying experimental and molecular validations. J. Food Process Eng. 2023, 46, e14230. [Google Scholar] [CrossRef]
- Hareharen, K.; Panneerselvam, T.; Raj Mohan, R. Improving the performance of machine learning model predicting phase and crystal structure of high entropy alloys by the synthetic minority oversampling technique. J. Alloys Compd. 2024, 991, 174494. [Google Scholar] [CrossRef]
- Feng, H.; Tian, H. Improving Crystal Property Prediction from a Multiplex Graph Perspective. J. Chem. Inf. Model. 2024, 64, 7376–7385. [Google Scholar] [CrossRef]
- Jin, L.; Du, Z.; Shu, L.; Cen, Y.; Xu, Y.; Mei, Y.; Zhang, H. Transformer-generated atomic embeddings to enhance prediction accuracy of crystal properties with machine learning. Nat. Commun. 2025, 16, 1210. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Q.; Zhou, W.; Zang, H.; Xu, L.; Ren, Y.; Xu, J.; Zhan, S.; Ma, W. Reinforce crystal material property prediction with comprehensive message passing via deep graph networks. Comput. Mater. Sci. 2024, 239, 112958. [Google Scholar] [CrossRef]
- Luo, X.; Wang, Z.; Gao, P.; Lv, J.; Wang, Y.; Chen, C.; Ma, Y. Deep learning generative model for crystal structure prediction. Npj Comput. Mater. 2024, 10, 254. [Google Scholar] [CrossRef]
- Ye, C.-Y.; Weng, H.-M.; Wu, Q.-S. Con-CDVAE: A method for the conditional generation of crystal structures. Comput. Mater. Today 2024, 1, 100003. [Google Scholar] [CrossRef]
- Jiao, R.; Huang, W.; Lin, P.; Han, J.; Chen, P.; Lu, Y.; Liu, Y. Crystal structure prediction by joint equivariant diffusion. Adv. Neural Inf. Process. Syst. 2023, 36, 17464–17497. [Google Scholar]
- Wang, J.; Gao, H.; Han, Y.; Ding, C.; Pan, S.; Wang, Y.; Jia, Q.; Wang, H.-T.; Xing, D.; Sun, J. MAGUS: Machine learning and graph theory assisted universal structure searcher. Natl. Sci. Rev. 2023, 10, nwad128. [Google Scholar] [CrossRef]
- Li, C.-N.; Liang, H.-P.; Zhao, B.-Q.; Wei, S.-H.; Zhang, X. Machine learning assisted crystal structure prediction made simple. J. Mater. Inform. 2024, 4, 15. [Google Scholar] [CrossRef]
- Shiraki, Y.; Kaneko, H. Correlations between the constituent molecules, crystal structures, and dielectric constants in organic crystals. Chemom. Intell. Lab. Syst. 2025, 261, 105376. [Google Scholar] [CrossRef]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A review of ensemble learning and data augmentation models for class imbalanced problems: Combination, implementation and evaluation. Expert Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Nguyen, N.; Ngo, D. Comparative analysis of boosting algorithms for predicting personal default. Cogent Econ. Financ. 2025, 13, 2465971. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Ab initio random structure searching. J. Phys. Condens. Matter 2011, 23, 053201. [Google Scholar] [CrossRef]
- Glass, C.W.; Oganov, A.R.; Hansen, N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Commun. 2006, 175, 713–720. [Google Scholar] [CrossRef]
- Hunnisett, L.M.; Nyman, J.; Francia, N.; Abraham, N.S.; Adjiman, C.S.; Aitipamula, S.; Alkhidir, T.; Almehairbi, M.; Anelli, A.; Anstine, D.M.; et al. The seventh blind test of crystal structure prediction: Structure generation methods. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2024, 80, 517–547. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. High-Pressure Phases of Silane. Phys. Rev. Lett. 2006, 97, 045504. [Google Scholar] [CrossRef]
- Doll, K.; Schön, J.C.; Jansen, M. Global exploration of the energy landscape of solids on the ab initio level. Phys. Chem. Chem. Phys. 2007, 9, 6128–6133. [Google Scholar] [CrossRef]
- Goedecker, S. Minima hopping: An efficient search method for the global minimum of the potential energy surface of complex molecular systems. J. Chem. Phys. 2004, 120, 9911–9917. [Google Scholar] [CrossRef]
- Goedecker, S.; Hellmann, W.; Lenosky, T. Global Minimum Determination of the Born-Oppenheimer Surface within Density Functional Theory. Phys. Rev. Lett. 2005, 95, 055501. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Ma, Y.; Eremets, M.; Oganov, A.R.; Xie, Y.; Trojan, I.; Medvedev, S.; Lyakhov, A.O.; Valle, M.; Prakapenka, V. Transparent dense sodium. Nature 2009, 458, 182–185. [Google Scholar] [CrossRef]
- Lv, J.; Wang, Y.; Zhu, L.; Ma, Y. Predicted Novel High-Pressure Phases of Lithium. Phys. Rev. Lett. 2011, 106, 015503. [Google Scholar] [CrossRef]
- Zhang, W.; Oganov, A.R.; Goncharov, A.F.; Zhu, Q.; Boulfelfel, S.E.; Lyakhov, A.O.; Stavrou, E.; Somayazulu, M.; Prakapenka, V.B.; Konôpková, Z. Unexpected Stable Stoichiometries of Sodium Chlorides. Science 2013, 342, 1502–1505. [Google Scholar] [CrossRef] [PubMed]
- Lonie, D.C.; Zurek, E. XtalOpt: An open-source evolutionary algorithm for crystal structure prediction. Comput. Phys. Commun. 2011, 182, 372–387. [Google Scholar] [CrossRef]
- Baettig, P.; Zurek, E. Pressure-Stabilized Sodium Polyhydrides: NaHn (n > 1). Phys. Rev. Lett. 2011, 106, 237002. [Google Scholar] [CrossRef] [PubMed]
- Hermann, A.; Ashcroft, N.W.; Hoffmann, R. High pressure ices. Proc. Natl. Acad. Sci. USA 2012, 109, 745–750. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Highly compressed ammonia forms an ionic crystal. Nat. Mater. 2008, 7, 775–779. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Naumov, I.I.; Hoffmann, R.; Ashcroft, N.W.; Hemley, R.J. Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl. Acad. Sci. USA 2017, 114, 6990–6995. [Google Scholar] [CrossRef] [PubMed]
- Tipton, W.W.; Hennig, R.G. A grand canonical genetic algorithm for the prediction of multi-component phase diagrams and testing of empirical potentials. J. Phys. Condens. Matter 2013, 25, 495401. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Hennig, R.G.; Ashcroft, N.W.; Hoffmann, R. Emergent reduction of electronic state dimensionality in dense ordered Li-Be alloys. Nature 2008, 451, 445–448. [Google Scholar] [CrossRef]
- Tipton, W.W.; Bealing, C.R.; Mathew, K.; Hennig, R.G. Structures, phase stabilities, and electrical potentials of Li-Si battery anode materials. Phys. Rev. B 2013, 87, 184114. [Google Scholar] [CrossRef]
- Wu, S.Q.; Ji, M.; Wang, C.Z.; Nguyen, M.C.; Zhao, X.; Umemoto, K.; Wentzcovitch, R.M.; Ho, K.M. An adaptive genetic algorithm for crystal structure prediction. J. Phys. Condens. Matter 2014, 26, 035402. [Google Scholar] [CrossRef]
- Zhao, X.; Nguyen, M.C.; Zhang, W.Y.; Wang, C.Z.; Kramer, M.J.; Sellmyer, D.J.; Li, X.Z.; Zhang, F.; Ke, L.Q.; Antropov, V.P.; et al. Exploring the Structural Complexity of Intermetallic Compounds by an Adaptive Genetic Algorithm. Phys. Rev. Lett. 2014, 112, 045502. [Google Scholar] [CrossRef]
- Umemoto, K.; Wentzcovitch, R.M.; Wu, S.; Ji, M.; Wang, C.-Z.; Ho, K.-M. Phase transitions in MgSiO3 post-perovskite in super-Earth mantles. Earth Planet. Sci. Lett. 2017, 478, 40–45. [Google Scholar] [CrossRef]
- Liu, Z.-L. Muse: Multi-algorithm collaborative crystal structure prediction. Comput. Phys. Commun. 2014, 185, 1893–1900. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Lv, J.; Liu, Z. Phase diagram and physical properties of iridium tetraboride from first principles. Phys. Chem. Chem. Phys. 2016, 18, 12569–12575. [Google Scholar] [CrossRef]
- Liu, Z.-L.; Jia, H.; Li, R.; Zhang, X.-L.; Cai, L.-C. Unexpected coordination number and phase diagram of niobium diselenide under compression. Phys. Chem. Chem. Phys. 2017, 19, 13219–13229. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Gao, W.; Chen, S.; Xiang, H.; Gong, X.-G. Inverse design of materials by multi-objective differential evolution. Comput. Mater. Sci. 2015, 98, 51–55. [Google Scholar] [CrossRef]
- Chen, H.-Z.; Zhang, Y.-Y.; Gong, X.; Xiang, H. Predicting New TiO2 Phases with Low Band Gaps by a Multiobjective Global Optimization Approach. J. Phys. Chem. C 2014, 118, 2333–2337. [Google Scholar] [CrossRef]
- Yang, J.-H.; Zhang, Y.; Yin, W.-J.; Gong, X.G.; Yakobson, B.I.; Wei, S.-H. Two-Dimensional SiS Layers with Promising Electronic and Optoelectronic Properties: Theoretical Prediction. Nano Lett. 2016, 16, 1110–1117. [Google Scholar] [CrossRef] [PubMed]
- Olson, M.A.; Bhatia, S.; Larson, P.; Militzer, B. Prediction of chlorine and fluorine crystal structures at high pressure using symmetry driven structure search with geometric constraints. J. Chem. Phys. 2020, 153, 094111. [Google Scholar] [CrossRef] [PubMed]
- Hajinazar, S.; Thorn, A.; Sandoval, E.D.; Kharabadze, S.; Kolmogorov, A.N. MAISE: Construction of neural network interatomic models and evolutionary structure optimization. Comput. Phys. Commun. 2021, 259, 107679. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Shah, S.; Margine, E.R.; Bialon, A.F.; Hammerschmidt, T.; Drautz, R. New Superconducting and Semiconducting Fe-B Compounds Predicted with an Ab Initio Evolutionary Search. Phys. Rev. Lett. 2010, 105, 217003. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Beaufils, C.; Kolmogorov, A.N. Ab initio engineering of materials with stacked hexagonal tin frameworks. Sci. Rep. 2016, 6, 28369. [Google Scholar] [CrossRef]
- Xia, K.; Gao, H.; Liu, C.; Yuan, J.; Sun, J.; Wang, H.-T.; Xing, D. A novel superhard tungsten nitride predicted by machine-learning accelerated crystal structure search. Sci. Bull. 2018, 63, 817–824. [Google Scholar] [CrossRef]
- Liu, C.; Gao, H.; Wang, Y.; Needs, R.J.; Pickard, C.J.; Sun, J.; Wang, H.-T.; Xing, D. Multiple superionic states in helium–water compounds. Nat. Phys. 2019, 15, 1065–1070. [Google Scholar] [CrossRef]
- Li, C.; Liang, H.; Duan, Y.; Lin, Z. Machine-learning accelerated annealing with fitting-search style for multicomponent alloy structure predictions. Phys. Rev. Mater. 2023, 7, 033802. [Google Scholar] [CrossRef]
- Liang, H.-P.; Geng, S.; Jia, T.; Li, C.-N.; Xu, X.; Zhang, X.; Wei, S.-H. Unveiling disparities and promises of Cu and Ag chalcopyrites for thermoelectrics. Phys. Rev. B 2024, 109, 035205. [Google Scholar] [CrossRef]
- Yang, S.; Cho, K.; Merchant, A.; Abbeel, P.; Schuurmans, D.; Mordatch, I.; Cubuk, E.D. Scalable diffusion for materials generation. arXiv 2023, arXiv:2311.09235. [Google Scholar] [CrossRef]
- Gruver, N.; Sriram, A.; Madotto, A.; Wilson, A.G.; Zitnick, C.L.; Ulissi, Z. Fine-tuned language models generate stable inorganic materials as text. arXiv 2024, arXiv:2402.04379. [Google Scholar] [CrossRef]
- Bisbo, M.K.; Hammer, B. Efficient Global Structure Optimization with a Machine-Learned Surrogate Model. Phys. Rev. Lett. 2020, 124, 086102. [Google Scholar] [CrossRef] [PubMed]
- Terayama, K.; Yamashita, T.; Oguchi, T.; Tsuda, K. Fine-grained optimization method for crystal structure prediction. Npj Comput. Mater. 2018, 4, 32. [Google Scholar] [CrossRef]
- Cai, W.; Nix, W.D. Imperfections in Crystalline Solids; MRS-Cambridge Materials Fundamentals; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.; Zou, G.; Zhang, L.; Han, S.; Li, Y.; Liu, D.; Fernandez, C.; Li, L.; Ren, L.; et al. Crystal-defect engineering of electrode materials for energy storage and conversion. Mater. Today Nano 2023, 22, 100336. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, D.; Zhang, C.; Zhou, X.; Wu, H.-H.; Wang, F.; Wang, S.; Wu, G.; Gao, J.; Zhao, H.; et al. A review of crystal defect-induced element segregation in multi-component alloy steels. Prog. Nat. Sci. Mater. Int. 2024, 34, 840–858. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Britton, D.; Hinojos, A.; Hummel, M.; Adams, D.P.; Medlin, D.L. Application of the polyhedral template matching method for characterization of 2D atomic resolution electron microscopy images. Mater. Charact. 2024, 213, 114017. [Google Scholar] [CrossRef]
- Wang, F.; Kurc, T.; Widener, P.; Pan, T.; Kong, J.; Cooper, L.; Gutman, D.; Sharma, A.; Cholleti, S.; Kumar, V.; et al. High-Performance Systems for in Silico Microscopy Imaging Studies. In Data Integration in the Life Sciences; Springer: Berlin/Heidelberg, Germany, 2010; pp. 3–18. [Google Scholar]
- Khan, N.; Asad, H.; Khan, S.; Riccio, A. Towards defect-free lattice structures in additive manufacturing: A holistic review of machine learning advancements. J. Manuf. Process. 2025, 144, 1–53. [Google Scholar] [CrossRef]
- Wu, L.; Wang, W.; Shi, Z.; Zhang, H.; Ke, L.; Liang, X.; Tian, D.; Zhang, H.; Bi, H.; Chen, W.; et al. Rapid identification of defects in doped organic crystalline films via machine learning-enhanced hyperspectral imaging. Chem. Eng. J. 2025, 513, 162696. [Google Scholar] [CrossRef]
- Klunnikova, Y.V.; Anikeev, M.V.; Filimonov, A.V.; Kumar, R. Machine learning application for prediction of sapphire crystals defects. J. Electron. Sci. Technol. 2020, 18, 100029. [Google Scholar] [CrossRef]
- Rodriguez-Guillen, D.; Díez, A.; Andrés, M.V.; Velazquez-Ibarra, L. Inverse design of photonic crystal fibers for dispersion engineering using neural networks. Opt. Commun. 2025, 587, 131891. [Google Scholar] [CrossRef]
- Ding, C.-j.; Wang, X.-y.; Li, X.-y.; Yang, W.-s.; Li, X.-l.; Zhang, Y.-g.; Xu, Y.-c.; Liu, C.-s.; Wu, X. Machine learning-based interatomic potential for simulating irradiation damage mechanisms in ZrC. J. Mater. Sci. Technol. 2026, 242, 75–91. [Google Scholar] [CrossRef]
- Luo, Y.; Byggmästar, J.; Daymond, M.R.; Béland, L.K. Interatomic force fields for zirconium based on the embedded atom method and the tabulated Gaussian Approximation Potential. Comput. Mater. Sci. 2024, 233, 112730. [Google Scholar] [CrossRef]
- Chen, H.; Yuan, D.; Geng, H.; Hu, W.; Huang, B. Development of a machine-learning interatomic potential for uranium under the moment tensor potential framework. Comput. Mater. Sci. 2023, 229, 112376. [Google Scholar] [CrossRef]
- Williams, L.; Sargsyan, K.; Rohskopf, A.; Najm, H.N. Active learning for SNAP interatomic potentials via Bayesian predictive uncertainty. Comput. Mater. Sci. 2024, 242, 113074. [Google Scholar] [CrossRef]
- Keshavarz, S.; Mao, Y.; Reid, A.C.E.; Agrawal, A. Advancing material simulations: Physics-Informed Neural Networks and Object-Oriented Crystal Plasticity Finite Element Methods. Int. J. Plast. 2025, 185, 104221. [Google Scholar] [CrossRef]
- Hussein, R.; Schmidt, J.; Barros, T.; Marques, M.A.L.; Botti, S. Machine-learning correction to density-functional crystal structure optimization. MRS Bull. 2022, 47, 765–771. [Google Scholar] [CrossRef]
- Li, X.; Mai, Y.; Meng, H.; Bi, H.; Ng, C.H.; Teo, S.H.; Lan, C.; Zhang, P.; Li, S. Machine learning quantification of grain boundary defects for high efficiency perovskite solar cells. Adv. Compos. Hybrid Mater. 2024, 7, 241. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, L.; Zhu, G.; Diehl, M.; Maldar, A.; Shang, X.; Zeng, X. Predicting grain boundary damage by machine learning. Int. J. Plast. 2022, 150, 103186. [Google Scholar] [CrossRef]
- He, Z.; Bi, S.; Asare-Yeboah, K. Study of Grain Boundary: From Crystallization Engineering to Machine Learning. Coatings 2025, 15, 164. [Google Scholar] [CrossRef]
- Salmenjoki, H.; Papanikolaou, S.; Shi, D.; Tourret, D.; Cepeda-Jiménez, C.M.; Pérez-Prado, M.T.; Laurson, L.; Alava, M.J. Machine learning dislocation density correlations and solute effects in Mg-based alloys. Sci. Rep. 2023, 13, 11114. [Google Scholar] [CrossRef]
- Deng, F.; Wu, H.; He, R.; Yang, P.; Zhong, Z. Large-scale atomistic simulation of dislocation core structure in face-centered cubic metal with Deep Potential method. Comput. Mater. Sci. 2023, 218, 111941. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, X.; Li, Y.; Lv, Q.; Chen, C.Y.-C.; Shen, L. Efficient equivariant model for machine learning interatomic potentials. Npj Comput. Mater. 2025, 11, 49. [Google Scholar] [CrossRef]
- Wang, G.; Wang, C.; Zhang, X.; Li, Z.; Zhou, J.; Sun, Z. Machine learning interatomic potential: Bridge the gap between small-scale models and realistic device-scale simulations. iScience 2024, 27, 109673. [Google Scholar] [CrossRef]
- Goryaeva, A.M.; Dérès, J.; Lapointe, C.; Grigorev, P.; Swinburne, T.D.; Kermode, J.R.; Ventelon, L.; Baima, J.; Marinica, M.-C. Efficient and transferable machine learning potentials for the simulation of crystal defects in bcc Fe and W. Phys. Rev. Mater. 2021, 5, 103803. [Google Scholar] [CrossRef]
- Borges, Y.; Huber, L.; Zapolsky, H.; Patte, R.; Demange, G. Insights from symmetry: Improving machine-learned models for grain boundary segregation. Comput. Mater. Sci. 2024, 232, 112663. [Google Scholar] [CrossRef]
- Wang, X.; Valdevit, L.; Cao, P. Neural network for predicting Peierls barrier spectrum and its influence on dislocation motion. Acta Mater. 2024, 267, 119696. [Google Scholar] [CrossRef]
- Zhang, L.; Csányi, G.; van der Giessen, E.; Maresca, F. Efficiency, accuracy, and transferability of machine learning potentials: Application to dislocations and cracks in iron. Acta Mater. 2024, 270, 119788. [Google Scholar] [CrossRef]
- Barros de Moraes, E.A.; D’Elia, M.; Zayernouri, M. Machine learning of nonlocal micro-structural defect evolutions in crystalline materials. Comput. Methods Appl. Mech. Eng. 2023, 403, 115743. [Google Scholar] [CrossRef]
- Alarfaj, A.A.; Hosni Mahmoud, H.A. Feature Fusion Deep Learning Model for Defects Prediction in Crystal Structures. Crystals 2022, 12, 1324. [Google Scholar] [CrossRef]
- Honrao, S.; Anthonio, B.E.; Ramanathan, R.; Gabriel, J.J.; Hennig, R.G. Machine learning of ab-initio energy landscapes for crystal structure predictions. Comput. Mater. Sci. 2019, 158, 414–419. [Google Scholar] [CrossRef]
- Sidnov, K.; Konov, D.; Smirnova, E.A.; Ponomareva, A.V.; Belov, M.P. Machine Learning-Based Prediction of Elastic Properties Using Reduced Datasets of Accurate Calculations Results. Metals 2024, 14, 438. [Google Scholar] [CrossRef]
- Kholtobina, A.; Lončarić, I. Exploring elastic properties of molecular crystals with universal machine learning interatomic potentials. Mater. Des. 2025, 254, 114047. [Google Scholar] [CrossRef]
- Kazeev, N.; Al-Maeeni, A.R.; Romanov, I.; Faleev, M.; Lukin, R.; Tormasov, A.; Castro Neto, A.H.; Novoselov, K.S.; Huang, P.; Ustyuzhanin, A. Sparse representation for machine learning the properties of defects in 2D materials. Npj Comput. Mater. 2023, 9, 113. [Google Scholar] [CrossRef]
- Dembitskiy, A.D.; Humonen, I.S.; Eremin, R.A.; Aksyonov, D.A.; Fedotov, S.S.; Budennyy, S.A. Benchmarking machine learning models for predicting lithium ion migration. Npj Comput. Mater. 2025, 11, 131. [Google Scholar] [CrossRef]
- Wei, H.; Bao, H.; Ruan, X. Perspective: Predicting and optimizing thermal transport properties with machine learning methods. Energy AI 2022, 8, 100153. [Google Scholar] [CrossRef]
- Chen, H.; Cai, J.; Zhang, Y.; Lv, X.; Hu, W.; Huang, B. Development of machine learning potentials for Ce-Ti and Ce-Ta binary systems and studies of the liquid-solid interfaces. Corros. Sci. 2025, 246, 112766. [Google Scholar] [CrossRef]
- Thampiriyanon, J.; Khumkoa, S. Machine Learning–Based Prediction of Complex Combination Phases in High-Entropy Alloys. Metals 2025, 15, 227. [Google Scholar] [CrossRef]
- Jang, Y.; Kim, C.H.; Go, A. Classification of magnetic order from electronic structure by using machine learning. Sci. Rep. 2023, 13, 12445. [Google Scholar] [CrossRef]
- Freitas, R.; Cao, Y. Machine-learning potentials for crystal defects. MRS Commun. 2022, 12, 510–520. [Google Scholar] [CrossRef]
- Tanaka, M.; Sasaki, K.; Punyafu, J.; Muramatsu, M.; Murayama, M. Machine-learning-aided analysis of relationship between crystal defects and macroscopic mechanical properties of TWIP steel. Sci. Rep. 2025, 15, 14435. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.-J. First-principles approaches and models for crystal defect energetics in metallic alloys. Comput. Mater. Sci. 2023, 216, 111831. [Google Scholar] [CrossRef]
- Domínguez-Gutiérrez, F.J.; Byggmästar, J.; Nordlund, K.; Djurabekova, F.; von Toussaint, U. Computational study of crystal defect formation in Mo by a machine learning molecular dynamics potential. Model. Simul. Mater. Sci. Eng. 2021, 29, 055001. [Google Scholar] [CrossRef]
- Dragoni, D.; Daff, T.D.; Csányi, G.; Marzari, N. Achieving DFT accuracy with a machine-learning interatomic potential: Thermomechanics and defects in bcc ferromagnetic iron. Phys. Rev. Mater. 2018, 2, 013808. [Google Scholar] [CrossRef]
- Goryaeva, A.M.; Lapointe, C.; Dai, C.; Dérès, J.; Maillet, J.-B.; Marinica, M.-C. Reinforcing materials modelling by encoding the structures of defects in crystalline solids into distortion scores. Nat. Commun. 2020, 11, 4691. [Google Scholar] [CrossRef]
- Vandermause, J.; Torrisi, S.B.; Batzner, S.; Xie, Y.; Sun, L.; Kolpak, A.M.; Kozinsky, B. On-the-fly active learning of interpretable Bayesian force fields for atomistic rare events. Npj Comput. Mater. 2020, 6, 20. [Google Scholar] [CrossRef]
- Asilian Bidgoli, A.; Rahnamayan, S.; Erdem, B.; Erdem, Z.; Ibrahim, A.; Deb, K.; Grami, A. Machine learning-based framework to cover optimal Pareto-front in many-objective optimization. Complex Intell. Syst. 2022, 8, 5287–5308. [Google Scholar] [CrossRef]
- Tan, C.S.; Gupta, A.; Ong, Y.-S.; Pratama, M.; Tan, P.S.; Lam, S.K. Pareto optimization with small data by learning across common objective spaces. Sci. Rep. 2023, 13, 7842. [Google Scholar] [CrossRef]

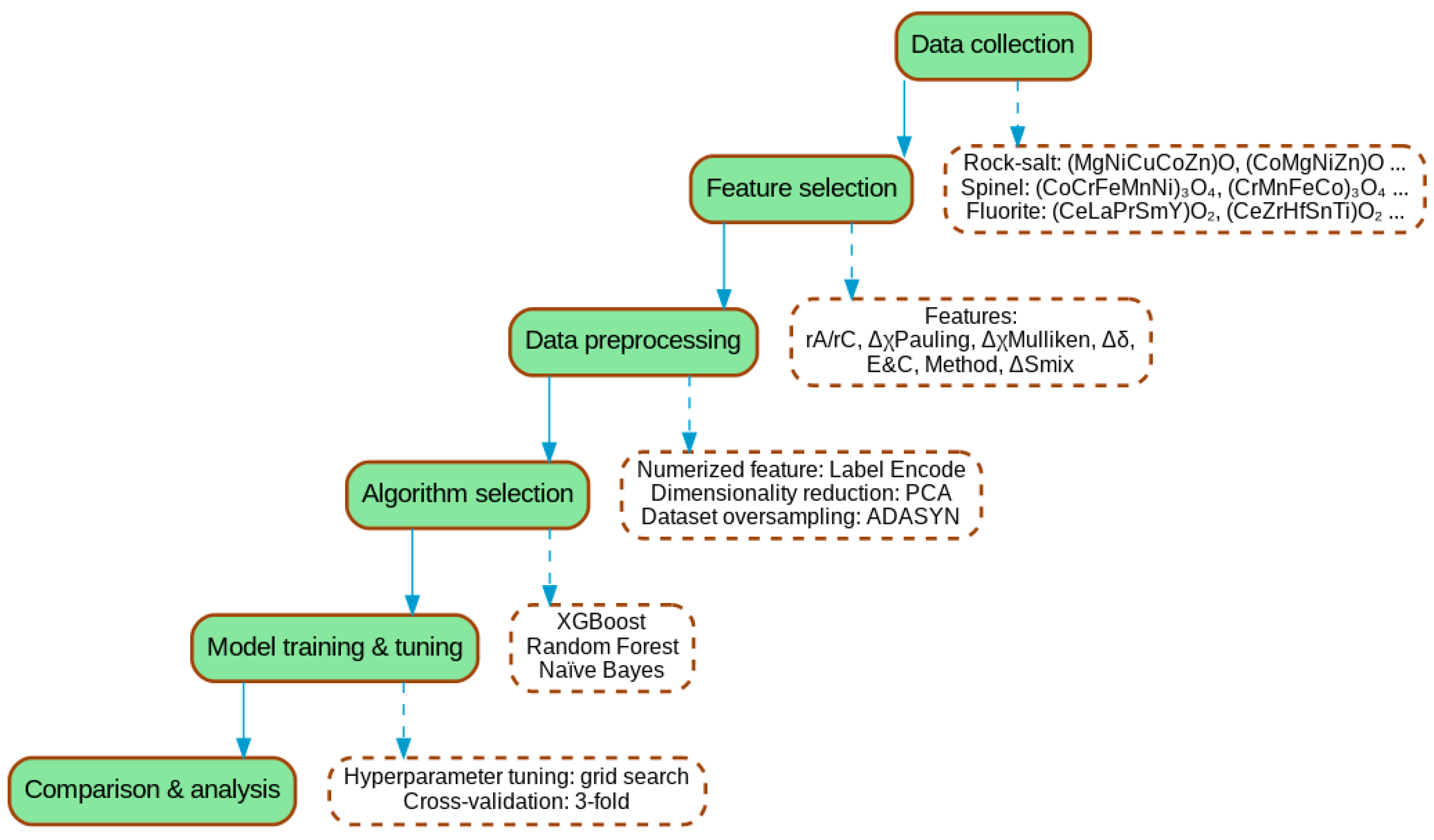
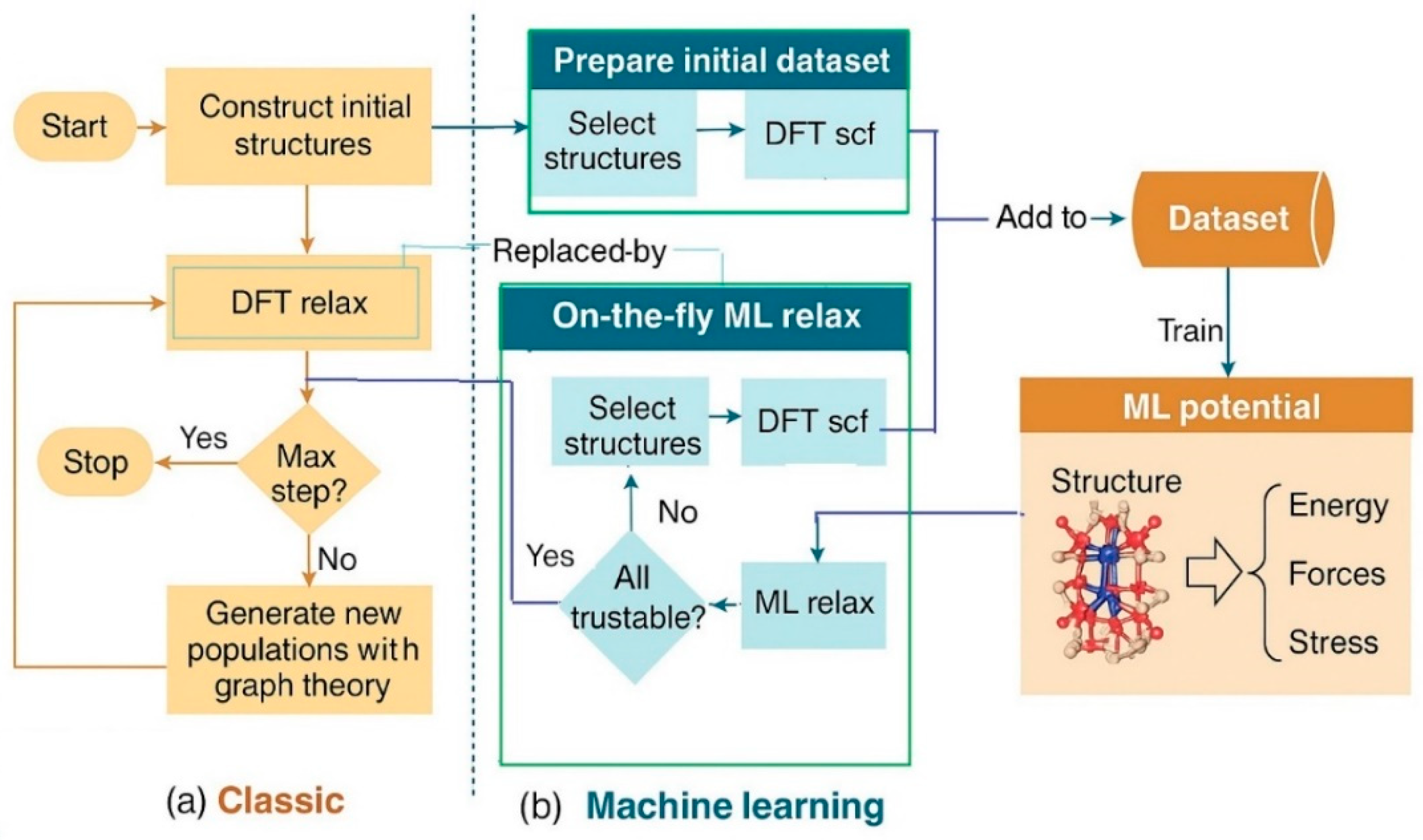

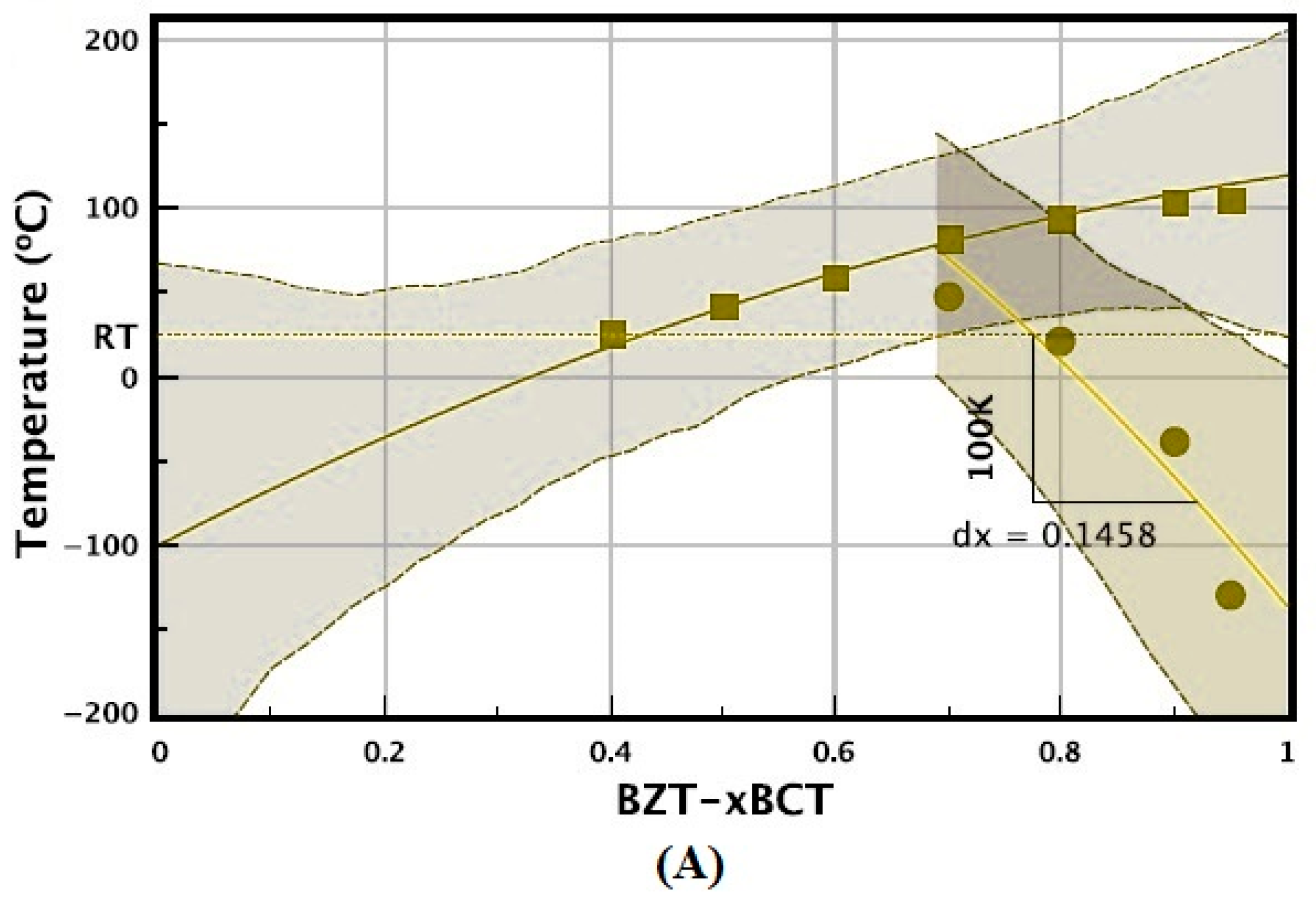
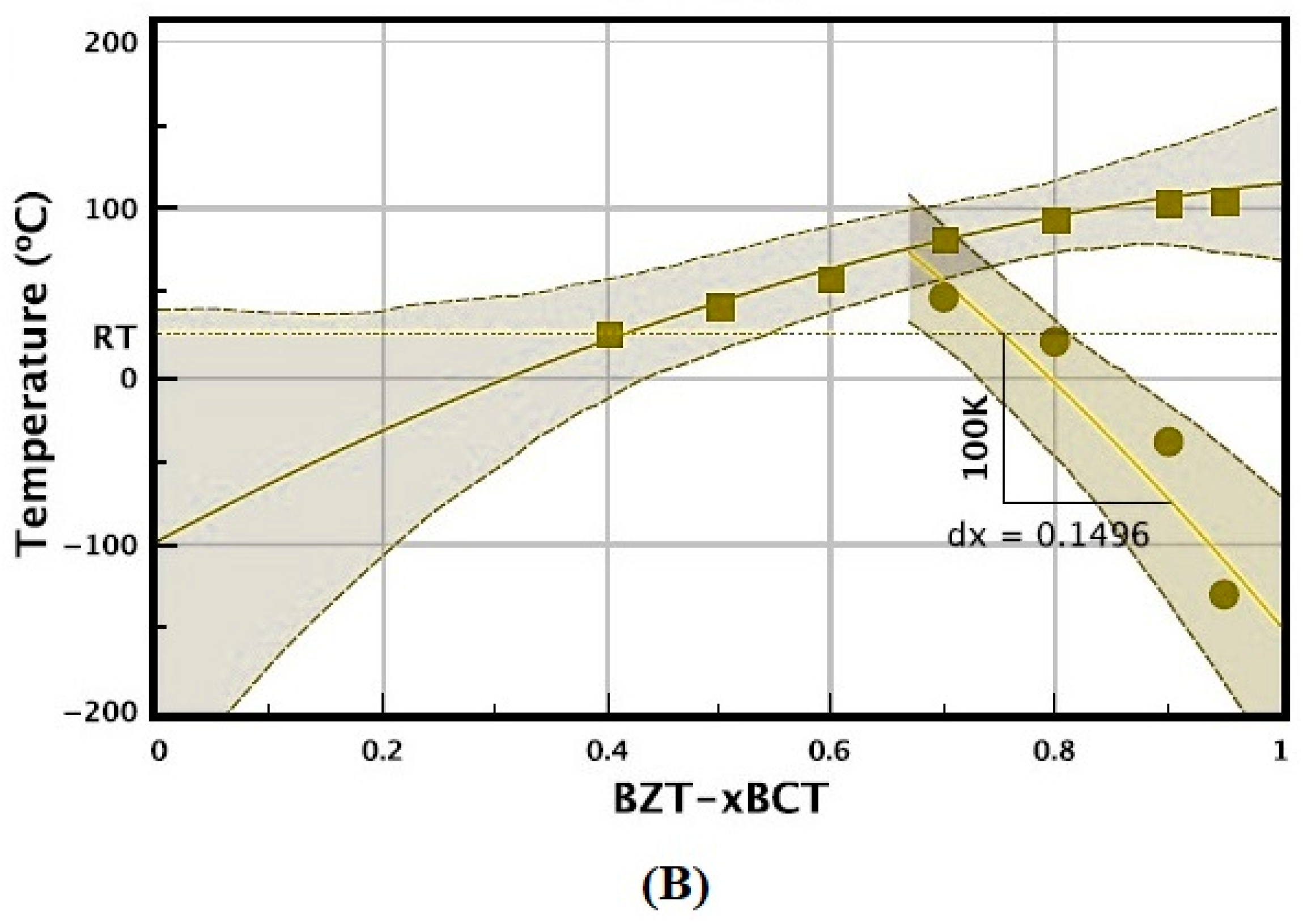
| ML Algorithm | Advantages | Challenges | Typical Use Cases/Scenarios to Avoid |
|---|---|---|---|
| Linear Regression | Simple, transparent, and easy to interpret; computationally efficient; provides direct insights into variable relationships. | Poor prediction for nonlinear problems; sensitive to outliers; unreliable when predictors are colinear | Use for: Quick baseline modeling, trend estimation, or problems with clear linear relationships. Avoid for: Highly nonlinear systems or datasets with strong multicollinearity. |
| k-NN | Nonparametric and intuitive; adapts naturally to nonlinear data; no training phase required. | Slow for large datasets; suffers from dimensionality; sensitive to outliers | Use for: Pattern recognition, anomaly detection, and small to medium datasets with local similarity patterns. Avoid for: Real-time applications or large-scale data requiring fast predictions. |
| NB | Fast and efficient; works well with small or sparse data; effective for categorical features. | Assumes feature independence; low accuracy probability outputs; requires representative training data | Use for: Text classification, spam filtering, or quick baseline models. Avoid for: Tasks involving dependent or continuous variables. |
| SVM | High accuracy in high-dimensional spaces; robust to overfitting; effective with limited data | Not suitable for very large datasets; poor performance with overlapping classes; sensitive to kernel selection | Use for: Image recognition, bioinformatics, or moderate-size, high-dimensional problems. Avoid for: Very large or noisy datasets. |
| Decision Trees | No need for normalization; deals with missing data effectively; easy to visualize and interpret | Prone to overfitting; sensitive to training data variations; longer training times | Use for: Feature selection and interpretable classification tasks. Avoid for: Small, noisy datasets or where stability is critical. |
| ANNs | Highly flexible; captures complex nonlinear relationships; scales well to large datasets. | Requires large training data; computationally expensive; low interpretability | Use for: Predicting complex material or process properties, image/spectra analysis, or multi-output regression. Avoid for: Small datasets or when interpretability is required. |
| Classifier | Precision (%) | Accuracy (%) | F1 Score | Recall (%) |
|---|---|---|---|---|
| AdaBoost | 68.93 | 67.92 | 0.681 | 67.56 |
| LightGBM | 90.07 | 90.07 | 0.899 | 90.08 |
| XGBoost | 86.12 | 85.45 | 0.859 | 85.86 |
| Gradient Boosting | 75.14 | 75.81 | 0.754 | 75.94 |
| CatBoost | 76.95 | 79.60 | 0.783 | 79.98 |
| Software | Applications | Methods |
|---|---|---|
| USPEX [109] | NaCl [124], W-B [86] | Evolutionary algorithm |
| XtalOPT [118] | NaHn [125], H2O [126] | Evolutionary algorithm |
| AIRSS [108] | SiH4 [111], NH3±x [127] | Random search |
| CALYPSO [24] | Li [117], LaH10 [128], P | Particle swarm optimization |
| GASP [119] | Li-Be [129], Li-Si [130] | Evolutionary algorithm |
| AGA [120] | Zr-Co [131], MgO-SiO2 [132] | Adaptive GA |
| MUSE [121] | IrB4 [133], NbSe2 [134] | Evolutionary algorithm |
| IM2ODE [122] | TiO2 [135], 2D SiS [136] | Differential evolution |
| SYDSS [15] | H2O-NaCl [15], Cl-F [137] | Random search |
| MAISE [123] | Fe-B [138], NaSn2 [139] | Evolutionary algorithm |
| Software | Applications | Methods |
|---|---|---|
| FTCP [82] | Au2Sc2O3 [82], Y2Zn2As2O3 [82] | VAE |
| GN-OA [23] | Tested on typical compounds [23] | Optimization algorithms and GNNs |
| MAGUS [103] | WN6 [140], HeH2O [141] | BO and GA |
| SCCOP [87] | B-C-N [142], AgBiS2 [143] | Simulated annealing and GNNs |
| iMatGen [81] | V-O [81] | VAE |
| CrystalGAN [83] | Pd-Ni-H [83], Mg-Ti-H [83] | GAN |
| CCDCGAN [84] | MoSe2 [84] | GAN |
| MatterGen [85] | V-Sr-O [85] | Diffusion model |
| UniMat [144] | Tested on typical compounds [144] | Diffusion model |
| DiffCSP [102] | Tested on typical compounds [102] | Diffusion model |
| LLaMA-2 [145] | Tested on typical compounds [145] | Large language-based model |
| GOFEE [146] | C24 [31], Carbon clusters [31] | Large language-based model |
| BEACON [29,30] | Cu15 [29], CuNi clusters [30] | BO |
| CrySPY [52] | Y2Co17 [147], Al2O3 [147] | VAE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghian, M.; Palevicius, A.; Janusas, G. A Comprehensive Review of Machine-Learning Approaches for Crystal Structure/Property Prediction. Crystals 2025, 15, 925. https://doi.org/10.3390/cryst15110925
Sadeghian M, Palevicius A, Janusas G. A Comprehensive Review of Machine-Learning Approaches for Crystal Structure/Property Prediction. Crystals. 2025; 15(11):925. https://doi.org/10.3390/cryst15110925
Chicago/Turabian StyleSadeghian, Mostafa, Arvydas Palevicius, and Giedrius Janusas. 2025. "A Comprehensive Review of Machine-Learning Approaches for Crystal Structure/Property Prediction" Crystals 15, no. 11: 925. https://doi.org/10.3390/cryst15110925
APA StyleSadeghian, M., Palevicius, A., & Janusas, G. (2025). A Comprehensive Review of Machine-Learning Approaches for Crystal Structure/Property Prediction. Crystals, 15(11), 925. https://doi.org/10.3390/cryst15110925







