Exploring Structural, Optoelectronic, Phonon, Spintronic, and Thermodynamic Properties of Novel Full-Heusler Compounds TiMCu2 (M = Al, Ga, In): Eco-Friendly Materials for Next-Generation Renewable Energy Technologies
Abstract
1. Introduction
2. Materials and Methods
3. Results
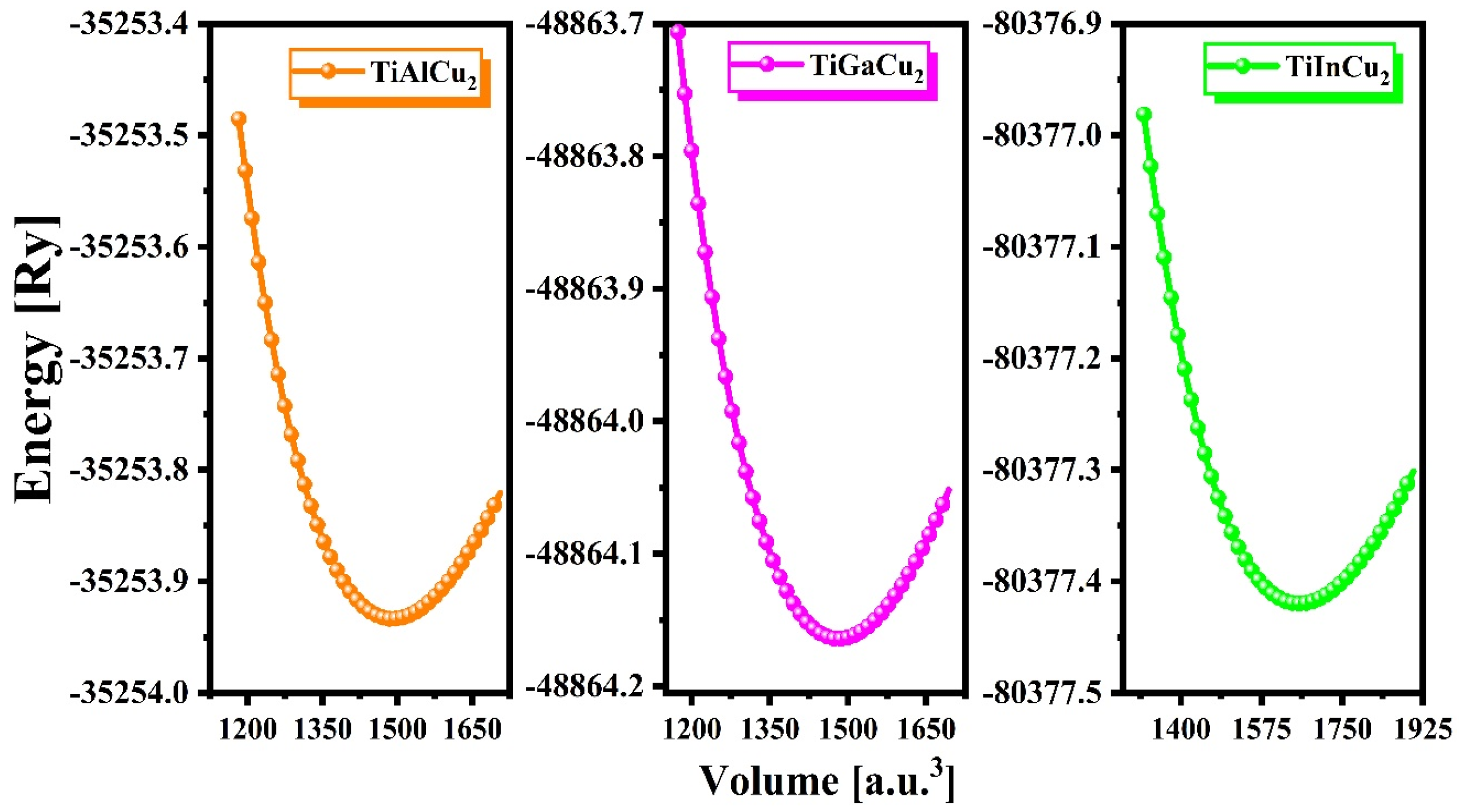
3.1. Structural Properties
3.2. Electronic Properties
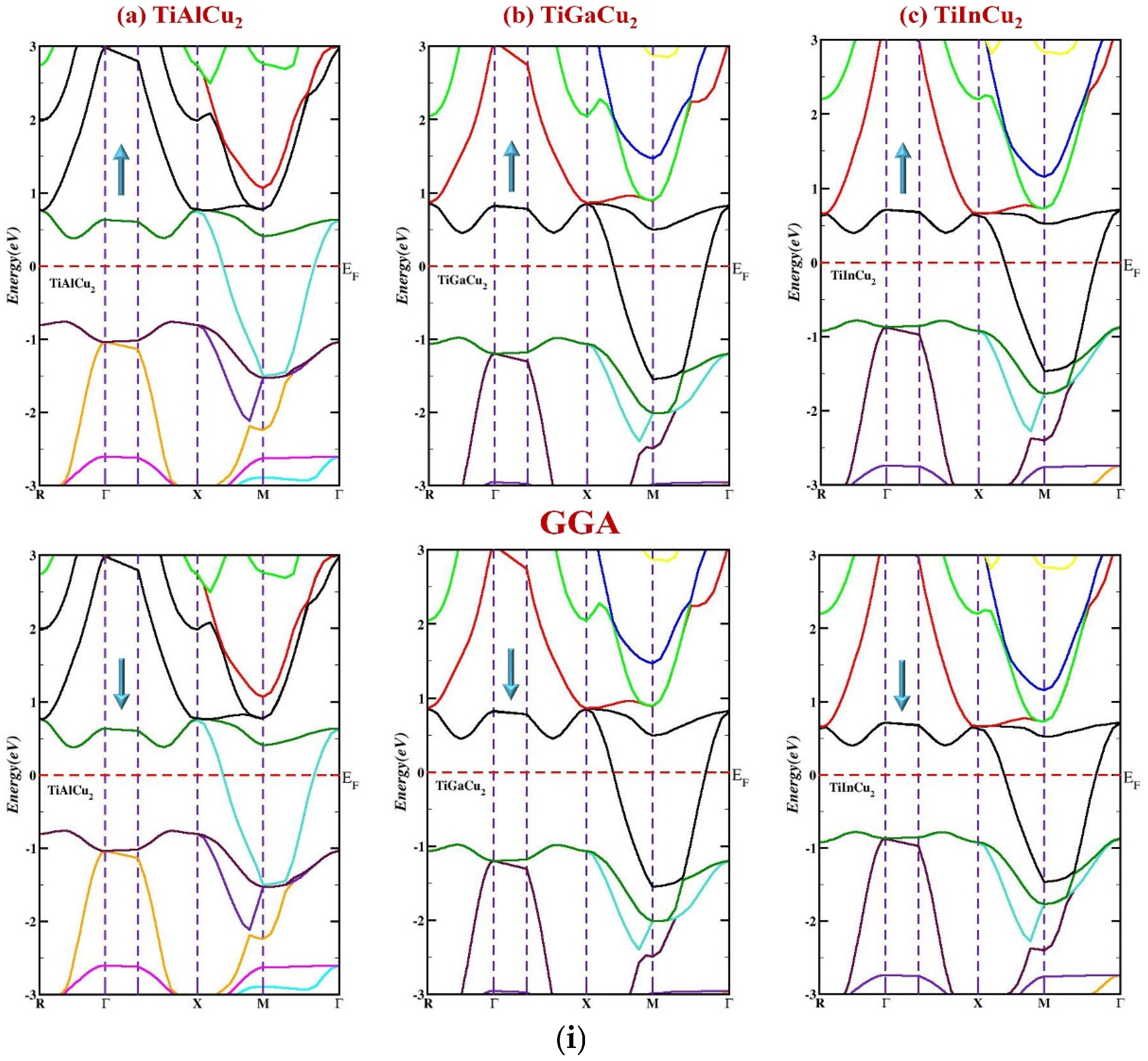
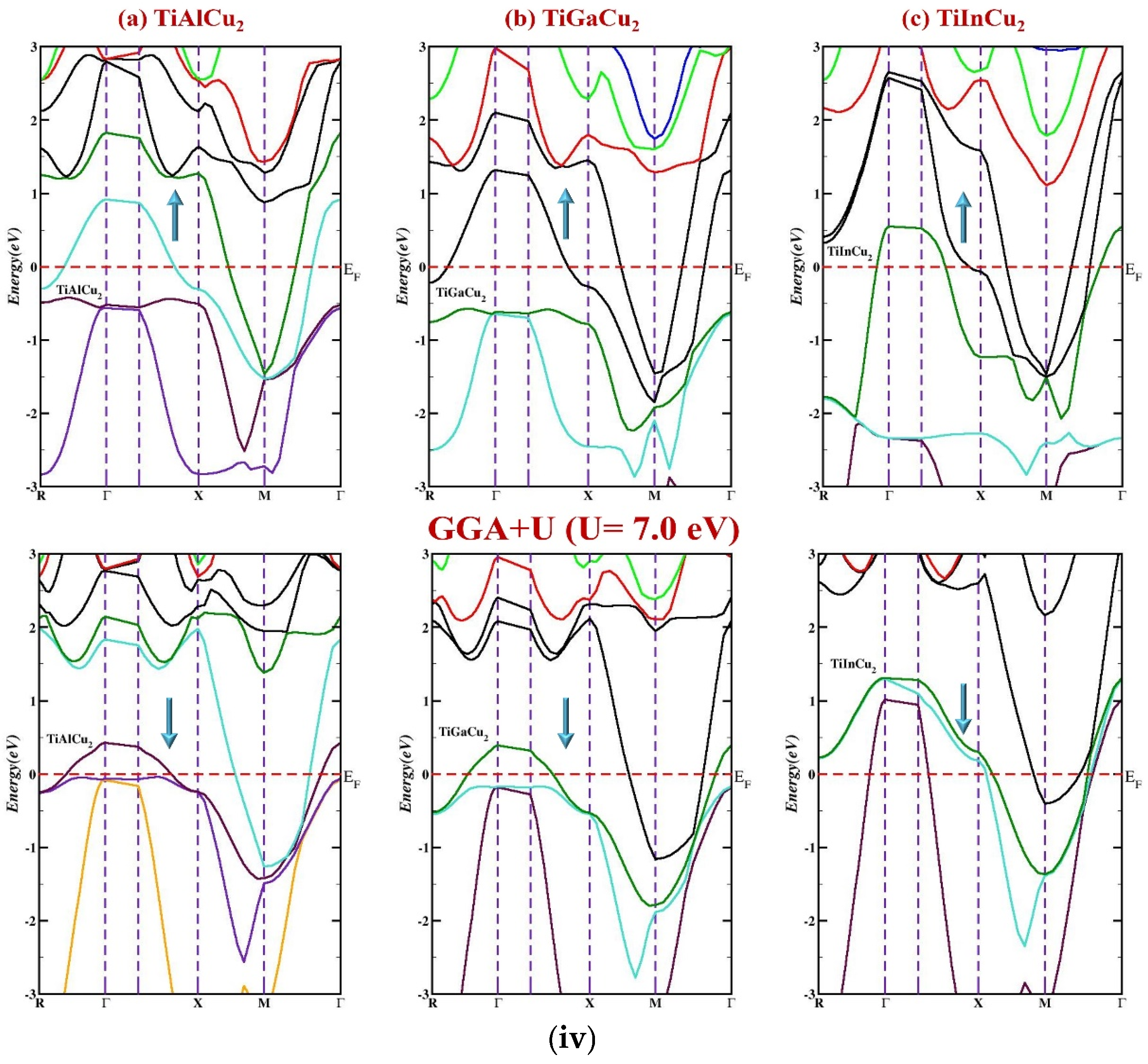
3.2.1. Energy Band Structures
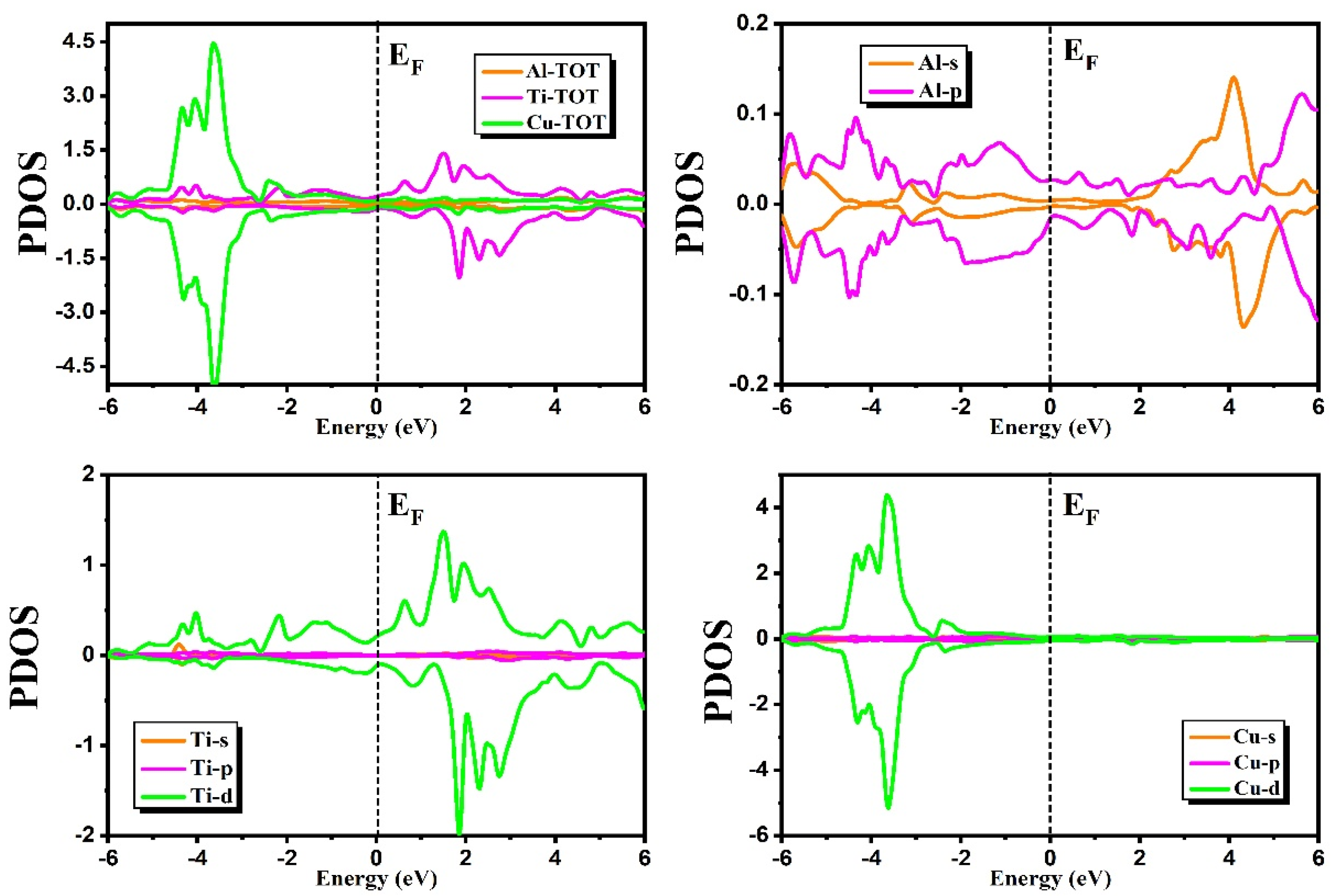
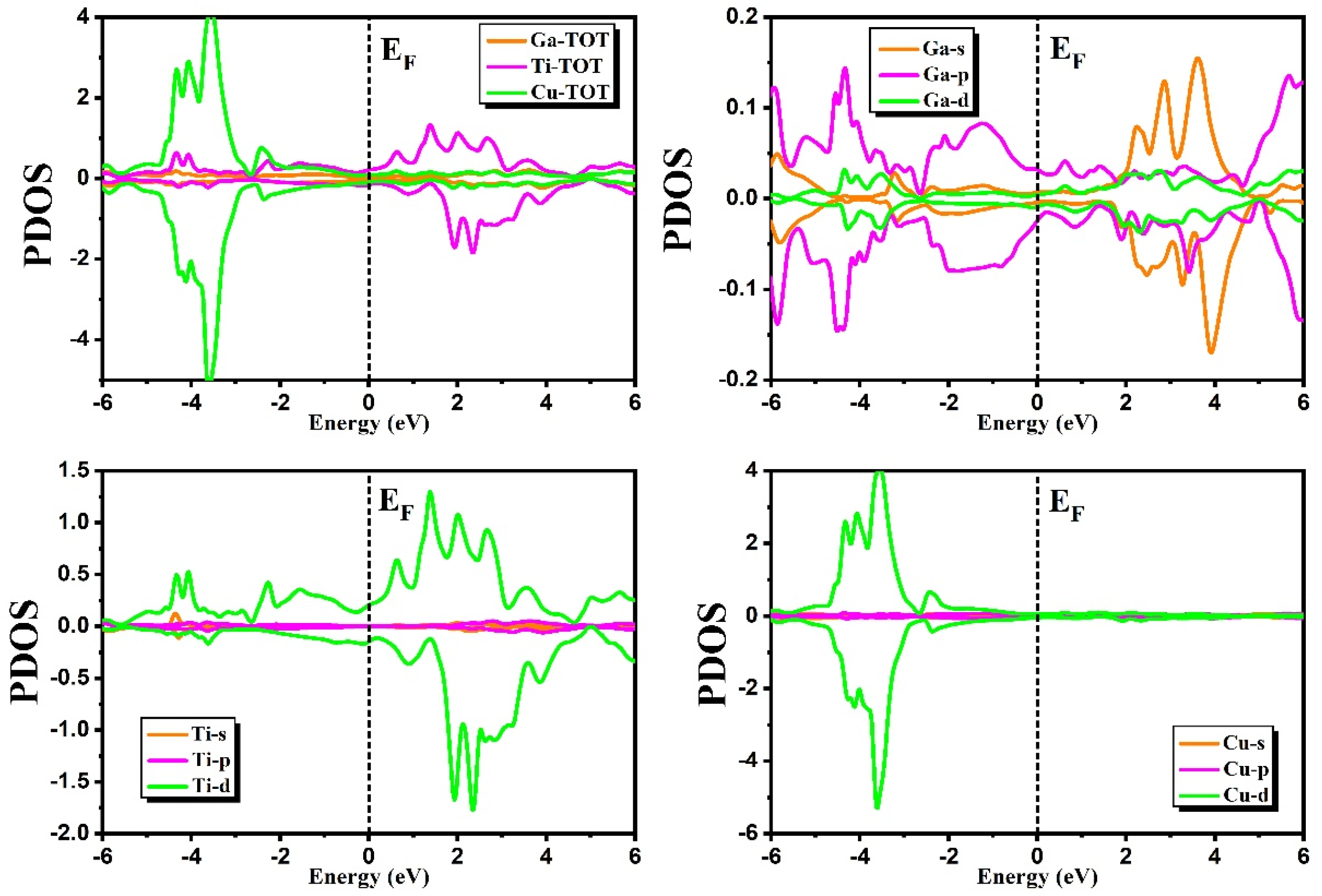
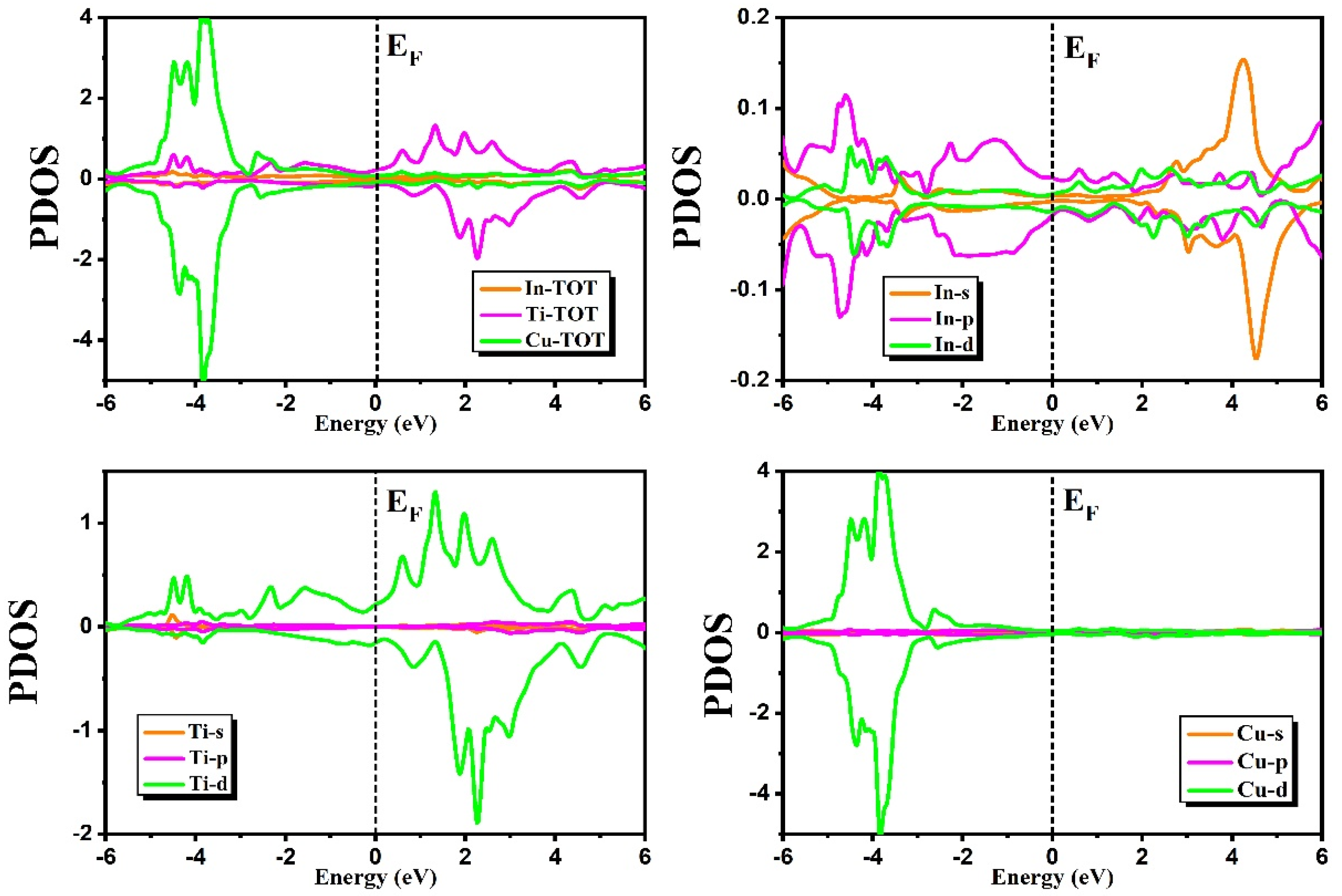
3.2.2. Density of States
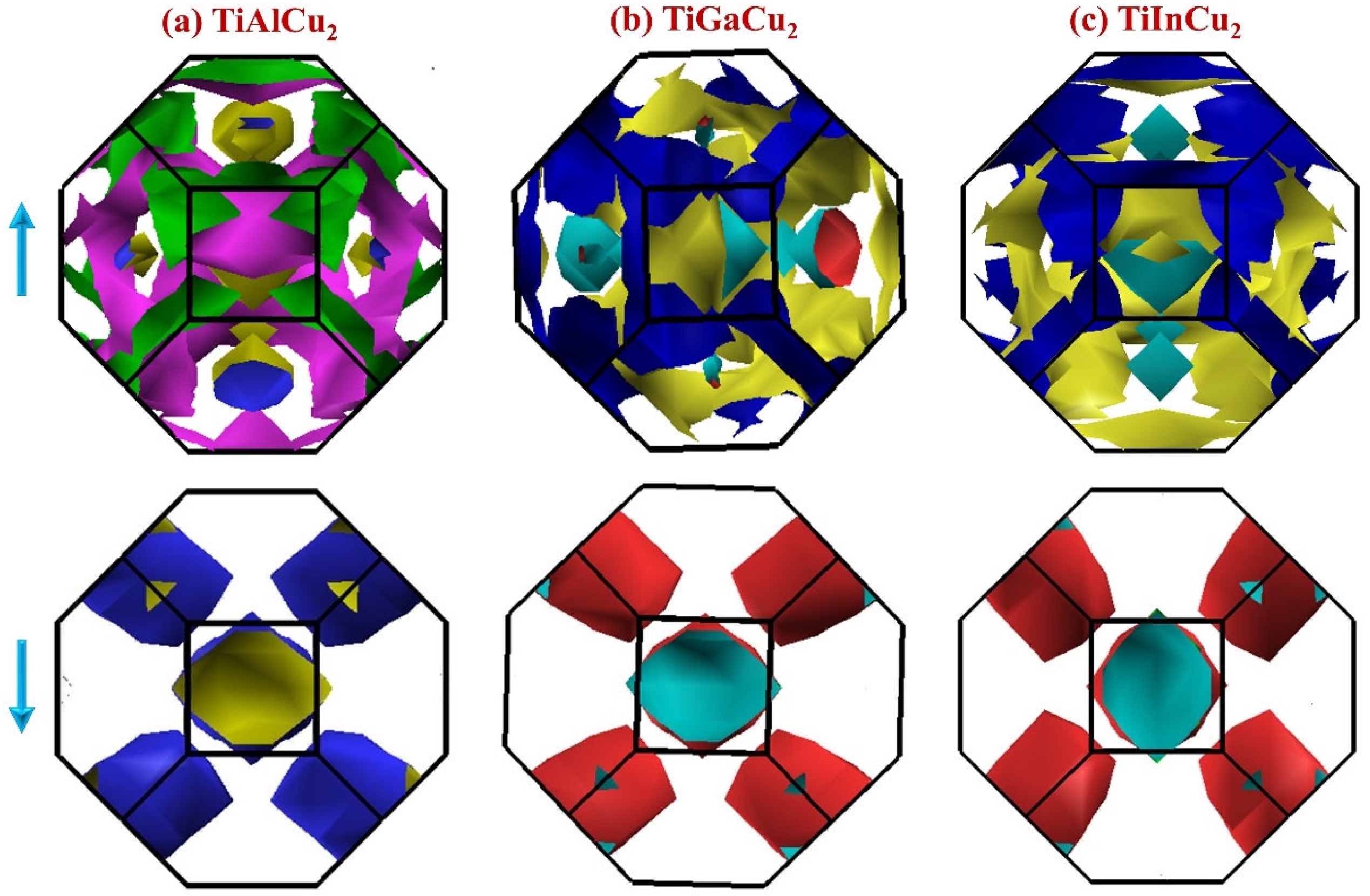
3.3. Fermi Surface
3.4. Phonon Dispersions
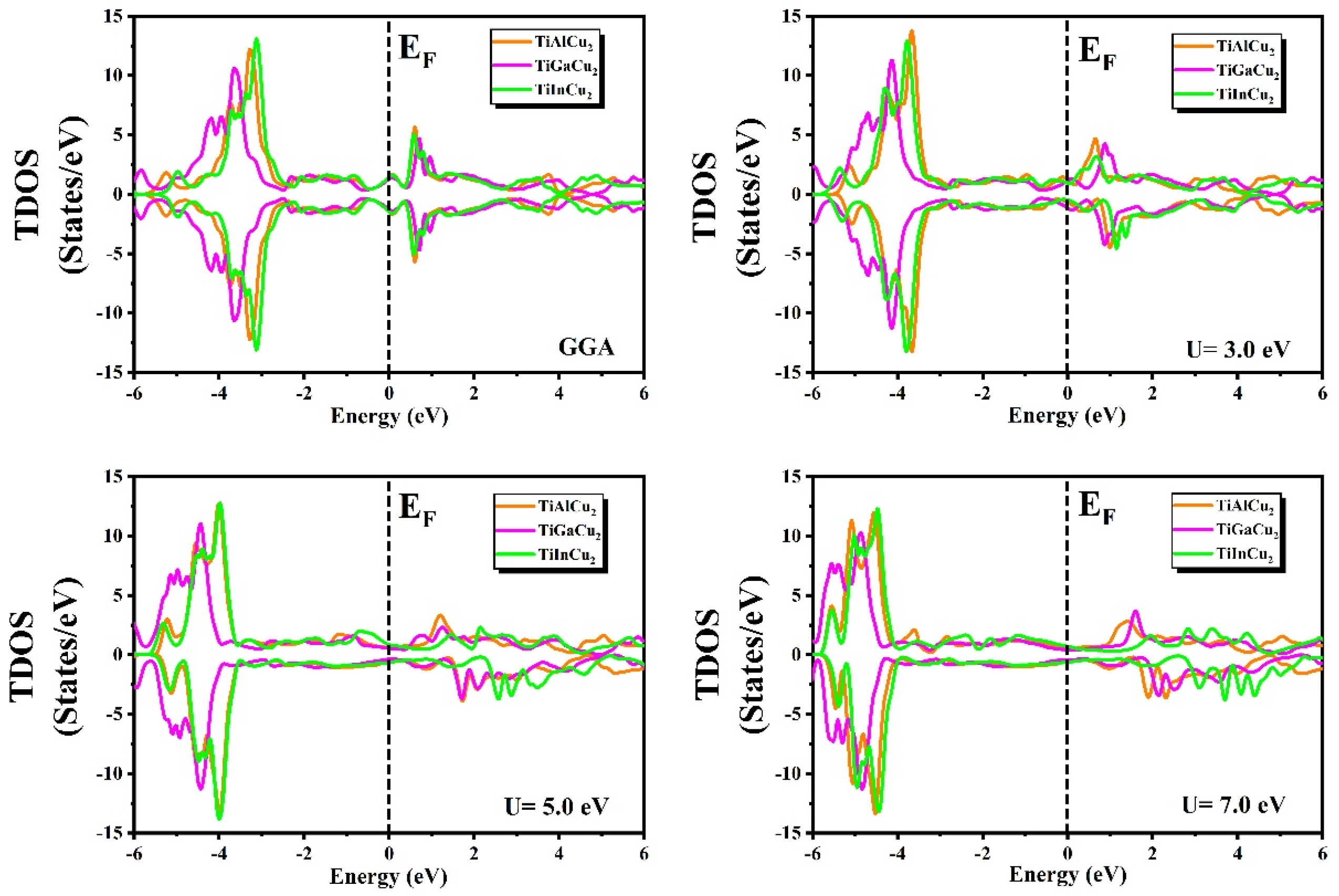
3.5. Magnetic Properties
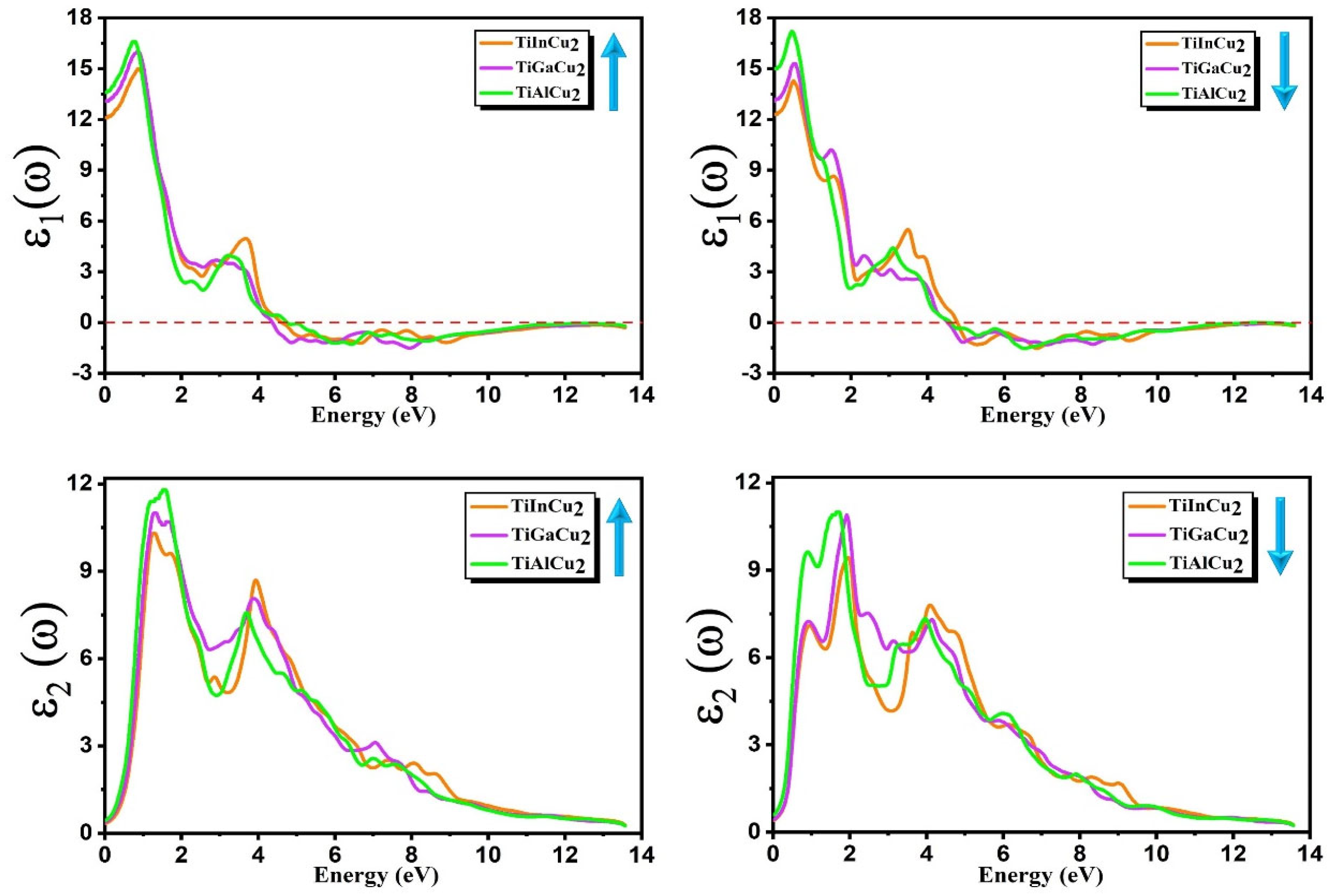
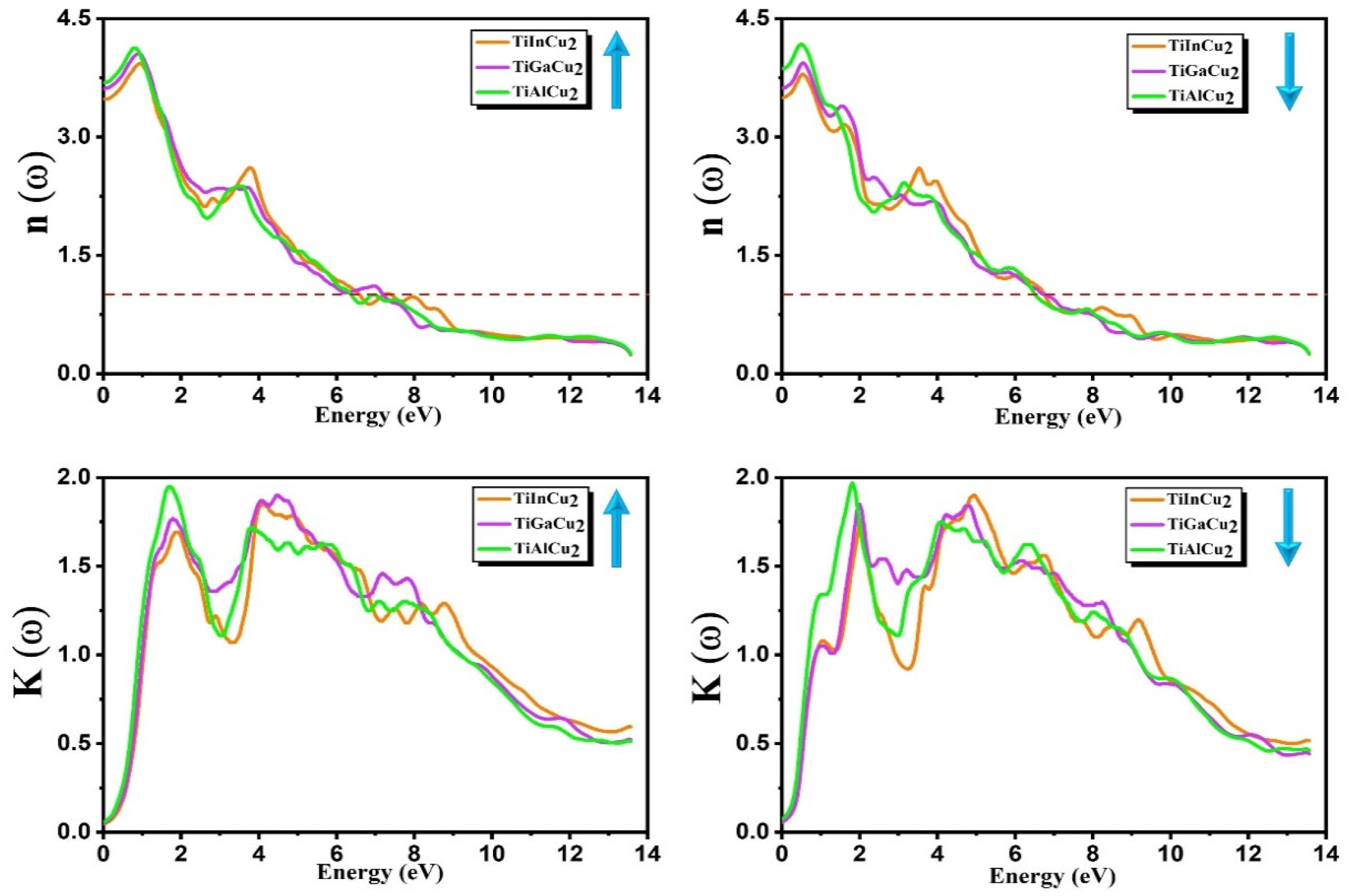
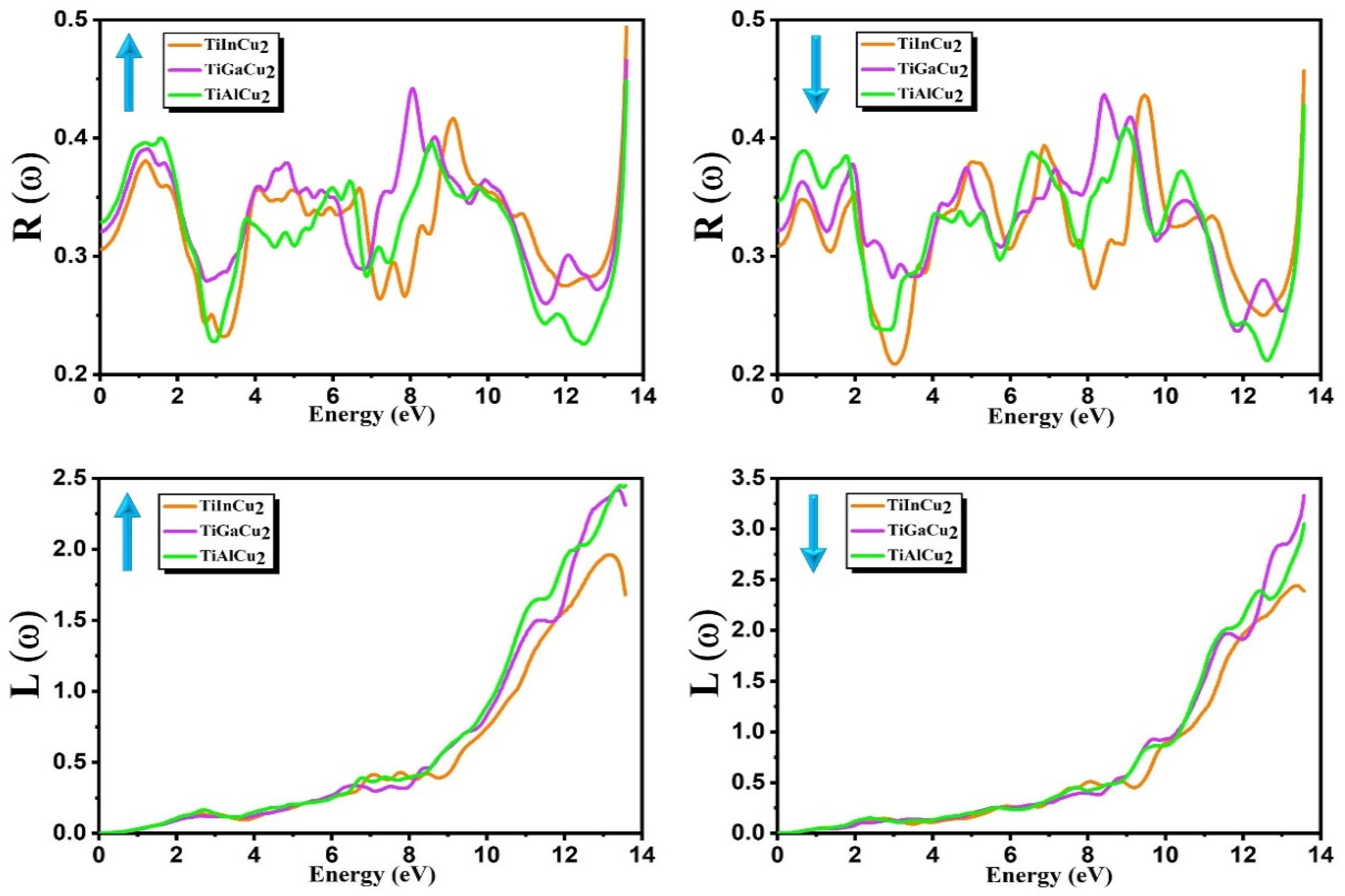
3.6. Optical Properties
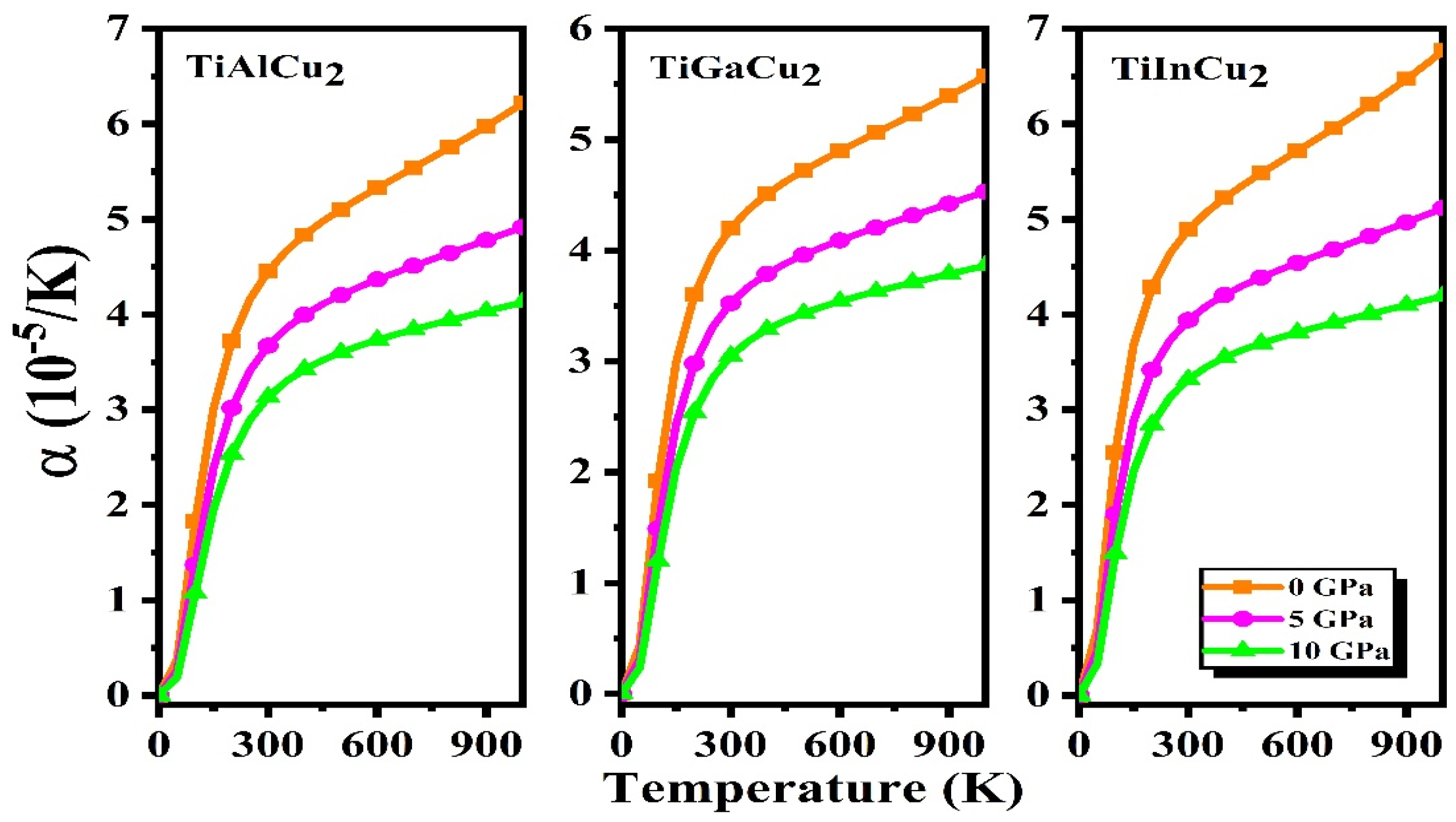
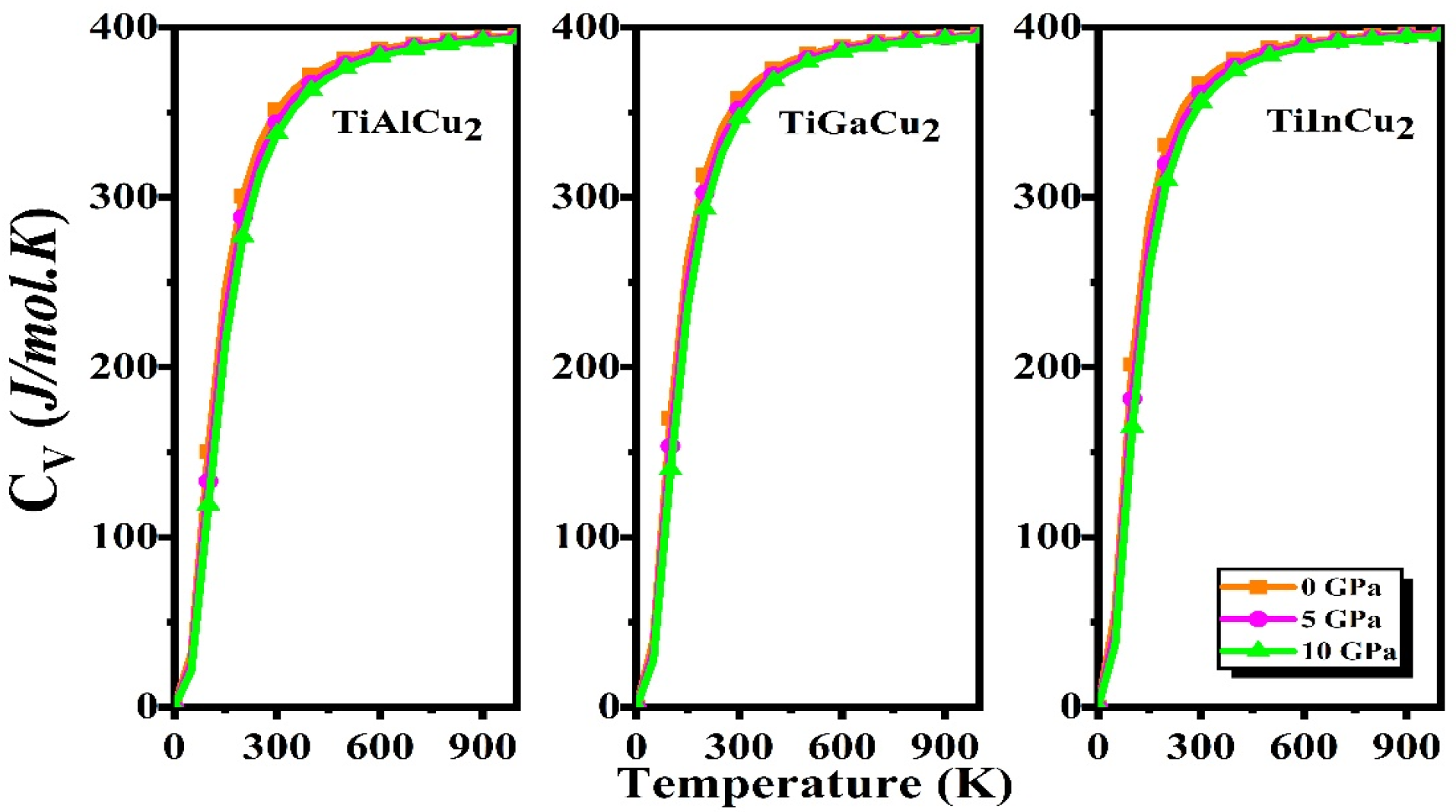
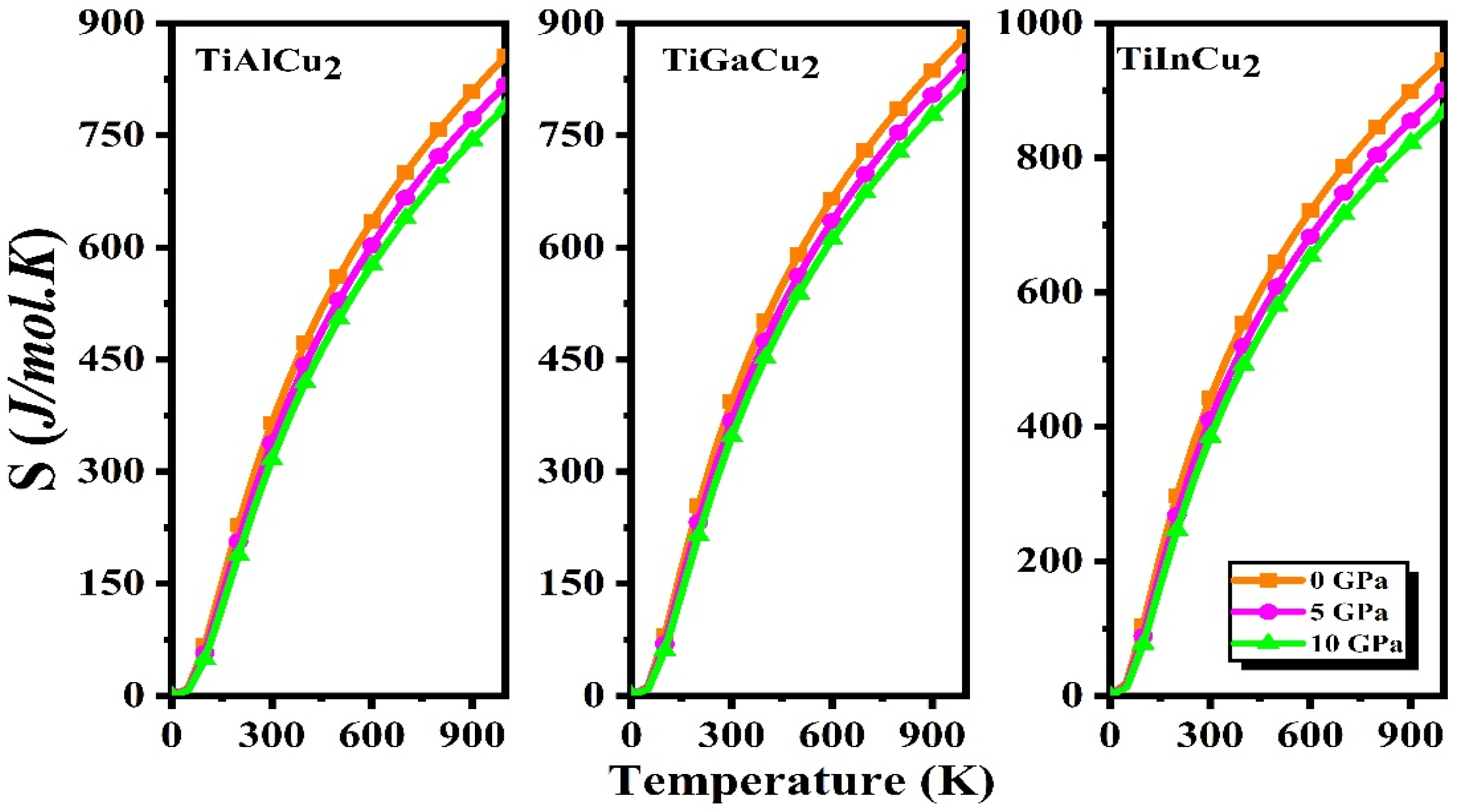
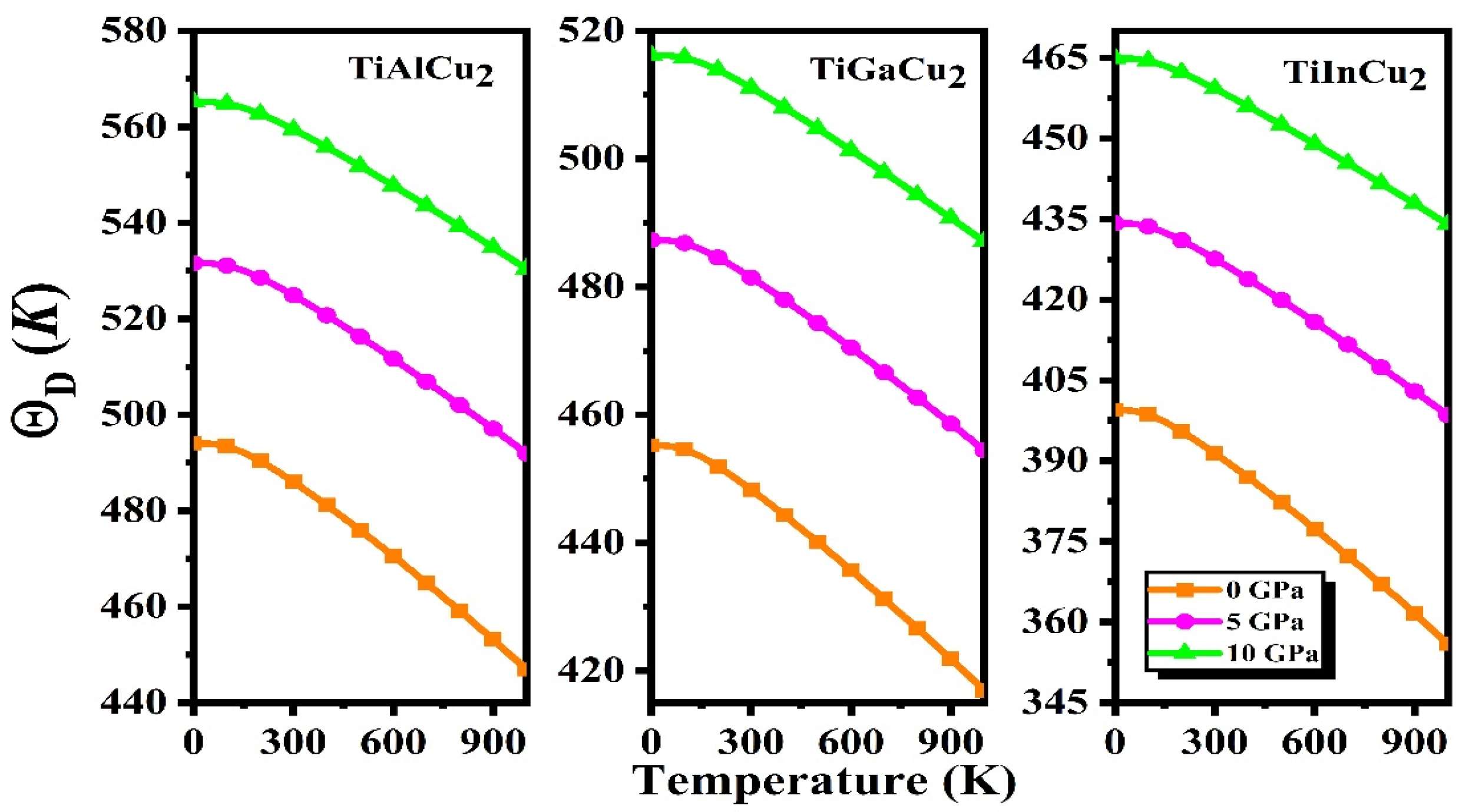
3.7. Thermodynamic Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tindibale, E.; Mulwa, W.M.; Adetunji, B.I. Elastic, anisotropic, lattice dynamics and electronic properties of XNiM and XNi2M (X= Ti, Zr, Hf; M= Sn, Ge, Si): DFT comparison study. Phys. B Condens. Matter. 2023, 665, 415029. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Cai, R.; Zhang, J.; Xia, S.; Li, Z.; Yu, C.; Wu, J.; Wang, P.; Wu, Y. Enhanced Local CO Coverage on Cu Quantum Dots for Boosting Electrocatalytic CO2 Reduction to Ethylene. Adv. Funct. Mater. 2025, 35, 2417764. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, C.; Xie, L.; Zhang, L.; Chai, X.; Wu, C.; Wang, S.; Peng, W.; Du, G.; Xu, K. Facile fabrication of electrospun hybrid nanofibers integrated cellulose, chitosan with ZIF-8 for efficient remediation of copper ions. Carbohydr. Polym. 2025, 359, 123574. [Google Scholar] [CrossRef] [PubMed]
- Luo, R.; Zhang, K.; Qin, Y.; Xie, L.; Chai, X.; Zhang, L.; Du, G.; Ge, S.; Rezakazemi, M.; Aminabhavi, T.M.; et al. Amine-functionalized UiO-66 incorporated electrospun cellulose/chitosan porous nanofibrous membranes for removing copper ions. Chem. Eng. J. 2024, 480, 148077. [Google Scholar] [CrossRef]
- Xu, K.; Li, Q.; Xie, L.; Shi, Z.; Su, G.; Harper, D.; Tang, Z.; Zhou, J.; Du, G.; Wang, S. Novel flexible, strong, thermal-stable, and high-barrier switchgrass-based lignin-containing cellulose nanofibrils/chitosan biocomposites for food packaging. Ind. Crops Prod. 2022, 179, 114661. [Google Scholar] [CrossRef]
- Amudhavalli, A.; Dharmaraj, P.; Manikandan, M.; RajeswaraPalanichamy, R.; Iyakutti, K. Investigation of optical properties of Zr2CoZ (Z= Al, Ga, In) full Heusler alloys. Solid State Sci. 2023, 144, 107307. [Google Scholar] [CrossRef]
- Yu, L.; Lei, Y.; Ma, Y.; Liu, M.; Zheng, J.; Dan, D.; Gao, P. A comprehensive review of fluorescence correlation spectroscopy. Front. Phys. 2021, 9, 644450. [Google Scholar] [CrossRef]
- Ren, H.; Xia, X.; Sun, Y.; Zhai, Y.; Zhang, Z.; Wu, J.; Li, J.; Liu, M. Electrolyte engineering for the mass exfoliation of graphene oxide across wide oxidation degrees. J. Mater. Chem. A 2024, 12, 23416–23424. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, X.; He, N.; Song, F.; Zhang, X. Physical absorption and thermodynamic modeling of CO2 in new deep eutectic solvents. J. Mol. Liq. 2024, 402, 124752. [Google Scholar] [CrossRef]
- Buschow, K.; Van Engen, P. Magnetic and magneto-optical properties of Heusler alloys based on aluminium and gallium. J. Magn. Magn. Mater. 1981, 25, 90–96. [Google Scholar] [CrossRef]
- Kimura, Y.; Tamura, Y.; Kita, T. Thermoelectric properties of directionally solidified half-Heusler compound NbCoSn alloys. Appl. Phys. Lett. 2008, 92, 012105. [Google Scholar] [CrossRef]
- Rai, D.; Sandeep, S.; Shankar, A.; Khenata, R.; Reshak, A.; Ekuma, C.; Thapa, R.; Ke, S.-H. Electronic, optical, and thermoelectric properties of Fe2+ xV1− xAl. AIP Adv. 2017, 7, 045118. [Google Scholar] [CrossRef]
- Winterlik, J.; Fecher, G.H.; Thomas, A.; Felser, C. Superconductivity in palladium-based Heusler compounds. Phys. Rev. B 2009, 79, 064508. [Google Scholar] [CrossRef]
- Liang, S.; Gao, Y.; Hu, C.; Hao, A.; Qin, H. Efficient Photon Beam Diffusion for Directional Subsurface Scattering. IEEE Trans. Vis. Comput. Graph. 2024. [Google Scholar] [CrossRef]
- Meng, S.; Meng, F.; Zhang, F.; Li, Q.; Zhang, Y.; Zemouche, A. Observer design method for nonlinear generalized systems with nonlinear algebraic constraints with applications. Automatica 2024, 162, 111512. [Google Scholar] [CrossRef]
- Spataru, C.D.; He, Y.; Léonard, F. Atomistic study of an ideal metal/thermoelectric contact: The full-Heusler/half-Heusler interface. APL Mater. 2019, 7, 013202. [Google Scholar] [CrossRef]
- Poon, S.J. Half Heusler compounds: Promising materials for mid-to-high temperature thermoelectric conversion. J. Phys. D Appl. Phys. 2019, 52, 493001. [Google Scholar] [CrossRef]
- Luo, Y.; Dong, Y. Strain Measurement at up to 3000° C Based on Ultraviolet-Digital Image Correlation. NDT E Int. 2024, 146, 103155. [Google Scholar] [CrossRef]
- Bachagha, T.; Suñol, J.-J. All-d-metal Heusler alloys: A review. Metals 2023, 13, 111. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, H.; Wang, Y.; Gao, X.; Wang, Z.; Wang, N.; Zang, D. Ultrasound induced grain refinement of crystallization in evaporative saline droplets. Ultrason. Sonochemistry 2024, 107, 106938. [Google Scholar] [CrossRef]
- Abbas, Z.; Fatima, K.; Butt, K.; Butt, F.; Hussain, S.; Muhammad, S. Structural, electronic, optical, magnetic and thermodynamics properties of novel half-heusler alloys XNiSb (X= Er, Ho, Yb): First-principles calculations. Opt. Quantum Electron. 2023, 55, 1070. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, X. Cracking elements method for dynamic brittle fracture. Theor. Appl. Fract. Mech. 2019, 102, 1–9. [Google Scholar] [CrossRef]
- Meng, S.; Meng, F.; Chi, H.; Chen, H.; Pang, A. A robust observer based on the nonlinear descriptor systems application to estimate the state of charge of lithium-ion batteries. J. Frankl. Inst. 2023, 360, 11397–11413. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Zhang, H.; Xu, T.; Zhang, Z.; Han, Q.; Liu, T.; Zou, Y.; Cheng, Z. Mid-Infrared Hyperuniform Disordered Solids Waveguide Devices with Morphology Engineering and Wall-Network Regulation. Laser Photonics Rev. 2025, 19, 2400469. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Rozale, H.; Lu, J.-W.; Wang, L.-Y. Half-Metallicity and Tetragonal Deformation of Ti 2 RhAl, Ti 2 RhGa, and Ti 2 RhIn: A first-principle study. J. Supercond. Nov. Magn. 2016, 29, 349–356. [Google Scholar] [CrossRef]
- De Groot, R.A.; Mueller, F.M.; van Engen, P.v.; Buschow, K. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, R.; Xiao, N.; Wang, Z.; Chen, L.; Wen, Y.; Li, P. Wireless multiferroic memristor with coupled giant impedance and artificial synapse application. Adv. Electron. Mater. 2022, 8, 2200370. [Google Scholar] [CrossRef]
- Fang, Q.-L.; Zhang, J.-M.; Xu, K.-W. Magnetic properties and origin of the half-metallicity of Ti2MnZ (Z= Al, Ga, In, Si, Ge, Sn) Heusler alloys with the Hg2CuTi-type structure. J. Magn. Magn. Mater. 2014, 349, 104–108. [Google Scholar] [CrossRef]
- Wang, G.; Feng, W. On-chip Mach-Zehnder interferometer sensor with a double-slot hybrid plasmonic waveguide for high-sensitivity hydrogen detection. Opt. Express 2023, 31, 39500–39513. [Google Scholar] [CrossRef]
- Li, Y.; Liu, G.; Wang, X.; Liu, E.; Xi, X.; Wang, W.; Wu, G.; Wang, L.; Dai, X. First-principles study on electronic structure, magnetism and half-metallicity of the NbCoCrAl and NbRhCrAl compounds. Results Phys. 2017, 7, 2248–2254. [Google Scholar] [CrossRef]
- Doumi, B.; Mokaddem, A.; Sayede, A.; Dahmane, F.; Mogulkoc, Y.; Tadjer, A. First-principles investigations on ferromagnetic behaviour of Be1− xVxZ (Z= S, Se and Te)(x= 0.25). Superlattices Microstruct. 2015, 88, 139–149. [Google Scholar] [CrossRef]
- Han, Y.; Khenata, R.; Li, T.; Wang, L.; Wang, X. Search for a new member of parabolic-like spin-gapless semiconductors: The case of diamond-like quaternary compound CuMn2InSe4. Results Phys. 2018, 10, 301–303. [Google Scholar] [CrossRef]
- Dahmane, F.; Benalia, S.; Djoudi, L.; Tadjer, A.; Khenata, R.; Doumi, B.; Aourag, H. First-principles study of structural, electronic, magnetic and half-metallic properties of the Heusler alloys Ti 2 ZAl (Z= Co, Fe, Mn). J. Supercond. Nov. Magn. 2015, 28, 3099–3104. [Google Scholar] [CrossRef]
- Dahmane, F.; Doumi, B.; Mogulkoc, Y.; Tadjer, A.; Prakash, D.; Verma, K.; Varshney, D.; Ghebouli, M.; Omran, S.B.; Khenata, R. Investigations of the structural, electronic, magnetic, and half-metallic behavior of Co 2 MnZ (Z= Al, Ge, Si, Ga) Full-Heusler compounds. J. Supercond. Nov. Magn. 2016, 29, 809–817. [Google Scholar] [CrossRef]
- Haque, E.; Hossain, M.A. First-principles study of elastic, electronic, thermodynamic, and thermoelectric transport properties of TaCoSn. Results Phys. 2018, 10, 458–465. [Google Scholar] [CrossRef]
- Han, Y.; Chen, Z.; Kuang, M.; Liu, Z.; Wang, X.; Wang, X. 171 Scandium-based full Heusler compounds: A comprehensive study of competition between XA and L21 atomic ordering. Results Phys. 2019, 12, 435–446. [Google Scholar] [CrossRef]
- Han, Y.; Wu, M.; Kuang, M.; Yang, T.; Chen, X.; Wang, X. All-d-metal equiatomic quaternary Heusler hypothetical alloys ZnCdTMn (T= Fe, Ru, Os, Rh, Ir, Ni, Pd, Pt): A first-principle investigation of electronic structures, magnetism, and possible martensitic transformations. Results Phys. 2018, 11, 1134–1141. [Google Scholar] [CrossRef]
- Dahmane, F.; Mesri, D.; Tadjer, A.; Khenata, R.; Benalia, S.; Djoudi, L.; Doumi, B.; Boumia, L.; Aourag, H. Electronic structure, magnetism and stability of Co2CrX (X= Al, Ga, In) ab initio study. Mod. Phys. Lett. B 2016, 30, 1550265. [Google Scholar] [CrossRef]
- Anjami, A.; Boochani, A.; Elahi, S.M.; Akbari, H. Ab-initio study of mechanical, half-metallic and optical properties of Mn2ZrX (X= Ge, Si) compounds. Results Phys. 2017, 7, 3522–3529. [Google Scholar] [CrossRef]
- Yousuf, S.; Gupta, D.C. Investigation of electronic, magnetic and thermoelectric properties of Zr2NiZ (Z= Al, Ga) ferromagnets. Mater. Chem. Phys. 2017, 192, 33–40. [Google Scholar] [CrossRef]
- Wang, X.; Cui, Y.; Liu, X.; Liu, G. Electronic structures and magnetism in the Li2AgSb-type Heusler alloys, Zr2CoZ (Z= Al, Ga, In, Si, Ge, Sn, Pb, Sb): A first-principles study. J. Magn. Magn. Mater. 2015, 394, 50–59. [Google Scholar] [CrossRef]
- Yan, P.-L.; Zhang, J.-M.; Xu, K.-W. Electronic structures, magnetic properties and half-metallicity in Heusler alloys Zr2CoZ (Z= Al, Ga, In, Sn). J. Magn. Magn. Mater. 2015, 391, 43–48. [Google Scholar] [CrossRef]
- Yousuf, S.; Gupta, D.C. Chemical stability and thermodynamics of new Zr2-based heusler alloys. Mater. Eng. Res. 2019, 1, 1–6. [Google Scholar] [CrossRef]
- Meng, F.; Hao, H.; Ma, Y.; Guo, X.; Luo, H. Site preference of Zr in Heusler alloys Zr2YAl (Y= Cr, Mn, Fe, Co, Ni) and its influence on the electronic properties. J. Alloys Compd. 2017, 695, 2995–3001. [Google Scholar] [CrossRef]
- Khaliq, A.; Zhou, X.; Chai, H.; Ali, M.; Wu, H.; Gassab, O.; Liu, H.; Xiao, D.; Yang, X.-G.; Du, S. Illumination Induced Negative Differential Resistance in InGaAs Avalanche Photodiode. IEEE Access 2024, 12, 50595–50604. [Google Scholar] [CrossRef]
- Heusler, F.; Starck, W.; Haupt, E. Magnetisch-chemische studien. Verh. Dtsch. Phys. Ges 1903, 5, 219–232. [Google Scholar]
- Chen, Y.; Li, C.; Yang, X. Simultaneous measurement of trace dimethyl methyl phosphate and temperature using all fiber Michaelson interferometer cascaded FBG. Opt. Express 2023, 31, 6203–6216. [Google Scholar] [CrossRef]
- Seema, K.; Umran, N.; Kumar, R. Effect of Disorder on Electronic, Magnetic, and Optical Properties of Co 2 CrZ Heusler Alloys (Z= Al, Ga, Si, Ge). J. Supercond. Nov. Magn. 2016, 29, 401–408. [Google Scholar]
- Zhou, H.; Guo, J.; Zhu, G.; Xie, F.; Tang, X.; Luo, X. Highly efficient preparation of crystalline yttrium carbonate in sodium carbonate system: Formation and growth mechanism. J. Rare Earths 2025, 43, 1492–1501. [Google Scholar] [CrossRef]
- Long, Q.; Yan, H.; Wu, H.; Qiu, S.; Zhou, X.; Qiu, T. Influence mechanism of leaching agent anions on the leaching of aluminium impurities in ionic-type rare earth ores: A DFT simulation combined with experimental verification. Sep. Purif. Technol. 2025, 354, 128768. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, Y.; Wang, H.; Xie, L.; Chai, X.; Zhang, L.; Peng, W.; Wang, S.; Du, G.; Xu, K. Electrospun biomass carbon-based porous nanofibers modified by green-dry cold plasma for gaseous formaldehyde adsorption. Ind. Crops Prod. 2024, 222, 119769. [Google Scholar] [CrossRef]
- Elkoua, I.A.; Masrour, R. A comparative study of physical and thermoelectrical characteristics of the new full-Heusler alloys Ag2TiGa and Ag2VGa with ab initio calculations. Int. J. Quantum Chem. 2024, 124, e27307. [Google Scholar] [CrossRef]
- Elkoua, I.A.; Masrour, R. DFT and Monte Carlo study of the structural, elastic, electronic, magnetic and magnetocaloric properties of Ni2MnSi full-Heusler alloys. Mater. Sci. Semicond. Process. 2025, 190, 109266. [Google Scholar] [CrossRef]
- Galta, A.E.; Masrour, R. Exploring the theoretical properties of Rh2TbY (Y = Ga, In) Full-Heusler alloys: Structural, Magneto-electronic, Thermodynamic, and thermoelectric Perspectives. Comput. Theor. Chem. 2025, 1244, 115008. [Google Scholar] [CrossRef]
- Abbas, Z.; Naz, A.; Hussain, S.; Muhammad, S.; Algarni, H.; Ali, A.; Jung, J. First-Principles Calculations to Investigate Structural, Electronic, Optical and Magnetic Properties of Pyrochlore Oxides Eu2Tm2O7 (Tm= Hf, Sn, Zr) for Energy Applications. Inorganics 2023, 11, 193. [Google Scholar] [CrossRef]
- Cai, Y.; Lan, J.; Zhang, G.; Zhang, Y.-W. Lattice vibrational modes and phonon thermal conductivity of monolayer MoS 2. Physical Review B 2014, 89, 035438. [Google Scholar] [CrossRef]
- Rauf, S.; Arif, S.; Haneef, M.; Amin, B. The first principle study of magnetic properties of Mn2WSn, Fe2YSn (Y= Ti, V), Co2YSn (Y= Ti, Zr, Hf, V, Mn) and Ni2YSn (Y= Ti, Zr, Hf, V, Mn) heusler alloys. J. Phys. Chem. Solids 2015, 76, 153–169. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, L.; Zhong, A.; Huang, G.; Wu, F.; Li, D.; Teng, M.; Wang, J.; Han, D. Deep red PhOLED from dimeric salophen Platinum (II) complexes. Dye. Pigment. 2019, 162, 590–598. [Google Scholar] [CrossRef]
- Blanco, M.; Francisco, E.; Luana, V. GIBBS: Isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model. Comput. Phys. Commun. 2004, 158, 57–72. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Kaur, N.; Srivastava, V.; Dar, S.A.; Khenata, R.; Sharma, R. A unified DFT exploration on transport and thermodynamic properties of L21 structure of Rh2XZn (X= Mn, Fe) ferromagnets. Mater. Sci. Eng. B 2023, 287, 116099. [Google Scholar] [CrossRef]




| Compound | Element | Wycoff | x | y | z |
|---|---|---|---|---|---|
| TiAlCu2 | Ti | 4a | 0 | 0 | 0 |
| Al | 4b | 0 | 1/2 | 0 | |
| Cu | 8c | 3/4 | 1/4 | 3/4 | |
| TiGaCu2 | Ti | 4a | 0 | 0 | 0 |
| Ga | 4b | 0 | 1/2 | 0 | |
| Cu | 8c | 3/4 | 1/4 | 3/4 | |
| TiInCu2 | Ti | 4a | 0 | 0 | 0 |
| In | 4b | 0 | 1/2 | 0 | |
| Cu | 8c | 3/4 | 1/4 | 3/4 |
| Compounds | a | V | B | (XA) | ) | ||
|---|---|---|---|---|---|---|---|
| (Å) | (Å3) | (GPa) | (GPa) | (Ry) | (Ry) | (eV) | |
| TiAlCu2 | 6.04 | 1490.02 | 135.09 | 4.57 | −35,253.93 | −35,253.67 | Metallic |
| TiGaCu2 | 6.03 | 1482.05 | 138.23 | 4.36 | −48,864.16 | −48,863.71 | |
| TiInCu2 | 6.26 | 1656.44 | 121.78 | 4.75 | −80,377.42 | −80,377.15 |
| Compounds | GGA | GGA+U | ||
|---|---|---|---|---|
| 3.0 | 5.0 | 7.0 | ||
| TiAlCu2 | 0.035 | 28.42 | 1.08 | 5.70 |
| TiGaCu2 | 0.009 | 0.067 | 22.31 | 0.014 |
| TiInCu2 | 0.016 | 33.69 | 13.89 | 7.63 |
| Compounds | Method | Magnetic Moment () | ||||
|---|---|---|---|---|---|---|
| TiAlCu2 | GGA | −0.0001 | −0.0006 | 0.00002 | 0.0001 | −0.0007 |
| GGA+U | 0.0283 | −0.0222 | 0.6982 | −0.0449 | 0.6594 | |
| TiGaCu2 | GGA | 0.00000 | −0.00007 | 0.0000 | 0.00001 | −0.00006 |
| GGA+U | 0.0545 | −0.0222 | 0.7546 | −0.0313 | 0.7556 | |
| TiInCu2 | GGA | −0.00002 | −0.00006 | 0.0000 | 0.0000 | −0.00008 |
| GGA+U | 0.0555 | −0.0173 | 0.7354 | −0.0283 | 0.7452 | |
| Compounds | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | |
| TiAlCu2 | 1.58 | 1.63 | 1.67 | 1.78 | 13.37 | 13.52 | 3.64 | 3.97 | 8.34 | 6.43 |
| TiGaCu2 | 1.33 | 1.91 | 4.12 | 1.97 | 13.40 | 13.58 | 3.91 | 4.17 | 7.90 | 8.31 |
| TiInCu2 | 1.27 | 1.97 | 4.46 | 4.95 | 13.15 | 13.32 | 3.96 | 4.70 | 8.84 | 9.19 |
| Compounds | ||||||
|---|---|---|---|---|---|---|
| ↑ | ↓ | ↑ | ↓ | ↑ | ↓ | |
| TiAlCu2 | 13.6 | 15.0 | 3.69 | 3.87 | 0.33 | 0.35 |
| TiGaCu2 | 13.1 | 13.1 | 3.61 | 3.62 | 0.32 | 0.32 |
| TiInCu2 | 12.1 | 12.3 | 3.48 | 3.50 | 0.31 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, Z.; Parveen, A.; Elsaeedy, H.I.; Mahjoub Said, N.; Khan, M.T. Exploring Structural, Optoelectronic, Phonon, Spintronic, and Thermodynamic Properties of Novel Full-Heusler Compounds TiMCu2 (M = Al, Ga, In): Eco-Friendly Materials for Next-Generation Renewable Energy Technologies. Crystals 2025, 15, 876. https://doi.org/10.3390/cryst15100876
Abbas Z, Parveen A, Elsaeedy HI, Mahjoub Said N, Khan MT. Exploring Structural, Optoelectronic, Phonon, Spintronic, and Thermodynamic Properties of Novel Full-Heusler Compounds TiMCu2 (M = Al, Ga, In): Eco-Friendly Materials for Next-Generation Renewable Energy Technologies. Crystals. 2025; 15(10):876. https://doi.org/10.3390/cryst15100876
Chicago/Turabian StyleAbbas, Zeesham, Amna Parveen, H. I. Elsaeedy, Nejla Mahjoub Said, and Mohd Taukeer Khan. 2025. "Exploring Structural, Optoelectronic, Phonon, Spintronic, and Thermodynamic Properties of Novel Full-Heusler Compounds TiMCu2 (M = Al, Ga, In): Eco-Friendly Materials for Next-Generation Renewable Energy Technologies" Crystals 15, no. 10: 876. https://doi.org/10.3390/cryst15100876
APA StyleAbbas, Z., Parveen, A., Elsaeedy, H. I., Mahjoub Said, N., & Khan, M. T. (2025). Exploring Structural, Optoelectronic, Phonon, Spintronic, and Thermodynamic Properties of Novel Full-Heusler Compounds TiMCu2 (M = Al, Ga, In): Eco-Friendly Materials for Next-Generation Renewable Energy Technologies. Crystals, 15(10), 876. https://doi.org/10.3390/cryst15100876





