Abstract
Multiple-Q magnetic states encompass a broad class of noncollinear and noncoplanar spin textures generated by the superposition of spin density waves. In this study, we theoretically explore the emergence of vortex crystals formed by multiple-Q spin density waves on a two-dimensional triangular lattice with point group symmetry. Using simulated annealing applied to an effective spin model, we demonstrate that the synergy among the easy-plane single-ion anisotropy, the biquadratic interaction, and the out-of-plane Dzyaloshinsky–Moriya interaction defined in momentum space can give rise to a variety of double-Q and triple-Q vortex crystals. We further examine the role of easy-plane single-ion anisotropy in triple-Q vortex crystals and show that weakening the anisotropy drives topological transitions into skyrmion crystals with skyrmion numbers and . The influence of an external magnetic field is also analyzed, revealing a field-induced phase transition from vortex crystals to single-Q conical spirals. These findings highlight the crucial role of out-of-plane Dzyaloshinskii–Moriya interactions in stabilizing unconventional vortex crystals, which cannot be realized in systems with purely polar or chiral symmetries.
1. Introduction
Noncollinear and noncoplanar spin textures have become a central focus in condensed matter physics, as they provide a natural platform for realizing topologically nontrivial states and the associated exotic transport and magnetoelectric phenomena. A hallmark of such textures is the topological Hall effect, in which a Hall voltage arises not from external magnetic fields or net magnetization but from the real-space Berry phase associated with finite scalar spin chirality [1,2,3,4,5,6,7]. Beyond transport signatures, such noncollinear and noncoplanar magnetic orders frequently engender multiferroic responses [8,9,10,11,12,13,14,15] and nonreciprocal transport [16,17,18,19,20,21], reflecting the intimate coupling between spin, charge, and lattice degrees of freedom. These functionalities establish noncollinear and noncoplanar spin textures as a key platform for both fundamental studies and the design of next-generation topological and multifunctional devices.
A widely studied route to generating noncollinear and noncoplanar magnetic textures is through multiple-Q magnetic states, which arise from the superposition of spin density waves with distinct ordering wave vectors [22,23]. Well-known examples include skyrmion crystals stabilized by a triple-Q superposition on a triangular lattice, as observed in MnSi [24,25,26], Si [27,28], FeGe [29,30], O [8,31,32], Pd [33,34,35,36,37,38], [39,40,41,42], and EuPtSi [43,44,45,46,47] and double-Q superpositions on a square lattice, as observed in Gd [48,49,50,51]. In addition, various multiple-Q states have been found, such as the meron–antimeron crystal in [52] and the hedgehog lattices in Mn [53,54,55,56] and SrFe [57,58,59,60], and the vortex crystal in [61].
From the theoretical side, the stabilization mechanisms of noncollinear and noncoplanar spin textures have been extensively investigated [62]. In noncentrosymmetric systems, the competition between ferromagnetic exchange and the antisymmetric Dzyaloshinski–Moriya (DM) interaction [63,64], together with external magnetic fields, provides the canonical route to the formation of skyrmion crystals in chiral, polar, and () systems [65,66,67,68,69,70,71,72]. In centrosymmetric systems, where intrinsic DM interactions are forbidden by inversion symmetry, alternative mechanisms, such as frustration among short- and/or long-range exchange interactions [73,74,75], anisotropic symmetric exchange interactions [76,77,78,79,80,81,82], and dipolar interactions [83,84], have been shown to generate multiple-Q orderings. The interplay of these competing tendencies can stabilize a rich variety of multiple-Q orderings, ranging from skyrmion crystals to meron crystals and hedgehog lattices, even in the absence of inversion-symmetry breaking [62,85,86,87].
In this work, we focus on a less explored class of multiple-Q states—vortex crystals—on the triangular lattice in noncentrosymmetric environments distinct from chiral, polar, and () point-group symmetries. The essential mechanism underlying their stabilization is the cooperative interplay between multi-spin interactions and the out-of-plane DM interaction inherent to the point group symmetry [88]. By performing simulated annealing for an effective spin model, we demonstrate that the combination of easy-plane single-ion anisotropy, a momentum-resolved biquadratic interaction, and the out-of-plane DM interaction stabilizes a rich variety of double-Q and triple-Q vortex crystals. We further show that weakening the easy-plane anisotropy triggers topological transitions into skyrmion crystals with quantized skyrmion numbers and , while the application of an external magnetic field drives the system into a single-Q conical spiral state. These findings underscore the pivotal role of out-of-plane DM interactions in stabilizing unconventional vortex crystals, which cannot be realized within purely polar or chiral symmetry classes, thereby opening new avenues for designing and controlling topological magnetic phases beyond conventional skyrmion-hosting systems.
The rest of this paper is organized as follows. In Section 2, we present the effective spin model on the two-dimensional triangular lattice, which incorporates the biquadratic interaction, the out-of-plane DM interaction, and the easy-plane single-ion anisotropy, and frustrated exchange interactions. We also describe the numerical approach based on simulated annealing. In Section 3, we investigate the stabilization of double-Q and triple-Q vortex crystals as functions of the model parameters. We then provide a detailed analysis of the magnetic phases appearing in the low-temperature phase diagram and examine the influence of easy-plane single-ion anisotropy and out-of-plane magnetic fields. Finally, in Section 4, we summarize our main findings.
2. Model and Method
We study a classical spin model defined on a two-dimensional triangular lattice subject to the point-group symmetry. The triangular-lattice layer is embedded in the plane, with the lattice constant set to unity. Each magnetic site is assumed to be coordinated by ligands forming a triangular prism under symmetry [88]. Such ligand arrangements are known to occur in several van der Waals magnets [89], including transition-metal dichalcogenides [90,91] and Ge [92,93,94]. The symmetry eliminates inversion centers on the bonds but preserves a mirror plane parallel to the triangular layer. As a consequence, the DM vectors are constrained to lie along the out-of-plane (z) direction, regardless of the bonds. This situation differs from chiral or polar systems, where the DM vectors lie in the plane and vary with bond orientation [95,96,97].
To incorporate the out-of-plane DM interaction, the bilinear exchange Hamiltonian can be expressed as
where denotes a classical spin of unit length at site i, . The first term represents the conventional isotropic Heisenberg exchange interaction, while the second embodies the antisymmetric DM interaction with the DM vector aligned along the z axis. The latter arises microscopically from spin-dependent electron hopping processes mediated by spin–orbit coupling in the presence of broken inversion symmetry. This form contrasts with chiral or polar systems, where the DM vectors typically lie in the lattice plane and depend on the specific bond direction.
By applying a Fourier transformation, the bilinear Hamiltonian can be reformulated in momentum space as
where denotes the Fourier component of the classical localized spin and the crystal momentum. The first and second terms describe the contributions of the Heisenberg and DM interactions, respectively. Here, and are the Fourier transforms of the real-space coupling constants and , respectively. For clarity, we restrict our attention to the effects of the out-of-plane DM interaction on magnetic ordering and therefore omit additional bond-dependent exchange terms that are allowed under point-group symmetry [98].
The momentum dependence of and originates from the underlying real-space exchange paths. To construct a tractable low-temperature phase diagram, we restrict the model to the dominant Fourier components in Equation (2). Specifically, we assume that the leading instabilities occur at a set of symmetry-related ordering wave vectors, , , and with , which lie away from both and the Brillouin-zone boundary. These three vectors are connected by the threefold rotational symmetry of the triangular lattice, enforcing the relations and ; it is noted that , , and so on. The momentum-space interactions are related to the real-space bilinear exchange interactions as a combination of a nearest-neighbor ferromagnetic exchange and further-neighbor antiferromagnetic couplings and . For instance, the commensurate ordering wave vectors at – under periodic boundary conditions are realized by setting and with . The qualitative results do not depend on the precise value of Q, as long as the ordering vectors remain away from the zone center and boundary. Under these assumptions, the bilinear Hamiltonian reduces to [82]
where the subscript of and is omitted for notational simplicity. Because of the underlying symmetry, spin states with spectral weight at , , or are strictly degenerate. Moreover, in the absence of bond-dependent exchange interaction, the model contains no intrinsic anisotropy within the spin plane.
Equation (3) can be interpreted as an effective spin Hamiltonian that captures the low-energy ground-state properties of the original real-space model in noncentrosymmetric magnets with relativistic spin–orbit coupling. The momentum-space interactions correspond to the Fourier transforms of real-space short-range couplings, such as frustrated exchange interactions, or long-range interactions in itinerant electron systems. For the latter case, Equation (3) serves as an effective representation of long-range spin interactions mediated by conduction electrons, such as those described by the Ruderman–Kittel–Kasuya–Yosida (RKKY) mechanism [99,100,101].
The ground state of the bilinear model in Equation (3) is described by the single-Q spiral state, where the ordering wave vector is selected out of –. In other words, there are no instabilities toward multiple-Q states. To promote instabilities toward multiple-Q formation in the presence of the out-of-plane DM interaction, we additionally consider three effects. One is the biquadratic interaction, which is given by
where N is the total number of sites. This term arises from the fourth-order perturbation expansion in terms of the spin–charge coupling in the Kondo lattice model, which corresponds to the higher-order RKKY interaction [102]. We suppose that the coupling constant is positive () by considering the dominant contribution of the Fermi surface nesting [102]. The second is the easy-plane single-ion anisotropy, which is represented as
with favoring spin alignment in the plane. The third is the Zeeman coupling in the presence of an external magnetic field, which is given by
where H is the magnitude of the magnetic field. We examine the instability toward multiple-Q states for the total Hamiltonian defined as
where we adopt as the unit of energy. In the following, we treat D, K, A, and H as phenomenological parameters. Specifically, we calculate the phase diagram in a wide range of model parameters as and to illustrate the qualitative phase behavior. While in realistic materials the bilinear exchange is usually much larger than the DM interaction and biquadratic interaction terms, our choice emphasizes the competition between these interactions. Similar parameter regimes have been suggested in itinerant magnets, e.g., Pd [103] and MnGe [53,104], where higher-order interactions play a significant role. As shown below, we have confirmed that the main qualitative features of the phase diagrams, such as the stabilization of multiple-Q vortex crystals, are robust against moderate changes in the relative ratios of and .
The effective spin model in Equation (7) can be used to search for new stabilization mechanisms of multiple-Q states and to reproduce the experimental phase diagram including multiple-Q phases [62]. In particular, by incorporating the momentum-resolved DM interaction, the effective spin model is capable of reproducing the complex transitions observed between distinct short-period skyrmion crystal phases in EuNi [105].
To obtain the low-temperature magnetic phase diagrams for the model defined in Equation (7), we employed unbiased simulated annealing on clusters containing spins. The simulations were performed using the standard Metropolis algorithm with local spin updates in real space. For each set of model parameters , the system was initialized from a random spin configuration at high temperatures, typically chosen within the range –5. The temperature was then gradually reduced according to a multiplicative cooling schedule with rates –, until a final target temperature of was reached. At the lowest temperature, – Monte Carlo sweeps were performed for equilibration and subsequent measurements. To accurately identify phase boundaries, especially in regions where competing spin configurations appeared, additional simulations were initialized from low-temperature spin states previously obtained in neighboring parameter regions. This procedure allowed us to avoid metastability effects and determine the phase diagram with higher reliability.
To characterize the numerically obtained spin states, we analyze both spin-related and chirality-related quantities. In the spin sector, we evaluate the Fourier components of the magnetic moment for each spin direction at wave vector , , and the spin structure factor, , defined as
where is the real-space position of site j on the triangular lattice. For convenience, we also compute the total structure factor, . The uniform magnetization is obtained from the site-averaged spin component .
In the chirality sector, we calculate the scalar spin chirality, which measures the noncoplanarity of three neighboring spins on each triangular plaquette. It is given by
where denotes the triangle plaquette center, and the spins , , and are taken in counterclockwise order on upward and downward triangles. A finite value of serves as a hallmark of topologically nontrivial spin textures, such as skyrmion crystals.
3. Results
In this section, we explore how double-Q and triple-Q vortex crystals are stabilized as functions of the underlying model parameters. We begin in Section 3.1 with a detailed characterization of the magnetic phases that emerge in the low-temperature phase diagram. The role of easy-plane single-ion anisotropy is then examined in Section 3.2, followed by an analysis of the effects of an out-of-plane magnetic field in Section 3.3.
3.1. Magnetic Phase Diagram
We construct the low-temperature phase diagram of the effective spin model in Equation (7) on the triangular lattice with symmetry, focusing on the competition between the biquadratic interaction and the out-of-plane DM interaction; in this section, we fix and . The phase diagram, summarized in Figure 1, is presented as functions of the DM coupling constant D and the biquadratic coupling constant K. Four distinct ordered phases are stabilized: the single-Q spiral state denoted as 1Q, the double-Q vortex crystal denoted as 2Q VX, and two symmetry-inequivalent triple-Q vortex crystals denoted as 3Q VX I and 3Q VX II. All of these phases are characterized by coplanar spin configurations in the plane, which is attributed to the strong easy-plane anisotropy. The phase diagram thus reveals that the present model can host a remarkably rich set of vortex-type spin textures, with the triple-Q vortex crystal II phase stabilized only when both D and K are finite, indicating the importance of their cooperative effect.
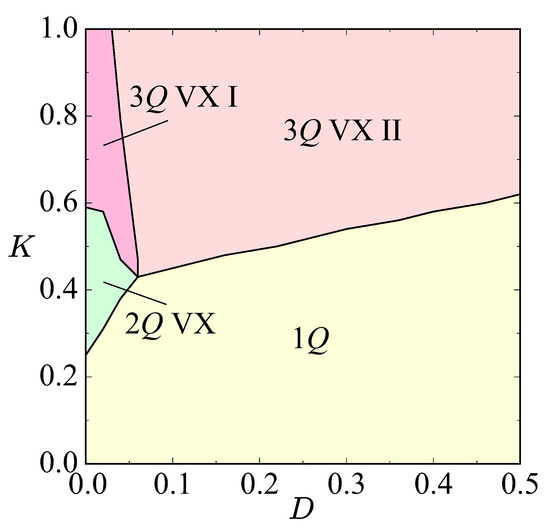
Figure 1.
Magnetic phase diagram of the model in Equation (7) at low temperatures as functions of the DM interaction D and the biquadratic interaction K at and . 1Q, 2Q VX, and 3Q VX denote the single-Q state, double-Q vortex crystal, and triple-Q vortex crystal, respectively. The labels I and II following 3Q VX serve as identifiers to distinguish between different phases.
For small K and finite D, the system stabilizes the single-Q spiral state, which is characterized by a single ordering wave vector and a coplanar spiral configuration of spins in the plane. This spin configuration maximizes the energy gain from the DM interaction and the easy-plane anisotropy. The spin structure factor exhibits a single pair of Bragg peaks at [Figure 2a], and the corresponding real-space configuration shows uniform spirals without any topological winding, as shown in Figure 3a. We note that the periodicities observed in the real-space spin textures are not attributed to incommensurate modulations within the Brillouin zone [106,107]. Instead, these commensurate periodicities are predetermined by the specific form of the exchange interaction in momentum space, which selects the ordering vector at . Therefore, the resulting spin textures naturally lock into simple commensurate periods without invoking additional lock-in effects or artifacts of the finite simulation box. This phase is topologically trivial and serves as a reference state for more complex multiple-Q phases.
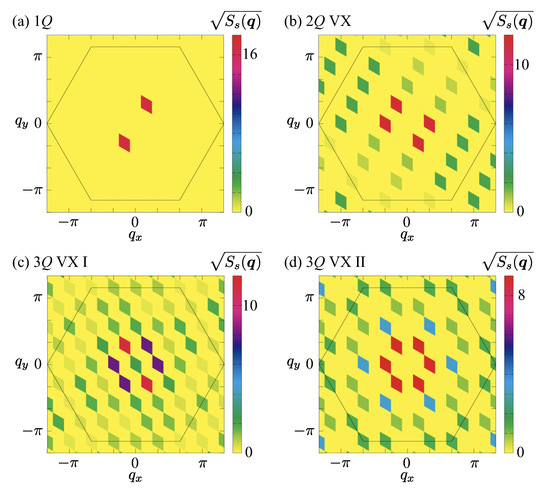
Figure 2.
Square root of the spin structure factor in (a) the single-Q state at and , (b) the double-Q vortex crystal at and , (c) the triple-Q vortex crystal I at and , and (d) the triple-Q vortex crystal II at and .
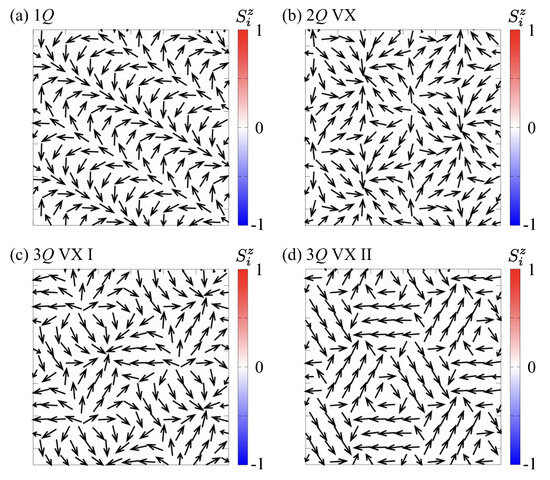
Figure 3.
Real-space plot of the spin configurations in (a) the single-Q state at and , (b) the double-Q vortex crystal at and , (c) the triple-Q vortex crystal I at and , and (d) the triple-Q vortex crystal II at and . The arrows denote the direction of spin moments, and the color shows the z-spin polarization.
Upon increasing K at small D, the system undergoes a transition from the single-Q spiral phase to the double-Q vortex crystal phase. In this state, two symmetry-related ordering wave vectors condense simultaneously, producing a periodic array of vortices and antivortices in the spin texture, as found by the real-space spin configuration in Figure 3b. The corresponding spin structure factor shown in Figure 2b exhibits two pairs of sharp Bragg peaks at and , signaling the spontaneous breaking of the threefold rotational symmetry of the triangular-lattice system. Because the spin configuration remains coplanar, the scalar spin chirality vanishes, and the phase is topologically trivial despite its vortex–antivortex structure.
At larger values of K, two distinct triple-Q vortex crystal phases appear. They are classified into type I and type II, which can be clearly distinguished by their spin structure factors and real-space spin textures. In the triple-Q vortex crystal I phase, which emerges at relatively small D, the three ordering wave vectors contribute unequally, leading to anisotropic intensity distributions in the spin structure factor [Figure 2c]. This signals a spontaneous breaking of the threefold rotational symmetry, analogous to the double-Q vortex crystal. The corresponding real-space spin configuration consists of a vortex-antivortex lattice where the positions of vortex cores lack threefold rotational symmetry, giving rise to a distorted triangular arrangement, as shown in Figure 3c. This state can thus be regarded as an intermediate phase between the double-Q vortex crystal and the fully symmetric triple-Q configurations corresponding to the triple-Q vortex crystal II described below.
In contrast, the triple-Q vortex crystal II phase emerges at larger values of D, where the three ordering vectors , , and contribute equally. In this case, the spin structure factor exhibits three Bragg peaks of identical intensity [Figure 2d], demonstrating the restoration of the threefold rotational symmetry of the triangular lattice. The real-space spin texture shown in Figure 3d reveals a highly ordered triangular array of vortices and antivortices, with the vortex cores arranged periodically to maintain the threefold rotational symmetry. Compared to the triple-Q vortex crystal I state, the triple-Q vortex crystal II state therefore exhibits a more symmetric and robust vortex–crystal arrangement, stabilized by the larger DM interaction, which enforces equal weight among the three symmetry-related ordering wave vectors. Notably, similar triple-Q vortex crystals preserving threefold rotational symmetry have been reported in frustrated spin models of centrosymmetric systems subjected to an external magnetic field [108,109].
The evolution of phases with increasing K at weak D can therefore be summarized as a sequence from the single-Q spiral state to the double-Q vortex crystal, followed by the triple-Q vortex crystal I and finally the triple-Q vortex crystal II, with the threefold rotational symmetry gradually restored as K increases. Conversely, strengthening the DM interaction at fixed K suppresses multiple-Q superpositions and favors the single-Q spiral state. This reflects the fact that the DM interaction stabilizes a unique single-Q spiral order by fixing the spiral rotation, whereas the biquadratic interaction promotes the coexistence of multiple ordering wave vectors, thereby driving the emergence of multiple-Q vortex crystals. The transitions between these magnetic phases are generally of first-order character, as expected from the absence of group–subgroup relations among the competing orders. In our simulated annealing calculations, the phase boundaries are identified from abrupt changes in order parameters such as magnetization, scalar spin chirality, and spin structure factors. While this approach allows us to delimit equilibrium phase boundaries, the precise determination of spinodal and binodal lines is beyond the present scope, since metastability effects and finite-size limitations prevent us from accessing such details in a strict thermodynamic sense.
Overall, the phase diagram highlights the delicate balance between the DM and biquadratic interactions in shaping the landscape of vortex-type spin textures. The identification of two distinct triple-Q vortex crystals demonstrates that even within coplanar spin configurations enforced by easy-plane anisotropy, symmetry-distinct vortex crystals can arise. These results suggest that out-of-plane DM interactions in -symmetric systems provide a promising route to engineer unconventional multiple-Q states, offering theoretical guidance for exploring real materials where diverse vortex crystals and their characteristic responses may be realized.
3.2. Effect of Single-Ion Anisotropy
Next, we examine how the easy-plane single-ion anisotropy A affects the stability of vortex crystals, focusing in particular on the two types of triple-Q vortex crystals. For weak DM interaction () and moderate , large negative A stabilizes the triple-Q vortex crystal I phase, as shown in Figure 4a. Its spin structure factor shows three Bragg intensities of unequal magnitude at –, as shown in Figure 4b, indicating spontaneous breaking of the threefold rotational symmetry, which is consistent with the results in Figure 2c.
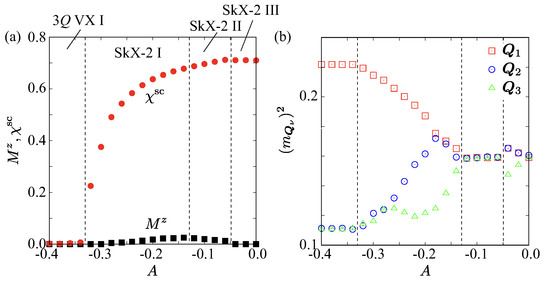
Figure 4.
Easy-plane single-ion anisotropy A dependence of (a) the out-of-plane component in the magnetization and the scalar spin chirality , and (b) the squared magnetic moments at – for and . The vertical dashed lines mark the separations between distinct magnetic phases. SkX-2 stands for the skyrmion crystal with the skyrmion number of 2.
As A increases toward zero, the system undergoes a transition into a skyrmion crystal with the skyrmion number of , which is indicated by the onset of finite scalar spin chirality in Figure 4a. The skyrmion number corresponding to the topological charge is defined as
where is the number of magnetic unit cells and is the skyrmion density at plaquette [110]:
This equation indicates that the skrymion number is related to the scalar spin chirality in Equation (10). By summing the local scalar spin chirality over all plaquettes in the magnetic unit cell and normalizing by , we directly obtain the skyrmion number corresponding to the topological charge. As a result of the calculations, we refer to this state as the SkX-2 I. Although the behavior of squared magnetic moments is continuously connected to the triple-Q vortex crystal I, the finite z-spin components generate noncoplanar spin textures with a nonzero skyrmion number, as shown in Figure 5a. The continuous variations of both and across the phase boundary suggest that this transition is of second-order character. We note, however, that in finite-size simulations, weakly first-order transitions may also appear continuous, and a more detailed finite-size scaling analysis would be required to rigorously confirm the transition order. This skyrmion crystal has analogs in square-lattice models with compass-type anisotropy and/or biquadratic interactions [111,112]. Because bond-dependent anisotropy is absent, states with positive and negative are energetically degenerate [113]. This state also exhibits a finite net , as shown in Figure 4a. As A increases, the modulation of the z-spin component becomes more pronounced compared with the spin configurations shown in Figure 5a,b. Accordingly, the scalar spin chirality is also more pronounced compared with the configurations shown in Figure 6a,b. In the SkX-2 I phase, the squared magnetic moments at and exhibit non-monotonic variations as a function of A. This behavior might originate from the continuous redistribution of spectral weight among the three ordering vectors during the crossover from the triple-Q vortex crystal I to the SkX-2 II state, the latter of which appears for smaller . The local extremum of (or ) does not signify a phase transition but rather a smooth rearrangement of the real-space skyrmion spin configuration.
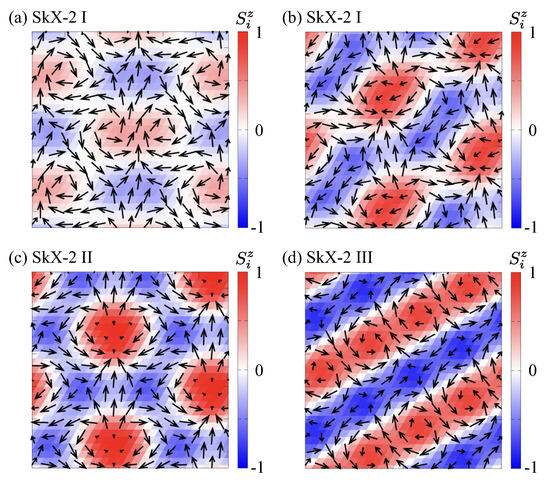
Figure 5.
Real-space plot of the spin configurations in (a) the SkX-2 I at , (b) the SkX-2 I at , (c) the SkX-2 II at , and (d) the SkX-2 III at . The arrows denote the direction of spin moments, and the color shows the z-spin polarization.
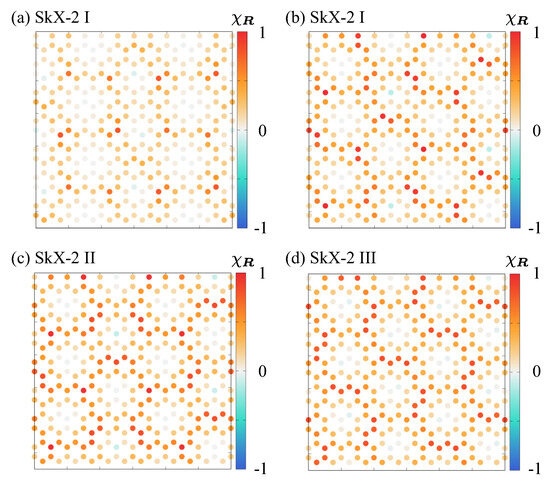
Figure 6.
Real-space plot of the scalar spin chirality configurations in (a) the SkX-2 I at , (b) the SkX-2 I at , (c) the SkX-2 II at , and (d) the SkX-2 III at ; for the trinagle vertices i, j, and k.
At weaker , the system transitions to another skyrmion crystal, denoted SkX-2 II, characterized by threefold-symmetric Bragg peaks of equal intensity at –, as shown in Figure 4b. The threefold symmetric Bragg peaks imply that the spin ansatz of this state is given by
This expression indicates that the spin configuration of the SkX-2 II is represented by a superposition of triple-Q sinusoidal waves at –, giving rise to the real-space texture shown in Figure 5c and scalar spin chirality texture shown in Figure 6c. Such a spin configuration has also been reported even in a centrosymmetric spin model incorporating the effect of the biquadratic interaction and easy-plane anisotropy but without the DM interaction [114].
As A approaches zero, the system undergoes another transition to the SkX-2 III phase, as shown in Figure 5d and Figure 6d. We refer to this state as the SkX-2 III. The magnitudes of at – are slightly different for , but they become the same for , as shown in Figure 4b. The spin ansatz of this state is given by
where the parameter depends on A, and () for (). Similar to Equation (13), this spin configuration is also described by a superposition of triple-Q sinusoidal waves at –, but with a distinct pattern of spin density wave superposition. The continuous transition between SkX-2 II and SkX-2 III with varying A has also been observed in the Kondo lattice models with single-ion anisotropy [115].
For intermediate DM interaction at and , the system at large negative A stabilizes the triple-Q vortex crystal II phase. As A is increased, the energy gain by A gradually decreases, and hence, the out-of-plane spin modulations and the associated scalar spin chirality appear, as shown by the A dependence of the magnetization and scalar spin chirality in Figure 7a and the square magnetic moments in Figure 7b. In other words, the system undergoes a phase transition into a noncoplanar state with nonzero scalar spin chirality, where the real-space spin configurations are presented in the presence of A in Figure 8a and in the absence of A in Figure 8b; the threefold rotational symmetry of the spin structure is broken. The observed continuous variations in and across the phase boundary imply that the transition is likely of second-order type. By calculating the skyrmion number of this state, one finds that the spin configuration exhibits the skyrmion number of , which is in contrast to the skyrmion crystal with the skyrmion number of two obtained for small D. We refer to this state as the SkX-1. By looking into the real-space spin configuration, this skyrmion crystal is characterized by two types of meron with the same sign of the scalar spin chirality, that is, the bimeron structure [116,117]. It is noted that the present bimeron structure is stabilized even without the external magnetic field, which is distinct from the previous one [116,117]. In other words, the interplay between the biquadratic interaction and the out-of-plane DM interaction can lead to the zero-field skyrmion crystal with when the magnitude of the easy-plane single-ion anisotropy is weak [118].
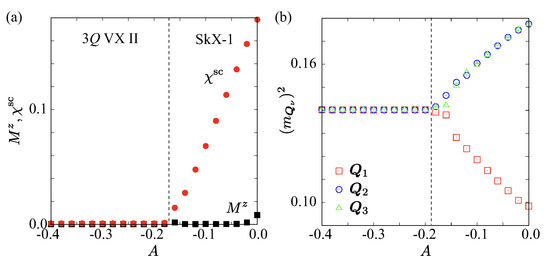
Figure 7.
Easy-plane single-ion anisotropy A dependence of (a) the out-of-plane component in the magnetization and the scalar spin chirality , and (b) the squared magnetic moments at – for and . The vertical dashed lines mark the separations between distinct magnetic phases. SkX-1 stands for the skyrmion crystal with the skyrmion number of 1.
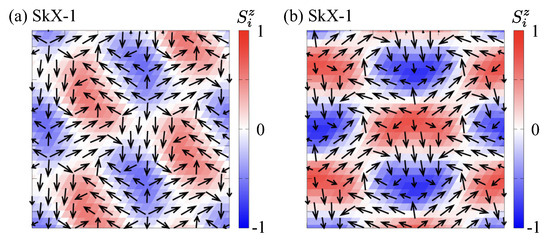
Figure 8.
Real-space plot of the spin configurations in the SkX-1 at (a) and (b) . The arrows denote the direction of spin moments, and the color shows the z-spin polarization.
For strong DM interaction () combined with large , the system exhibits qualitatively different behavior. In this regime, the triple-Q vortex crystal II phase is robustly stabilized across the entire range of A, as shown in Figure 9. The Bragg intensities at – remain nearly unchanged with varying A, and both and stay vanishingly small (not shown). This robustness indicates that once the DM interaction and the biquadratic interaction become sufficiently strong, they enforce a coplanar triple-Q state with high symmetry, effectively suppressing any topological instability toward skyrmion formation. In other words, the large D and K parameters lock the system into a vortex–crystal configuration that is insensitive to the competing effects of single-ion anisotropy.
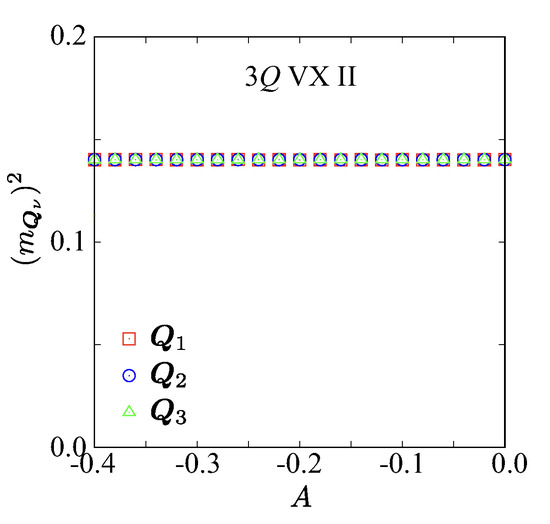
Figure 9.
Easy-plane single-ion anisotropy A dependence of the squared magnetic moments at – for and .
Taken together, these results clarify the dual role of A and D in controlling the stability of vortex and skyrmion crystals. Negative A generally favors coplanar vortex crystals by enforcing in-plane spin alignment, while reducing relaxes this constraint and allows the emergence of noncoplanar textures that stabilize skyrmion crystals. The skyrmion number realized depends sensitively on the DM interaction D: for weak DM (), the system hosts the skyrmion crystals with , for intermediate DM (), the skyrmion crystals with emerges, and for strong DM (), skyrmion crystals are completely suppressed as the triple-Q vortex crystal II phase dominates.
These systematic trends establish single-ion anisotropy A as an essential tuning parameter for controlling the phase transition between vortex crystals and skyrmion crystals. At the same time, the DM interaction D acts as a selector of the skyrmion number, thereby governing the topological character of the emergent spin textures. The cooperative and competitive interplay of A and D thus provides a framework for engineering a variety of nontrivial magnetic phases in noncentrosymmetric magnets with symmetry.
3.3. Effect of Magnetic Field
We next investigate the influence of an out-of-plane magnetic field H on the stability of vortex crystal phases. Figure 10 and Figure 11 summarize the low-temperature results against H at fixed , , and , where the triple-Q vortex crystal II state is stabilized at zero field. As shown in Figure 10a, the uniform magnetization increases monotonically with increasing H, exhibiting small kinks that signal successive phase transitions. By contrast, the corresponding scalar spin chirality remains nearly zero throughout the entire field range, indicating the absence of topologically nontrivial spin textures in this parameter regime.
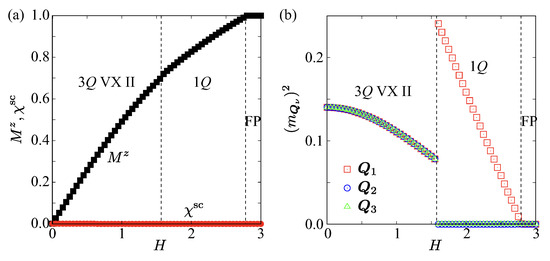
Figure 10.
Magnetic field H dependence of (a) the out-of-plane component in the magnetization and the scalar spin chirality , and (b) the squared magnetic moments at – for and . The vertical dashed lines mark the separations between distinct magnetic phases. FP stands for the fully polarized state.
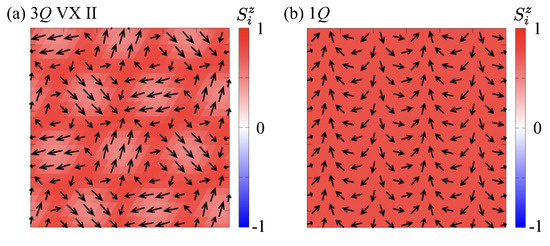
Figure 11.
Real-space plot of the spin configurations in (a) the triple-Q vortex crystal II at and (b) the single-Q state at . The arrows denote the direction of spin moments, and the color shows the z-spin polarization.
The evolution of the spin structure factor in Figure 10b reveals a clear sequence of magnetic phases. At low fields, the system resides in the triple-Q vortex crystal II phase, characterized by three symmetry-related Bragg peaks of equal intensity. Upon increasing H, the system undergoes a transition to the single-Q spiral phase, in which only a single pair of Bragg peaks persists, as shown in Figure 2a. At sufficiently large H, these finite-Q peaks vanish, signaling the phase transition into the fully polarized state.
Real-space spin textures corresponding to these phases are displayed in Figure 11. At , the spin configuration in Figure 11a exhibits a well-ordered triangular lattice of vortices and antivortices, consistent with the triple-Q vortex crystal II, as shown in Figure 3d. At , the spin pattern evolves into a spiral texture with a dominant modulation along a single ordering wave vector [Figure 11b], as expected in the single-Q spiral phase shown in Figure 3a. At even higher fields, all spins are uniformly aligned with the magnetic field, resulting in the fully polarized state. These findings demonstrate that the out-of-plane magnetic field destabilizes the multiple-Q vortex crystal states, driving the system through a continuous sequence from the triple-Q vortex crystal II to the single-Q spiral state, and finally into the fully polarized state.
4. Conclusions
We have shown that a momentum-space effective spin model on a triangular lattice with symmetry, comprising an out-of-plane DM interaction , a positive biquadratic coupling , and easy-plane single-ion anisotropy , stabilizes a rich hierarchy of vortex-type multiple-Q states at low temperatures. In the plane, four ordered phases are realized: the single-Q spiral state, the double-Q vortex crystal, and two symmetry-inequivalent triple-Q vortex crystals. Among them, one of the triple-Q vortex crystals emerges only when both D and K are finite, underscoring the cooperative role of these two interactions.
Tuning the easy-plane single-ion anisotropy A controls the phase transition between coplanar vortex crystals and noncoplanar skyrmion crystals. For weak DM interaction, weakening the magnitude of the single-ion anisotropy converts the anisotropic triple-Q vortex crystal into skyrmion crystals with the skyrmion number of two, while for intermediate DM interaction, an analogous route yields the skyrmion crystal with the skyrmion number of one from the isotropic triple-Q vortex crystal. By contrast, for strong DM interaction, the threefold-symmetric triple-Q vortex crystal remains robust against variations in A, indicating that large D enforces coplanar order and suppresses topological transitions. These trends show that the DM interaction, as well as the easy-axis single-ion anisotropy, primarily determine the degree of out-of-plane spin modulation and scalar spin chirality, thereby enabling the stabilization of skyrmion textures. Applying an external out-of-plane magnetic field H further drives the system through a sequence of phases: from the triple-Q vortex crystal at low fields, to the single-Q spiral state at intermediate fields, and finally to the fully polarized state at high fields. In this process, the uniform magnetization increases monotonically with H, while the scalar spin chirality remains negligible, reflecting the suppression of nontrivial topology under strong field alignment.
Altogether, our findings identify the out-of-plane DM interaction allowed by symmetry as a key ingredient for realizing unconventional vortex crystal states that are inaccessible in purely polar or chiral magnetic systems. This establishes a new design principle for engineering exotic magnetic textures, highlighting noncentrosymmetric magnets with symmetry as promising platforms for exploring emergent electrodynamics and topological responses.
Funding
This research was supported by JSPS KAKENHI Grants Numbers JP21H01037, JP22H00101, JP22H01183, JP23H04869, JP23K03288, JP23K20827, and by JST CREST (JPMJCR23O4) and JST FOREST (JPMJFR2366).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflict of interest.
References
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Shindou, R.; Nagaosa, N. Orbital Ferromagnetism and Anomalous Hall Effect in Antiferromagnets on the Distorted fcc Lattice. Phys. Rev. Lett. 2001, 87, 116801. [Google Scholar] [CrossRef]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Martin, I.; Batista, C.D. Itinerant Electron-Driven Chiral Magnetic Ordering and Spontaneous Quantum Hall Effect in Triangular Lattice Models. Phys. Rev. Lett. 2008, 101, 156402. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Nakazawa, K.; Bibes, M.; Kohno, H. Topological Hall effect from strong to weak coupling. J. Phys. Soc. Jpn. 2018, 87, 033705. [Google Scholar] [CrossRef]
- Matsui, A.; Nomoto, T.; Arita, R. Skyrmion-size dependence of the topological Hall effect: A real-space calculation. Phys. Rev. B 2021, 104, 174432. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef]
- White, J.S.; Levatić, I.; Omrani, A.; Egetenmeyer, N.; Prša, K.; Živković, I.; Gavilano, J.L.; Kohlbrecher, J.; Bartkowiak, M.; Berger, H.; et al. Electric field control of the skyrmion lattice in Cu2OSeO3. J. Phys. Condens. Matter 2012, 24, 432201. [Google Scholar] [CrossRef]
- Okamura, Y.; Kagawa, F.; Mochizuki, M.; Kubota, M.; Seki, S.; Ishiwata, S.; Kawasaki, M.; Onose, Y.; Tokura, Y. Microwave magnetoelectric effect via skyrmion resonance modes in a helimagnetic multiferroic. Nat. Commun. 2013, 4, 2391. [Google Scholar] [CrossRef]
- Mochizuki, M.; Seki, S. Magnetoelectric resonances and predicted microwave diode effect of the skyrmion crystal in a multiferroic chiral-lattice magnet. Phys. Rev. B 2013, 87, 134403. [Google Scholar] [CrossRef]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef] [PubMed]
- Mochizuki, M.; Seki, S. Dynamical magnetoelectric phenomena of multiferroic skyrmions. J. Phys. Condens. Matter 2015, 27, 503001. [Google Scholar] [CrossRef]
- Christensen, M.H.; Andersen, B.M.; Kotetes, P. Unravelling Incommensurate Magnetism and Its Emergence in Iron-Based Superconductors. Phys. Rev. X 2018, 8, 041022. [Google Scholar] [CrossRef]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I. Magnetoelectric effect and orbital magnetization in skyrmion crystals: Detection and characterization of skyrmions. Phys. Rev. B 2019, 99, 060406. [Google Scholar] [CrossRef]
- Tokura, Y.; Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 2018, 9, 3740. [Google Scholar] [CrossRef]
- Hoshino, S.; Nagaosa, N. Theory of the magnetic skyrmion glass. Phys. Rev. B 2018, 97, 024413. [Google Scholar] [CrossRef]
- Ishizuka, H.; Nagaosa, N. Anomalous electrical magnetochiral effect by chiral spin-cluster scattering. Nat. Commun. 2020, 11, 2986. [Google Scholar] [CrossRef]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yatsushiro, M. Nonlinear nonreciprocal transport in antiferromagnets free from spin-orbit coupling. Phys. Rev. B 2022, 106, 014420. [Google Scholar] [CrossRef]
- Eto, R.; Pohle, R.; Mochizuki, M. Low-Energy Excitations of Skyrmion Crystals in a Centrosymmetric Kondo-Lattice Magnet: Decoupled Spin-Charge Excitations and Nonreciprocity. Phys. Rev. Lett. 2022, 129, 017201. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, Y.; Tajima, K.; Bloch, D.; Roth, M. Helical spin structure in manganese silicide MnSi. Solid State Commun. 1976, 19, 525–528. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Beille, J.; Voiron, J.; Roth, M. Long period helimagnetism in the cubic B20 FexCo1-xSi and CoxMn1-x Si alloys. Solid State Commun. 1983, 47, 399–402. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Lebech, B.; Bernhard, J.; Freltoft, T. Magnetic structures of cubic FeGe studied by small-angle neutron scattering. J. Phys. Condens. Matter 1989, 1, 6105. [Google Scholar] [CrossRef]
- Adams, T.; Chacon, A.; Wagner, M.; Bauer, A.; Brandl, G.; Pedersen, B.; Berger, H.; Lemmens, P.; Pfleiderer, C. Long-Wavelength Helimagnetic Order and Skyrmion Lattice Phase in Cu2OSeO3. Phys. Rev. Lett. 2012, 108, 237204. [Google Scholar] [CrossRef] [PubMed]
- Seki, S.; Kim, J.H.; Inosov, D.S.; Georgii, R.; Keimer, B.; Ishiwata, S.; Tokura, Y. Formation and rotation of skyrmion crystal in the chiral-lattice insulator Cu2OSeO3. Phys. Rev. B 2012, 85, 220406. [Google Scholar] [CrossRef]
- Saha, S.R.; Sugawara, H.; Matsuda, T.D.; Sato, H.; Mallik, R.; Sampathkumaran, E.V. Magnetic anisotropy, first-order-like metamagnetic transitions, and large negative magnetoresistance in single-crystal Gd2PdSi3. Phys. Rev. B 1999, 60, 12162–12165. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.H.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef]
- Sampathkumaran, E.V. A report of (topological) Hall anomaly two decades ago in Gd2PdSi3, and its relevance to the history of the field of Topological Hall Effect due to magnetic skyrmions. arXiv 2019, arXiv:1910.09194. [Google Scholar]
- Hirschberger, M.; Nakajima, T.; Kriener, M.; Kurumaji, T.; Spitz, L.; Gao, S.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. High-field depinned phase and planar Hall effect in the skyrmion host Gd2PdSi3. Phys. Rev. B 2020, 101, 220401(R). [Google Scholar] [CrossRef]
- Kumar, R.; Iyer, K.K.; Paulose, P.L.; Sampathkumaran, E.V. Magnetic and transport anomalies in R2RhSi3 (R = Gd, Tb, and Dy) resembling those of the exotic magnetic material Gd2PdSi3. Phys. Rev. B 2020, 101, 144440. [Google Scholar] [CrossRef]
- Spachmann, S.; Elghandour, A.; Frontzek, M.; Löser, W.; Klingeler, R. Magnetoelastic coupling and phases in the skyrmion lattice magnet Gd2PdSi3 discovered by high-resolution dilatometry. Phys. Rev. B 2021, 103, 184424. [Google Scholar] [CrossRef]
- Chandragiri, V.; Iyer, K.K.; Sampathkumaran, E. Magnetic behavior of Gd3Ru4Al12, a layered compound with distorted kagomé net. J. Phys. Condens. Matter 2016, 28, 286002. [Google Scholar] [CrossRef]
- Nakamura, S.; Kabeya, N.; Kobayashi, M.; Araki, K.; Katoh, K.; Ochiai, A. Spin trimer formation in the metallic compound Gd3Ru4Al12 with a distorted kagome lattice structure. Phys. Rev. B 2018, 98, 054410. [Google Scholar] [CrossRef]
- Hirschberger, M.; Nakajima, T.; Gao, S.; Peng, L.; Kikkawa, A.; Kurumaji, T.; Kriener, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. Skyrmion phase and competing magnetic orders on a breathing kagome lattice. Nat. Commun. 2019, 10, 5831. [Google Scholar] [CrossRef]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Nakamura, S.; Sakakibara, T.; Hedo, M.; Nakama, T.; et al. Giant Hall resistivity and magnetoresistance in cubic chiral antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2018, 87, 023701. [Google Scholar] [CrossRef]
- Kaneko, K.; Frontzek, M.D.; Matsuda, M.; Nakao, A.; Munakata, K.; Ohhara, T.; Kakihana, M.; Haga, Y.; Hedo, M.; Nakama, T.; et al. Unique Helical Magnetic Order and Field-Induced Phase in Trillium Lattice Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 013702. [Google Scholar] [CrossRef]
- Tabata, C.; Matsumura, T.; Nakao, H.; Michimura, S.; Kakihana, M.; Inami, T.; Kaneko, K.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic Field Induced Triple-q Magnetic Order in Trillium Lattice Antiferromagnet EuPtSi Studied by Resonant X-Ray Scattering. J. Phys. Soc. Jpn. 2019, 88, 093704. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Takeuchi, T.; Harima, H.; Hedo, M.; Nakama, T.; et al. Unique Magnetic Phases in the Skyrmion Lattice and Fermi Surface Properties in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 094705. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Field-Direction Sensitive Skyrmion Crystals in Cubic Chiral Systems: Implication to 4f-Electron Compound EuPtSi. J. Phys. Soc. Jpn. 2021, 90, 073705. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef]
- Huddart, B.M.; Hernández-Melián, A.; Wood, G.D.A.; Mayoh, D.A.; Gomilšek, M.; Guguchia, Z.; Wang, C.; Hicken, T.J.; Blundell, S.J.; Balakrishnan, G.; et al. Field-orientation-dependent magnetic phases in GdRu2Si2 probed with muon-spin spectroscopy. Phys. Rev. B 2025, 111, 054440. [Google Scholar] [CrossRef]
- Yu, X.Z.; Koshibae, W.; Tokunaga, Y.; Shibata, K.; Taguchi, Y.; Nagaosa, N.; Tokura, Y. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 2018, 564, 95–98. [Google Scholar] [CrossRef]
- Tanigaki, T.; Shibata, K.; Kanazawa, N.; Yu, X.; Onose, Y.; Park, H.S.; Shindo, D.; Tokura, Y. Real-space observation of short-period cubic lattice of skyrmions in MnGe. Nano Lett. 2015, 15, 5438–5442. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, N.; Seki, S.; Tokura, Y. Noncentrosymmetric magnets hosting magnetic skyrmions. Adv. Mater. 2017, 29, 1603227. [Google Scholar] [CrossRef]
- Fujishiro, Y.; Kanazawa, N.; Nakajima, T.; Yu, X.Z.; Ohishi, K.; Kawamura, Y.; Kakurai, K.; Arima, T.; Mitamura, H.; Miyake, A.; et al. Topological transitions among skyrmion-and hedgehog-lattice states in cubic chiral magnets. Nat. Commun. 2019, 10, 1059. [Google Scholar] [CrossRef]
- Kanazawa, N.; Kitaori, A.; White, J.S.; Ukleev, V.; Rønnow, H.M.; Tsukazaki, A.; Ichikawa, M.; Kawasaki, M.; Tokura, Y. Direct Observation of the Statics and Dynamics of Emergent Magnetic Monopoles in a Chiral Magnet. Phys. Rev. Lett. 2020, 125, 137202. [Google Scholar] [CrossRef]
- Ishiwata, S.; Tokunaga, M.; Kaneko, Y.; Okuyama, D.; Tokunaga, Y.; Wakimoto, S.; Kakurai, K.; Arima, T.; Taguchi, Y.; Tokura, Y. Versatile helimagnetic phases under magnetic fields in cubic perovskite SrFeO3. Phys. Rev. B 2011, 84, 054427. [Google Scholar] [CrossRef]
- Ishiwata, S.; Nakajima, T.; Kim, J.H.; Inosov, D.S.; Kanazawa, N.; White, J.S.; Gavilano, J.L.; Georgii, R.; Seemann, K.M.; Brandl, G.; et al. Emergent topological spin structures in the centrosymmetric cubic perovskite SrFeO3. Phys. Rev. B 2020, 101, 134406. [Google Scholar] [CrossRef]
- Rogge, P.C.; Green, R.J.; Sutarto, R.; May, S.J. Itinerancy-dependent noncollinear spin textures in SrFeO3, CaFeO3, and CaFeO3/SrFeO3 heterostructures probed via resonant X-ray scattering. Phys. Rev. Mater. 2019, 3, 084404. [Google Scholar] [CrossRef]
- Onose, M.; Takahashi, H.; Sagayama, H.; Yamasaki, Y.; Ishiwata, S. Complete phase diagram of Sr1-xLaxFeO3 with versatile magnetic and charge ordering. Phys. Rev. Mater. 2020, 4, 114420. [Google Scholar] [CrossRef]
- Takagi, R.; White, J.; Hayami, S.; Arita, R.; Honecker, D.; Rønnow, H.; Tokura, Y.; Seki, S. Multiple-q noncollinear magnetism in an itinerant hexagonal magnet. Sci. Adv. 2018, 4, eaau3402. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Butenko, A.B.; Leonov, A.A.; Rößler, U.K.; Bogdanov, A.N. Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets. Phys. Rev. B 2010, 82, 052403. [Google Scholar] [CrossRef]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.B.; Bogdanov, A.N.; Monchesky, T.L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Mochizuki, M. Spin-Wave Modes and Their Intense Excitation Effects in Skyrmion Crystals. Phys. Rev. Lett. 2012, 108, 017601. [Google Scholar] [CrossRef]
- Momoi, T.; Kubo, K.; Niki, K. Possible Chiral Phase Transition in Two-Dimensional Solid 3He. Phys. Rev. Lett. 1997, 79, 2081–2084. [Google Scholar] [CrossRef]
- Okubo, T.; Chung, S.; Kawamura, H. Multiple-q States and the Skyrmion Lattice of the Triangular-Lattice Heisenberg Antiferromagnet Under Magnetic Fields. Phys. Rev. Lett. 2012, 108, 017206. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef]
- Becker, M.; Hermanns, M.; Bauer, B.; Garst, M.; Trebst, S. Spin-orbit physics of Mott insulators on the triangular lattice. Phys. Rev. B 2015, 91, 155135. [Google Scholar] [CrossRef]
- Rousochatzakis, I.; Rössler, U.K.; van den Brink, J.; Daghofer, M. Kitaev anisotropy induces mesoscopic Z2 vortex crystals in frustrated hexagonal antiferromagnets. Phys. Rev. B 2016, 93, 104417. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a Ni-halide monolayer. Nat. Commun. 2020, 11, 5784. [Google Scholar] [CrossRef] [PubMed]
- Yambe, R.; Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 2021, 11, 11184. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Interplay between Single-Ion and Two-Ion Anisotropies in Frustrated 2D Semiconductors and Tuning of Magnetic Structures Topology. Nanomaterials 2021, 11, 1873. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Utesov, O.I. Thermodynamically stable skyrmion lattice in a tetragonal frustrated antiferromagnet with dipolar interaction. Phys. Rev. B 2021, 103, 064414. [Google Scholar] [CrossRef]
- Utesov, O.I. Mean-field description of skyrmion lattice in hexagonal frustrated antiferromagnets. Phys. Rev. B 2022, 105, 054435. [Google Scholar] [CrossRef]
- Grytsiuk, S.; Hanke, J.P.; Hoffmann, M.; Bouaziz, J.; Gomonay, O.; Bihlmayer, G.; Lounis, S.; Mokrousov, Y.; Blügel, S. Topological–chiral magnetic interactions driven by emergent orbital magnetism. Nat. Commun. 2020, 11, 511. [Google Scholar] [CrossRef] [PubMed]
- Aoyama, K.; Kawamura, H. Hedgehog-lattice spin texture in classical Heisenberg antiferromagnets on the breathing pyrochlore lattice. Phys. Rev. B 2021, 103, 014406. [Google Scholar] [CrossRef]
- Mendive-Tapia, E.; dos Santos Dias, M.; Grytsiuk, S.; Staunton, J.B.; Blügel, S.; Lounis, S. Short period magnetization texture of B20-MnGe explained by thermally fluctuating local moments. Phys. Rev. B 2021, 103, 024410. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Skyrmion crystal under D3h point group: Role of out-of-plane Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 105, 224423. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, Q.; Xing, J.; Liu, N.; Guo, Y.; Liu, Z.; Zhao, J. Recent progress on 2D magnets: Fundamental mechanism, structural design and modification. Appl. Phys. Rev. 2021, 8, 031305. [Google Scholar] [CrossRef]
- Puotinen, D.; Newnham, R. The crystal structure of MoTe2. Acta Crystallogr. 1961, 14, 691–692. [Google Scholar] [CrossRef]
- Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 1–15. [Google Scholar] [CrossRef]
- Deiseroth, H.J.; Aleksandrov, K.; Reiner, C.; Kienle, L.; Kremer, R.K. Fe3GeTe2 and Ni3GeTe2–Two New Layered Transition-Metal Compounds: Crystal Structures, HRTEM Investigations, and Magnetic and Electrical Properties. Eur. J. Inorg. Chem. 2006, 2006, 1561–1567. [Google Scholar] [CrossRef]
- Park, T.E.; Peng, L.; Liang, J.; Hallal, A.; Yasin, F.S.; Zhang, X.; Song, K.M.; Kim, S.J.; Kim, K.; Weigand, M.; et al. Néel-type skyrmions and their current-induced motion in van der Waals ferromagnet-based heterostructures. Phys. Rev. B 2021, 103, 104410. [Google Scholar] [CrossRef]
- Ding, B.; Li, Z.; Xu, G.; Li, H.; Hou, Z.; Liu, E.; Xi, X.; Xu, F.; Yao, Y.; Wang, W. Observation of magnetic skyrmion bubbles in a van der Waals ferromagnet Fe3GeTe2. Nano Lett. 2019, 20, 868–873. [Google Scholar] [CrossRef]
- Banerjee, S.; Rowland, J.; Erten, O.; Randeria, M. Enhanced Stability of Skyrmions in Two-Dimensional Chiral Magnets with Rashba Spin-Orbit Coupling. Phys. Rev. X 2014, 4, 031045. [Google Scholar] [CrossRef]
- Kathyat, D.S.; Mukherjee, A.; Kumar, S. Microscopic magnetic Hamiltonian for exotic spin textures in metals. Phys. Rev. B 2020, 102, 075106. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kathyat, D.S.; Kumar, S. Antiferromagnetic skyrmions and skyrmion density wave in a Rashba-coupled Hund insulator. Phys. Rev. B 2021, 103, 134424. [Google Scholar] [CrossRef]
- Kaplan, T. Single-band Hubbard model with spin-orbit coupling. Z. Phys. B Condens. Matter 1983, 49, 313–317. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Akagi, Y.; Udagawa, M.; Motome, Y. Hidden Multiple-Spin Interactions as an Origin of Spin Scalar Chiral Order in Frustrated Kondo Lattice Models. Phys. Rev. Lett. 2012, 108, 096401. [Google Scholar] [CrossRef]
- Bouaziz, J.; Mendive-Tapia, E.; Blügel, S.; Staunton, J.B. Fermi-Surface Origin of Skyrmion Lattices in Centrosymmetric Rare-Earth Intermetallics. Phys. Rev. Lett. 2022, 128, 157206. [Google Scholar] [CrossRef]
- Okumura, S.; Hayami, S.; Kato, Y.; Motome, Y. Magnetic hedgehog lattices in noncentrosymmetric metals. Phys. Rev. B 2020, 101, 144416. [Google Scholar] [CrossRef]
- Singh, D.; Fujishiro, Y.; Hayami, S.; Moody, S.H.; Nomoto, T.; Baral, P.R.; Ukleev, V.; Cubitt, R.; Steinke, N.J.; Gawryluk, D.J.; et al. Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet. Nat. Commun. 2023, 14, 8050. [Google Scholar] [CrossRef]
- Janssen, T.; Janner, A. Incommensurability in crystals. Adv. Phys. 1987, 36, 519–624. [Google Scholar] [CrossRef]
- Janssen, T.; Janner, A.; Looijenga-Vos, A.; De Wolff, P. Incommensurate and commensurate modulated structures. In International Tables for Crystallography Volume C: Mathematical, Physical and Chemical Tables; Springer: Dordrecht, The Netherlands, 2006; pp. 907–955. [Google Scholar]
- Kamiya, Y.; Batista, C.D. Magnetic Vortex Crystals in Frustrated Mott Insulator. Phys. Rev. X 2014, 4, 011023. [Google Scholar] [CrossRef]
- Hayami, S.; Lin, S.Z.; Kamiya, Y.; Batista, C.D. Vortices, skyrmions, and chirality waves in frustrated Mott insulators with a quenched periodic array of impurities. Phys. Rev. B 2016, 94, 174420. [Google Scholar] [CrossRef]
- Berg, B.; Lüscher, M. Definition and statistical distributions of a topological number in the lattice O(3) σ-model. Nucl. Phys. B 1981, 190, 412–424. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Degeneracy Lifting of Néel, Bloch, and Anti-Skyrmion Crystals in Centrosymmetric Tetragonal Systems. J. Phys. Soc. Jpn. 2020, 89, 103702. [Google Scholar] [CrossRef]
- Hayami, S. Multiple-Q magnetism by anisotropic bilinear-biquadratic interactions in momentum space. J. Magn. Magn. Mater. 2020, 513, 167181. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I.; Tretiakov, O.A. Magnetic bimerons as skyrmion analogues in in-plane magnets. Phys. Rev. B 2019, 99, 060407(R). [Google Scholar] [CrossRef]
- Hayami, S. In-plane magnetic field-induced skyrmion crystal in frustrated magnets with easy-plane anisotropy. Phys. Rev. B 2021, 103, 224418. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Meron–antimeron crystals in noncentrosymmetric itinerant magnets on a triangular lattice. Phys. Rev. B 2021, 104, 094425. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).