Abstract
In this article, the mechanism of relaxation polarization currents occurring at a constant temperature (isothermal process) in crystals with ionic-molecular chemical bonds (CIMBs) in an alternating electric field was investigated. Methods of the quasi-classical kinetic theory of dielectric relaxation, based on solutions of the nonlinear system of Fokker–Planck and Poisson equations (for the blocking electrode model) and perturbation theory (by expanding into an infinite series in powers of a dimensionless small parameter) were used. Generalized nonlinear mathematical expressions for calculating the complex amplitudes of relaxation modes of the volume-charge distribution of the main charge carriers (ions, protons, water molecules, etc.) were obtained. On this basis, formulas for the current density of relaxation polarization (for transient processes in a dielectric) in the k-th approximation of perturbation theory were constructed. The isothermal polarization currents are investigated in detail in the first four approximations (k = 1, 2, 3, 4) of perturbation theory. These expressions will be applied in the future to compare the results of theory and experiment, in analytical studies of the kinetics of isothermal ion-relaxation (in crystals with hydrogen bonds (HBC), proton-relaxation) polarization and in calculating the parameters of relaxers (molecular characteristics of charge carriers and crystal lattice parameters) in a wide range of field parameters (0.1–1000 MV/m) and temperatures (1–1550 K). Asymptotic (far from transient processes) recurrent formulas are constructed for complex amplitudes of relaxation modes and for the polarization current density in an arbitrary approximation k of perturbation theory with a multiplicity r by the polarizing field (a multiple of the fundamental frequency of the field). The high degree of reliability of the theoretical results obtained is justified by the complete agreement of the equations of the mathematical model for transient and stationary processes in the system with a harmonic external disturbance. This work is of a theoretical nature and is focused on the construction and analysis of nonlinear properties of a physical and mathematical model of isothermal ion-relaxation polarization in CIMB crystals under various parameters of electrical and temperature effects. The theoretical foundations for research (construction of equations and working formulas, algorithms, and computer programs for numerical calculations) of nonlinear kinetic phenomena during thermally stimulated relaxation polarization have been laid. This allows, with a higher degree of resolution of measuring instruments, to reveal the physical mechanisms of dielectric relaxation and conductivity and to calculate the parameters of a wide class of relaxators in dielectrics in a wide experimental temperature range (25–550 K).
Keywords:
crystals with ion-molecular chemical bonds (CIMBs); hydrogen-bonded crystals (HBC); isothermal ion-relaxation polarization (in CIMBs); isothermal proton-relaxation polarization (in HBC); isothermal relaxation polarization current (ITRPC); thermally stimulated relaxation polarization current (TSRPC); nonlinear quasi-classical kinetic theory of dielectric relaxation; nonlinear space-charge polarization (in ionic dielectrics); proton relaxation and conductivity (in HBC); thermally stimulated polarization currents (TSPC); thermally stimulated depolarization currents (TSDC); Fokker–Planck kinetic equation (solved together with the Poisson equation); diffusion-relaxation polarization (for the ionic subsystem in CIMBs); complex amplitudes of relaxation modes of the space-charge distribution 1. Introduction
Studies of the electrophysical properties of crystals with ionic-molecular chemical bonds (CIMBs) are carried out using dielectric spectroscopy methods by measuring the temperature spectra of thermally stimulated depolarization currents (TSDC) and the frequency-temperature spectra of the dielectric loss tangent [1,2,3,4,5,6].
Theoretical methods for research and analysis of electrical conductivity and dielectric relaxation parameters in CIMB class crystals (including HBC) have developed quite well over the past 10 years and make it possible to achieve a high degree of consistency between the results of theory and experiment [1,2,3,4,5]. The quasi-classical kinetic theory of dielectric relaxation is the most effective for mathematical and numerical analysis of ion-relaxation polarization (IRP) and ionic conductivity (IC) processes in CIMB. It is based on a nonlinear system of equations of a phenomenological model describing the processes of diffusion transport (including both thermally activated (classical) and quantum tunnel transitions of ions on chemical bonds) for various types of charge carriers in a dielectric in a wide range of field parameters (0.1–1000 MV/m) and temperatures (0–1550 K) [5].
The aim of this scientific article is to develop and analyze the properties and parameters of a nonlinear universal quasi-classical model of isothermal polarization and ionic conductivity processes in crystals with ionic-molecular chemical bonds (CIMBs) in an alternating electric field, with the aim of a detailed theoretical study of the influence of high orders (r > 1) of polarization nonlinearities (quantum low-temperature; space-charge high-temperature) on the structure and properties of mathematical expressions describing the theoretical spectra of polarization current density in a wide range of field parameters (3 kHz–300 MHz and 3 GHz–300 GHz; 0.1–1000 MV/m) and temperatures (1–1550 K).
The construction of a rigorous nonlinear quantum-mechanical model (based on solutions of the Schrödinger equation and construction of a non-stationary (non-equilibrium) density matrix for an ensemble of majority charge carriers (primarily protons in HBC)) for ion-relaxation polarization is not included in the objectives of this work and is the subject of a separate study.
This article is of an analytical calculation nature and is focused on the preparation and detailed analysis of nonlinear properties of the physical and mathematical model of ion-relaxation polarization directly, without performing numerical calculations, which are also deferred to the future.
Note: To simplify the procedure of familiarization with our previously published works, primarily, the fundamental articles [2,3,4,5] and with the basic physical principles of physical and mathematical models of ion-relaxation polarization in CIMB class crystals (in particular, with the quantum-mechanical principles of proton motion in the hydrogen sublattice of HBC), before studying this work or in the process of studying it, we recommend familiarizing yourself with Section 4.2 (see Figure 1, Figure 2 and Figure 3 and their analysis) of this work.
Figure 1.
Scheme of the migration of ions due to the gradual movement of a proton within the layered structure, in a crystal of chemically pure chalcanthite [3]. Arrows indicate the directions of proton movements between conditions 1–6; the vertical arrow shows the direction of the external electric (polarizing) field .
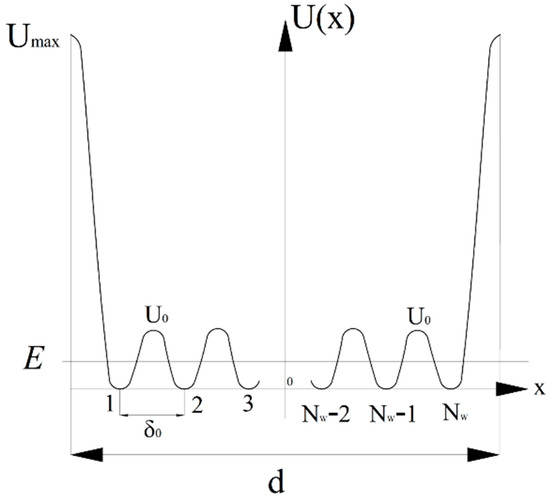
Figure 2.
The model of an unperturbed one-dimensional multi-well symmetric crystalline potential for the ion in CIMBs (for the proton in HBC).
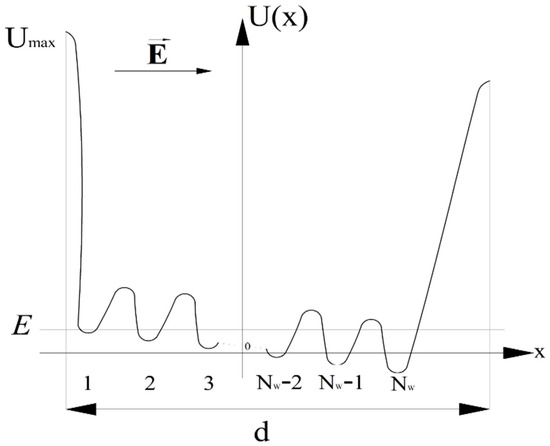
Figure 3.
The model of a perturbed by an electric field one-dimensional multi-well symmetric crystalline potential for the ion in CIMBs (for the proton in HBC).
2. Materials and Methods
2.1. Justification of the Relevance and Scientific and Practical Significance of the Chosen Research Area
The applied scientific and technical significance of CIMBs class crystals relates to a wide range of modern industry sectors [1,2,3,4,5], including industrial electrical engineering and high-voltage technology (insulating materials; electrically adjustable capacitors) [1,6], microelectronics (MIS, MSM structures; quantum field-effect transistors; resonant tunnel diodes) [7,8,9,10,11,12,13], radio engineering, radio electronics and microwave technologies (radar, communication technologies and systems, microwave detection of the properties of various working media, shells and housings of structures of radar, energy, cryogenic and space installations and systems (solid reflective surfaces of receiving and location devices; high-temperature dense and super-dense (non-ideal) plasma in technological circuits of thermonuclear reactors, etc.)) [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32], non-linear optics (non-linear receivers and converters of coherent electromagnetic waves in the optical range) and laser technology (regulators of laser radiation parameters based on ferroelectric crystals) [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52], electrochemical technologies and alternative energy technologies [53,54,55,56] (in the development of solid-state fuel cells based on proton semiconductors and conductors with high proton conductivity) etc. Of greatest applied practical interest are materials operating under extreme conditions of ultra-low and ultra-high temperatures, strong and super-strong electric and magnetic fields, intense laser radiation, mechanical stress, and deformation [1,5,6].
The application of numerical optimization methods to the results of theory and experiment from a comparison of the experimental and theoretical graphs of the measured macroscopic quantity (polarization; density of thermally stimulated polarization current (TSPC) and depolarization current (TSDC); real and imaginary components of the complex dielectric permittivity (CDP)), allows to calculate a set of theoretical values of molecular parameters for each type of relaxers (the most mobile charge carriers), activated in the vicinity of the corresponding temperatures or frequencies of the alternating electric field maxima on the basic experimental graph [2,3,4,5,57,58,59,60,61,62].
Presently, theoretical achievements in the field of electrophysics of CIMBs class materials are nonlinear physical and mathematical models of ion-relaxation polarization and conductivity, based on a nonlinear quasi-classical kinetic equation written in the form of the equation of balance of the number of particles (relaxers) in potential wells of a spatially inhomogeneous one-dimensional crystalline potential field perturbed by a polarizing electric field [1,2,3,4,5]. The solution of this equation is carried out in conjunction with the Poisson equation, taking into account the boundary and initial conditions arising from the experimental conditions for a given electrode model [57,58,59]. The results of this method, as applied to the descriptions of the temperature spectra of TSDC density and the frequency-temperature spectra of dielectric losses, are consistent with the experimental data in the entire experimental range of temperatures (50–450 K) and external electric field strengths (0.1–1 MV/m) [2,3,4,5].
Consideration of the influence of quantum transitions of massive (in comparison with protons) ions on dielectric relaxation in CIMBs does not have any special physical meaning, since, due to the small De Broglie wavelengths and small transparencies of the potential barrier for heavy ions (sulfate anions, phosphate anions, carbonate anions in crystal hydrates; silicate anions in natural minerals of the layered silicate class), formal consideration in the kinetic coefficients of the statistically averaged over energy levels (continuous spectrum) quantum permeability (depending on temperature in a certain way), from a physical point of view, has practically no effect on the parameters of the TSDC density spectra J and [2,5].
Hydrogen-bonded crystals (HBCs), a subclass of CIMBs, are characterized by the presence in the crystal structure of a hydrogen sublattice consisting of hydrogen ions (protons) interacting through electrostatic forces (hydrogen bonds) with ions of the anionic sublattice and water molecules (structural and adsorbed). The activation energies of protons in hydrogen bonds are distributed, according to experimental data, depending on the level of chemical complexity of the bond (on the type of ion with which the proton is bound), in the range of 0.01–1 eV, and the equilibrium concentration of the most mobile charge carriers (protons) in HBC, depending on the temperature range T K, is approximately [58,60]. Under this conditions, polarization in HBC, in the radio wave range (3 kHz–300 MHz) and microwave range (3 GHz–300 GHz), in the region of weak fields is determined by the diffusion-relaxation movement of protons along hydrogen bonds in the direction of the lines of force of the external electric field (proton conductivity) [59,61]. The set of polarization processes associated with the relaxation motion of protons in HBC can be defined as proton-relaxation polarization. The natural frequencies of vibrations of protons on hydrogen bonds in HBC are approximately . The width of the potential barrier for protons in HBC takes numerical values of . Transitions of protons along hydrogen bond lines can be carried out, taking into account the parameters of the structure, both due to thermal activation (classical transitions) and by quantum tunneling (quantum transitions) [62,63].
The equations of the quasi-classical nonlinear model of ion-relaxation polarization in CIMBs, as applied to the studies of proton-relaxation polarization in hydrogen-bonded crystals (HBC), are adapted at the mathematical level to the influence of proton tunneling on dielectric relaxation. In this case, high transparencies of the potential barrier for protons (0.001–0.1) significantly affect the numerical values of the kinetic coefficients [60]. At the same time, the numerical calculation indicates the determining influence of the parameters of the potential barrier (activation energy (potential barrier height) and barrier width on the temperature position and amplitude of the statistically averaged over energy levels (continuous spectrum) quantum permeability (calculated in [61] for the model of a one-dimensional parabolic potential barrier perturbed by a stationary polarizing field) by the WKB method The highest calculated values of this function are achieved at 0.01–0.1 eV, and the proton oscillation frequency in the temperature range T K and are equal to 0.01–0.2 [62], respectively. These regularities are confirmed by studies of low-temperature theoretical maxima in temperature spectra (see figures 10–13 in [5]) and frequency spectra (see figures 6 and 8 in [5]). The authors of [1,4,5] have unambiguously confirmed, both experimentally and theoretically, the dominant role of proton tunneling in the low temperature range (50–100 K), as well as a certain (not the main, but quite significant against the background of thermal activation) role of proton tunneling in the high temperature range (150–550 K) in HBC. In [2,3,4,5], the determining role of quantum effects in the region of anomalously high polarization nonlinearities in HBC, extending to the ranges of ultra-low (1–10 K) and ultra-high (550–1550 K) temperatures, was theoretically substantiated using various quantum-mechanical approximations. The transition to more rigorous, in comparison with the WKB method, direct quantum-mechanical calculations (based on the model of the discrete energy spectrum of protons), in estimating the values confirms the above established quantum effects.
Currently, it is expedient and scientifically sound to move on to detailed theoretical studies of the effects of quantum tunneling of protons on thermally stimulated polarization and depolarization in HBC in a wide theoretical range of temperatures (1–1550 K) and fields (0.1–1000 MV/m) [1,57,58,59,60,62].
Algorithms for theoretical studies of the temperature spectra of the density of thermally stimulated polarization currents (TSPC) and depolarization currents (TSDC), as in the case of frequency-temperature spectra of the dielectric loss tangent , should be based on the methods of nonlinear quasi-classical [1,2,3,5] and quantum [1,4] kinetic theories of dielectric relaxation in crystals with ionic-molecular chemical bonds (CIMBs), exhibiting the properties of ionic dielectrics with a layered crystalline structure (ceramics; natural minerals; perovskites; crystal hydrates, etc.). The nonlinear quasi-classical kinetic theory of dielectric relaxation [2,5] works successfully, both in formal mathematical and physical terms, in describing the mechanisms of ion-relaxation polarization and conductivity in almost all CIMB class crystals in a wide theoretical range of field parameters (0.1–1000 MV/m) and temperatures (1–550 K). Polarization nonlinearities, within the framework of the quasi-classical kinetic theory [2,5], unfold when compared with the experiment in the field of nonlinear space-charge polarization (450–550 K), and in theoretical terms they extend to a much wider range of temperatures, up to 1550 K in the region of strong fields (10–1000 MV/m). The nonlinear quantum theory of dielectric relaxation [4], in physical terms, is successfully applied, first of all, to hydrogen-bonded crystals (HBC), which exhibit, in the low temperature region (50–100 K), the effects of nonlinear quantum relaxation caused by the tunneling motion of hydrogen ions (protons) in the space of the anion sublattice of HBC [1,4]. Experimentally established quantum polarization nonlinearities in HBC manifest at low temperatures (50–100 K) with a sample thickness of 1000–10,000 nm, and theoretically extend to the region of ultra-low temperatures (4–25 K) with a sample thickness of 1–10 nm and are characterized by anomalously high polarization currents (3–4 orders of magnitude higher than at T = 50–100 K and d = 1000–10,000 nm). With this type of size effects, the low-temperature theoretical maximum shifts from the region of nitrogen to the region of helium temperatures with a decrease in the amplitude of the maximum by 3–4 orders of magnitude, which is accompanied by an increase in the ferroelectric properties of proton semiconductors [1,4].
In [3], the studies of the influence of quantum tunneling of protons on the theoretical TSDC temperature spectra were carried out within the framework of the quasi-classical kinetic theory [1], taking into account high-order polarization nonlinearities in the field, but for a model of the crystal potential in the form of a one-dimensional double symmetric potential well [3]. Moreover, the methods [3] led to satisfactory agreement between the experimental results and theory when calculating the characteristic parameters of relaxers in a wide temperature range (50–550 K). However, the methods of [3], even from the point of view of the nonlinear quasi-classical kinetic theory [2,5], are insufficient for a detailed analysis of the effects of ion tunneling (primarily protons in HBC) on the nonlinear properties of TSDC spectra, in particular on the electret effect, since in [3], in contrast to [2,5], a multi-well (closer to the real crystal structure than a double-well) model of the crystalline potential field for conduction ions moving by relaxation (reciprocating, due to ion transitions between adjacent potential wells, against the background of their thermal motion) in a crystalline potential field perturbed by an external electric field was not used. Additionally, with a rigorous theoretical approach, the methods developed in [2,5], which are consistent when comparing theory with experiment for spectra are insufficiently rigorous for the study of the temperature spectra of thermally stimulated polarization and depolarization currents in CIMBs, since in [5] polarization harmonics multiples of the field powers higher than the first (r > 1) were not taken into account. The analytical apparatus, built on recurrence formulas for complex amplitudes of relaxation modes of the space-charge density in a dielectric, was investigated in [2], in a generalized sense, for arbitrary orders of perturbation theory k with an arbitrary multiplicity of frequency harmonics of polarization r. At the same time, in [5], when calculating theoretical spectra using the methods of [2], only the first frequency harmonic of polarization (r = 1) was used. Although it was calculated in the infinite approximation of perturbation theory (at k = 1, 2, 3, etc., to infinity), it is insufficient for a rigorous analysis of nonlinearities in the phenomena of thermally stimulated polarization and depolarization, characterized by a higher resolution or sensitivity of the system to temperature than the spectra . Thus, in a rigorous theoretical study of quantum nonlinearities in the TSPC and TSDC spectra in alternating current, at the level of quasi-classical kinetic theory [2], it is necessary, in continuation of [5], to construct formulas for the polarization of the crystal, with an accuracy of up to an arbitrary order in frequency harmonics of the space-charge distribution (r > 1), which corresponds, in the radio frequency range, to nonlinear electrophysical effects such as secondary harmonic polarization generation (SHPG) and self-generation of high-order polarization. This approach will form the basis of the calculation schemes for calculating the polarization of a dielectric in this article. When calculating the kinetic coefficients in this article, as in [2], the model of the crystal potential in the format of a one-dimensional multi-well symmetric potential field [5] will be used. Potential barriers are assumed to be parabolic [2,3,4,5]. In the general case, the barrier can take an arbitrary shape, including rectangular [1]. In this sense, the parabolic potential barrier is closest in its properties to the real crystalline structure of a dielectric [2,3,4,5].
In view of the specificity of the mathematical apparatus of the quantum kinetic theory of dielectric relaxation, direct quantum mechanical studies of the theoretical spectra of TSPC and TSDC, using the density matrix apparatus by analogy with the methods of [4], will be carried out in subsequent works.
The mathematical expressions obtained in this article, will be extended to materials of a wider class, primarily to CIMBs, without limiting the generality of the results.
2.2. Theoretical Bases of Physical and Mathematical Models of Relaxation Polarization in Solid Dielectrics
In modern fundamental physical science, the question of the applied, scientific, and technical significance of the results of the research direction developed in a certain area of research is of great importance. At the same time, the aspects of the applied scientific concept and the strategy for its development are determined both by the specifics of a given scientific direction and by its relevance to the practical needs of a modern scientific and technical industry (or group of industries).
The state of condensed matter physics, covering a wide range of different materials and methods in the field of solid state physics and physics of dielectrics and semiconductors, is characterized by colossal achievements in the issues of condensed matter theory in the format of classical and quantum theories of various directions (in particular, the theory of quantum liquids, such as helium-II at ultra-low temperatures; the theory of quantum macroscopic phenomena, in particular, the superfluidity of liquid helium (2.19 K), low-temperature superconductivity in metals (4–25 K)), including the quasi-classical [1,2,5,57,59] and quantum [1,4,5,60,61,62] kinetic theories of dielectric relaxation and conductivity in solid dielectrics, which are of practical importance for the physics of dielectrics and its practical applications, such as industrial electrical engineering (capacitor technology (electrically controlled capacitor devices); insulation and cable technology; high voltage technology); electric power engineering (insulating surfaces of current-carrying lines; electric generators and their auxiliary equipment in industrial power plants); radio engineering and radio physics (electronically controlled radio frequency systems (3 kHz–300 MHz) and microwave technologies and devices (3–300 GHz), in particular, generators and converters of microwave coherent waves (3–300 THz) [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]) for radio communication systems, television communications, radar and microwave diagnostics of the state of materials in extreme technological conditions (microwave diagnostics of plasma in thermonuclear reactors and auxiliary nuclear fusion installations); electrochemical technologies (solid-state fuel cells based on transition metal oxides (TMO), perovskites, high-temperature ionic superconductors [40–58] in [5]); optoelectronics (fiber optic elements of sensors for deformation parameters of construction and building materials [18–26] in [5]); nonlinear optics and laser technology (laser control elements [27–39] in [5], laser radiation parameter controllers (KDP, DKDP ([79–92] in [5])) based on nonlinear optical materials that exhibit nonlinear optical effects when interacting with intense coherent electromagnetic waves (3000 THz) of the optical range nonlinear absorption of light; generation of multiple frequency harmonics; photoelectric effect; combination scattering of light); microelectronics and quantum electronics (MIS, MSM-elements, necessary for the development of quantum superconducting nonlinear elements such as resonant and tunnel diodes ([9–17] in [5])); space technologies and cryogenic equipment (functional elements for panels of local photovoltaic devices for space stations; photoconverters of electrical energy based on dielectrics with high ionic conductivity and proton semiconductors with ultra-high proton conductivity in the region of ultra-low (helium) temperatures).
The quasi-classical nonlinear kinetic theory of dielectric relaxation in HBC [2,5], at the level of coefficients (formulas (5)–(10) in [5]) of the nonlinear generalized kinetic equation (formulas (16) and (17) in [5]), considers the influence of proton tunnel transitions (inside the hydrogen sublattice during the interaction of protons with ions of the anion sublattice) on the mechanism of proton-relaxation polarization and conductivity in proton semiconductors and dielectrics (PSD) in the low-temperature region (50–100 K), against the background of low values of proton activation energies (0.01–0.1 eV), when the transparency values of the potential barrier for protons are sufficiently large (0.001–0.1) [3,4], which, under the conditions of a crystalline structure (in a solid), is quite significant for such heavy (in comparison with electrons) particles as protons. The quasi-classical nonlinear model [5] allows, at the theoretical level (formulas (150), (120), (121) and (122) in [5]), to detect and analyze the behavior of low-temperature maxima (50–100 K) in the spectra in HBC (see figures 10–13 in [5]), which presently cannot be achieved experimentally for a number of technical reasons [1]. Additionally, in [5], theoretical frequency spectra , , were investigated at constant temperatures in HBC (see figures 6–9 in [5]).
The use of direct quantum-mechanical calculations allows, using the apparatus of the density matrix, to take into account the influence of the configuration of the discrete energy spectrum of relaxers (protons) on the properties and parameters of low-temperature spectra in HBC (see graphs 6, in figures 1 and 2 in [4], constructed using the quantum-mechanical expression (27) from [4]). Furthermore, in [4], the size effects associated with anomalous shifts of low-temperature maxima from the region of nitrogen (50–100 K) to the region of helium (4–25 K) temperatures were investigated, with a decrease in the amplitude of the theoretical maximum from to with the decrease in the thickness of the dielectric from 30,000 nm to 3 nm (see tables 3 and 4 in [4]).
Similarly, in [1], taking into account the quasi-discrete structure of the energy spectrum of protons in HBC, in the region of ultra-low temperatures (1–10 K), in nanosized crystalline structures (1–10 m) of HBC, leads to anomalously high numerical values of the transparency of the potential barrier in the range of 0.5–0.9. The tangent of the dielectric loss angle, according to the results in [1], decreases in amplitude by 3–4 orders of magnitude in comparison with the low-temperature region. This effect, which manifests in anomalously large values of the real component of the dielectric constant of crystals (2.5–5.5 million) in the region of helium temperatures (4–25 K), can be defined as a low-temperature quasi-ferroelectric effect in HBC.
From numerical studies of quasi-classical nonlinear models of thermally stimulated depolarization in HBC in the high-temperature region (150–550 K), the quantum transparencies of the potential barrier for protons are also large (0.01–0.1), and high-temperature nonlinear space-charge polarization in HBC is largely determined by quantum tunnel transitions of protons. Thus, quantum effects in HBC play a significant role in the formation of proton-relaxation polarization in a wide temperature range (1–1550 K) [2,3].
Based on the comparative analysis of the influence of quantum effects on theoretical spectra [4,5] performed in this Section 2.1, it can be argued that it is necessary to expand the methods of quasi-classical and quantum theories of dielectric relaxation for studying the properties and parameters of theoretical spectra of thermally stimulated depolarization currents in HBC, including the study of the transformations of the TSDC density spectra caused by size effects due to tunneling (with abnormally high transparency) movement of hydrogen ions (protons) in the temperature range (4–25 K), which is most scientifically and practically significant for cryogenic technology and the physics and technology of low-temperature superconductivity.
The physical and mathematical models constructed in this way could be extended to a wide class of crystals with ionic-molecular chemical bonds (CIMB) and their composites.
As noted in the introduction, the analytical apparatus of the models developed in this article will be based on the methods of the nonlinear quasi-classical kinetic theory of dielectric relaxation [2,5] in an arbitrary approximation by the multiplicity of frequency harmonics of polarization above the first (r > 1), in combination with the methods of statistical physics and electrodynamics of continuous media, with elements of nonrelativistic quantum mechanics (necessary to reflect, at the mathematical level, the influence of quantum effects on the nonlinear properties of proton migration processes in HBC [2,5]).
In the general case, the physical and mathematical model of nonlinear relaxation processes during thermally stimulated depolarization in CIMBs should consist of two sequentially implemented parts. In the first part of the model, the dielectric relaxation during polarization of a crystal in a constant (stationary) external electric field at a given polarization temperature is investigated, and in the second part, a study of the kinetics of thermally stimulated depolarization (in the absence of an external field) is performed in a sample rapidly cooled to liquid nitrogen temperatures (in the classical experimental scheme [1,3]), and in the general case to liquid helium temperatures (in theoretical schemes [2,5]) and heated according to a certain time law T = f(t), in the simplest case, linear. Of significant theoretical interest is the study, in the first part of the general model, of the kinetics of nonlinear thermally stimulated polarization in an alternating external electric field, with a subsequent transition, in the second stage of the modeled solutions, to the study of depolarization according to the scheme described above (in the absence of an external voltage source). This approach would allow, at a sufficiently high theoretical level, to demonstrate the influence of polarization nonlinearities of various natures (quantum-mechanical; space-charge; associated with size effects, etc.) in the process of preparing the sample for depolarization, to establish the influence of quantum tunneling [1,3] and interactions of relaxation modes of the volume-charge on the mechanism of thermally stimulated polarization currents (TSPC) and, subsequently, on thermally stimulated depolarization currents (TSDC).
Due to the complexity of the equations and calculation formulas of the general nonlinear physical and mathematical model of thermally stimulated polarization and depolarization, the methodological apparatus of this article will be simplified when setting research objectives, with the expectation of implementing the general scheme of theoretical research in subsequent works. At this stage of research, such simplifications are technically necessary and, as will be shown below, are entirely justified from a methodological point of view. In this regard, firstly, we take all polarization processes as isothermal (the polarization temperature is taken as a constant value in this model) and, secondly, we will consider kinetic phenomena only for polarization processes (in an alternating field), and we will not describe depolarization (in the absence of an external electric field) in this article and will defer this procedure to subsequent works. The polarization process is similar in this regard and represents a separate problem, the solution of which will be described in the future.
The methodology of this work will be based on the study of the nonlinear phenomenological system of Fokker–Planck and Poisson equations for a given model of electrodes [5]. The crystal temperature is assumed to be constant in the zero approximation for the polarizing field in the model under study. At the initial moment of time, polarization is absent. The solutions of this system of equations are constructed in a quasi-classical model with an accuracy of up to multiples of an arbitrary order in the frequency of the field of space-charge distributions frequency harmonics for the most mobile ions across the thickness of the crystal .
The space-charge distribution for relaxers (conduction ions) , calculated in the k-th approximation of perturbation theory (by a small dimensionless parameter < 1) at a frequency harmonic of multiplicity r to the fundamental frequency of the alternating field is determined using a Fourier series expansion in spatial harmonics on the interval 0, according to the formula , where is the complex amplitude of the space-charge distribution . This model uses dimensionless spatial variable and time t. Here is the lattice constant (in the crystal structure of the simulated dielectric); is the probability rate of transition (flip) of a relaxer (conduction ion) between adjacent potential wells in a crystal potential field, calculated in the approximation l = 0 from the dimensionless parameter , at a crystal temperature T [2,5]. In this expression, q is the charge of the relaxer. In the work [5], generalized nonlinear formulas are constructed for calculating the function in an arbitrary approximation l from a dimensionless parameter with coefficients . The electric field strength in a dielectric calculated in the general case from the solution of the Poisson equation [5] and has the form =, where is the strength of the alternating in time external electric field, and is the strength of the induced field excited by the external electric field during polarization of the crystal. The induced field in the quasi-classical model [2,5] is taken to be a spatially inhomogeneous non-stationary function varying weakly (adiabatic) along the x coordinate in the region of an arbitrary potential well in the crystalline potential field perturbed by the field . In the special case = , with blocking electrodes at the crystal boundaries, the boundary condition is satisfied, where d is the amplitude of the EMF, , is the amplitude value and cyclic frequency of the polarizing field strength, d is the thickness of the crystal.
In continuation of the work [5], in which the polarization of the crystal was calculated at the fundamental frequency of the alternating field (r = 1), in this work the study of the polarization of the dielectric will be constructed using the same methods of the nonlinear quasi-classical model [2,5], but in an arbitrary approximation of the multiplicity r by the frequency of the external polarizing field , and the current polarization density corresponding to the partial harmonic of multiplicity r, upon transition of the dimensionless variable t, is equal to .
The calculation of the space-charge distribution in the crystal at the fundamental (r = 1) frequency of the alternating field results in the expression [5]
Here, the parameters , , , =, , , are used [5]. is the probability rate of transfer of a conductivity ion between adjacent potential wells, calculated in the l-th approximation from the dimensionless parameter [5]. Additionally, the high-frequency (in the optical frequency range) dielectric constant of the crystal was used. The theorem was applied during transformations [2]. Relaxation times , where is the diffusion relaxation time, is the zero component of the diffusion relaxation time by the spatial harmonic number (n = 0), is the Maxwell relaxation time [2,5], corresponds to the n-th relaxation mode of the space-charge distribution (in this case, at the fundamental frequency of the alternating field )
with a complex amplitude expanded into an infinite power series in components corresponding to the k-th approximation of perturbation theory in a small dimensionless parameter [2]. An arbitrary k-th component of the complex amplitude is calculated using the recurrence formula . Based on the component of order k = 1 of perturbation theory and summing the elements by number k from 1 to infinity, we obtain the resulting expression
which corresponds to the generalized complex amplitude
The dimensionless quasi-classical parameter of the kinetic theory of dielectric relaxation is a small parameter of perturbation theory, complementary to .
Using the power series the generalized formula for the polarization of a dielectric at the fundamental frequency of an alternating field can be rewritten in a compact form , from which we have
Thus, the generalized (calculated in the infinite approximation of perturbation theory by a small parameter of perturbation theory , at the fundamental frequency of the alternating field) polarization of the crystal is a function based on the first approximation of perturbation theory at the same fundamental frequency of the field
where —the basic component of polarization calculated in the first approximation of perturbation theory. Here .
It is evident, that a power series of successive approximations is performed
Here
Thus, it is obvious
where, respectively, the degree of the additional small parameter of the model is the ratio
Accordingly .
Everything fits together.
In the general case, the study of polarization at the fundamental (r = 1) frequency of the alternating field leads to the function [5]
The quasi-classical relaxation coefficients are complex functions of temperature = = − i, investigated in [2,5].
Let us apply the complex coefficient of relaxation polarization ==, also calculated at the fundamental frequency of the alternating field. Simultaneously
Then
The density of the relaxation polarization current, established at the first (fundamental) frequency harmonic of the external electric field, is calculated from the expression
Based on the equality , let us rewrite the generalized formula for the relaxation polarization current density at the fundamental frequency of the alternating field in the dielectric
in a compact form , from where we have
Here, the equalities
are used.
Accordingly with the equality an infinite power series of successive approximations is fulfilled
where
Respectively,
Distinguishing the real and imaginary components of the relaxation polarization current density
we have
The following formulas are convenient for comparison with the experiment
The formulas obtained, which correspond to relaxation polarization currents, cannot be considered complete from the point of view of a strict comprehensive assessment of the parameters and mechanisms of currents excited in a dielectric with a complex crystalline structure, in particular, in dielectrics with ionic-molecular chemical bonds (mica; ceramics; crystal hydrates; vermiculites, etc.). In addition to relaxation-polarization processes, which are realized due to relaxation (reciprocating) transitions of the main charge carriers in a crystalline potential field perturbed by an external electric field, with an average relaxation time s, induction polarization processes occur in the crystal, which are realized due to almost instantaneous transitions of the main charge carriers on elements of the crystal structure such as atoms, molecules, ions, dipoles, etc., when an external electric field is turned on, with an average relaxation time of s. In the general case, for polarization processes in a harmonically changing over time external (polarizing) electric field , the electrostatic induction in a dielectric is [1,2], where is the value of inductive polarization (occurring in the high-frequency range (in the optical frequency region), and characterized by permeability ) [1,3], is —the magnitude of relaxation polarization occurring in a dielectric in an alternating electric field, in the radio frequency and microwave range, and characterized, according to the nonlinear quasi-classical kinetic theory, at the fundamental frequency of the field [2,5], by the permittivity [2,5]. Then, the value of the total polarization current density in a dielectric is . Therefore, we have
From where we get
The following formulas are convenient for comparison with the experiment
Based on (3c,d) let us write the dispersion relations
Averaging in the left parts of relations (3e–h) is performed over the period of the electric field fluctuations .
An important consequence of the analytical relations for the components of the total polarization current density (3e–h) are the following equalities
2.3. General Provisions of the Physical Model of Thermally Stimulated Polarization in Ionic Dielectrics
In the general case, for an experimental sample (dielectric; semiconductor; composite material) of thickness d, connected in the direction of the crystal axis (in the direction of the lines of force of the external electric field ) to a source of alternating electric voltage V(t), with a given model of electrodes, the boundary condition (applied to the Poisson equation) for the electrical circuit is satisfied
A spatially inhomogeneous non-stationary (alternating) electric field inside a crystal is formed as a result of conductivity and polarization phenomena of various natures (depending on the type of chemical bonds and the structure of the crystal lattice); it is the sum of the external field and the field induced in the crystal as a result of electrophysical processes
In the general case, the experimental methodology for studying thermally stimulated depolarization currents in dielectrics is based on a combined measurement scheme consisting of two parts (or stages) [1,3]. At the first stage, the experimental sample (crystal) is polarized in a uniform harmonically changing over time external (polarizing) electric field of intensity at a constant polarization temperature , during the polarization time . The voltage source, in this case, is characterized by an alternating EMF , where is the amplitude and frequency of the EMF, and d is the thickness of the crystal placed in the space between the plates of a flat capacitor, with a plate area of S. The shape of the electrode plates (electrodes) and the near-electrode processes that depend on the geometry of the electrodes do not have a significant effect on the polarization mechanism within the framework of this model, therefore the shape of the electrodes of the measuring cell can be arbitrary. The second Kirchhoff rule, as applied to this equivalent measurement scheme, under the assumption of non-uniformity of the field inside the dielectric, when , where is induced by the external polarizing field component of the field , satisfies the boundary condition [1,2,5]. Then, the boundary condition for the Poisson equation [2,5], when calculating the total spatially inhomogeneous polarization field distributed over the thickness of the dielectric, takes the form
At the second stage of measurements, the experimental sample is disconnected from the EMF source , cooled rapidly to a temperature near the temperature of liquid nitrogen, connected to a source of alternating EMF of a harmonic type and begins to heat up according to a linear law (thermally stimulated polarization). The numerical values of the amplitude and frequency of the EMF, in the general case, are different from the corresponding parameters in the first part of the experiment , At the same time, in the experiments described in [1,3], the heating rate of the crystal and the polarization temperature were set within the range of , K. The polarizing field in [1,3] was assumed to be stationary . In the general case, at the second stage of the experiment, the mathematical description of the processes of thermally stimulated polarization of a dielectric in an external field should be constructed using the total spatially inhomogeneous field of thermally stimulated polarization distributed over the thickness of the dielectric, satisfying, when solving the Poisson equation [2,5], the boundary condition
The range of changes in the parameters , , c, , , , , d, in the theoretical study of thermally stimulated space-charge polarization is selected in compliance with the formal requirements for the smallness of the dimensionless parameters [1,5]
At the same time, the diffusion and mobility coefficients for the first stage of the measurement scheme (isothermal polarization) are calculated at a constant temperature , and for the second stage of the measurement scheme (thermal polarization) the calculations are based on the expressions [1,5]
The kinetic coefficients , , , , in the general case, within the framework of the quasi-classical model of dielectric relaxation, in the absence of the influence of the phonon subsystem on the motion of relaxers [1,2,5], have the meaning of the first two components of the expansion of the probability rate of the transfer of a relaxer (an ion; a proton in HBC) through a potential barrier separating the i-th and j-th neighboring potential wells, in powers of a small dimensionless parameter , where for the process of isothermal polarization (in an alternating field and , where for the process of thermal polarization (in an alternating field . Parameters , , are model constants, and parameters , are functions of crystal temperature, as they relate to the process of thermally stimulated polarization, occurring at a variable monotonically increasing temperature T. To simplify the mathematical model of thermal polarization, when calculating the parameters , , , we will take the zero approximation in the vicinity (on the set of points of the continuum measure) of the temperatures of the corresponding experimental (monorelaxation) maxima of the current density of thermally stimulated polarization . Thus, in the numerical study of the quasi-classical kinetic model of thermal polarization, the method of minimizing the comparison function (MCF) [1,5] will be applied, which is reduced to minimizing the difference in the amplitudes of the theoretical and experimental maxima of the density of the thermally stimulated polarization current in the vicinity of the temperature of the corresponding experimental maximum .
The calculation of kinetic coefficients , , , will be based on the recurrent formulas of the quasi-classical theory [1,2,5], using perturbation theory methods in the approximation l by a small dimensionless parameter , where , [2,5]
In (5), the averaged over the energy levels of the continuous spectrum of the main charge carriers (ions; protons in HBC) quasi-classical quantum transparency of the potential barrier is used, which is calculated in the approximation l by a small dimensionless parameter for the parabolic shape of the one-dimensional barrier [2,5]. In the general case, the application of the WKB approximation to calculate quantum transparency can be used for an arbitrary shape of a one-dimensional potential barrier
Applying for l = 0, l = 1, respectively, , , we obtain
where , .
2.4. Nonlinear Quasi-Classical Model of Isothermal Relaxation Polarization in Ionic Dielectrics in a Non-Stationary Electric Field
The structure and properties of the nonlinear kinetic equation of the phenomenological Fokker–Planck model [2,5] and the solution schemes of this equation are determined by the influence of the parameters (amplitude and frequency) of the alternating polarizing field, the characteristic parameters of relaxers and the temperature on the small parameter of the perturbation theory.
In Section 2.2, the basic principles of the physical model of relaxation polarization in dielectrics with a complex crystal lattice structure, including CIMBs and, in particular, HBC crystals, were described. There, two main stages of the implementation of the research schemes are identified, including the first stage, which amounts to isothermal polarization at temperature in an alternating electric field , and the second stage, which amounts to thermal polarization in an alternating electric field .
A variant of this scheme, which is closer to the conditions of a real experiment, assumes, at the first stage, the same isothermal polarization at temperature in a non-stationary electric field , and, at the second stage, thermally stimulated depolarization, when the external electric field is switched off completely and is not switched on again , , and the sample is rapidly cooled to a temperature near the temperature of liquid nitrogen and begins to heat up according to a linear law (thermally stimulated depolarization).
Within the framework of the methodology and structure of this scientific article, we will investigate only the first stage of the measuring circuit, namely, isothermal polarization in a non-stationary field, and the study of thermal polarization and, in particular, thermally stimulated depolarization, will be deferred to subsequent publications.
At the first stage of the research of the measuring circuit for the mathematical model of isothermal polarization in an alternating field , the formal form of the system of nonlinear equations of the phenomenological model (57)–(61) from [5], including the quasi-classical kinetic equation in the form of the nonlinear Fokker–Planck equation (57) and the associated Poisson Equation (58) and the initial and boundary conditions (59)–(61) to (57) and (58) from [5], is completely preserved and the solutions of equations (57) and (58) from [5] must be rewritten taking into account the kinetic coefficients calculated at temperature , , Where , . Taking dimensionless variables , and dimensionless field , let us rewrite (57)–(61) from [5] in the form
In the general case, solutions of Equations (6) and (7) are constructed by expanding into infinite series in powers of the polarization dimensionless small parameter in the form
In the k-th approximation of perturbation theory, the solution of Equations (6) and (7) on the interval is constructed using Fourier series
The complex amplitudes of functions (12) and (13) are calculated from the solution of the operator equation (69) from [5], according to the recurrent expression (70) from [5], rewritten in the notations corresponding to the process of isothermal polarization (in the notations from Section 2.2)
Here .
In [2,5] similar (14) complex amplitudes were calculated according to the recurrent expression (70) from [5], in the asymptotic approximation, in the stationary polarization mode (under the condition ), which is established upon transition to the limit in the final expression for the function . This limit expression is constructed in [5] and has the form of a recurrent formula (73). This mathematical approach, from the point of view of the physical content of polarization processes, is justified in the study of dielectric loss mechanisms, when the ultimate goal of analytical studies is the construction of theoretical spectra of complex dielectric permittivity (CDP). These spectra, at the fundamental frequency of the alternating field , are calculated, as noted in Section 2.1, based on the formula for the polarization of the crystal and take the form =. When studying the kinetics of dielectric losses, it is unnecessary to continuously (throughout the entire time of studying the process itself, comparable to the polarization time) analyze the transient processes excited in the dielectric due to the action of an external electric field and, further, developed under the influence of the electric field induced in the dielectric during the interaction of the external field with the substance. In the equations of the mathematical model, when studying the CDP spectra, it is sufficient to move to a time far from the transient processes (when the observation time of the process is much longer than the relaxation time ), which is reflected in the properties of the asymptotic function , represented by formula (73) from [5].
Studies of the recurrent expression (13) for processes associated with polarization currents (as well as with depolarization currents) must be carried out from the point of view of a detailed study of the kinetics of the polarization process over a period of time comparable to the relaxation time (under the condition ). In this case, the study of the dependencies for the complex amplitudes of relaxation modes (the n-th number in the k-th approximation of perturbation theory for a small dimensionless parameter ) must be carried out in a continuous mode, from the point of view of a detailed analysis of the relaxation mechanism of the space-charge distribution over a time comparable to the polarization time. The study of complex amplitudes is performed for the most mobile charge carriers (in the general case, ions) moving in a dielectric (in the space between the electrodes) in an alternating polarizing field . Mathematical modeling of the distribution of the space-charge density across the thickness of the crystal, within the framework of the quasi-classical kinetic theory [2,5], is carried out as a function of the spatial variable and time in a nonlinear approximation in the field using perturbation theory methods, by expansions into infinite power series in a small parameter according to expressions (10) and (11).
In (13), the component of the dimensionless field of the k-th order is generated by the space-charge distribution of the corresponding order , formed under the action of the field of the previous k-1-th order . The process of polarization of a dielectric in the zero approximation (k = 0) is described by a system of equations , , , from which follows the expression for the “zero” dimensionless field , corresponding to the strength of the external field .
In subsequent approximations of perturbation theory , integration of the equation taking into account the boundary condition , gives a recurrent expression for the k-th component of the function , in the form
In the first approximation (k = 1) from (14), noting that
taking into account , we have
Based on in view of (16), we obtain a previously linear solution by a small parameter of the Fokker–Planck equation for the isothermal polarization process
Substituting (16) into (13), along with (17) into (15), yields a linear by a small parameter component of the dimensionless field
In the approximation k = 2, from (14)
substituting (17) and (18) into (19), applying the expression
we ultimately have
Based on , in view of (20), we obtain a quadratic solution of the Fokker–Planck equation by a small parameter
Substituting (20) into (13), as well as (21) into (15), yields a quadratic component of the dimensionless field by a small parameter
In the approximation k = 3, from (14) we have
The result of calculating the third-order complex amplitude of perturbation theory (k = 3), constructed on the basis of (23), together with (17), (18), (21) and (22), is presented in the format of a transition function of time in the form of expression (S1) in Section S1.
The calculation of the space-charge density for relaxers (ions) in the third approximation k = 3 of perturbation theory is based on (12) in the form and, due to (S1), in the form (S2), is a cubic solution by a small parameter of the Fokker–Planck equation (Equation (6) in this article; (57) in [5]).
Further calculations of the components of perturbation theory for the space-charge density in the approximations are rather cumbersome transformations (in comparison with those previously performed in the approximations k = 1, 2, 3). A detailed presentation of these calculation schemes, even for the case k = 4, does not seem appropriate within the framework of the main part of this work due to their cumbersomeness.
Thus, in the approximation k = 4, from (14)
The final expression for the complex amplitude in the fourth approximation of perturbation theory (k = 4) is constructed in Section S2, based on (24), taking into account (S2), (S3), (21), (22), (17) and (18) and is formulated as a function of time (S4), containing eight terms on the right-hand side, each of which contains a time part that is a multiple of the corresponding field frequency , 2, 3, 4.
The calculation of the space-charge density for relaxers in the k = 4 approximation of perturbation theory is based on (12) in the form and, by virtue of (S4), is a fourth-order solution of the Fokker–Planck equation by a small parameter ((57) from [5]).
It is obvious that knowledge of the space-time function and expressions (17), (21) and (S2) reveals the possibility of calculating the isothermal polarization current density , with an accuracy of up to the fourth term of perturbation theory by a small parameter when solving the Fokker–Planck equation ((57) from [5])
The component of the k-th approximation of perturbation theory by a small parameter for the relaxation polarization current density is calculated by virtue of the expression for the k-th component of polarization, taking into account , by the formula
The recurrent expression (25) must be investigated in combination with Formula (14) for complex amplitudes of the space-charge distribution of various orders k of perturbation theory by a small parameter (12) in the form . Moreover, in Section 2.3 rigorous formulas for the first four approximations by a small parameter in the form of expressions (17) for k = 1, (20) for k = 2, (S1) for k = 3 and (S4) in the case of k = 4 were constructed.
For transitioning to the studies of the components of the polarization current density by Formula (25) for values of k = 5 and higher, a more compact recurrent expression than (14) is necessary, allowing, in a continuous time mode (for process times comparable to relaxation times), to express a function of arbitrary order k through similar functions of all orders preceding the given one, starting from k = 1 to k − 1. For this purpose, the analytical expression (71) constructed in [5], in which the embedded complex amplitudes are calculated for time intervals comparable to is convenient. Then
It evident that Formula (20) can be obtained on the basis of (26) for k = 2, using the result of (16). Similarly, according to (26), for k = 3, using (16) and (20), it is easy to obtain (S1), and for k = 4, using (16), (20) and (S1), respectively, (S4). In this regard, from the point of view of the effectiveness of analytical research and the application of relaxation functions in the study of polarization processes in a dielectric, expression (26) is more rational than (14). Although, the general methodological role of Formula (14) is retained, since this expression, for different values of the parameter k, forms a clear representation of the connections of different orders of perturbation theory when studying the complex amplitudes of relaxation modes for k = 1, 2, 3, 4. At higher orders, when k > 4, Formula (26) is significantly more convenient.
The analytical advantages of the recurrent expression (26), compared to (14), are even more obvious when studying the formulas of the element for the relaxation polarization current density in the format (25). Thus, when calculating the terms on the right-hand side of (26), for the first element
we have
for the second element
we get
For the relaxation polarization current density, in the approximation k of perturbation theory by a small parameter , at frequencies of an alternating field of multiplicity r = (1, 2, 3), in the right-hand side of (25), at process times close to the relaxation time , but after some transformations, we have, respectively,
In (27), the following notations are used
Noting that = 0 from (27b) we obtain the identity . In a similar way, we obtain recurrent identities , for = 1, 2, 3, …, which indicate that the polarization current density, at frequency harmonics of even multiplicity to the fundamental frequency of the field , is equal to zero.
In (27a–c) the relaxation time corresponding to the relaxation mode of number s is determined from the expressions constructed in [2,5], in combination with formulas (4) and (5) in the form
Similar calculations are performed for the expression .
For a more accurate calculation of the relaxation polarization current density in a given approximation k of perturbation theory, it is necessary to substitute the complete expressions for the complex amplitudes calculated from (14) and (26), into (25).
It is easy to see that substituting the function и from (16) into (25) for k = 1 results in
Next, substituting the second-order perturbation theory function from (19) into (25) for k = 2 results in
Due to = 0 the second term on the right-hand side of (29) is equal to zero. At the same time, Пpи этoм, the first term in the formula for the polarization current density at k = 2, associated with the first power of the polarizing field, respectively, a multiple of the fundamental frequency harmonic , is equal to
To determine the component of the polarization current density in the third approximation of perturbation theory, it is necessary to substitute the function from (S1) into the recurrent Formula (25), with k = 3. Due to the cumbersomeness of the final expression for the desired function , the result is placed in Section S3 (see Expression (S5)). After some auxiliary transformations, Formula (S5) takes a form convenient for numerical calculations and comparison of the results of theoretical and experimental studies. Thus, we obtain
In this case, the first and second terms in Formula (31) for the polarization current density at k = 3, associated respectively with the first and third power of the polarizing field, are calculated from components with coefficients , that are multiples of the first two frequency harmonics of the alternating electric field
To determine the component of the polarization current density in the fourth approximation of perturbation theory, it is necessary to substitute the function from (S4) into the recurrent Formula (25), with k = 4. Due to the cumbersomeness of the final expression for the desired function , the result is placed in Section S4 (see Expression (S7)).
After some auxiliary transformations, Formula (S7) takes a simplified form convenient for numerical calculations and comparison of the results of theoretical and experimental studies (see Expression (S8)). In this case, in the right part of the Formula (S8) there are five terms, the first of which, with a coefficient is a multiple of the first odd frequency harmonic , and the other four components, with the corresponding coefficients , , , , are multiples of the second odd frequency harmonic of the alternating electric field.
The value of the polarization current density calculated with an accuracy of up to the fourth order (k = 1, 2, 3, 4) by the power of the small dimensionless parameter of perturbation theory is constructed on the basis of the general expression , taking into account the formulas for individual components, calculated, respectively, for k = 1 (expression (28)), k = 2 (expression (30)), k = 3 (expression (31)) and k = 4 (expression (S8)).
Due to the fact that all terms in expressions (28), (30), (31) and (S8) contain an element of the form , the lines described by these formulas can be considered relaxation in a time interval of the order of the relaxation time of the process .
Let us make a transition in the element to the dimensional relaxation time . Here, the expression for the n-th spatial relaxation mode of the space-charge distribution can be applied. The inverse diffusion relaxation time for the n-th spatial relaxation mode has the form . The dimensional inverse Maxwell relaxation time has the form .
Let us move on to the study of the polarization current density in the stationary mode. Taking the limiting condition , in expression (28), we obtain an asymptotic approximation characterizing the stationary polarization mode
From this .
In the limit, from (30), (31) and (S8) we have
Accordingly, we obtain the expansion of the asymptotic expression for the polarization current density with an accuracy of up to the fourth order (k = 1, 2, 3, 4) of the perturbation theory by a small parameter by the asymptotics of the current density components that are multiples of the frequency harmonics of the first and second orders
To study expansions of the type (36) of higher orders by a small parameter , starting with k = 5, etc., it is necessary to calculate the components of the corresponding orders using the recurrent Formula (25) in combination with (14) and (26). Due to the cumbersomeness of the mathematical operations in this area, at this stage of the research, we will move on to the analysis of asymptotic expressions , taking in Formulas (25) and (26) to the formal limit , corresponding to the stationary polarization mode (far from transient processes), when the approximation is fulfilled. In this case, against the background of asymptotic limit expressions for complex amplitudes of the space-charge distribution in the approximation k by a small parameter of perturbation theory , when they are expanded into components of even and odd multiplicity in the frequency of the alternating field , when the limit equality
is satisfied, only asymptotic components that are odd-order multiples of the frequency of the alternating field are preserved
In a similar way, we obtain recurrent identities , for = 1, 2, 3 …, which indicate that the components of the polarization current density that are multiples of even orders in the fundamental frequency of the field , are equal to zero.
Thus, when studying the kinetics of both isothermal and thermally stimulated polarization of a dielectric in an alternating field, the calculation of time-asymptotic expressions for complex amplitudes of the space-charge density in the k-th approximation by a small parameter by transitioning to the limit expressions (37) is of significant interest, from an applied point of view.
From (13), taking into account (37), we have
Based on (10)–(12)
taking
we construct a time-asymptotic expression for the total complex amplitude of the space-charge density
To calculate the partial complex amplitudes , included in the total complex amplitude of the k-th approximation and, accordingly, the total complex amplitude , it is necessary to construct a recurrent expression for the functions , which is satisfied in the k-th approximation by a small parameter and in the r approximation in the field frequency . For this purpose, we will first analyze, using Formula (26), the previously obtained partial expressions for the components , , , , defined by Formulas (16), (20), (S1) and (S4).
For k = 1, based on (37), (16) we have
For k = 2, applying (37), (20) we write
Here
For k = 3, applying (37) and (S1) we write
Here
For k = 4, based on (37) and (S4), accordingly
Here
Based on (26) and special cases (16), (20), (S1) and (S3), the property of the asymptotic approximation for the function is obvious, which states
Thus, the calculation of the asymptotic values of the current density for the first four approximations (k = 1, 2, 3, 4) of function (25), using (42)–(45), in combination with (46), confirms expressions (32)–(34) completely and expression (35) partially. The result obtained can be considered to be one of the criteria of reliability of the methodological apparatus developed in this article. In this case, asymptotic Formulas (32)–(35) are limit expressions of the form
In (47) the asymptotic expressions (37) are used.
The regularities established in expressions (32)–(35) and (42)–(45) confirm the feasibility of constructing a generalized expression (47) in combination with an asymptotic expression in the form (37) for the recurrent Formula (26). Next, using practical experience in calculating complex amplitudes (15), (18), (21) and (24) and their asymptotic approximations (42)–(45), we will move on to develop an analytical scheme for obtaining recurrent formulas for functions , in arbitrary approximations by parameters k, r. To do this, we transform the recurrent in parameter k (the order of perturbation theory when solving the system of Equations (6) and (7)) expression (26), taking into account (37)
In the stationary polarization mode, taking into account the limiting condition in (26), by virtue of the equalities
In the general case, in a given approximation of perturbation theory k, recurrent expressions (47)–(49) are used together in numerical studies of the density of relaxation polarization currents. Additional transformations of these equalities and the application of a number of model assumptions (simplification of the initial formulas; transition to limit formulas in a certain range of variation of the model parameters, etc.) are applied depending on the properties of the function at the frequency of the alternating field in a given temperature range.
Based on (49), performing, for r = 1, 2, 3, transformations in accordance with the scheme described in [2,5], we write down recurrent formulas for partial complex amplitudes . With r = 1, we have
With r = 2, we write
where .
With r = 3, we have
It is convenient to reduce parameter to the form
We will also present the parameter in expanded form
In (52), it is indicated .
We will conduct studies of the influence of subsequent approximations of k > 4 perturbation theory by a small parameter on the structure and properties of partial complex amplitudes with values of order r > 4 in field frequency on the basis of an approximate recurrent formula, which is satisfied under the condition of smallness of the dimensionless parameter , and follows from the analysis of Formula (51) in approximations of order k = 2 and k > 2 and expression (52) for parameter values k = 3 and k > 3, using the method of mathematical induction, having prepared rigorous formulas for , , ,…, constructed on the basis of (51), and formulas for , , ,…, . constructed on the basis of (52). Then
where the parameter is introduced, satisfying a number of properties (1) ; (2) , , ; (3) . In the general case, the complex parameters , for cases r = 1, 2, 3 are equal to, respectively
Based on (40) and (34), with r = 4, we have
Here
where given the parameter
Then, assuming
and restricting ourselves to the coefficient , we construct an approximate recurrent expression of order r = 4,
It is obvious that (53) is a logical complement to the series of expressions (50)–(52), although it gives only an approximate value of partial complex amplitudes .
It is easy to see that expressions (50)–(53) are in complete agreement with (42)–(45), which can be defined as one of the reliability criteria of the generalized stationary recurrent expression (53), which allows us to strictly calculate partial complex amplitudes for any values of k, r.
The studies conducted in Section 2 of this article lead to the conclusion and physical justification of asymptotic expressions for polarization complex amplitudes , which are complex amplitudes that change harmonically over time at a space-charge density distributed over the thickness of the dielectric in the stationary polarization mode , when relaxation processes have virtually no effect on the amplitude of the steady state polarization current density (47).
The most informative, from a physical point of view and in terms of applying the results of theory to experiment (in the development of schemes for the theoretical analysis of the structural features and properties of crystals with ionic-molecular chemical bonds), research method is the method based on the measurement and calculation of the spectra of thermally stimulated polarization currents in a wide range of field parameters (0.1–1 MV/m) and temperatures (50–550 K). The theoretical ranges of external impact parameters are significantly wider than the available experimental ranges and are, from 10 MV/m to 1000 MV/m for the amplitude of the external electric field and from 1 K to 1500 K for the temperature. Studies of the kinetics of ion-relaxation (primarily proton-relaxation) polarization in IMBCs class crystals (in particular, in HBC) in the temperature range near T = 0 K have not yet been conducted, due to the rather complex, in physical nature, and not fully investigated, at the theoretical level, mechanism of quantum electrophysical phenomena in these crystals [3,5]. It has been preliminarily established that quantum kinetic phenomena in nanometer layers (1–10 nm) of proton semiconductors and dielectrics (PSD) in the range of helium temperatures (4–25 K) lead to abnormally high amplitudes of the density of the thermally stimulated depolarization current (3–4 orders of magnitude higher than in the range of nitrogen temperatures (50–100 K) with a micrometer sample thickness) [1]. These polarization effects are nonlinear, quantum (caused by the ultra-high values of quantum transparency (0.85–0.95) of the potential barrier for hydrogen ions (protons) in PSD) and are associated with the quantum-mechanical interaction of the proton (formed by fairly mobile protons that do not interact with each other) and phonon (associated with the vibrations of heavy, low-mobility, in comparison with protons, ions and ionic groups) subsystems in PSD (for example, in HBC) [3]. It is difficult to directly interpret nonlinear quantum polarization effects in PSD as quantum macroscopic effects similar to the effects of superconductivity in metals (for electron and phonon subsystems; Cooper pairs, etc.), due to the fact that the Hamiltonian of the proton-phonon interaction and the contribution of this operator to the density matrix for an ensemble of conduction protons and to the general statistical matrix of the simulated crystal have not been fully and comprehensively (by comparing the quasi-classical and strict quantum models) studied at the theoretical level, within the framework of the quantum-mechanical approximations we are developing for proton conductivity and relaxation in HBC [1,3,5].
Thus, at this stage of research, we can consider both quasi-classical (built on the solution of the Fokker–Planck Equation (6) in combination with the Poisson Equation (7)) and quantum-mechanical (built on the solution of the Liouville equation, together with the Poisson operator equation) [1,3] models of isothermal quantum nonlinear polarization and depolarization, including thermally stimulated quantum polarization and depolarization, for the temperature range T = 1–1500 K, taking field parameters from 0.1 MV/m to 1000 MV/m.
In this article, we operate with the apparatus of the quasi-classical nonlinear kinetic theory of ion-relaxation polarization [1,5], with elements of the quantum theory of ion relaxation and conductivity, limiting ourselves to the quasi-classical formula for the transparency of a parabolic one-dimensional potential barrier [4,5] in the coefficients of the kinetic Equation (6).
The strict quantum-mechanical approach, based on the calculation of the density of polarization and depolarization currents, using the apparatus of the density matrix and the apparatus of nonlinear quantum kinetic theory, will be deferred for the future and carried out within the framework of a separate work.
The main subject of the quasi-classical kinetic theory of ion relaxation in solid dielectrics is the development and study of an analytical apparatus for calculating complex amplitudes for an arbitrary value of the parameter k and their asymptotic approximations for arbitrary values of the parameters k, r. In essence, the solution to this problem has already been accomplished in Formulas (50)–(52) and approximated in Formulas (53) and (55), etc. The further problem is reduced to adapting these expressions to Formula (47) for the polarization current density. The problem of calculating the density of depolarization currents (isothermal; thermally stimulated) will be solved in a similar way, with the difference in the format of the time dependences in the recurrent expressions (48) and (49), calculated from the solutions of the Fokker–Planck (6) and Poisson (7) equations, taking into account the initial conditions corresponding to the depolarization process. In this case, the initial expressions (14) and (26) for depolarization processes will change.
The scheme for measuring thermally stimulated depolarization currents developed by Bucci and Riva [1,4] is reduced, at the first stage, to isothermal (at a constant temperature ) polarization of the investigated sample in a uniform non-stationary electric field and the resulting spatially inhomogeneous electric field inside the dielectric is calculated taking into account the internal field induced by the polarizing field , satisfies the condition for the total field in a dielectric . Amplitude of alternating EMF where d is the thickness of the crystal. At the second stage of measurements (when describing thermally stimulated depolarization), the external field is switched off , , the dielectric is rapidly cooled to low temperatures (50–80 K), is connected to an electrometer (or quality meter) and begins to heat up according to a linear law . The electric field inside the dielectric during depolarization satisfies the short circuit condition .
Thus, the field frequency and the amplitude of the EMF source are excluded from the set of variable external parameters of the mathematical model of thermally stimulated depolarization.
The solution of the problem of isothermal polarization, in the limit, will allow us to construct initial conditions for the complex amplitudes of the relaxation modes of the space-charge during depolarization. In this case, based on (48):
For k = 1, r = 1, from (50) we have
For k = 2, r = (1, 2), from (50) and (51) we have
Here
For k = 3, r = (1, 2, 3), from (50)–(52) we have
Here
For k = 4, r = (1, 2, 3, 4), from (50)–(52) and (55) we have
Thus, based on the results of additional calculations, Formulas (56)–(59) are, taking into account their explanatory formulas designated by the symbols a, b, c, d, completely consistent with Formulas (42)–(45) and their explanatory formulas designated by the additional symbols a, b, c, d. At the same time, both groups of asymptotic formulas for the components of the complex amplitudes of the relaxation modes of the space-charge , at the values of the orders k = (1, 2, 3, 4), r = (1, 2, 3, 4), induced during the polarization of the dielectric, are consistent with Formulas (32)–(35) for the asymptotic expressions for the components of the polarization current density , , , . These comprehensively verified expressions are, in view of their complete consistency, absolutely correct from a mathematical point of view and represent special cases of solutions and consequences of solutions of a quasi-classical nonlinear kinetic equation in the format of the Fokker–Planck Equation (6), solved together with the Poisson Equation (7) in the first four approximations k = (1, 2, 3, 4) of perturbation theory by a small dimensionless parameter (having the meaning of a comparison parameter for this model of polarization processes) . When moving to higher orders of perturbation theory by the parameter , in the asymptotic formulas for the components of complex amplitudes , stationary terms (summands) accumulate in increasingly higher orders in the index r. The same terms, except with odd r, are accumulated in the asymptotic formulas for the components of the polarization current density
It is easy to see that Formula (60) works in conjunction with (49), and the agreement at the first four orders of perturbation theory allows us to assert the reliability of the results of calculations performed using the recurrent Formula (53) substituted into (60).
In conclusion of Section 2, let us focus on the issue of the matrix representation of stationary (in this case, asymptotic) expressions for the complex amplitudes of the space-charge and the polarization current density , the most visual, in comparison with the algebraic, representation. For this purpose, we represent the total stationary complex amplitude of the n-th relaxation mode as an operator equivalent to a column vector
Multiplying the operator (61) by a column vector, matrix elements of which are the corresponding powers k of the small parameter
yields the expression.
Modeling operator (61) taking into account (36)
where ,
by multiplying by a column vector
The function is introduced in (65)
Thus, the action of the operator on the operator of the complete stationary (asymptotic) total amplitude of the n-th relaxation mode transforms it into algebraic sums
allowing to calculate the space-charge distributions studied in the experiment, defined in the form of harmonic series (10) and (12)
3. Results: Properties of a Nonlinear Quasi-Classical Model of Polarization Currents in an Alternating Polarizing Field
The studies of the mechanism of isothermal polarization currents in an alternating field will be conducted according to the model described in Section 2, identifying the value of the total polarization current density measured in the experiment with the operator
In the general case, the operator must reflect the kinetics of relaxation processes, represented mathematically, in the form of matrix elements that depend on time in a certain way and correspond to the k-th approximation of perturbation theory, with relaxation times . Analogously with (61), we have
In this case, the matrix elements of the operator (67) are calculated according to (25), where . The operator (67) is modeled taking into account (68)
Analogously (51), the action of the operator on the operator (69) gives
where .
The shift to limits , transitions relaxation expressions (69) and (70) to images of the form
where .
Combining (60) and (25) we find, in the general form, the partial currents formed in the k-th approximation of perturbation theory at the field frequency
Substituting the recurrence Formulas (48) and (49) into (73), as expected, gives, in the case of even orders of r, the expression
where .
In the case of odd orders of r, we have
where .
In the general case
According to (72), the asymptotic density of the total current can be represented as a sum of frequency harmonics
where
Based on (73) and (76), with r = 0, 1, 2,…, we have
substituting the recurrence Formula (53) into (77)
taking , , we have
Taking r = 0 in (78), considering the identity , at the fundamental field frequency , we have
Here .
When deriving Formula (79), the parameter was used. Also, due to , in the functions of the polarization temperature , quasi-classical parameters, similar to those constructed in [2,5] are constructed
In (80), dimensional relaxation times , calculated at temperature , are used, where the diffusion relaxation time for the n-th relaxation mode is calculated using the formula , in which is calculated using the zero-order diffusion coefficient by a small parameter of the theory of successive approximations (see Section 2) and corresponds to the first-order relaxation mode (n = 1). The Maxwell relaxation time is calculated using the first order mobility coefficient . Next, according to , parameters (80) are reduced to the form
The representations of the parameters , in the form (80a–d), despite their cumbersomeness in comparison with the original expressions (80), are more convenient from the point of view of a detailed theoretical and numerical analysis of the influence of frequency and temperature on the current density of isothermal polarization (79), including further practical applications of this issue in the field of optimization of computer research processes and forecasting of the values of the parameters of the structure and electrophysical characteristics of functional dielectric and semiconductor elements of installations and systems. Due to the formal analogy of Formula (80a–d), studies of the properties of expanded power series embedded in expression (80a–d), depending on the relations , , can be performed in accordance with the results presented in [2,5].
4. Discussions: Analysis of the Properties of the Investigated Model
4.1. Construction and Analysis of Recurrent Analytical Expressions for the Density of Isothermal Polarization Current
A complete description of relaxation polarization in ionic dielectrics with a complex crystalline structure, including HBC (crystal hydrates, layered silicates), when calculating the electrostatic induction vector of a crystal (semiconductor, dielectric) , [1,57,58,62], the polarization vector of the crystal, in the general case, is taken as a sum [59,62], where polarization of the inductive or inertialess type is established almost instantly, with a relaxation time of the order of s, and polarization of the inertial or relaxation type manifests itself in a wide range of polarizing field strengths and temperatures, in the optical range of field frequencies, with a relaxation time of the order of s [1,2,5]. High-frequency permittivity [57,62], where , , are the corresponding coefficients of electron, elastic-ionic and elastic-dipole polarization.
Relaxation polarization in HBC, according to the results of measurements of , in the temperature range T = 100–350 K, at polarizing field strengths , is realized in the vicinity of frequency maxima Hz (at T = const), with relaxation time s [59,62]. Since , the high-frequency permittivity , when constructing a physical-mathematical model of relaxation polarization in ion-molecular dielectrics, in particular, in HBC, can be considered a constant value. We define the complex polarization coefficient for the processes of ion-relaxation and dipole-relaxation polarization [57], associated with the relaxation motion of water molecules, various ions and polar groups (A, K—dipoles, polar vacancies) [58]. Then, for the one-dimensional model of ion-relaxation polarization in crystals of the IMBC class, we write
We will calculate the total current density in dielectric taking into account the conduction current density (caused by the drift motion of conduction ions in an electric field) and the relaxation current density (associated with ion-relaxation polarization in the crystal) The value of the relaxation polarization is calculated using a nonlinear quasi-classical model of dielectric relaxation at the fundamental frequency of the polarizing electric field, according to the expressions , [1,2,5], taking into account the complex form of the quasi-classical relaxation coefficient . The components of the parameter , defined as quasi-classical relaxation coefficients, are investigated in various approximations, by various methods taking into account a sufficient amount of evidence of the calculation rigor in [2,5]. Thus, we write
From the point of view of the classical theory of conductivity [1,5], assuming the ionic conductivity current density being equal to, respectively, [1], we accordingly calculate , , where is the static conductivity coefficient calculated for conductivity ions, determined by the equilibrium concentration of conductivity ions in dielectric , their effective mass and the relaxation time for conductivity ions . Here q is the ion charge modulus. Further, taking the coefficient of electrical (in the general case, ionic, and in particular, for HBC, proton) conductivity as a complex value of the form and, separating the real and imaginary parts of the total current density, we have
Averaging the expressions , over time, for the period of oscillations of the external variable field, noting that
we find the imaginary component of the energy of the alternating electric field dissipated per unit time in a unit volume of the dielectric (the imaginary component of the volumetric power density) [1], in the quadratic approximation by the field
Also, noting that
we obtain the real component of the volumetric power density [1] of the alternating electric field in dielectric in the quadratic approximation by the field
The investigation of expressions (87) and (88) should be carried out in accordance with the analytical dependencies (83) and (84).
Based on the recurrent expression (53), for r = 3, taking into account the identity , applying the recurrent Formula (73) and summing by k from k = 3 to infinity , we obtain a formula for calculating the total component of the polarization current density at the second odd frequency of the field . In this case, at r = 3, as well as at all subsequent orders by the field r = 5, 7, 9, etc., when calculating the multiples of the parameter r of the components of the polarization current density , we limit ourselves to the corresponding components of the multiplicity r for the density of the relaxation polarization current Thus, for r = 3, according to the above considered scheme, we have
The same result is obtained by substituting the parameter r = 1 into the recurrent expression (78).
Applying the identity [2,5]
, taking into account the designations , ,, , , , we ultimately have
Let us convert (90) to the form
In (91) the following notations are adopted
Let us write the resulting expression for the second frequency harmonic of the current density
In (92) the following notations are adopted
Separating the real and imaginary parts in (92)
we calculate the quantities proportional to the sixth power of the field strength amplitude
Based on
according to the formula
taking the component of the complex dielectric permittivity (CDP) in the form , we have
we obtain the dispersion relations of the components of the CDP
Substituting (95) and (96) into (101) and (102), we obtain
Thus, Formulas (86) and (87) show how the cubic term in the field of the polarization current density can be used to calculate the corresponding components in the second power of the expansion of CDP in a series in powers of the field strength
In expression (105), the fourth-order component in powers written, accordingly, at the fourth power of the expansion of CDP in powers of the field strength , will be calculated on the basis of dispersion relations analogous to (101) and (102)
By virtue of the recurrent equalities (73) and (53), taking the component of the density of the relaxation current of polarization in the dielectric proportional to the first power of the field (in accordance with (82)) in the form , we calculate the density of the total polarization current in the linear approximation for the polarizing field (in the case of multiplicity r = 1) . Based on , we have
Based on (108) it is evident that
Applying , [1,2,5] to the calculation of the function , when
substituting (111) into (109) and (110), we obtain expressions for the components at the zero degree of the expansion of CDP by powers of the field strength, in the form of dispersion relations [5]
Expressions (112) and (113) are in complete agreement with (83)–(86), which can be considered as another additional criterion for the reliability of the calculations performed in Section 3 and Section 4.
From the results obtained above, it is obvious that the calculation of the component of the CDP for an arbitrary even degree of the field in (86) can be performed on the basis of generalized expressions
The component of the polarization current density (equal to the density of the relaxation polarization current at field multiplicities of order r > 1) that are multiples of the frequency harmonic of order will be calculated on the basis of recurrent Formulas (73) and (53) using expressions of the form . Then
Calculating parameter from recurrence formula
and denoting , , …, , we have
The final complex expression for function (117), in the general case, will be written as
In (118) the following notations are adopted
The complex parameter is presented in (91d).
Combining (114), (115), and (118) we have
.
The dispersion expressions (119) and (120) are satisfied at a set of frequencies
Formula (118), with comments to it in the form of expressions (118a–e), represent generalized asymptotic (calculated far from transient processes) recurrent expressions for calculating the polarization current density in dielectrics of the crystals with ionic-molecular chemical bonds class (IMBCs), in particular in HBC, at a constant temperature (isothermal polarization) , in an arbitrary approximation at , by the magnitude of the polarizing electric field strength .
Expressions (119) and (120), following from the generalized dispersion relations (114) and (115), are recurrent expressions for calculating the components of the complex dielectric permittivity (CDP) in the approximation of multiplicity by the polarizing electric field.
Expression (116), which, as (118), denotes a generalized recurrent formula for the isothermal polarization current density in ion-molecular dielectrics, provides, in addition to (118), the possibility of analyzing the properties and parameters of the theoretical frequency spectrum in an arbitrary approximation by a dimensionless small parameter of perturbation theory . The description of the properties of functional temperature and field dependences for the parameter included in the nonlinear quasi-classical kinetic Equation (6) is carried out in the works [2,5]. Expression (117) is equivalent to (116) and (118).
In this article, we will not touch upon the issues of theoretical study of the regularities of relaxation polarization at variable temperature (thermally stimulated polarization) in IMHCs crystals. A study of thermal polarization in dielectrics will be conducted in subsequent work.
In this work, only the theoretical aspects of the problem of the quasi-classical calculation of isothermal relaxation polarization currents in dielectrics were investigated, and the basic recurrent formulas for calculating the components of the sought value of the polarization current density at different multiplicities r in the frequency of the external alternating field were constructed. Recurrent formulas for calculating the CDP components are also constructed in various approximations for the polarizing field strength.
The problem of the experimental justifications of the solutions obtained will be solved in subsequent articles, specifically dedicated to the application of various methods to the numerical calculation and analysis of the properties and parameters of theoretical frequency spectra in arbitrary approximations by a dimensionless small parameter . There, a numerical calculation of the parameters of relaxers (in the general case, ions of both charge signs; in HBC, protons) will be performed in a wide range of temperatures, amplitudes, and frequencies of the external electric field.
From the point of view of comparative analysis of the results of theory and experiment, the construction of a nonlinear physical and mathematical model and numerical analysis of the spectra of thermally stimulated polarization (TSPC) and depolarization (TSDC) currents in IMBCs class crystals is more qualitative and informative. The TSDC method applied to the model of a symmetric double potential well for relaxers in [3] will be further improved using the methods of the quasi-classical kinetic theory used in this article, but for a more scientifically rigorous model of a one-dimensional spatially periodic potential relief for relaxers, and will be reduced to the calculation of theoretical frequency spectra in arbitrary approximations by a dimensionless small parameter . Additionally, recurrent expressions for calculating the components of complex CDP in the approximation of multiplicity by the polarizing electric field will be investigated. When solving the kinetic equation of ionic (in HBC, proton) relaxation during thermally stimulated depolarization, by analogy with (6)–(9) and (10)–(13), a phenomenological system of equations with their boundary conditions will be constructed, and the initial conditions for the Fokker–Planck equation will be constructed using asymptotic expressions for the polarization complex amplitudes of the relaxation modes of the space-charge in the form (47), (49), (50)–(53) and (56)–(59). This concerns the hetero-charge associated with the accumulation and spatially inhomogeneous distribution of space-charge, formed due to the diffusion movement of conductivity ions along chemical bonds in the space between the electrodes, during the polarization process. Regarding the initial distribution of the homo-charge associated with the injection of charge carriers (ions, protons) from the surface of the electrodes into the depth of the crystal, as well as with the localization of charge carriers on vacancies and electron traps, we will calculate the corresponding semi-empirical distributions [1,5].
4.2. Comparative Analysis of the Results in This Work and in Previous Articles on This Research Direction
In the proposed scientific article, direct non-stationary solutions of the system of nonlinear equations of the quasi-classical kinetic theory of dielectric relaxation are considered and investigated for the first time, as applied to a specific phenomenon of the isothermal polarization current associated with ion-relaxation polarization caused by the diffusion transfer of relaxers (ions of both charge signs) and the rotation of water molecules in crystals with ion-molecular bonds (CIMBs) in an electric field. Hydrogen-bonded crystals (HBCs) are a special case of crystals of this class. They are characterized, as noted above, by the presence of a hydrogen sublattice in their structure and, accordingly, the property of proton conductivity associated with the diffusion transfer of hydrogen ions (protons) in a polarizing electric field [1,2,3,4,5]. In HBC, the hydrogen sublattice is formed by hydrogen ions, which are localized on hydrogen bonds and perform small oscillations near the points of fixation or equilibrium positions. It is in a state of dynamic equilibrium with the anion sublattice, formed by acidic residues of inorganic salts (carbonates, sulfates, phosphates, silicates, etc.), which are massive, low-mobility anions of various types (according to the chemical structure and the structure of the crystal lattice cell). In this case, in HBC, one can distinguish carbonate anions, sulfate anions, silicate anions, phosphate anions, etc. [1].
In many cases, in CIMB class crystals, one type of charge carriers (relaxers) is the most mobile, in comparison with other types of charge carriers [2,4,8].
Ions and polar groups act as mobile relaxers in dielectrics with a complex crystal structure (layered minerals, ceramics), in particular, in HBC they are Bjerrum defects (ionization , ; orientation defects—L, D), orientation defects associated with ion vacancies (VL, VD defects) and hydrogen ions (protons) localized on hydrogen bonds [1]. For example, in Ih ice crystals, the greatest mobility is exhibited by [2,4,8] defects.
In [3], a detailed analysis of the mechanisms of migration of structural defects in HBC was carried out, experimental and theoretical graphs of the density of thermally stimulated depolarization currents (TSDC) were presented, using the example of phlogopite (Figure 1 in [3]), mica of Onot talc (Figure 2 in [3]), muscovite (Figure 3 in [3]), chemically pure chalcanthite (Figure 4 in [3]). Experimental and theoretical values of molecular parameters for each type of relaxers in these crystals are given in tables 1–4 (see [3]). The dominant influence of quantum effects caused by proton tunneling between ions of the anion sublattice in the region of the low-temperature maximum of the TSDT density in HBC (50–100 K) was established. A distinct influence of quantum transitions of protons on thermally stimulated depolarization in the high temperature region (150–550 K) was discovered [3]. Theoretical studies of the kinetics of thermally stimulated depolarization were carried out in [3] based on the nonlinear phenomenological kinetic theory for the model of a double symmetric potential well (a simplified model of potential relief for relaxers). Thus, in [3], already within the framework of a simplified model of the crystalline potential field for conductivity ions (in HBC, for protons), the significant role of quantum tunneling of protons in HBC was proven at a sufficiently high level (from comparisons of theoretical and experimental results), in a wide range of temperatures (50–550 K), and not only at low temperatures (near nitrogen temperatures). This is of high significance from the point of view of practical applications of the electrophysical properties of HBC in microelectronics and radio engineering. In [3], schemes for the migration of ions in the HBC are proposed, due to the relaxation movement of a proton in the layered structure of a dielectric, between layers of water molecules or between a layer of water molecules and a layer of anions [1,5]. The movement of the proton, in this physical model, is diffusional (depending largely on the action of thermal motion forces) and occurs under the action of external electric field forces in the direction of the hydrogen bond lines oriented along the crystal axis C. Figure 1 shows a diagram of the migration of ions due to the gradual movement of the proton using the example of chemically pure chalcanthite (Figure 5 in [3]; Figure 1 in this paper).
The results of calculations of the parameters of relaxers in the investigated sample are performed in [3] (Table 4 in [3]).
The following stages of proton movement are discerned
1. The formation of defects of the type occurs as a result of proton fluctuations in layers of water molecules or the introduction of a proton-donor impurity (HCl; HF)
2. The transfer of a proton between the ion and the sulfate anion , with the formation of the protonated anion
3. Reorientation of the protonated anion due to the displacement of the proton along the sulfate anion in the first layer
4. Reorientation of the protonated anion due to the displacement of the proton between the first and second layers of sulfate anions
5. Reorientation of the protonated anion due to the displacement of the proton along the sulfate anion in the second layer of anions
6. The transfer of a proton between the protonated anion and a water molecule with the formation of a sulfate anion and an ion
A similar pattern of proton displacements is also observed in phlogopite , with the only difference being that proton displacements occur between silicate anions and in protonated anions , .
Based on the considered mechanisms of ionic conductivity, we can take the geometric model of proton-relaxation polarization of HBC, as well as the ion-relaxation polarization of CIMB, to be one-dimensional.
In the mathematical model, expressions (6)–(9) and their solutions (10) and (11) in this article formally match the basic equations (57)–(61) and their solutions (62) in [5]. In expressions (10) and (11) in this work, which are equivalent in a formal sense to expression (62), methods of perturbation theory are used in the form of expansions of the sought functions into infinite power series by the small dimensionless parameter [2,5]. Along with the classical (calculated without taking into account the quantum tunneling of ions) dimensionless small parameter , the value of the basic quasi-classical small parameter , which appears in calculations when taking into account the quantum tunneling of ions (which is most effective when considering the relaxation motion of protons in HBC), even within the framework of the quasi-classical kinetic theory (not to mention the structure of quantum-mechanical kinetic theory) is largely determined by the ratio of the kinetic coefficients , These coefficients are calculated as functions of the crystal temperature T using the known formulas of the quasi-classical kinetic theory [5], in the form of the first two approximations l = 0, l = 1 from the expansions of the generalized non-stationary velocity of the probability of the transfer of an ion (in HBC, a proton) between adjacent potential wells (equilibrium positions) in the one-dimensional mathematical model by additional small dimensionless parameters , These parameters, in turn, are calculated in a one-dimensional model of the crystalline potential relief for an ion moving in the direction of the coordinate axis OX, chosen in the direction of the crystalline axis C (Figure 2).
Here is the correction to the potential energy of an ion due to its movement in a spatially inhomogeneous non-stationary electric , where , are, respectively, the strength of the external non-stationary polarizing electric field and the electric field induced in the dielectric as a result of its polarization in the external field; x is the coordinate of the ion in the one-dimensional model [2,5]. The crystalline potential relief , disturbed by the electric field , is shown in Figure 3. In this model is the height of the potential barrier (the activation energy of the ion on the bond); is the width of the potential barrier; is the potential energy of the ion at the crystal boundaries (the work function of the ion from the dielectric); is the total number of potential wells in the model; d is the thickness of the crystal; is the energy level in the unperturbed continuous energy spectrum of the ion; is the lattice constant, is the ion charge.
The calculation of the electric field strength is performed, in this model, using the Poisson equation , where is the concentration of ions excessing the equilibrium ; is the high-frequency dielectric permittivity. The function is constructed from solutions of the nonlinear Fokker–Planck kinetic equation (expression (6) in this article; equation (57) in article [5]).
The study of the function , when calculating the value of , is carried out in [2,5] near the equilibrium position for an ion with coordinate x, taken as a continuous value in the Poisson equation (expression (7) in this article; equation (58) in article [5]). Let us rewrite the non-stationary velocity of the probability of transfer of an ion (in HBC, a proton) through a potential barrier (see expression (9) in [5]) in the form
Statistical averaging of the non-stationary quasi-classical transparency is carried out in [5] using classical Boltzmann statistics for ions of mass m, distributed over the energy levels of the continuous spectrum E, in the case of a one-dimensional potential barrier of arbitrary shape , perturbed by an electric field Then, taking
in the generalized case we obtain
Preceding [5] the equation is solved.
In [5], in the case of a one-dimensional potential barrier of parabolic shape, perturbed by an electric field , where is the width of the potential barrier, in the WKB approximation the quantum transparency of the potential barrier, calculated in the approximation of a small perturbing correction to the potential energy of an ion moving with energy E, equals to
In this case, the quantum transparency of a potential barrier perturbed by an external field, statistically averaged over the stationary energy levels of the continuous spectrum E takes the form (see (9) in [5])
Here , are auxiliary dimensionless parameters. The identity is satisfied.
Using expression (4) from [5], we write
The coefficients of this expression represent the probability rate of an ion transfer across a potential barrier calculated in the approximation of l using the parameter (formula (5) in [5])
In relation to the parabolic potential barrier, taking we obtain
In particular, for the sought approximations of orders l = 0, l = 1, according to equalities (10b) and (10c) from [5], we have
For an arbitrary value
Thus
We also note the recurrent expression that is important for this model
In this expression, the value has the meaning of the probability rate of thermally activated (classical) transitions of ions through a potential barrier. The parameter is also a function of temperature.
Here is the critical temperature separating the temperature zones of quantum and thermally activated transitions of ions, calculated from the condition .
The fundamental equation of the quasi-classical kinetic theory of ion-relaxation polarization of solid dielectrics is the generalized nonlinear kinetic equation (expression (17) in the article [5]), constructed on the basis of a mathematical model of a one-dimensional potential crystal field, shown in Figure 1 and Figure 2. Thus, taking the coordinate of the ion in the model x, we write equation (17) from [5]
in which the generalized nonlinear diffusion coefficients and mobility of ions in the simulated crystal in an electric field are introduced, with the generalized non-stationary velocity of ion transport in the electric field (see expressions (18) in article [5]).
The generalized nonlinear quasi-classical kinetic equation (17) from [5] is reduced to the differential continuity equation where total current density in the system
is equal to the sum of the conduction current density and diffusion current These expressions allow us to formulate the boundary conditions for the kinetic equation in the blocking electrode model, when where d is the crystal thickness. Then, we obtain
At the initial moment of time polarization is absent .
The solution of the kinetic equation in [5] is constructed together with the Poisson equation (the d’Alembert wave equation, transformed in the radio wave wavelength region) (see expression (22) in [5]), where are, respectively, the equilibrium and nonequilibrium concentrations of ions in the crystal; is the permittivity in the high-frequency region. The boundary condition, according to the blocking electrode model, takes the form [5] . The source of external voltage is taken to be , where are the amplitude and circular frequency of the EMF, respectively; is the amplitude of the external polarizing electric field .
Further transformations in the work [5] were reduced to simplifying the kinetic equation to a form corresponding to the approximations l = 0 and l = 1 in power series
Respectively, we have
For the kinetic equation we take
Then, we get the system
The Fokker–Planck and Poisson equations (expressions (6) and (7) in this article; expressions (57) and (58) in [5]) follow from the above-described equations of the system for the quantity , by applying dimensionless variables , . The dimensionless field and the excess concentration of conductivity ions are also introduced. In this case, these equations are taken in the form (57) and (58) from [5], respectively (6), and (7) from this article
In these nonlinear equations, the dimensionless small parameter of perturbation theory is a function of the crystal temperature, the amplitude of the polarizing field strength E0, and also the molecular parameters of the relaxers . Additional designations , are also accepted.
The initial and boundary conditions for the kinetic equation in this article are formulated in the form (8), and in [5] in the form (59) and (60)
The boundary condition takes the form corresponding to the boundary condition (9) for the Poisson equation in this article
The solutions of the system of nonlinear Equations (6)–(9) in this article, which match, in a formal sense, equations (57)–(61) from the article [5], are constructed using expansions in infinite power series by the small dimensionless parameter of perturbation theory , introduced in [5]. Moreover, expressions (10) and (11) of this article formally match the expressions (62) from [5] , . In the methodology of this work and the article [5], some coincidences take place only in a formal sense, but in the physical sense, in the present article, more detailed processes associated with ion-relaxation polarization are considered (as in [5]), but, in relation to the model of isothermal polarization (at a constant temperature) and are investigated not in the approximation of time asymptotics (in the stationary mode of polarization in an alternating field), but in the mode of transient (nonequilibrium, from the point of view of kinetics) processes in a dielectric in an electric field. These differences are manifested in the mathematical model, starting with the generalized analytical expression (14) for the complex amplitudes of relaxation modes of number n in the k-th approximation by the parameter for the volume-charge induced in the crystal during the polarization process. Further mathematical operations, omitted in this article due to their cumbersomeness, in [5], consist of the construction of a recurrent system of equations (63)–(67) for the approximation k of perturbation theory.
It should be noted that equation (63) in [5] is original and has no analogues in the issue of constructing analytical solutions of nonlinear kinetic equations of the Fokker–Planck type, which contains a fairly high degree of scientific novelty within the framework of this range of theoretical problems to be solved. Further mathematical operations contained in expressions (68)–(70) in [5] are reduced in this article to transformations in the form of Fourier series (12)
allowing, on the interval , in the image , to write equation (63) from [5] in operator form (expression (69) in the article [5])
The solution to this equation is given by the recurrent expression (70) in the article [5], which is formally equivalent to the expression (14) in the present article for the complex amplitudes of the relaxation modes of the volume-charge for the spatial harmonic n of the Fourier series in the k-th approximation by the parameter
Here Let us reiterate that the formal equivalence of this expression in [5] and in this work does not mean the physical equivalence of these formulas. In this expression, the dimensionless electric field in the k − 1-th and m-th approximations by the parameter is calculated by analogy with the k-th approximation for the “zero” field (expression (13) in this article)
This expression is a consequence (essentially equivalent) to expression (15) in this article.
In the article [5], the solution of the operator equation (69) in the form (70) is investigated in the asymptotic approximation (far from transient processes) and is written for an arbitrary order of perturbation theory k with a frequency harmonic of multiplicity r in the form of a non-stationary expression
Here, asymptotic integral operators are applied
The operators are deciphered in [5].
In contrast to the earlier work [5], in the present work the functions are presented in the form of transient non-stationary functions of time, calculated on the basis of formula (14), respectively, in the approximations k = 1, 2, 3, 4 (expressions (16), (20), (S1) and (S4)), as applied to a specific phenomenon of the isothermal polarization current flowing through the cross-section of the dielectric (due to the diffusion movement of conductivity ions in the space between the electrodes in the model of a flat capacitor with an arbitrary shape of the electrodes) at a constant crystal temperature, which can be interpreted as the evolution in time for the function described above for a given value of the parameter k. For the sake of brevity, omitting the index “pol”, we write the recurrence formula (see equation (26) in this article)
Based on (14), and also from (26), partial expressions are constructed for the nonequilibrium functions , for k = 1 (see Formula (16)), applying ; for k = 2 (see Formulas (19) and (20)), applying (see expressions (17) and (18)); for k = 3 (see Formulas (23) and (S1)), applying, in addition to (17) and (18), the expressions (see (21) and (22)); for k = 4 (see Formulas (24) and (S4)), applying, in addition to (17), (18), (21) and (22), the expressions (see (S2) and (S3)). Due to the cumbersome nature of these expressions, in this Section 4.2 only the numbers of the main working formulas and their connections and correspondences in the model are used. The transition to higher approximations of perturbation theory for k = 5, 6, 7, etc. in Formulas (14) and (26) leads to even more cumbersome calculation schemes and their elements, which is not appropriate within the framework of the purpose of this work. If necessary, performing these calculations will not be particularly difficult from the point of view of the logic of the calculations. In this article, for the first time, based on the recurrent Formula (25)
using partial expressions for complex amplitudes of the space-charge distribution in the first four approximations by the small dimensionless parameter , for k = 1, 2, 3, 4, nonlinear quasi-classical formulas are constructed for calculating the current density of isothermal polarization in a dielectric. This, in relation to polarization current, has never been done before, from the point of view of the scientific direction being developed. Thus, expressions are constructed for the functions (see Formula (28)), (see Formula (30)), (see Formula (S6)), (see Formula (S8)).
5. Conclusions
Due to the cumbersomeness of the mathematical apparatus developed in this scientific article, with the significant importance of analytical conclusions and solutions of the main and additional equations of the physical-mathematical model, taking into account that the work is purely theoretical (with a high-quality experimental base of previous studies) and each intermediate solution, along with solutions of the basic equations, is informative and important for further developments (theoretical, experimental), and numerical optimizations of the studied models in the field of nonlinear relaxation polarization and electrical conductivity in crystals with ionic-molecular bonds, in this work, we have adopted an expanded form of conclusions on the work. This approach will allow to examine the main conclusions and also, in an abbreviated form, to return to the results of the mathematical calculations (formulas, equations and their solutions) and transformations performed in the work.
The following conclusions could be drawn from the work conducted
The following extended conclusions (with the explanations and comments) could be drawn upon based the results of the work performed
1. Using the methods of the quasi-classical kinetic theory of dielectric relaxation [1,2,3,4,5], a system of nonlinear Equations (6)–(9) was constructed, describing the process of isothermal polarization. The solution of the system of Equations (6)–(9) is carried out in dimensionless variables , , using the methods of perturbation theory, by expansions in infinite series by powers of a polarization dimensionless small parameter (10). The kinetic coefficients , are calculated by the methods described in Section 2, using Formula (5a,b), at a temperature equal to the polarization temperature . In this case, the expressions for the space-charge density and the dimensionless electric field are modeled in the k-th approximation by a small parameter , on the segment , using harmonic Fourier series (12) and (13)
The parameter , where d is the thickness of the dielectric and a is the lattice constant, describes the influence of size effects on polarization. The parameter is a measure of the inverse field and has the dimension of the equilibrium concentration of particles . Here −is the high-frequency permittivity; —is the amplitude of external electric field strength ; q is the ion charge. The complex amplitudes of relaxation modes of the n-th order for a spatially inhomogeneous space-charge (12) are calculated in the k-th approximation by a small parameter , for isothermal polarization (at a constant polarization temperature), using the recurrent Formula (14).
2. Expressions for the functions , are obtained in the first four approximations of perturbation theory k = 1 (see Formulas (16) and (17)); k = 2 (see Formulas (20) and (21)); k = 3 (see Formulas (S1) and (S2)); k = 4 (see Formula (S4)).
3. The expression for the polarization current density operator (25), calculated in the k-th approximation by a small parameter (25), is written and investigated . Relaxation times for relaxation modes of the n-th order for the isothermal polarization process are calculated, where —is the diffusion relaxation time for the n-th, and —for the first relaxation mode, —is the Maxwell relaxation time. The diffusion and mobility coefficients are calculated at temperature .
4. Based on the main expression (see Formula (14)), an additional recurrent expression is proposed for calculating the polarization complex amplitudes of the relaxation modes of the space-charge density, calculated in the k-th approximation by a small parameter , taking into account all previous approximations, starting from k = 1 to k − 1 (see Formula (26)). The expression for the current density (25) works in the system with Formula (26).
5. Based on the recurrent expression (25) in combination with Formulas (16), (21), (S1) and (S4), partial expressions are constructed for the polarization current density calculated in the approximations k = 1, 2, 3, 4 by a small parameter , see Formulas (28) with k = 1 for ; (30) with k = 2 for ; (31) with k = 3 for ; (S8) with k = 4 for . The expressions obtained will be applied in the future to calculate theoretical spectra in the field of relaxation processes in the first four approximations of perturbation theory. Using an analogous method, from the recurrent expression (25), in combination with Formula (26), spectra can be constructed in subsequent approximations of perturbation theory k = 5, 6, 7, etc.
6. By transitioning to the limits in special Formulas (28), (30), (31) and (S8), far from transient processes , with the formal fulfillment of the condition , asymptotic (stationary) expressions for the polarization current density in the approximations k = 1, 2, 3, 4 by a small parameter of perturbation theory are constructed, see Formulas (32) with k = 1 for the function ; (33) with k = 2 for the function ; (34) with k = 3 for the function ; (35) with k = 4, for the function .
7. Additionally, far from transient processes , asymptotic (stationary) expressions for polarization complex amplitudes of relaxation modes in approximations k = 1, 2, 3, 4 by a small parameter are constructed, see Formulas (42) with k = 1 for ; (43) with k = 2 for ; (44) with k = 3 for ; (45) with k = 4 for . It was established that expressions (42)–(45) are consistent with (32)–(35) through the recurrent Formula (25). Thus, we have formulated the first criterion for the reliability of the calculations performed in Section 2.3.
8. When studying the kinetics of isothermal polarization of a dielectric in an alternating field in a stationary polarization mode, from the point of view of practical applications (in mathematical modeling of nonlinear polarization in radio engineering devices and microwave technology devices), the calculation of asymptotic expressions over time for complex amplitudes of the space-charge and polarization current density in an arbitrary k-th approximation by a small parameter , is of interest, by transitioning to the limit expressions (47)–(49)
9. Recurrent asymptotic formulas for partial complex amplitudes of relaxation modes of space-charge are written for arbitrary values of orders of perturbation theory k and multiplicity r in the frequency of the polarizing field (53)
where only the evaluation of the structure and numerical values of the complex parameter , calculated as sums of power series, represents a certain computational complexity. The properties of the parameter (1) ; (2) , ; (3) are investigated, where the additional parameter . is introduced.
10. As a special case of equality (53), an additional recurrent expression for the frequency multiplicity r = 4, of orders , is proposed (Formula (55)). Based on the results of calculating the functions , at 1, 2, 3, 4, the formulas for calculating the functions (50)–(53) are completely consistent with Formulas (32)–(35) and (42)–(45). Thus, we have formulated the second criterion for the reliability of the calculations performed in Section 2.3, Section 3 and Section 4.
11. To simplify the scheme of mathematical description of relaxation polarization, along with algebraic formats (25), (47) and (60), a generalized operator representation of the polarization current density (67) is proposed
A matrix interpretation of the polarization current density in the form of a column vector —is performed, see expression (69). The current density operator works in conjunction with the operator of complex amplitudes of relaxation modes of the space-charge
see expression (68). It has been established that the action of the operator —(see expression (62)) on the current density operator (69) yields the value measured in the experiment (see expression (70)). For the stationary mode of the isothermal polarization process , a matrix expression for the polarization current density —is proposed (see (71)). Operator (71) works in combination with the asymptotic operator of complex amplitudes —(see (61)). It has been established that the action of the operator on the operator (56) gives (see Formula (72)), with matrix elements calculated from expression (47)
Partial current densities are calculated in the k-th approximation of perturbation theory at the field frequency
Formula (73) —(see Formula (73)) works in conjunction with (53).
12. A recurrence expression is constructed for the partial current density generated in a dielectric during isothermal polarization and established in a stationary polarization mode at an odd field frequency —(see (116)).
Expressions are written for the partial current densities of stationary isothermal polarization, calculated at field frequencies that are multiples of r = 1, Formula (82) is constructed taking into account the conduction currents ; r = 3, —(Formula (89)).
13. A generalized recurrent formula (see expression (118)) has been constructed, which, in combination with additional model equalities (118a–e), makes it possible to calculate the numerical values of the polarization current density in the asymptotic (stationary) approximation (far from transient processes) in an arbitrary approximation at , based on the magnitude of the polarizing electric field strength in dielectrics of the class of crystals with ionic-molecular chemical bonds (IMBCs), in particular in HBC, at a constant temperature (isothermal polarization).
14. Based on the generalized dispersion relations (114) and (115), recurrent expressions are constructed for calculating the components of the complex dielectric permittivity (CDP) in the approximation of multiplicity by the polarizing electric field.
15. The main theoretical principles of the physical-mathematical model of nonlinear isothermal and thermally stimulated polarization in solid dielectrics exhibiting the property of ionic conductivity and ionic relaxation polarization in a wide range of field parameters (100 kV/m–1000 MV/m) and temperatures (0–1500 K) are formulated. A calculation scheme has been developed for studying the processes of thermally stimulated polarization in materials with complex crystal lattice structure and ionic-molecular type of chemical bonds. Hydrogen-bonded crystals (HBC) are characterized by the presence of a hydrogen sublattice in the crystal structure (consisting of hydrogen ions (protons) that do not interact with each other and move inside the anion sublattice between its ions) and the manifestation of the property of proton conductivity, caused by the diffusion transfer of protons along hydrogen bonds in a polarizing field.
16. The physical-mathematical model of isothermal relaxation polarization and conductivity, constructed using the methods of nonlinear quasi-classical kinetic theory of dielectric relaxation [1,2,3,4,5], is based on the study of the system of nonlinear equations of the phenomenological model (6)–(9), as applied to the properties of ionic-molecular dielectrics. The theoretical results obtained will allow, in the future, to trantition to a numerical study of the regularities for anomalously high polarization nonlinearities, manifested at the theoretical level, during the transition from micrometer (1–10 μm) to nanosized (1–10 nm) HBC layers, when the maximum (peak) of the dielectric permittivity experiences a shift from the region of low (50–100 K) to the region of ultra-low (4–25 K) with an increase in the amplitude of the maximum to values of the order of 1.5–2.5 million. The electrical conductivity coefficient of the dielectric, at the same time, increases by 3–4 orders of magnitude. In the general case, in IMBs class crystals, theoretical nonlinearities of this type usually appear in the ranges (1) ultra-low temperatures (1–10 K) and weak fields (100–1000 kV/m), which is especially characteristic of proton semiconductors and dielectrics (PSD), exhibiting the property of quantum (tunnel) low-temperature conductivity [1,5]; (2) ultra-high temperatures (550–1550 K) and strong fields (10–1000 MV/m), when IMBs exhibit nonlinear space-charge polarization [1,2].
17. Theoretical manifestations of polarization nonlinearities in dielectrics with an ion-molecular type of chemical bond are provided by taking into account the high-order terms (starting from the third k = 3, 4, 5,…, etc., up to infinity) of the perturbation theory by the small dimensionless parameter (see Formulas (10) and (11)) in the mathematical modeling of the spatially inhomogeneous space-charge distribution (12) and (13) formed in the model crystal under the action of an electric field.
18. The theoretical foundations of the schemes of analytical studies of nonlinear thermally stimulated polarization processes are laid, which are reduced to measuring the temperature spectra of thermally stimulated depolarization currents described in Section 2.1, when, at the first stage of the experiment, the process of isothermal (at a constant polarization temperature ) polarization of the sample in a uniform stationary electric field of strength is studied, during the polarization time , and at the second stage of the experiment, the external field is switched off , , the dielectric is rapidly cooled to low temperatures (50–80 K), shorted to an electrometer (or quality meter) and begins to heat up according to a linear law .
The main conclusions could be drawn summarizing the results obtained (in brief form):
1. Analytical solutions of the nonlinear quasi-classical kinetic equation of dielectric relaxation in crystals with ionic-molecular chemical bonds (CIMBs) are constructed in the first four approximations of perturbation theory (k = 1, 2, 3, 4). In contrast to the previously presented review article [5], these solutions are written in the form of nonequilibrium volume-charge distributions describing transient (in time) isothermal processes in dielectrics in an electric field (expressions (17), (21), (S2), and (S4)). Previously, these solutions were constructed far from transient processes, as non-stationary asymptotic functions (in the previous article [5]), but in this work, they differ, both in physical and mathematical content, and relate to specific processes in dielectrics the isothermal relaxation polarization currents All fundamental model differences in solving this theoretical problem are reflected in Section 2.2, Section 2.3, and Section 4.2 of this work. (see paragraphs 1, 2, and 4 of the extended conclusions).
2. For the first time, the nonlinear quasi-classical formulas for calculating the current density of isothermal relaxation polarization as a function of time in a dielectric were constructed by us. This has never been done before in relation to current in the context of the scientific problem under study (Expressions (28), (30), (S5) and (S7)). (see extended conclusions, p.3).
3. A recurrence expression for the partial current density generated in a dielectric in the stationary polarization mode at an odd field frequency is constructed (see (116) and (118) and extended conclusions, sections 5–17). All original calculation mechanisms for solving this theoretical problem are evident throughout Section 2, Section 3 and Section 4 of this work.
4. The theoretical foundations of analytical research schemes for nonlinear thermally stimulated depolarization processes have been laid (see extended conclusions, paragraphs 17 and 18). Previously, this issue has not been studied within the framework of the developing scientific direction. The solutions of the system of nonlinear Fokker–Planck and Poisson equations (expressions (6)–(9)) for the process of isothermal relaxation polarization in the approximations of perturbation theory k = 1, 2, 3, 4 (expressions (16), (20), (S1), (S4)) and for k > 4, will be used in constructing the initial conditions for the Fokker–Planck equation and its particular solutions as applied to the process of thermally stimulated relaxation depolarization.
5. This work is a continuation of the article [5] (and all earlier publications related to it), in the direction of a narrower area of specialization, for the development of theoretical schemes for studying transient (non-steady-state nonequilibrium processes) isothermal polarization currents (and not only relaxation polarization, as in [5]) in CIMBs-type crystals and in dielectrics and semiconductors related to them in structure and properties. This is reflected in the title of the work, the Introduction, the Objectives of the article (p. 9), and its methodology, described in Section 2.2, Section 2.3, Section 3 and Section 4.
Note In this article, in the process of constructing and analyzing the properties and parametric dependencies in the final formulas and equations of the model, the basic expressions from the work [5] are used in between, but no more than to justify the consistency of the equations of the new and previous models, as criteria for the reliability of new results and their applications. All these circumstances are stipulated in the process of mathematical description of the new model.
6. Prospects of Further Theoretical Research
When constructing calculation formulas for the TSDC density, as a function of temperature, the formulas of the equation of the nonlinear generalized quasi-classical theory of ion-relaxation polarization and conductivity in CIMBs will be applied, taking into account the components of the density of the thermally stimulated current associated with the relaxation of the homocharge in the dielectric, disconnected from an external source of electrical energy (EMF) [5,57,58,59]. The methodological basis of the phenomenological theory of thermally stimulated polarization currents (TSPC) and depolarization currents (TSDC) will be based on the equations of the nonlinear quasi-classical theory of isothermal (proceeding at a constant temperature of the experimental sample) polarization currents, investigated in this article.
Depolarization effects caused by the relaxation of the volume-charge accumulated in the crystal during polarization in an external polarizing field (in the presence of an EMF source) at a constant temperature (isothermal process) or variable temperature are called electret. The depolarization process caused by the relaxation of the charge accumulated in the crystal due to the diffusion movement of the main charge carriers in the polarizing field can be defined as hetero-charge relaxation. The depolarization process caused by the relaxation of homo-charge particles (accumulated due to charge injection from the surface of the electrodes into the depth of the dielectric and electron traps) can be defined as the relaxation of homo- and hetero-charge.
The experimental basis for thermally stimulated polarization and depolarization schemes is the Bucci-Riva method, which involves preliminary freezing of a shorted to an electrometer dielectric to a low temperature (50–100 K). Next, the experimental sample is heated according to a determined time law = f(t). The current flowing through the sample is defined as the thermally stimulated depolarization current. The initial value of the charge on the capacitor plates during thermally stimulated depolarization is defined as the sum of the initial values of the hetero- and homo-charge.
The methods developed for calculating thermally stimulated depolarization currents are also applicable to HBC.
As a model of the unperturbed crystal potential for relaxers (ions in CIMB; protons in HBC), let us adopt a one-dimensional spatially periodic potential field [5]. Potential barriers in this model are assumed to be one-dimensional parabolic [2,3,4,5].
Direct quantum mechanical studies of the theoretical spectra of thermally stimulated polarization (TSPC) and depolarization (TSDC) currents are the subject of a separate work to be performed in the future.
The study of the electrophysical properties of thin films of transition metals (TMO) for the development of high-speed non-volatile memory elements with high thermal and mechanical stability (DRAM, FeRAM (ferroelectrics with a rectangular hysteresis loop (FRHL); neuromorphic elements based on TMM)) is a topical applied direction in the field of nonlinear theory of thermally stimulated polarization and depolarization of dielectrics ([93–100] in [5]). Ferroelectric materials of the FRHL type (TMO, some types of ceramics, micas) are characterized by abnormally high residual polarizations and colossal polarization relaxation times (up to 10 years) ([100–110] in [5]) and can be used in the development of elements of neural networks and artificial intelligence, which is relevant for modern information technologies and electronic computing and measuring equipment ([111–121] in [5]).
The methods of nonlinear quasi-classical kinetic ([67,69,71–73] in [5]) and quantum kinetic ([68,70,122,123,136,138] in [5]) theories of ion-relaxation polarization and conductivity of solid dielectrics [2,3,4,5] developed by us, in combination with methods of numerical optimization of theoretical and experimental results ([1,128,138–140] in [5]) (in particular, using the MCF-method), form the theoretical basis of branched multiparameter algorithms ([75,76] in [5]) for sets of computer programs for computer modeling and prediction of properties and parameters (electrical; geometric; molecular; crystallographic) of heterogeneous functional elements based on crystals with ion-molecular chemical bonds (CIMBs) ([1,8,138] in [5]) The methods of the quantum kinetic theory of proton conductivity will be applicable in the study of the properties of ferroelectrics with hydrogen bonds and the development of physical and mathematical models of the quantum theory of ferroelectric phenomena caused by the tunneling motion of protons in the hydrogen sublattice of FRHL crystals near the temperature of the second-order phase transition. A direct quantum-mechanical approach to modeling the Hamiltonian operator of the proton and anion sublattices (taking into account proton-phonon and proton-proton interactions) will allow, with a sufficiently high degree of mathematical accuracy, to describe the mechanism of quantum behavior of the proton gas in ferroelectric HBCs with the possibility of exhibiting anomalously high, close to 0.95–0.98 ([122,123] in [5]), statistically averaged quantum transparencies of the potential barrier for protons moving in nanosized HBC layers at liquid helium temperatures (4–25 K) [60]. The material component of the dielectric constant of crystals under these conditions also reaches abnormally high values (2.5–5.5 million) [61,62]. The quantum properties of the proton in HBC at low (50–100 K) and, especially, ultra-low (1–10 K) temperatures can be tentatively explained, (since a strict theory of this effect has not yet been constructed), by the influence of two factors. Firstly, in the temperature range of liquid helium (4–25 K), the oscillations of the anion sublattice ions, specifically in nanosized layers (1–10 nm), occur with low frequencies, the average amplitudes of the anion oscillations decrease, the potential barrier for protons decreases in width to 0.05–0.07 nm (versus 0.085–0.095 nm at nitrogen temperatures) and the probability of proton penetration through the barrier (despite its enormous mass, compared to an electron, and, accordingly, the small De Broglie wavelength) at this stationary energy level of the discrete spectrum reaches abnormally high values of 0.95–0.99 [60,61]. It should be noted that the transformation of the proton energy spectrum from continuous to discrete is also caused by the specific behavior of the ions of the anion sublattice at helium temperatures and is associated with a reduction in both the crystal thickness d (macroscopic characteristic) and the lattice parameter a (these parameters are used in the formula for calculating the proton energy levels in HBC). Additionally, the spectrum of proton energies at T = 1–10 K, in contrast to the region T = 50–100 K, as shown by numerical calculations, due to the same layer thickness (1–10 nm), inclusively, leads to degeneration of the energy spectrum, and the width of the energy bands, at given parameters (1–10 nm; 1–10 K) is noticeably higher than at T = 50–100 K, d = 1000–10,000 nm [60,61].
High proton concentrations and, accordingly, anomalously high amplitudes of theoretical maxima of thermally stimulated current and anomalously low amplitudes of theoretical maxima of loss tangent in the region of ultra-low temperatures (1–10 K) at a layer thickness of d = 1–10 nm in HBC (in comparison with the temperature region T = 50–100 K at a layer thickness of 1–10 μm) are explained by a significant increase in stationary quantum transparency (up to 0.9–0.95) [60,61] due to transformations of the parameters of the discrete spectrum of proton energies in nanosized crystalline structures against the background of small values of the height and width of the potential barrier. The quantum behavior of the proton gas in HBC at ultra-low temperatures can arguably be explained by the formation of proton-proton pairs, which are formed due to the increasing interaction of protons with the phonon subsystem with the transition of the proton gas into boson gas, despite the low concentrations of relaxing protons (conduction protons) in the proton gas (an ensemble of non-interacting protons, distributed over energy levels in the field of the crystal lattice) in HBC (in comparison with the concentrations of conduction electrons in metallic superconductors).
When forming the schemes of analytical and numerical calculations of the temperature spectra of TSPC and TSDC, the methods developed during the patent research in [64,65,66] will be used.
7. Patents
1. Kalytka V.A., Baimukhanov Z.K., Bashirov A.V., Khanov T.A., Isaev V.L., and Suleimanov S.R. Patent of the Republic of Kazakhstan for utility model. Universal setup for measuring the parameters of microscopic structural defects. No. 5016. 06/05/2020. Bulletin No. (21)2020/0477.2.
2. Issayev V.L., Ospanov A.K., Kyzyrov K.B., Dandybaev E.S., Kalytka V.A., Reshetnikova O.S., and Mitussov A.A. Patent of the Republic of Kazakhstan for Invention. Hydraulic Hammer. No. 35366. (45)12/11/2021. Bulletin No. (21)2020/0613.1. The advantages of this Patent for Invention described in the Article lie, first and foremost, in the identical structure and methodology for solving the differential equations of inelastic displacements of continuous medium flows (in the mechanical model of the working substance motion (fluid) described in the Patent) and the differential equations in the model of electric charge transport in dielectric structures (in the kinetic and electrodynamic models described in the Article). In both the Patent and the Article, the objects of study are formally identical (continuous media, albeit of different physical natures) and the methods of analytical investigation of the differential equations in the studied models are mathematically equivalent. In the Article, the equation for electric charge transport is formulated and solved in the form of the continuity equation for the medium, whereas in the Patent, the dynamics of flow are analyzed and solved. Secondly, both in the Patent and in the Article, the numerical calculation of model parameters employs the same optimization scheme proposed by the authors—the method of minimizing the comparison function (MCF-method). This method is an original contribution by the authors in the field of mathematical modeling of mechanical, hydrodynamic, electrodynamic, and kinetic phenomena.
3. Issayev V.L., Kamarova S.N., Kalytka V.A., Kaidanovich O. Yu., Draganova M.A. Patent of the Republic of Kazakhstan for Invention. Boiler. No. 36790. (45)14/06/2024. Bulletin No. (21) 2023/0306.1.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15100863/s1.
Author Contributions
Conceptualization: V.K.; Methodology: V.K.; Software: Y.N., A.Y. and F.B.; Validation: V.K., A.M., Y.N., A.Y., D.L., D.K. and A.Z.; Investigation: V.K., A.M., Y.N., A.Y., A.A., F.B., V.I., K.M., D.L., D.K. and A.Z.; Formal analysis: V.K., A.M., Y.N., A.Y., A.A., F.B., V.I., K.M., D.L., D.K. and A.Z.; Recourses: A.M., Y.N., A.Y., K.M., D.K. and A.Z.; Data curation: V.K., V.I., A.Y. and K.M.; Writing—original draft preparation: V.K.; Writing—review and editing: V.K.; Project administration: Y.N. and A.M. Supervision: V.K., Y.N. and A.Y.; Visualization: K.M. and A.A.; Funding acquisition: A.Y., A.M., Y.N. and D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out at the expense of a grant from the Russian Science Foundation № 22-19-00389, https://rscf.ru/project/22-19-00389/ (accessed on 1 September 2024).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author(s).
Acknowledgments
During the preparation of this manuscript, the author(s) used Corel Draw, Graphics Suite 2025 for the purposes of constructing graphical representations (Figure 1, Figure 2 and Figure 3 in this article) of the physical-mathematical model of relaxation polarization developed in this study. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kalytka, V.A. Electrophysics of Proton Semiconductors and Dielectrics; Karaganda Technical University, KTU Publishing House: Karaganda, Kazahstan, 2021; Volume 133. [Google Scholar]
- Kalytka, V.; Bulatbayev, F.; Neshina, Y.; Bilichenko, Y.; Bilichenko, A.; Bashirov, A.; Sidorina, Y.; Naboko, Y.; Malikov, N.; Senina, Y. Theoretical Studies of Nonlinear Relaxation Electrophysical Phenomena in Dielectrics with Ionic–Molecular Chemical Bonds in a Wide Range of Fields and Temperatures. Appl. Sci. Sect. Appl. Phys. 2022, 12, 6555. [Google Scholar] [CrossRef]
- Kalytka, V.; Baimukhanov, Z.; Neshina, Y.; Mekhtiyev, A.; Dunayev, P.; Galtseva, O.; Senina, Y. Influence of Quantum Effects on Dielectric Relaxation in Functional Electrical and Electric Energy Elements Based on Proton Semiconductors and Dielectrics. Appl. Sci. Sect. Appl. Phys. 2023, 13, 8755. [Google Scholar] [CrossRef]
- Kalytka, V.; Mekhtiyev, A.; Neshina, Y.; Alkina, A.; Aimagambetova, R.; Mukhambetov, G.; Bashirov, A.; Afanasyev, D.; Bilichenko, A.; Zhumagulova, D.; et al. Physical and Mathematical Models of Quantum Dielectric Relaxation in Electrical and Optoelectric Elements Based on Hydrogen-Bonded Crystals. Crystals 2023, 13, 1353. [Google Scholar] [CrossRef]
- Kalytka, V.; Mekhtiyev, A.; Neshina, Y.; Alkina, A.; Senina, Y.; Bilichenko, A.; Sidorina, Y.; Beissekov, A.; Tatkeyeva, G.; Sarsikeyev, Y. Quasi-Classical Models of Nonlinear Relaxation Polarization and Conductivity in Electric, Optoelectric, and Fiber Optic Elements Based on Materials with Ionic–Molecular Chemical Bonds. Appl. Sci. Sect. Appl. Phys. 2024, 14, 11830. [Google Scholar] [CrossRef]
- Tonkonogov, M.P. Dielectric spectroscopy of hydrogen-bonded crystals, and proton relaxation. Uspekhi Fiz. Nauk. 1998, 41, 25–48. [Google Scholar] [CrossRef]
- Cai, J.; Lan, S.; Wei, B.; Qi, J.; Nan, C.W.; Lin, Y.H. Colossal permittivity in high-entropy CaTiO3 ceramics by chemical bonding engineering. Nat. Commun. 2025, 16, 4008. [Google Scholar] [CrossRef]
- Grodecka, A.; Machnikowski, P.; Förstner, J. Phonon-assisted tunneling between singlet states in two-electron quantum dot molecules. Phys. Rev. B 2008, 78, 085302. [Google Scholar] [CrossRef][Green Version]
- Imry, Y.; Tinkham, M. Introduction to Mesoscopic Physics. Phys. Today 1998, 51, 60. [Google Scholar] [CrossRef]
- Iogansen, L.V. On the possibility of resonant transfer of electrons in crystals through the barrier system. ZhETF 1963, 45, 207–218. [Google Scholar]
- Iogansen, L. Thin-film electron interferometers. Uspekhi Fiz. Nauk. 1965, 86, 175–179. [Google Scholar] [CrossRef]
- Abrikosov, A.A. Resonance tunneling in high-temperature superconductors. Uspekhi Fiz. Nauk. 1998, 168, 683–695. [Google Scholar] [CrossRef]
- Panda, P.K.; Sahoo, B. PZT to Lead Free Piezo Ceramics: A Review. Ferroelectrics 2015, 474, 128–143. [Google Scholar] [CrossRef]
- Abdel-Latif, I.A.; Gad, S.A.; Moustafa, A.M. Utilization of nanohexaferrites for application in microwave devices. In Nanostructured Hexagonal Ferrites; Elsevier: Amsterdam, The Netherlands, 2024; pp. 253–269. [Google Scholar] [CrossRef]
- Silver, K.; Li, J.; Porch, A.; Jamieson, W.D.; Castell, O.; Dimitriou, P.; Kallnik, C.; Barrow, D. 3D-printed microfluidic-microwave device for droplet network formation and characterization. Lab Chip 2024, 24, 5101–5112. [Google Scholar] [CrossRef]
- Avrutov, V.; Rupich, S.; Tsisarzh, V. Trends Of The Microwave Photonic Radars. Bull. Kyiv Polytech. Inst. Ser. Instrum. Mak. 2024, 67, 5–12. [Google Scholar] [CrossRef]
- Jirauschek, C. Theory of Hybrid Microwave–Photonic Quantum Devices. Laser Photonics Rev. 2023, 17, 2300461. [Google Scholar] [CrossRef]
- Horikoshi, S.; Catalá-Civera, J.M.; Schiffmann, R.F.; Fukushima, J.; Mitani, T.; Serpone, N. Engineering of Microwave Heating. In Microwave Chemical and Materials Processing; Springer Nature: Singapore, 2024; pp. 163–221. [Google Scholar] [CrossRef]
- Horikoshi, S.; Catalá-Civera, J.M.; Schiffmann, R.F.; Fukushima, J.; Mitani, T.; Serpone, N. Physics of Microwave Heating. In Microwave Chemical and Materials Processing; Springer Nature: Singapore, 2024; pp. 95–161. [Google Scholar] [CrossRef]
- Kadyrov, R.R. Adaptive microwave heating control for oily waste processing. In Proceedings of the IOP Conference Series Materials Science and Engineering, Krasnoyarsk, Russia, 29–30 April 2021; Volume 1155, p. 012098. [Google Scholar] [CrossRef]
- Origlia, C.; Rodriguez-Duarte, D.O.; Vasquez, J.A.T.; Bolomey, J.-C.; Vipiana, F. Review of Microwave Near-Field Sensing and Imaging Devices in Medical Applications. Sensors 2024, 24, 4515. [Google Scholar] [CrossRef]
- Syssoev, V.S.; Basov, E.V.; Orlov, A.I.; Zudin, I.Y.; Gushchin, M.E.; Mareev, E.A.; Shvets, N.N. Experimental simulation of the generation of microwave radiation during the interaction of a lightning discharge with an aircraft. Saf. Reliab. Power Ind. 2024, 17, 49–57. [Google Scholar] [CrossRef]
- Panda, S.S.S.; Panigrahi, T.; Parne, S.R.; Sabat, S.L.; Cenkeramaddi, L.R. Recent Advances and Future Directions of Microwave Photonic Radars: A Review. IEEE Sens. J. 2021, 21, 21144–21158. [Google Scholar] [CrossRef]
- Foong, P.Y.; Voon, C.H.; Lim, B.Y.; Teh, P.L.; Yeoh, C.K.; Rojan, M.A.; Parmin, N.A.; Gopinath, S.C.B.; Low, F.W.; Kashif, M.; et al. A Comparative Study of Microwave Welding Using Multiwalled Carbon Nanotubes and Silicon Carbide Nanowhiskers as Microwave Susceptors. Int. J. Nanoelectron. Mater. 2024, 17, 535–540. [Google Scholar] [CrossRef]
- Sun, Y.L.; Zhang, X.G.; Huang, Z.; Tian, H.W.; Cui, T.J.; Jiang, W.X. Intelligent Transmissive Microwave Metasurface with Optical Sensing and Transparency. Research 2024, 7, 7–9. [Google Scholar] [CrossRef]
- Hartnagel, H.L.; Quay, R.; Rohde, U.L.; Rudolph, M. (Eds.) Fundamentals of RF and Microwave Techniques and Technologies; Springer: Cham, Switzerland, 2023; Volume 23, p. 1539. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Adhikari, A.; Pallipamu, N.; Singh, M.; Nusrat, T.; Gaddam, S.; Samaddar, P.; Rajagopal, A.; Cherukuri, A.S.S.; Yadav, A.; et al. Applications of Microwaves in Medicine Leveraging Artificial Intelligence: Future Perspectives. Electronics 2023, 12, 1101. [Google Scholar] [CrossRef]
- Shao, W.; McCollough, T. Advances in Microwave Near-Field Imaging: Prototypes, Systems, and Applications. IEEE Microw. Mag. 2020, 21, 94–119. [Google Scholar] [CrossRef]
- Gartshore, A.; Kidd, M.; Joshi, L.T. Applications of Microwave Energy in Medicine. Biosensors 2021, 11, 96. [Google Scholar] [CrossRef]
- Lui, H.-S.; Persson, M. Microwave and Antenna Systems in Medical Applications. Sensors 2024, 24, 1059. [Google Scholar] [CrossRef] [PubMed]
- Serafino, G.; Scotti, F.; Lembo, L.; Hussain, B.; Porzi, C.; Malacarne, A.; Maresca, S.; Onori, D.; Ghelfi, P.; Bogoni, A. Toward a New Generation of Radar Systems Based on Microwave Photonic Technologies. J. Light. Technol. 2019, 37, 643–650. [Google Scholar] [CrossRef]
- Mittal, S.; R, V. Microwave Photonics Advancements in Radar Application. Blue Eyes Intell. Eng. Sci. Publ. 2022, 11, 35–40. [Google Scholar] [CrossRef]
- Belonenko, M.B. Characteristic features of nonlinear dynamics of a laser pulse in a photorefractive ferroelectric with hydrogen bonds. Quantum Electron. 1998, 28, 247–250. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Liu, J.H.; Biegalski, M.D.; Hu, J.-M.; Shang, S.L.; Ji, Y.; Wang, J.M.; Hsu, S.L.; Wong, A.T.; Cordill, M.J.; et al. Electrically reversible cracks in an intermetallic film controlled by an electric field. Nat. Commun. 2018, 9, 41. [Google Scholar] [CrossRef]
- Oh, S.; Hwang, H.; Yoo, I.K. Ferroelectric materials for neuromorphic computing. APL Mater. 2019, 7, 091109. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Kurtz, S.K.; Jamieson, P.B. Atomic displacement relationship to Curie temperature and spontaneous polarization in displacive ferroelectrics. Phys. Rev. 1968, 172, 551–553. [Google Scholar] [CrossRef]
- Kulagin, I.A. Components of the third-order nonlinear susceptibility tensors in KDP, DKDP and LiNbO3 nonlinear optical crystals. Quantum Electron. 2004, 34, 657. Available online: https://iopscience.iop.org/article/10.1070/QE2004v034n07ABEH002823 (accessed on 23 July 2023). [CrossRef]
- Bystrov, V.S.; Paramonova, E.V.; Meng, X.; Shen, H.; Wang, J.; Fridkin, V.M. Polarization switching in nanoscale ferroelectric composites containing PVDF polymer film and graphene layers. Ferroelectrics 2022, 590, 27–40. [Google Scholar] [CrossRef]
- Strukov, B.A.; Levanyuk, A.P. Ferroelectric Phenomena in Crystals. Physical Foundations; Springer: Berlin/Heidelberg, Germany, 1998; Volume 308. [Google Scholar] [CrossRef]
- Hu, J.; Chen, L.; Nan, C. Multiferroichetero structures integrating ferroelectric and magnetic materials. Adv. Mater. 2016, 28, 15–39. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, H.; Liu, X.; Bai, Q.; Zhang, H.; Gao, Y.; Jin, B.A. Comprehensive Study of Optical Fiber Acoustic Sensing. IEEE Access 2019, 7, 85821–85837. [Google Scholar] [CrossRef]
- Movchikova, A.; Suchaneck, G.; Malyshkina, O.V.; Pedko, B.B.; Gerlach, G. Thermal wave study of piezoelectric coefficient distribution in PMN-PT single crystals. Adv. Appl. Ceram. 2010, 109, 131–134. [Google Scholar] [CrossRef]
- Mukhortov, V.M.; Golovko, Y.I.; Mamatov, A.A.; Zhigalina, O.M.; Kuskova, A.N.; Chuvilin, A.L. Influence of Internal Deformation Fields on the Controllability of Nanosized Ferroelectric Films in a Planar Capacitor. Tech. Phys. Lett. 2010, 80, 77–82. Available online: https://journals.ioffe.ru/articles/viewPDF/9945 (accessed on 23 July 2023).
- Ezhilvalavan, S.; Tseng, T.-Y. Progress in the developments of (Ba,Sr)TiO3 (BST) thin films for Gigabitera DRAMs. Mater. Chem. Phys. 2000, 65, 227–248. [Google Scholar] [CrossRef]
- Huber, S.P.; Zoupanos, S.; Uhrin, M.; Talirz, L.; Kahle, L.; Häuselmann, R.; Gresch, D.; Müller, T.; Yakutovich, A.V.; Andersen, C.W.; et al. AiiDA 1.0, a scalable computational infrastructure for automated reproducible workflows and data provenance. Sci. Data 2020, 7, 300. [Google Scholar] [CrossRef]
- Magdău, I.-B.; Liu, X.-H.; Kuroda, M.A.; Shaw, T.M.; Crain, J.; Solomon, P.M.; Newns, D.M.; Martyna, G.J. The piezoelectronic stress transduction switch for very large-scale integration, low voltage sensor computation, and radio frequency applications. Appl. Phys. Lett. 2015, 107, 073505. [Google Scholar] [CrossRef]
- Chang, J.B.; Miyazoe, H.; Copel, M.; Solomon, P.M.; Liu, X.-H.; Shaw, T.M.; Schrott, A.G.; Gignac, L.M.; Martyna, G.J.; Newns, D.M. First realization of the piezo-electronic stress-based transduction device. Nanotechnology 2015, 26, 375201. [Google Scholar] [CrossRef]
- Chernikova, A.G.; Kozodaev, M.G.; Negrov, D.V.; Korostylev, E.V.; Park, M.H.; Schroeder, U.; Hwang, C.S.; Markeev, A.M. Improved ferroelectric switching endurance of La-doped Hf0.5Zr0.5O2 thin films. ACS Appl. Mater. Interfaces 2018, 10, 2701–2708. [Google Scholar] [CrossRef]
- Delimova, L.; Guschina, E.; Zaitseva, N.; Pavlov, S.; Seregin, D.; Vorotilov, K.; Sigov, A. Effect of seed layer with low lead content on electrical properties of PZT thin films. J. Mater. Res. 2017, 32, 1618–1627. [Google Scholar] [CrossRef]
- Udd, E.; Spillman, W.B. The Emergence of Fiber Optic Sensor Technology. In Fiber Optic Sensors: An Introduction for Engineers and Scientists; Wiley: Hoboken, NJ, USA, 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Marichev, V.A. Anomalous electrical conductivity of aqueous solutions in submicron cracks and gaps. J. Appl. Electrochem. 2005, 35, 17. [Google Scholar] [CrossRef]
- PPereira, L.; Mesquita, E.; Alberto, N.; Melo, J.; Marques, C.; Antunes, P.; André, P.S.; Varum, H. Fiber Bragg Grating Sensors for Reinforcing Bar Slippage Detection and Bond-Slip Gradient Characterization. Sensors 2022, 22, 8866. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, C.; Sankar, R.; Kumar, R.M.; Jayavel, R. Effect of Amino Acid Doping on The Growth and Ferroelectric Properties of TriglycineSulphate Single Crystals. Mater. Res. Bull. 2008, 43, 305–311. [Google Scholar] [CrossRef]
- Yaroslavtsev, A.B. Solid electrolytes: Main prospects of research and development. Russ. Chem. Rev. 2016, 85, 1255–1276. [Google Scholar] [CrossRef]
- Farhana, K.; Jiban, P. Structural and Optical Properties of Triglycine Sulfate Single Crystals Doped with Potassium Bromide. J. Cryst. Process Technol. 2011, 1, 26–31. [Google Scholar] [CrossRef]
- Dadayan, A.K.; Borisov, Y.A.; Zolotarev, Y.A.; Bocharov, E.V.; Nagaev, I.Y.; Myasoedov, N.F. Solid-State Catalytic Hydrogen/Deuterium Exchange in Mexidol Russ. J. Phys. Chem. 2021, 95, 273–278. [Google Scholar] [CrossRef]
- Kalytka, V.A.; Korovkin, M.V.; Mekhtiyev, A.D.; Yurchenko, A.V. Nonlinear Polarization Effects in Dielectrics with Hydrogen Bonds. Russ. Phys. J. 2018, 61, 757–769. [Google Scholar] [CrossRef]
- Kalytka, V.A. The mathematical description of the nonlinear relaxation of polarization in dielectrics with hydrogen bonds. Bull. Samara Univ. Nat. Sci. Ser. 2017, 23, 71–83. [Google Scholar] [CrossRef][Green Version]
- Kalytka, V.A. Nonlinear kinetic phenomena under polarization in solid dielectrics. Bull. Mosc. Reg. State Univ. Ser. Phys. Math. 2018, 2, 61–75. [Google Scholar] [CrossRef]
- Kalytka, V. Nonlinear Quantum Phenomena During the Polarization of Nanometer Layers of Proton Semiconductors and Dielectrics. Izv. Altai State Univ. 2021, 4, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Kalytka, V.; Aliferov, A.; Korovkin, M.; Mehtiyev, A.; Madi, P. Quantum properties of dielectric losses in nanometer layers of solid dielectrics at ultra-low temperatures. Proc. Russ High Sch. Acad. Sci. 2021, 51, 14–33. [Google Scholar] [CrossRef]
- Kalytka, V.A.; Korovkin, M.V. Proton conductivity. In Monograph; Publishing House: Saarbrücken, Germany; LAP LAMBERT Academic Publishing: Saarbrücken, Germany, 2015; Volume 180, Available online: http://www.lap-publishing.com (accessed on 21 June 2025).
- Kalytka, V.A.; Korovkin, M.V.; Madi, P.S.; Kalacheva, S.A.; Sidorina, Y.A. Universal installation for studying structural defects in electrical and optical fiber materials. IOP Conf. Ser. J. Phys. 2020, 1499, 012046. [Google Scholar] [CrossRef]
- Kalytka, V.A.; Baimukhanov, Z.K.; Bashirov, A.V.; Khanov, T.A.; Isaev, V.L.; Suleimanov, S.R. Universal Setup for Measuring the Parameters of Microscopic Structural Defects. Patent of the Republic of Kazakhstan for Utility Model. No. 5016. 06/05/2020; Bulletin No. (21)2020/0477.2, 6 May 2020. [Google Scholar]
- Issayev, V.L.; Ospanov, A.K.; Kyzyrov, K.B.; Dandybaev, E.S.; Kalytka, V.A.; Reshetnikova, O.S.; Mitussov, A.A. Hydraulic Hammer. Patent of the Republic of Kazakhstan for Invention. No. 35366. (45)12/11/2021; Bulletin No. (21)2020/0613.1, 12 November 2021. [Google Scholar]
- Issayev, V.L.; Kamarova, S.N.; Kalytka, V.A.; Kaidanovich, O.Y.; Draganova, M.A. Boiler. Patent of the Republic of Kazakhstan for Invention No. 36790. (45)14/06/2024; Bulletin No. (21) 2023/0306.1, 14 June 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).