Hybrid Kinetic Modelling of Protein Crystallization: Hanging Drop and Langmuir–Blodgett Conditions

Abstract

The understanding and control of protein crystallization are crucial in structural biology, drug development, and biomaterial design. This study introduces a unified framework for modeling and comparing crystallization kinetics using selected growth functions. Experimental datasets from the literature for four proteins, Lysozyme, Thaumatin, Ribonuclease A, and Proteinase K, under Hanging Drop and Langmuir–Blodgett conditions were analyzed. Five kinetic models, Avrami, Kashchiev, Hill, Logistic, and Generalized Sigmoid (GSM), were fitted to size–time data of the four benchmark proteins. From each fit, four descriptors were extracted: crystallization half-time, time of maximum growth, width at half-maximum, and peak growth rate. These metrics summarize crystallization dynamics and enable cross-comparison of proteins and methods. Langmuir–Blodgett templating accelerated onset and improved synchrony, though the effect varied by protein and model. Logistic, Hill, and GSM models provided consistent fits across most conditions, while Avrami and Kashchiev were more sensitive to early or late deviations. Notably, descriptor extraction remained reliable even with limited or uneven sampling, revealing kinetic regimes such as synchrony, asymmetry, or prolonged nucleation, not evident in raw data. This transferable analytical framework supports quantitative evaluation of crystallization behavior, aiding screening, process optimization, and time-resolved structural studies.

1. Introduction

Protein crystallization underpins structural biology by providing crystals suitable for high-resolution X-ray diffraction and, more recently, for preparing cryo-electron microscopy (cryo-EM) grids [1,2,3]. Despite major advances in automation and high-throughput screening [4], the fundamental kinetics of nucleation and crystal growth remain poorly characterized, particularly in terms of their temporal progression and synchrony [5,6,7].

The hanging–drop (HD) vapor–diffusion method remains the most widely employed technique in crystallization trials. It offers simplicity, compatibility with high–throughput formats, and requires only minimal sample volumes [8,9]. In this method, a protein droplet equilibrates against a reservoir of higher osmotic strength, leading to progressive concentration increase and eventual nucleation. However, HD often produces stochastic nucleation events, yielding heterogeneous crystal sizes and dispersed growth kinetics [10]. Alternative approaches, such as Langmuir–Blodgett (LB) film–assisted crystallization, aim to exert greater control on nucleation by organizing protein molecules at the air–water interface [10,11]. In this approach, protein molecules are softly organized into thin layers at the air–water interface, which helps initiate crystallization in a more controlled way. In model systems such as Lysozyme and Thaumatin, LB templating accelerates nucleation and produced larger, better–ordered crystals [12,13,14,15,16,17]. These methods employ monolayer films or self–assembled substrates to promote collective activation and accelerate crystallization [18]. However, despite these advantages, LB remains rarely applied and relatively underutilized and direct kinetic comparisons with HD are surprisingly limited.

A quantitative understanding of crystallization kinetics is crucial not only for refining experimental protocols but also for ensuring reproducibility and developing predictive models [19,20,21,22]. The crystallization process is typically represented by growth curves X(t) which track the increase in crystallized volume or fraction as a function of time [23]. The first derivative dX/dt makes the dynamics more explicit, revealing incubation delays preceding nucleation, bursts of cooperative growth, and the eventual deceleration toward saturation.

Several models have been employed to describe these crystallization trajectories. Classical nucleation–growth models, exemplified by the Avrami and Kashchiev equations [24], capture continuous or distributed nucleation coupled with isotropic crystal growth. Cooperative activation models, exemplified by the Hill function [25], represent synchronized transitions typical of templated conditions. Phenomenological sigmoidal descriptions, including the Logistic [26] and the more flexible Generalized Sigmoid (GSM) form [27], provide shape-controlled behaviors that accommodate symmetry or asymmetry without mechanistic assumptions.

From the models fitted to the experimental data, four key descriptors are extracted: the crystallization half–time; the time of maximum growth; the peak growth rate; and the width at half-maximum of the derivative peak, summarizing onset, rate, synchrony of the crystallization process and spread of cooperative growth event.

These descriptors are significant because they translate complex growth trajectories into a concise, quantitative framework. They facilitate direct comparisons of timing, synchrony, and intensity across different proteins and conditions, overcoming the limitations of qualitative or endpoint-only assessments.

However, comprehensive X(t) trajectories and the above descriptors are reported infrequently. Many crystallization studies still emphasize endpoint yields or static snapshots. In particular, LB studies often focus on the morphology or diffraction quality of the resulting crystals, while neglecting kinetic details. Consequently, the absence in the literature of comparisons between HD and LB in these terms leaves a key question unanswered: not only how templating changes the outcome, but also how it reshapes the timing and coordination of the growth process.

2. Methods

2.1. Protein Selection and Kinetic Data Processing

Time–resolved crystallization measurements were reported under both HD and LB conditions for Lysozyme, Thaumatin, Ribonuclease A, and Proteinase K [28,29]. Lysozyme was selected as a benchmark protein due to its extensively characterized crystallization kinetics using optical microscopy and direct growth–rate measurements. For Thaumatin, kinetic profiles under LB conditions were derived from in situ μGISAXS experiments [30,31], while HD trajectories were reconstructed from reported onset times and qualitative screening data. Ribonuclease A datasets were compiled from published growth profiles obtained under both HD and LB environments, providing complementary examples of stochastic versus templated nucleation. Proteinase K was also included, but the available series contain only a limited number of measurement points in the transition region, restricting the precision of fitted descriptors primarily serving as an illustration of the importance of denser kinetic sampling in the critical region.

Crystallization was performed under standardized conditions (18–22 °C) for all proteins, using literature-reported protocols compatible with either HD or LB film-assisted methods [28,29,30]. Lysozyme was crystallized in 0.1 M sodium acetate (pH 4.5) with 3% NaCl at 25–30 mg/mL; Thaumatin was studied under LB using 0.1 M sodium tartrate (pH 6.5) at 30–35 mg/mL, with HD data reconstructed from earlier sources. For Ribonuclease A, 2.5 M ammonium sulfate (pH 6.0) and 15–25 mg/mL protein were used, and Proteinase K in 0.1 M Tris-HCl (pH 8.0) with 0.5 M NaCl at ~30 mg/mL.

HD experiments were typically sampled once daily via optical microscopy; LB trajectories included sub-daily or SAXS-derived data (Thaumatin). Specifically, Lysozyme and Ribonuclease A trajectories contained ~10 time points, Thaumatin 6–8, while Proteinase K was limited to 4, hence serving mainly to illustrate the modeling limitations arising from sparse kinetic sampling. Thus, while the protein crystallization experiments in the literature were performed under slightly different conditions (protein concentrations, temperatures, buffer systems), these conditions reported in the original publications are considered to be comparable for the purposes of this analysis. The availability of more experimental findings would allow a more consistent analysis than allowed at present.

Data placement, not merely data count, governs descriptor reliability. We define the transition window as the 30–70% segment of the growth trajectory relative to the empirical plateau. Reliable estimation of synchrony and intensity (W_1⁄2, (dX/dt)_max) requires at least 3–4 measurements within this window plus ≥ 1 pre-onset anchor. Proteinase K contains a number of points comparable to Ribonuclease A, yet lacks mid-slope coverage, which explains its model-dependence despite a similar number of points.

All crystallization data employed in this study were obtained from single published growth curves as reported above under HD and LB conditions, without replicate measurements. Consequently, experimental uncertainty originates from both the measurement techniques used to determine crystal size and the sample preparation steps.

The dataset used in this study was primarily obtained from Pechkova et al. (2014) [29], who reported crystal growth trajectories under HD and LB conditions. The crystal size X(t) was defined as the longest linear dimension observable in each sample (e.g., crystal length), measured from optical microscopy and SAXS data without averaging over multiple axes. Supplementary Figure S1 illustrates this procedure for Thaumatin. For the other proteins, analogous morphological features were used to define the principal growth direction. This convention consistently applied throughout the study. Optical resolution and SAXS calibration contribute an estimated 3–5% variability in size determination for HD-grown crystals, while standard handling procedures (e.g., pipetting, alignment) add approximately 2–3%. For LB-grown crystals, nanogravimetric surface measurements carry an estimated uncertainty of ~5%. To account for all sources of error and potential compounding effects, a conservative overall uncertainty of ±10% in crystal size was adopted. This uncertainty is reflected in Figure 1, Figure 2, Figure 3 and Figure 4 and was propagated into all model descriptors and kinetic parameters (Figure 5, Figure 6 and Figure 7), as discussed in more detail in Supplementary Sections S2.3 and S2.4.

2.2. Modeling Crystallization Kinetics: Classical, Cooperative, and Diffusion–Limited Regimes

Crystallization dynamics were analyzed using a suite of kinetic models chosen to represent distinct mechanistic regimes: traditional nucleation–growth, cooperative activation, shape–controlled sigmoids, and time–distributed nucleation. This diverse modeling approach allowed us to evaluate not only quantitative fit quality but also key qualitative features of the crystallization process, including synchronization, depletion effects, and asymmetry.

The Avrami model, a widely established reference, assumes continuous nucleation with isotropic crystal growth, thus capturing the smooth sigmoidal kinetics of untemplated crystallization. The crystallized fraction evolves according to Equation (1), where k is a kinetic constant and n reflects the combined influence of dimensionality and the nucleation regime:

$$X\left(t\right)=1-e^{-k({t-\tau )}^n}$$

(1)

The exponent n in the Avrami model integrates both nucleation mode and growth dimensionality (e.g., 1D linear, 2D surface, 3D volumetric growth), while k represents the rate constant. The parameter τ represents a lag phase and indicates the time at which nucleation becomes kinetically active. This model is well-suited for describing smooth crystallization profiles that are not significantly limited by mass transport effects.

To account for cooperative nucleation, we employed the Hill model [25], which describes activation events as discussed above and expressed as in Equation (2). Here, k is a pseudo–equilibrium time parameter and n is the Hill coefficient.

$$X\left(t\right)={\displaystyle \frac{t^n}{k^n+t^n}}$$

(2)

In this model, values of n > 1 indicate positive cooperativity, where nucleation accelerates after the initial activation. Such effects are commonly observed in templated environments, such as LB films, where molecular organization facilitates synchronized nucleation.

Asymmetric kinetics were described by the Generalized Sigmoid (GSM) [32,33], which incorporates an asymmetry parameter m. The functional form is given in Equation (3).

$$X\left(t\right)=A{\left(1+e^{-k(t-t_0)}\right)}^{-1∕m}$$

(3)

Here, A represents the asymptotic plateau, k and t₀ govern the steepness and inflection point, respectively, and m modulates the asymmetry. For m > 1, the onset is delayed but completion is rapid; for m < 1, the onset is sharp with an extended saturation phase. This form is appropriate for systems where nucleation and growth are temporally decoupled, such as those involving transient energy barriers or metastable intermediate states. Unlike τ in the Avrami and Kashchiev models, which represents the time at which crystallization begins, t₀ in the GSM model corresponds to the inflection point, typically near the time of fastest growth but not necessarily the onset. For comparison, we also tested the simpler, symmetric Logistic model [34] as expressed in Equation (4):

$$X\left(t\right)={\displaystyle \frac{1}{1+e^{-k\left(t-t_0\right)}}}$$

(4)

The Logistic model is purely phenomenological: t₀ coincides with both the inflection and the half–time, while k determines the slope. Its symmetry makes it a useful descriptive tool across different experimental conditions for cases where mechanistic detail is not required.

The Kashchiev model [35,36] differs from the Avrami model by incorporating progressive, time–distributed nucleation. Instead of an abrupt onset, it describes a gradual initiation window, as expressed in Equation (5):

$$X\left(t\right)={\displaystyle \frac{{\left(k(t- \tau )\right)}^n}{1+{\left(k(t-\tau \right))}^n}}$$

(5)

As in Avrami model, τ represents the nucleation induction time. This model is particularly well-suited for systems where nucleation events continue to occur during the growth phase.

Finally, we considered the possibility of two–step nucleation [34,37,38], in which crystallization proceeds via metastable dense liquid intermediates. Although no unique functional form exists, such mechanisms are often manifested in kinetic profiles by delayed but sharp rises, frequently producing high Hill coefficients or asymmetric GSM fits. In this context, strong asymmetry or elevated n values can serve as indirect signatures of intermediate–mediated nucleation.

All model equations and their parameter definitions are summarized in Supplementary Table S1.

2.3. Model Fitting and Descriptor Extraction

Each crystallization dataset was fitted to all kinetic models using nonlinear least–squares minimization. The fitting procedure minimized the residual sum of squares between experimental data and model predictions for X(t).

Table 1. Model Parameters for HD and LB Crystallization Fits. Comparison of fitted parameters for five kinetic models across Hanging Drop (HD) and Langmuir–Blodgett (LB) conditions for all proteins.

Protein	Model	Best Fit Parameters HD	Best Fit Parameters LB
Lysozyme	Avrami	k = 5.30, n= 0.73, τ = 1.73	k = 1.54, n = 0.732, τ = 0.798
	Kashchiev	k = 1.54, n = 2.96, τ = 1.178	k = 3.426, n= 1.12, τ = 0.7979
	Hill	k = 1.684, n= 6.02	k = 1.14, n= 2.72
	Logistic	k = 5.841, t0 = 1.768	k = 2.049, t0 = 1.197
	GSM	k = 7.289, t0 = 1.768, = 1.51	k = 2.047, t0 = 1.197, m = 0.979
Thaumatin	Avrami	k = 0.5186, n= 1, τ = 2.784	k = 0.6467, n= 1, τ = 2.552
	Kashchiev	k = 0.9041, n= 1.24, τ = 2.784	k = 1.181, n = 1.26, τ = 2.552
	Hill	k = 3.977, n = 3.5	k = 3.646, n= 3.25
	Logistic	k = 0.8501, t0 = 4.176	k = 0.7873, t0 = 3.829
	GSM	k = 0.823, t0 = 4.176, m = 0.925	k = 0.8236, t0 = 3.829, m = 1.16
Ribonuclease A	Avrami	k = 0.8007, n= 2.65, τ = 1.075	k = 1.66, n = 1, τ = 0.566
	Kashchiev	k = 1.211, n = 5.88, τ = 1.205	k = 3.32, n= 1.13, τ = 0.566
	Hill	k = 0.9369, n= 1.49	k = 0.8086, n= 1.83
	Logistic	k = 1.267, t0 = 0.9837	k = 2.305, t0 = 0.849
	GSM	k = 1.207, t0 = 0.9837, m = 0.679	k = 1.843, t0 = 0.849, m = 0.799
Proteinase K	Avrami	k = 48.77, n= 1.88, τ = 0.5307	k = 13.44, n= 1.87, τ = 0.5563
	Kashchiev	k = 269.7, n= 1, τ = 0.3635	k = 19.31, n= 1.93, τ = 0.7589
	Hill	k = 0.5193, n= 5.96	k = 0.5421, n= 4.92
	Logistic	k = 27.13, t0 = 0.5453	k = 7.514, t0 = 0.5692
	GSM	k = 27.71, t0 = 0.5453, m = 1.08	k = 9.197, t0 = 0.5692, m = 0.368

reports all fitted parameters and descriptors for Lysozyme, Thaumatin, Ribonuclease A, and Proteinase K under HD and LB conditions. The corresponding fitted curves and their derivatives are depicted in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 respectively.

All models describe crystallization as a monotonic increase, with no intrinsic maximum in X(t). In contrast, the derivative dX/dt exhibits a distinct peak that corresponds to the maximum rate of crystal growth; this derivative profile serves as the basis for extracting time–resolved descriptors as follows:

(i)

crystallization half–time (t_1⁄2, when X(t) reaches 50% of its plateau), which describes the timing of crystallization onset.

(ii)

time of maximum growth rate (t_max) which identifies the point of maximum growth acceleration.

(iii)

the peak growth rate (dX/dt)_max which measures the intensity of the crystallization process.

(iv)

width at half–maximum (W_1⁄2) of the dX/dt profile quantifying the duration of the cooperative growth phase.

These descriptors are expressed in physical units (days, μm/day) and were computed either analytically from model derivatives or numerically from finite-difference approximations. Analytical solutions were used wherever possible; descriptors for asymmetric GSM fits were validated numerically when required (Figure S3).

Model diagnostics prioritized coverage of the mid-slope region. When the 30–70% window was undersampled, as for Proteinase K, we reported timing descriptors (t_1⁄2, t_max) with caution and treated W_1/2 and (dX/dt)_max as provisional, reflecting increased model-dependence.

Curve fitting was performed using custom Python 3.10 scripts that leveraged the numpy, scipy.optimize, and matplotlib libraries. Rate profiles from fitted models were obtained either analytically by differentiation or numerically via central finite differences (using forward/backward differences at the boundaries). Descriptor uncertainty was estimated from the covariance matrix of parameters returned by the nonlinear least-squares fitting routine (scipy.optimize.curve_fit).

When a closed-form analytical solution for uncertainty propagation was unavailable for a given descriptor, confidence intervals were approximated using finite differences applied to the fitted function. This approach provides a reasonable estimate of descriptor robustness without assuming specific parametric distributions. Visual inspection of the residuals was also performed to assess potential biases in the model fits, particularly under conditions of sparse experimental sampling. The rate of crystal growth dX(t)/dt was estimated using finite differences between consecutive size measurements. Propagation of the ±10% uncertainty in crystal size into the numerical derivative results in rate uncertainties typically around 25%, depending on the growth rate and time interval. This propagated error was included as vertical error bars in the derivative plots (Figure 5, Figure 6 and Figure 7). Detailed information is reported in Supplementary Materials at Sections S2.3 and S2.4.

2.4. Statistical Evaluation of Model Fits

Model performance was assessed using both goodness–of–fit metrics and information criteria. Specifically, for each protein and condition, the coefficient of determination (R²) and the root–mean–square error (RMSE) was calculated to quantify the explained variance and absolute deviation between experimental and fitted values. To account for differences in model complexity, the Akaike Information Criterion (AIC) was also computed, balancing fit accuracy against the number of parameters. All statistical evaluations were performed using built-in routines in Python (scipy.stats, numpy.linalg).

Uncertainty in fitted parameters was estimated from the covariance matrix returned by the nonlinear least–squares routine (scipy.optimize.curve_fit). Confidence intervals (95%) for the four descriptors defined above were obtained via analytical error propagation when closed forms were available, or by Monte Carlo resampling of residuals otherwise, as detailed in Section 2.3.

All fit statistics, including standard deviations of the residuals and pairwise AIC differences between models, are provided in the Supplementary Materials and, in particular, in Table S4.

3. Results: Growth and Rate Profiles

This section presents the crystallization growth curves X(t) for Lysozyme, Thaumatin, Ribonuclease A, and Proteinase K under HD and LB conditions. Experimental trajectories are compared with predictions of five kinetic models—Avrami, Kashchiev, Hill, Logistic, and the Generalized Sigmoid Model (GSM)—using the fixed parameter values reported in Table 1. All growth curves are expressed in physical units, e.g., time in days and crystal size in micrometers, without normalization or rescaling.

The comparisons highlight key kinetic features: the onset of crystallization t₀, the steepness of the central rise (controlled by parameters k, n, or m, the symmetry or asymmetry of the transition, and the final plateau size. Together, these elements provide a direct physical interpretation of the experimental series and clarify how each model represents the balance between onset timing, growth synchrony, and saturation under HD and LB conditions. Model comparisons are based on visual agreement, which helps to identify the kinetic forms that helps to identify the biophysical signatures of HD and LB crystallization. Detailed statistical metrics (RMSE, AIC) are provided in Supplementary Materials and, in particular, in Supplementary Materials to support these qualitative assessments.

Section 3.1, Section 3.2, Section 3.3 and Section 3.4 present per-protein experiments obtained from the literature and the time behavior of the models in eqn. 1 and the fitted parameters in Table 1. Section 3.5 synthesizes cross-system trends via descriptors and 3.6 reports statistical model comparison.

3.1. Lysozyme—HD and LB Kinetics

Based on the analysis of Figure 1, the crystallization kinetics of Lysozyme under HD and LB conditions are presented below. Under HD conditions, Lysozyme shows a lag phase until approximately day 1.5–2, followed by a smooth rise to a plateau near 800 μm. Logistic and GSM models closely reproduce the sigmoidal inflection and the rounded progression toward saturation. The Hill model captures the rise but overemphasizes steepness. Avrami and Kashchiev underestimate early growth but align at the plateau.

Under LB conditions, crystallization is advanced: onset occurs earlier, the rise is steeper, and completion to a plateau near 800 μm is reached within 2–3 days. Logistic and Hill models best match the synchronized transition, while GSM captures the slight asymmetry after the inflection. Avrami and Kashchiev again lag at early times but ultimately recover the final size. LB templating thus compresses the crystallization timeline for Lysozyme, reducing onset delays and enhancing synchrony. Models capable of sharper or asymmetric transitions—Logistic, Hill, and GSM—align most closely with the experimental profiles under both regimes, whereas Avrami and Kashchiev provide conservative envelopes that systematically understate the onset.

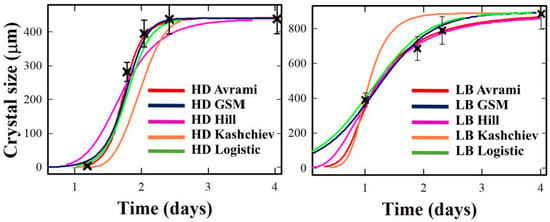
Figure 1. Crystallization growth curves X(t) for Lysozyme under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data (black crosses) are compared with fits from Avrami (red), GSM (cyan), Hill (purple), Kashchiev (orange), and Logistic (dark blue). Error bars are reported as discussed in detail in the Supplementary Materials.

Figure 1. Crystallization growth curves X(t) for Lysozyme under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data (black crosses) are compared with fits from Avrami (red), GSM (cyan), Hill (purple), Kashchiev (orange), and Logistic (dark blue). Error bars are reported as discussed in detail in the Supplementary Materials.

3.2. Thaumatin: Accelerated and Amplified Growth Under LB Conditions

Based on the analysis of Figure 2, the crystallization kinetics of Thaumatin under HD and LB conditions are presented below. Under HD conditions, Thaumatin displays a delayed onset, becoming detectable only after day 2, and saturates around day 6–7, with final sizes exceeding 900 μm. Logistic and GSM reproduce both the inflection and the plateau, while the Hill model overestimates the steepness of the rise. Avrami and Kashchiev underestimate early growth but converge to the observed plateau.

Under LB conditions, Thaumatin crystallization accelerates markedly: onset occurs within 24 h, peaking near day 2.5. The process is both faster and more intense, with nearly double the peak rate versus HD. Hill captures this steep mid–phase most accurately, while GSM accounts for the slight asymmetry in the trajectory. Logistic provides a reasonable but more conservative description, whereas Avrami and Kashchiev fail to reproduce the rapid early transition.

LB templating thus advances onset and amplifies the growth rate while preserving sigmoidal character. This response indicates Thaumatin as a system particularly sensitive to cooperative enhancement and synchronization at the interface.

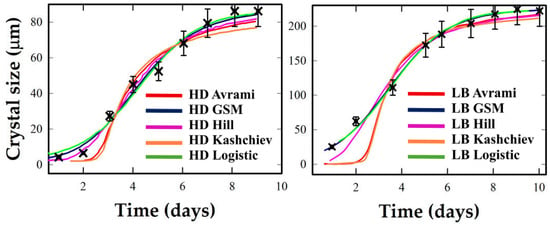
Figure 2. Crystallization kinetics of Thaumatin under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data (black crosses) are compared with model fits from the five models, represented by the same choice of colors as in Figure 1.

Figure 2. Crystallization kinetics of Thaumatin under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data (black crosses) are compared with model fits from the five models, represented by the same choice of colors as in Figure 1.

3.3. Ribonuclease A: Sharp Transition and High Synchrony Under LB Conditions

Based on the analysis of Figure 3, the crystallization kinetics of Ribonuclease A under HD and LB conditions are presented below. Under HD conditions, Ribonuclease A exhibits a broad and gradual rise extending over the entire 4–day window, with modest growth rates and final crystal sizes around 60 μm. Logistic and Avrami reproduce the general trend, capturing the overall sigmoidal trend and moderate steepness. GSM slightly underestimates early slope but aligns post-inflection. Hill and Kashchiev fail to reproduce the extended onset, resulting in compressed or distorted profiles.

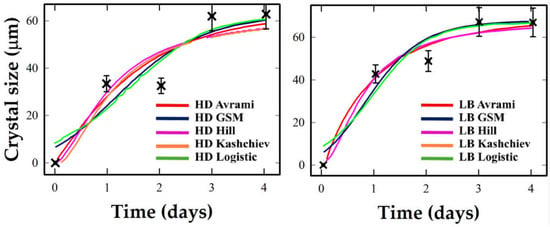
Figure 3. Crystallization kinetics of Ribonuclease A under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data and the five models are represented by the same choice of colors as in Figure 1.

Figure 3. Crystallization kinetics of Ribonuclease A under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data and the five models are represented by the same choice of colors as in Figure 1.

In contrast, under LB conditions, transition is abrupt, with onset within 1–1.5 days and rapid completion suggesting a highly synchronized crystallization process with minimal stochastic delay. Hill best captures the steep onset and narrow transition width, consistent with strong cooperative behavior.

Models allowing steeper or mildly asymmetric transitions (Logistic, GSM) capture the LB-induced sharpening, whereas Avrami/Kashchiev understate early growth

LB templating shifts Ribonuclease A into a tightly coordinated crystallization regime, best described by models that handle narrow transitions and strong cooperativity.

3.4. Proteinase K: Diffuse Growth with Weak LB Response and Limited Experimental Resolution

The crystallization kinetics of Proteinase K under HD and LB conditions are presented in Figure 4. The analysis of Figure 4 shows that Proteinase K exhibits a rapid, step-like transition under both HD and LB conditions, saturating within one day. Inflection is poorly resolved due to abrupt growth and limited time points. The results of the kinetic model fitting for Proteinase K should be interpreted with caution, given the limited number of data points and their position, as stated above. The lack of intermediate points between 30 and 70% growth, precisely where model discrimination and descriptor sensitivity are highest, limits the reliability of model comparisons. This protein mainly illustrates the challenges of sparse sampling.

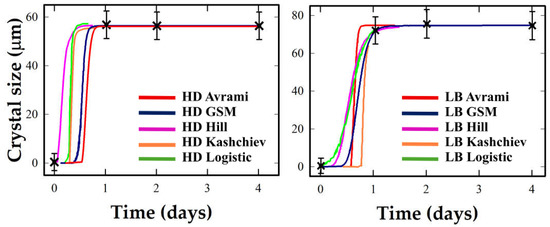
Figure 4. Crystallization kinetics of Proteinase K under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data and the five models are represented by the same choice of colors as in Figure 1.

Figure 4. Crystallization kinetics of Proteinase K under Hanging Drop (HD, (left)) and Langmuir–Blodgett (LB, (right)) conditions. Experimental data and the five models are represented by the same choice of colors as in Figure 1.

3.5. Overall Results

The extracted kinetic descriptors enable a comparative assessment of crystallization dynamics across the four proteins under HD and LB conditions. For Lysozyme, Thaumatin, and Ribonuclease A, LB templating consistently reduces the crystallization half-time t_1/2 and advances the growth time t_max. These shifts are accompanied not only by faster activation but also by enhanced synchrony. Under LB, peak rates (dX/dt)_max tend to increase while W_1⁄2 narrows, showing that templating both accelerates growth and concentrates it into a shorter, more coherent time window.

Among the systems, Thaumatin exhibits the most pronounced response. Its maximum rate almost doubles, while W_1⁄2 contracts from roughly 2.8 days to under 1.5, a clear sign of compressed cooperative growth. Ribonuclease A follows the same trend but with an even sharper character: under LB the growth burst centers well before t_1⁄2, which is a classic marker of cooperative, synchronized transitions. Lysozyme behaves more modestly, its curve shifts left and steepens, but the change is less dramatic.

Proteinase K behaves differently. While Logistic and GSM models suggest a broader and somewhat slower transition under LB conditions (e.g., W_1⁄2 from 0.13 to 0.47 days, and (dX/dt)max dropping from 381 to 140 μm/day), these values must be interpreted with caution. Only four time points per condition were available, with limited coverage of the 30–70% transition range. Avrami and Kashchiev fits often yielded pathological descriptors—e.g., unrealistically sharp peaks with near-zero W₁⁄₂—due to undersampled onset. Therefore, apparent sluggishness is likely a modeling artifact, not an intrinsic kinetic feature. In this case, Logistic and GSM provide the most stable—but still tentative—descriptions.

All descriptor values and their variation across proteins and conditions are further discussed in the Supplementary Materials.

3.6. Statistical Evaluation of Model Fits

Model performance was assessed using three standard metrics: the coefficient of determination (R²), the root–mean–square error (RMSE), and the Akaike Information Criterion (AIC) [39] which, respectively, evaluate explained variance, residual magnitude, and the trade-off between fit quality and model complexity. The overall pattern was consistent across proteins. Logistic and GSM generally produced excellent fits with R² values between 0.94 and 0.99, and low RMSE, consistent with their ability to balance timing and shape across diverse crystallization curves. Hill often performed equally well, particularly for synchronized transitions, such as Lysozyme and Ribonuclease A under LB conditions. In broader transitions, however, Hill tended to overemphasize the steepest mid-slopes. Avrami and Kashchiev accounted for part of the variance but consistently produced higher AIC values, indicating that the additional parameters they employ did not improve fits.

Inspection of residuals supported these patterns: Logistic and GSM left structureless residuals; Hill was well balanced in narrow transitions but biased in broader ones. Avrami and Kashchiev exhibited systematic under- and overestimation at early and late stages, respectively. Lysozyme showed major statistical improvement under LB, with reduced RMSE and AIC. Ribonuclease A showed similar gains, with higher R² and fewer systematic deviations, especially under Hill and GSM. Thaumatin was well fitted in both regimes (R² > 0.98); LB variability stemmed from noisy late-stage data, not poor model alignment. For Proteinase K, the lack of experimental data in the transition time region produced high R² and closely spaced AIC values across all models. For Proteinase K, statistical quality is weak under both HD and LB conditions, as reflected in low R² (0.33 and 0.70, respectively) and unstable AIC metrics. These limitations confirm that kinetic descriptors derived from such sparse data are unreliable and must be interpreted with caution. Supplementary Table S4 shows that Hill and GSM outperform it in specific cases, and these models were retained in

Table 2. Kinetic descriptors of protein crystallization under Hanging Drop and Langmuir–Blodgett conditions. Reported values are the half–time (t_1⁄2), the time of maximum rate (t_max), the width at half–maximum (W_1⁄2), and the peak growth rate (dX/dt)_max.

Protein	Model	t1/2 (days)	tmax (days)	W1/2 (days)	(dX/dt)max (μm/day)	Model	t1/2 (days)	tmax (days)	W1/2 (days)	(dX/dt)max (μm/day)
	Hanging Drop (HD)					Langmuir-Blodgett (LB)
Lysozyme	Hill	1.68	1.59	0.949	404	Hill	1.14	0.859	1.22	617
Thaumatin	Logistic	4.18	4.18	4.15	18.3	GSM	3.75	3.83	4.47	43.7
Ribonuclease A	Hill	0.937	0.315	1.09	40.8	Hill	0.809	0.414	0.992	52.2
Proteinase K	Logistic	0.545	0.545	0.13	381	Hill	0.542	0.498	0.366	177

when statistically justified. Figure 5, Figure 6 and Figure 7 show derivative profiles from each model, illustrating how transitions differ in timing, symmetry, and sharpness.

The values of t₀ obtained from GSM and Logistic model fits (Table 1) are overall consistent with the inflection points observed in the experimental X(t) curves (Figure 5, Figure 6 and Figure 7), confirming that the fitted parameters reliably capture the kinetics of maximal crystal growth rate. This internal consistency reinforces the physical interpretability of t₀ as the characteristic time of synchronized growth onset under each condition.

The onset time τ, defined as the point where X(t) begins to deviate from zero, generally aligns well between the fitted model and the experimental growth curves except in Ribonuclease A, where the agreement is less precise. This is likely due to the shallower initial slope and more gradual emergence of crystallization in this system. This may reflect either a slower nucleation process or increased variability in the early stages of growth, which may affect the accuracy of τ estimation.

4. Discussion: Interpretation of Kinetic Descriptors

4.1. Comparative Interpretation of Crystallization Profiles

Crystallization profiles across the four proteins can be interpreted through four macroscopic descriptors extracted from the X(t) growth curves—previously introduced in Section 2 and Section 3—that can be reorganized into four macroscopic features: (i) the onset window (e.g., t_1⁄2, t₀ , or τ), (ii) the mid-slope steepness (which reflects growth synchrony), (iii) the symmetry or skewness of the transition, and (iv) the final plateau, which represents the total crystal size. While these features are not tied to any specific model, they can be interpreted through fitted parameters such as the rate constant k, the shape exponent n, and the asymmetric factor m. Together, they provide a physical tool for interpreting the kinetic response under different crystallization regimes.

A first macroscopic contrast arises between HD and LB conditions [40]. In general, HD profiles tend to display broader onset windows and more gradual completions, features that are consistent with stochastic nucleation and asynchronous growth across the droplet. By contrast, LB templating systematically reduces the onset lag and sharpens the slope of the transition, suggesting that LB deposition may modulate nucleation pathways via altered interfacial conditions or cooperative feedback mechanisms. Notably, while timing and synchrony are affected, the plateau size remains largely protein-dependent and shows less sensitivity to the method of deposition.

Looking at individual proteins, Lysozyme under HD (Figure 1, left) exhibits a delayed onset and a smooth sigmoidal rise, saturating near 400 μm after approximately three days. Logistic and GSM models reproduce this shape well, capturing the inflection region and gradual completion. The Hill model sharpens the rise excessively, while Avrami and Kashchiev tend to underestimate early growth but align with the plateau. Under LB (Figure 1, right), the curve shifts leftward: onset occurs earlier, the slope steepens, and growth completes by day two. Here, Logistic and Hill perform best, while GSM captures subtle asymmetries beyond the inflection.

Thaumatin shows the clearest symmetric sigmoidal character under both HD and LB (Figure 2). Under HD, onset is delayed until day 2–3, and the growth reaches over 900 μm by day 6. Under LB, W_1⁄2 nearly halves while (dX/dt)_max rises, suggesting that LB not only synchronizes but also amplifies growth intensity. Logistic and GSM track the full curve with accurate fits, while Hill is slightly too steep. This makes Thaumatin a model case for synchronized, yet balanced, crystallization kinetics.

Ribonuclease A exhibits a weaker HD response (Figure 3, left), with slow growth spread across four days. Logistic and Avrami offer the best description here. Under LB (Figure 3, right), however, the growth is sharply compressed: the inflection and maximum rate occur much earlier, and the width W_1⁄2 narrows significantly. Hill and GSM perform best in capturing this synchronized burst. The Logistic model is adequate, but symmetric; Avrami and Kashchiev struggle with the early rise.

Proteinase K presents a different case. Both HD and LB conditions exhibit step-like transitions with limited temporal resolution, making descriptor estimation highly uncertain. The apparent growth synchrony may reflect genuine dynamics, but more likely arises from undersampling near the transition midpoint. Avrami and Kashchiev often yield extreme or non-physical descriptors, while Logistic and GSM produce more stable, albeit tentative, fits. Here, LB effects are difficult to quantify, and no robust mechanistic conclusion should be drawn from this profile.

Taken together, these results demonstrate that each model captures different features of the crystallization process: Logistic describes symmetric transitions reliably; GSM handles mild asymmetries; Hill excels in narrow, cooperative bursts; both Avrami and Kashchiev favor gradual onsets. Model selection should be driven by the morphology of X(t), not by a single mechanistic assumption.

4.2. Descriptor-Based Kinetic Analysis and Model Performance

The derivative profiles dX/dt provide a more direct window into crystallization kinetics, isolating the onset, growth synchrony, and duration of the transition. For each protein under HD and LB conditions, experimental rate markers are compared to analytical derivatives of the five fitted models. These rate profiles reveal how each system distributes growth over time, and how model shape parameters map onto real physical features such as nucleation delay, maximum rate (t_max), and transition width (W_1⁄2).

Figure 5, Figure 6 and Figure 7 show that LB templating consistently advances the onset of crystallization and sharpens the central burst. For Lysozyme and Thaumatin, HD profiles are smooth and bell-shaped, with Logistic and GSM offering balanced fits. Hill often exaggerates the central burst, producing artificially narrow W_1⁄2 values.

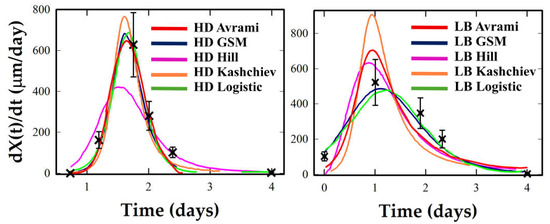
Figure 5. Crystallization rate profiles under HD and LB conditions for Lysozyme. Experimental rate estimates (black crosses) are compared with analytical derivatives from the five kinetic models (colored curves).

Figure 5. Crystallization rate profiles under HD and LB conditions for Lysozyme. Experimental rate estimates (black crosses) are compared with analytical derivatives from the five kinetic models (colored curves).

Figure 6. Crystallization rate profiles under HD and LB conditions for Thaumatin. Experimental rate estimates (black crosses) are compared with analytical derivatives from the five kinetic models (colored curves).

Figure 6. Crystallization rate profiles under HD and LB conditions for Thaumatin. Experimental rate estimates (black crosses) are compared with analytical derivatives from the five kinetic models (colored curves).

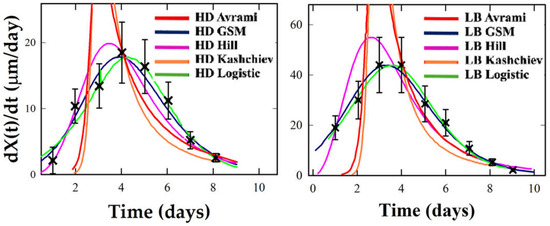
Figure 7. Crystallization rate profiles under HD and LB conditions for Ribonuclease A. Experimental rate estimates (black crosses) are compared with analytical derivatives from the five kinetic models (colored curves).

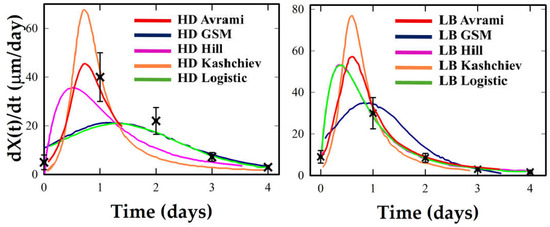
Figure 7. Crystallization rate profiles under HD and LB conditions for Ribonuclease A. Experimental rate estimates (black crosses) are compared with analytical derivatives from the five kinetic models (colored curves).

Avrami and Kashchiev tend to underestimate early growth and to overshoot at later stages. Under LB, the same systems show taller, earlier peaks and narrower W1⁄2, particularly in Lysozyme, where Logistic and Hill offer strong fits, and GSM captures the asymmetry. Thaumatin retains moderate symmetry under LB but shows a significant increase in peak rate. Hill captures this best, though GSM remains reliable. Proteinase K is again ambiguous: sparse data near the inflection preclude robust descriptor extraction. Logistic and GSM give stable but tentative fits, while Avrami and Kashchiev yield non-physical rates. Ribonuclease A offers the most intense transformation. Its LB profile exhibits an early, sharply concentrated rate peak, a classic marker of cooperative crystallization consistent with a strongly synchronized nucleation burst under LB templating. Here, Hill and GSM fit best, with Logistic underestimating peak sharpness.

Table 2 summarizes the four key descriptors extracted from each model: time of half-crystallization (t_1⁄2), time of maximum growth rate (t_max), maximum rate (dX/dt)_max, and width at half maximum (W_1⁄2). These quantities enable objective cross-comparisons. LB conditions consistently shift t_1⁄2 and t_max earlier, especially in Lysozyme and Ribonuclease A, while amplifying (dX/dt)_max and reducing W_1⁄2, i.e., growth is concentrated into a narrower, more synchronized window. For Thaumatin, LB also increases (dX/dt)_max but retains a moderate W_1⁄2, consistent with preserved symmetry. Proteinase K again shows minimal apparent change, but this likely reflects insufficient temporal resolution and unstable descriptors rather than a genuine absence of LB response. Model performance aligns with curve morphology. Logistic and GSM provide robust fits across most conditions, handling symmetry and mild asymmetry well. Hill performs best under synchronized conditions (low W_1⁄2, early t_max), such as LB–Ribonuclease A. Avrami and Kashchiev capture early lag and are useful when growth is gradual or sparse but tend to overemphasize early rise when data density is low.

Residual analysis supports these conclusions. Logistic and GSM yield unstructured residuals with low root–mean–square error (RMSE), while Hill may underfit the tail. Avrami and Kashchiev show systematic early–late mismatches, reflected in higher AIC scores. In proteins like Lysozyme and Thaumatin, LB conditions improve fit quality: RMSE drops and AIC decreases, indicating better model–data alignment. Ribonuclease A shows the clearest improvement: both R² and residual structure favor Hill and GSM under LB. Proteinase K again precludes strong statistical evaluation; its low data density inflates R² and undermines AIC, warning against interpretations, as already observed above.

Altogether, these descriptor trends show that LB templating does more than accelerate crystallization: it reorganizes timing and intensity, shifting growth into a focused cooperative burst.

This has interpretive value beyond fit quality: narrower W_1⁄2 and earlier t_max suggest tighter molecular synchrony, while higher (dX/dt)_max reveals amplified growth dynamics. The comparative effectiveness of models thus reflects not only mathematical convenience but their alignment with the physical regime of the crystallization process.

Table 2 presents a comparison of kinetic descriptors (t_1⁄2, t_max, W_1⁄2, and (dX/dt)_max) for each protein under HD and LB conditions. For each dataset, the model providing the best statistical fit—based on AIC and R²—was selected. Depending on the system, this corresponded to the Logistic, Hill, or GSM model, reflecting the absence of a universally optimal function. Each model emphasizes distinct kinetic features: Logistic provides symmetric fits suited to balanced growth, Hill captures cooperative and synchronized transitions, and GSM accommodates asymmetry. Including the best-fitting model in each case allows the descriptor set to highlight both general trends across crystallization conditions and protein-specific kinetic signatures. As noted previously, results for Proteinase K remain provisional.

4.3. Descriptor Ratios: Cross-System Mechanistic Signatures

To clarify the mechanistic implications of LB templating across systems, descriptor ratios between LB and HD conditions were computed using three kinetic metrics t_1⁄2, t_max and (dX/dt)_max. As shown in Table 2, LB generally compresses the crystallization timeline, but responses vary across proteins. In Lysozyme, both t_1⁄2 and t_max decrease from 1.77 to 1.20 days (ratio 0.68), while (dX/dt)_max decreases modestly (ratio 0.71). This does not indicate reduced growth capacity, but rather a symmetric acceleration in which onset and peak remain aligned (t_max ≈ t_1⁄2). Thaumatin shows a different pattern: t_1⁄2 shifts only slightly (ratio 0.92), yet (dX/dt)_max more than doubles (ratio 2.41), demonstrating that LB enhances cooperative throughput while preserving symmetry. Ribonuclease A undergoes the sharpest transformation: t_1⁄2 shortens (ratio 0.86), (dX/dt)max rises 2.6-fold, and t_max advances disproportionately (ratio 0.42). In this case, Logistic fits under-represent the sharpness of the transition, while Hill captures the strong cooperativity where t_max < t_1⁄2. This reflects synchronized, templating-induced nucleation. Proteinase K remains excluded from ratio analysis due to undersampled profiles, underscoring that such metrics require sufficient temporal coverage to be meaningful.

These ratio trends reveal meaningful differences in how LB templating reorganizes crystallization. Lysozyme experiences an early but moderate transformation, driven mainly by reduced lag. Thaumatin responds with enhanced cooperative rate while retaining symmetric growth. Ribonuclease A demonstrates a tightly synchronized burst with both temporal contraction and intensity amplification. These patterns illustrate a continuum of mechanistic responses to templating from uniform timing shifts to concentrated acceleration with advanced inflection.

Cross-model interpretation further reinforces this view. Logistic and GSM models reflect balanced or mildly asymmetric transitions where t_max ≈ t_1⁄2. In these cases, LB effects are seen as coherent shifts with modest changes in peak rate. Hill models reveal systems with pre-inflection acceleration (t_max < t_1⁄2) and amplified peaks, ideal for characterizing synchronized responses like that seen in LB–Ribonuclease A. Meanwhile, Avrami and Kashchiev, though less emphasized here, consistently predict earlier t_max and inflated peaks in Supplementary Table S3, acting as bounds for early-onset scenarios.

Altogether, descriptor ratios provide a powerful compact language for comparing protein crystallization behavior. They separate kinetic acceleration from synchrony enhancement and reveal distinct mechanistic classes of LB response.

4.4. Model Families, Descriptor Robustness, and Cross-System Interpretation

The five kinetic models used in this study fall into two functional families: mechanistic nucleation–growth models (Avrami, Kashchiev) and empirical sigmoid functions (Hill, Logistic, GSM). The mechanistic models are grounded in explicit assumptions about incubation times and growth dimensionality, while the empirical ones shape the kinetic profile—steepness, symmetry, and inflection—without invoking microscopic mechanisms. These structural distinctions affect how each model captures LB-induced acceleration.

Avrami and Kashchiev reflect barrier lowering through earlier values of τ or t₀, and by adjusting the exponent n to capture changes in dimensionality or nucleation dispersion. However, the Avrami form often requires shifting the onset to avoid artificially steep early growth, especially under LB conditions, but such onset shifts often yield unstable descriptors, with artificially inflated (dX/dt)_max values. For n < 1, the model can yield diverging derivatives immediately after τ, a mathematical artifact that distorts interpretation of (dX/dt)max and W_1/2. The Kashchiev model mitigates this by distributing nucleation over a finite interval, producing more stable descriptors when early growth is adequately sampled.

Sigmoidal models offer flexible and robust baselines. The Logistic model assumes symmetry, with t₀ at the inflection point and k governing slope. GSM introduces asymmetry via the exponent m, allowing skewed transitions while maintaining fit stability. The Hill function emphasizes cooperativity: increasing n sharpens the profile, capturing burst-like growth typical of synchronized nucleation in LB films.

Across the four proteins analyzed, both convergences and divergences are observed:

• Lysozyme: All models capture LB-induced shifts to earlier t_1/2 and t_max. Mechanistic fits produce higher peaks and narrower W_1/2 while sigmoid models yield smoother, broader transitions. This suggests LB promotes earlier onset with only moderate synchronization, consistent with a modest narrowing of W_1⁄2.
• Thaumatin: LB consistently increases growth rates and advances t_max, yet W_1/2 remains wide, but (dX/dt)_max rises strongly, indicating intensified but still temporally extended growth. This indicates acceleration without sharp temporal confinement, and model outputs agree closely.
• Ribonuclease A: Model choice influences interpretation most strongly. Logistic and Hill fits both show advanced onset and steeper slopes, with Hill notably indicating t_max < t_1/2, consistent with synchronized bursts. The Logistic model underestimates this burst, while Hill more faithfully captures the cooperative peak. Avrami and Kashchiev vary more in peak width but confirm accelerated crystallization.
• Proteinase K: Sparse data preclude reliable conclusions. Logistic and GSM yield interpretable trends; Avrami and Kashchiev produce unstable or nonphysical parameters (e.g., inflated peak rates, near-zero W_1/2). Hill over-concentrates the profile. Only shape-controlled models provide reliable fits.

As detailed in Supplementary Table S3, timing descriptors such as t_1/2 and t_max are relatively stable across model families. In contrast, synchrony (W_1/2) and growth intensity (dX/dt)_max) are model-dependent, especially under conditions of asymmetry or sparse sampling.

Two practical conclusions emerge. First, timing-related parameters, including τ, t₀, and empirical t_1/2, are the most transferable and robust. Second, model selection significantly impacts derived descriptors like synchrony and peak intensity. Logistic and GSM offer stable and conservative profiles; Hill detects cooperative amplification; Avrami and Kashchiev reflect barrier-driven onset shifts.

Overall, the data support our central conclusion: LB templating lowers the nucleation barrier and narrows the cooperative window. The manifestation of this effect, however, varies by protein and by model. Divergences between models do not indicate inconsistency, but rather reflect complementary emphases: shape versus mechanism, symmetry versus asymmetry, continuity versus discreteness. When early and mid-growth phases are well sampled, models converge on core kinetic features. Where sampling is sparse, as in Proteinase K, model disagreement highlights which descriptors remain unconstrained, guiding where experimental refinement is most needed.

4.5. Model Discrimination via AIC Analysis

While model performance and mechanistic behavior have been discussed individually for each protein and condition in Section 3.1, Section 3.2, Section 3.3, Section 3.4 and Section 3.5, a broader statistical comparison provides additional perspective on model suitability. Supplementary Table S4 summarizes the Akaike Information Criterion (AIC), ΔAIC, and residual variance for all fits, offering an objective basis for comparing models across systems and crystallization regimes.

In several LB-assisted conditions, particularly for Lysozyme and Ribonuclease A, models such as Hill and GSM consistently achieve the lowest AIC values, reflecting their capacity to capture rapid, cooperative, or asymmetric growth profiles. For instance, in Ribonuclease A–LB, Hill outperforms all other models by a ΔAIC of >4.8 relative to Logistic and >6.0 relative to GSM, despite its lower parameter count. This result reinforces observations made earlier about the highly synchronized character of LB-induced nucleation in this system. For Thaumatin under LB, GSM provides the lowest AIC, consistent with its ability to capture symmetric yet intensified transitions. Conversely, in conditions where the transition is broader or asymmetric (e.g., Proteinase K–HD), Logistic and GSM perform better, while classical nucleation–growth models (Avrami and Kashchiev) consistently show higher AIC and are statistically disfavored.

These findings support the notion that model selection reflects not only statistical fit quality but also mechanistic alignment with the dominant kinetic regime—whether spontaneous, heterogeneous, cooperative, or templated—and highlights the importance of considering both data quality and physical plausibility when comparing models.

5. Conclusions

This work introduces a comparative, descriptor–based framework that translates heterogeneous crystallization curves into a unified set of kinetic metrics, expressed in physical units and applicable to multiple proteins and experimental setups. This approach translates complex crystallization profiles into directly comparable measures of timing, synchrony, and intensity, providing a transferable basis for cross–protein and cross–condition analysis. When described in physical terms, descriptors can be applied across proteins and models, while LB/HD ratios offer a concise method for assessing templating effects without specifying a particular mechanistic approach.

Across Lysozyme, Thaumatin, and Ribonuclease A, LB consistently compresses the time scale and advances the time of maximum growth rate. Yet, the amplitude response was protein–dependent: Lysozyme showed a coherent left-shift with modestly reduced peak intensity; Thaumatin combined modest acceleration with a twofold increase in throughput; Ribonuclease A exhibited the strongest synchronization, with T_max pulled well before T_1⁄2 and peak growth rates more than doubled. These three outcomes define distinct regimes of templating action: consistent shift, balanced enhancement, and synchronized sharpening. Proteinase K was included deliberately as a counterexample: its incomplete sampling of the inflection and mid-slope region prevents reliable descriptor extraction, illustrating how limited coverage makes descriptors unstable, making them model-driven rather than data-constrained, and therefore unreliable for mechanistic interpretation. This case highlights that a key experimental priority is to ensure indispensable dense sampling in the transition window.

Reliable descriptors require (i) dense sampling across the inflection, (ii) at least one early anchor point before visible growth, and (iii) systematic reporting of descriptors alongside raw X(t) curves as standard practice. Descriptor ratios also serve as internal consistency checks: in balanced transitions, t_max should remain close to t_1⁄2, while genuine synchrony is indicated only when experimental data clearly support narrower, earlier rises.

In summary, LB templating consistently accelerates crystallization but redistributes growth rates in protein–specific ways. The descriptor framework provides a quantitative basis for capturing such differences, supports meaningful cross-system comparison, and highlights experimental priorities. Applying this approach, especially through improved temporal resolution in the critical transition region, will allow templating effects to be exploited more effectively and extend kinetic analysis to new proteins and interfacial conditions.