Ferroaxial Property Under Hybrid Skyrmion Crystals
Abstract
1. Introduction
2. Model
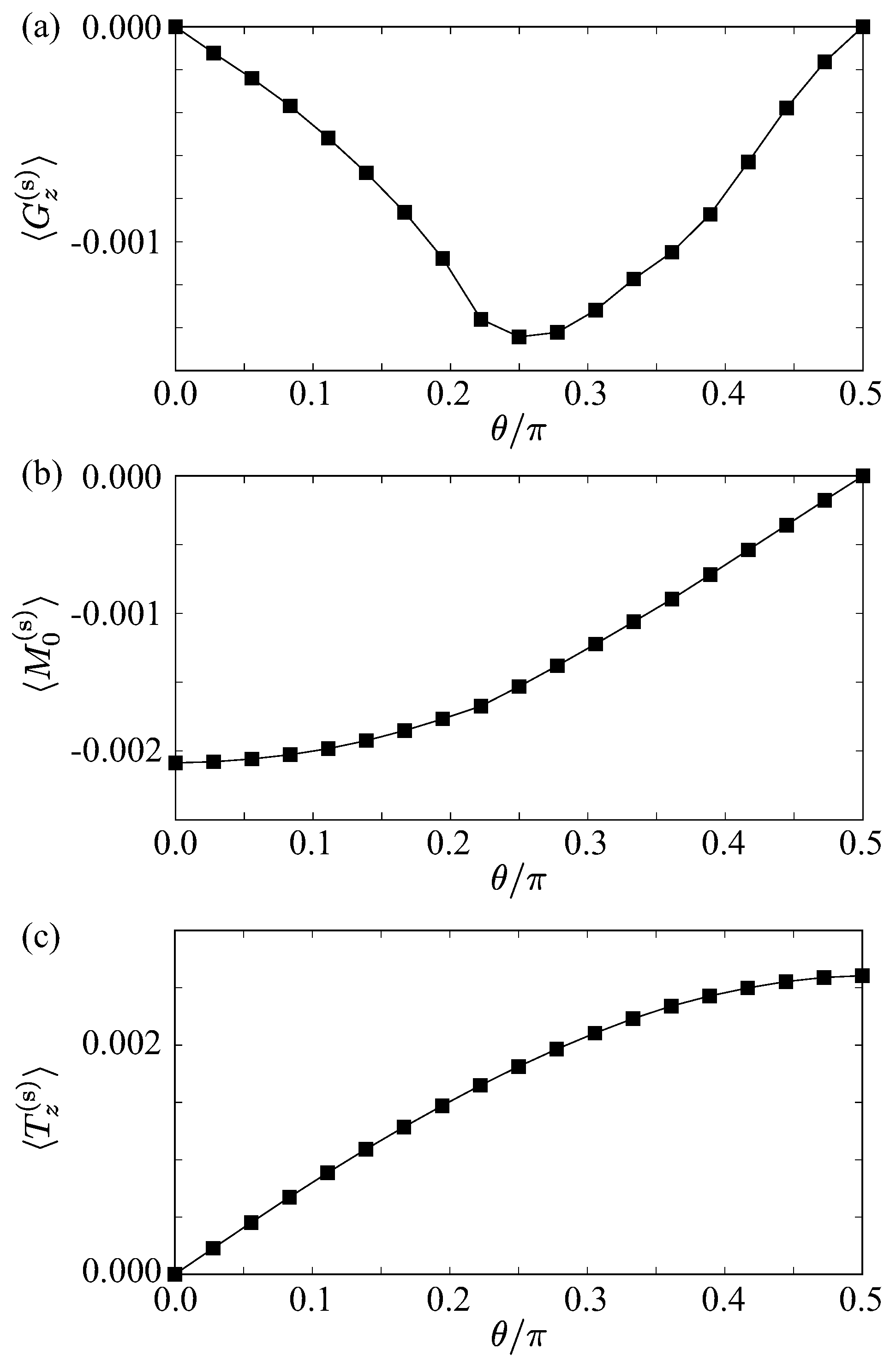
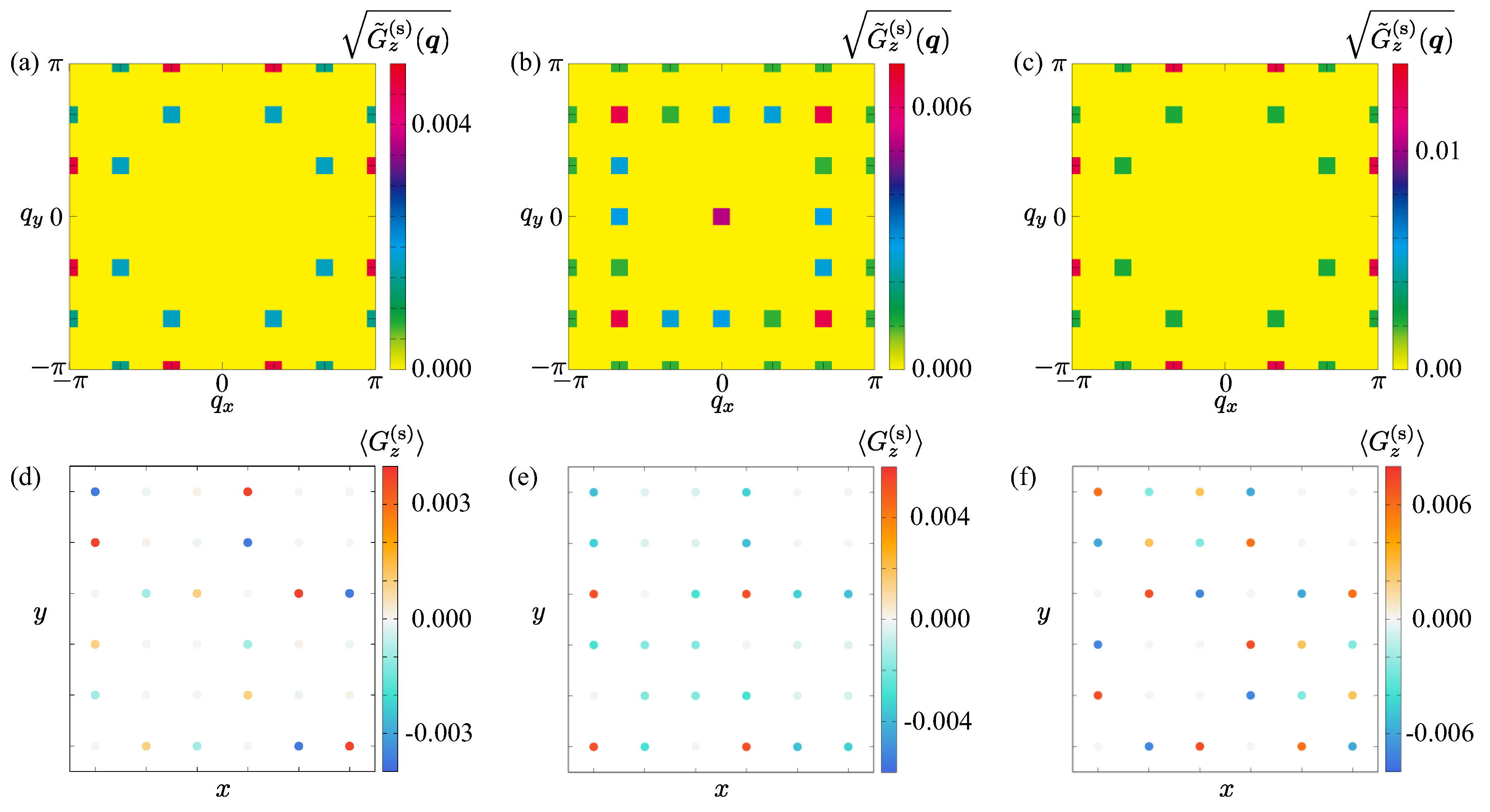
3. Ferroaxiality Under Skyrmion Spin Textures
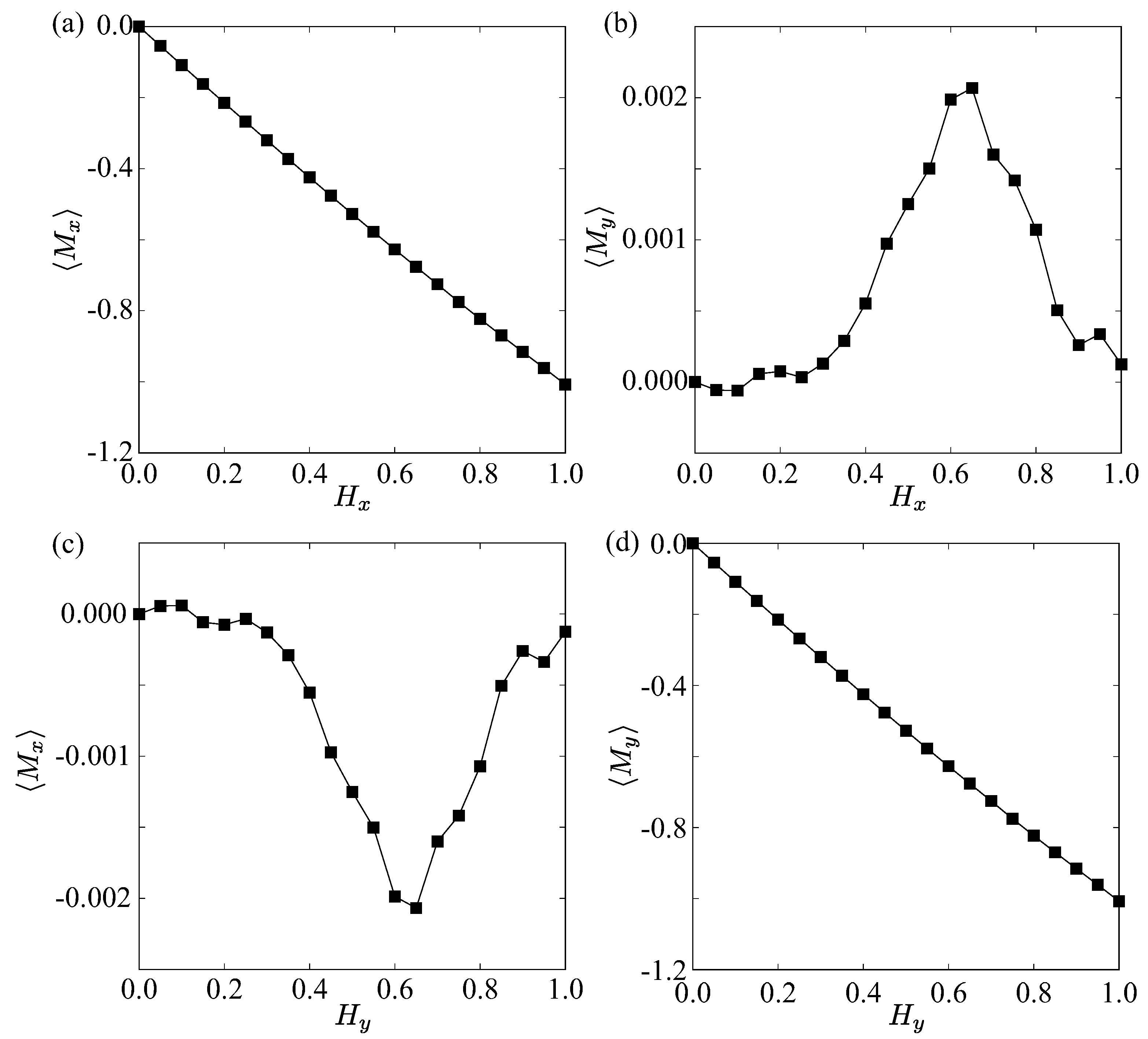
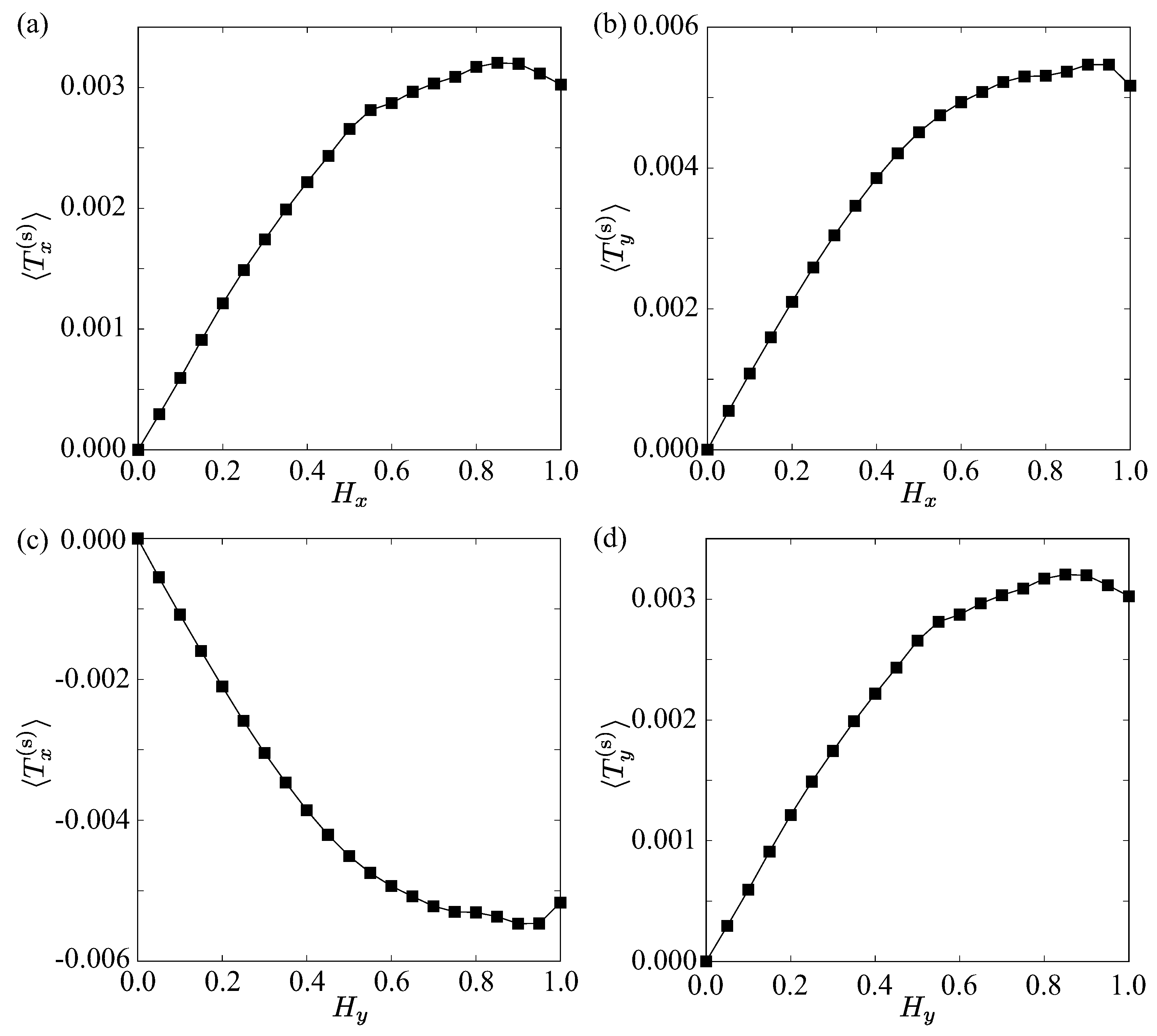
4. Transverse Responses Under an External Magnetic Field
5. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dubovik, V.; Cheshkov, A. Multipole expansion in classical and quantum field theory and radiation. Sov. J. Part. Nucl. 1975, 5, 318–337. [Google Scholar]
- Dubovik, V.; Tugushev, V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 1990, 187, 145–202. [Google Scholar] [CrossRef]
- Gorbatsevich, A.; Kopaev, Y.V. Toroidal order in crystals. Ferroelectrics 1994, 161, 321–334. [Google Scholar] [CrossRef]
- Kuramoto, Y.; Kusunose, H.; Kiss, A. Multipole orders and fluctuations in strongly correlated electron systems. J. Phys. Soc. Jpn. 2009, 78, 072001. [Google Scholar] [CrossRef]
- Santini, P.; Carretta, S.; Amoretti, G.; Caciuffo, R.; Magnani, N.; Lander, G.H. Multipolar interactions in f-electron systems: The paradigm of actinide dioxides. Rev. Mod. Phys. 2009, 81, 807–863. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Ikeda, H.; Oppeneer, P.M. First-principles theory of magnetic multipoles in condensed matter systems. J. Phys. Soc. Jpn. 2018, 87, 041008. [Google Scholar] [CrossRef]
- Kusunose, H.; Hayami, S. Generalization of microscopic multipoles and cross-correlated phenomena by their orderings. J. Phys. Condens. Matter 2022, 34, 464002. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Gao, Y.; Vanderbilt, D.; Xiao, D. Microscopic theory of spin toroidization in periodic crystals. Phys. Rev. B 2018, 97, 134423. [Google Scholar] [CrossRef]
- Shitade, A.; Watanabe, H.; Yanase, Y. Theory of orbital magnetic quadrupole moment and magnetoelectric susceptibility. Phys. Rev. B 2018, 98, 020407(R). [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, D. Orbital magnetic quadrupole moment and nonlinear anomalous thermoelectric transport. Phys. Rev. B 2018, 98, 060402(R). [Google Scholar] [CrossRef]
- Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
- Popov, Y.F.; Kadomtseva, A.; Belov, D.; Vorob’ev, G.; Zvezdin, A. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. J. Exp. Theor. Phys. Lett. 1999, 69, 330–335. [Google Scholar] [CrossRef]
- Schmid, H. On ferrotoroidics and electrotoroidic, magnetotoroidic and piezotoroidic effects. Ferroelectrics 2001, 252, 41–50. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 2007, 76, 214404. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Thöle, F.; Spaldin, N.A. Magnetoelectric multipoles in metals. Philos. Trans. R. Soc. A 2018, 376, 20170450. [Google Scholar] [CrossRef]
- Saito, H.; Uenishi, K.; Miura, N.; Tabata, C.; Hidaka, H.; Yanagisawa, T.; Amitsuka, H. Evidence of a New Current-Induced Magnetoelectric Effect in a Toroidal Magnetic Ordered State of UNi4B. J. Phys. Soc. Jpn. 2018, 87, 033702. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4 (A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in PT-symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Hlinka, J. Eight Types of Symmetrically Distinct Vectorlike Physical Quantities. Phys. Rev. Lett. 2014, 113, 165502. [Google Scholar] [CrossRef] [PubMed]
- Hlinka, J.; Privratska, J.; Ondrejkovic, P.; Janovec, V. Symmetry Guide to Ferroaxial Transitions. Phys. Rev. Lett. 2016, 116, 177602. [Google Scholar] [CrossRef]
- Jin, W.; Drueke, E.; Li, S.; Admasu, A.; Owen, R.; Day, M.; Sun, K.; Cheong, S.W.; Zhao, L. Observation of a ferro-rotational order coupled with second-order nonlinear optical fields. Nat. Phys. 2020, 16, 42–46. [Google Scholar] [CrossRef]
- Cheong, S.W.; Lim, S.; Du, K.; Huang, F.T. Permutable SOS (symmetry operational similarity). npj Quantum Mater. 2021, 6, 58. [Google Scholar] [CrossRef]
- Cheong, S.W.; Huang, F.T.; Kim, M. Linking emergent phenomena and broken symmetries through one-dimensional objects and their dot/cross products. Rep. Prog. Phys. 2022, 85, 124501. [Google Scholar] [CrossRef]
- Hayami, S.; Oiwa, R.; Kusunose, H. Electric Ferro-Axial Moment as Nanometric Rotator and Source of Longitudinal Spin Current. J. Phys. Soc. Jpn. 2022, 91, 113702. [Google Scholar] [CrossRef]
- Nasu, J.; Hayami, S. Antisymmetric thermopolarization by electric toroidicity. Phys. Rev. B 2022, 105, 245125. [Google Scholar] [CrossRef]
- Roy, A.; Guimarães, M.H.D.; Sławińska, J. Unconventional spin Hall effects in nonmagnetic solids. Phys. Rev. Mater. 2022, 6, 045004. [Google Scholar] [CrossRef]
- Inda, A.; Hayami, S. Nonlinear Transverse Magnetic Susceptibility under Electric Toroidal Dipole Ordering. J. Phys. Soc. Jpn. 2023, 92, 043701. [Google Scholar] [CrossRef]
- Johnson, R.D.; Nair, S.; Chapon, L.C.; Bombardi, A.; Vecchini, C.; Prabhakaran, D.; Boothroyd, A.T.; Radaelli, P.G. Cu3Nb2O8: A Multiferroic with Chiral Coupling to the Crystal Structure. Phys. Rev. Lett. 2011, 107, 137205. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.D.; Chapon, L.C.; Khalyavin, D.D.; Manuel, P.; Radaelli, P.G.; Martin, C. Giant Improper Ferroelectricity in the Ferroaxial Magnet CaMn7O12. Phys. Rev. Lett. 2012, 108, 067201. [Google Scholar] [CrossRef]
- Hayashida, T.; Uemura, Y.; Kimura, K.; Matsuoka, S.; Hagihala, M.; Hirose, S.; Morioka, H.; Hasegawa, T.; Kimura, T. Phase transition and domain formation in ferroaxial crystals. Phys. Rev. Mater. 2021, 5, 124409. [Google Scholar] [CrossRef]
- Hayashida, T.; Uemura, Y.; Kimura, K.; Matsuoka, S.; Morikawa, D.; Hirose, S.; Tsuda, K.; Hasegawa, T.; Kimura, T. Visualization of ferroaxial domains in an order-disorder type ferroaxial crystal. Nat. Commun. 2020, 11, 4582. [Google Scholar] [CrossRef] [PubMed]
- Yokota, H.; Hayashida, T.; Kitahara, D.; Kimura, T. Three-dimensional imaging of ferroaxial domains using circularly polarized second harmonic generation microscopy. npj Quantum Mater. 2022, 7, 106. [Google Scholar] [CrossRef]
- Bhowal, S.; Spaldin, N.A. Electric toroidal dipole order and hidden spin polarization in ferroaxial materials. Phys. Rev. Res. 2024, 6, 043141. [Google Scholar] [CrossRef]
- Hasegawa, T.; Yoshida, W.; Nakamura, K.; Ogita, N.; Matsuhira, K. Raman Scattering Investigation of Structural Transition in Ca5Ir3O12. J. Phys. Soc. Jpn. 2020, 89, 054602. [Google Scholar] [CrossRef]
- Hanate, H.; Hasegawa, T.; Hayami, S.; Tsutsui, S.; Kawano, S.; Matsuhira, K. First Observation of Superlattice Reflections in the Hidden Order at 105 K of Spin–Orbit Coupled Iridium Oxide Ca5Ir3O12. J. Phys. Soc. Jpn. 2021, 90, 063702. [Google Scholar] [CrossRef]
- Hayami, S.; Tsutsui, S.; Hanate, H.; Nagasawa, N.; Yoda, Y.; Matsuhira, K. Cluster Toroidal Multipoles Formed by Electric-Quadrupole and Magnetic-Octupole Trimers: A Possible Scenario for Hidden Orders in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 033702. [Google Scholar] [CrossRef]
- Hanate, H.; Tsutsui, S.; Yajima, T.; Nakao, H.; Sagayama, H.; Hasegawa, T.; Matsuhira, K. Space-Group Determination of Superlattice Structure Due to Electric Toroidal Ordering in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 063601. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.T.; Admasu, A.S.; Kratochvílová, M.; Chu, M.W.; Park, J.G.; Cheong, S.W. Multiple ferroic orders and toroidal magnetoelectricity in the chiral magnet BaCoSiO4. Phys. Rev. B 2022, 105, 184407. [Google Scholar] [CrossRef]
- Yamagishi, S.; Hayashida, T.; Misawa, R.; Kimura, K.; Hagihala, M.; Murata, T.; Hirose, S.; Kimura, T. Ferroaxial Transitions in Glaserite-type Compounds: Database Screening, Phonon Calculations, and Experimental Verification. Chem. Mater. 2023, 35, 747–754. [Google Scholar] [CrossRef]
- Nagai, T.; Kimura, T. Chemical Switching of Ferroaxial and Nonferroaxial Structures Based on Second-Order Jahn–Teller Activity in (Na,K)2Hf(BO3)2. Chem. Mater. 2023, 35, 4109–4115. [Google Scholar] [CrossRef]
- Nagai, T.; Mochizuki, Y.; Yoshida, S.; Kimura, T. Chemical Aspect of Displacive-Type Ferroaxial Phase Transition from Perspective of Second-Order Jahn–Teller Effect: NASICON Systems as an Example. J. Am. Chem. Soc. 2023, 145, 8090–8098. [Google Scholar] [CrossRef]
- Kajita, Y.; Nagai, T.; Yamagishi, S.; Kimura, K.; Hagihala, M.; Kimura, T. Ferroaxial transitions in glaserite-type Na2BaM(PO4)2 (M = Mg, Mn, Co, and Ni). Chem. Mater. 2024, 36, 7451–7458. [Google Scholar] [CrossRef]
- Sekine, D.; Sato, T.; Tokunaga, Y.; Arima, T.h.; Matsubara, M. Second harmonic imaging of antiferromagnetic domains and confirmation of absence of ferroaxial twins in MnTiO3. Phys. Rev. Mater. 2024, 8, 064406. [Google Scholar] [CrossRef]
- Martinez, V.A.; Gao, Y.; Yang, J.; Lyzwa, F.; Liu, Z.; Won, C.J.; Du, K.; Kiryukhin, V.; Cheong, S.W.; Sirenko, A.A. Ferroaxial phonons in chiral and polar NiCo2TeO6. Phys. Rev. B 2025, 112, 064411. [Google Scholar] [CrossRef]
- Alekseev, S.; Ghorashi, S.A.A.; Fernandes, R.M.; Cano, J. Charge density waves with nontrivial orbital textures in rare earth tritellurides. Phys. Rev. B 2024, 110, 205103. [Google Scholar] [CrossRef]
- Hayami, S. Ferroaxial moment induced by vortex spin texture. Phys. Rev. B 2022, 106, 144402. [Google Scholar] [CrossRef]
- Zener, C. Interaction between the d-Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Anderson, P.W.; Hasegawa, H. Considerations on double exchange. Phys. Rev. 1955, 100, 675. [Google Scholar] [CrossRef]
- Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge Studies in Magnetism Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Adams, T.; Chacon, A.; Wagner, M.; Bauer, A.; Brandl, G.; Pedersen, B.; Berger, H.; Lemmens, P.; Pfleiderer, C. Long-Wavelength Helimagnetic Order and Skyrmion Lattice Phase in Cu2OSeO3. Phys. Rev. Lett. 2012, 108, 237204. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857. [Google Scholar] [CrossRef]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.M.; White, J.S.; Rønnow, H.M.; Dewhurst, C.D.; Mochizuki, M.; Yanai, K.; et al. Neel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef] [PubMed]
- Bordács, S.; Butykai, A.; Szigeti, B.G.; White, J.S.; Cubitt, R.; Leonov, A.O.; Widmann, S.; Ehlers, D.; von Nidda, H.A.K.; Tsurkan, V.; et al. Equilibrium skyrmion lattice ground state in a polar easy-plane magnet. Sci. Rep. 2017, 7, 7584. [Google Scholar] [CrossRef] [PubMed]
- Fujima, Y.; Abe, N.; Tokunaga, Y.; Arima, T. Thermodynamically stable skyrmion lattice at low temperatures in a bulk crystal of lacunar spinel GaV4Se8. Phys. Rev. B 2017, 95, 180410. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Ukleev, V.; Feoktystov, A.; Arima, T.h.; Kakurai, K.; Tokura, Y. Néel-Type Skyrmion Lattice in the Tetragonal Polar Magnet VOSe2O5. Phys. Rev. Lett. 2017, 119, 237201. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I. Theory of helicoidal structures in antiferromagnets. I. Nonmetals. Sov. Phys. JETP 1964, 19, 960–971. [Google Scholar]
- Kataoka, M.; Nakanishi, O. Helical spin density wave due to antisymmetric exchange interaction. J. Phys. Soc. Jpn. 1981, 50, 3888–3896. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Tokunaga, Y.; Yu, X.; White, J.; Rønnow, H.M.; Morikawa, D.; Taguchi, Y.; Tokura, Y. A new class of chiral materials hosting magnetic skyrmions beyond room temperature. Nat. Commun. 2015, 6, 7638. [Google Scholar] [CrossRef]
- Karube, K.; White, J.; Reynolds, N.; Gavilano, J.; Oike, H.; Kikkawa, A.; Kagawa, F.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; et al. Robust metastable skyrmions and their triangular–square lattice structural transition in a high-temperature chiral magnet. Nat. Mater. 2016, 15, 1237. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Morikawa, D.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Yu, X.; Tokunaga, Y.; Arima, T.h.; Rønnow, H.M.; et al. Disordered skyrmion phase stabilized by magnetic frustration in a chiral magnet. Sci. Adv. 2018, 4, eaar7043. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Ukleev, V.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; Taguchi, Y. Metastable skyrmion lattices governed by magnetic disorder and anisotropy in β-Mn-type chiral magnets. Phys. Rev. B 2020, 102, 064408. [Google Scholar] [CrossRef]
- Henderson, M.E.; Bleuel, M.; Beare, J.; Cory, D.G.; Heacock, B.; Huber, M.G.; Luke, G.M.; Pula, M.; Sarenac, D.; Sharma, S.; et al. Skyrmion alignment and pinning effects in the disordered multiphase skyrmion material Co8Zn8Mn4. Phys. Rev. B 2022, 106, 094435. [Google Scholar] [CrossRef]
- Chacon, A.; Heinen, L.; Halder, M.; Bauer, A.; Simeth, W.; Mühlbauer, S.; Berger, H.; Garst, M.; Rosch, A.; Pfleiderer, C. Observation of two independent skyrmion phases in a chiral magnetic material. Nat. Phys. 2018, 14, 936–941. [Google Scholar] [CrossRef]
- Takagi, R.; Yamasaki, Y.; Yokouchi, T.; Ukleev, V.; Yokoyama, Y.; Nakao, H.; Arima, T.; Tokura, Y.; Seki, S. Particle-size dependent structural transformation of skyrmion lattice. Nat. Commun. 2020, 11, 5685. [Google Scholar] [CrossRef] [PubMed]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Hayami, S.; Gao, S.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Takagi, R.; Motome, Y.; Tokura, Y.; et al. Zoology of Multiple-Q Spin Textures in a Centrosymmetric Tetragonal Magnet with Itinerant Electrons. Adv. Sci. 2022, 9, 2105452. [Google Scholar] [CrossRef]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef]
- Yoshimochi, H.; Takagi, R.; Ju, J.; Khanh, N.; Saito, H.; Sagayama, H.; Nakao, H.; Itoh, S.; Tokura, Y.; Arima, T.; et al. Multistep topological transitions among meron and skyrmion crystals in a centrosymmetric magnet. Nat. Phys. 2024, 20, 1001. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Utesov, O.I. Thermodynamically stable skyrmion lattice in a tetragonal frustrated antiferromagnet with dipolar interaction. Phys. Rev. B 2021, 103, 064414. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Degeneracy Lifting of Néel, Bloch, and Anti-Skyrmion Crystals in Centrosymmetric Tetragonal Systems. J. Phys. Soc. Jpn. 2020, 89, 103702. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Helicity locking of a square skyrmion crystal in a centrosymmetric lattice system without vertical mirror symmetry. Phys. Rev. B 2022, 105, 104428. [Google Scholar] [CrossRef]
- Legrand, W.; Chauleau, J.Y.; Maccariello, D.; Reyren, N.; Collin, S.; Bouzehouane, K.; Jaouen, N.; Cros, V.; Fert, A. Hybrid chiral domain walls and skyrmions in magnetic multilayers. Sci. Adv. 2018, 4, eaat0415. [Google Scholar] [CrossRef]
- Li, W.; Bykova, I.; Zhang, S.; Yu, G.; Tomasello, R.; Carpentieri, M.; Liu, Y.; Guang, Y.; Gräfe, J.; Weigand, M.; et al. Anatomy of skyrmionic textures in magnetic multilayers. Adv. Mater. 2019, 31, 1807683. [Google Scholar] [CrossRef]
- Liyanage, W.L.N.C.; Tang, N.; Quigley, L.; Borchers, J.A.; Grutter, A.J.; Maranville, B.B.; Sinha, S.K.; Reyren, N.; Montoya, S.A.; Fullerton, E.E.; et al. Three-dimensional structure of hybrid magnetic skyrmions determined by neutron scattering. Phys. Rev. B 2023, 107, 184412. [Google Scholar] [CrossRef]
- Singh, D.; Fujishiro, Y.; Hayami, S.; Moody, S.H.; Nomoto, T.; Baral, P.R.; Ukleev, V.; Cubitt, R.; Steinke, N.J.; Gawryluk, D.J.; et al. Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet. Nat. Commun. 2023, 14, 8050. [Google Scholar] [CrossRef]
- Matsumura, T.; Kurauchi, K.; Tsukagoshi, M.; Higa, N.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Helicity Unification by Triangular Skyrmion Lattice Formation in the Noncentrosymmetric Tetragonal Magnet EuNiGe3. J. Phys. Soc. Jpn. 2024, 93, 074705. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef]
- Kim, K.W.; Moon, K.W.; Kerber, N.; Nothhelfer, J.; Everschor-Sitte, K. Asymmetric skyrmion Hall effect in systems with a hybrid Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2018, 97, 224427. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Complete Multipole Basis Set for Single-Centered Electron Systems. J. Phys. Soc. Jpn. 2020, 89, 104704. [Google Scholar] [CrossRef]
- Inda, A.; Hayami, S. Emergent cross-product-type spin-orbit coupling under ferroaxial ordering. Phys. Rev. B 2025, 111, L041104. [Google Scholar] [CrossRef]
- Bhowal, S.; Spaldin, N.A. Magnetoelectric Classification of Skyrmions. Phys. Rev. Lett. 2022, 128, 227204. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Sawada, K.; Nagaosa, N. Optical Magnetoelectric Effect in Multiferroic Materials: Evidence for a Lorentz Force Acting on a Ray of Light. Phys. Rev. Lett. 2005, 95, 237402. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, H.; Tatara, G. Effective Hamiltonian theory for nonreciprocal light propagation in magnetic Rashba conductor. Phys. Rev. B 2016, 94, 235148. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Nonlinear electric transport in odd-parity magnetic multipole systems: Application to Mn-based compounds. Phys. Rev. Res. 2020, 2, 043081. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Ullah, A.; Li, X.; Jin, Y.; Pahari, R.; Yue, L.; Xu, X.; Balasubramanian, B.; Sellmyer, D.J.; Skomski, R. Topological phase transitions and Berry-phase hysteresis in exchange-coupled nanomagnets. Phys. Rev. B 2022, 106, 134430. [Google Scholar] [CrossRef]
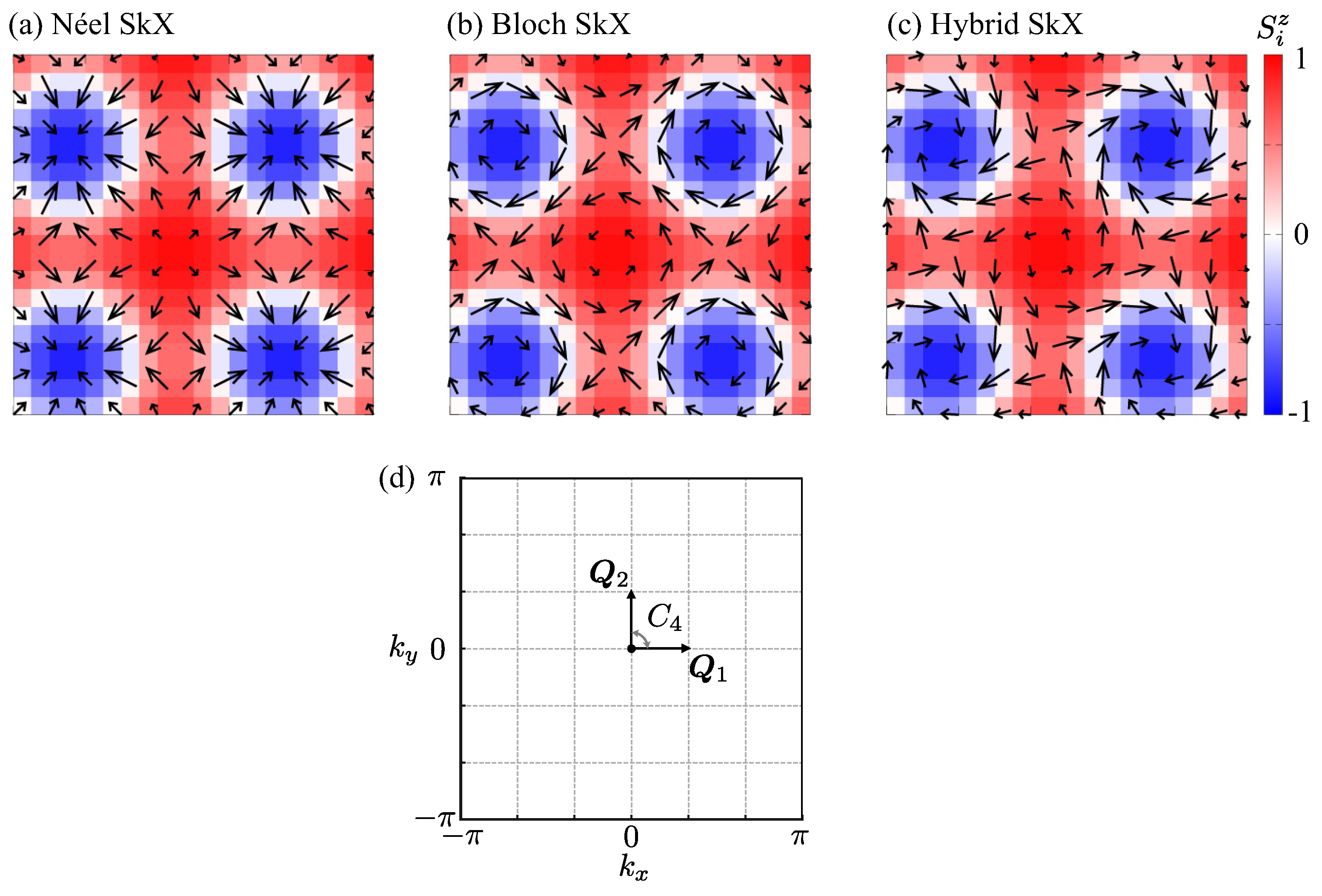
| SkX | MPG | Allowed Multipoles | Forbidden Multipoles | Irrep. |
|---|---|---|---|---|
| Néel-type | , | , | ||
| Bloch-type | , | , | ||
| Hybrid-type | 4 | , , | – | , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Ferroaxial Property Under Hybrid Skyrmion Crystals. Crystals 2025, 15, 831. https://doi.org/10.3390/cryst15100831
Hayami S. Ferroaxial Property Under Hybrid Skyrmion Crystals. Crystals. 2025; 15(10):831. https://doi.org/10.3390/cryst15100831
Chicago/Turabian StyleHayami, Satoru. 2025. "Ferroaxial Property Under Hybrid Skyrmion Crystals" Crystals 15, no. 10: 831. https://doi.org/10.3390/cryst15100831
APA StyleHayami, S. (2025). Ferroaxial Property Under Hybrid Skyrmion Crystals. Crystals, 15(10), 831. https://doi.org/10.3390/cryst15100831






