Abstract
The superconductivity of CaC6 as a function of pressure and Ca isotopic composition was revisited using DFT calculations on a 2c–double hexagonal superlattice. The introduction of superlattices was motivated by previous synchrotron absorption and Raman spectroscopy results on other superconductors that showed evidence of superlattice vibrations at low (THz) frequencies. For CaC6, superlattices have previously been invoked to explain the ARPES data. A superlattice along the hexagonal c-axis direction is also illustrative of atomic orbital symmetry and periodicity, including bonding and antibonding s-orbital character implied by cosine-modulated electronic bands. Inspection of the cosine band revealed that the cosine function has a small (meV) energy difference between the bonding and antibonding regions, relative to a midpoint non-bonding energy. Fermi surface nesting was apparent in an appropriately folded Fermi surface using a superlattice construct. Nesting relationships identified phonon vectors for the conservation of energy and for phase coherency between coupled electrons at opposite sides of the Fermi surface. A detailed analysis of this Fermi surface nesting provided accurate estimates of the superconducting gaps for CaC6 with the change in applied pressure. The recognition of superlattices within a rhombohedral or hexagonal representation provides consistent mechanistic insight on superconductivity and electron−phonon coupling in CaC6.
Keywords:
superconductivity; CaC6; Fermi surface; Fermi level; superlattice; tight binding; cosine; band structure 1. Introduction
Superlattices, quantum wells, and other related nanoscale heterostructures have played, and continue to play, important roles in technological applications, such as resonant tunnelling devices and lasers [1,2,3]. Many familiar superlattices are layered, nanoscale periodic structures of two materials, resulting in compositional and/or lattice spacing modulations that are perpendicular to the layers. Modulations and new periodicities introduced to artificial superlattices can also be engineered to advantageously modify electronic properties and material behavior [1,2,3]. More recent styles of superlattices, such as Moiré-like [4,5,6,7,8] and ordered arrays of nanocrystals [9,10,11], have also been experimentally fabricated and/or used conceptually to explain the observed electronic phenomena [12].
Superlattice concepts are used to explain the phenomena closely related to superconducting materials, particularly the tuning of properties in the proximity of electronic topological transitions (ETTs) and Feshbach resonances as a function of pressure and strain, as well as the appearance of Van Hove singularities [13,14]. In addition, superlattices have been used to model striped structures, experimentally observed in superconductors at both nano [15] and atomic [16] scales. The effects of modulated strain on superconducting materials, both from the intrinsic crystal structure of the complex metal oxide [3] or artificially created to mimic those strain modulations [17], are also linked to superlattice observations and models.
Experimental observations of superlattice vibration modes in synchrotron THz absorption spectroscopy [18] and Raman spectroscopy [19] on MgB2 compounds, characterized by vibration modes of low frequency, have provided complementary numerical and mechanistic insights on the superconductivity of MgB2. These low-frequency modes are substantially below the lowest absorption frequency predicted for the conventional P6/mmm symmetry ascribed to MgB2 based on atomic positions [18,20]. The recognition of a superlattice in MgB2 enabled the identification of bonding and antibonding regions, and the role of Fermi surface (FS) nesting and phase relationships that were not otherwise apparent [18,21].
For CaC6, Yang et al. [12] introduced Ca-folded Brillouin zones to explain the ARPES measurements of the Fermi surface maps and the observations of π* pockets near Γ (see Figure 1 of reference [12]). These triangular π* pockets are attributed to a Ca superlattice [12] and denote the existence of a superconducting gap that is distinct from the carbon interlayer superconducting gap in CaC6. This detailed ARPES study clarified that both the interlayer and the π* bands contribute to superconductivity in CaC6 [12] and that a superlattice construct offers an effective means to understand superconductivity mechanisms. Other ARPES studies on CaC6 [22,23] are addressed below.
For layer-structured superconductors, cosine-shaped electronic bands (EBs) are important indicators of conduction mechanisms. These cosine bands resemble tight-binding descriptors for the EBs of the semiconductors [21,24,25,26]. However, for many superconductors, the bonding (lower energy) and antibonding (higher energy) regions of the cosine amplitudes are marginally asymmetric. For CaC6, cosine-shaped bands were identified as free-electron-like interlayer states, with a substantial Ca-4s orbital character with a contribution to superconductivity and gap appearance [12,27,28,29,30,31,32].
Theoretical double-cell superlattice constructs for DFT calculations split the energy (and/or phase), and explicitly, the bonding and antibonding regions of these cosine bands [18,21,33]. As discussed below, a double superlattice construct, combined with the use of reduced symmetry, provides a useful approximation for the orbital character of crystal symmetry and includes informative site symmetry detail [34].
We evaluated the asymmetry of cosine EBs for CaC6 using DFT calculations with a high grid resolution and demonstrated a direct correlation with the superconducting gap at different pressures. The CaC6 superconductor [35,36] is a hexagonal layered compound with a lower axial symmetry than MgB2. This compound can be described in either hexagonal or rhombohedral lattices [35]. We utilized both types of lattice in this paper to demonstrate the equivalence of the results and to highlight the specific features. In addition, we considered the importance of phonon dispersions and the critical role played by acoustic phonons in superconductivity.
2. Materials and Methods
We conducted comprehensive DFT analyses on EB Structures (EBSs) and FSs for CaC6 within a pressure range from 0 GPa to 16 GPa using Quantum ESPRESSO (QE) Version QE-7.3 [37] and Materials Studio CASTEP 2023 [38] for the comparison. Details of these analyses are given in an article published separately [39]. The crystal structures were visualized using Crystal Maker V11.0.2 using geometry-optimized cell parameters of the experimentally determined values [35].
Key parameters, such as plane wave cut-off energies, pseudopotentials, and k-point grids, are critical enablers of meV resolution for EBS and phonon dispersion (PD) calculations, as noted in earlier publications [20,40]. Using QE, we employed a cut-off energy of 120 Ry (=1632.68 eV), a k-point grid of 24 × 24 × 24 sampling density, ultrasoft pseudopotentials [41], and a generalized gradient approximation (GGA) [42,43] for the exchange–correlation functional. We also explored norm-conserving pseudopotentials within the LDA and GGA approximations using CASTEP with a cut-off energy of 990 eV and Δk-grid 0.005 Å−1 for the additional comparisons.
The DFT calculations considered both the primitive rhombohedral unit cell and the hexagonal counterpart. The specific lattice constants were taken from the X-ray diffraction results of bulk CaC6 [35]. We have also explored several superlattice variants, acknowledging their significance in accurately portraying the symmetry and phases of the orbitals [21]. Further evaluation of the essential parameters that enable the systematic detailed interpretation of the DFT calculations are provided in our earlier work [40,44]. For consistency, we show calculation outputs using the LDA functional, although equivalent calculations using the GGA functional show similar trends.
Constructing a supercell is a routine procedure for the DFT calculations of the electronic properties, although the context can differ substantially. For example, a supercell can be a “multiple of the smallest unit cell” or “a unit cell of a superlattice” structure. We initially built a supercell as a multiple of the smallest unit cell, and then we imposed reduced symmetry that contained symmetry elements of the parent space group, as shown in earlier work [19,45].
In a dynamic environment, we may also consider the other forms of a superlattice. For example, an elastic acoustic wave imposed on an initially symmetric, homogeneous structure [9,46,47]. In this case, at a particular instant of time, there will be a modulated expansion and contraction of the sub-units (e.g., the original smallest units) of a superlattice. According to the elastic theory, the structure will show a modulation of the lattice constants with a wavelength given by the acoustic wavelength. A positional modulation of the atoms will create a superlattice.
The smallest superlattice that can be created using elastic waves is a double-unit supercell, where one cell is contracted, and the other adjacent cell is expanded. In general, a cosine-shaped band in an EBS, particularly in superconductors, can be associated with nearly free electrons [27]. Such a band corresponds to a cosine wavefunction; that is, the real part of a plane wave or complex exponential. Thus, the electron density in that cosine band is modulated as the square of the cosine function and is periodically modulated as a superlattice structure.
3. Results and Discussion
In our earlier work on MgB2, we showed that atomic orbital symmetry provides added detailed mechanistic understanding of superconductivity [21] compared with the atomic position symmetry of the space group P6/mmm. We utilized a similar strategy for the DFT calculations on CaC6 by first identifying key bands–particularly along an equivalent real space layer direction–that demonstrate a cosine format across or near the Fermi level. We developed an argument for the construction of a double supercell, starting with a band that approximates a cosine function. Using a double cell for the DFT calculations, several features related to the superconductivity of CaC6 were derived in a fashion consistent with that previously described for MgB2 [18,21].
3.1. Cosine Functions and Linear Chains of Atoms
There is strong agreement that cosine-shaped bands in the EBS of CaC6, as shown in Supplemental Figure S1, show nearly-free Ca 4s orbital character [27]. The cosine function for the EB has argument ckz, implying that planes separated by the lattice parameter c are out of phase [48]. This phase relationship in the c-direction is identical to that encountered in discussions on chain(s) of atoms with s-orbitals [49,50], as exemplified by a chain of H-atoms or H ‘n-merization’ [33]. A schematic of this important phase relationship and change from predominantly bonding to predominantly antibonding states is shown in Figure 1.
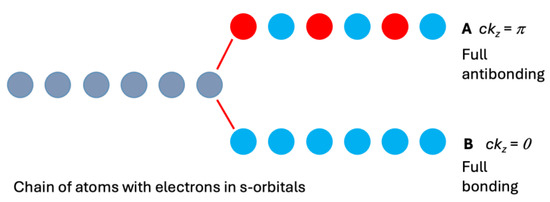
Figure 1.
Schematic of a chain of atoms with s-orbitals (e.g., a chain of H-atoms) in the bonding (bottom of a cosine band) and anti-bonding (top of a cosine band) orbital configurations. Grey circles represent the combined orbital designations.
For a group symmetry to appropriately represent the periodicity implied by an antibonding orbital arrangement, a reduced symmetry with a double supercell in the c-direction must be used [18,21]. In this case, reduced symmetry is a better representation of a compound for which the orbital character of electrons and likely effects on atomic positions are considered. This representation is analogous to that shown for MgB2 [18,21], noting that for the c and ab-directions at Γ, the bands showed opposite bonding/antibonding character (see e.g., Figure 1 of reference [21]). In contrast, for CaC6, in both the c and ab-directions at Γ, the bands showed the same bonding character. This band characteristic is reasonable for s-orbitals with local spherical symmetry; thus, the same orbital character was maintained in the entire set of spherical directions.
3.2. Electronic Band Structures for Superlattices
We calculated the EBS for three types of CaC6 unit cells of Space Group 166 (R-3m) at a pressure of 0 GPa: (i) a rhombohedral lattice, (ii) an equivalent hexagonal lattice of the same Space Group 166, and (iii) an equivalent hexagonal lattice with a double c-axis, 2c. In the reciprocal space, a key visualization format for the EBS and Brillouin zones, doubling a real-space dimension (e.g., a unit cell dimension, c, increased to 2c) can be effected by folding along the appropriate reciprocal direction [36]. For the hexagonal lattice of Space Group R-3m, the Γ–Z direction is along c*. Hence, the focus of this work was along the Γ–Z directions in reciprocal space. The calculated EBSs for the conventional reciprocal directions for each CaC6 format are provided in Figures S1–S3 in the Supplementary File. The key c* directions that contain cosine-shaped band(s) are identified in Figures S1–S3.
3.3. Antibonding-Bonding Asymmetry
Careful inspection of the shape for the interlayer cosine band of CaC6 using a rhombohedral structure (Space Group 166 or R-3m) indicated that the cosine function was not perfectly symmetrical (see Figure 2a and Figure S1). We delineated this asymmetry as previously discussed in our evaluation of cosine sigma bands for MgB2 [21]. The asymmetry of a cosine band suggests that adjustments to the tight-binding equations are appropriate in order to describe the EB along the c* direction [21], as shown below.
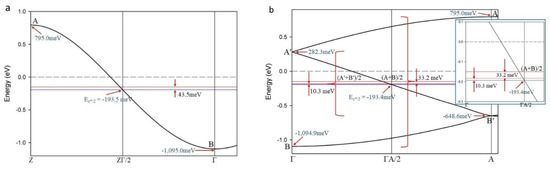
Figure 2.
Electronic band structures of CaC6 at 0 GPa (Space Group R-3m) calculated for: (a) rhombohedral symmetry and (b) equivalent hexagonal symmetry. The cosine-shaped interlayer band along the c* direction crosses the Fermi level (dotted horizontal line) in both cases. In (a), the energy, Ec*/2, is –193.5 meV and the average energy, Eav, between the antibonding (A) and bonding (B) nodes of the cosine band is –150.0 meV. This energy difference, ΔE, reflects the marginal asymmetry of the cosine band. In (b), the same cosine band is folded in the hexagonal configuration and results in the two bonding (B, B′) and two antibonding (A, A′) nodes of the cosine band. Similarly, Eav and E′av show different energy values to Ec*/2 with a net ΔE of 43.5 meV (at higher magnification in the inset). EBS plots showing conventional reciprocal directions and the location of the cosine band are provided in Supplemental Figures S1–S3.
An asymmetry, or difference in energy, ΔE, is schematically shown for CaC6 at 0 GPa calculated with a rhombohedral lattice in Figure 2a. The bonding and anti-bonding nodes, denoted “B” and “A”, respectively, of the cosine band along Γ–Z are shown in Figure 2a. The energy, Ec*/2, at the intersection of the cosine band with the reciprocal mid-point, ΓZ/2, is −193.5 meV. The average energy, Eav, between the bonding (B) and antibonding (A) nodes at Γ and at Z, respectively, was 43.5 meV higher than Ec*/2 (i.e., at −150.0 meV) and is denoted by a red horizontal line. This difference in energy, ΔE, represents the asymmetry of the cosine band for this rhombohedral lattice. A perfectly symmetric cosine band will show zero difference in energy between Ec*/2 and Eav (i.e., for the equivalent bonding and antibonding regions). In the following sections, we describe how a superconducting gap can be determined from this antibonding–bonding energy asymmetry.
Figure 2b shows the band structure along the c* direction for a hexagonal lattice equivalent to the rhombohedral configuration shown in Figure 2a. In this case, there was a folding of the c* direction because the a and b directions are multiples of the C-C bonds in CaC6. This folding resulted in two distinct bonding and antibonding nodes in the band structure, as identified in Figure 2b. The energy at the intersection of the A′–B′ band at ΓA/2 was Ec*/2 and is denoted by a blue horizontal line in Figure 2b. For the hexagonal case, we determined Eav for both A–B and A′–B′, as shown by the red horizontal lines in Figure 2b. The asymmetries, or ΔE’ and ΔE, were 10.3 meV and 43.5 meV (ΔE = 10.3 + 33.2 meV), respectively, relative to the energy at Ec*/2.
Figure 3 shows the band structure along the c* direction for CaC6 at 0 GPa and at 7.5 GPa with a hexagonal 2c superlattice. For 2c superlattice symmetry, the Brillouin zone boundary line of the unfolded reciprocal space folded onto the Γ-direction. In an ideal structure, the bonding and antibonding bands will adopt a symmetric appearance relative to the mid-point energy (i.e., with the symmetry axis at a constant energy, Ec*/2), as shown by the blue horizontal line in Figure 3a (inset).
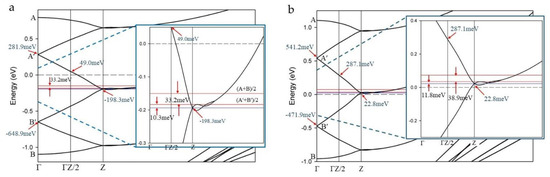
Figure 3.
Electronic band structures of CaC6 (Space Group R-3m) calculated for a 2c hexagonal lattice: (a) at 0 GPa and (b) at 7.5 GPa. In both cases, the folded cosine-shaped interlayer band along the c* direction crosses the Fermi level (dotted horizontal line). In (a) the energy, Ec*/2, is –198.5 meV and is at the intersection on Z where the two branches of the cosine curve from A′ and B′ meet. The net energy difference, ΔE, is 43.5 meV. This energy difference, ΔE, reflects the marginal asymmetry of the cosine band for a 2c superlattice at 0 GPa. The calculation for CaC6 at 7.5 GPa, shows a shift of the folded bands along c* towards higher energy, with Ec*/2 above the Fermi level at 22.8 meV. In addition, the net ΔE value is 50.7 meV, an increase of 7.2 meV compared with 0 GPa.
In Figure 3a, Ec*/2 is now at the intersection on Z, where the two branches of the cosine curve from A′ and B′ meet (i.e., blue line clearly shown in the inset). The energy for Ec*/2 was at a nominally lower energy (~5 meV) compared with Ec*/2 for the hexagonal cell, shown in Figure 2b. Again, measuring the values for Eav and E′av, as shown in Figure 3a, the difference in energy for ΔE’ and ΔE was 10.3 meV and 43.5 meV (= 10.3 + 33.2 meV), respectively (inset, Figure 3a; red lines relative to the blue line).
A similar configuration for the folded cosine band of a 2c superlattice at 7.5 GPa is shown in Figure 3b. In this case, the folded band along c* is at a higher energy compared with the calculations at 0 GPa, consistent with the experimental data showing a higher Tc at 7.5 GPa [38]. Similar trends were observed for the DFT calculations of hexagonal 2c superlattices at other pressures (Supplemental Figure S4).
3.4. Revised Tight-Binding Equations
To accommodate the condition for CaC6, we proposed the following adjustments to the tight-binding equations of the form shown in Equations (1) and (2):
The highest asymmetry offset at Γ is given by the equation:
where ETB Gap@Γ is a tight-binding gap. Asymmetry values or tight-binding gaps vary with respect to the choice of unit cell symmetry or the type of supercell. However, the values are interrelated by the symmetry relationships between the hexagonal and rhombohedral lattice systems.
The dependence of Eav as function of kz, Eav(kz) is shown in Figure 4. Eav(kz) has a cosine dependence itself, with half the reciprocal space period of that of the cosine-shaped band (=½ × 2π/c = 2π/2c), and for a bonding–antibonding format of the Eav(kz) cosine, we halve this reciprocal distance (=2π/4c). That is, in real space, the periodicity is double that of the bonding–antibonding folded periodicity (=2 × 2c = 4c). A 4c superlattice periodicity has previously been identified for MgB2 [18,21,51]. This result suggests that the origin of this super-periodicity also relates to electronic behavior, as represented by the EBS.
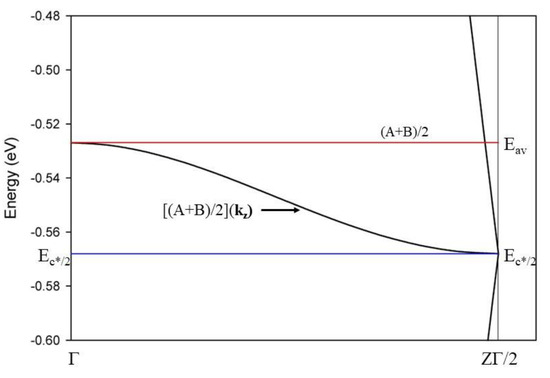
Figure 4.
Enlarged view of the electronic band structure for CaC6 at 0 GPa calculated for rhombohedral symmetry and folded at the midpoint ΓZ/2. The average energy Eav = ½(A + B) at Γ is plotted as the red line. Eav = ½(A + B) as a function of kz is plotted as the dark continuous line between Eav and Ec*/2 (blue line) with a cosine shape and a full period of π/c.
Figure S4 (Supplemental) shows the band structure calculations for two other pressures, at 4 GPa and 12 GPa, to delineate the trends in this modelling approach. We show in Figure 3 that at a pressure of 7.5 GPa, the non-bonding-point Ec*/2, is near the Fermi level (at 22.8 meV). The position of the bonding to antibonding crossing at this pressure corresponds to the highest experimentally determined Tc for CaC6 as shown in Figure 5 (extracted and adapted from ref. [52]). The drop in Tc at about 8 GPa can be correlated to an electronic topological transition of the superlattice FS and is discussed in a separate publication. As shown in Figure S4, the cosine band crosses the Fermi level with different proportions of bonding and antibonding character, depending on the external pressure. This relative shift in the bonding–antibonding character is also consistent with the changes in Tc observed with pressure.
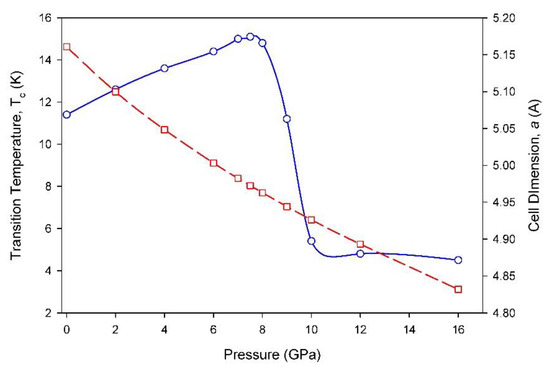
Figure 5.
Graph of the experimentally determined superconducting transition temperature (blue circles) for CaC6 as function of pressure (re-plotted and adapted from reference [52]). The rhombohedral cell dimension, a, as function of pressure is also plotted as red squares (right-hand axis).
As discussed in detail below, to determine the superconducting gap, the tight-binding gap ETB Gap@Γ (the highest asymmetry offset) must be corrected by a factor determined by the fraction of the Fermi surface that participates in unencumbered, or non-interfering, nesting between the open loops. If other Fermi surface bands cross the nested region, or the Fermi surface curvature deviates substantially, a different nesting vector is required. In such a case, additional phonons of different energy/frequency must become involved for the conservation of energy and momentum. In this case, coupling between electrons at opposite sides of the Fermi surface, requiring additional phonons, translates into the equivalent of scattering events.
3.5. Superlattice Nesting Vectors and Key Phonon Wavevectors
Figure 6 shows the schematics of the rhombohedral and hexagonal representations of CaC6. The rhombohedral and hexagonal reciprocal unit cells of CaC6 are related by the following equations:
ΓZR = 3ΓAH
ΓZR = π/c
c = 13.572 Å
(a1* + a2* + a3*)/3 = π/c
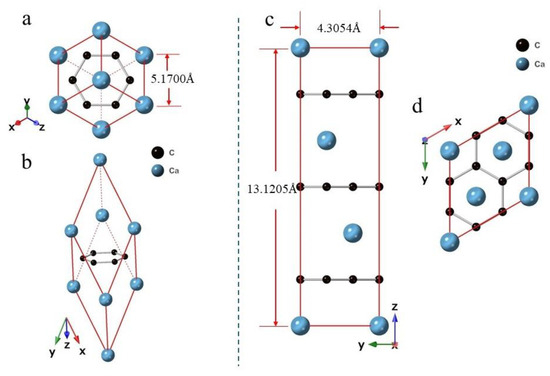
Figure 6.
Schematics of the CaC6 crystal structure, represented using: (a,b) rhombohedral and (c,d) hexagonal symmetry. (a) Shows a view of the rhombohedral cell along the [111]-direction and (b) a view along c*; (c) shows a view of the hexagonal cell along [100] and (d) shows a view along [001].
Thus, twice the ΓAH distance of the reciprocal hexagonal unit cell (2π/3c), and half of the reciprocal distance (π/3c = 2π/6c), correspond to the distances between the Brillouin zone (BZ) boundaries or between Γ and the BZ boundary for the 2c-real space hexagonal superlattice. For Fermi surface features, this real space superlattice corresponds to a repeat distance of a folded hexagonal supercell in reciprocal space.
This reciprocal space vector and the related dimensional relationships to the primitive rhombohedral cell are particularly useful for understanding the crystallographic relationships in the CaC6 structure. For example, the reciprocal space vector is itself a ‘nesting’ vector in the perpendicular c or c*-direction for the Fermi surfaces of the CaC6 2c superlattice, as shown in Figure 7a. This nesting vector joins significant proportions of the folded Fermi surfaces and can be considered a vertical component of diagonal nesting vectors [21].
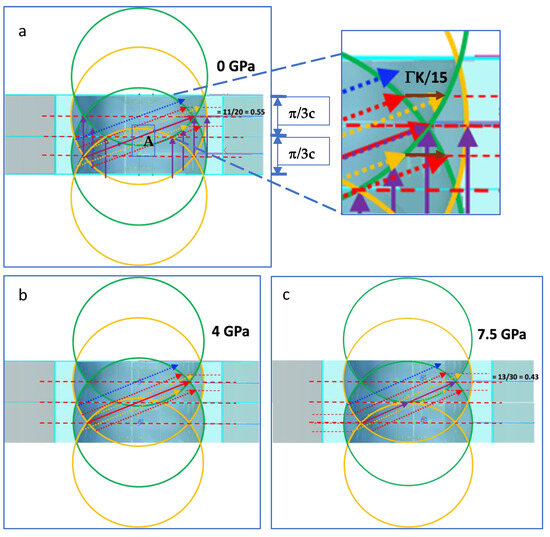
Figure 7.
Cross-sectional views of the Ca-4s Fermi surfaces for CaC6, calculated for 2c hexagonal supercells at pressures: (a) 0 GPa, with detailed view of the Fermi surface crossing point (inset), (b) 4 GPa, and (c) 7.5 GPa. Two of the first Brillouin zone sections along the c* reciprocal direction are displayed. The contours for the Fermi surfaces are green- and orange-colored lines. Nesting vectors of identical length that join opposite sides of the Fermi surface, parallel to the vector that crosses the center point or origin (A), are shown by red, orange, and purple arrows. Blue lines represent vectors that do not connect Fermi surface regions. See text for further details.
The extent of the diagonal nesting vectors is clear in MgB2 [21], which has a cosine-shaped Fermi surface profile. For MgB2, nesting using parallel reciprocal vectors of identical magnitude spanned the entire warped tubular Fermi surfaces of MgB2 [21]. The same condition cannot be said for CaC6.
In CaC6, the approximately circular profiles of the Fermi surface cross-sections significantly reduced the extent of nesting, although the nesting conditions did not require existence over the entire Fermi surface [48]. Consequently, for CaC6, the nesting extent was difficult to determine accurately with comparable error or uncertainty to that followed for MgB2 [21]. Another source of error was the thermal energy width (~kBT) that occurred around the Fermi surface at temperatures above absolute zero. The width of this thermal energy nominally extended the region by ~1.4 meV at 16 K, where nesting by the same original phonon vector was maintained.
Figure 7 shows cross-sections of the Ca-4s-dominated Fermi surfaces for CaC6 at selected pressures. In Figure 7, the green- and orange-colored circles delineate the contours of the Fermi surfaces, as well as indicating a change in phase introduced by folding on the alternating (approximate) spherical Fermi surfaces. Note that the changes in phase between the bonding and antibonding regions for the same Fermi surfaces exist as indicated by the phase of the cosine functions themselves, where the plane perpendicular to ΓZ at the mid-point Z/2 defines the transition boundary between the bonding and antibonding behaviors (see Supplementary Figure S5). Therefore, the folded Fermi surfaces require careful identification of phase variation, which may be complex and/or convoluted and so, is difficult to track and represent graphically.
In Figure 7, the blue lines that are parallel to the nesting vectors and of the same magnitude do not connect the Fermi surface regions. Thus, the extent of nesting is limited to a window around the ‘crossing’ of the Fermi surfaces (joined by the red and purple lines that cross the center of the double-stacked Brillouin zones). The brown arrows (circled) in the inset of Figure 7a correspond to the maximum electron momentum transfer between the y and z directions (~ΓK/15), which are coherently accommodated through nesting by a phonon of appropriate frequency for energy conservation.
At 0 GPa, both the red and orange vectors produced a nesting relationship that crossed the Γ point center at the midpoint. The diagonal nesting relationships had vectors qD and qd (in Figure 7a, D and d stand for long and short diagonals, respectively, where qD = 3qd) with projections approximately given by:
qD = 2ΓK/3 ± ΓAH = 2ΓK/3 ± (π/3c) kz
qd = qD/3 = 2ΓK/9 ± ΓAH/3 = 2ΓK/9 ± (π/9c) kz
The nesting vectors connected open loops with kF and −kF at opposite sides through the origin. Thus, these nesting vectors connected the bonding and antibonding branches of the relevant band, and are associated with Cooper pairing [21]. In this case, the nesting vector corresponded to the primary phonon in electron–phonon coupling through the relationships:
−kF1 + qD,d = kF1′
−kF2 − qD,d = kF2′
At 7.5 GPa, the diagonal nesting relationships had vectors qD and qd (in Figure 7c, where qD = 2qd) with projections approximately given by:
qD = 4ΓK/11 ± ΓAH = 4ΓK/11 ± (π/3c) kz
qd = qD/2 = 2ΓK/11 ± ΓAH/2 = 2ΓK/11 ± (π/6c) kz
Coherent Electron–Phonon Coupling via Acoustic Nesting
As schematically shown in Figure 7a–c, the nesting between mid-points in different Brillouin zones established favorable reference points for an electron–phonon coupling condition between the opposite sides of the Fermi surface. These points are non-bonding and establish a reference for the phase relationships. However, the coherence of the electrons coupled by this same nesting phonon vector only survives without disturbance while an intersection with any new Fermi surface associated with a different band of unrelated symmetry is absent. Coherent coupling is also lost when the curvature of the Fermi surfaces change, such that a nesting vector of fixed magnitude does not link electron states on the opposite sides of the Fermi surface. For CaC6, examples of this loss of connectivity by nesting vectors on opposite sides of the Fermi surface are shown as blue (dotted) arrows in Figure 7a–c.
Figure 7 also enables the identification of two general types of nesting. These two types are:
Closed loops alone do not appear to be conducive to superconductivity but may be indirectly involved in superconducting behavior. However, for this CaC6 system, open loops were continuously connected in the extended Brillouin zone scheme. Thus, the open loops correlated with superconductivity through the magnitude of the nesting vectors and the extent of the nested regions. In Figure 7a, the purple-colored vectors are parallel to the red and orange arrows but are shorter in length. By comparing these vectors at pressures of 0 GPa and 7.5 GPa, we identified other features, including the densities of states. In Figure 7a,c, the purple-colored vectors are approximately one third and one half of the red nesting vectors, respectively. This relationship suggests that the shorter purple vectors are nesting vectors themselves, and given their multiplicity, they are indicators of the relative population of the densities of states.
The proportions of a Fermi surface that participates, and remains, with a given acoustic nesting vector, define a proportion of the cosine amplitude that remains coherently coupled. This fraction, multiplied by the above-mentioned tight-binding gap, ETB Gap@Γ, provides an accurate estimate of the superconducting gap (provided DFT calculations are carried out with sufficient resolution [40]).
The superconducting TB gap value at 0 GPa is the ETB Gap@Γ value at Γ divided by three, because of the three parallel nesting vectors that fit between the nested Fermi surface spheres, multiplied by the fraction of the folded z*-axis that is nested, which is ~0.55 (see Figure 7a). The superconducting TB gap value at 7.5 GPa is the value at Γ divided by two, because there are two parallel nesting vectors that fit between the nested Fermi surface spheres, multiplied by the fraction of the folded z*-axis that is nested, which is ~0.43 (see Figure 7c).
The superconducting TB gap value at 4 GPa was obtained by linearly extrapolating the number of parallel nesting vectors that fit between the nested Fermi surface spheres, multiplied by the linear extrapolation of the fraction of the folded z*-axis that is nested. These extrapolations resulted in 3.21 + (5.49 − 3.21) × (4/7.5) = 4.43, 0.55 − (0.55 − 0.43) × (4/7.5) = 0.486, and 4.43 × 0.486 = 2.15 for (i) the parallel nesting vectors, (ii) the fraction of the z*-axis that can be nested, and (iii) the superconducting TB gap, respectively (see Table 1). We estimate the error in determining the superconducting TB gap at ±0.09 meV. The values of the calculated gaps for the other pressures are given in Table 1.

Table 1.
Geometry optimized cell parameters for CaC6 at selected pressures; other parameters extracted from calculated EBS.
If we include the additional periodicity identified in Section 3.2 from the cosine dependence of the average of the bonding and antibonding energies, we obtain a 4c superlattice symmetry. This superlattice symmetry introduces an extra folding in the reciprocal space at π/4c. This additional folding more accurately reflects the dynamic symmetry of the structure, compared to calculations without additional folding. We suggest that calculations in which the full z*-axis participates in nesting are more likely to effectively represent coherent superconducting transport behavior. In addition, this additional folding brings the non-bonding, cosine inflection points to Γ. This condition is, intuitively, an appropriate locus for electron phonon coupling, which initiates the exchange of sound velocity between the y- and z-directions, as the electrons travel the cosine bands or the corresponding Fermi surface.
The highest Tc was obtained when the Fermi level and the non-bonding energy of the cosine-shaped band coincide. This represents the most balanced distribution between the fully occupied bonding states and the fully unoccupied antibonding states. This configuration suggests that the optimal conditions for superconductivity occur when the smallest energy is needed for the excitation of electrons in the filled bonding states into the empty antibonding states, and that this energy, translated for interactions between quasiparticles, corresponds to the superconducting gap.
3.6. Phonon Frequencies and the Superconducting Gap Energy
This section focuses on the 0 GPa case with a similar extension to the DFT calculations for CaC6 under higher-pressure conditions. The difference in the phonon vectors for conserved momentum transfers in the y- and z-directions of the nested regions were approximately ΓK/15 and 3ΓK/10 (=(9/2) ΓK/15), and ΓAH and ΓAH/3, respectively, as shown in the inset of Figure 7a.
Figure 8 shows an expanded view of the phonon dispersion (PD) for 40CaC6, calculated using the LDA functional and k-grid Δk = 0.015 Å−1, with the CASTEP Materials Studio 2023 software. A PD for CaC6 with the Ca isotope 44 is also provided in the Supplemental section (Figure S6).
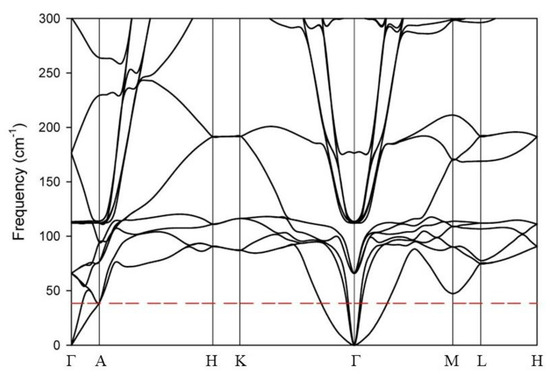
Figure 8.
Phonon dispersion (PD) for CaC6 calculated with a hexagonal unit cell using DFT with the LDA functional and k-grid 0.015 Å–1. The red dotted line is a constant frequency (or energy) reference at 39.6 cm–1. The intersections of the red dotted line with the branches of the PD occurred approximately at all the vectors identified using nesting and coherent conservation of momentum.
Figure 8 shows that all the phonon vectors associated with nesting (ΓK/15, 3ΓK/10, ΓAH, and ΓAH/3) had values on the acoustic PD branches with a similar energy at 39.6 cm−1 (i.e., 4.91 meV). These acoustic energies (or multiples of energy depending on degeneracy or multiplicity) accompanying the nested momentum transfers must be exchanged (absorbed or provided) in an electron–phonon coupling, for the coupled electron movement along the nested regions on either side of the Fermi surface to conserve energy and remain coherent [21].
These calculations of PDs for CaC6 using the hexagonal unit cell shown in Figure 6c,d are consistent with the calculated PDs for CaC6 using the rhombohedral cell by Calandra and Mauri [29]. The latter gave the values of frequency for the equivalent of ~ ΓM/15 and ΓK/15 that closely matched half the energy of the asymmetry in the cosine function (i.e., the tight-binding gap) at Γ, as listed in Table 1 for the LDA (i.e., 10.3/2 meV = 5.15 meV; although, depending on the pseudopotential, values as low as 9.8/2 = 4.9 meV were obtained). In Figure 8, the frequency of 39.6 cm−1 was ~4.91 meV (=3 × 1.63 meV), or approximately three times the superconducting gap energy [52,53] at 0 GPa. Thus, we showed that there is a clear geometrical origin for the phonons engaged in the conservation of energy, with electrons coupled via these nesting relationships.
The rhombohedral calculations by Calandra and Mauri [29] also showed that:
or, alternatively, from our hexagonal calculations:
ωL(ΓZ/6) = ωT(ΓZ/2) ≈ ωT(ΓT/2)
ωL(ΓA/3) = ωT(ΓA) ≈ ωT, L(ΓK/15) = ωT(3ΓK/10)
These equivalences suggest that the interconversion of transverse phonons into longitudinal phonons, and vice versa, by addition and subtraction is highly probable. Similarly, longitudinal and transverse vibrations in the kx ky-plane may convert to the transverse and longitudinal vibrations in the kz-direction, respectively [40]. This interaction favors energy conversion between the different acoustic phonon branches and perhaps enhances the creation of optical phonons; the latter may also be required to maintain coherency.
An outcome from the above is an emphasis on low-frequency phonons and the sensitivity of superconducting mechanisms on the low energy (meV) domain. Photon energies used for ARPES are often higher than the 9 eV used by Yang et al. [12]. Typical studies are undertaken between 40 eV and 50 eV [22,23] or higher. Concentrated photon illumination at these high energies is likely to excite electrons far below and far above the Fermi level. This likelihood implies localized heating effects and complex interactions that may not be inimical to superconductivity. For example, the Eliashberg calculations for CaC6 [14] suggest that anomalies in the ARPES spectra originate from the out-of-plane and in-plane vibrations of carbon atoms. However, these anomalies occur at energies that are equivalent to temperatures well above room temperature.
The Isotope Effect for CaC6
Employing the McMillan formula [54], the critical transition temperature for 40Ca, computed by Calandra and Mauri, [29] aligned well with the experimental data. Notably, the calculated isotope effect for 44Ca relative to 40Ca differed by 0.24 K. This value contrasts with the experimental observation of a larger isotope effect, a ~0.5 K difference in Tc reported by Hinks et al. [55].
Figure 9 shows an overlay of the PDs calculated for a single hexagonal unit cell of CaC6 using the two most abundant isotopes of Ca, namely 40Ca and 44Ca. Figure 9b is an enlarged view of the acoustic region in the ΓA direction, highlighted by the orange rectangle in Figure 9a. Figure 10 shows the low-frequency region of the phonon density of states (PDOS), calculated for a single hexagonal unit cell of CaC6 and also using 40Ca and 44Ca. The PDOS for the full frequency range is given in Supplementary Figure S7. The reference lines are guides to the eye for the relative changes in frequency (or energy) with the colors matching the respective isotopes.
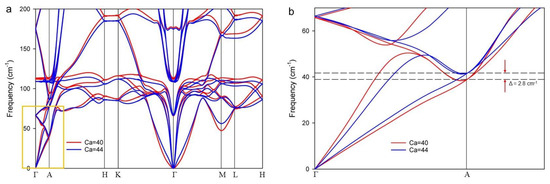
Figure 9.
(a) Phonon dispersion (PD) for CaC6 calculated with a hexagonal unit cell, using DFT with the LDA functional and k-grid value 0.015 Å–1. The PD in red was calculated for 40Ca and the PD in blue for 44Ca isotope, respectively. (b) Magnification of the orange rectangle in (a), showing differences in frequency (Δω = 3.0 ± 0.4 cm–1) between both isotopes at reciprocal point A.
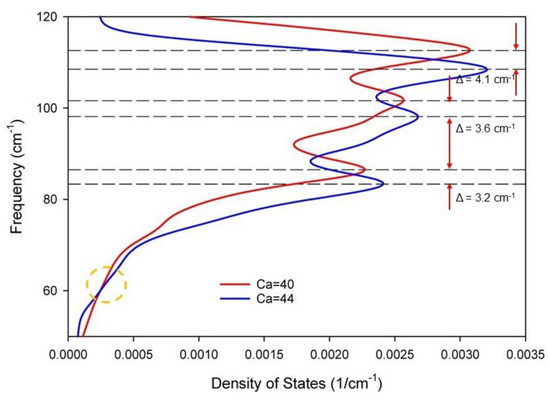
Figure 10.
Phonon density of states (PDOS) for 40Ca and for the 44Ca isotopes, showing relative shifts in peak density (and differences in frequency, Δω) with the increase in phonon frequency. A shift in relative frequencies of Ca isotopes occurs at ~60 cm–1 (yellow dotted circle).
The difference in acoustic frequencies at the Brillouin zone boundary, A, was 3.0 ± 0.4 cm−1 (=0.37 ± 0.05 meV). For the midpoint A/2, which corresponds to the Brillouin zone boundary of the folded reciprocal space of the 2c superlattice, ~1.5 cm−1 (=0.18 meV). Therefore, if the isotope effect is predominantly controlled by the acoustic frequencies, the change in Tc for the isotope effect should be proportional to the frequency difference at the Brillouin zone boundaries of the 2c superlattice for the same nesting phonon vector. We assume that the frequency of 39.6 cm−1 is proportional to the experimentally determined Tc of 11.4 K (see Figure 5 and Section 3.4). Therefore, 1.5 cm−1 corresponds to 11.4 K × (1.5/39.6) = 0.43 ± 0.06 K. This calculated value for the difference in Tc for the Ca isotopes is in close agreement with the experimentally measured isotope shift determined by Hinks et al. [55].
Comparing the PDOS for the Ca isotopes (see Figure 10 and Supplementary Figure S7), a change to their relative position occurs at ~60 cm−1 (see the dotted circle in Figure 10). The first PDOS peak at low frequency shows a frequency difference in the 40Ca and 44Ca peak positions that exceed the calculated value determined above for the isotope effect using PDs. Moreover, the difference in the peak positions increases as the calculated frequencies approach the range of the optical phonons.
This variation in the peak positions suggests that the Tc estimates based on the density of states calculations will be inaccurate, particularly at higher frequencies than acoustic. This inaccuracy may account for a limited success with the accuracy of the McMillan equations and similar approaches, particularly for complex compounds. For the calculated PDs of complex compounds, some optical modes may contribute non-linearities to the dispersion. As stated by Jones and March [56], densities of states are a conceptual compromise when the full PD and EBS calculations are not available.
4. Conclusions
We used a systematic approach to DFT modelling that extracts superconductivity parameters from band structure and phonon dispersion calculations, enabled by a fine k-grid and a large cut-off radius for meV resolution. This theoretical approach is employed for CaC6, for which the superlattice constructs, motivated by experimental observations on other layered superconductors and the topological similarities of EBs, are consistent with the cosine-shaped band structures along the layer direction. Interrogation of Fermi surfaces reveal important bonding–antibonding and nesting relationships that display an asymmetry with a strong connection to superconductivity and the identification of a superconductivity gap. The extent and nature of this asymmetry, evidenced in band structures and Fermi surface projections, aligns with the experimentally determined change in Tc with applied pressure. The gap energy was determined from the tight-binding bands and the approximate nesting relationship, resulting in a good match with the experimentally determined values as shown above. The approximate phonon nesting vectors identified from the superlattice FS reciprocal space geometry results in phonon wavevectors that have approximately the same frequency (or energy), which also match the experimentally determined superconducting gap.
These results demonstrate that superconductivity is largely a geometrically tuned phenomenon, implicit in the observations of superconductivity in many different crystal structures of widely varying geometry. We have shown that accurate and mechanistic information on superconductivity can be extracted from an analytical interrogation of EBS, the Fermi surface, and PD calculations. Superlattice constructs, supported by extensive experimental observations of their manifestation, for example using Raman and THz spectroscopy, are useful tools for understanding this important phenomenon. We encourage further experimental investigations on CaC6 with a focus on the low-frequency, acoustic region. The acoustic phonon region is a key spectral region for superconductivity and an energy domain that is commensurate with superconducting gap energies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst14060499/s1, Figures S1–S3: Calculated EBS for CaC6 with rhombohedral and hexagonal cells; Figure S4: Calculated EBS for CaC6 with 2c hexagonal cells at 0 GPa and 7.5 GPa; Figure S5: Schematic of the CaC6 Fermi Surface; Figure S6: Calculated phonon dispersions for 40CaC6 and 44CaC6; Figure S7: Calculated phonon density of states for 40CaC6 and 44CaC6.
Author Contributions
Conceptualization, J.A.A. and I.D.R.M.; methodology, B.W., A.B. and J.A.A.; software, B.W. and J.A.A.; validation, J.A.A., I.D.R.M. and A.B.; formal analysis, A.B. and J.A.A.; investigation, B.W.; resources, J.A.A.; writing—original draft preparation, B.W. and J.A.A.; writing—review and editing, J.A.A. and I.D.R.M.; visualization, I.D.R.M. and J.A.A.; supervision, J.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request due to privacy of many unpublished results and their relevance for subsequent planned publications.
Acknowledgments
The authors are grateful to the e-Research Office at QUT for access to high-performance computing (HPC) and assistance, and to QUT for a scholarship award to B.W. The authors are also thankful for access to the Bunya HPC facilities and the ongoing assistance from Marlies Hankel at UQ.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Patterson, J.; Bailey, B. Solid-State Physics: Introduction to the Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ferreira, R. Chapter 1: Introduction to Semiconductor Heterostructures. In Semiconductor Modelling Techniques; Mari, X., Balkan, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 159. [Google Scholar]
- Ivchenko, E.L.; Pikus, G.E. Superlattices and Other Heterostructures: Symmetry and Optical Phenomena, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- He, F.; Zhou, Y.; Ye, Z.; Cho, S.H.; Jeong, J.; Meng, X.; Wang, Y. Moiré patterns in 2D materials: A review. ACS Nano 2021, 15, 5944–5958. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lai, J.M.; Zhang, J. Review of phonons in moiré superlattices. J. Semicond. 2023, 44, 011902. [Google Scholar] [CrossRef]
- Li, Y.; Wan, Q.; Xu, N. Recent Advances in Moiré Superlattice Systems by Angle-Resolved Photoemission Spectroscopy. Adv. Mater. 2023, 2305175. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Mataira, R.C.; Crump, W.P. Classifying superconductivity in Moiré graphene superlattices. Sci. Rep. 2020, 10, 212. [Google Scholar] [CrossRef]
- Mangold, M.A.; Holleitner, A.W.; Agustsson, J.S.; Calame, M. Nanoparticle Arrays. In Handbook of Nanoparticles; Aliofkhazraei, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Cargnello, M.; Johnston-Peck, A.C.; Diroll, B.T.; Wong, E.; Datta, B.; Damodhar, D.; Doan-Nguyen, V.V.T.; Herzing, A.A.; Kagan, C.R.; Murray, C.B. Substitutional doping in nanocrystal superlattices. Nature 2015, 524, 450. [Google Scholar] [CrossRef]
- Yazdani, N.; Jansen, M.; Bozyigit, D.; Lin, W.M.M.; Volk, S.; Yarema, O.; Yarema, M.; Juranyi, F.; Huber, S.D.; Wood, V. Nanocrystal superlattices as phonon-engineered solids and acoustic metamaterials. Nat. Commun. 2019, 10, 4236. [Google Scholar] [CrossRef]
- Yang, S.L.; Sobota, J.A.; Howard, C.A.; Pickard, C.J.; Hashimoto, M.; Lu, D.H.; Mo, S.K.; Kirchmann, P.S.; Shen, Z.X. Superconducting graphene sheets in CaC6 enabled by phonon-mediated interband interactions. Nat. Commun. 2014, 5, 3493. [Google Scholar] [CrossRef] [PubMed]
- Logvenov, G.; Bonmassar, N.; Christiani, G.; Campi, G.; Valletta, A.; Bianconi, A. The Superconducting Dome in Artificial High-Tc Superlattices Tuned at the Fano–Feshbach Resonance by Quantum Design. Condens. Matter 2023, 8, 78–84. [Google Scholar] [CrossRef]
- Bianconi, A. Feshbach shape resonance in multiband superconductivity in heterostructures. J. Supercond. Inc. Nov. Magn. 2005, 18, 626–636. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. High Tc superconductivity in a superlattice of quantum stripes. Solid State Commun. 1997, 102, 369–374. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Agrestini, S.; Campi, G.; Saini, N.L.; Saccone, A.; De Negri, S.; Giovannini, M. A superconductor made by a metal heterostructure at the atomic limit tuned at the ‘shape resonance’: MgB2. J. Phys. Condens. Matter 2001, 13, 7383–7390. [Google Scholar] [CrossRef]
- Sboychakov, A.O.; Kugel, K.I.; Bianconi, A. Moiré-like Superlattice Generated van Hove Singularities in a Strained CuO2 Double Layer. Condens. Matter 2022, 7, 50–59. [Google Scholar] [CrossRef]
- Alarco, J.A.; Gupta, B.; Shahbazi, M.; Appadoo, D.; Mackinnon, I.D.R. THz/Far infrared synchrotron observations of superlattice frequencies in MgB2. Phys. Chem. Chem. Phys. 2021, 23, 23922–23932. [Google Scholar] [CrossRef] [PubMed]
- Alarco, J.A.; Chou, A.; Talbot, P.C.; Mackinnon, I.D.R. Phonon Modes of MgB2: Super-lattice Structures and Spectral Response. Phys. Chem. Chem. Phys. 2014, 16, 24443–24456. [Google Scholar] [CrossRef] [PubMed]
- Alarco, J.A.; Mackinnon, I.D.R. Phonon dispersions as indicators of dynamic symmetry reduction in superconductors. In Phonons in Low Dimensional Structures; Stavrou, V.N., Ed.; InTech Open: London, UK, 2018; pp. 75–101. [Google Scholar]
- Alarco, J.A.; Mackinnon, I.D.R. Superlattices, Bonding-Antibonding, Fermi Surface Nesting, and Superconductivity. Condens. Matter 2023, 8, 72. [Google Scholar] [CrossRef]
- Sugawara, K.; Sato, T.; Takahashi, T. Fermi-surface-dependent superconducting gap in C6Ca. Nat. Phys. 2009, 5, 40–43. [Google Scholar] [CrossRef]
- Valla, T.; Pan, Z. Superconductivity and Electron-Phonon Coupling in Graphite Intercalation Compunds. In Physics and Applications of Graphene-Experiments; IntechOpen: London, UK, 2011. [Google Scholar]
- Askerzade, I. Unconventional Superconductors—Anisotropy and Multiband Effects; Springer: Berlin/Heidelberg, Germany, 2012; Volume 153. [Google Scholar]
- Askerzade, I.N. Effect of Coulomb Repulsion on the Critical Temperature in Layered Superconductors with Arbitrary Layer Thicknesses. J. Korean Phys.Soc. 2004, 45, 475–478. [Google Scholar]
- Askerzade, I.N. Reviews of Topical Problems—Study of layered superconductors in the theory of an electron—Phonon coupling mechanism. Phys. Uspekhi 2009, 52, 977–988. [Google Scholar] [CrossRef]
- Csányi, G.; Littlewood, P.B.; Nevidomskyy, A.H. The role of the interlayer state in the electronic structure of superconducting graphite intercalated compounds. Nat. Phys. 2005, 1, 42–45. [Google Scholar] [CrossRef]
- Mazin, I. Intercalant-driven superconductivity in YbC6 and CaC6. Phys. Rev. Lett. 2005, 95, 227001. [Google Scholar] [CrossRef] [PubMed]
- Calandra, M.; Mauri, F. Theoretical Explanation of Superconductivity in CaC6. Phys. Rev. Lett. 2005, 95, 237002. [Google Scholar] [CrossRef] [PubMed]
- Sanna, A.; Profeta, G.; Floris, A.; Marini, A.; Gross, E.; Massidda, S. Anisotropic gap of superconducting CaC6: A first-principles density functional calculation. Phys. Rev. B 2007, 75, 020511. [Google Scholar] [CrossRef]
- Boeri, L.; Bachelet, G.B.; Giantomassi, M.; Andersen, O.K. Electron-phonon interaction in graphite intercalation compounds. Phys. Rev. B 2007, 76, 064510. [Google Scholar] [CrossRef]
- Lamura, G.; Aurino, M.; Cifariello, G.; Di Gennaro, E.; Andreone, A.; Emery, N.; Hérold, C.; Marêché, J.F.; Lagrange, P. Experimental Evidence of s-Wave Superconductivity in Bulk CaC6. Phys. Rev. Lett. 2006, 96, 107008. [Google Scholar] [CrossRef] [PubMed]
- Canadell, E.; Doublet, M.-L.; Lung, C. Orbital Approach to the Electronic Structure of Solids; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Evarestov, R.A.; Smirnov, V.P. Site Symmetry in Crystals: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 108. [Google Scholar]
- Emery, N.; Hérold, C.; d’Astuto, M.; Garcia, V.; Bellin, C.; Marêché, J.F.; Lagrange, P.; Loupias, G. Superconductivity of Bulk CaC6. Phys. Rev. Lett. 2005, 95, 087003. [Google Scholar] [CrossRef] [PubMed]
- Weller, T.E.; Ellerby, M.; Saxena, S.S.; Smith, R.P.; Skipper, N.T. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nat. Phys. 2005, 1, 39–41. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Wang, B.; Bianconi, A.; Mackinnon, I.D.R.; Alarco, J.A. Superlattices Reveal Electronic Topological Transition in CaC6 with Pressure. Crystals 2024, in press. [Google Scholar]
- Mackinnon, I.D.R.; Almutairi, A.; Alarco, J.A. Insights from systematic DFT calculations on superconductors. In Real Perspectives of Fourier Transforms and Current Developments in Superconductivity; Arcos, J.M.V., Ed.; IntechOpen Ltd.: London, UK, 2021; pp. 1–29. [Google Scholar] [CrossRef]
- Bartók, A.P.; Yates, J.R. Ultrasoft pseudopotentials with kinetic energy density support: Implementing the Tran-Blaha potential. Phys. Rev. B 2019, 99, 235103. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Alarco, J.A.; Talbot, P.C.; Mackinnon, I.D.R. Comparison of functionals for metal hexaboride band structure calculations. Mod. Numer. Sim. Mater. Sci. 2014, 4, 53–69. [Google Scholar] [CrossRef]
- Alarco, J.A.; Shahbazi, M.; Talbot, P.C.; Mackinnon, I.D.R. Spectroscopy of metal hexaborides: Phonon dispersion models. J. Raman Spect. 2018, 49, 1985–1998. [Google Scholar] [CrossRef]
- Klingshirn, C.F.; Klingshirn, C.F. Crystals, Lattices, Lattice Vibrations and Phonons. In Semiconductor Optics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 135–166. [Google Scholar]
- Deymier, P.A. Acoustic Metamaterials and Phononic Crystals; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 173. [Google Scholar]
- Grüner, G. Density Waves in Solids; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Ferry, D.K. Semiconductors: Bonds and Bands; IoP Publishing: Bristol, UK, 2019. [Google Scholar]
- Huebener, R.P. Conductors, Semiconductors, Superconductors; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Campi, G.; Ricci, A.; Bianconi, A. Local Structure in Mg1−xAlxB2 System by High Resolution Neutron Diffraction. J. Supercond. Nov. Magn. 2012, 25, 1319–1322. [Google Scholar] [CrossRef]
- Gauzzi, A.; Takashima, S.; Takeshita, N.; Terakura, C.; Takagi, H.; Emery, N.; Hérold, C.; Lagrange, P.; Loupias, G. Enhancement of superconductivity and evidence of structural instability in intercalated graphite CaC6 under high pressure. Phys. Rev. Lett. 2007, 98, 067002. [Google Scholar] [CrossRef]
- Gonnelli, R.S.; Daghero, D.; Delaude, D. Evidence for Gap Anisotropy in CaC6 from Directional Point-Contact Spectroscopy. Phys. Rev. Lett. 2008, 100, 207004. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition Temperature of Strong-Coupled Superconductors. Phys. Rev. 1968, 167, 331–344. [Google Scholar] [CrossRef]
- Hinks, D.G.; Rosenmann, D.; Claus, H.; Bailey, M.S.; Jorgensen, J.D. Large Ca isotope effect in the CaC6 superconductor. Phys. Rev. B 2007, 75, 014509. [Google Scholar] [CrossRef]
- Jones, W.; March, N.H. Theoretical Solid State Physics; Courier Corporation: Chelmsford, MA, USA, 1985; Volume 35. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).