3.1. Electronic Structures of Pristine Magnesium Oxide
The electronic structure of undoped MgO was investigated first. Considering that the cutoff energy of plane wave expansion and the dimension of the k point mesh are two parameters that largely determine the calculation accuracy, convergence tests were conducted in a MgO unit cell. As shown in
Figure 2, cutoff energies ranging from 400 to 700 eV were tested. The lattice constant converged at 4.25 Å, independent of the cutoff energy.
The converged lattice constant agrees well with other calculation results [
6,
19,
29,
30] but is slightly larger than the experimental value of 4.21 Å [
18]. The overestimation of the lattice constant was also observed in other previous simulations [
6,
29]. The reason has been suggested to be the underestimation of bonding in the oxide. As these simulations all employed GGA, the reason for an overestimated lattice constant can be further explained: GGA approximates the true exchange-correlation functional, which means the Coulombic repulsions are still overestimated, including the repulsions between the 2p orbitals of O and 3s orbital of Mg. This results in a greater Mg-O bond length, which further results in a greater lattice constant (Mg-O-Mg). (Another possible reason for the discrepancy between the current calculations and the experimental results could be the differing temperature conditions, with calculations performed at 0 K while experimental measurements are conducted at higher temperatures.) At the converged lattice constant, the energy difference between cutoff energies of 600 eV and 700 eV was on the scale of 1 meV. The dimension of k point mesh was tested from 1 to 10 (10 × 10 × 10). The energy differences were on the scale of 1 meV when the k point mesh dimension was greater than 6 (6 × 6 × 6). Therefore, the plane wave cutoff energy of 600 eV and the k point mesh of 6 × 6 × 6 were used, considering a balance between computation accuracy and expense.
Figure 3 shows a combined graph of the band structure (BS) and density of states (DOS) of pristine MgO. BS and DOS provide information about the distribution of electronic states. Whereas the former shows the electronic energy along high symmetry lines in the irreducible Brillouin zone, the latter covers the whole Brillouin zone of the lattice. The high symmetry lines connected with high symmetry points of Γ (0.000, 0.000, 0.000), X (0.500, 0.000, 0.000), U (0.625, 0.250, 0.625), K (0.375, 0.375, 0.750), W (0.500, 0.250, 0.750), and L (0.500, 0.500, 0.500), in fractal coordinates, of the reciprocal lattice were used according to the method proposed by Tanaka and colleagues [
31,
32].
The valence band maximum and conduction band minimum of the band gap were located at the Γ point, indicating that the simulated MgO is a direct band gap material, in agreement with other calculation results. The calculated band gap was 4.58 eV, which is smaller than reported experimental values of 5.5 eV [
15], 5.8–5.9 eV [
15,
18], and 7.2 eV [
23]. This difference has been attributed to the framework of density functional theory, where the mutually interacting nature between electrons is approximated by the exchange-correlation functional, which is not exact. The projected contributions from the orbitals of the Mg and O atoms to the band structure of MgO are shown in
Figure 4. Both Mg and O atomic orbitals are distributed throughout the valence band and conduction band. The VBM (valence band maximum) is mainly composed of the 2p orbital of the O atom. 2s, 2p of the O atom and 3s of the Mg atom contribute to CBM (conduction band minimum). The O 2p orbital had the most dispersive distribution throughout the band structure of pristine MgO.
3.2. Hubbard Onsite Parameters of Rare Earth Dopants in Magnesium Oxide
When doping a rare earth ion into a host, it could either replace an occupied site—the substitution site—or occupy an empty site—the interstitial site. Experimentally, it has been proven by X-ray diffraction characterisations [
4,
21,
23] that the structure of rare-earth-doped crystalline MgO remained cubic, indicating that rare earth dopants occupy the substitution sites. In the current simulations, the rare earth elements were placed in substitutional Mg sites. To aid the localisation of the 4f states of the Nd and Er dopants, U
eff on-site correction terms were applied. The electronic structures of the single-rare-earth-atom-doped MgO were calculated and compared using different U
eff (integer values from 0 to 8 eV). One Mg atom was substituted by one Nd or Er atom in a 2 × 2 × 2 MgO supercell. The aim of these tests was to determine a U
eff for each of Nd and Er and use them in the subsequent calculations in the next parts, where the influence of Li will be investigated in systems with defect complexes.
Different U
eff values resulted in changes in the following two aspects: (1) the position of the 4f ground states in the band gap and (2) the splitting of the 4f ground state energy. The latter shows how dispersive the energy of the 4f state is, which indicates the localisation status of 4f states. The results are shown in
Figure 5a,b, in which the 4f states are highlighted with vertical black lines. When choosing the optimal U
eff parameters according to the calculated density of states, the priority was to see whether the applications of U
eff positively influence the localisations of 4f states.
For the Nd dopant, as shown in
Figure 5a, when no on-site correction is applied (U
eff = 0 eV), two main ground state 4f peaks of similar intensity locate near the CBM, and the energy gap between the two peaks is 0.62 eV. When increasing U
eff from 1 to 4 eV, the peak of the highest intensity 4f states for each applied U
eff remains near the CBM, but multiple splitting peaks appear. The highest-intensity peak moves towards the top of the conduction band with U
eff = 5 eV. As U
eff increases to 6 eV and 7 eV, compared to U
eff = 0 eV, the energy gap between the splitting 4f peaks becomes larger because of the peak location near the top of the conduction band. When U
eff = 8 eV, the 4f ground state spikes near the CBM with small peaks close to its lower energy side. By comparing, U
eff = 8 eV gives the most localised 4f ground state in energy. Since no other U
eff parameters aid the localisation of 4f of Nd as U
eff = 8 eV does, U
eff = 8 eV was chosen for the Nd 4f orbitals.
For the Er dopant, as shown in
Figure 5b, the 4f ground states distribute mainly between the VBM and the middle of the band gap. U
eff = 0 eV gives two 4f ground state peaks of comparable intensities and an energy gap of 0.4 eV, located at 0.9 eV and 1.3 eV above the VBM. The 4f states show good localisations when using U
eff = 1 eV, 2 eV, 3 eV, and 4 eV. Though there is a peak 0.1 eV above the VBM for U
eff = 2 eV, its intensity is much lower than the main peak, and the 4f energy states mostly localise 0.88 eV above the VBM. Increasing the U
eff to larger than 4 eV results in a large splitting of the energy of the 4f states. For example, when U
eff = 6 eV, there is a 4f peak at the bottom of the valence band, the other located 0.81 eV above the VBM. When U
eff = 8 eV, 4f peaks distribute from the bottom of the valence band to the bottom of the conduction band. To choose a U
eff from 1 eV, 2 eV, 3 eV, and 4 eV for Er 4f orbitals, the locations of the 4f states in the band gap were compared with the energy level diagram built by Oliveira et al. [
21], where the 4f state of trivalent Er locates 0.4 eV below the VBM. In the current results, the gaps between the main 4f states of Er and the VBM using U
eff = 1 eV, 2 eV, 3 eV, and 4 eV are 3.2 eV, 0.9 eV, 1.5 eV, and 2.9 eV, respectively. The 4f state of Er is relatively closer to the VBM when using U
eff = 2 eV than using 1 eV, 3 eV, and 4 eV. Thus, U
eff = 2 eV was chosen for the Er 4f orbitals.
3.3. Electronic Structures of Rare-Earth-Doped Magnesium Oxide and Roles of Li
The unfilled 4f orbitals of rare earth elements are the inner orbitals. When putting rare earth dopants in a crystalline host, the outer orbitals, the filled 5s and 5p orbitals weaken or screen the perturbation on 4f orbitals from the crystal field. Therefore, the wavelength of the characteristic 4f-4f emission is considered to remain similar in various hosts with similar moderate crystal field strength. But, the energy level in the band gap may change due to the defects in the doped systems. The calculations in this part include electroneutral defect clusters
and
in 2 × 2 × 2 supercells, where RE = rare earth = Nd or Er. The initial and relaxed structures of the simulated supercells are shown in
Figure 6.
As shown in
Figure 6, after relaxation, the coordination polyhedra of RE dopants were distorted from the perfect octahedron of Mg of perfect centre-symmetry in pristine MgO. The octahedral coordination remained for substitutional dopants, considering the ionic size and that the rock salt is a compact crystal structure. Changes were more readily observable in the Nd-doped systems than in Er-doped systems. The mismatch in the ionic radii between rare earth and Mg undoubtedly distorts the coordination polyhedron. Quantitively, the octahedra of two rare earth dopants in the defect complexes were included in the brief statistical analysis of each doped system, as shown in
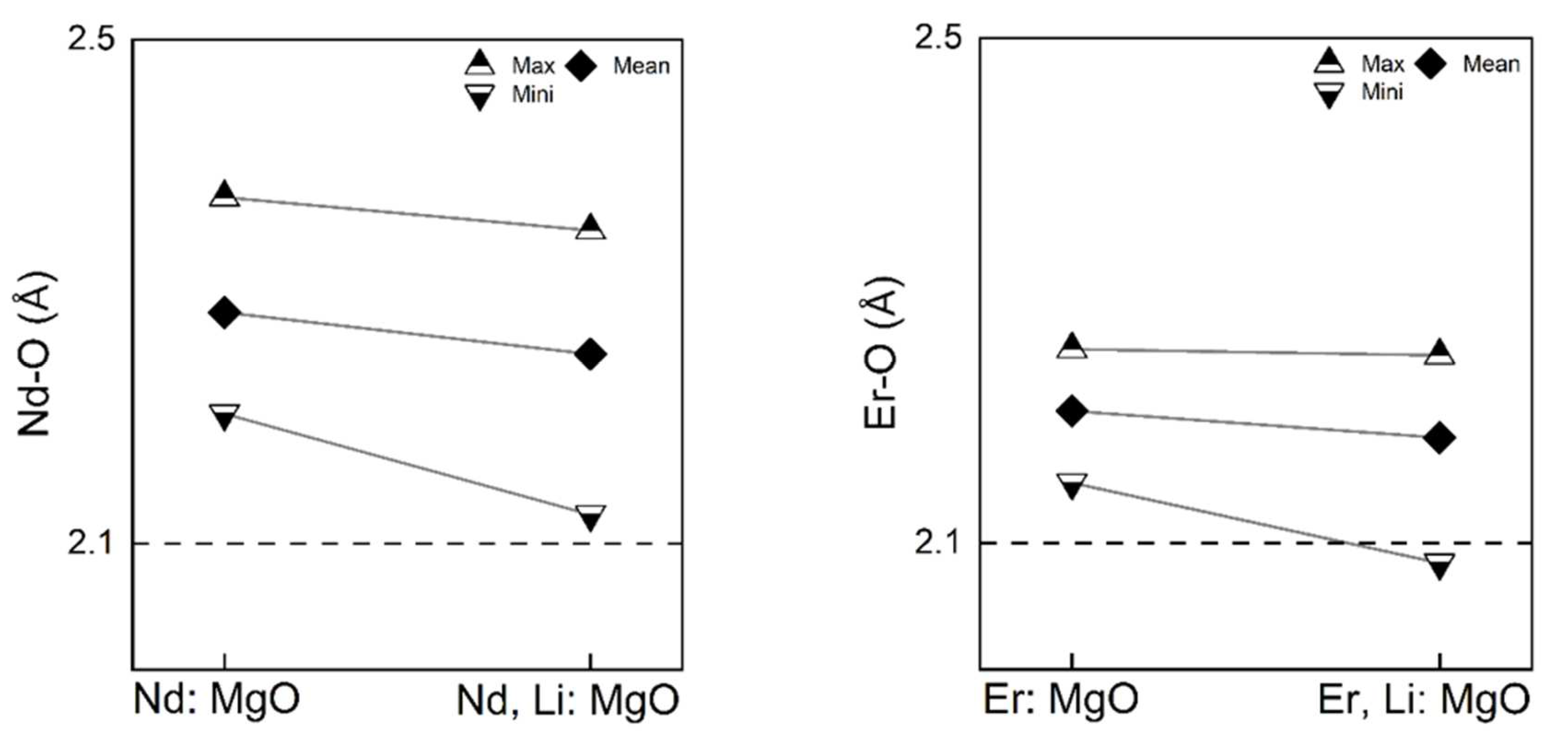
Figure 7.
The dashed line in the middle indicates the Mg-O bond length in the pristine MgO, which is 2.125 Å. The bond lengths of the rare earth dopant are the interatomic distances between the rare earth dopant and its six nearest oxygen atoms. As the coordinates of each atom in the system are available from the calculations, the inter-atomic distances can be readily obtained. There are six RE-O bonds in each coordination polyhedron. The mean RE-O bond lengths in all four calculated systems were greater than 2.125 Å. This increase in the bond length is understandable as both Nd and Er possess larger ionic radii than Mg. Under the energy equilibrium condition, oxygen atoms move to a farther distance to relax. As ionic Nd is larger than Er, the mean Nd-O length is larger than the mean Er-O length. Decreases in the mean, maximum, and minimum bond lengths were found in Li co-doped systems. The decrease is more apparent in Nd-doped MgO than in Er-doped MgO.
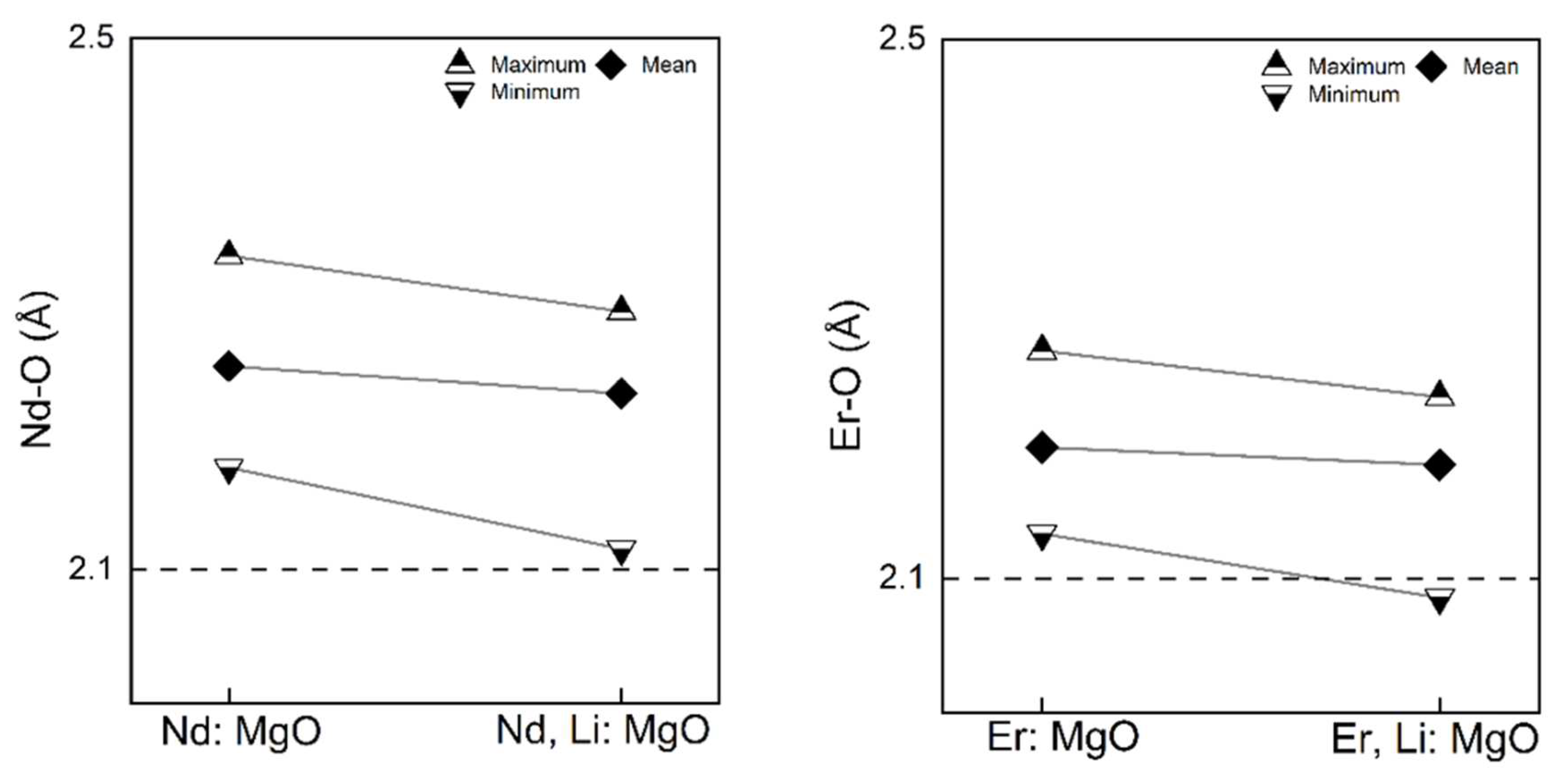
Comparing the current results in
Figure 7 with the results in our previous work [
27], as shown in
Figure 8, the extent of the relaxations in the bond lengths of the dopant-centred octahedra are consistent, such as the maximum, mean, and minimum bond lengths. The results in
Figure 8 were obtained using a classical force-field method—the static lattice method—where the defect relaxations were performed under the Mott–Littleton scheme. The bond lengths considered were also the six nearest oxygen atoms around the rare earth dopant. Both results show that RE, Li: MgO possesses a slightly more contracted octahedra with smaller bond lengths than RE: MgO. Additionally, the distortions of the coordination octahedra of rare earth dopants were quantified using Baur’s Distortion Indices (DI) [
33,
34], as shown in
Table 1. The DI of bond length (TO), bond angle (OTO), and edge length (OO) are expressed as follows:
The DI of the coordination octahedra of the rare earth dopants increased after co-doping Li. However, in the previous simulations based on the classical static lattice method [
27], the DI was found to decrease after co-doping Li. This discrepancy results from the different simulation methodologies applied in the two investigations. The defect structures in the static lattice method were relaxed under the Mott–Littleton scheme, and the DFT calculations were based on the periodic boundary condition, where the size of the supercell is of the volume of several unit cells. The size the supercell is limited to the computational resources/power available.
The DOS calculation results of defect complexes containing RE: MgO (RE = Nd or Er) with and without Li are shown in
Figure 9a,b. For Nd: MgO, by comparing the DOS curves in
Figure 5a, which involves no defect cluster, changes can be found mainly in the multiple additional energy levels, especially in the band gap, which are dominated by Nd dopants. The distributions of 4f states were found to be different. The introduction of the complex contributes to a broader spread of 4f ground states, which is due to the interaction between the closely situated dopants [
35]. According to
Figure 9a, overlapping of 4f and 5d states was observed in the CB (conduction band), and the peak of the highest intensity of Nd 4f states lies at a higher energy than that of 5d states in the CB. With this energy distribution, the parity allowed 4f-5d transitions become more accessible. At the same time, this may depress the forbidden intra-configurational 4f-4f transitions. On the other hand, since 5d states lie in the CB, where electrons are delocalised, 4f-5d transitions would be hard to observe experimentally. In a cluster-free system, 5d states lie right below the CBM. When using the band gap of the experimental value (~7.2 eV) [
23], for the systems with defect complexes, the 5d states lie below the CBM with an energy gap smaller than 1 eV. This is smaller than the one in the system with an isolated dopant. This indicates that the probability of electrons being excited from 5d to the conduction band is higher in clustered systems. Two peaks were observed in the band gap, contributed by the 4f states of the two Nd dopants. One lies around 0.1 eV above VBM, and the other lies around 3.2 eV above VBM, giving a width of 3.1 eV. The former peak possesses a higher intensity. The grey area between the peaks is used to indicate this gap.
The distribution of 4f states in the band gap was a critical change when comparing cluster-doped systems with and without Li co-doping. In Nd, Li: MgO, two peaks of the 4f states were located at 0.3 eV and 3.1 eV above VBM with an increased density of states, giving a smaller energy width of 2.8 eV. Some 4f peaks were found at the lower energy side of the 5d states in Nd: MgO, but these peaks disappeared in Nd, Li: MgO. This change may discourage the absorption transition from 4f to 5d ground states, as the energy gap between 5d and the lower energy 4f states vastly increases.
In the Er: MgO with defect complexes, as shown in
Figure 9b, the distribution of the 4f ground states of Er was found to be relatively more dispersive than in
Figure 5b. The energies of the 4f states of Er: MgO and Er, Li: MgO range from 0.06 to 2.1 eV and from 0.4 to 1.2 eV in the band gap, respectively, giving energy widths of 2.04 eV and 0.8 eV. A larger energy width means a more dispersive energy distribution of the 4f states. In Er: MgO, one Er dopant contributes to the peaks of lower energies, and the other Er dopant contributes to the peaks of higher energies in the band gap. In Er, Li: MgO, each Er dopant contributes to all peaks in the band gap. An essential difference between the distributions of the 4f states of Nd and Er is that the 4f states of Er distribute within the band gap. Its 5d states remain in the CB without overlapping with 4f states. In the Nd-doped system, 4f states emerge on both the lower and higher energy sides of the 5d states, indicating that both absorption and emission towards 5d may occur. Nevertheless, in the Er-doped system, only absorbing energy can excite electrons from 4f to 5d states. The probability of 4f-5d transitions in Nd: MgO may be higher than in Er: MgO, regardless of Li. Additionally, after the cooperation of Li, the number of Er 4f levels in the band gap decreased. The intensity of peaks of the lower energy increased, while peak intensities of the higher energy decreased. Compared to Er: MgO, the distribution of the ground 4f states in the band gap of Er, Li: MgO are more localised. This is favourable to obtain a narrow emission peak and increased emission intensity.
The projected DOS from Li orbitals are shown in
Figure 10. Both the s and p orbitals of Li spread through the valence band, the conduction band, and the band gap but with a very low peak intensity. An overlapping with the peaks of 4f states in the band gap was observed.
A simplified illustration of the band structures of calculated systems is shown in
Figure 11. The blue lines are 4f levels, and the green lines are 5d levels. Given the physical origin of energy level splitting in a crystal field, the calculated ground 4f energy levels in the band gap of Nd- and Er-doped systems can be interpreted as the Stark levels, which belong to the ground state manifolds of
4I
9/2 and
4I
15/2, respectively.
4I
9/2 and
4I
15/2 possess 10 and 16 (2J + 1) degeneracies in total, respectively. Since Nd
3+ and Er
3+ ions possess an odd number of 4f electrons, each Stark level has a minimum of 2-fold degeneracy, independent of the point symmetry of the crystal field [
15,
36]. The calculated 4f energy levels were not given further notation as the reduction degree of the respective ground state manifolds was not resolved so far. However, the number of calculated main 4f peaks contributed by each dopant were fewer than five for Nd or eight for Er. The results do not conflict with the degeneracy characteristics of 4f
3 and 4f
11. The VBMs were shifted to zero. The CBM was positioned according to experimental results of the band gap of pristine crystalline MgO [
23], which is around 7.2 eV above the VBM. Possible resonant absorptions of photons can be presumed from the energy gaps between the calculated energy levels in the band gap. As for the popular wavelength of Nd and Er, 1060 nm (~1.2 eV) is expected to have good transparency in Nd (Li): MgO. Li was not found to induce electronic energy levels for resonant absorption at that wavelength. In Er, Li: MgO, resonant absorptions of 1550 nm (~0.8 eV) may happen. However, Er possesses multiple emissions in the range of 1538–1574 nm. Good transparency can be expected as well in this range. As indicated by the black arrows, potential absorptions of wavelength in the visible range in Nd: MgO include 400 nm from the occupied to upper 4f states and 517 nm from the lower to upper 4f states. In Nd, Li: MgO, a possible absorption is 443 nm from the 4f states in the band gap. In Er: MgO, potential absorptions include 729 nm, 653 nm, and 620 nm among the 4f states in the band gap. However, no potential resonant absorptions are expected in the visible range in Er, Li: MgO.
Based on the above, Li co-doping may influence the transparency of Nd- and Er-doped MgO in the visible range. Er, Li: MgO has better visible transparency than Nd, Li: MgO. This may partially explain the experimental results of the relative visible transparency between Er- and Nd-doped MgO co-doped with Li [
4]. The starting levels of these potential absorptions are from the low Stark levels. The depopulation of the electrons on these levels may be beneficial for maintaining the population inversion between them and the Stark levels which belong to upper excited manifolds. The equilibrium between this absorption and the stimulated/spontaneous emission will determine the ultimate optical properties.
In all, the changes in the electronic structures by co-doping Li include the following aspects: (1) density of the 4f states (peak intensity) in the band gap, (2) energy gap between the 5d states and the 4f states, and (3) position and splitting of the 4f states in the band gap. For potential laser applications where a reverse population between the excited and the ground 4f states is the basis, if fewer 4f electrons jump upwards to 5d states, more would be available for 4f-4f transitions. These results suggest that Li co-doping may contribute to the laser property of both Nd: MgO and Er: MgO, but the underlying mechanisms are considered to be different. The former two aspects may weigh more for Nd: MgO, and the latter may weigh more for Er: MgO, depending on in which system those changes are relatively more apparent.