Batch Cooling Crystallization of a Model System Using Direct Nucleation Control and High-Performance In Situ Microscopy
Abstract
1. Introduction
High-Performance In Situ Microscopy (HPM)
2. Materials and Methods
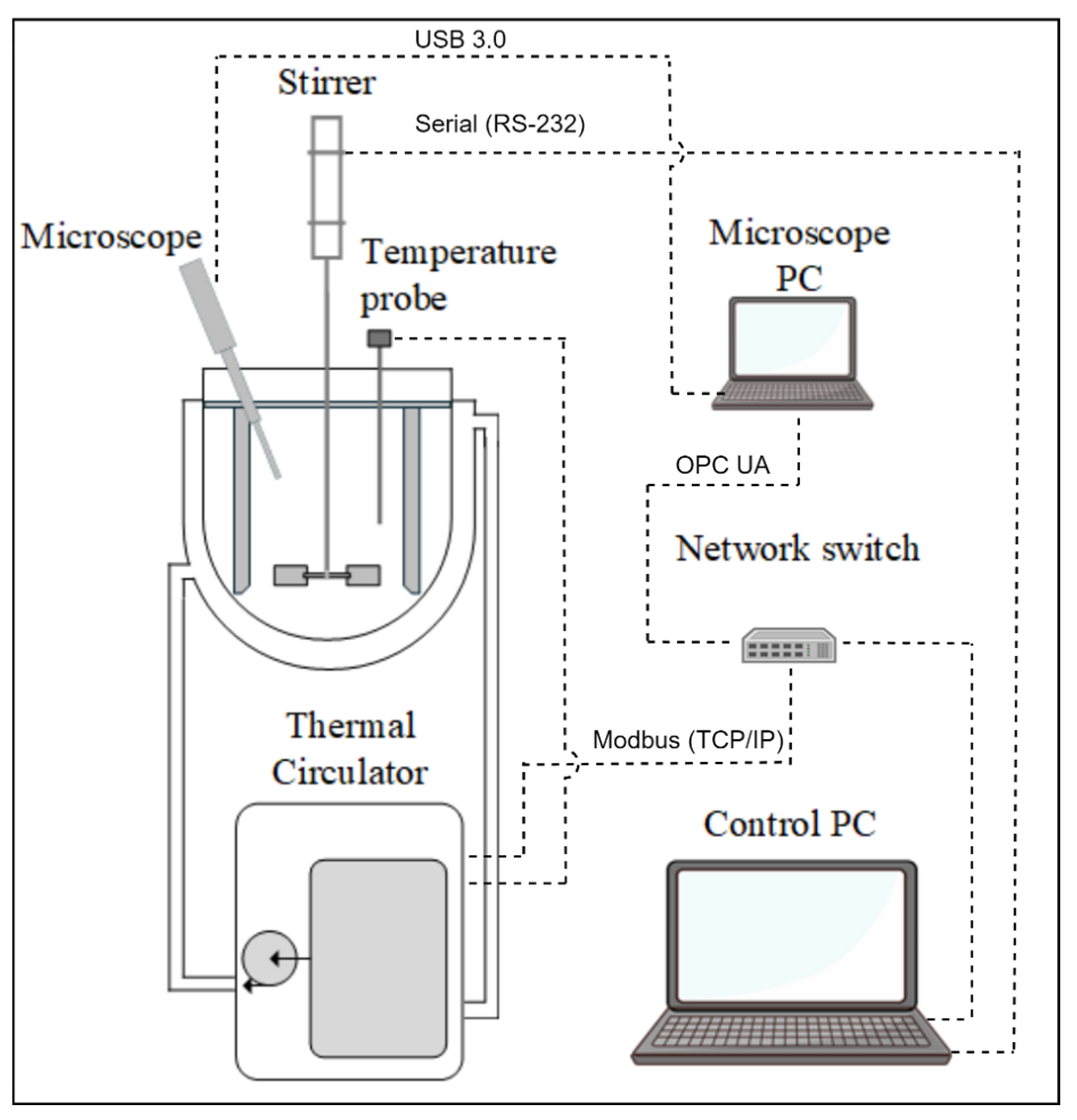
2.1. Laboratory System Configuration
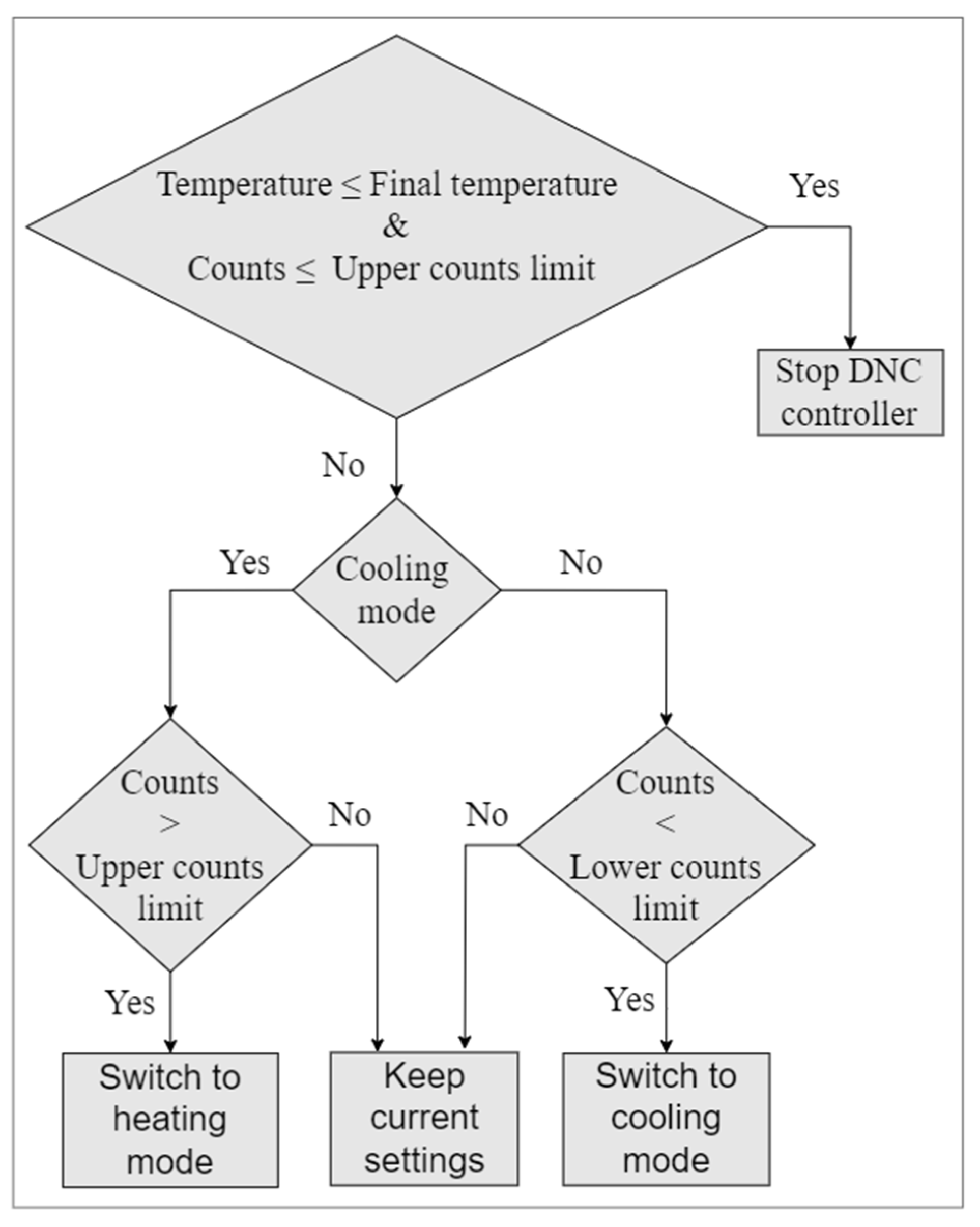
2.2. DNC Controller Algorithm and Controlled Variable Selection
2.3. Microscope Properties and Configuration Settings
2.4. Experimental Procedure
3. Results and Discussion
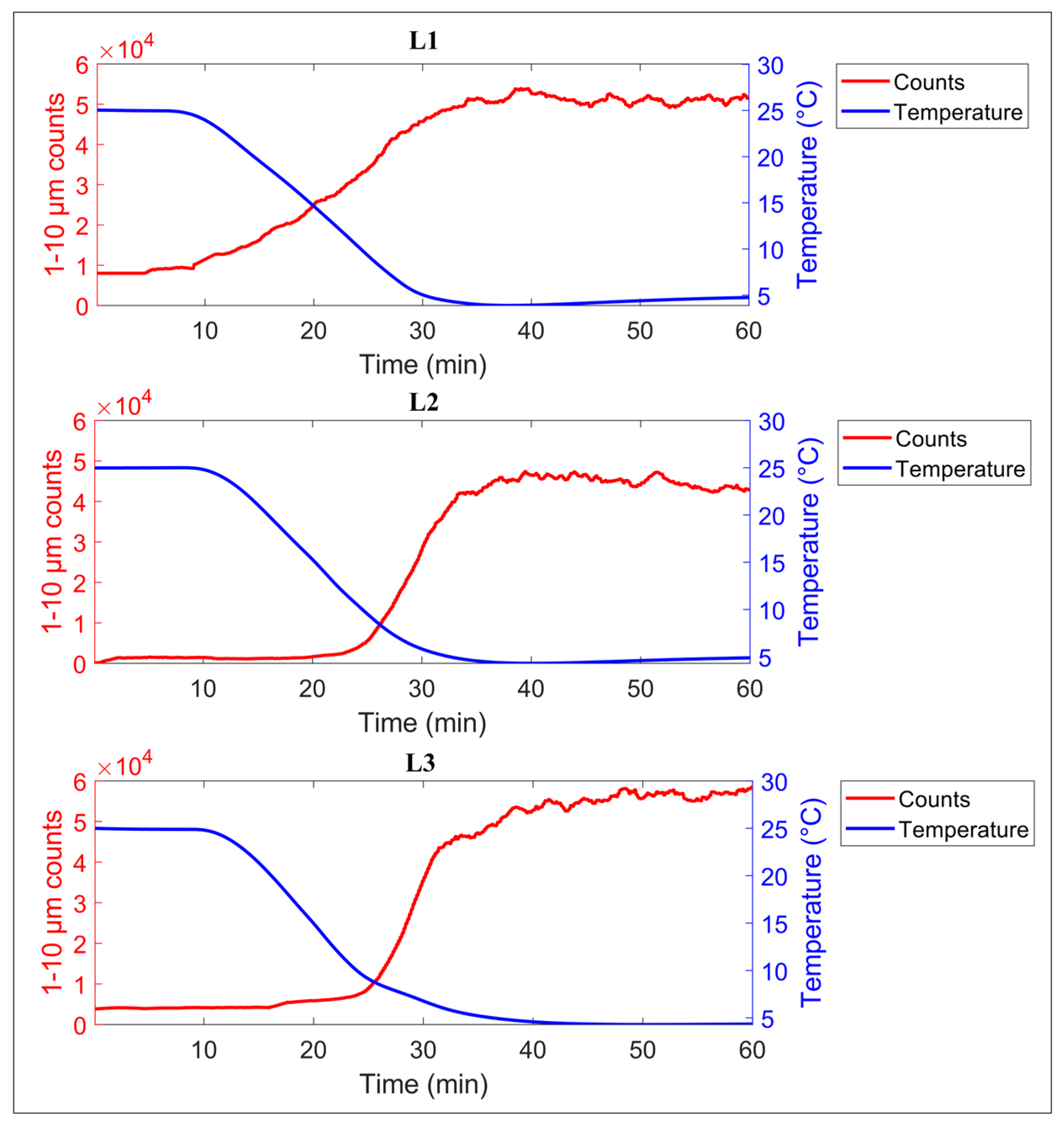
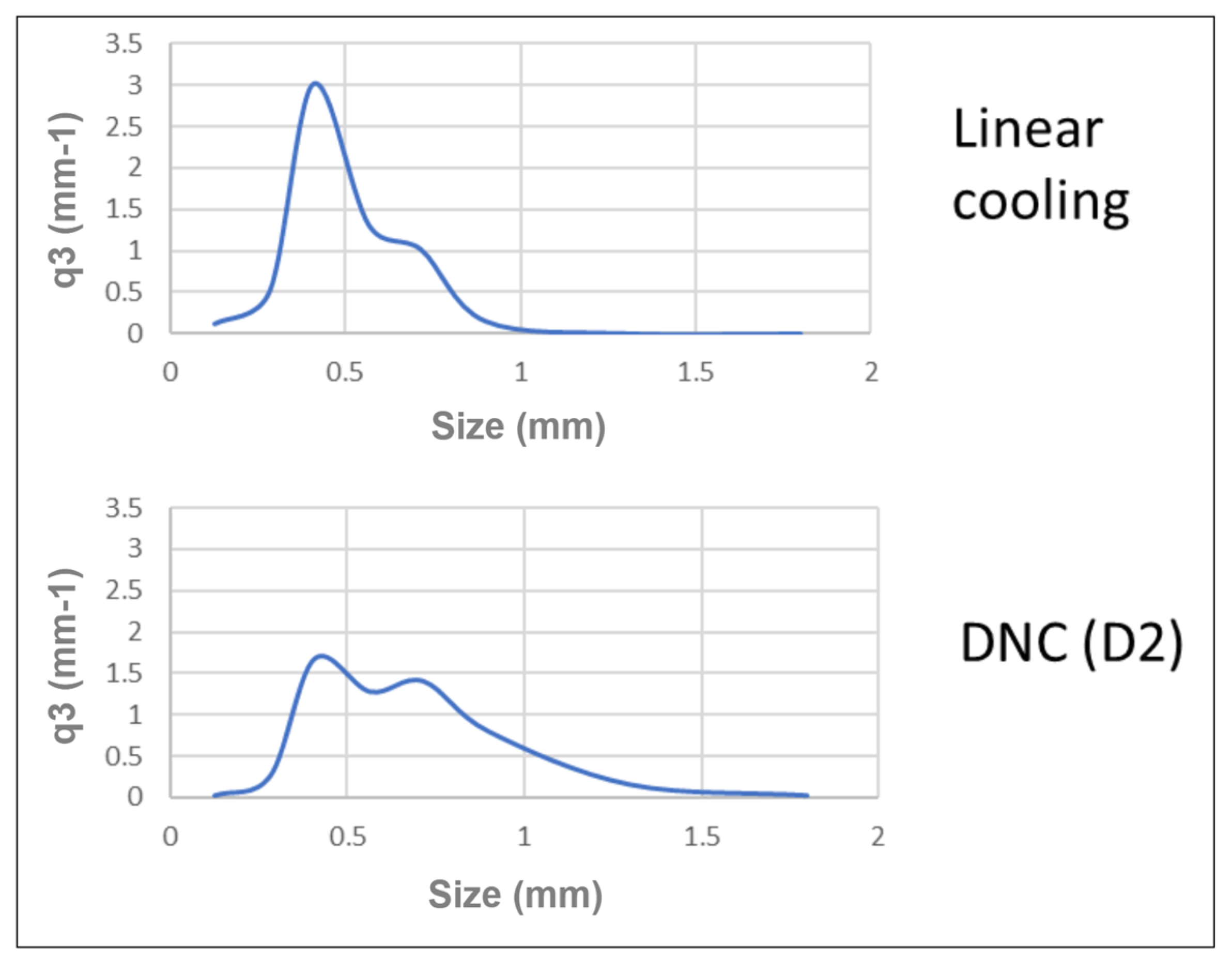
3.1. Linear Cooling Experiments
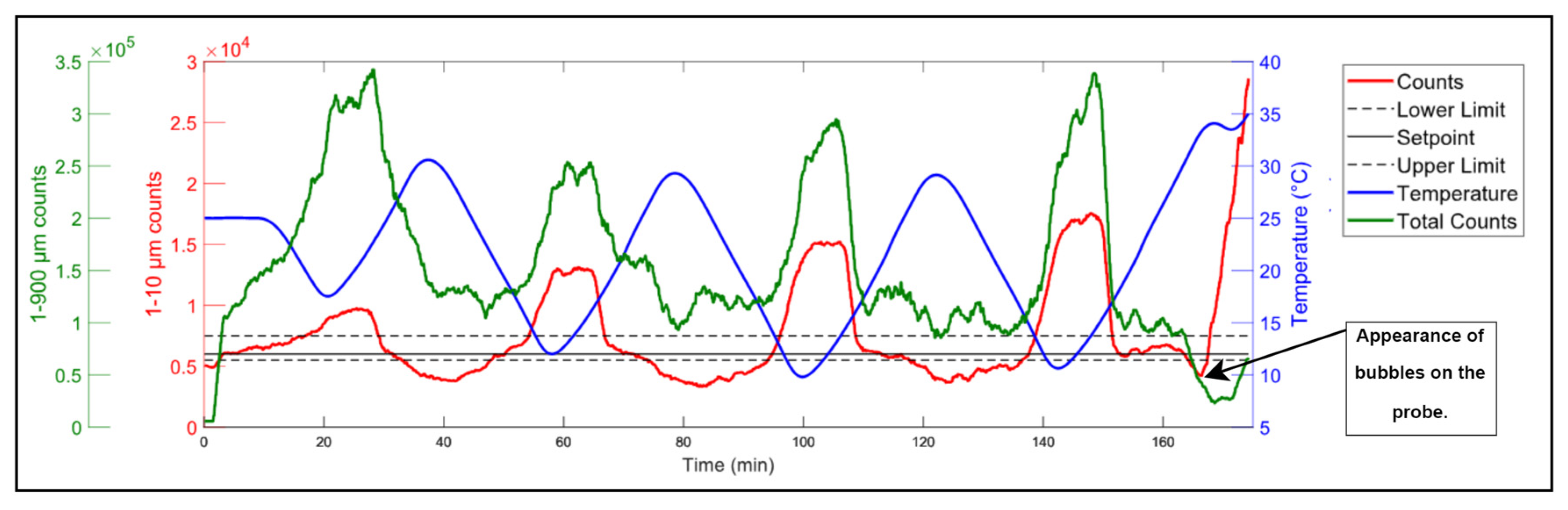
3.2. DNC Experiments
Experiment D3 Analysis
3.3. Comparison of DNC and Linear Cooling
4. Conclusions
5. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tung, H.-H. Crystallization of Organic Compounds: An Industrial Perspective; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Swami, A.; Hatolkar, S.; Patil, A.; Dhumal, K.; Shastri, A. Process analytical technology (PAT): Enhancing quality and efficiency in pharmaceutical development and production. Korean J. Physiol. Pharmacol. 2023, 27, 394–408. [Google Scholar]
- Bhavin, S.E.; Anuradha, G. Process analytical technology (PAT) in quality assurance: A detailed review. Int. J. Pharm. Sci. Nanotechnol. 2022, 15, 5763–5770. [Google Scholar]
- Chianese, A.; Kramer, H.J. Industrial Crystallization Process Monitoring and Control; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Szilagyi, B.; Eren, A.; Quon, J.L.; Papageorgiou, C.D.; Nagy, Z.K. Application of model-free and model-based quality-by-control (QbC) for the efficient design of pharmaceutical crystallization processes. Cryst. Growth Des. 2020, 20, 3979–3996. [Google Scholar] [CrossRef]
- ASaleemi, N.; Steele, G.; Pedge, N.I.; Freeman, A.; Nagy, Z.K. Enhancing crystalline properties of a cardiovascular active pharmaceutical ingredient using a process analytical technology based crystallization feedback control strategy. Int. J. Pharm. 2012, 430, 56–64. [Google Scholar] [CrossRef]
- Trampuž, M.; Teslić, D.; Likozar, B.; Dejanović, I. Batch crystallization of active pharmaceutical ingredient: Kinetics and equilibrium modelling. Kem. Ind. 2018, 67, 43–48. [Google Scholar] [CrossRef]
- de Moraes, M.G.F.; Grover, M.A.; de Souza, M.B.; Lage, P.L.C.; Secchi, A.R. Optimal control of crystal size and shape in batch crystallization using a bivariate population balance modeling. IFAC-PapersOnLine 2021, 54, 653–660. [Google Scholar] [CrossRef]
- Bötschi, S.; Rajagopalan, A.K.; Morari, M.; Mazzotti, M. Feedback control for the size and shape evolution of needle-like crystals in suspension I Concepts and simulation studies. Cryst. Growth Des. 2018, 18, 4470–4483. [Google Scholar] [CrossRef]
- Rajagopalan, A.K.; Bötschi, S.; Morari, M.; Mazzotti, M. Feedback control for the size and shape evolution of needle-like crystals in suspension II Cooling crystallization experiments. Cryst. Growth Des. 2018, 18, 6185–6196. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, T.; Ma, Y.; Xue, F.; Gao, Z.; Hou, B.; Gong, J. Application of pat-based feedback control approaches in pharmaceutical crystallization. Crystals 2021, 11, 221. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Fevotte, G.; Kramer, H.; Simon, L.L. Recent advances in the monitoring, modelling and control of crystallization systems. Chem. Eng. Res. Des. 2013, 91, 1903–1922. [Google Scholar] [CrossRef]
- Liotta, V.; Sabesan, V. Monitoring and feedback control of supersaturation using ATR-FTIR to produce an active pharmaceutical ingredient of a desired crystal size. Org. Process Res. Dev. 2004, 8, 488–494. [Google Scholar] [CrossRef]
- Gavran, M.; Andrijić, Ž.U.; Bolf, N.; Rimac, N.; Sacher, J.; Šahnić, D. Development of a calibration model for real-time solute concentration monitoring during crystallization of ceritinib using raman spectroscopy and in-line process microscopy. Processes 2023, 11, 3439. [Google Scholar] [CrossRef]
- Zhang, T.; Nagy, B.; Szilágyi, B.; Gong, J.; Nagy, Z.K. Simulation and experimental investigation of a novel supersaturation feedback control strategy for cooling crystallization in semi-batch implementation. Chem. Eng. Sci. 2020, 225, 115807. [Google Scholar] [CrossRef]
- Zhang, T.; Szilágyi, B.; Gong, J.; Nagy, Z.K. Novel semibatch supersaturation control approach for the cooling crystallization of heat-sensitive materials. AIChE J. 2020, 66, 16955. [Google Scholar] [CrossRef]
- Bakar, M.R.A.; Nagy, Z.K.; Saleemi, A.N.; Rielly, C.D. The impact of direct nucleation control on crystal size distribution in pharmaceutical crystallization processes. Cryst. Growth Des. 2009, 9, 1378–1384. [Google Scholar] [CrossRef]
- Saleemi, A.N.; Rielly, C.D.; Nagy, Z.K. Comparative investigation of supersaturation and automated direct nucleation control of crystal size distributions using ATR-UV/vis spectroscopy and FBRM. Cryst. Growth Des. 2012, 12, 1792–1807. [Google Scholar] [CrossRef]
- Saleemi, A.; Rielly, C.; Nagy, Z.K. Automated direct nucleation control for in situ dynamic fines removal in batch cooling crystallization. CrystEngComm 2012, 14, 2196–2203. [Google Scholar] [CrossRef]
- Ostergaard, I.; Szilagyi, B.; De Diego, H.L.; Qu, H.; Nagy, Z.K. Polymorphic Control and Scale-Up Strategy for Antisolvent Crystallization Using a Sequential Supersaturation and Direct Nucleation Control Approach. Cryst. Growth Des. 2020, 20, 5538–5550. [Google Scholar] [CrossRef]
- Ostergaard, I.; Szilagyi, B.; De Diego, H.L.; Qu, H.; Nagy, Z.K. Polymorphic Control and Scale-Up Strategy for Antisolvent Crystallization Using Direct Nucleation Control. Cryst. Growth Des. 2020, 20, 2683–2697. [Google Scholar] [CrossRef]
- Simone, E.; Othman, R.; Vladisavljević, G.T.; Nagy, Z.K. Preventing crystal agglomeration of pharmaceutical crystals using temperature cycling and a novel membrane crystallization procedure for seed crystal generation. Pharmaceutics 2018, 10, 17. [Google Scholar] [CrossRef]
- Simone, E.; Zhang, W.; Nagy, Z.K. Application of process analytical technology-based feedback control strategies to improve purity and size distribution in biopharmaceutical crystallization. Cryst. Growth Des. 2015, 15, 2908–2919. [Google Scholar] [CrossRef]
- Yao, T.; Liu, J.; Wan, X.; Li, B.; Rohani, S.; Gao, Z.; Gong, J. Deep-learning based in situ image monitoring crystal polymorph and size distribution: Modeling and validation. AIChE J. 2024, 70, 18279. [Google Scholar] [CrossRef]
- Barhate, Y.; Boyle, C.; Salami, H.; Wu, W.L.; Taherimakhsousi, N.; Rabinowitz, C.; Bommarius, A.; Cardona, J.; Nagy, Z.K.; Rousseau, R.; et al. OpenCrystalData: An open-access particle image database to facilitate learning, experimentation, and development of image analysis models for crystallization processes. Digit. Chem. Eng. 2024, 11, 100150. [Google Scholar] [CrossRef]
- Wu, W.L.; Chappelow, C.; Hanspal, N.; Larsen, P.; Patton, J.; Shinkle, A.; Nagy, Z.K. Implementation and application of image analysis-based turbidity direct nucleation control for rapid agrochemical crystallization process design and scale-up. Ind. Eng. Chem. Res. 2022, 61, 14561–14572. [Google Scholar] [CrossRef]
- Borsos, Á.; Szilágyi, B.; Agachi, P.Ş.; Nagy, Z.K. Real-Time Image Processing Based Online Feedback Control System for Cooling Batch Crystallization. Org. Process Res. Dev. 2017, 21, 511–519. [Google Scholar] [CrossRef]
- Jul-Jørgensen, I.; Oliver, R.; Gernaey, K.V.; Hundahl, C.A. Modernizing non-classical protein crystallization through industry 4.0: Advanced monitoring and modelling utilizing process analytical technology. Chem. Eng. Res. Des. 2024, 204, 382–389. [Google Scholar] [CrossRef]
- Pickles, T.; Svoboda, V.; Marziano, I.; Brown, C.J.; Florence, A.J. Integration of a model-driven workflow into an industrial pharmaceutical facility: Supporting process development of API crystallisation. CrystEngComm 2024, 26, 4678–4689. [Google Scholar] [CrossRef]
- BlazeMetrics. Available online: https://www.blazemetrics.com/ (accessed on 2 December 2024).
- Rabesiaka, M.; Sghaier, M.; Fraisse, B.; Porte, C.; Havet, J.L.; Dichi, E. Preparation of glycine polymorphs crystallized in water and physicochemical characterizations. J. Cryst. Growth 2010, 312, 1860–1865. [Google Scholar] [CrossRef]
- Surovtsev, N.V.; Adichtchev, S.V.; Malinovsky, V.K.; Ogienko, A.G.; Drebushchak, V.A.; Manakov, A.Y.; Ancharov, A.I.; Yunoshev, A.S.; Boldyreva, E.V. Glycine phases formed from frozen aqueous solutions: Revisited. J. Chem. Phys. 2012, 137, 065103. [Google Scholar] [CrossRef]
- Yang, X.; Wang, X.; Ching, C.B. Solubility of form α and form γ of glycine in aqueous solutions. J. Chem. Eng. Data 2008, 53, 1133–1137. [Google Scholar] [CrossRef]
- Szilágyi, B. External fine particle removal for crystallization processes: Introduction and systematic comparison with the temperature cycling-based fines removal. Chem. Eng. Process. 2022, 179, 109074. [Google Scholar] [CrossRef]




| Experiment | L1 | L2 | L3 |
|---|---|---|---|
| Seed loading (percent of dissolved mass) | 1.041 | 0.91 | 0.85 |
| Experiment | D1 | D2 | D3 |
|---|---|---|---|
| Upper counts limit | 29,000 | 10,000 | 7500 |
| Counts setpoint | 25,000 | 8000 | 6000 |
| Lower counts limit | 22,000 | 6000 | 5500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Budimir Sacher, J.; Bolf, N.; Sejdić, M. Batch Cooling Crystallization of a Model System Using Direct Nucleation Control and High-Performance In Situ Microscopy. Crystals 2024, 14, 1079. https://doi.org/10.3390/cryst14121079
Budimir Sacher J, Bolf N, Sejdić M. Batch Cooling Crystallization of a Model System Using Direct Nucleation Control and High-Performance In Situ Microscopy. Crystals. 2024; 14(12):1079. https://doi.org/10.3390/cryst14121079
Chicago/Turabian StyleBudimir Sacher, Josip, Nenad Bolf, and Marko Sejdić. 2024. "Batch Cooling Crystallization of a Model System Using Direct Nucleation Control and High-Performance In Situ Microscopy" Crystals 14, no. 12: 1079. https://doi.org/10.3390/cryst14121079
APA StyleBudimir Sacher, J., Bolf, N., & Sejdić, M. (2024). Batch Cooling Crystallization of a Model System Using Direct Nucleation Control and High-Performance In Situ Microscopy. Crystals, 14(12), 1079. https://doi.org/10.3390/cryst14121079






