First-Principles Calculations of the Structural, Mechanical, Optical, and Electronic Properties of X2Bi4Ti5O18 (X = Pb, Ba, Ca, and Sr) Bismuth-Layered Materials for Photovoltaic Applications
Abstract
1. Introduction
2. Methodology
3. Results and Discussion
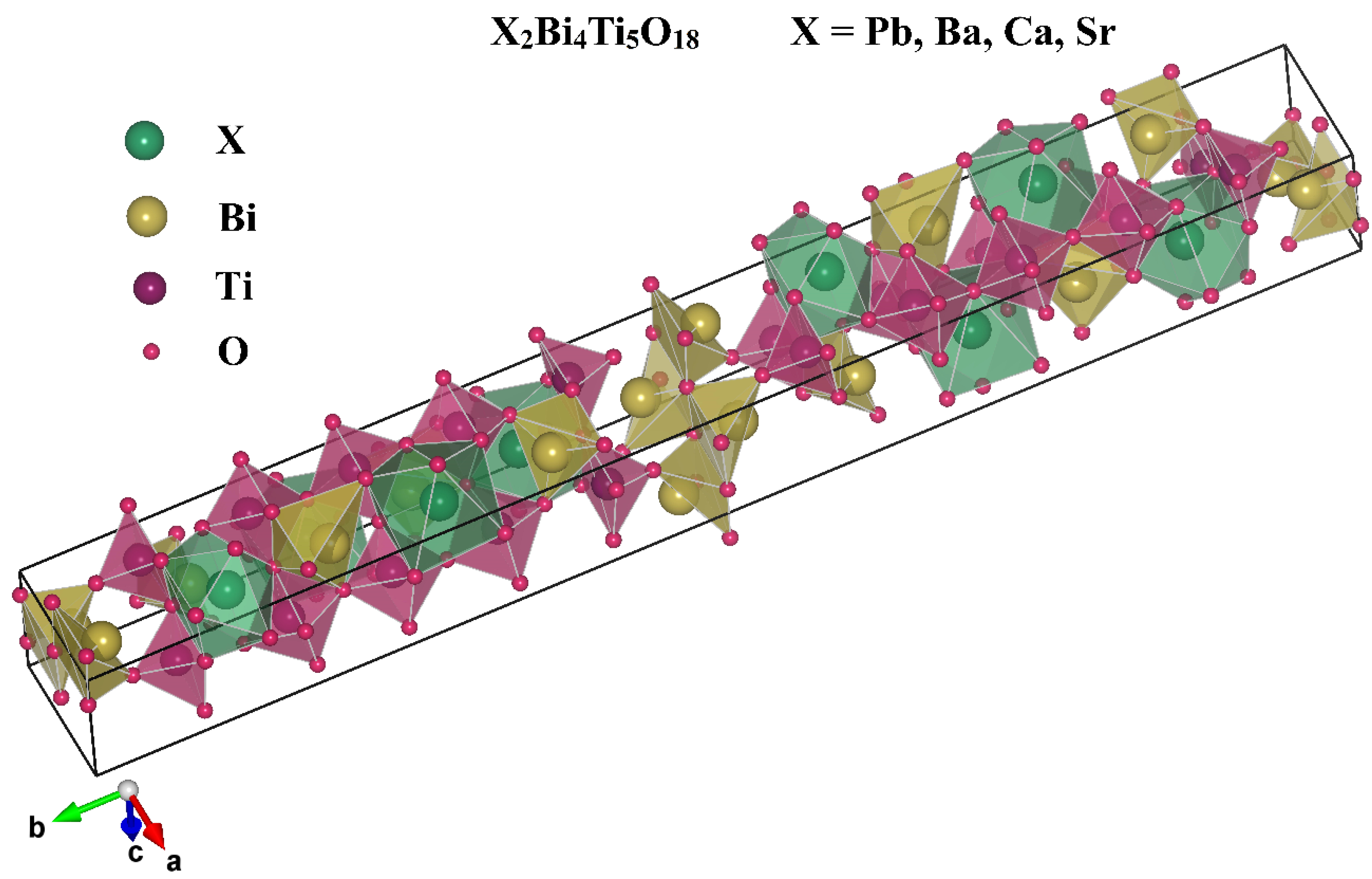
3.1. Structural Properties
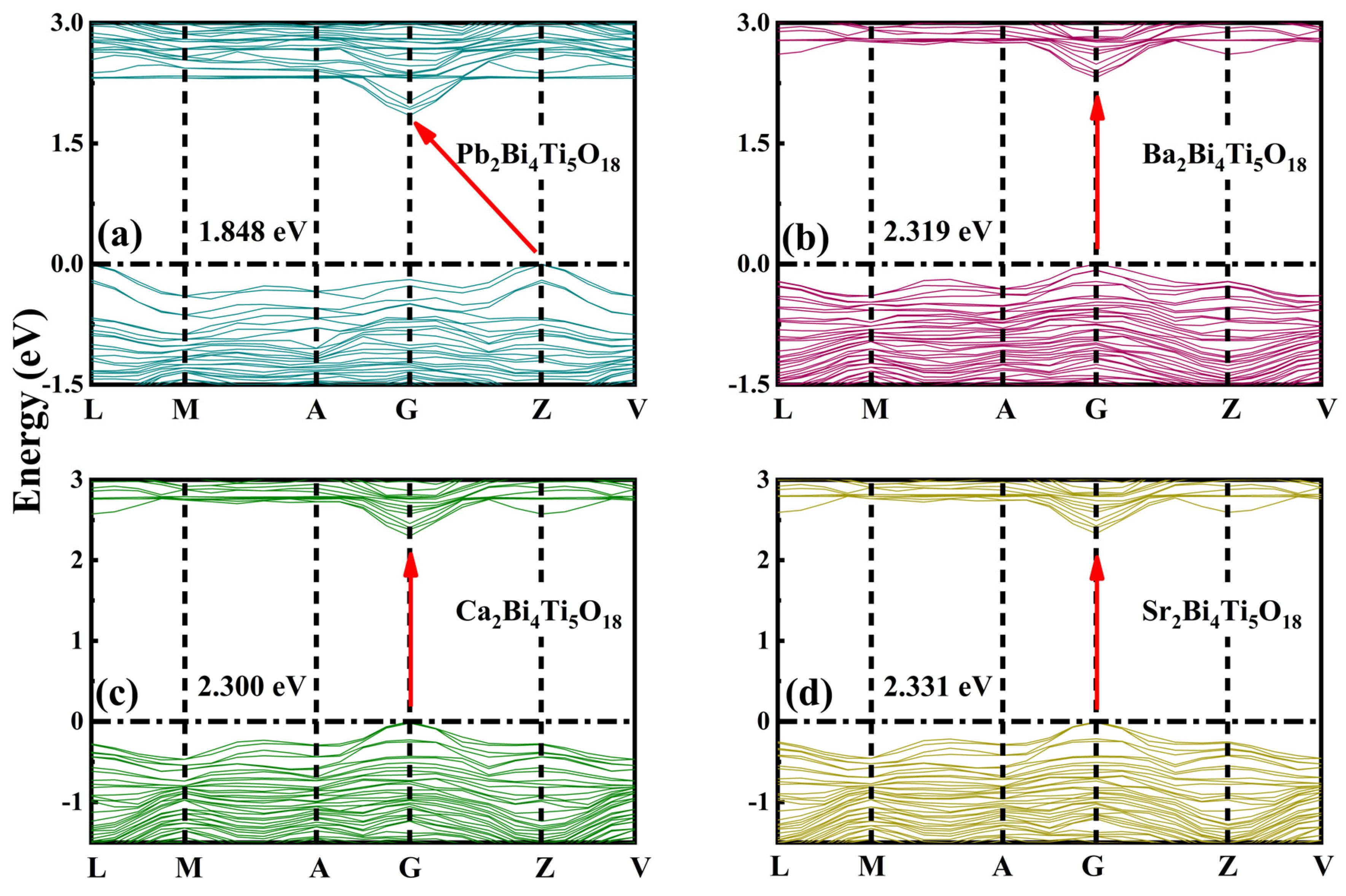
3.2. Band Structure
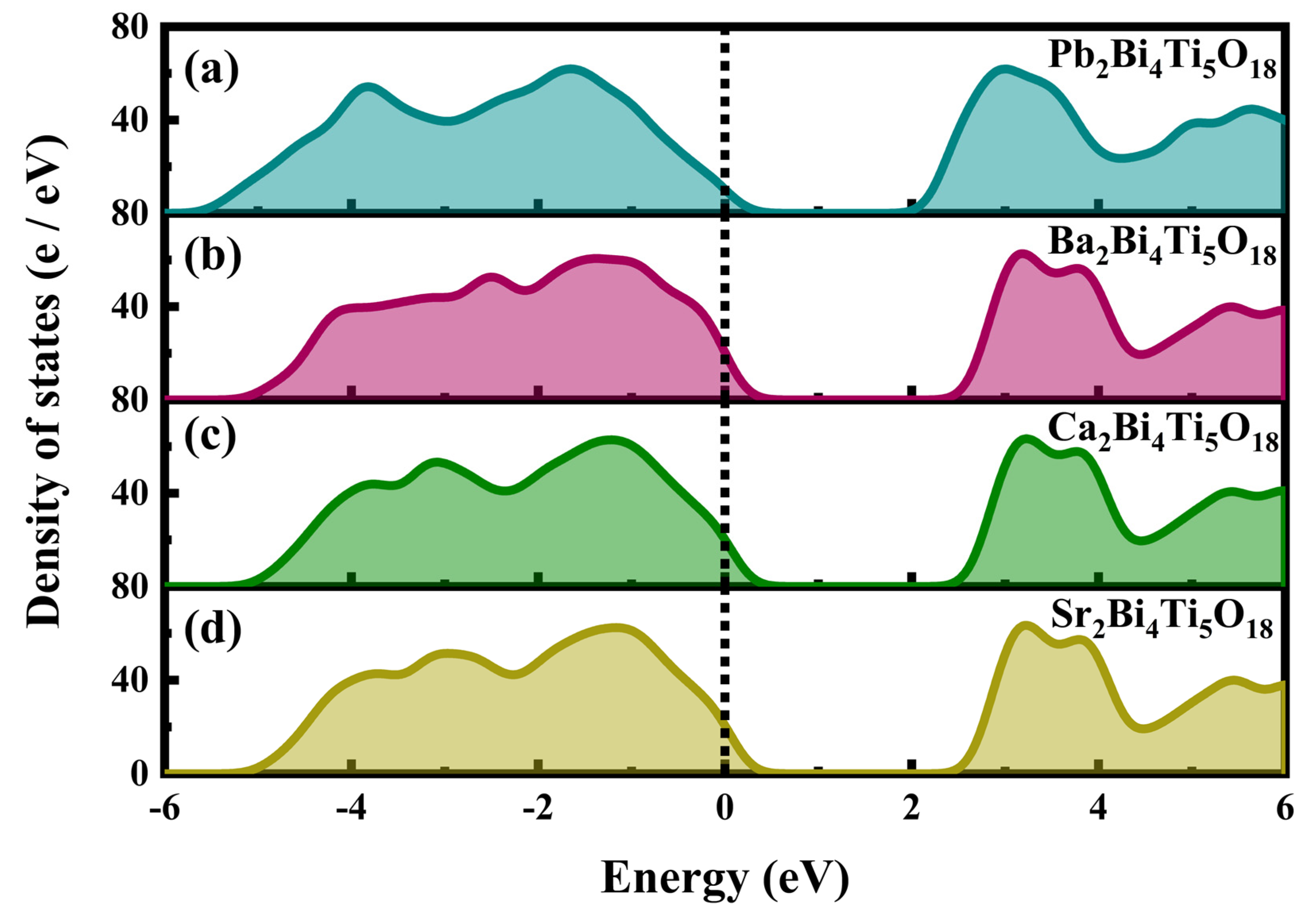
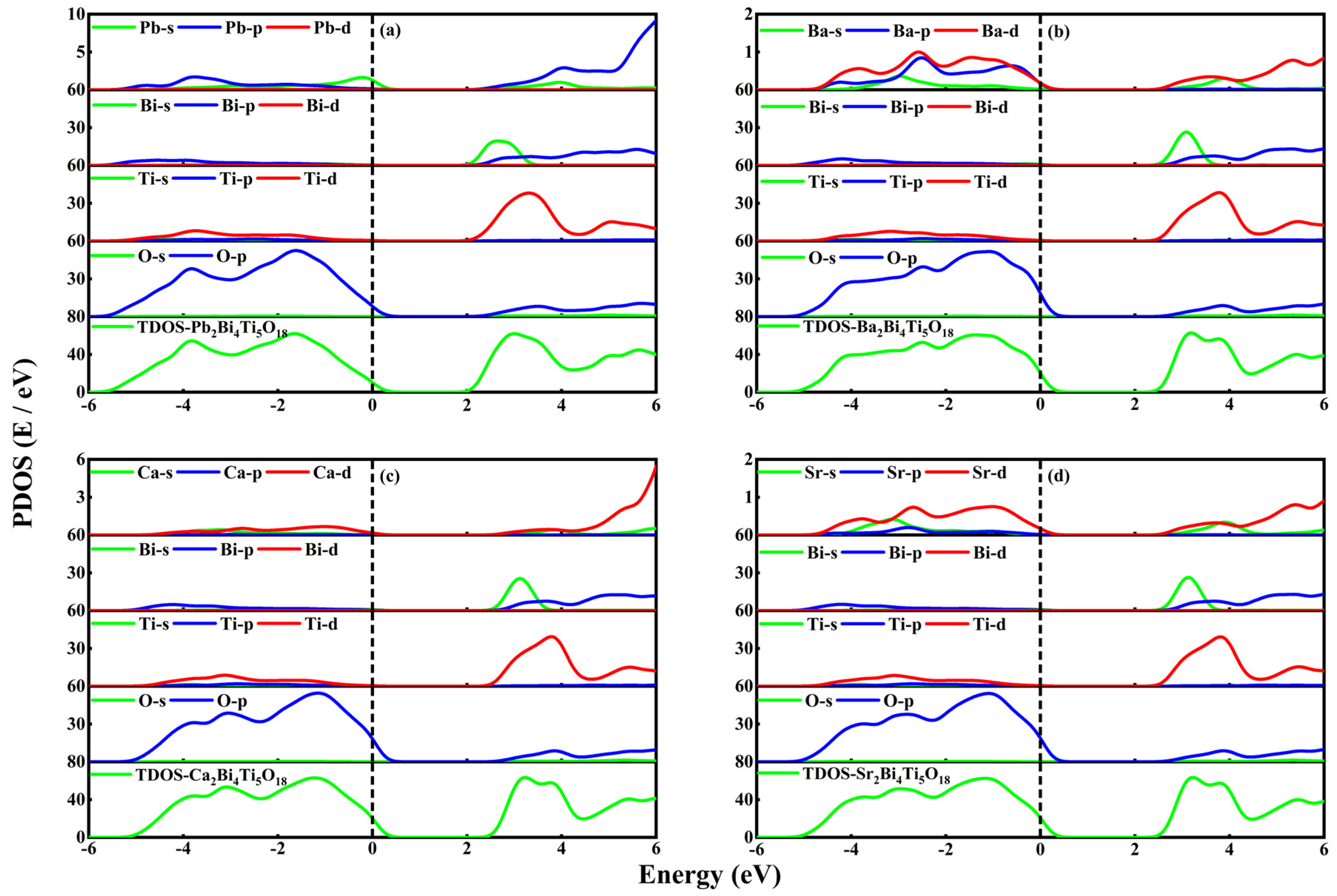
3.3. Density of States
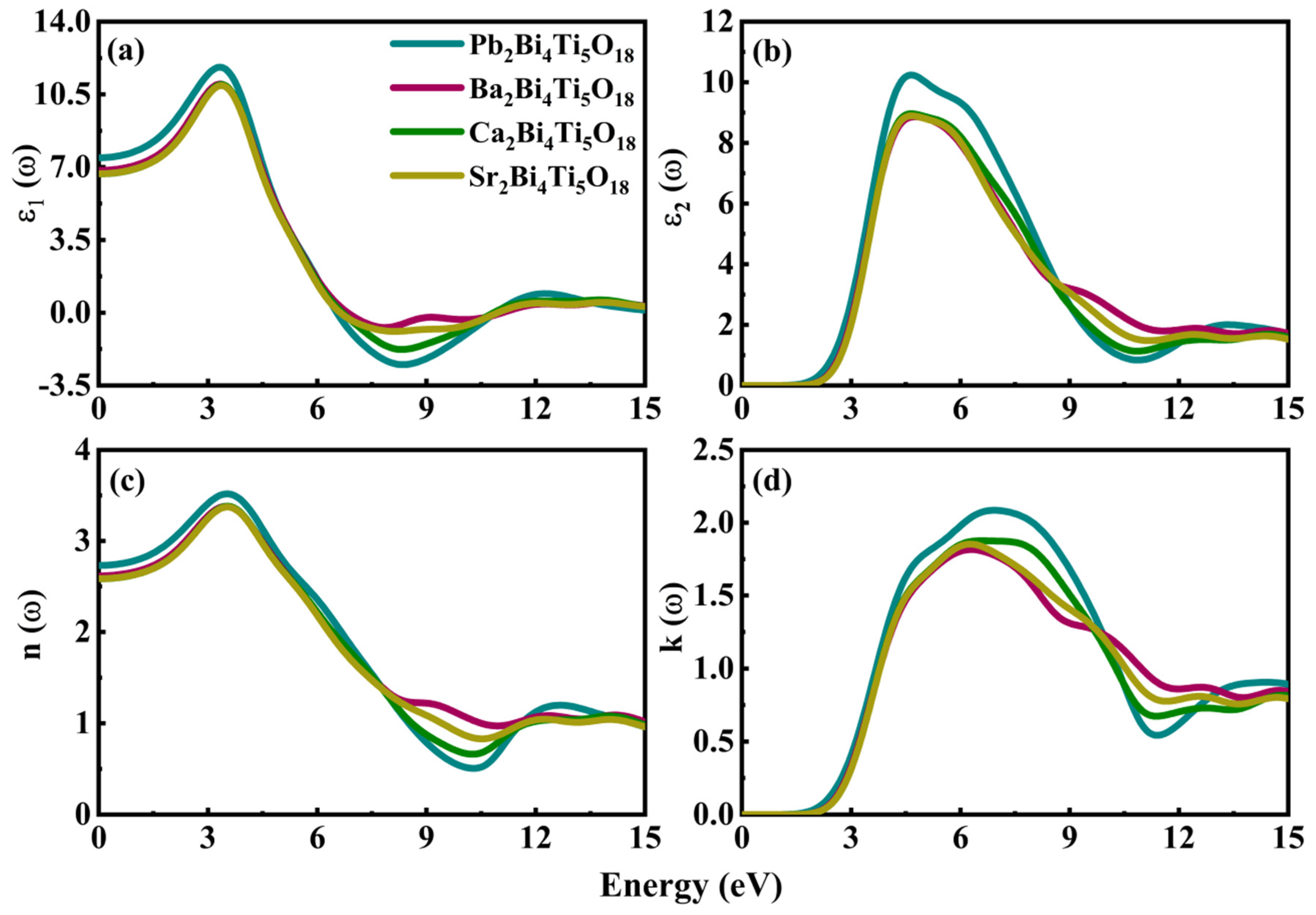
3.4. Dielectric and Optical Properties
3.5. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rabaia, M.K.H.; Abdelkareem, M.A.; Sayed, E.T.; Elsaid, K.; Chae, K.J.; Wilberforce, T.; Olabi, A.G. Environmental impacts of solar energy systems: A review. Sci. Total Environ. 2021, 754, 141989. [Google Scholar] [CrossRef] [PubMed]
- Güney, T. Solar energy and sustainable development: Evidence from 35 countries. Int. J. Sustain. Dev. World Ecol. 2022, 29, 187–194. [Google Scholar] [CrossRef]
- Kabir, E.; Kumar, P.; Kumar, S.; Adelodun, A.A.; Kim, K.H. Solar energy: Potential and future prospects. Renew. Sustain. Energy Rev. 2018, 82, 894–900. [Google Scholar] [CrossRef]
- Hernández-Callejo, L.; Gallardo-Saavedra, S.; Alonso-Gómez, V. A review of photovoltaic systems: Design, operation and maintenance. Sol. Energy 2019, 188, 426–440. [Google Scholar] [CrossRef]
- Chaves, A.; Azadani, J.G.; Alsalman, H.; Da Costa, D.R.; Frisenda, R.; Chaves, A.J.; Song, S.H.; Kim, Y.D.; He, D.; Zhou, J.; et al. Bandgap engineering of two-dimensional semiconductor materials. NPJ 2D Mater. Appl. 2020, 4, 29. [Google Scholar] [CrossRef]
- Yang, T.; Wang, M.; Duan, C.; Hu, X.; Huang, L.; Peng, J.; Huang, F.; Gong, X. Inverted polymer solar cells with 8.4% efficiency by conjugated polyelectrolyte. Energy Environ. Sci. 2012, 5, 8208–8214. [Google Scholar] [CrossRef]
- Li, X.; Choy, W.C.; Huo, L.; Xie, F.; Sha, W.E.I.; Ding, B.; Guo, X.; Li, Y.; Hou, J.; You, J.; et al. Dual plasmonic nanostructures for high performance inverted organic solar cells. Adv. Mater. 2012, 24, 3046–3052. [Google Scholar] [CrossRef]
- He, Z.; Zhong, C.; Su, S.; Xu, M.; Wu, H.; Cao, Y. Enhanced power-conversion efficiency in polymer solar cells using an inverted device structure. Nat. Photonics 2012, 6, 591–595. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.; Xu, M.; Ma, W.; Li, R.; Wang, P. Design of high-efficiency organic dyes for titania solar cells based on the chromophoric core of cyclopentadithiophene-benzothiadiazole. Energy Environ. Sci. 2013, 6, 2944–2949. [Google Scholar] [CrossRef]
- de Wild, J.; Meijerink, A.; Rath, J.K.; Van Sark, W.G.J.H.M.; Schropp, R.E.I. Upconverter solar cells: Materials and applications. Energy Environ. Sci. 2011, 4, 4835–4848. [Google Scholar] [CrossRef]
- Cao, Q.; Peng, D.; Zou, H.; Li, J.; Wang, X.; Yao, X. Up-conversion luminescence of Er3+ and Yb3+ co-doped CaBi2Ta2O9 multifunctional ferroelectrics. J. Adv. Dielectr. 2014, 4, 1450018. [Google Scholar] [CrossRef]
- Banerjee, P.; Franco, A., Jr. Role of higher valent substituent on the dielectric and optical properties of Sr0.8Bi2.2Nb2O9 ceramics. Mater. Chem. Phys. 2019, 225, 213–218. [Google Scholar] [CrossRef]
- Hussain, A.; Jabeen, N.; Hassan, N.U.; Rahman, A.U.; Khan, M.U.; Naz, A.; Yousef, E.S. Influence of Mn Ions’ Insertion in Pseudo-Tetragonal Phased CaBi4Ti4O15-Based Ceramics for Highly Efficient Energy Storage Devices and High-Temperature Piezoelectric Applications. Int. J. Mol. Sci. 2022, 23, 12723. [Google Scholar] [CrossRef] [PubMed]
- Rizwan, M.; Qaiser, M.A.; Hussain, A.; Ghazanfar, U.; Dahshan, A. Influence of MnO2 on the ferroelectric properties, energy storage efficiency and piezoelectric properties of hightemperature Bi3TaTiO9 ceramics. New J. Chem. 2024, 48, 8158–8163. [Google Scholar] [CrossRef]
- Jabeen, N.; Hussain, A.; Rahman, A.U.; Faiza, I.; El-Bahy, S.M. Novel, diverse and ultra-high ferroelectric, piezoelectric and dielectric performances of Mn added La2Ti2O7-based ceramics for high-temperature applications. Solid State Ion. 2024, 414, 116637. [Google Scholar] [CrossRef]
- Hussain, A.; Jabeen, N.; Tabassum, A.; Khan, M.U.; Basharat, L.; El Azab, I.H. Multifunctional Experimental Studies of Sm-Ion-Influenced Pseudo-Cubic Morphotropic Phase Boundary Regional BiFeO3-xSrTiO3 Ceramics for High-Temperature Applications. Crystals 2024, 14, 540. [Google Scholar] [CrossRef]
- Ramirez, M.O.; Kumar, A.; Denev, S.A.; Chu, Y.H.; Seidel, J.; Martin, L.W.; Yang, S.-Y.; Rai, R.C.; Xue, X.S.; Ihlefeld, J.F.; et al. Spin-charge-lattice coupling through resonant multimagnon excitations in multiferroic BiFeO3. Appl. Phys. Lett. 2009, 94, 161905. [Google Scholar] [CrossRef]
- Fu, H.; Zhang, L.; Yao, W.; Zhu, Y. Photocatalytic properties of nanosized Bi2WO6 catalysts synthesized via a hydrothermal process. Appl. Catal. B Environ. 2006, 66, 100–110. [Google Scholar] [CrossRef]
- Walsh, A.; Yan, Y.; Huda, M.N.; Al-Jassim, M.M.; Wei, S.H. Band edge electronic structure of BiVO4: Elucidating the role of the Bi s and V d orbitals. Chem. Mater. 2009, 21, 547–551. [Google Scholar] [CrossRef]
- Gao, F.; Chen, X.Y.; Yin, K.B.; Dong, S.; Ren, Z.F.; Yuan, F.; Yu, T.; Zou, Z.G.; Liu, J.M. Visible-light photocatalytic properties of weak magnetic BiFeO3 nanoparticles. Adv. Mater. 2007, 19, 2889–2892. [Google Scholar] [CrossRef]
- Zhang, L.W.; Wang, Y.J.; Cheng, H.Y.; Yao, W.Q.; Zhu, Y.F. Synthesis of Porous Bi2WO6 Thin Films as Efficient Visible-Light-Active Photocatalysts. ChemInform 2009, 40. [Google Scholar] [CrossRef]
- Joshi, U.A.; Jang, J.S.; Borse, P.H.; Lee, J.S. Microwave synthesis of single-crystalline perovskite BiFeO3 nanocubes for photoelectrode and photocatalytic applications. Appl. Phys. Lett. 2008, 92, 242106. [Google Scholar] [CrossRef]
- Yi, H.T.; Choi, T.; Choi, S.G.; Oh, Y.S.; Cheong, S.W. Mechanism of the switchable photovoltaic effect in ferroelectric BiFeO3. Adv. Mater. 2011, 23, 3403–3407. [Google Scholar] [CrossRef] [PubMed]
- Shu, H.B.; Sun, L.Z.; Zhong, X.L.; Wang, J.B.; Zhou, Y.C. Bonding mechanism and relaxation energy of SrBi2B2O9 (B = Ta, Nb): First-principles study. J. Phys. Chem. Solids 2009, 70, 707–712. [Google Scholar] [CrossRef]
- Li, Q.; Wang, J.; Li, M.; Guo, S.; Zhang, J.; Hu, Z.; Zhou, Z.; Wang, G.; Dong, X.; Chu, J. Structure evolution mechanism of Na0.5Bi2.5Nb2−xWxO9+δ ferroelectric ceramics: Temperature-dependent optical evidence and first-principles calculations. Phys. Rev. B 2017, 96, 024101. [Google Scholar] [CrossRef]
- Kainat, F.; Jabeen, N.; Yaqoob, A.; Hassan, N.U.; Hussain, A.; Khalifa, M.E. Effect of Ca, Ba, Be, Mg, and Sr Substitution on Electronic and Optical Properties of XNb2Bi2O9 for Energy Conversion Application Using Generalized Gradient Approximation–Perdew–Burke–Ernzerhof. Crystals 2024, 14, 710. [Google Scholar] [CrossRef]
- Li, G.; He, C.; Xiong, Y.; Zou, Z.; Liu, Y.; Chen, Q.; Zhang, W.; Yan, S.; Xiao, Y.; Tang, M.; et al. Coexistence of ferroelectricity and metallicity in M-doped BaTiO3 (M = Al, V, Cr, Fe, Ni, and Nb): First-principles study. Mater. Today Commun. 2021, 27, 102394. [Google Scholar] [CrossRef]
- Wu, L.; Luo, B.; Tian, E. Ferroelectric properties of BaTiO3-BiScO3 weakly coupled relaxor energy-storage ceramics from first-principles calculations. J. Alloys Compd. 2021, 866, 158933. [Google Scholar] [CrossRef]
- Stambouli, N.B.; Ouahrani, T.; Badawi, M.; Reshak, A.H.; Azizi, S. Untangling electronic, optical and bonding properties of hexagonal bismuth borate SrBi2B2O7 crystal for ultraviolet opto-electronic applications: An ab initio study. J. Alloys Compd. 2019, 803, 1127–1135. [Google Scholar] [CrossRef]
- Cai, M.Q.; Yin, Z.; Zhang, M.S.; Li, Y.Z. Electronic structure of the ferroelectric-layered perovskite bismuth titanate by ab initio calculation within density functional theory. Chem. Phys. Lett. 2004, 399, 89–93. [Google Scholar] [CrossRef]
- Han, J.Y.; Bark, C.W. Structural and optical properties of Fe doped bismuth titanate thin film deposited by RF sputtering. Jpn. J. Appl. Phys. 2016, 55, 02BC09. [Google Scholar] [CrossRef]
- Hussain, A.; Jabeen, N.; Rahman, A.U.; Qaiser, M.A.; Tariq, Z.; Abd El-Gawad, H.H. Experimental and theoretical study of Gd2O3 added pseudo-tetragonal Bi3TaTiO9-based ceramics for ferroelectric, electric and high-temperature piezoelectric applications. Ceram. Int. 2024, 50, 18177–18184. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Momin, M.A.; Islam, M.A.; Nesa, M.; Sharmin, M.; Rahman, M.J.; Bhuiyan, A.H. Effect of M (Ni, Cu, Zn) doping on the structural, electronic, optical, and thermal properties of CdI2: DFT based theoretical studies. AIP Adv. 2021, 11, 055203. [Google Scholar] [CrossRef]
- Faizan, M.; Bhamu, K.C.; Murtaza, G.; He, X.; Kulhari, N.; AL-Anazy, M.M.; Khan, S.H. Electronic and optical properties of vacancy ordered double perovskites A2BX6 (A = Rb, Cs; B = Sn, Pd, Pt; and X = Cl, Br, I): A first principles study. Sci. Rep. 2021, 11, 6965. [Google Scholar] [CrossRef]
- Desjarlais, M.P. Density functional calculations of the reflectivity of shocked xenon with ionization based gap corrections. Contrib. Plasma Phys. 2005, 45, 300–304. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Hadi, M.A. New ternary nanolaminated carbide Mo2Ga2C: A first-principles comparison with the MAX phase counterpart Mo2GaC. Comput. Mater. Sci. 2016, 117, 422–427. [Google Scholar] [CrossRef]
- Gao, X.P.; Jiang, Y.H.; Liu, Y.Z.; Zhou, R.; Feng, J. Stability and elastic properties of NbxCy compounds. Chin. Phys. B 2014, 23, 097704. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]

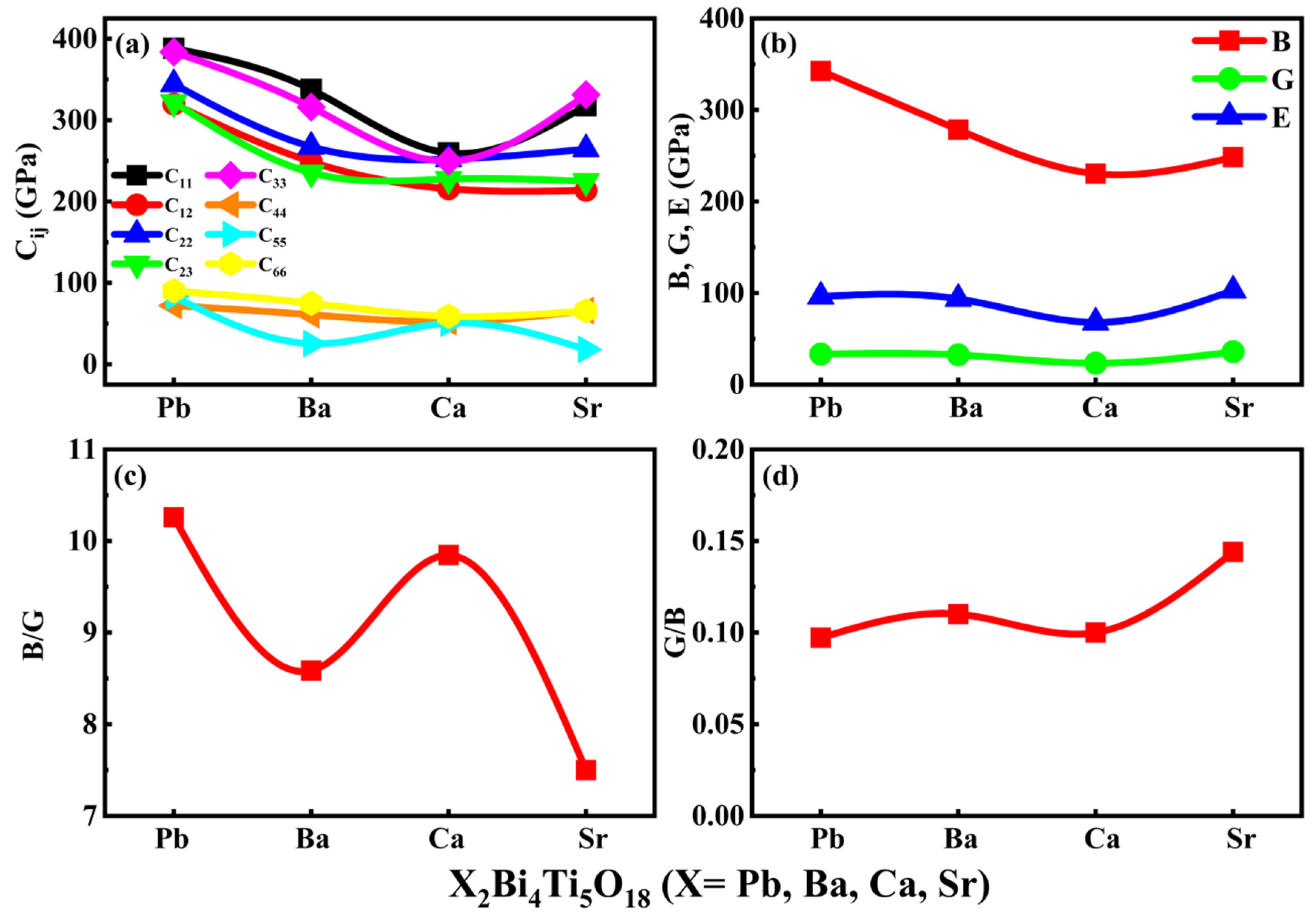
| NAME | Pb2Bi4Ti5O18 | Ba2Bi4Ti5O18 | Ca2Bi4Ti5O18 | Sr2Bi4Ti5O18 |
|---|---|---|---|---|
| C11 | 308.61 | 309.02 | 278.90 | 285.10 |
| C12 | 275.85 | 267.58 | 239.51 | 250.68 |
| C22 | 325.12 | 321.62 | 259.26 | 257.94 |
| C33 | 294.90 | 320.07 | 265.49 | 272.27 |
| C44 | 35.83 | 80.45 | 56.41 | 58.66 |
| C55 | 97.43 | 81.74 | 76.31 | 81.05 |
| C66 | 51.01 | 64.48 | 58.86 | 61.49 |
| B | 342.673 | 278.48 | 230.343 | 248.34 |
| G | 16.45 | 93.64 | 67.972 | 102.72 |
| E | 33.4 | 32.42 | 23.392 | 35.891 |
| B/G | 10.259 | 8.587 | 9.847 | 7.5 |
| G/B | 0.09 | 0.11 | 0.1 | 0.144 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Kainat, F.; Jabeen, N.; Yaqoob, A.; Abbas, T.; Khan, M.U.; Qaiser, M.A.; Mahmoud, M.H.H. First-Principles Calculations of the Structural, Mechanical, Optical, and Electronic Properties of X2Bi4Ti5O18 (X = Pb, Ba, Ca, and Sr) Bismuth-Layered Materials for Photovoltaic Applications. Crystals 2024, 14, 870. https://doi.org/10.3390/cryst14100870
Hussain A, Kainat F, Jabeen N, Yaqoob A, Abbas T, Khan MU, Qaiser MA, Mahmoud MHH. First-Principles Calculations of the Structural, Mechanical, Optical, and Electronic Properties of X2Bi4Ti5O18 (X = Pb, Ba, Ca, and Sr) Bismuth-Layered Materials for Photovoltaic Applications. Crystals. 2024; 14(10):870. https://doi.org/10.3390/cryst14100870
Chicago/Turabian StyleHussain, Ahmad, Fatima Kainat, Nawishta Jabeen, Ali Yaqoob, Tassawar Abbas, Muhammad Usman Khan, Muhammad Adnan Qaiser, and M. H. H. Mahmoud. 2024. "First-Principles Calculations of the Structural, Mechanical, Optical, and Electronic Properties of X2Bi4Ti5O18 (X = Pb, Ba, Ca, and Sr) Bismuth-Layered Materials for Photovoltaic Applications" Crystals 14, no. 10: 870. https://doi.org/10.3390/cryst14100870
APA StyleHussain, A., Kainat, F., Jabeen, N., Yaqoob, A., Abbas, T., Khan, M. U., Qaiser, M. A., & Mahmoud, M. H. H. (2024). First-Principles Calculations of the Structural, Mechanical, Optical, and Electronic Properties of X2Bi4Ti5O18 (X = Pb, Ba, Ca, and Sr) Bismuth-Layered Materials for Photovoltaic Applications. Crystals, 14(10), 870. https://doi.org/10.3390/cryst14100870









