Asymptotic Solutions of Steady Lamellar Eutectic Growth in Directional Solidification for Small Tangent Values of the Contact Angles
Abstract
1. Introduction
2. Mathematical Formulation
3. Outer Solutions in the Region Far from the Liqiud–Solid Interface
4. Solutions in the Region Near the Liquid–Solid Interface
5. Uniformly Valid Solutions
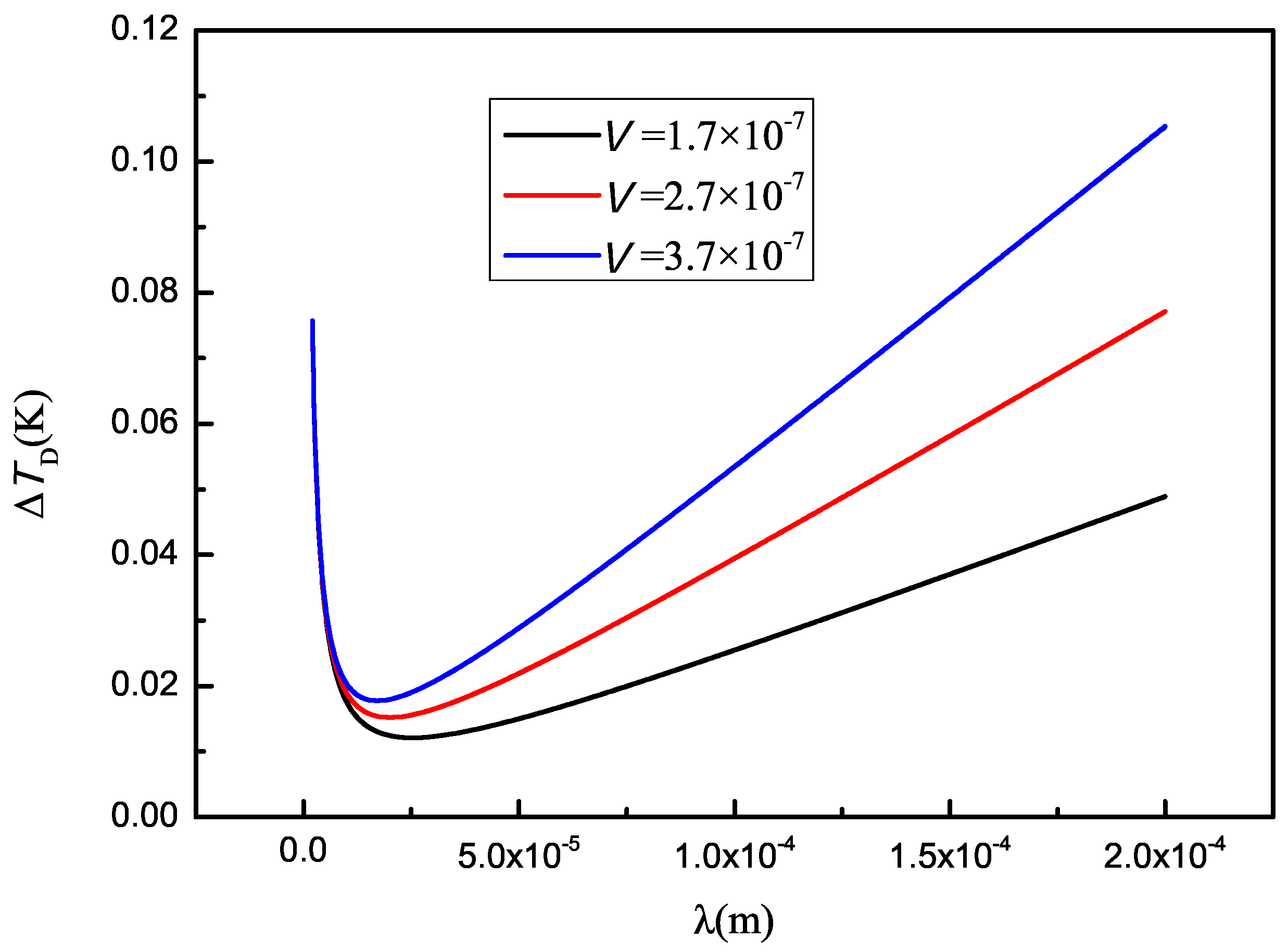
6. Average Undercooling of the Solid–Liquid Interface
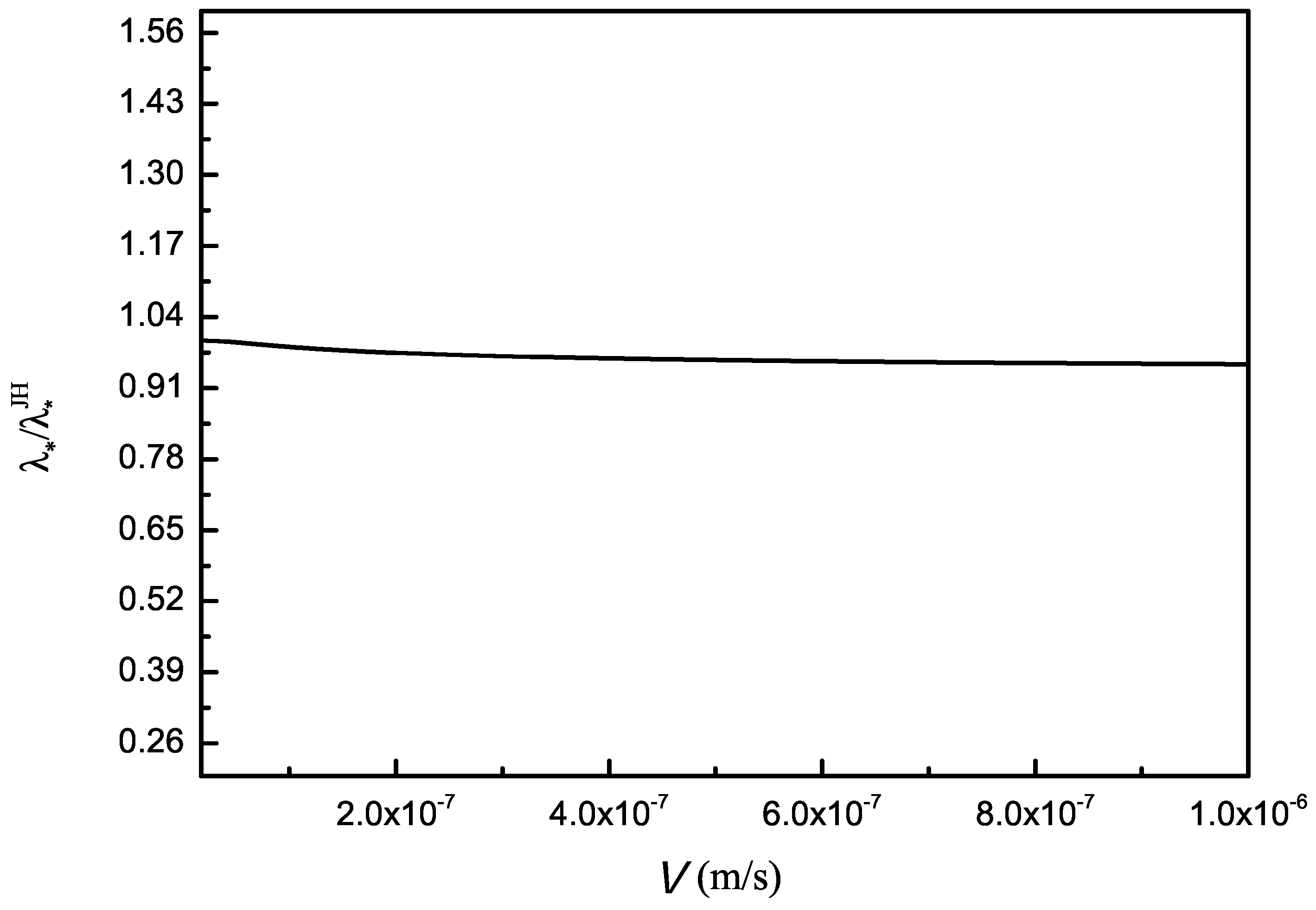
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Glicksman, M.E. Principles of Soldification; Springer: London, UK, 2011; pp. 398–424. [Google Scholar]
- Faivre, G. Morphological instabilities of lamellar eutectic growth fronts: A survey of recent experimental and numerical results. J. Cryst. Growth 1996, 166, 29–39. [Google Scholar] [CrossRef]
- Ginibre, M.; Akamatsu, S.; Faivre, G. Experimental determination of the stability diagram of a lamellar eutectic growth front. Phys. Rev. E 1997, 56, 780–796. [Google Scholar] [CrossRef]
- Mergy, J.; Faivre, G.; Guthmann, C.C.; Mellet, R. Quantitative determination of the physical parameters relevant to the thin-film directional solidification of the CBr4-C2Cl6 eutectic alloy. J. Cryst. Growth 1981, 134, 353–368. [Google Scholar] [CrossRef]
- Akamatsu, S.; Plapp, S.; Faivre, G.; Karma, A. Pattern stability and trijunction motion in eutectic solidification. Phys. Rev. E 2002, 66, 030501. [Google Scholar] [CrossRef] [PubMed]
- Bottin-Rousseau, S.; Medjkoune, M.; Senninger, O.; Carroz, L.; Soucek, R.; Hecht, U.; Akamatus, S. Loked-lamellar eutectic growth in thin Al-Al2Cu samples: In situ directional solidification and crystal orientation analysis. J. Cryst. Growth 2021, 570, 126203. [Google Scholar] [CrossRef]
- Bottin-Rousseau, S.; Witusiewicz, V.; Hecht, U.; Fernandez, J.; Laveron-Simavilla, A.; Akamatus, S. Coexistence of rod-like and lamellar eutectic growth patterns. Scr. Mater. 2022, 207, 11314. [Google Scholar] [CrossRef]
- Serefoglu, M.; Bottin-Rousseau, S.; Akamatsu, S. Lamella-rod pattern transition and confinement effects during eutectic growth. Acta Mater. 2023, 242, 118425. [Google Scholar] [CrossRef]
- Liu, J.; Elliott, R. A numerical model for eutectic spacing selection in the CBr4C2cl6 eutectic system. J. Cryst. Growth 1995, 148, 406–414. [Google Scholar] [CrossRef]
- Pusztai, T.; Tatkai, L.; Szallas, A.; Granasy, L. Spiraling eutectic dendrites. Phys. Rev. E 2013, 87, 032401. [Google Scholar] [CrossRef]
- Folch, R.; Plapp, M. Quantitative phase-field modeling of two-phase growth. Phys. Rev. E 2005, 72, 011602. [Google Scholar] [CrossRef]
- Feng, L.; Feng, X.; Lu, Y.; Zhu, C.; Jia, B. Phase field modeling of lamellar eutectic growth under the influence of fluid flow. Comp. Mater. Sci. 2017, 137, 171–178. [Google Scholar] [CrossRef]
- Zhang, A.; Guo, Z.; Xiong, S.M. Quantitative phase-field lattice-Boltzmann study of lamellar eutectic growth under natural convection. Phys. Rev. E 2018, 97, 053302. [Google Scholar] [CrossRef] [PubMed]
- Lei, W.; Cao, Y.; Xin, L.; Kun, C.; Huang, W. Globular to lamellar transition during anomalous eutectic growth. Model. Simul. Mater. Sci. Eng. 2020, 28, 065014. [Google Scholar] [CrossRef]
- Pusztai, T.; Ratkai, L.; Horvath, L.; Granasy, L. Phase-field modeling of directional melting lamellar and rod eutectic structures. Acta Mater. 2022, 227, 117678. [Google Scholar] [CrossRef]
- Tu, Z.; Zhou, J.; Tong, L.; Guo, Z. A phase-field study of lamellar eutectic growth with solid-solid boundary anisotropy. J. Cryst. Growth 2019, 532, 125439. [Google Scholar] [CrossRef]
- Akamatsu, S.; Bottin-Rousseau, S. Numerical Simulations of Locked Lamellar Eutectic Growth Patterns. Metall. Mater. Trans. A 2021, 52, 4533–4545. [Google Scholar] [CrossRef]
- Ogawa, J.; Natsume, Y. Cellular automaton model for predicting the three-dimensional eutectic structure of binary alloys. Comp. Mater. Sci. 2021, 195, 110497. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, A.; Jiang, B.; Gao, L.; Guo, Z.; Song, J.; Xiong, S.; Pan, F. Numerical investigation of eutectic growth dynamics under convection by 3D phase-field method. Comp. Math. App. 2022, 114, 83–94. [Google Scholar] [CrossRef]
- Seiz, M.; Kellner, M.; Nestler, B. Simulation of dendritic-eutectic growth with the phase-field method. Acta Mater. 2023, 254, 118965. [Google Scholar] [CrossRef]
- Jackson, K.A.; Hunt, J.D. Lamellar and rod eutectic growth. Trans. Metall. Soc. AIME 1966, 236, 1129. [Google Scholar]
- Datye, V.; Langer, J.S. Stability of thin eutectic growth. Phys. Rev. B 1981, 24, 4155–4169. [Google Scholar] [CrossRef]
- Brattkus, K.; Caroli, B.; Caroli, C.; Roulet, B. Lamellar eutectic growth at large thermal-gradient. 1. stationary pattern. J. Phys. Fr. 1990, 51, 1847–1864. [Google Scholar] [CrossRef]
- Chen, Y.J.; Davis, S.H. Instability of triple junctions in lamellar eutectic growth. Acta Mater. 2001, 49, 1363–1372. [Google Scholar] [CrossRef]
- Akamatsu, S.; Bottin-Rousseau, S.; Serefoglu, M.; Faivre, G. A theory of thin lamellar eutectic growth with anisotropic interphase boundaries. Acta Mater. 2012, 60, 3199–3205. [Google Scholar] [CrossRef]
- Li, X.M.; Li, W.Q.; Jin, Q.L.; Zhou, R. A steady solution of the gasar eutectic growth in directional solidification. Chin. Phys. B 2022, 80, 078101. [Google Scholar] [CrossRef]
- Xu, J.J.; Li, X.M. Global steady state solutions for lamellar eutectic growth in directional solidification. J. Cryst. Growth 2014, 401, 93–98. [Google Scholar] [CrossRef]
- Xu, J.J.; Chen, Y.Q. Steady spatially-periodic eutectic growth with the effect of triple point in directional solidification. Acta Mater. 2014, 80, 220. [Google Scholar] [CrossRef]
- Li, X.M.; Xu, F. Uniformly valid asymptotic solutions of rod eutectic growth in directional solidification for contact angles being the normal order. J. Cryst. Growth 2017, 468, 945–949. [Google Scholar] [CrossRef]
- Li, X.M.; Chen, X.K.; Xu, F. Uniformly valid asymptotic solutions of rod eutectic growth in directional solidification for liquid-solid interface slopes of small order. J. Cryst. Growth 2019, 507, 453–458. [Google Scholar] [CrossRef]
- Gan, Y.L.; Li, X.M. Global instability of rod eutectic growth in directional solidification. Crystals 2023, 13, 548. [Google Scholar] [CrossRef]
- Tu, Z.; Zhou, J.; Zhang, Y.; Li, W.; Yu, W. An analytic theory for the symmetry breaking of growth-front in lamellar eutectic growth influenced by solid-solid anisotropy. J. Cryst. Growth 2020, 549, 125851. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; Li, X. Asymptotic Solutions of Steady Lamellar Eutectic Growth in Directional Solidification for Small Tangent Values of the Contact Angles. Crystals 2024, 14, 93. https://doi.org/10.3390/cryst14010093
Xiao J, Li X. Asymptotic Solutions of Steady Lamellar Eutectic Growth in Directional Solidification for Small Tangent Values of the Contact Angles. Crystals. 2024; 14(1):93. https://doi.org/10.3390/cryst14010093
Chicago/Turabian StyleXiao, Jing, and Xiangming Li. 2024. "Asymptotic Solutions of Steady Lamellar Eutectic Growth in Directional Solidification for Small Tangent Values of the Contact Angles" Crystals 14, no. 1: 93. https://doi.org/10.3390/cryst14010093
APA StyleXiao, J., & Li, X. (2024). Asymptotic Solutions of Steady Lamellar Eutectic Growth in Directional Solidification for Small Tangent Values of the Contact Angles. Crystals, 14(1), 93. https://doi.org/10.3390/cryst14010093




