Experimental Investigation of Laser Damage Limit for ZPG Infrared Single Crystal Using Deep Magnetorheological Polishing of Working Surfaces
Abstract
:1. Introduction
2. Estimation of the Influence of Various Parameters on the Magnitude of Optical Breakdown
3. Investigated Samples and Their Parameters
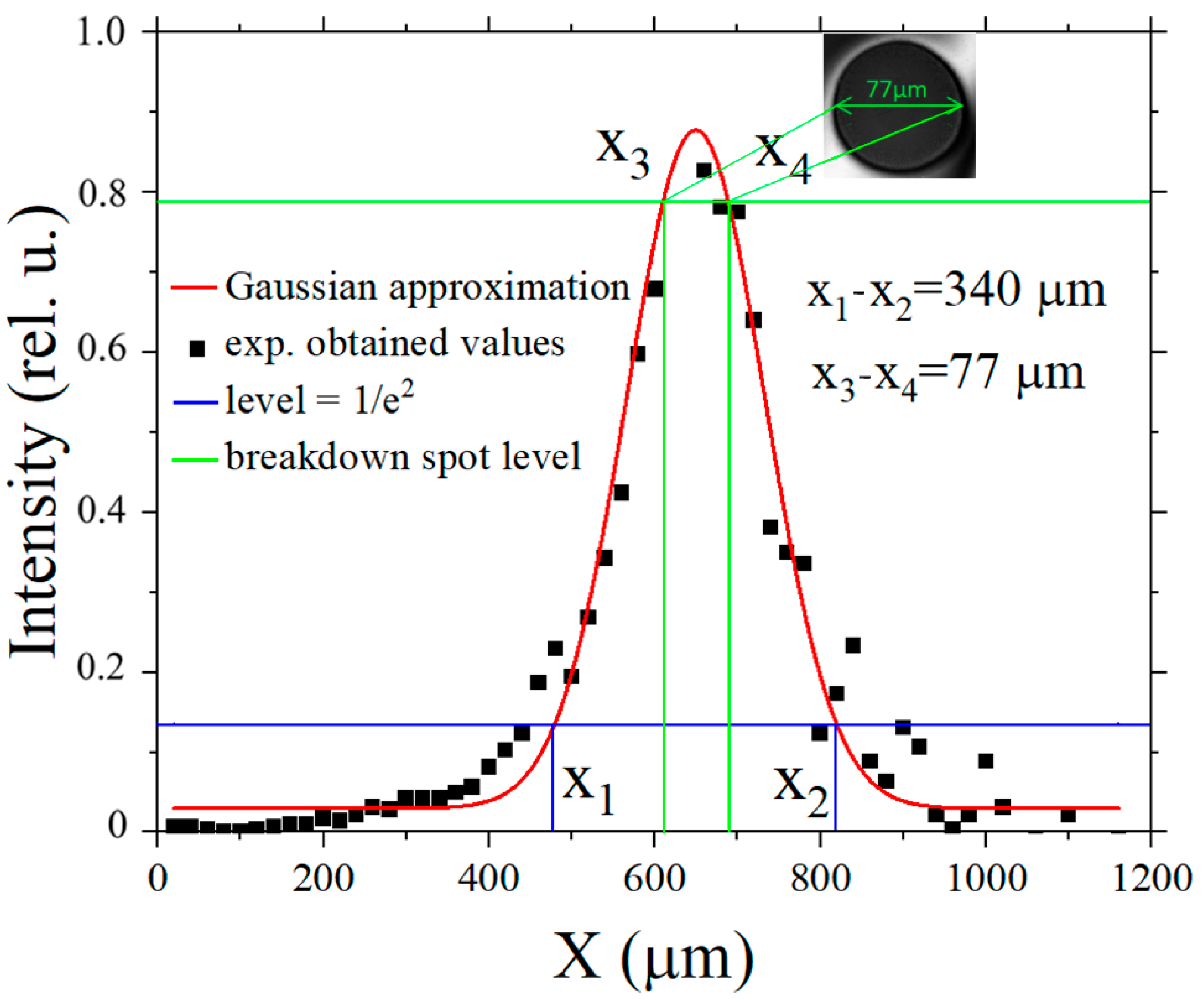
4. Parameters of the Setup and Methodology for Determining the LIDT of the Studied Samples
5. Experimental Results and Discussion
6. Conclusions
- A comprehensive assessment of the influence of various parameters on the magnitude of optical breakdown was carried out during deep removal (up to 150 μm) from the surface of a ZGP single crystal by magnetic rheological polishing.
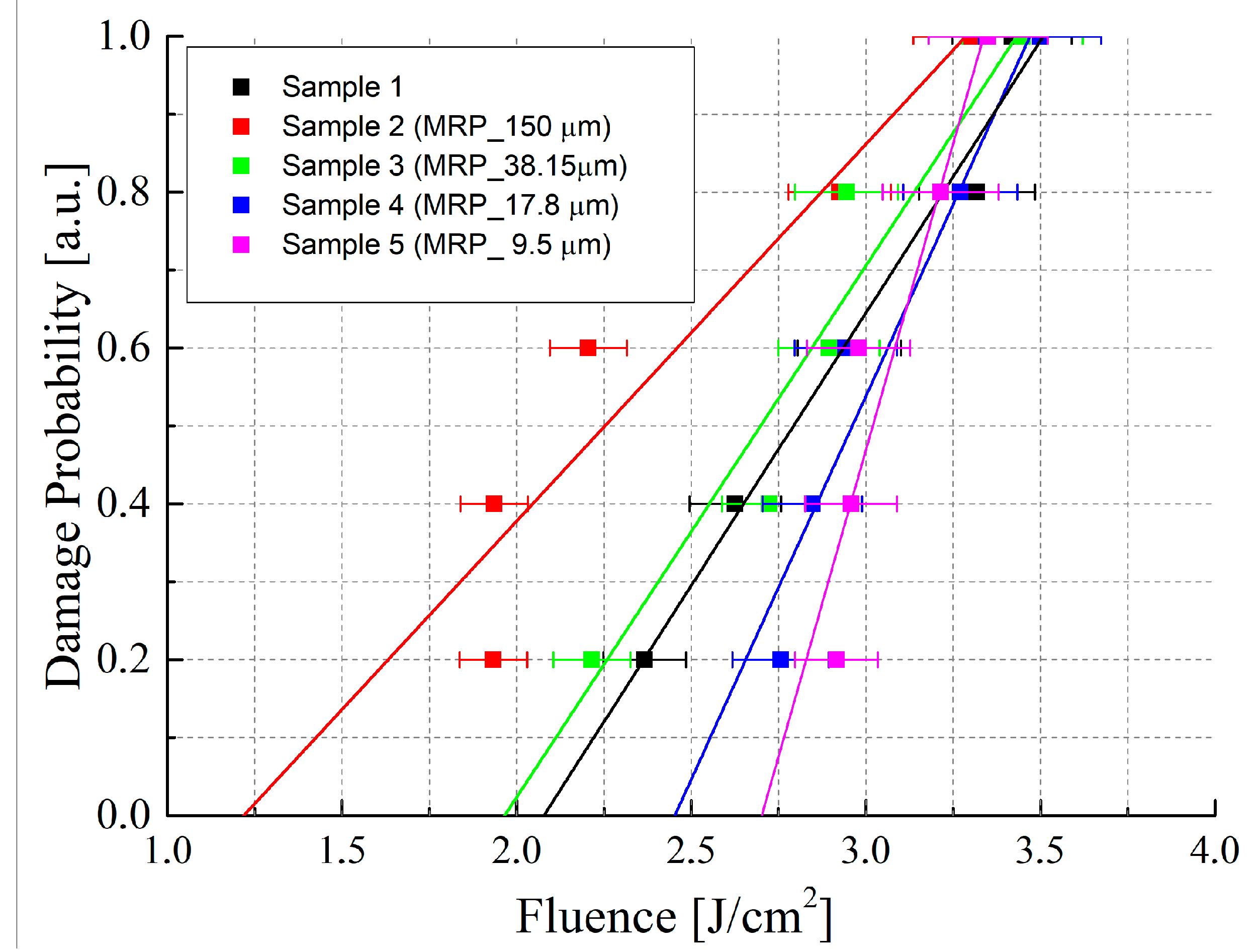
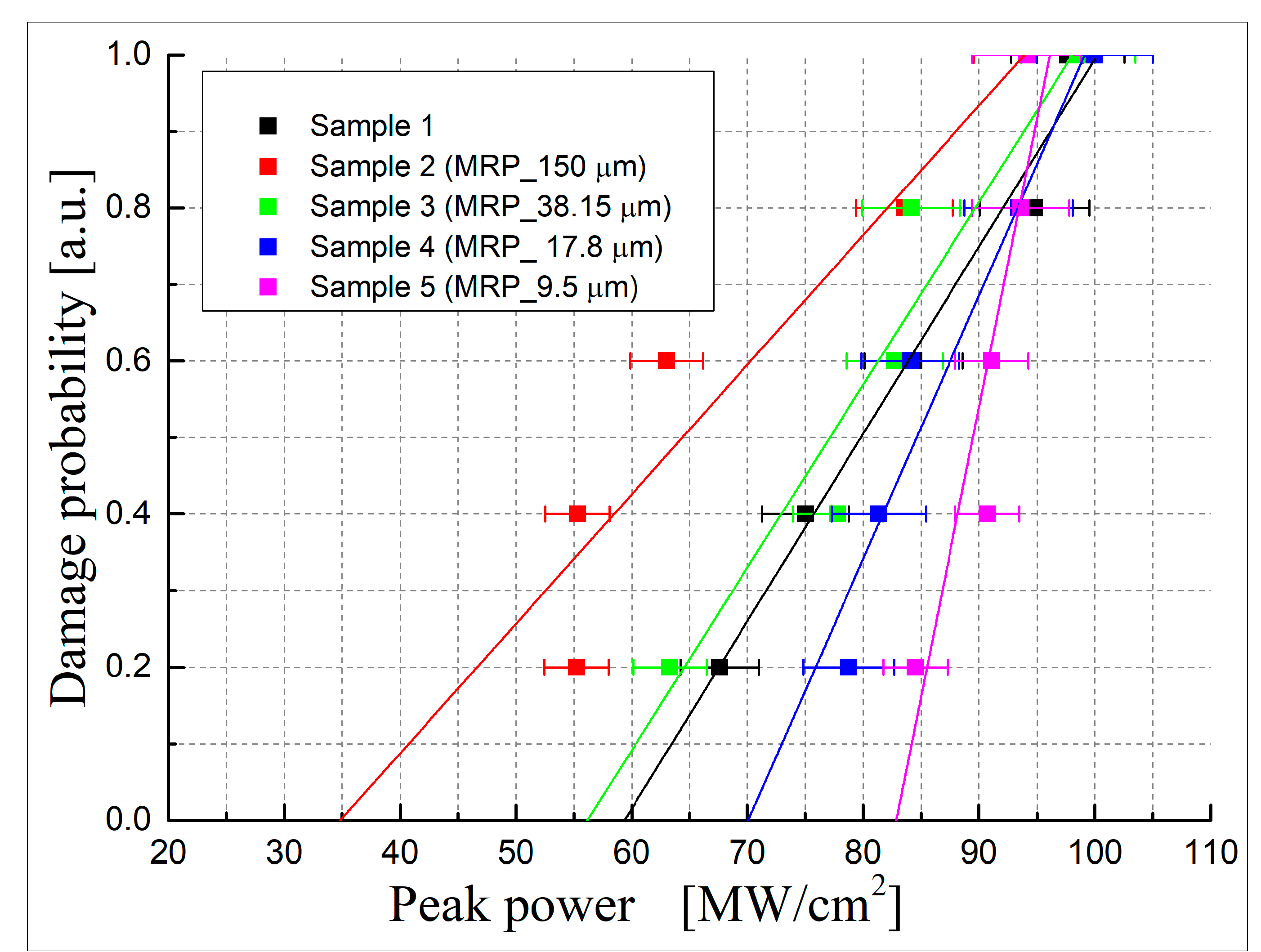
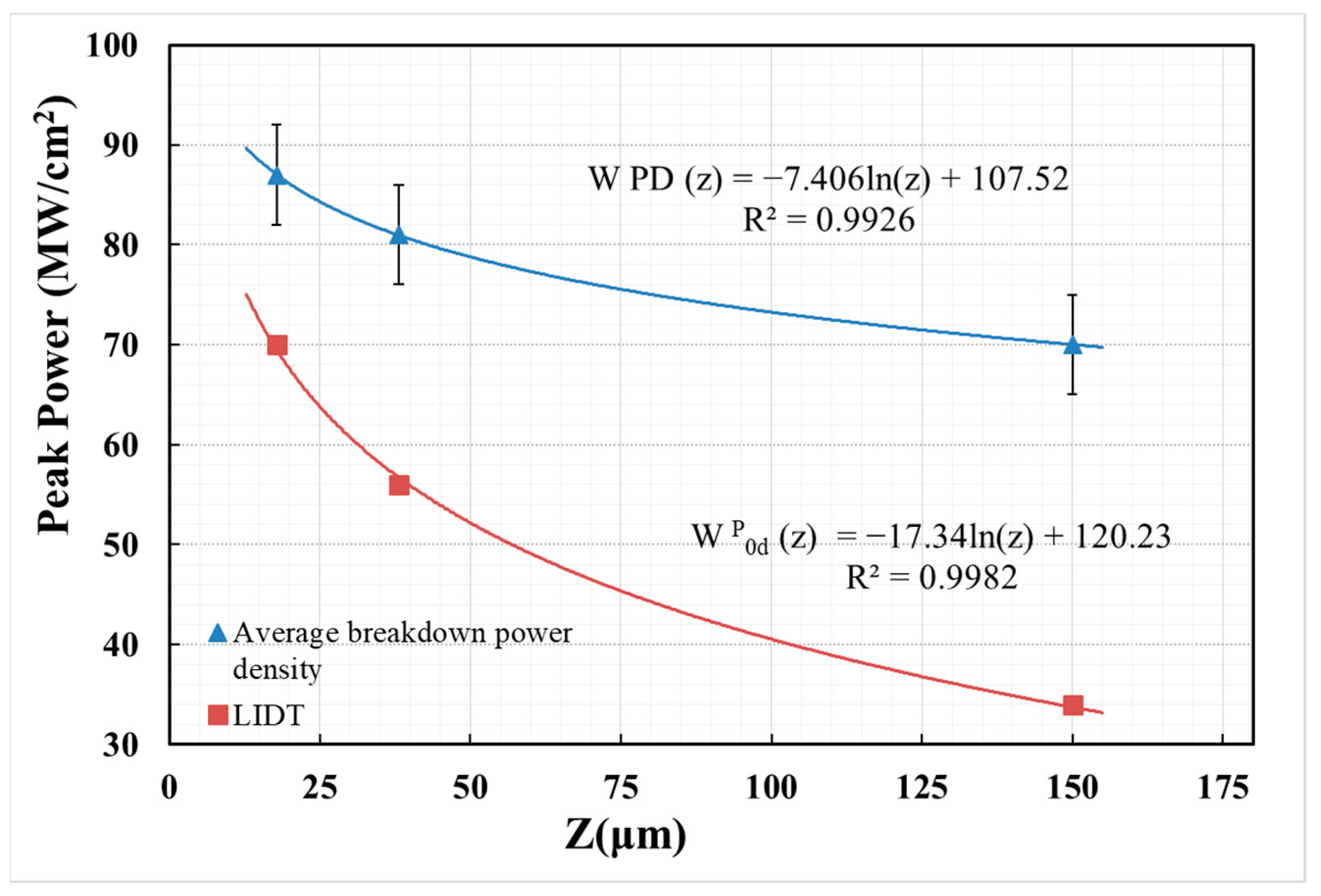
- Experimental studies of the influence of MPO polishing parameters on the LIDT of ZGP crystals were carried out. It was shown that the depth of MPO polishing has a significant effect on the LIDT of a ZGP crystal. With MPO removal of material from the surface of the crystal of more than 30 μm, a significant decrease in the LIDT of the ZGP surface was observed, whereas for the depth of MPO polishing of 17.8 μm, an increase in the LIDT was observed compared to a ZGP crystal with standard polishing. With a depth of material removal of 17.8 μm, the LIDT increased by 1.18 times.
- It was shown that the dependence of the LIDT of ZGP on the depth of MPO polishing is a smooth monotonically decreasing logarithmic function. It is assumed that the obtained logarithmic dependence indicates the thermal nature of optical breakdown and the dependence of the LIDT of ZGP on the concentration of surface absorbing defects. The obtained dependencies predict that a decrease in the depth of MPO polishing to several microns will lead to a further increase in the LIDT. However, these theoretical assumptions require experimental confirmation.
- It is recommended that, in practice, MRO processing of ZGP crystals be carried out with material removal from the surface of no more than 20 μm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, Y.; Meng, J.; Wei, T.; Xie, Z.; Jia, S.; Wenlong, T.; Zhu, J.; Wang, W. 150 Gbps multi-wavelength FSO transmission with 25-GHz ITU-T grid in the mid-infrared region. Opt. Express 2023, 31, 15156–15169. [Google Scholar] [CrossRef] [PubMed]
- Yevtushenko, A.; Rozniakowska-Klosinska, M. Encyclopedia of Thermal Stresses, Laser-Induced Thermal Splitting in Homo-Geneous Body with Coating; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Parfenov, V.A. Laser Materials Microprocessing; SPbGETU “LETI”: Sankt-Petersburg, Russia, 2011; pp. 5–11. [Google Scholar]
- Soldatov, A.N.; Vasilyeva, A.V.; Polunin, Y.P.; Kuksgauzen, D.A.; Kostyrya, I.D. Strontium vapor generator-amplifier system for bone ablation. Bio-Technosphere 2012, 3–4, 47. [Google Scholar]
- Kozub, J.; Ivanov, B.; Jayasinghe, A.; Prasad, R.; Shen, J.; Klosner, M.; Heller, D.; Mendenhall, M.; Piston, D.W.; Joos, K.; et al. Raman-shifted alexandrite laser for soft tissue ablation in the 6- to 7-µm wavelength range. Biomed. Opt. Express 2011, 2, 1275–1281. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.; Shen, Y.; Zong, N.; Bian, Q.; Wang, E.-P.; Chang, J.-Q.; Bo, Y.; Cui, D.-F.; Peng, Q.-J. 1.53 W all-solid-state nanosecond pulsed mid-infrared laser at 6.45 µm. Opt. Lett. 2022, 47, 1359–1362. [Google Scholar] [CrossRef] [PubMed]
- Bobrovnikov, S.M.; Matvienko, G.G.; Romanovsky, O.A.; Serikov, I.B.; Sukhanov, A.Y. Lidar Spectroscopic Gas Analysis of the Atmosphere; IOA SB RAS: Tomsk, Russia, 2014; p. 510. [Google Scholar]
- Romanovskii, O.; Sadovnikov, S.; Kharchenko, O.; Yakovlev, S. Development of Near/Mid IR differential absorption OPO lidar system for sensing of atmospheric gases. Opt. Laser Technol. 2019, 116, 43–47. [Google Scholar] [CrossRef]
- Bochkovskii, D.A.; Vasil’eva, A.V.; Matvienko, G.G.; Polunin, Y.P.; Romanovskii, O.A.; Soldatov, A.N.; Kharchenko, O.V.; Yudin, N.A.; Yakovlev, S.V. Application of a strontium vapor laser to laser remote sounding of atmospheric composition. Atmos. Ocean. Opt. 2012, 25, 166–170. [Google Scholar] [CrossRef]
- Schunemann, P.G.; Zawilski, K.T.; Pomeranz, L.A.; Creeden, D.J.; Budni, P.A. Advances in nonlinear optical crystals for mid-infrared coherent sources. J. Opt. Soc. Am. B 2016, 33, D36–D43. [Google Scholar] [CrossRef]
- Hemming, A.; Richards, J.; Davidson, A.; Carmody, N.; Bennetts, S.; Simakov, N.; Haub, J. 99 W mid-IR operation of a ZGP OPO at 25% duty cycle. Opt. Express 2013, 21, 10062–10069. [Google Scholar] [CrossRef]
- Haakestad, M.W.; Fonnum, H.; Lippert, E. Mid-infrared source with 02 J pulse energy based on nonlinear conversion of Q-switched pulses in ZnGeP_2. Opt. Express 2014, 22, 8556–8564. [Google Scholar] [CrossRef]
- Qian, C.-P.; Yao, B.-Q.; Zhao, B.-R.; Liu, G.-Y.; Duan, X.-M.; Dai, T.-Y.; Ju, Y.-L.; Wang, Y.-Z. High repetition rate 102 W middle infrared ZnGeP2 master oscillator power amplifier system with thermal lens compensation. Opt. Lett. 2019, 44, 715–718. [Google Scholar] [CrossRef]
- Hildenbrand, A.; Kieleck, C.; Tyazhev, A.; Marchev, G.; Stöppler, G.; Eichhorn, M.; Schunemann, P.G.; Panyutin, V.L.; Petrov, V.P. Laser damage of the nonlinear crystals CdSiP2 and ZnGeP2 studied with nanosecond pulses at 1064 and 2090 nm. Opt. Eng. 2014, 53, 122511. [Google Scholar] [CrossRef]
- Gribenyukov, A.I.; Dyomin, V.V.; Olshukov, A.S.; Podzyvalov, S.N.; Polovtsev, I.G.; Yudin, N.N. Investigation of the process of laserinduced damage of ZnGeP2 crystals using digital holography. Russ. Phys. J. 2019, 61, 2042–2052. [Google Scholar] [CrossRef]
- Chumside, J.H.; Wilson, J.J.; Gribenyukov, A.I.; Shubin, S.F.; Dolgii, S.I.; Andreev, Y.M.; Zuev, V.V.; Boulder, V. Frequency conversion of a CO2 laser with ZnGeP2. In NOAA Technical Memorandum ERL WPL-224 WPL-224WPL; Air Resources Laboratory: Silver Spring, MD, USA, 1992; p. 18. [Google Scholar]
- Yudin, N.; Antipov, O.; Gribenyukov, A.; Eranov, I.; Podzyvalov, S.; Zinoviev, M.; Voronin, L.; Zhuravleva, E.; Zykova, M. Effect of postgrowth processing technology and laser radiation parameters at wavelengths of 2091 and 1064 nm on the laser-induced damage threshold in ZnGeP2 single crystal. Quantum Electron. 2021, 51, 306–316. [Google Scholar] [CrossRef]
- Andreev, Y.M.; Badikov, V.V.; Voevodin, V.G.; Geiko, L.G.; Geiko, P.P.; Ivashchenko, M.V.; I Karapuzikov, A.; Sherstov, I.V. Radiation resistance of nonlinear crystals at a wavelength of 9.55 μm. Quantum Electron. 2001, 31, 1075–1078. [Google Scholar] [CrossRef]
- Peterson, R.D.; Schepler, K.L.; Brown, J.L.; Schunemann, P.G. Damage properties of ZnGeP_2 at 2 μm. J. Opt. Soc. Am. B 1995, 12, 2142–2146. [Google Scholar] [CrossRef]
- Zawilski, K.T.; Setzler, S.D.; Schunemann, P.G.; Pollak, T.M. Increasing the laser-induced damage threshold of single-crystal ZnGeP_2. J. Opt. Soc. Am. B 2006, 23, 2310–2316. [Google Scholar] [CrossRef]
- Yudin, N.; Zinoviev, M.; Kuznetsov, V.; Slyunko, E.; Podzvalov, S.; Voevodin, V.; Lysenko, A.; Kalsin, A.; Shaimerdenova, L.; Baalbaki, H.; et al. Effect of Dopants on Laser-Induced Damage Threshold of ZnGeP2. Crystals 2023, 13, 1940737. [Google Scholar] [CrossRef]
- Guha, S.; Bartsch, M.; Hopkins, F.K.; Eaton, M.P.; Setzler, S.D.; Schunemann, P.G.; Pollak, T.M. Nonlinear absorption and laser damage threshold measurements of doped ZnGeP2. In Operational Characteristics and Crystal Growth of Nonlinear Optical Materials; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3793, pp. 9–12. [Google Scholar] [CrossRef]
- Peng, Y.; Wei, X.; Wang, W. Mid-infrared optical parametric oscillator based on ZnGeP2 pumped by 2-m laser. Chin. Opt. Lett. 2011, 9, 061403. [Google Scholar] [CrossRef]
- Yudin, N.; Khudoley, A.; Zinoviev, M.; Podzvalov, S.; Slyunko, E.; Zhuravleva, E.; Kulesh, M.; Gorodkin, G.; Kumeysha, P.; Antipov, O. The Influence of Angstrom-Scale Roughness on the Laser-Induced Damage Threshold of Single-Crystal ZnGeP2. Crystals 2022, 12, 83. [Google Scholar] [CrossRef]
- Yudin, N.; Antipov, O.; Eranov, I.; Gribenyukov, A.; Verozubova, G.; Lei, Z.; Zinoviev, M.; Podzvalov, S.; Slyunko, E.; Voevodin, V.; et al. Laser-Induced Damage Threshold of Single Crystal ZnGeP2 at 2.1 µm: The Effect of Crystal Lattice Quality at Various Pulse Widths and Repetition Rates. Crystals 2022, 12, 652. [Google Scholar] [CrossRef]
- Verozubova, G.A.; Gribenyukov, A.I.; Mironov, Y.P. Two-temperature synthesis of ZnGeP2. Inorg. Mater. 2007, 43, 1040–1045. [Google Scholar] [CrossRef]
- ISO 11146-1:2005; Lasers and Laser-Related Equipment—Test Methods for Laser Beam Widths, Divergence Angles and Beam Propagation Ratios. International Organization for Standardization: Geneva, Switzerland, 2005.
- ISO 2602:1980; Statistical Interpretation of Test Results—Estimation of the Mean—Confidence Interval. International Organization for Standardization: Geneva, Switzerland, 1980.
- Fisher, R.A.; Rothamsted, M.A. Statistical methods for research workers. Metron 1925, 5, 90. [Google Scholar]
- Dyomin, V.; Gribenyukov, A.; Davydova, A.; Zinoviev, M.; Olshukov, A.; Podzyvalov, S.; Polovtsev, I.; Yudin, N. Holography of particles for diagnostics tasks. Appl. Opt. 2019, 58, 300–310. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, L.; Shao, T.; Liu, H.; Huang, J.; Ye, X.; Wang, F.; Yang, L.; Zheng, W. Statistically Correlating Laser-Induced Damage Performance with Photothermal Absorption for Fused Silica Optics in a High-Power Laser System. Photonics 2022, 9, 137. [Google Scholar] [CrossRef]

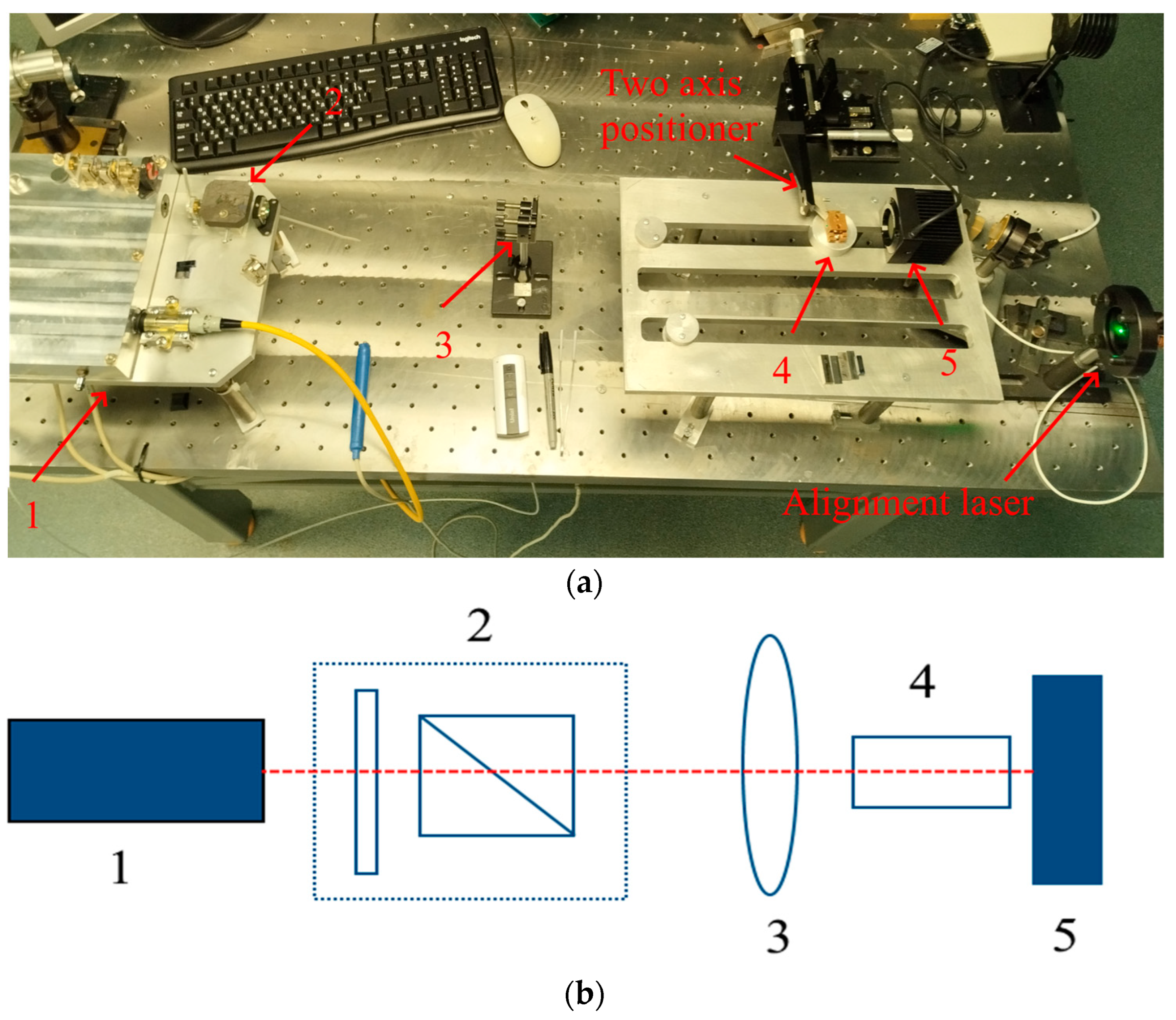

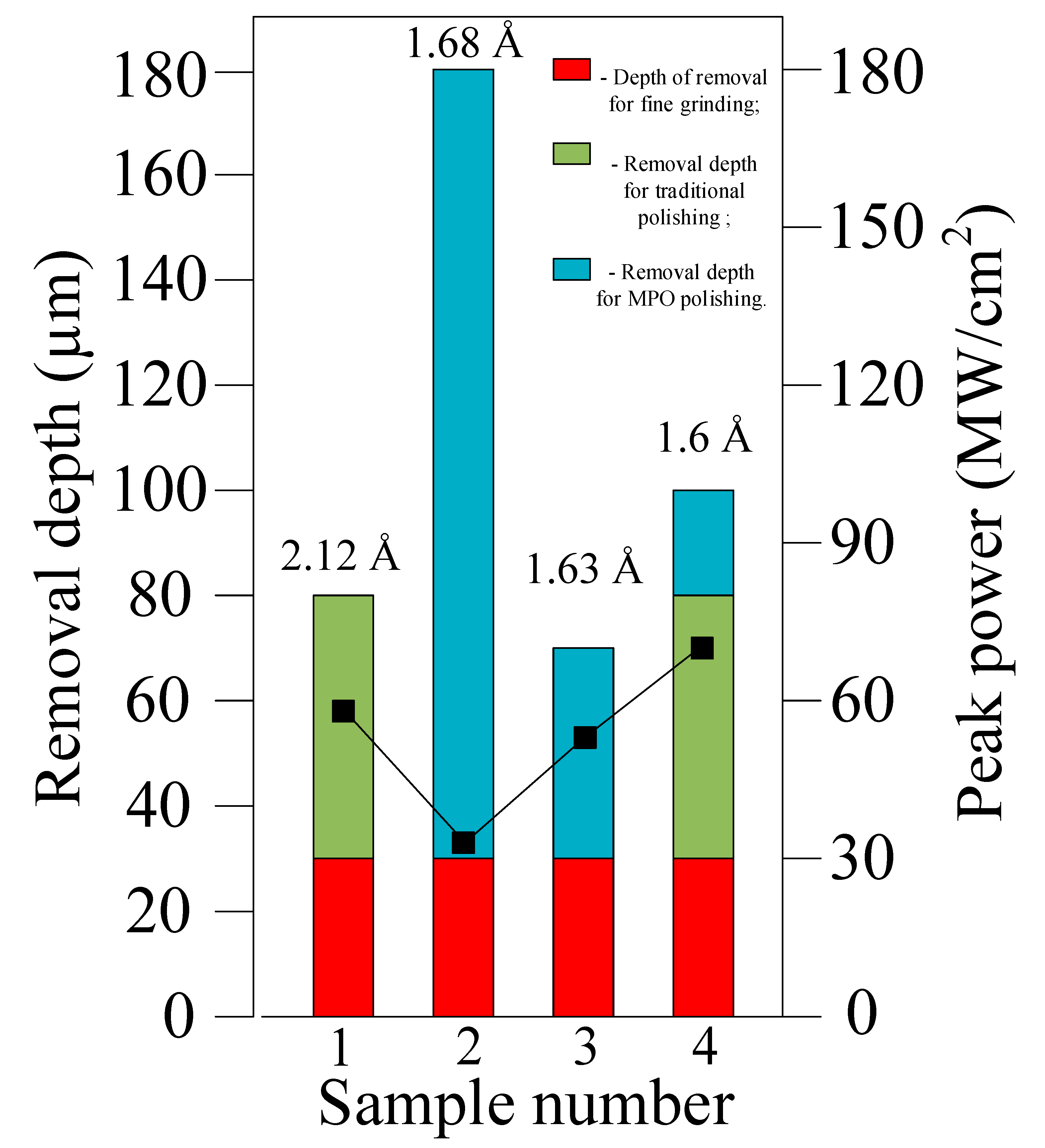
| Roughness Parameter (×50 Lens), nm | Sample 1 (Traditional Polishing) | Sample 2 | Sample 3 | Sample 4 | |||
|---|---|---|---|---|---|---|---|
| Fine Grinding | MPO | Fine Grinding | MPO | Traditional Polishing | MPO | ||
| Rz | 1.67 | 2204.0 | 1.16 | 2175.0 | 1.140 | 1.28 | 1.13 |
| Ra | 0.212 | 274.0 | 0.168 | 262.0 | 0.163 | 0.184 | 0.16 |
| Rq | 0.294 | 355.0 | 0.213 | 341.0 | 0.207 | 0.233 | 0.204 |
| Sample | MPO Removal Depth, µm | k | , J/cm2 | , J/cm2 | , MW/cm2 | , MW/cm2 |
|---|---|---|---|---|---|---|
| 1 | 0 | 2.8 | (2.9 ± 0.5) | 2.08 | 59 | (88 ± 15) |
| 2 | 150 | 2.8 | (2.5 ± 0.7) | 1.22 | 34 | (70 ± 22) |
| 3 | 38.15 | 2.8 | (2.8 ± 0.5) | 1.96 | 56 | (81 ± 15) |
| 4 | 17.8 | 2.8 | (3.0 ± 0.5) | 2.45 | 70 | (87 ± 11) |
| 5 | 9.5 | 2.8 | (3.2 ± 0.2) | 2.9 | 82 | (90 ± 5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yudin, N.N.; Khudoley, A.; Zinovev, M.; Slyunko, E.; Podzyvalov, S.; Kuznetsov, V.; Gorodkin, G.; Kumeysha, P.; Lysenko, A.; Kalsin, A.; et al. Experimental Investigation of Laser Damage Limit for ZPG Infrared Single Crystal Using Deep Magnetorheological Polishing of Working Surfaces. Crystals 2024, 14, 32. https://doi.org/10.3390/cryst14010032
Yudin NN, Khudoley A, Zinovev M, Slyunko E, Podzyvalov S, Kuznetsov V, Gorodkin G, Kumeysha P, Lysenko A, Kalsin A, et al. Experimental Investigation of Laser Damage Limit for ZPG Infrared Single Crystal Using Deep Magnetorheological Polishing of Working Surfaces. Crystals. 2024; 14(1):32. https://doi.org/10.3390/cryst14010032
Chicago/Turabian StyleYudin, Nikolay N., Andrei Khudoley, Mikhail Zinovev, Elena Slyunko, Sergey Podzyvalov, Vladimir Kuznetsov, Gennady Gorodkin, Pavel Kumeysha, Alexey Lysenko, Andrey Kalsin, and et al. 2024. "Experimental Investigation of Laser Damage Limit for ZPG Infrared Single Crystal Using Deep Magnetorheological Polishing of Working Surfaces" Crystals 14, no. 1: 32. https://doi.org/10.3390/cryst14010032
APA StyleYudin, N. N., Khudoley, A., Zinovev, M., Slyunko, E., Podzyvalov, S., Kuznetsov, V., Gorodkin, G., Kumeysha, P., Lysenko, A., Kalsin, A., Gabdrakhmanov, A., Romanovskii, O. A., Kashevsky, S., & Baalbaki, H. (2024). Experimental Investigation of Laser Damage Limit for ZPG Infrared Single Crystal Using Deep Magnetorheological Polishing of Working Surfaces. Crystals, 14(1), 32. https://doi.org/10.3390/cryst14010032







