Active Control Topological Valley Modes in Metamaterial Plates
Abstract
1. Introduction
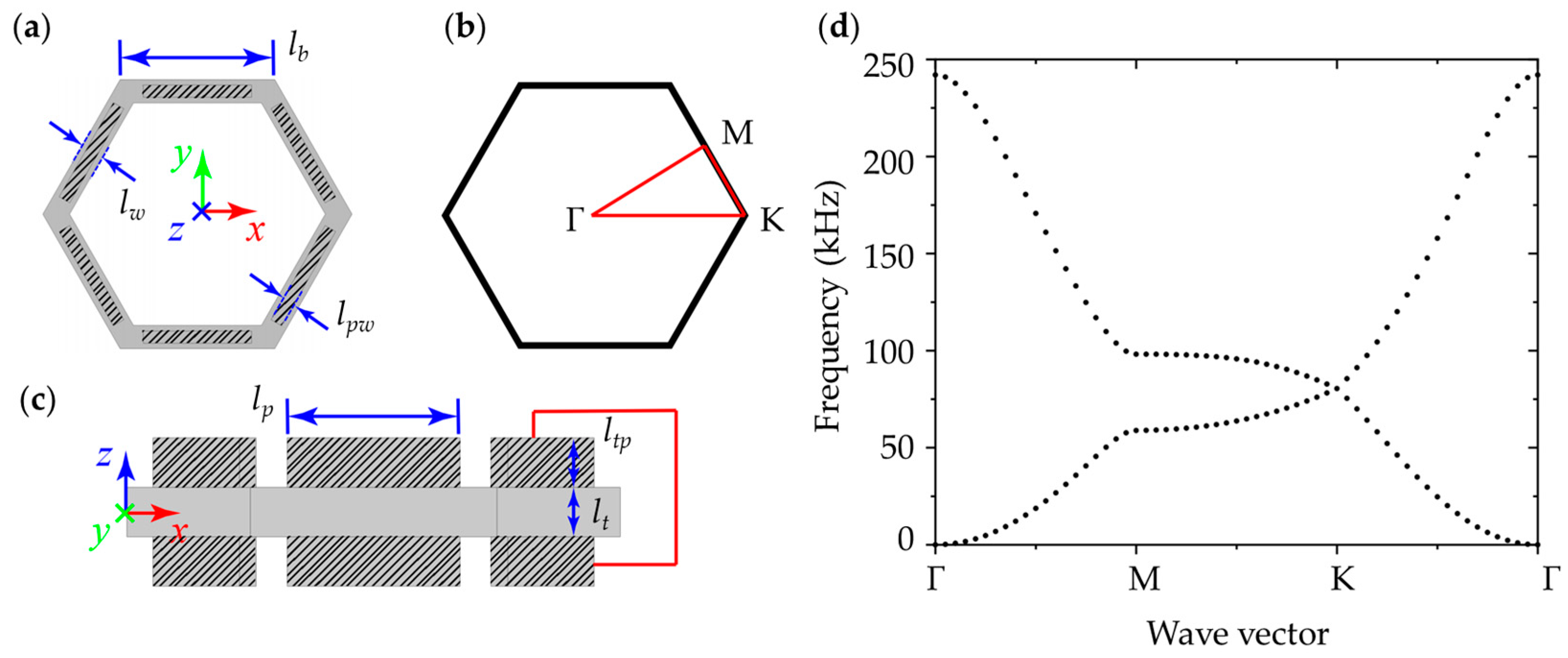
2. Design of the Hexagonal Metamaterial Plate
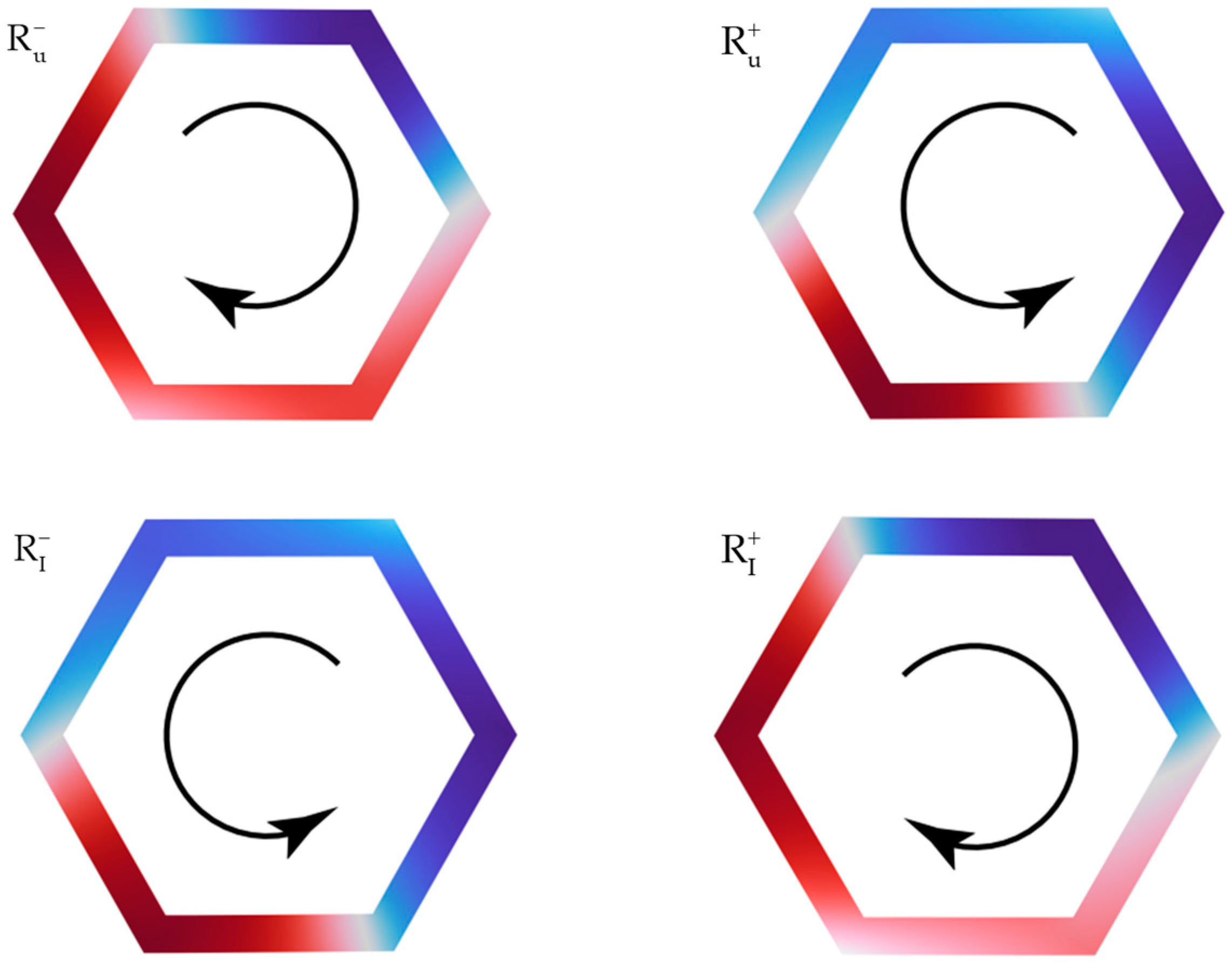
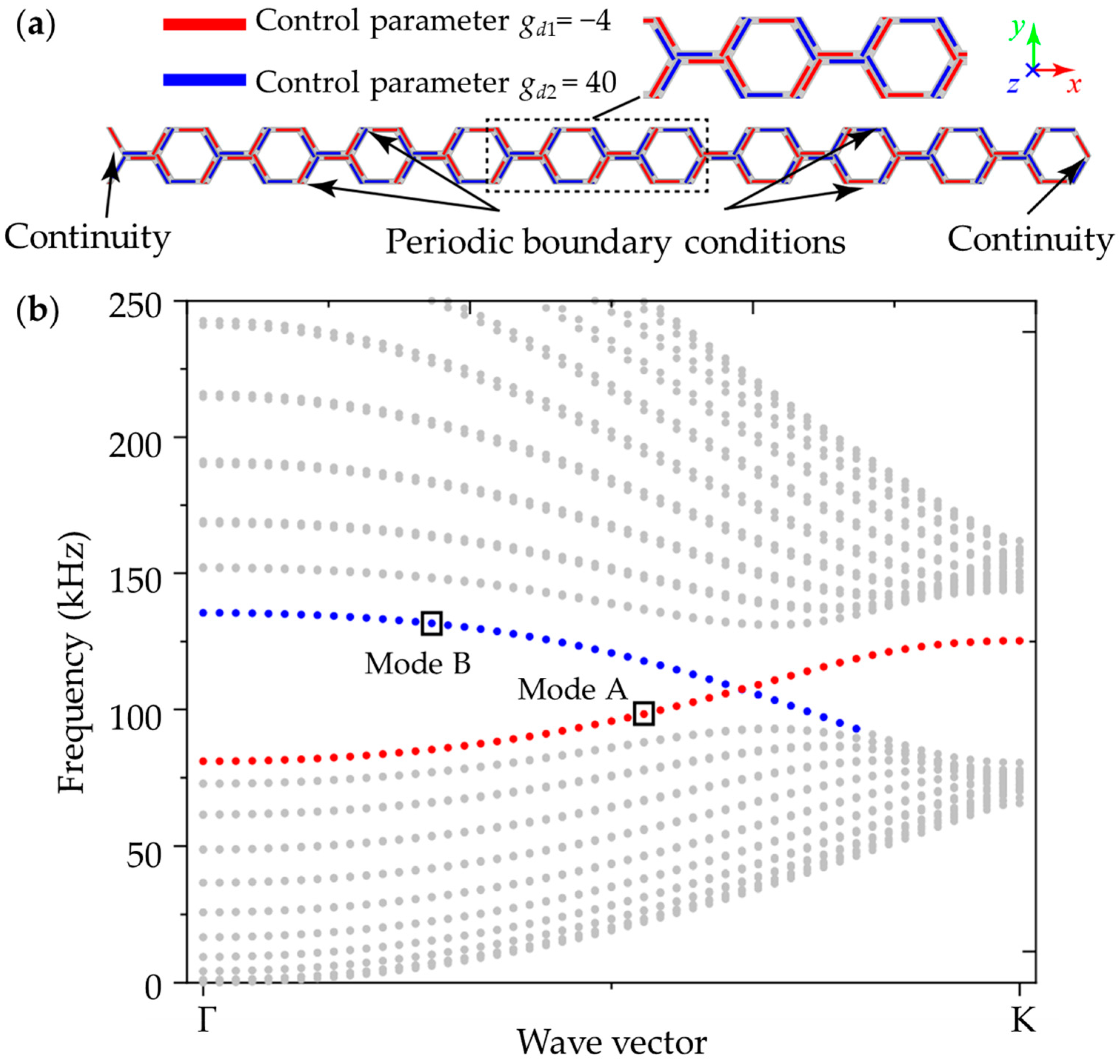
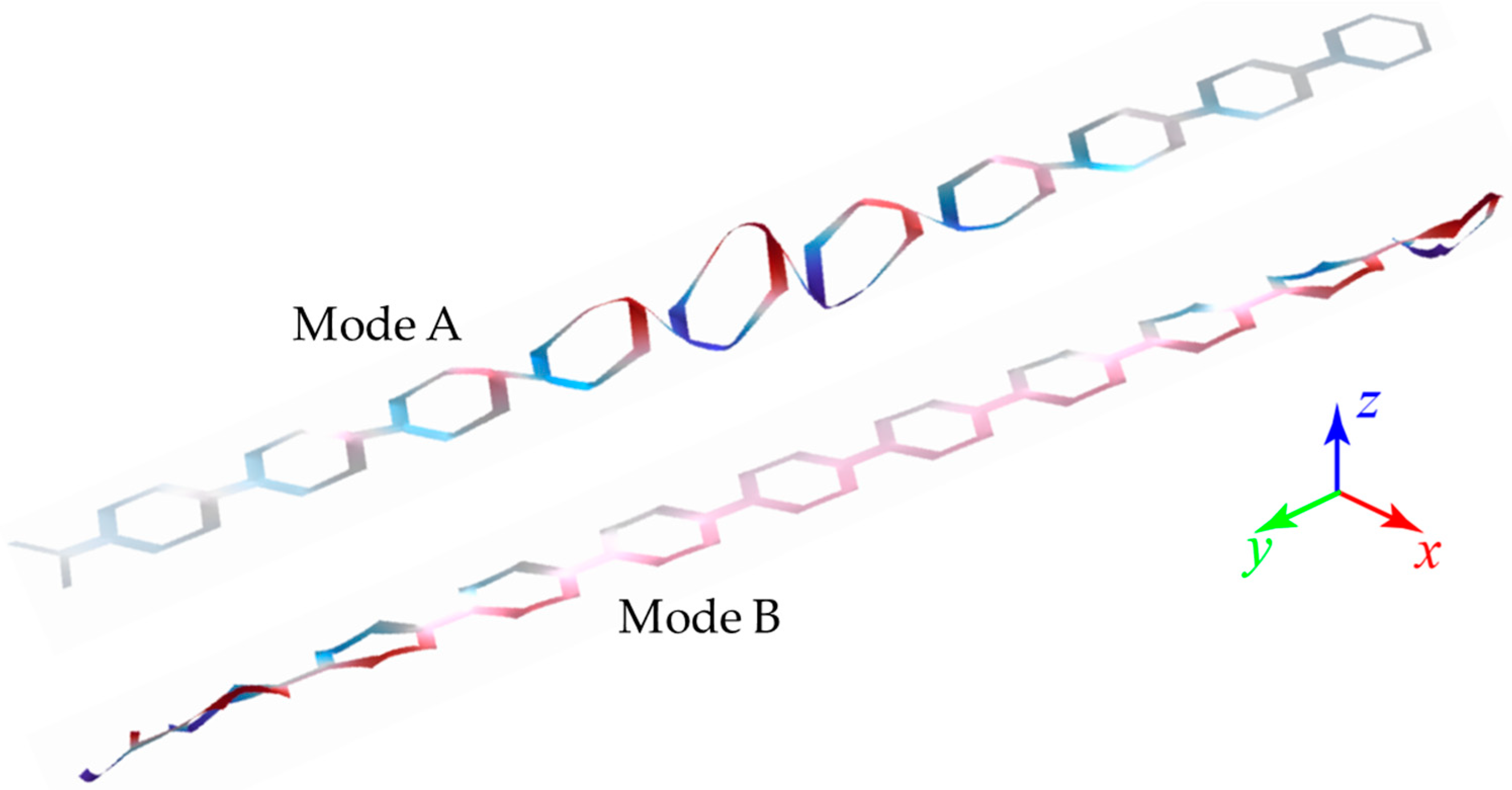
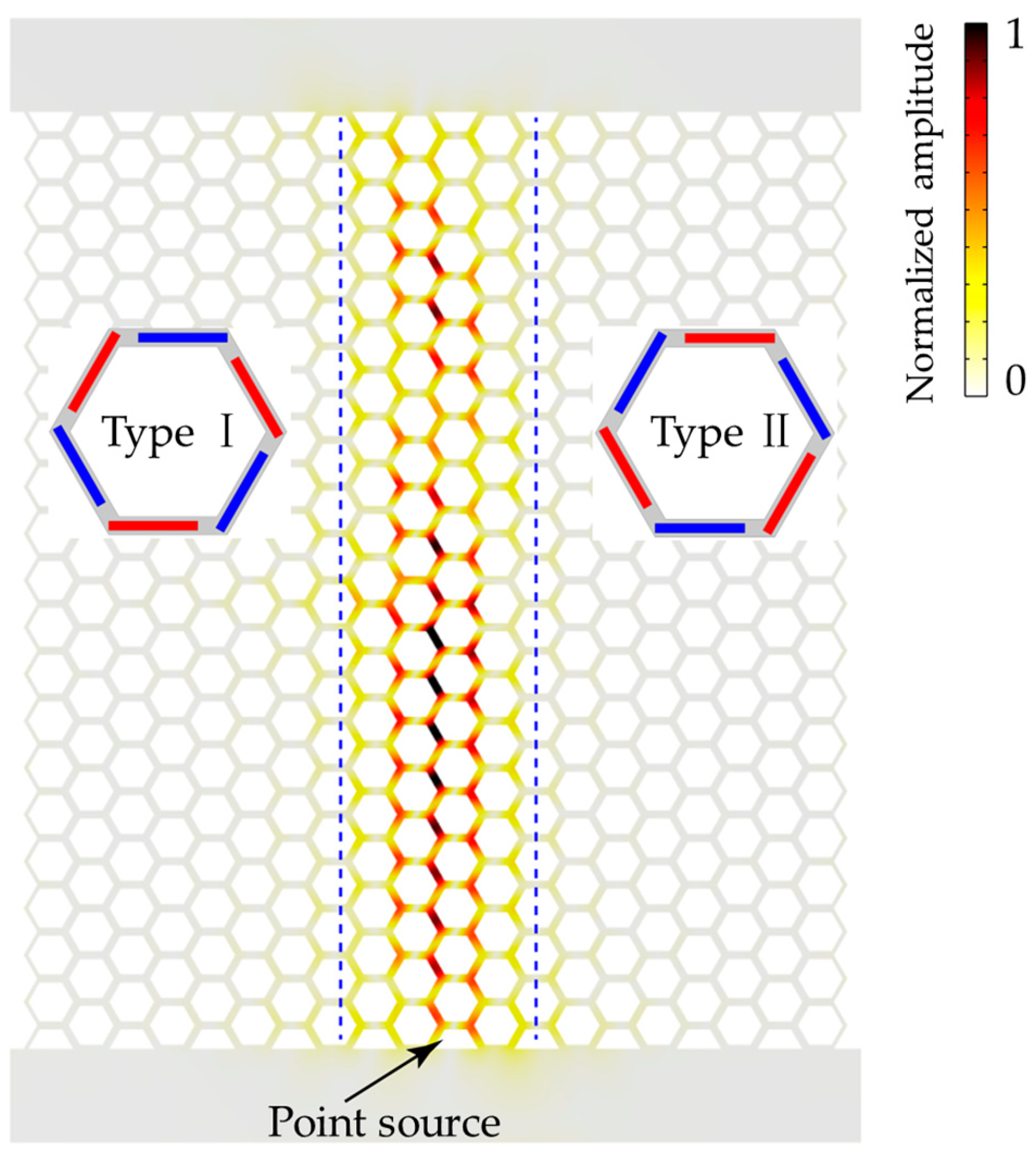
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.L.; Wang, Y.; Chuang, K.C.; Wu, F.G.; Wang, Q.X.; Lin, W.Q.; Jiang, H.Q. A brief review of dynamic mechanical metamaterials for mechanical energy manipulation. Mater. Today 2021, 44, 168–193. [Google Scholar] [CrossRef]
- Hou, Z.; Wu, F.; Liu, Y. Phononic crystals containing piezoelectric material. Solid State Commun. 2004, 130, 745–749. [Google Scholar] [CrossRef]
- Kherraz, N.; Chikh-Bled, F.H.; Sainidou, R.; Morvan, B.; Rembert, P. Tunable phononic structures using lamb waves in a piezoceramic plate. Phys. Rev. B 2019, 99, 094302. [Google Scholar] [CrossRef]
- Chikh-Bled, F.H.; Kherraz, N.; Sainidou, R.; Rembert, P.; Morvan, B. Piezoelectric phononic plates: Retrieving the frequency band structure via all-electric experiments. Smart. Mater. Struct. 2019, 28, 115046. [Google Scholar] [CrossRef]
- Kherraz, N.; Haumesser, L.; Levassort, F.; Benard, P.; Morvan, B. Controlling bragg gaps induced by electric boundary conditions in phononic piezoelectric plates. Appl. Phys. Lett. 2016, 108, 093503. [Google Scholar] [CrossRef]
- Kutsenko, A.A.; Shuvalov, A.L.; Poncelet, O.; Darinskii, A.N. Tunable effective constants of the one-dimensional piezoelectric phononic crystal with internal connected electrodes. J. Acoust. Soc. Am. 2015, 137, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, Y.; Ma, T.; Zhang, C. Smart piezoelectric phononic crystals and metamaterials:State-of-the-art review and outlook. Chin. Sci. Bull. 2022, 67, 1305–1325. [Google Scholar] [CrossRef]
- Nassar, H.; Xu, X.C.; Norris, A.N.; Huang, G.L. Modulated phononic crystals: Non-reciprocal wave propagation and willis materials. J. Mech. Phys. Solids 2017, 101, 10–29. [Google Scholar] [CrossRef]
- Croënne, C.; Vasseur, J.O.; Bou Matar, O.; Ponge, M.F.; Deymier, P.A.; Hladky-Hennion, A.C.; Dubus, B. Brillouin scattering-like effect and non-reciprocal propagation of elastic waves due to spatio-temporal modulation of electrical boundary conditions in piezoelectric media. Appl. Phys. Lett. 2017, 110, 061901. [Google Scholar] [CrossRef]
- Degraeve, S.; Granger, C.; Dubus, B.; Vasseur, J.O.; Pham Thi, M.; Hladky-Hennion, A.C. Bragg band gaps tunability in an homogeneous piezoelectric rod with periodic electrical boundary conditions. J. Appl. Phys. 2014, 115, 194508. [Google Scholar] [CrossRef]
- Flores Parra, E.A.; Bergamini, A.; Lossouarn, B.; Van Damme, B.; Cenedese, M.; Ermanni, P. Bandgap control with local and interconnected lc piezoelectric shunts. Appl. Phys. Lett. 2017, 111, 111902. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Ke, M.; Liu, Z. Valley vortex states in sonic crystals. Phys. Rev. Lett. 2016, 116, 093901. [Google Scholar] [CrossRef]
- Rocklin, D.Z.; Chen, B.G.; Falk, M.; Vitelli, V.; Lubensky, T.C. Mechanical weyl modes in topological maxwell lattices. Phys. Rev. Lett. 2016, 116, 135503. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 2016, 13, 369–374. [Google Scholar] [CrossRef]
- Ningyuan, J.; Owens, C.; Sommer, A.; Schuster, D.; Simon, J. Time- and site-resolved dynamics in a topological circuit. Phys. Rev. X 2015, 5, 021031. [Google Scholar] [CrossRef]
- Prodan, E.; Dobiszewski, K.; Kanwal, A.; Palmieri, J.; Prodan, C. Dynamical majorana edge modes in a broad class of topological mechanical systems. Nat. Commun. 2017, 8, 14587. [Google Scholar] [CrossRef]
- Paulose, J.; Meeussen, A.S.; Vitelli, V. Selective buckling via states of self-stress in topological metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 7639–7644. [Google Scholar] [CrossRef]
- Kane, C.L.; Lubensky, T.C. Topological boundary modes in isostatic lattices. Nat. Phys. 2013, 10, 39–45. [Google Scholar] [CrossRef]
- Peano, V.; Brendel, C.; Schmidt, M.; Marquardt, F. Topological phases of sound and light. Phys. Rev. X 2015, 5, 031011. [Google Scholar] [CrossRef]
- Chaunsali, R.; Kim, E.; Thakkar, A.; Kevrekidis, P.G.; Yang, J. Demonstrating an in situ topological band transition in cylindrical granular chains. Phys. Rev. Lett. 2017, 119, 024301. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Li, Z.; Ni, X.; Sun, X.-C.; Yu, S.-Y.; Lu, M.-H.; Liu, X.-P.; Chen, Y.-F. Topological phononic states of underwater sound based on coupled ring resonators. Appl. Phys. Lett. 2016, 108, 031904. [Google Scholar] [CrossRef]
- Pal, R.K.; Ruzzene, M. Edge waves in plates with resonators: An elastic analogue of the quantum valley hall effect. New J. Phys. 2017, 19, 025001. [Google Scholar] [CrossRef]
- Zhang, F.; Jung, J.; Fiete, G.A.; Niu, Q.; MacDonald, A.H. Spontaneous quantum hall states in chirally stacked few-layer graphene systems. Phys. Rev. Lett. 2011, 106, 156801. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2013, 12, 233–239. [Google Scholar] [CrossRef]
- Ma, T.; Shvets, G. All-si valley-hall photonic topological insulator. New J. Phys. 2016, 18, 025012. [Google Scholar] [CrossRef]
- Dorin, P.; Wang, K.W. Broadband frequency and spatial on-demand tailoring of topological wave propagation harnessing piezoelectric metamaterials. Front. Mater. 2021, 7, 602996. [Google Scholar] [CrossRef]
- Rocklin, D.Z. Directional mechanical response in the bulk of topological metamaterials. New J. Phys. 2017, 19, 065004. [Google Scholar] [CrossRef]
- Pal, R.K.; Schaeffer, M.; Ruzzene, M. Helical edge states and topological phase transitions in phononic systems using bi-layered lattices. J. Appl. Phys. 2016, 119, 084305. [Google Scholar] [CrossRef]
- Huber, S.D. Topological mechanics. Nat. Phys. 2016, 12, 621–623. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Yang, L.; Wang, T.; Chen, A.L.; Laude, V.; Wang, Y.-S. Guided lamb waves in reconfigurable phononic crystal waveguides. APL Mater. 2021, 9, 081110. [Google Scholar] [CrossRef]
- Wang, Y.; Perras, E.; Golub, M.V.; Fomenko, S.I.; Zhang, C.; Chen, W. Manipulation of the guided wave propagation in multilayered phononic plates by introducing interface delaminations. Eur. J. Mech. A Solids 2021, 88, 104266. [Google Scholar] [CrossRef]
- Dong, H.-W.; Wang, Y.-S.; Zhang, C. Inverse design of high-q wave filters in two-dimensional phononic crystals by topology optimization. Ultrasonics 2017, 76, 109–124. [Google Scholar] [CrossRef]
- Swinteck, N.; Matsuo, S.; Runge, K.; Vasseur, J.O.; Lucas, P.; Deymier, P.A. Bulk elastic waves with unidirectional backscattering-immune topological states in a time-dependent superlattice. J. Appl. Phys. 2015, 118, 063103. [Google Scholar] [CrossRef]
- Nash, L.M.; Kleckner, D.; Read, A.; Vitelli, V.; Turner, A.M.; Irvine, W.T. Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 14495–14500. [Google Scholar] [CrossRef]
- Croënne, C.; Vasseur, J.O.; Bou Matar, O.; Hladky-Hennion, A.C.; Dubus, B. Non-reciprocal behavior of one-dimensional piezoelectric structures with space-time modulated electrical boundary conditions. J. Appl. Phys. 2019, 126, 145108. [Google Scholar] [CrossRef]
- Brendel, C.; Peano, V.; Painter, O.; Marquardt, F. Snowflake phononic topological insulator at the nanoscale. Phys. Rev. B 2018, 97, 020102. [Google Scholar] [CrossRef]
- Wang, P.; Lu, L.; Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 2015, 115, 104302. [Google Scholar] [CrossRef]
- Zhou, W.; Wu, B.; Chen, Z.; Chen, W.; Lim, C.W.; Reddy, J.N. Actively controllable topological phase transition in homogeneous piezoelectric rod system. J. Mech. Phys. Solids 2020, 137, 103824. [Google Scholar] [CrossRef]
- Darabi, A.; Collet, M.; Leamy, M.J. Experimental realization of a reconfigurable electroacoustic topological insulator. Proc. Natl. Acad. Sci. USA 2020, 117, 16138–16142. [Google Scholar] [CrossRef]
- Susstrunk, R.; Huber, S.D. Observation of phononic helical edge states in a mechanical topological insulator. Science 2015, 349, 47–50. [Google Scholar] [CrossRef]
- Vila, J.; Pal, R.K.; Ruzzene, M. Observation of topological valley modes in an elastic hexagonal lattice. Phys. Rev. B 2017, 96, 134307. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef]
- Fleury, R.; Sounas, D.; Alu, A. Non-reciprocal acoustic devices based on spatio-temporal angular-momentum modulation. J. Acoust. Soc. Am. 2014, 136, 2281. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, T.; Ge, H.; Wang, W.; Chen, Z.G.; Lu, M.H.; Chen, Y.F. Topological boundary states transport in synthetic four-dimensional acoustic system. Sci. Bull. 2022, 67, 1950–1953. [Google Scholar] [CrossRef] [PubMed]
- Xiao, M.; Ma, G.; Yang, Z.; Sheng, P.; Zhang, Z.Q.; Chan, C.T. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 2015, 11, 240–244. [Google Scholar] [CrossRef]
- Miniaci, M.; Pal, R.K.; Morvan, B.; Ruzzene, M. Experimental observation of topologically protected helical edge modes in patterned elastic plates. Phys. Rev. X 2018, 8, 031074. [Google Scholar] [CrossRef]
- Ye, L.; Qiu, C.; Xiao, M.; Li, T.; Du, J.; Ke, M.; Liu, Z. Topological dislocation modes in three-dimensional acoustic topological insulators. Nat. Commun. 2022, 13, 508. [Google Scholar] [CrossRef]
- Du, J.; Li, T.; Fan, X.; Zhang, Q.; Qiu, C. Acoustic realization of surface-obstructed topological insulators. Phys. Rev. Lett. 2022, 128, 224301. [Google Scholar] [CrossRef]
- Ni, A.; Shi, Z. Complex dispersion relation and topologically protected flexural wave transport in viscoelastic periodic plates. Phys. Lett. A 2023, 458, 128584. [Google Scholar] [CrossRef]
- Luo, J.; Du, Z.; Chen, H.; Ding, X.; Liu, C.; Zhang, W.; Guo, X. Efficient design of helical higher-order topological insulators in 3d elastic medium. J. Mech. Phys. Solids 2023, 176, 105325. [Google Scholar] [CrossRef]
- Luo, J.; Du, Z.; Guo, Y.; Liu, C.; Zhang, W.; Guo, X. Multi-class, multi-functional design of photonic topological insulators by rational symmetry-indicators engineering. Nanophotonics 2021, 10, 4523–4531. [Google Scholar] [CrossRef]
- Du, Z.; Luo, J.; Xu, Z.; Jiang, Z.; Ding, X.; Cui, T.; Guo, X. Higher-order topological insulators by ml-enhanced topology optimization. Int. J. Mech. Sci. 2023, 255, 108441. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhou, Y.; Zheng, S.; Liu, J.; Xia, B. Waveguides induced by replacing defects in phononic crystal. Int. J. Mech. Sci. 2023, 255, 108464. [Google Scholar] [CrossRef]
- Ma, T.-X.; Fan, Q.-S.; Zhang, C.; Wang, Y.-S. Flexural wave energy harvesting by the topological interface state of a phononic crystal beam. Extreme Mech. Lett. 2022, 50, 101578. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Ma, T.-X.; Wang, Y.-Z.; Li, F.-M.; Zhang, C. Vibration isolation by novel meta-design of pyramid-core lattice sandwich structures. J. Sound Vib. 2020, 480, 115377. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, Y.; Liu, F.; Cao, L.; Yang, Z. Modulated flexural edge waves in a plate with its free edge structured by an array of grooves. J. Sound Vib. 2022, 536, 117173. [Google Scholar] [CrossRef]
- Tang, X.; Ma, T.-X.; Wang, Y.-S. Topological rainbow trapping and acoustic energy amplification in two-dimensional gradient phononic crystals. Appl. Phys. Lett. 2023, 122, 112201. [Google Scholar] [CrossRef]
- Matsuda, O.; Larciprete, M.C.; Li Voti, R.; Wright, O.B. Fundamentals of picosecond laser ultrasonics. Ultrasonics 2015, 56, 3–20. [Google Scholar] [CrossRef]
- Tomoda, M.; Matsuda, O.; Wright, O.B.; Li Voti, R. Tomographic reconstruction of picosecond acoustic strain propagation. Appl. Phys. Lett. 2007, 90, 041114. [Google Scholar] [CrossRef]
- Dehoux, T.; Wright, O.B.; Voti, R.L. Picosecond time scale imaging of mechanical contacts. Ultrasonics 2010, 50, 197–201. [Google Scholar] [CrossRef]
- Dehoux, T.; Wright, O.B.; Li Voti, R.; Gusev, V.E. Nanoscale mechanical contacts probed with ultrashort acoustic and thermal waves. Phys. Rev. B 2009, 80, 235409. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Ma, T.-X.; Wang, Y.-Z.; Chai, Y.-Y.; Zhang, C.; Li, F.-M. Active auto-adaptive metamaterial plates for flexural wave control. Int. J. Solids Struct. 2022, 254–255, 111865. [Google Scholar] [CrossRef]
- Li, Z.Y.; Wang, Y.Z.; Ma, T.X.; Zheng, Y.F.; Zhang, C.Z.; Li, F.M. A self-sensing and self-actuating metamaterial sandwich structure for the low-frequency vibration mitigation and isolation. Compos. Struct. 2022, 297, 115894. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zhang, J.; Chang, J.; Li, Z.-Y.; Yan, D. Active Control Topological Valley Modes in Metamaterial Plates. Crystals 2023, 13, 933. https://doi.org/10.3390/cryst13060933
Zhou J, Zhang J, Chang J, Li Z-Y, Yan D. Active Control Topological Valley Modes in Metamaterial Plates. Crystals. 2023; 13(6):933. https://doi.org/10.3390/cryst13060933
Chicago/Turabian StyleZhou, Jingxuan, Jie Zhang, Jiahui Chang, Zheng-Yang Li, and Dongjia Yan. 2023. "Active Control Topological Valley Modes in Metamaterial Plates" Crystals 13, no. 6: 933. https://doi.org/10.3390/cryst13060933
APA StyleZhou, J., Zhang, J., Chang, J., Li, Z.-Y., & Yan, D. (2023). Active Control Topological Valley Modes in Metamaterial Plates. Crystals, 13(6), 933. https://doi.org/10.3390/cryst13060933





