Abstract
Phononic crystals and metamaterials have a unique band structure that allows for the existence of topologically protected surface states. The topologically protected edge states can guide elastic waves without significant scattering or loss of energy. One of the most promising applications of topological insulators in wave guiding is in the field of acoustics, where they can be used to design highly efficient and robust acoustic wave guides. However, the high efficiency, precision, reconfigurability, and robustness of elastic waves remains challenging. The topological insulators provide a feasible method to design high-efficiency, robust, and low-backscattering waveguides. In this work, a novel design of hexagonal metamaterial plates composed of a base plate and piezoelectric patches is proposed. The hexagonal metamaterial plate can generate robust topologically protected edge waves via active control. The paths of the topologically protected edge waves can be tuned by adjusting the control parameters. The robustness and efficiency of the proposed hexagonal metamaterial plate are testified to by the numerical examples. These findings provide systematic theoretical guidelines for designing reconfigurable wave guides, elastic wave splitters, and novel elastic wave devices and hold great promise for the development of high-performance and versatile wave guide technologies with potential applications in a wide range of fields.
1. Introduction
The study of elastic wave propagation in various structures and materials has remained active in the past decades. Phononic crystals are periodic elastic composite materials that have broad application prospects in controlling and manipulating elastic waves due to the existence of a phononic band gap. When an elastic wave propagates in a phononic crystal, a special dispersion relationship or energy band can be produced. The frequency domain covered by the dispersion curve is called the passband, and the uncovered part is the stopband, namely the band gap. Theoretically, elastic waves in the band gap are forbidden to propagate in the phononic crystal, while elastic waves in the passband can propagate without energy loss. If there are point or line defects in the phononic crystal, the elastic waves within the band gap will be localized or propagate along the defects. Therefore, phononic crystals can be used to block or control elastic waves. The study of phononic crystals will not only give rise to developments in solid-state physics, materials science, and acoustics but also open up a variety of possible applications in vibration and sound control. Currently, phononic crystals and metamaterials offer effective solutions to the suppression, guidance, and modulation of elastic waves [1,2,3,4,5,6,7,8]. The traditional methods of elastic wave guidance are mainly based on the defect states and directional propagation properties of phononic crystals. However, the precision of the elastic wave control is largely affected by the strong elastic wave scattering effect when elastic waves propagate to the boundary or defects [9,10,11,12,13,14].
In recent years, the theory of topological physics has been introduced into the study of acoustics, mechanics, condensed matter physics, quantum physics, and the commonality between matter waves and classical waves [15,16,17]. Topology is a branch of mathematics that introduces the topological principles of mathematics into the field of condensed matter physics, and the resulting topological states have always garnered significant attention from researchers [18,19,20,21,22]. In the field of condensed matter physics, the discovery of the quantum hall effect, i.e., a phenomenon unique to quantum systems, has opened up the possibility of realizing materials with phase transitions, symmetries, and non-trivial topological properties [23,24,25]. Realizing phenomena similar to the quantum hall effect in the study of acoustic waves can provide new research ideas and implementation methods for elastic wave propagation and control.
Inspired by the topological phase transition and topological material theory, the elastic wave topological insulator is proposed by analogy with the idea of a topological insulator under the photoelectric wave band [26,27,28,29,30,31]. The essence of elastic wave propagation in an elastic wave topological insulator is the result of the action of surface states (boundary states). Compared with ordinary periodic waveguide structures [32,33,34], the elastic wave topological insulator breaks the time-reversal symmetry of elastic wave propagation and realizes the single control of elastic waves [35,36,37]. For example, in the case of acoustic or elastic waves, bulk waves with unidirectional backscattering immune topological edge states can be observed in a time-dependent elastic superlattice. Furthermore, the elastic wave topological insulator has obvious back scattering suppression and defect immunity for the regulation of elastic waves, which provides a new technical method for the precise regulation of elastic waves. The elastic wave topological insulator opens new avenues for the design of acoustic devices with special properties and functionalities on edges, surfaces, and interfaces [38,39,40,41,42,43,44].
Since the common material properties used to construct elastic wave topological insulators are insensitive to magnetic fields, the time inversion symmetry cannot be broken with reference to the method of the electron system. According to the method of breaking the time inversion symmetry, elastic wave topological insulators can be divided into two types: active elastic wave topological insulators and passive elastic wave topological insulators.
Active elastic wave topological insulators are usually constructed by an applied source field or external energy. If the source field or external energy can break the time-reversal symmetry, then the topological boundary states can be achieved by this spatio-temporal modulation method. The theory and design of a spatio-temporally modulated, fully linear, compact acoustic circulator based on effective acoustic indices are proposed [45]. The non-reciprocal propagation of elastic waves can be realized at any desired frequency. Topological boundary states can also be achieved by coordinate-dependent coupling waveguides that contribute two synthetic dimensions [46]. From a theoretical perspective, a gyroscopic structure with rotational inertia embedded periodically in the structure is designed, thus targeting topological edge states for both longitudinal and transverse waves in the structure [39]. All the above methods are based on the addition of an applied source field to the structure or medium to break the time-reversal symmetry to obtain the topological edge state, which has some limitations in engineering applications. Due to the limitations of active-type elastic wave topological insulators in engineering applications, there is a need to explore a method to construct elastic wave topological insulators without the need for an applied source field.
It is shown that breaking the spatial inversion symmetry of the structure can construct the quantum pseudo-spin hall effect of the elastic wave and realize the “topological phase transition” of the structure. The spatial structure inversion symmetry of the structure can be broken by a simple spatial structure design to construct an elastic wave topological insulator that does not require an external source field, which is called a passive type of elastic wave topological insulator. Xiao et al. [47] design a one-dimensional elastic wave topological insulator structure for the elastic waveguide. The topological phase transition is achieved by periodically designing the rectangular cross section, and the topological edge states of the longitudinal and transverse waves are experimentally verified. Miniaci et al. [48] design a novel two-bit elastic wave topological insulator for structural elastic waves with a series of triangular holes and a circular hole. It could generate a double Dirac cone, and then this Dirac cone can be broken by breaking the symmetry along the thickness direction. Then the acoustic pseudo-spin state is achieved, and the topologically protected helical mode in the elastic plate is investigated both numerically and experimentally. According to the current research on topological insulators, elastic wave topological insulators have achieved extensive results in terms of physical mechanisms and structural designs. Whereas the design of new structures to reduce the topological phase transition band in engineering applications still needs to be studied in depth.
In recent years, topological devices have been extensively studied [49,50,51]. Multiple optimization methods [52,53] and artificial intelligence [54] have been used to design the topological insulators. Different from traditional acoustic devices, frequency-selective transporters can be designed and manufactured based on topological insulators [55]. Furthermore, the topological insulators can be further utilized for energy harvesting [56]. Combining with the rainbow trapping phenomenon [57,58], the topological interfaces can be used as sensors, which could enhance signals [59].
In this work, we propose a hexagonal metamaterial with shunted piezoelectric patches. The topological valley hall effect is realized in the hexagonal metamaterial plate by active control. The propagation paths of elastic waves can be tuned by adjusting the control parameters. Taking advantage of this characteristic, the schematic diagram of an elastic wave splitter can be realized as shown in Figure 1, which is composed of two different topology types, namely type I and type II. The topology types are presented by different distributions, with red and blue in hexagons. The elastic waves are assumed to propagate normally from the bottom to the top boundaries of the elastic wave splitter. The different topologies of type I and type II unit cells are constructed by assigning different control parameters. Subsequently, the transmittance of the topologically protected edge waves along different paths can be examined. The results show that the topological insulators have potential applications in material parameter testing [60,61,62,63], energy harvesting, acoustic devices, and so on.
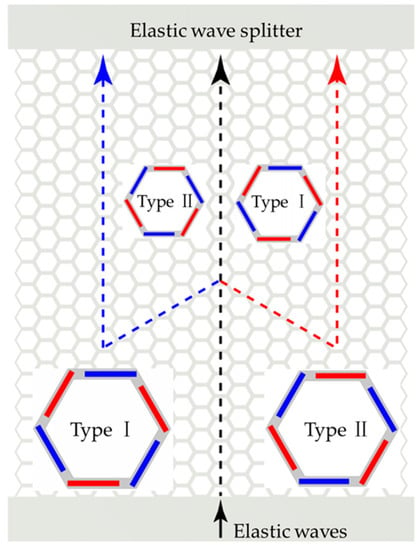
Figure 1.
Schematic diagram of an elastic wave splitter based on the topological valley hall effect, where the topology types are presented by different distributions with red and blue in hexagons.
2. Design of the Hexagonal Metamaterial Plate
The hexagonal metamaterial plate is composed of a base plate and piezoelectric patches (PZT) (shaded by oblique lines), as shown in Figure 2a,c. The length of the base plate (lb) is defined as 1 mm. The width of the base plate (lw) is defined as 0.3 mm. The PZT patches have a length lp = 0.75lb and a width (lpw) defined as 0.078 mm. The thickness of the base plate and PZT patches is the same: lt = ltp = 0.1 mm. In this study, aluminum (E = 70 GPa, ν = 0.33, ρ = 2700 kg·m−3) is chosen as the base plate, while PZT-5H (c11 = 60.6 GPa, ν = 0.29, ρ = 7500 kg·m−3, e31 = −6.623 C·m−2, κ33 = 1433.6 × 10−9 C2·N−1·m−2) is used as the PZT patches. The governing equation of the hexagonal metamaterial plate can be written as [64,65]:
in which
and
where E is the Young’s modulus of the base plate, ν is the Poisson’s ratio of the base plate, c11 is the elastic constant of the PZT patches, νp is the Poisson’s ratio of the PZT patches, e31 is the piezoelectric constant, κ33 is the permittivity constant under constant strain, and gd is the displacement control parameter. Then the band structures of the hexagonal metamaterial plate can be calculated by the finite element analyses. The most common method to analyze the propagation characteristics of the flexural wave in the hexagonal metamaterial plate is the investigation of the dispersion relations or band structures by considering a unit cell, as shown in Figure 3, where the Bloch periodic boundary conditions are applied to the two opposite boundaries of the unit cell.
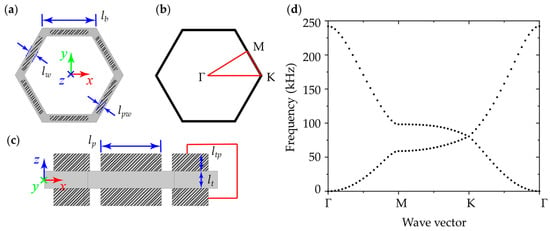
Figure 2.
(a) Top view of the unit cell of the hexagonal metamaterial plate and geometrical parameters. (b) The corresponding first Brillouin zone of the hexagonal lattice. (c) Side view of the unit cell of the hexagonal metamaterial plate and geometrical parameters. (d) The band structures of hexagonal metamaterial plates with an open circuit.
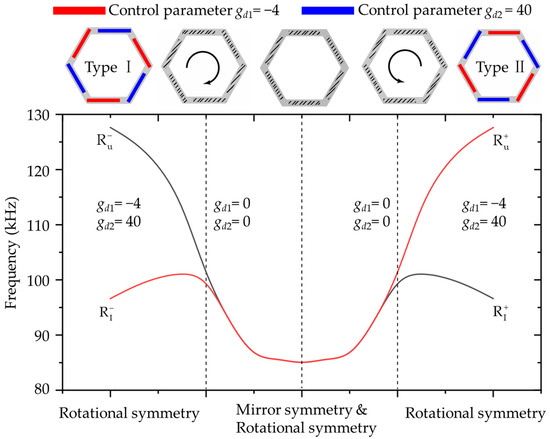
Figure 3.
The band-edge eigenfrequencies of two eigenmodes at valley K with different symmetries. The PZT patches are shaded by oblique lines. While the PZT patches with different control parameters gd1 = −4 and gd2 = 40 are colored red and blue, respectively.
Then the band structures of the unit cell are analyzed by the finite element method (FEM) via a common commercial FEM software. However, the real active control system is difficult and inefficient to carry out in the common commercial FEM software. Equation (1) can provide an alternative path. Based on Equation (1), the effects of active control and the piezoelectric effect can be considered as adding positive or negative stiffness to the base plate. Then the unit cell of the hexagonal metamaterial plate can be considered a pure elastic plate. By discretizing the unit cell by quadratic Lagrange elements with quadratic shape functions, following the standard procedure of the FEM, and taking into account the Bloch–Floquet periodic boundary conditions. The discrete eigenvalue equation in the frequency domain can be obtained as
in which K and M are the stiffness and mass matrices under consideration of the Bloch–Floquet periodicity, respectively, ω is the eigenfrequency, and is the transverse displacement vector of the element nodes.
Brillouin zones are polyhedral in reciprocal space in crystalline materials. Physically, Brillouin zone boundaries represent Bragg planes that reflect (diffract) waves having particular wave vectors so that they cause constructive interference. Therefore, the eigenfrequencies, each of which represents the propagation properties of the elastic waves, can be computed by varying the wave vector k along the boundaries of the first irreducible Brillouin zone of the unit cell, as shown in Figure 2b. When performing the parameter scanning along the boundaries of the first Brillouin zone in Figure 2b, the eigenvalue problems are solved by FEM with a 2D plate element by the ARPACK solver. Therefore, the eigenmodes in Figure 2d are all out-of-plane flexural modes.
Previous studies [43] have illustrated that the quantum valley hall effect can be realized in discrete hexagonal lattices. While two sufficient conditions must be satisfied to guarantee the existence of the topologically protected edge waves. The unit cell should satisfy C3 symmetry, while mirror symmetry must be violated.
In this case, to violate the mirror symmetry but maintain the C3 symmetry, the PZT patches are rotated clockwise or anti-clockwise, as shown in Figure 3. With the rotation of the PZT patches, the mirror symmetry is broken. The results turn out to be the opening of the Dirac cone at the K point in Figure 2d and forming a band gap. The band gap bounding frequencies are marked by R+ (red line) and R− (black line), as shown in Figure 3. However, the band gap is relatively narrow.
Since the rotation of the PZT patches has little effect on the band gap. To further break the mirror symmetry, different control parameters are assigned to the PZT patches based on the anticlockwise rotation, as shown in Figure 3. When the different control parameters are applied to the PZT patches, the eigenmodes and change to and . Furthermore, the assigned control parameters further break the mirror symmetry while maintaining the rotation symmetry. It can be seen that the band gap expands massively due to the break in the mirror symmetry.
The eigenmodes and phase of the bounding frequencies R+ and R− are shown in Figure 4. It can be observed that the bound frequencies have a refection change. That is because of the break in the C3v symmetry. It should be noted that the has a clockwise polarization while the has an anti-clockwise polarization. The changes in polarization suggest that the topologically protected edge waves exist along the interface between a lattice with different pairs of control parameters.
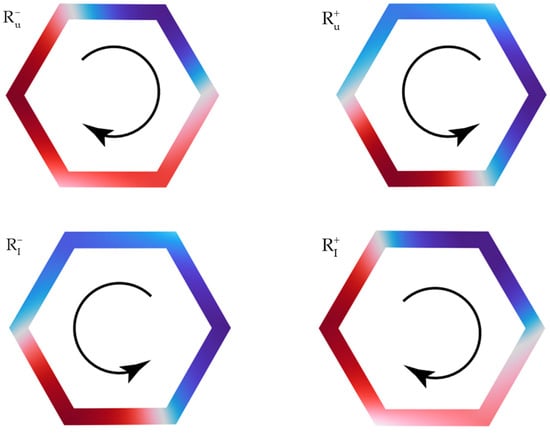
Figure 4.
The eigenmodes and phase of the bounding frequencies R+ and R− in Figure 3.
3. Results
To further study the topologically protected edge waves, the band structure of an elastic wave splitter including a finite number of unit cells is studied, as shown in Figure 5a. The elastic wave splitter consists of 10 type I and 10 type II unit cells with different topologies, as shown in Figure 3. The top and bottom boundaries of this elastic wave splitter are set as Bloch periodic boundary conditions. To isolate additional boundary modes, the left and right boundaries of this elastic wave splitter are considered to be in continuity.
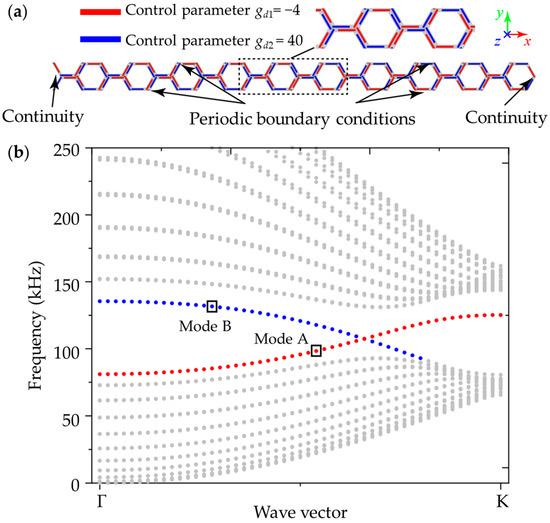
Figure 5.
(a) The illustration of the strip consists of 10 type I and 10 type II unit cells with the top and bottom boundaries set as periodic boundaries and the left and right boundaries considered to be continuity. (b) The corresponding band structure of the strip, where two additional eigenmodes A and B are marked by red and blue nodes, respectively.
The band structure of this elastic wave splitter can be calculated and shown in Figure 5b. All of the flexural modes are marked by gray dots, while the two different interface modes are marked by red and blue dots, respectively. These two additional eigenmodes A and B that appeared in the band gap can be easily observed, as shown in Figure 5b.
To further figure out the two additional different interface modes A and B, the corresponding distributions of displacement fields at modes A and B are calculated and presented in Figure 6. The results show that these two modes are interface modes, both of which are located at the interfaces between type I and type II unit cells. It can be clearly observed that the largest amplitude of the displacement field appears consequently at the interfaces of the type I and II unit cells, which indicates that the different symmetries of the topological state of this designed elastic wave splitter shown in Figure 3 lead to the topologically protected edge waves.
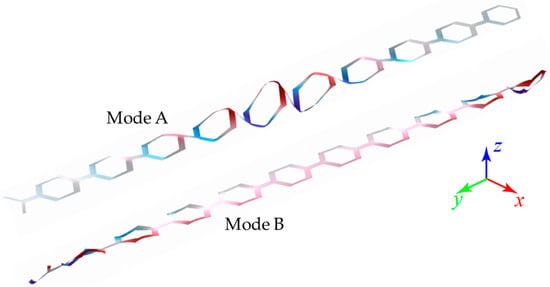
Figure 6.
The corresponding distributions of displacement fields at modes A and B in Figure 5.
4. Discussion
The above analyses illustrate the existence of topologically protected edge waves. The novel design of hexagonal metamaterial plates brings great advances for the real-time turnability of the topologically protected edge waves under active control. Therefore, the real-time target path turnability of the flexural waves in the elastic wave splitter with different topology types is examined in this section. In this section, the hexagonal metamaterial plate consisting of 20 × 20 unit cells is employed. Extend layers as damping domains are added at the top and bottom ends of the finite structure with an isotropic loss factor of 5. While other boundaries are set as free boundary conditions. To clearly illustrate the topologically protected edge waves, the amplitudes of the displacement fields are normalized to the amplitude of the stimulations. That is, if the amplitudes at certain points are equal to those of the stimulations, the normalized amplitudes should be regarded as 1.
Firstly, a straight path is considered, as shown in Figure 7. The point source is given at the lower boundary between the interface of type I and type II unit cells. It can be noticed that the topologically protected edge waves can transmit along the straight path. The largest normalized amplitude is localized around the interface of type I and type II unit cells. That illustrates the good back scattering suppression ability of the designed hexagonal metamaterial plate.
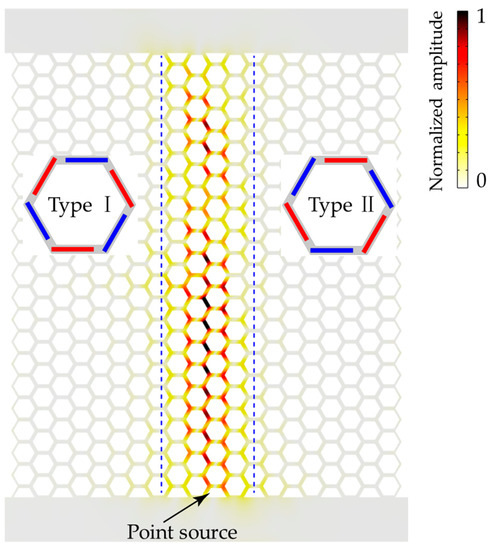
Figure 7.
The distributions of displacement fields along the straight path along the interface of type I and type II unit cells at 117 kHz.
Later, to study the robustness and defect immunity of the designed hexagonal metamaterial plate, two sharp bends (120° and 240°) are added to the interfaces between type I and type II unit cells. The Z-shaped path with sharp corners is examined in Figure 7. The topologically protected edge waves can still propagate through the Z-shaped path, similar to the straight path case. The largest normalized amplitude is also localized at the interfaces between type I and type II unit cells. The absence of significant backscattering at two sharp bends illustrates the robustness and defect immunity of the designed hexagonal metamaterial plate. The high efficiency of the topologically protected edge waves can be testified by the high normalized amplitudes at the top boundary of the interfaces between type I and type II unit cells in Figure 7 and Figure 8.
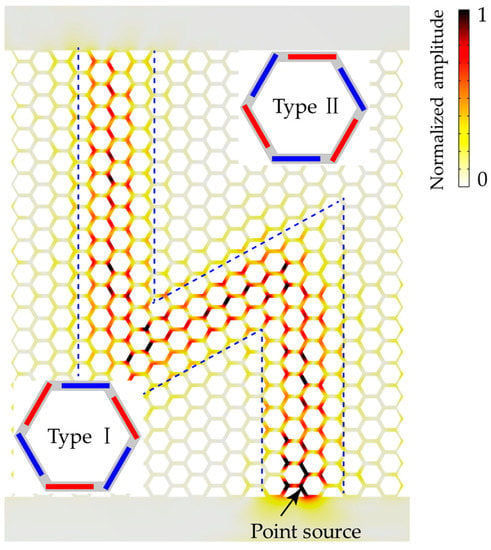
Figure 8.
Distributions of the displacement field of the Z-shaped path with sharp corners along the interface of type I and type II unit cells t at 110 kHz.
In a word, the topologically protected edge waves can be tuned by adjusting the control parameters. Real-time arbitrary propagation paths of the elastic waves with high robustness turn out to be realized. Considering the hexagonal metamaterial plate is designed as an acoustic or elastic device for different experiential testing techniques, only numerical simulations are carried out. The real-time path tuning of the flexural waves can be realized in the experiment, but it is inefficient to carry out in the numerical simulations. Therefore, only two typical paths are found in the numerical simulations. Further experiments can be carried out based on the numerical simulations to meet desirable targets.
5. Conclusions
In conclusion, a novel design of hexagonal metamaterial plates composed of a base plate and piezoelectric patches is proposed. The propagation paths of elastic waves can be tuned by adjusting the control parameters. The Dirac cone of the hexagonal metamaterial plate is opened by rotating the PZT patches under active control. By assigning different control parameters, type I and type II unit cells with different topologies are proposed. The topologically protected edge waves are found at the interfaces between the type I and type II unit cells. Subsequently, the transmittance of the topologically protected edge waves along different paths is examined. The paths can be tuned by adjusting the control parameters. The results show that the topologically protected edge waves can propagate past sharp corners without backscattering. It testified to the robustness of the novel hexagonal metamaterial plate. This work provides a theoretical basis for designing reconfigurable wave guides, elastic wave splitters, and novel elastic wave devices. Those findings show that the topological insulators have potential applications in sensing, energy harvesting, and acoustic devices and hold great promise for the development of high-performance and versatile waveguide technologies with potential applications in a wide range of fields.
Author Contributions
Conceptualization, J.Z. (Jingxuan Zhou), J.C., Z.-Y.L. and D.Y.; methodology, J.Z. (Jingxuan Zhou) and Z.-Y.L.; formal analysis, J.Z. (Jingxuan Zhou), J.Z. (Jie Zhang) and Z.-Y.L.; investigation, J.Z. (Jingxuan Zhou), J.Z. and Z.-Y.L.; data curation, J.Z. (Jie Zhang), J.C. and Z.-Y.L.; writing—original draft preparation, J.Z. (Jingxuan Zhou), J.Z. (Jie Zhang) and Z.-Y.L.; writing—review and editing, J.C. and D.Y.; visualization, J.Z. (Jingxuan Zhou) and J.C.; supervision, Z.-Y.L. and D.Y.; project administration, Z.-Y.L. and D.Y.; funding acquisition, Z.-Y.L. and D.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities (Grant Nos. FRF-TP-22-110A1, 00007492, and FRF-BD-20-08A), and the Interdisciplinary Research Project for Young Teachers of USTB (Fundamental Research Funds for the Central Universities, Grant No. FRF-IDRY-22-007).
Data Availability Statement
Data are made available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, L.L.; Wang, Y.; Chuang, K.C.; Wu, F.G.; Wang, Q.X.; Lin, W.Q.; Jiang, H.Q. A brief review of dynamic mechanical metamaterials for mechanical energy manipulation. Mater. Today 2021, 44, 168–193. [Google Scholar] [CrossRef]
- Hou, Z.; Wu, F.; Liu, Y. Phononic crystals containing piezoelectric material. Solid State Commun. 2004, 130, 745–749. [Google Scholar] [CrossRef]
- Kherraz, N.; Chikh-Bled, F.H.; Sainidou, R.; Morvan, B.; Rembert, P. Tunable phononic structures using lamb waves in a piezoceramic plate. Phys. Rev. B 2019, 99, 094302. [Google Scholar] [CrossRef]
- Chikh-Bled, F.H.; Kherraz, N.; Sainidou, R.; Rembert, P.; Morvan, B. Piezoelectric phononic plates: Retrieving the frequency band structure via all-electric experiments. Smart. Mater. Struct. 2019, 28, 115046. [Google Scholar] [CrossRef]
- Kherraz, N.; Haumesser, L.; Levassort, F.; Benard, P.; Morvan, B. Controlling bragg gaps induced by electric boundary conditions in phononic piezoelectric plates. Appl. Phys. Lett. 2016, 108, 093503. [Google Scholar] [CrossRef]
- Kutsenko, A.A.; Shuvalov, A.L.; Poncelet, O.; Darinskii, A.N. Tunable effective constants of the one-dimensional piezoelectric phononic crystal with internal connected electrodes. J. Acoust. Soc. Am. 2015, 137, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, Y.; Ma, T.; Zhang, C. Smart piezoelectric phononic crystals and metamaterials:State-of-the-art review and outlook. Chin. Sci. Bull. 2022, 67, 1305–1325. [Google Scholar] [CrossRef]
- Nassar, H.; Xu, X.C.; Norris, A.N.; Huang, G.L. Modulated phononic crystals: Non-reciprocal wave propagation and willis materials. J. Mech. Phys. Solids 2017, 101, 10–29. [Google Scholar] [CrossRef]
- Croënne, C.; Vasseur, J.O.; Bou Matar, O.; Ponge, M.F.; Deymier, P.A.; Hladky-Hennion, A.C.; Dubus, B. Brillouin scattering-like effect and non-reciprocal propagation of elastic waves due to spatio-temporal modulation of electrical boundary conditions in piezoelectric media. Appl. Phys. Lett. 2017, 110, 061901. [Google Scholar] [CrossRef]
- Degraeve, S.; Granger, C.; Dubus, B.; Vasseur, J.O.; Pham Thi, M.; Hladky-Hennion, A.C. Bragg band gaps tunability in an homogeneous piezoelectric rod with periodic electrical boundary conditions. J. Appl. Phys. 2014, 115, 194508. [Google Scholar] [CrossRef]
- Flores Parra, E.A.; Bergamini, A.; Lossouarn, B.; Van Damme, B.; Cenedese, M.; Ermanni, P. Bandgap control with local and interconnected lc piezoelectric shunts. Appl. Phys. Lett. 2017, 111, 111902. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Ke, M.; Liu, Z. Valley vortex states in sonic crystals. Phys. Rev. Lett. 2016, 116, 093901. [Google Scholar] [CrossRef]
- Rocklin, D.Z.; Chen, B.G.; Falk, M.; Vitelli, V.; Lubensky, T.C. Mechanical weyl modes in topological maxwell lattices. Phys. Rev. Lett. 2016, 116, 135503. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 2016, 13, 369–374. [Google Scholar] [CrossRef]
- Ningyuan, J.; Owens, C.; Sommer, A.; Schuster, D.; Simon, J. Time- and site-resolved dynamics in a topological circuit. Phys. Rev. X 2015, 5, 021031. [Google Scholar] [CrossRef]
- Prodan, E.; Dobiszewski, K.; Kanwal, A.; Palmieri, J.; Prodan, C. Dynamical majorana edge modes in a broad class of topological mechanical systems. Nat. Commun. 2017, 8, 14587. [Google Scholar] [CrossRef]
- Paulose, J.; Meeussen, A.S.; Vitelli, V. Selective buckling via states of self-stress in topological metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 7639–7644. [Google Scholar] [CrossRef]
- Kane, C.L.; Lubensky, T.C. Topological boundary modes in isostatic lattices. Nat. Phys. 2013, 10, 39–45. [Google Scholar] [CrossRef]
- Peano, V.; Brendel, C.; Schmidt, M.; Marquardt, F. Topological phases of sound and light. Phys. Rev. X 2015, 5, 031011. [Google Scholar] [CrossRef]
- Chaunsali, R.; Kim, E.; Thakkar, A.; Kevrekidis, P.G.; Yang, J. Demonstrating an in situ topological band transition in cylindrical granular chains. Phys. Rev. Lett. 2017, 119, 024301. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Li, Z.; Ni, X.; Sun, X.-C.; Yu, S.-Y.; Lu, M.-H.; Liu, X.-P.; Chen, Y.-F. Topological phononic states of underwater sound based on coupled ring resonators. Appl. Phys. Lett. 2016, 108, 031904. [Google Scholar] [CrossRef]
- Pal, R.K.; Ruzzene, M. Edge waves in plates with resonators: An elastic analogue of the quantum valley hall effect. New J. Phys. 2017, 19, 025001. [Google Scholar] [CrossRef]
- Zhang, F.; Jung, J.; Fiete, G.A.; Niu, Q.; MacDonald, A.H. Spontaneous quantum hall states in chirally stacked few-layer graphene systems. Phys. Rev. Lett. 2011, 106, 156801. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2013, 12, 233–239. [Google Scholar] [CrossRef]
- Ma, T.; Shvets, G. All-si valley-hall photonic topological insulator. New J. Phys. 2016, 18, 025012. [Google Scholar] [CrossRef]
- Dorin, P.; Wang, K.W. Broadband frequency and spatial on-demand tailoring of topological wave propagation harnessing piezoelectric metamaterials. Front. Mater. 2021, 7, 602996. [Google Scholar] [CrossRef]
- Rocklin, D.Z. Directional mechanical response in the bulk of topological metamaterials. New J. Phys. 2017, 19, 065004. [Google Scholar] [CrossRef]
- Pal, R.K.; Schaeffer, M.; Ruzzene, M. Helical edge states and topological phase transitions in phononic systems using bi-layered lattices. J. Appl. Phys. 2016, 119, 084305. [Google Scholar] [CrossRef]
- Huber, S.D. Topological mechanics. Nat. Phys. 2016, 12, 621–623. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Yang, L.; Wang, T.; Chen, A.L.; Laude, V.; Wang, Y.-S. Guided lamb waves in reconfigurable phononic crystal waveguides. APL Mater. 2021, 9, 081110. [Google Scholar] [CrossRef]
- Wang, Y.; Perras, E.; Golub, M.V.; Fomenko, S.I.; Zhang, C.; Chen, W. Manipulation of the guided wave propagation in multilayered phononic plates by introducing interface delaminations. Eur. J. Mech. A Solids 2021, 88, 104266. [Google Scholar] [CrossRef]
- Dong, H.-W.; Wang, Y.-S.; Zhang, C. Inverse design of high-q wave filters in two-dimensional phononic crystals by topology optimization. Ultrasonics 2017, 76, 109–124. [Google Scholar] [CrossRef]
- Swinteck, N.; Matsuo, S.; Runge, K.; Vasseur, J.O.; Lucas, P.; Deymier, P.A. Bulk elastic waves with unidirectional backscattering-immune topological states in a time-dependent superlattice. J. Appl. Phys. 2015, 118, 063103. [Google Scholar] [CrossRef]
- Nash, L.M.; Kleckner, D.; Read, A.; Vitelli, V.; Turner, A.M.; Irvine, W.T. Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 14495–14500. [Google Scholar] [CrossRef]
- Croënne, C.; Vasseur, J.O.; Bou Matar, O.; Hladky-Hennion, A.C.; Dubus, B. Non-reciprocal behavior of one-dimensional piezoelectric structures with space-time modulated electrical boundary conditions. J. Appl. Phys. 2019, 126, 145108. [Google Scholar] [CrossRef]
- Brendel, C.; Peano, V.; Painter, O.; Marquardt, F. Snowflake phononic topological insulator at the nanoscale. Phys. Rev. B 2018, 97, 020102. [Google Scholar] [CrossRef]
- Wang, P.; Lu, L.; Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 2015, 115, 104302. [Google Scholar] [CrossRef]
- Zhou, W.; Wu, B.; Chen, Z.; Chen, W.; Lim, C.W.; Reddy, J.N. Actively controllable topological phase transition in homogeneous piezoelectric rod system. J. Mech. Phys. Solids 2020, 137, 103824. [Google Scholar] [CrossRef]
- Darabi, A.; Collet, M.; Leamy, M.J. Experimental realization of a reconfigurable electroacoustic topological insulator. Proc. Natl. Acad. Sci. USA 2020, 117, 16138–16142. [Google Scholar] [CrossRef]
- Susstrunk, R.; Huber, S.D. Observation of phononic helical edge states in a mechanical topological insulator. Science 2015, 349, 47–50. [Google Scholar] [CrossRef]
- Vila, J.; Pal, R.K.; Ruzzene, M. Observation of topological valley modes in an elastic hexagonal lattice. Phys. Rev. B 2017, 96, 134307. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef]
- Fleury, R.; Sounas, D.; Alu, A. Non-reciprocal acoustic devices based on spatio-temporal angular-momentum modulation. J. Acoust. Soc. Am. 2014, 136, 2281. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, T.; Ge, H.; Wang, W.; Chen, Z.G.; Lu, M.H.; Chen, Y.F. Topological boundary states transport in synthetic four-dimensional acoustic system. Sci. Bull. 2022, 67, 1950–1953. [Google Scholar] [CrossRef] [PubMed]
- Xiao, M.; Ma, G.; Yang, Z.; Sheng, P.; Zhang, Z.Q.; Chan, C.T. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 2015, 11, 240–244. [Google Scholar] [CrossRef]
- Miniaci, M.; Pal, R.K.; Morvan, B.; Ruzzene, M. Experimental observation of topologically protected helical edge modes in patterned elastic plates. Phys. Rev. X 2018, 8, 031074. [Google Scholar] [CrossRef]
- Ye, L.; Qiu, C.; Xiao, M.; Li, T.; Du, J.; Ke, M.; Liu, Z. Topological dislocation modes in three-dimensional acoustic topological insulators. Nat. Commun. 2022, 13, 508. [Google Scholar] [CrossRef]
- Du, J.; Li, T.; Fan, X.; Zhang, Q.; Qiu, C. Acoustic realization of surface-obstructed topological insulators. Phys. Rev. Lett. 2022, 128, 224301. [Google Scholar] [CrossRef]
- Ni, A.; Shi, Z. Complex dispersion relation and topologically protected flexural wave transport in viscoelastic periodic plates. Phys. Lett. A 2023, 458, 128584. [Google Scholar] [CrossRef]
- Luo, J.; Du, Z.; Chen, H.; Ding, X.; Liu, C.; Zhang, W.; Guo, X. Efficient design of helical higher-order topological insulators in 3d elastic medium. J. Mech. Phys. Solids 2023, 176, 105325. [Google Scholar] [CrossRef]
- Luo, J.; Du, Z.; Guo, Y.; Liu, C.; Zhang, W.; Guo, X. Multi-class, multi-functional design of photonic topological insulators by rational symmetry-indicators engineering. Nanophotonics 2021, 10, 4523–4531. [Google Scholar] [CrossRef]
- Du, Z.; Luo, J.; Xu, Z.; Jiang, Z.; Ding, X.; Cui, T.; Guo, X. Higher-order topological insulators by ml-enhanced topology optimization. Int. J. Mech. Sci. 2023, 255, 108441. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhou, Y.; Zheng, S.; Liu, J.; Xia, B. Waveguides induced by replacing defects in phononic crystal. Int. J. Mech. Sci. 2023, 255, 108464. [Google Scholar] [CrossRef]
- Ma, T.-X.; Fan, Q.-S.; Zhang, C.; Wang, Y.-S. Flexural wave energy harvesting by the topological interface state of a phononic crystal beam. Extreme Mech. Lett. 2022, 50, 101578. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Ma, T.-X.; Wang, Y.-Z.; Li, F.-M.; Zhang, C. Vibration isolation by novel meta-design of pyramid-core lattice sandwich structures. J. Sound Vib. 2020, 480, 115377. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, Y.; Liu, F.; Cao, L.; Yang, Z. Modulated flexural edge waves in a plate with its free edge structured by an array of grooves. J. Sound Vib. 2022, 536, 117173. [Google Scholar] [CrossRef]
- Tang, X.; Ma, T.-X.; Wang, Y.-S. Topological rainbow trapping and acoustic energy amplification in two-dimensional gradient phononic crystals. Appl. Phys. Lett. 2023, 122, 112201. [Google Scholar] [CrossRef]
- Matsuda, O.; Larciprete, M.C.; Li Voti, R.; Wright, O.B. Fundamentals of picosecond laser ultrasonics. Ultrasonics 2015, 56, 3–20. [Google Scholar] [CrossRef]
- Tomoda, M.; Matsuda, O.; Wright, O.B.; Li Voti, R. Tomographic reconstruction of picosecond acoustic strain propagation. Appl. Phys. Lett. 2007, 90, 041114. [Google Scholar] [CrossRef]
- Dehoux, T.; Wright, O.B.; Voti, R.L. Picosecond time scale imaging of mechanical contacts. Ultrasonics 2010, 50, 197–201. [Google Scholar] [CrossRef]
- Dehoux, T.; Wright, O.B.; Li Voti, R.; Gusev, V.E. Nanoscale mechanical contacts probed with ultrashort acoustic and thermal waves. Phys. Rev. B 2009, 80, 235409. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Ma, T.-X.; Wang, Y.-Z.; Chai, Y.-Y.; Zhang, C.; Li, F.-M. Active auto-adaptive metamaterial plates for flexural wave control. Int. J. Solids Struct. 2022, 254–255, 111865. [Google Scholar] [CrossRef]
- Li, Z.Y.; Wang, Y.Z.; Ma, T.X.; Zheng, Y.F.; Zhang, C.Z.; Li, F.M. A self-sensing and self-actuating metamaterial sandwich structure for the low-frequency vibration mitigation and isolation. Compos. Struct. 2022, 297, 115894. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).