Abstract
Using a theory of homogenization that consists in the discretization of the inclusion of a binary phononic crystal in small volumes, in which the material parameters can be expanded in Fourier series, we have determined the dependence of the effective elastic parameters as a function of the frequency. In particular, the frequency dependence of all the elements that constitute the effective tensors of stiffness (moduli of elasticity) and density was analyzed for a 1D phononic crystal conformed of materials whose main characteristic is the high contrast between their elastic properties. In this dynamic case of homogenization, it was found that the effective parameters can reproduce the exact dispersion relations for the acoustic modes that propagate along the periodicity direction of the crystal. Particularly, in the second pass band (high-frequency branch) corresponding to the transverse vibrational modes, the homogenized elastic phononic crystal exhibits a metamaterial behavior because the effective C44-component (shear modulus) and dynamic mass density were found to be both negative. It is noteworthy that the study derived from this homogenization technique can lead to design of double negative metamaterial systems for potential applications.
1. Introduction
A phononic crystal is an artificial composite material with periodic distribution of at least two materials with different mechanical properties. A simple example is the periodic arrangement of solid cylinders in a fluid (water or air); in Refs. [1,2,3] by means of multiple-scattering theory and the plane waves method, a general study of these structures in the quasi-static limit is indicated for the calculation of the effective parameters of density, elastic modulus and the speed of sound propagation, in order to study its applications as sound filters and acoustic screens. Moreover, these structures due to the periodicity and the contrast between the elastic parameters of the materials that constitute them, give rise to the formation of forbidden bands in the band structure of the vibration modes [4,5]; this implies that artificial materials can be designed and manufactured to control the propagation of vibrational modes in predetermined frequency ranges [6,7,8].
Parallel to the study of phononic crystals, the elastic metamaterials are found. The main characteristic of these artificial structures lies in potentially extending their physical properties with respect to conventional materials existing in nature. For example, the elastic metamaterials can manifest unnatural physical properties such as bandgaps and negative values of mass, modulus of elasticity, Poisson’s ratio, refractive index, among other properties (e.g., see [9,10] and references).
Nowadays, the field of application and study of the metamaterials can be divided into six fundamental physical domains: mechanical, thermal, electromagnetic, seismic, mass transport and acoustic [9]. Their negative effective properties may lead to potential engineering applications. Auxetic materials are a branch of mechanical metamaterials; these materials, when subjected to tensile stress (elongation), increase their length in the direction perpendicular to the applied force, because they have a negative Poisson’s ratio. These types of structures have important mechanical properties such as high energy absorption and fracture resistance, with promising applications such as protection devices, smart sensors and filters, textile industry, and so on [11,12]. Typically, the auxetics have low density, e.g., structures type foam is an example of auxetic material [13,14,15]. Regarding heat conduction processes, in recent years studies have been reported on periodic structures known as thermal wave crystals (thermal metamaterials); through the use of the Bloch theorem and the transfer matrix method it has been possible to determine the relations dispersion for the propagation of thermal waves in these materials [16,17,18]. On the other hand, using the FDTD (finite difference in time domain) method, the system responses to the temperature have been calculated [18,19,20,21]; the potential applications of these materials lie in the reduction and insulation of the heat flow. In the case of thermal invisibility, it is interesting to highlight the design and manufacture of thermal metamaterials with negative thermal conductivity [22,23,24]. We can refer to the following references for a detailed review of the subsequent areas: electromagnetic metamaterials as well as photonic crystals (control of electromagnetic waves) [25,26,27], seismic metamaterials (manipulation of seismic waves for building protection) [28,29], and mass transport metamaterials (control of the mass flow in diffusion processes) [30,31]. In the context of recent perspectives on the future progress in the field of study of the metamaterials, we can mention as examples the following three works: (1) Soo-Ho Jo, et al. proposed the design of 2D phononic crystals introducing defects with piezoelectric patches; these structures allow the harvesting and localization of the energy of elastic waves in broadband frequencies [32]. (2) Yan Chen, et al. applying a method based on the perturbative analysis, studied the dynamic behavior of a 1D nonlinear mass-in-mass phononic crystal to calculate the dispersion relation and demonstrate that by modifying the wave amplitude and the degree of nonlinearity, the band-gap frequency range can be adjusted (validating the results with finite element simulations) [33]. Lastly, (3) Luyun Chen, et al. using a finite element model of a 2D hexachiral phononic crystal (whose main characteristic is that it does not have a complete mirror symmetry), investigated the acoustic transmission and tunneling in a Dirac-cone state, with applications oriented towards wave manipulation [34].
In the case of acoustic metamaterials, it is well known that their principal application is to control the acoustic or elastic waves [4,5,35,36,37]. Due to the extreme properties of their effective material parameters, within the framework of this field of study we can find elastic metamaterials that are able to possess negative effective values of modulus of elasticity, bulk modulus and mass. The most general case of these metamaterial structures are the double negative systems, which are characterized by having a negative refractive index (analogous to the study by Veselago [38] for the electromagnetic case) due to the effects of local resonances that produce simultaneous negative effective parameters of mass and modulus of elasticity. In Ref. [39] using the plane wave method, the authors characterize a double negative acoustic system for a periodic arrangement of rubber spheres in water; for different filling fractions of the inclusion they obtain simultaneous negative effective values of bulk modulus and density, which being respectively mathematically analogous to dielectric permittivity and magnetic permeability, satisfy the Veselago conditions for a negative refractive index. Another recent work that we can mention is the one developed in [40], in which they characterize and optimize the anisotropy of a broad band elastic system with double negative material parameters.
One of the common conditions to conform resonant metamaterials (i.e., negative simultaneous density and shear modulus) is the high contrast between the elastic properties of their constituents [39,40,41,42,43,44]. Considering the above, in this article we will analyze from a homogenization method that allows to study the material effective response for any form of the inclusions within the unit cell of a 3D phononic crystal and whose principle lies in the discretization of the inclusion [45], the frequency dependence of the effective tensors of moduli of elasticity and density for a transverse polarization of a 1D phononic crystal. For a filling fraction established for the inclusion, it is shown that the effective dynamic parameters can reproduce the exact dispersion relations for the acoustic modes that propagate along the periodicity direction of the crystal. Particularly, in the second pass band (high-frequency branch), the homogenized elastic phononic crystal exhibits a metamaterial behavior because the effective C44-component (shear modulus) and mass density were found to be both negative. This proposal allows us to analyze the conditions for the manifestation of the metamaterial behavior of homogenized phononic crystals, specifically for the design of double negative structures, whose novel and promising applications depending on the operating wavelength can be mentioned, such as acoustic cloaking [46,47,48,49,50] and superlensing (negative refractive index) [51,52,53,54].
2. Homogenization Theoretical Formalism
The numerical approximation used in this study is based on the recent theoretical homogenization technique described in [45]. In that work, the effective properties of the artificial composite material are derived from the fact that, as it is a periodic structure, both its material parameters (e.g., moduli of elasticity and density) as well as their reciprocals that are in function of the position, can be expanded into Fourier series. Furthermore, Bloch’s theorem can be used to express the displacement and stress fields as a plane wave with wave vector and angular frequency . From this formalism that implied the inversion and multiplication of very large matrices (especially for the 3D cases), an approximation was deduced for the calculation of the effective parameters in three-dimensional binary phononic crystals with solid components. The numerical results of the obtained formulas are based on the discretization of the volume of the inclusion () in a finite number of small parts (compared to the volume of the unit cell, ), and according to its geometry the value of its form factor , is introduced into the formulas as a function of the position () of its center of gravity and of the filling fraction in the unit cell of the phononic crystal, also showing a dependence in terms of summations on the vectors of the reciprocal lattice for the calculation of the effective response.
According to this approximation (see [45] and analytical deduction therein), the general equation for calculating the effective tensors of the effective material response as a function of the frequency and the wave vector (dynamic case), is given by the expression:
wherein the apostrophe in the summation that indicates that the term is excluded. In the quasi-static limit (k → 0, ω → 0), the above equation assumes the form:
where for both equations
here, Ω and stand for the matrices of angular frequency ω and of Bloch vector , respectively. Also, , and is the form factor of the inclusion, and the subscripts a and b correspond for the inclusion and host materials, respectively.
In addition, by using the Equation (2), numerical results were presented for the calculation of all the elements of the effective stiffness and density tensors in the quasi-static limit; the cases analyzed involve cubic lattices with solid constituents whose particularity lies in the geometry of the inclusions and filling fraction in the unit cell that go from a cube, parallelepiped and sphere centered in the cell to a non-centrosymmetric inclusion. Once that the 3D phononic crystal has been homogenized, it is shown that its effective density is defined by the average of its constituents (). Besides, it is possible to define its crystalline anisotropy as a function of the number of independent effective elastic constants obtained, which largely depends on the type of crystal lattice of the materials used for the inclusion and the host-matrix.
As mentioned in the introductory part, this work will extend to the dynamic study of the effective parameters through the application of Equation (1), for a one-dimensional binary phononic crystal that can be modeled as a 3D case from a cubic lattice with a geometry and inclusion volume type slab; see Figure 1.
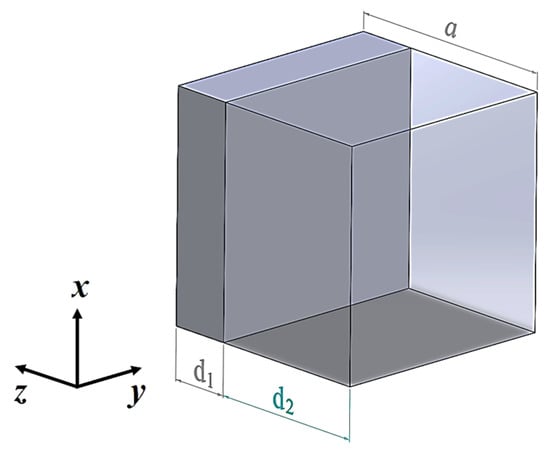
Figure 1.
Cubic unit cell with an inclusion of type slab (1D phononic crystal), a: lattice period and d1 (d2): width of the inclusion (host)-slab.
3. Numerical Results and Discussion
In this section, the vibrational properties are determined for a one-dimensional binary phononic crystal with periodicity in the z-direction, whose characteristic lies in the high contrast between the mechanical properties of its constituents. Indeed, there are multiple reported studies (e.g., [39,40,41,42,43,44] and references cited therein), in which binary phononic elastic compounds are designed where the inclusion material is a very rigid material with respect to the host material. This gives rise to a high contrast between the mechanical properties and acoustic impedances at the contact interfaces between the constituent materials in the unit cell. With these characteristics, the inclusion has very small transverse and longitudinal wave velocities with respect to the host, which gives rise to Mie resonances (dipolar and monopolar). These resonant structures in the metamaterial building blocks lead to effective dynamic parameter negatives. More specifically, a higher mass density of the inclusion with respect to the matrix, implies a greater oscillation amplitude for said component, therefore, the total momentum is opposite to the macroscopic velocity; these negative total momentums exhibited by the compound enhance the dipole resonances to produce a negative effective mass density [55,56]. Regarding the stiffness parameters, the above conditions generate a wave mechanism of quadrupolar resonances necessary to produce a negative shear modulus [41,42]. Although several schemes have been proposed for the design engineering of acoustic/elastic metamaterials, to date no strict criteria have been established to obtain these double negative effective parameters for a given band branch. The previous generalities must be carefully analyzed as a physical mechanism for choosing the appropriate materials that will conform the phononic crystal and that lead to negative effective material parameters. In the present work, the selected inclusion and host materials are aluminium (Al) and soft-rubber (sr), respectively. The transverse velocities are: = 3220.0 m/s and = 17.817 m/s, densities: = 2733 kg/m3 and = 945 kg/m3, and the elastic stiffness constants: = 106.8 GPa, = 60.7 GPa, = 28.2 GPa, = 511.5 MPa, = 510.9 MPa, and = 0.3 MPa [57,58].
The elastic waves propagate perpendicularly to the layers of the 1D phononic crystal with wave vector kz (see Figure 1). The Figure 2 shows the effective parameters as a function of the Al-filling fraction () in the quasi-static limit (kz → 0, ω → 0) by using the Equation (2). Note the influence of the high contrast between the materials on the values of the effective parameters. The effective density (Figure 2a) shows a linear behavior, which represents the average of the values of the density of the constituents of the periodic structure, characterized by the well-known expression [59]: . The behavior of the elastic stiffness constants is illustrated in the Figure 2b–d, when there is only one material as constituent ( = 0 and = 1), and 3 different elastic stiffness constants corresponding to the inclusion and host materials are observed, which implies a cubic crystalline symmetry for the constituents of the phononic periodic structure. But, as the inclusion fills the unit cell (0 < < 1), 6 different values are generated for the elastic stiffness constants, hence the anisotropy of the one-dimensional phononic crystal is of the tetragonal type.
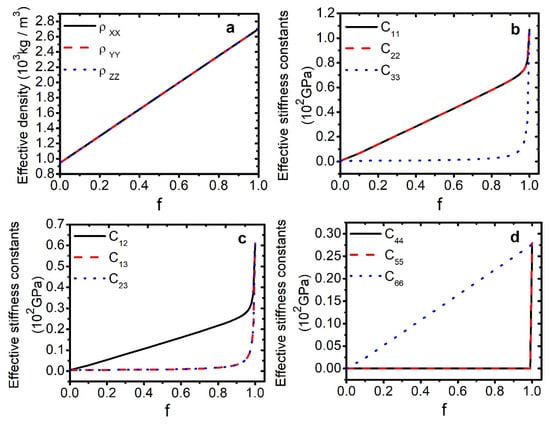
Figure 2.
Effective density (a) and effective stiffness constants (b–d) as a function of the Al-filling fraction in the quasi-static limit.
Now, the dispersion relation for propagating waves in the 1D phononic crystal aluminium/soft-rubber will be determined. For simplicity, we will focus our attention on transverse elastic waves propagating in 1D phononic binary periodic systems. An analytical method will be used to determine the bands structure of transverse elastic waves, and is given by the equation [60,61]:
where d is the width of the material layer (subscripts 1 and 2 correspond to the inclusion and host materials, respectively) and d1 + d2 is the period () of the phononic crystal. This analytical method refers to the application of boundary conditions and Bloch’s theorem, and is an alternative to determine the dispersion relation defined by the equation motion [60]:
here is the instantaneous vector of transverse displacement.
After using Equation (3), the Figure 3 shows the frequency ranges of the phononic band structure for the pass bands and forbidden band of the transverse phononic modes. For this calculation, the ratio of the thickness of the Al layer (inclusion) with respect to the unit cell ( = 10 mm) is 0.9. The graph presented, corresponds to the symmetric interval , known as the first Brillouin zone. The ranges of frequency values for the first and second pass bands are 0–1.11 kHz and 8.91–9.05 kHz, respectively.
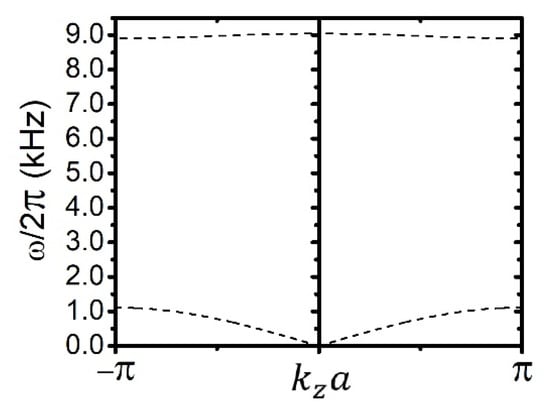
Figure 3.
Schematic representation of the transverse band structure of the 1D phononic crystal aluminium/soft-rubber in the first Brillouin zone.
The velocity of transverse propagation of the elastic waves in the subjacent materials that constitute the periodic structure, is given by the formula , where is the transverse modulus of elasticity, defined for this case by the elastic stiffness constant .
Next, to prove the utility and feasibility of our homogenization method for the dynamic case, we will establish an iterative method. Once that the filling fraction has been fixed and the exact values of obtained, they are substituted into the exact expression for the matrix defined by Equation (1) to calculate the corresponding effective parameters for a transverse polarization including a -finite in terms of the angular frequency (i.e., ). The Figure 4 and Figure 5 exhibit the variation of the effective parameters, and , as a function of the frequency corresponding to the low-frequency and high-frequency branches of the band structure.
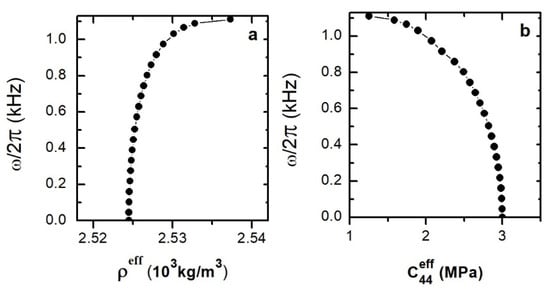
Figure 4.
Effective parameters (a) and (b) corresponding to the low-frequency branch of the band structure.
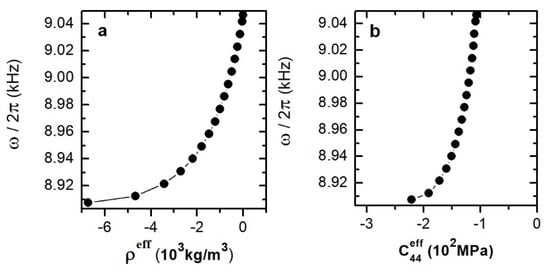
Figure 5.
Effective parameters (a) and (b) corresponding to the high-frequency branch of the band structure.
Our numerical results obtained positive values for the effective parameters of density and transverse stiffness for the frequency range of the first pass band. It is interesting to note that in contrast to the above, for the frequency range of the second pass band the 1D phononic crystal demonstrates a metamaterial behavior with two simultaneous negative effective components.
In order to verify our results, the effective parameters calculated must permit to obtain exactly the complete dispersion relation within the first Brillouin zone. The relation between the frequency () and the wave vector () for the propagation of transverse elastic waves in a homogenized solid periodic structure is given by:
where , the +(−) sign in the denominator allows obtaining the positive (negative) values of in the first Brillouin zone of the complete dispersion relation.
The comparison of the first and second pass bands of the transversal dispersion relation obtained of exact manner (Equation (3)) and through the calculation criteria by using effective parameters (Equation (5)) is illustrated in Figure 6.
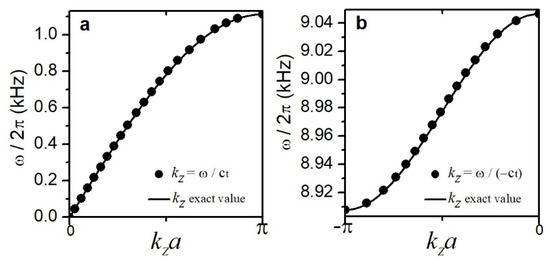
Figure 6.
Comparison of the low-frequency (a) and high-frequency (b) branches of the band structure for transverse modes calculated of exact manner (solid line) and by using effective parameters (dots).
We note that the exact dispersion relation agrees-well with the one that involves its calculation with the effective parameters using a -finite []. The quotient in the Equation (5) of between , implies obtaining a real result for .
Finally, the binary one-dimensional phononic crystal proposed here (aluminium/soft-rubber), possesses effective negative values of mass density and shear modulus in a determined range of band frequencies. This property leads to an interesting phenomenon known as negative refractive index of transverse waves (, the positive sign of the square root is selected for normal materials). The constituent materials have intrinsic mass and stiffness; both parameters define a resonant system that when is excited by the adequate sonic frequencies the mechanical resonance of the artificial structure is obtained. The key result here is a negative elastic value created from the resonance frequencies of the material [53,62,63,64,65].
4. Conclusions
From a general theory of homogenization, that expands the material parameters that appear in the wave equation in Fourier series and which consists in the discretization of the volume of the inclusion in small parts for a binary phononic crystal, we have calculated the values of the effective response of the material parameters of mass density and tensor of stiffness as a function of the frequency and a finite Bloch wave vector [ and ]. The numerical study realized was for a 1D solid phononic crystal whose unit cell is composed of an aluminium layer embedded in a soft-rubber host. The main characteristic of this binary compound is the high elastic contrast between the physical contact of the alternating aluminium/soft-rubber layers in the unit block, in order to characterize a double negative system. This design condition of high mismatches between the acoustic and material parameters of the constituents, implies introducing resonant structures in the unit blocks of the 1D phononic crystal, which increases the dipolar and quadrupolar resonances of the compound and gives rise to negative branches of the effective elastic parameters dependent of the frequency. For such a system, the analytical results determined correspond to a transverse polarization of the elastic waves. As can be seen in the previous sections, this homogenization of the dynamic type, provides graphs that show the evolution of the effective shear modulus or transverse modulus of elasticity () and mass density () with respect to frequency and how these reach negative values in certain defined frequency-regions, which they can change in function of the fraction of filling of the materials that constitute the unit cell. On the other hand, these effective parameters obtained allow us to calculate the low-frequency and high-frequency branches of the phononic band structure.
Here we have proved that the calculation of the dynamic effective elastic parameters totally satisfies two basic conditions: (i) the general conservation laws, and (ii) they reproduce the dispersion relations of the composite.
The usefulness and exactitude of the homogenization approach presented here was demonstrated by means of numerical examples, which leaves the breach open to continue boarding the problem of obtaining the dispersion relation by means of the effective parameters of mass density and elastic stiffness constants. Finally, it also allowed to analyze the conditions for the manifestation of the metamaterial behavior of the homogenized phononic crystal, in this particular case for the design of elastic metamaterials able to possess simultaneous negative values of mass density and shear modulus.
In summary, the results already reported for the quasi-static regime and those presented in this work for the dynamic regime, both with the use of the master Equation (1), demonstrate the generality of our homogenization theory, unlike other formalisms. An interesting feature of this approach is that from the design of 3D structures, these can be particularized to 2D and 1D models. A point to be noted about the application of our numerical iterative procedure in the case of dynamic homogenization, is the important condition of knowing an exact analytical formula to determine the bands structure of a phononic composite with a particular design (for the sake of practicality, we select to model numerically a 1D case). The foregoing should not be seen as a limitation for this approach, as currently there are methods to calculate the band structures of acoustic metamaterials and phononic crystals, each one with its own limitations that are based on the complexity of the structure and constituent materials; a previous analysis is important to choose the exact one.
As previously mentioned, the importance of the phenomenon of double negative metamaterials and applications, lies in the fact that when mechanical waves propagate through these structures, negative refraction, acoustic cloaking, and sound attenuation between other unnatural effects can be obtained.
Author Contributions
For Conceptualization, J.F.M. and A.C.P.R.; Formal analysis, J.F.M., G.M.M., M.M., J.A.L.L. and F.S.; Investigation, A.M.-S., M.M., J.A.L.L. and F.S.; Methodology, J.F.M., A.H.H.J., G.M.M. and A.C.P.R.; Software, J.F.M., A.M.-S. and M.M.; Validation, A.H.H.J. and A.M.-S.; Writing—original draft, J.F.M., G.M.M. and A.C.P.R.; Writing—review & editing, A.H.H.J., A.M.-S., M.M., J.A.L.L. and F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by Tecnológico Nacional de México (Grant No. 18862.23-P), VIEP-BUAP and UPAEP.
Data Availability Statement
Data will be made available on request, contacting to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ni, Q.; Cheng, J. Anisotropy of effective velocity for elastic wave propagation in two-dimensional phononic crystals at low frequencies. Phys. Rev. B 2005, 72, 014305. [Google Scholar] [CrossRef]
- Khelif, A.; Adibi, A. Phononic Crystals: Fundamentals and Applications, 1st ed.; Springer: New York, NY, USA, 2016; pp. 1–22. [Google Scholar]
- Gumen, L.N.; Arriaga, J.; Krokhin, A.A. Metafluid with anisotropic dynamic mass. Low Temp. Phys. 2011, 37, 975–978. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Sigalas, M.; Economou, E. Elastic and acoustic wave band structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Li, Y.F.; Huang, X.; Meng, F.; Zhou, S. Evolutionary topological design for phononic band gap crystals. Struct. Multidisc. Optim. 2016, 54, 595–617. [Google Scholar] [CrossRef]
- Li, Y.F.; Meng, F.; Li, S.; Jia, B.; Zhou, S.; Huang, X. Designing broad phononic band gaps for in-plane modes. Phys. Lett. A 2018, 382, 679–684. [Google Scholar] [CrossRef]
- Aravantinos-Zafiris, N.; Lucklum, F.; Sigalas, M.M. Complete phononic band gaps in the 3D Yablonovite structure with spheres. Ultrasonics 2021, 110, 106265. [Google Scholar] [CrossRef]
- Liu, J.; Guo, H.; Wang, T. A Review of Acoustic Metamaterials and Phononic Crystals. Crystals 2020, 10, 305. [Google Scholar] [CrossRef]
- Holliman, J.E., Jr.; Schaef, H.T.; McGrail, B.P.; Miller, Q.R. Review of foundational concepts and emerging directions in metamaterial research: Design, phenomena, and applications. Mater. Adv. 2022, 3, 8390–8406. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Han, D.; Ren, X.; Zhang, Y.; Zhang, X.Y.; Zhang, X.G.; Luo, C.; Xie, Y.M. Lightweight auxetic metamaterials: Design and characteristic study. Compos. Struct. 2022, 293, 115706. [Google Scholar] [CrossRef]
- Lakes, R.S. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Rothenburg, L.; Berlin, A.I.; Bathurst, R.J. Microstructure of isotropic materials with negative Poisson’s ratio. Nature 1991, 354, 470–472. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices, 1st ed.; McGraw-Hill Book Company Inc.: New York, NY, USA, 1953. [Google Scholar]
- Li, N.; Ren, J.; Wang, L.; Zhang, G.; Hänggi, P.; Li, B. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Modern Phys. 2012, 84, 1045–1066. [Google Scholar] [CrossRef]
- Chen, A.-L.; Li, Z.-Y.; Ma, T.-X.; Li, X.-S.; Wang, Y.-S. Heat reduction by thermal wave crystals. Int. J. Heat Mass Transf. 2018, 121, 215–222. [Google Scholar] [CrossRef]
- Yeung, W.K.; Lam, T.T. A numerical scheme for non-Fourier heat conduction Part I: One-dimensional problem formulation and applications. Numer. Heat Transf. Part B Fund. 1998, 33, 215–233. [Google Scholar] [CrossRef]
- Lam, T.T.; Yeung, W.K. A numerical scheme for non-Fourier heat conduction, Part II: Two-dimensional problem formulation and verification. Numer. Heat Transf. Part B Fund. 2002, 41, 543–564. [Google Scholar] [CrossRef]
- Zhang, M.K.; Cao, B.Y.; Guo, Y.C. Numerical studies on dispersion of thermal waves. Int. J. Heat Mass Transf. 2013, 67, 1072–1082. [Google Scholar] [CrossRef]
- Chen, T.; Weng, C.-N.; Chen, J.-S. Cloak for curvilinearly anisotropic media in conduction. Appl. Phys. Lett. 2008, 93, 114103. [Google Scholar] [CrossRef]
- Fan, C.Z.; Gao, Y.; Huang, J.P. Shaped graded materials with an apparent negative thermal conductivity. Appl. Phys. Lett. 2008, 92, 251907. [Google Scholar] [CrossRef]
- Kuon, I.; Ohtaka, K. Photonic Crystals: Physics, Fabrication and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Kuramochi, E. Manipulating and trapping light with photonic crystals from fundamental studies to practical applications. J. Mater. Chem. C 2016, 4, 11032–11049. [Google Scholar] [CrossRef]
- Milton, G.W.; Briane, M.; Willis, J.R. On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 2006, 8, 248. [Google Scholar] [CrossRef]
- Farhat, M.; Guenneau, S.; Enoch, S. Broadband cloaking of bending waves via homogenization of multiply perforated radially symmetric and isotropic thin elastic plates. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 85, 020301. [Google Scholar] [CrossRef]
- Restrepo-Florez, J.M.; Maldovan, M. Mass Separation by Metamaterials. Sci. Rep. 2016, 6, 21971. [Google Scholar] [CrossRef] [PubMed]
- Restrepo-Florez, J.M.; Maldovan, M. Rational design of mass diffusion metamaterial concentrators based on coordinate transformation. J. Appl. Phys. 2016, 120, 084902. [Google Scholar] [CrossRef]
- Jo, S.-H.; Youn, B.D. A Phononic Crystal with Differently Configured Double Defects for Broadband Elastic Wave Energy Localization and Harvesting. Crystals 2021, 11, 643. [Google Scholar] [CrossRef]
- Chen, Y.; Li, G.; Sun, R.; Chen, G. Wave Dispersion in One-Dimensional Nonlinear Local Resonance Phononic Crystals with Perturbation Method. Crystals 2021, 11, 774. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y.; Kong, H. Acoustic Tunneling Study for Hexachiral Phononic Crystals Based on Dirac-Cone Dispersion Properties. Crystals 2021, 11, 1577. [Google Scholar] [CrossRef]
- Sigalas, M.; Economou, E. Band structure of elastic waves in two dimensional systems. Solid State Commun. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 2014, 66, 38. [Google Scholar] [CrossRef]
- Laude, V. Phononic Crystals: Artificial Crystals for Sonic, Acoustic, and Elastic Waves; Walter de Gruyter GmbH & Co KG Llc.: Berlin/Heidelberg, Germany, 2015; Volume 26. [Google Scholar]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Usp. 1968, 10, 509. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. B 2004, 70, 055602(R). [Google Scholar] [CrossRef]
- Dong, H.-W.; Zhao, S.-D.; Wang, Y.-S.; Zhang, C. Topology optimization of anisotropic broadband double-negative elastic metamaterials. J. Mech. Phys. Solids 2017, 105, 54–80. [Google Scholar] [CrossRef]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Effective medium theory for elastic metamaterials in two dimensions. Phys. Rev. B 2007, 76, 205313. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, G. Analytic model of elastic metamaterials with local resonances. Phys. Rev. B 2009, 79, 195109. [Google Scholar] [CrossRef]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Elastic Metamaterials with Simultaneously Negative Effective Shear Modulus and Mass Density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef]
- Lai, Y.; Wu, Y.; Sheng, P.; Zhang, Z.-Q. Hybrid elastic solids. Nat. Mater 2011, 10, 620–624. [Google Scholar] [CrossRef]
- Flores Méndez, J.; Pinón Reyes, A.C.; Heredia Jiménez, A.H.; Ambrosio Lázaro, R.C.; Morales-Sánchez, A.; Moreno Moreno, M.; Luna-López, J.A.; Severiano Carrillo, F.; Meraz Melo, M.A. Discretization Approach for the Homogenization of Three-Dimensional Solid-Solid Phononic Crystals in the Quasi-Static Limit: Density and Elastic Moduli. Appl. Sci. 2022, 12, 2987. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, C.G.; Fang, N. Broadband Acoustic Cloak for Ultrasound Waves. Phys. Rev. Lett. 2011, 106, 024301. [Google Scholar] [CrossRef] [PubMed]
- Popa, B.I.; Zigoneanu, L.; Cummer, S.A. Experimental Acoustic Ground Cloak in Air. Phys. Rev. Lett. 2011, 106, 253901. [Google Scholar] [CrossRef] [PubMed]
- Zigoneanu, L.; Popa, B.I.; Cummer, S.A. Three-dimensional broadband omnidirectional acoustic ground cloak. Nat. Mater. 2014, 13, 352–355. [Google Scholar] [CrossRef]
- Bi, Y.; Jia, H.; Sun, Z.; Yang, Y.; Zhao, H.; Yang, J. Experimental demonstration of three-dimensional broadband underwater acoustic carpet cloak. Appl. Phys. Lett. 2018, 112, 223502. [Google Scholar] [CrossRef]
- Esfahlani, H.; Karkar, S.; Lissek, H.; Mosig, J.R. Acoustic carpet cloak based on an ultrathin metasurface. Phys. Rev. B 2016, 94, 014302. [Google Scholar] [CrossRef]
- Park, J.J.; Park, C.M.; Lee, K.J.B.; Lee, S.H. Acoustic superlens using membrane-based metamaterials. Appl. Phys. Lett. 2015, 106, 051901. [Google Scholar] [CrossRef]
- Yang, X.; Yin, J.; Yu, G.; Peng, L.; Wang, N. Acoustic superlens using Helmholtz-resonator-based metamaterials. Appl. Phys. Lett. 2015, 107, 193505. [Google Scholar] [CrossRef]
- Kaina, N.; Lemoult, F.; Fink, M.; Lerosey, G. Negative refractive index and acoustic superlens from multiple scattering in single negative metamaterials. Nature 2015, 525, 77–81. [Google Scholar] [CrossRef]
- Park, C.M.; Lee, S.H. Zero-reflection acoustic metamaterial with a negative refractive index. Sci. Rep. 2019, 9, 3372. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, Z.; Qiu, C.; Shi, J. Metamaterial with Simultaneously Negative Bulk Modulus and Mass Density. Phys. Rev. Lett. 2007, 99, 093904. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ciesielski, A. An Introduction to Rubber Technology, 1st ed.; RAPRA Technology: Shrewsbury, UK, 1999. [Google Scholar]
- Deymier, P.A. Acoustic Metamaterials and Phononic Crystals, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kushwaha, M.S. Classical band structure of periodic elastic composites. Int. J. Mod. Phys. B 1996, 10, 977–1094. [Google Scholar] [CrossRef]
- Rytov, S.M. Acoustic properties of a thinly laminated medium. Sov. Phys. Acoust. 1956, 2, 68. [Google Scholar]
- Lee, S.H.; Park, C.M.; Seo, Y.M.; Wang, Z.G.; Kim, C.K. Composite acoustic medium with simultaneously negative density and modulus. Phys. Rev. Lett. 2010, 104, 054301. [Google Scholar] [CrossRef]
- Liu, X.N.; Hu, G.K.; Huang, G.L.; Sun, C.T. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl. Phys. Lett. 2011, 98, 251907. [Google Scholar] [CrossRef]
- Liang, Z.; Feng, T.; Lok, S.; Liu, F.; Ng, K. Space-coiling metamaterials with double negativity and conical dispersion. Sci. Rep. 2013, 3, 1614. [Google Scholar] [CrossRef]
- Xie, Y.; Popa, B.I.; Zigoneanu, L.; Cummer, S.A. Measurement of a broadband negative index with space-coiling acoustic metamaterials. Phys. Rev. Lett. 2013, 110, 175501. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).