Prediction of Superconductivity in Clathrate Er Hydrides under High Pressure
Abstract
1. Introduction
2. Methods and Computational Details
3. Results and Discussion
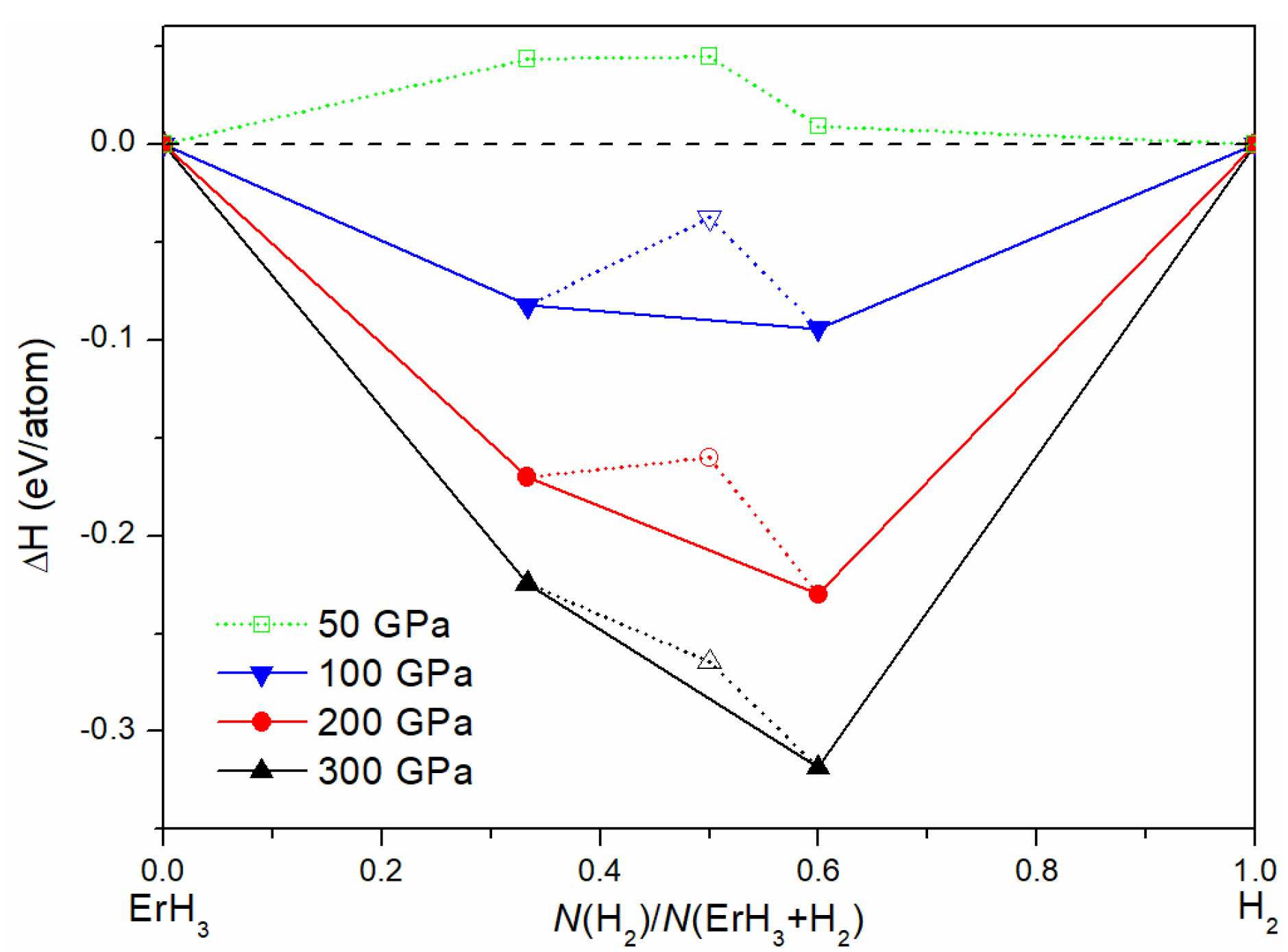
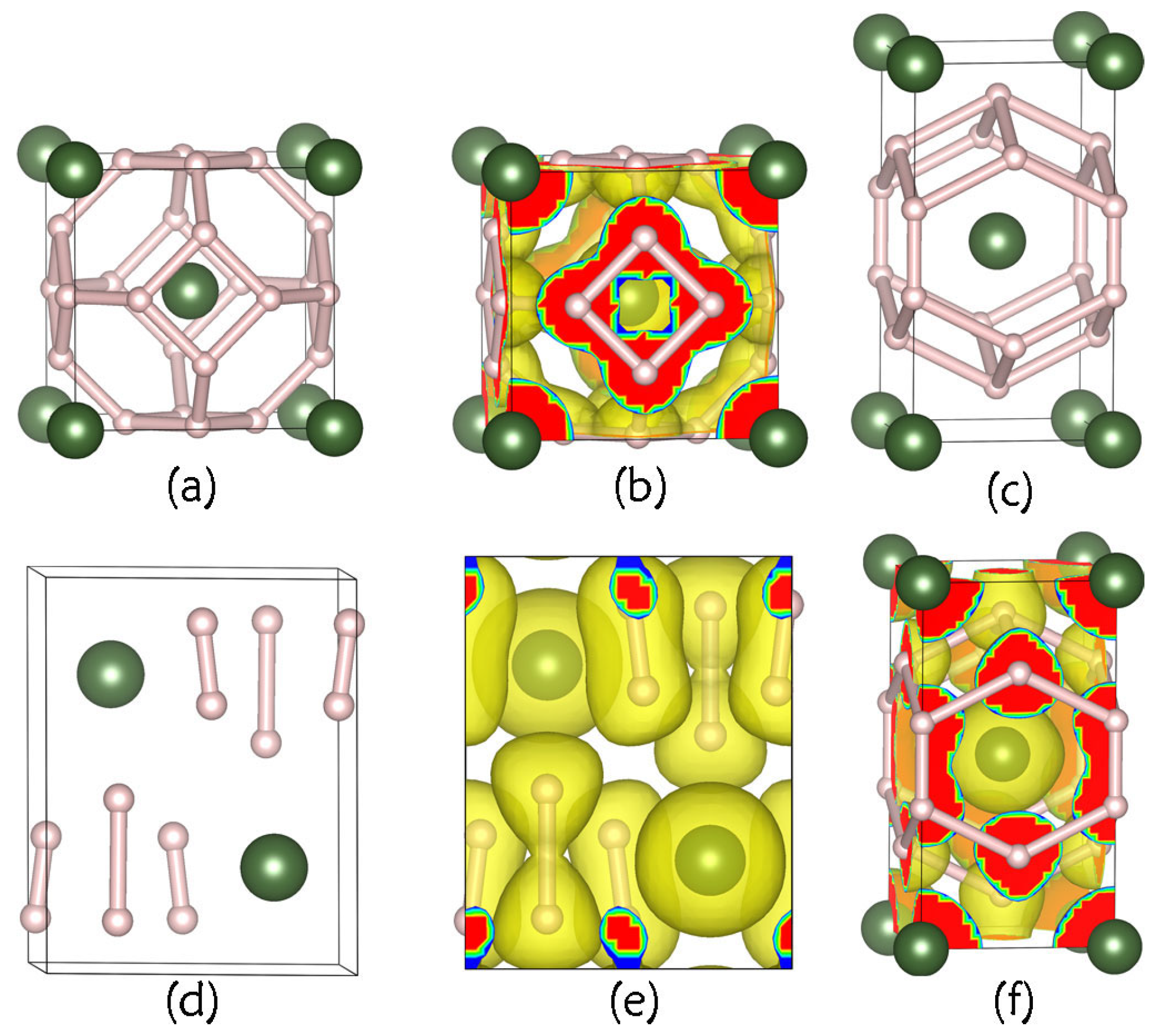
3.1. Crystal Structures and Stabilities
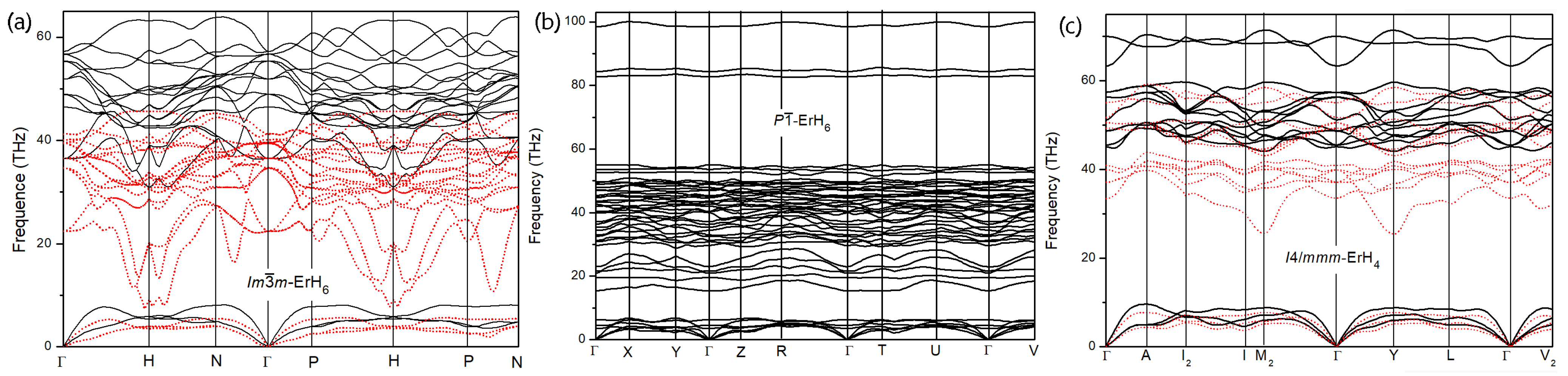
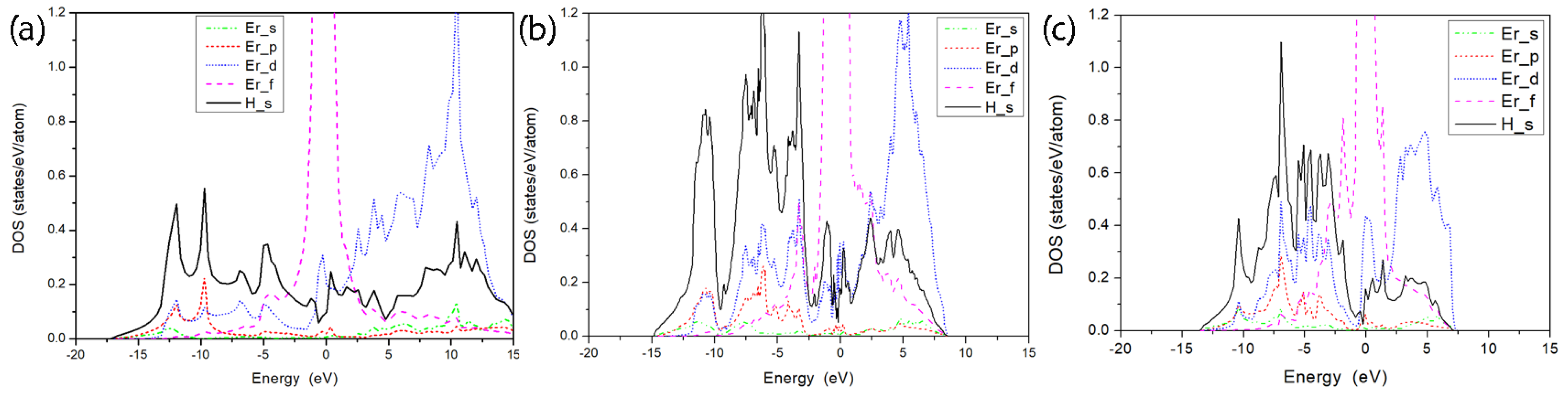
3.2. Electronic Characteristics and Superconductivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ashcroft, N.W. Metallic Hydrogen: A High-Temperature Superconductor? Phys. Rev. Lett. 1968, 21, 1748–1749. [Google Scholar] [CrossRef]
- Ashcroft, N.W. Hydrogen Dominant Metallic Alloys: High Temperature Superconductors? Phys. Rev. Lett. 2004, 92, 187002. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Naumov, I.I.; Hoffmann, R.; Ashcroft, N.W.; Hemley, R.J. Potential High-Tc Superconducting Lanthanum and Yttrium Hydrides at High Pressure. Proc. Natl. Acad. Sci. USA 2017, 114, 6990–6995. [Google Scholar] [CrossRef]
- Peng, F.; Sun, Y.; Pickard, C.J.; Needs, R.J.; Wu, Q.; Ma, Y. Hydrogen Clathrate Structures in Rare Earth Hydrides at High Pressures: Possible Route to Room-Temperature Superconductivity. Phys. Rev. Lett. 2017, 119, 107001. [Google Scholar] [CrossRef] [PubMed]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; et al. Superconductivity at 250 K in Lanthanum Hydride under High Pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef]
- Van Setten, M.J.; Popa, V.A.; de Wijs, G.A.; Brocks, G. Electronic Structure and Optical Properties of Lightweight Metal Hydrides. Phys. Rev. B 2007, 75, 035204. [Google Scholar] [CrossRef]
- Zurek, E.; Hoffmann, R.; Ashcroft, N.W.; Oganov, A.R.; Lyakhov, A.O. A Little Bit of Lithium Does a Lot for Hydrogen. Proc. Natl. Acad. Sci. USA 2009, 106, 17640–17643. [Google Scholar] [CrossRef]
- Chen, Y.; Geng, H.Y.; Yan, X.; Sun, Y.; Wu, Q.; Chen, X. Prediction of Stable Ground-State Lithium Polyhydrides under High Pressures. Inorg. Chem. 2017, 56, 3867–3874. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Q.; Oganov, A.R.; Wang, H. Superconductivity of Lithium-Doped Hydrogen under High Pressure. Acta Cryst. 2014, 70, 104–111. [Google Scholar] [CrossRef]
- Zhou, D.; Jin, X.; Meng, X.; Bao, G.; Ma, Y.; Liu, B.; Cui, T. Ab Initio Study Revealing a Layered Structure in Hydrogen-Rich KH6 under High Pressure. Phys. Rev. B 2012, 86, 014118. [Google Scholar] [CrossRef]
- Yu, S.; Zeng, Q.; Oganov, A.R.; Hu, C.; Frapper, G.; Zhang, L. Exploration of Stable Compounds, Crystal Structures, and Superconductivity in the Be-H System. AIP Adv. 2014, 4, 107118. [Google Scholar] [CrossRef]
- Lonie, D.C.; Hooper, J.; Altintas, B.; Zurek, E. Metallization of Magnesium Polyhydrides under Pressure. Phys. Rev. B 2013, 87, 054107. [Google Scholar] [CrossRef]
- Wang, H. Superconductive Sodalite-Like Clathrate Calcium Hydride at High Pressures. Proc. Natl. Acad. Sci. USA 2012, 109, 4. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, J.; Gao, G.; Liu, H.; Wang, H. Compressed Sodalite-Like MgH6 as a Potential High-Temperature Superconductor. RSC Adv. 2015, 5, 59292–59296. [Google Scholar] [CrossRef]
- Ma, L.; Wang, K.; Xie, Y.; Yang, X.; Wang, Y.; Zhou, M.; Liu, H.; Yu, X.; Zhao, Y.; Wang, H.; et al. High-Temperature Superconducting Phase in Clathrate Calcium Hydride CaH6 up to 215 K at a Pressure of 172 Gpa. Phys. Rev. Lett. 2022, 128, 167001. [Google Scholar] [CrossRef]
- Abe, K. Hydrogen-Rich Scandium Compounds at High Pressures. Phys. Rev. B 2017, 96, 144108. [Google Scholar] [CrossRef]
- Qian, S.; Sheng, X.; Yan, X.; Chen, Y.; Song, B. Theoretical Study of Stability and Superconductivity of ScHn (n = 4–8) at High Pressure. Phys. Rev. B 2017, 96, 094513. [Google Scholar] [CrossRef]
- Ye, X.; Zarifi, N.; Zurek, E.; Hoffmann, R.; Ashcroft, N.W. High Hydrides of Scandium under Pressure: Potential Superconductors. J. Phys. Chem. C 2018, 122, 6298–6309. [Google Scholar] [CrossRef]
- Heil, C.; Di Cataldo, S.; Bachelet, G.B.; Boeri, L. Superconductivity in Sodalite-Like Yttrium Hydride Clathrates. Phys. Rev. B 2019, 99, 220502. [Google Scholar] [CrossRef]
- Geballe, Z.M.; Liu, H.; Mishra, A.K.; Ahart, M.; Somayazulu, M.; Meng, Y.; Baldini, M.; Hemley, R.J. Synthesis and Stability of Lanthanum Superhydrides. Angew. Chem. Int. Edit. 2018, 57, 688–692. [Google Scholar] [CrossRef] [PubMed]
- Troyan, I.A.; Semenok, D.V.; Kvashnin, A.G.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Ivanova, A.G.; Prakapenka, V.B.; Greenberg, E.; Gavriliuk, A.G.; et al. Anomalous High-Temperature Superconductivity in YH6. Adv. Mater. 2021, 33, 2006832. [Google Scholar] [CrossRef] [PubMed]
- Kong, P.; Minkov, V.S.; Kuzovnikov, M.A.; Drozdov, A.P.; Besedin, S.P.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Prakapenka, V.B.; Chariton, S. Superconductivity up to 243 K in the Yttrium-Hydrogen System under High Pressure. Nat. Commun. 2021, 12, 5075. [Google Scholar] [CrossRef]
- Bi, J.; Nakamoto, Y.; Zhang, P.; Shimizu, K.; Zou, B.; Liu, H.; Zhou, M.; Liu, G.; Wang, H.; Ma, Y. Giant Enhancement of Superconducting Critical Temperature in Substitutional Alloy (La,Ce)H9. Nat. Commun. 2022, 13, 5952. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Semenok, D.V.; Huang, X.; Shu, H.; Li, X.; Duan, D.; Cui, T.; Oganov, A.R. High-Temperature Superconducting Phases in Cerium Superhydride with a Tc up to 115 K Below a Pressure of 1 Megabar. Phys. Rev. Lett. 2021, 127, 117001. [Google Scholar] [CrossRef]
- Salke, N.P.; Esfahani, M.M.D.; Zhang, Y.; Kruglov, I.A.; Zhou, J.; Wang, Y.; Greenberg, E.; Prakapenka, V.B.; Liu, J.; Oganov, A.R. Synthesis of Clathrate Cerium Superhydride CeH9 at 80-100 GPa with Atomic Hydrogen Sublattice. Nat. Commun. 2019, 10, 4453. [Google Scholar] [CrossRef]
- Li, X.-F.; Hu, Z.-Y.; Huang, B. Phase Diagram and Superconductivity of Compressed Zirconium Hydrides. Phys. Chem. Chem. Phys. 2017, 19, 3538–3543. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Duan, D.; Tian, F.; Liu, H.; Li, D.; Zhao, Z.; Sha, X.; Yu, H.; Zhang, H. First-Principles Study on the Structural and Electronic Properties of Metallic HfH2 under Pressure. Sci. Rep. 2015, 5, 11381. [Google Scholar] [CrossRef]
- Durajski, A.P. Phonon-Mediated Superconductivity in Compressed Nbh 4 Compound. Eur. Phys. J. B 2014, 87, 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Hao, J.; Liu, H.; Li, Y.; Ma, Y. The Metallization and Superconductivity of Dense Hydrogen Sulfide. J. Chem. Phys. 2014, 140, 174712. [Google Scholar] [CrossRef]
- Einaga, M.; Sakata, M.; Ishikawa, T.; Shimizu, K.; Eremets, M.I.; Drozdov, A.P.; Troyan, I.A.; Hirao, N.; Ohishi, Y. Crystal Structure of the Superconducting Phase of Sulfur Hydride. Nat. Phys. 2016, 12, 835–838. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, F.; Yao, Y. First-Principles Demonstration of Superconductivity at 280 K in Hydrogen Sulfide with Low Phosphorus Substitution. Phys. Rev. B 2016, 93, 224513. [Google Scholar] [CrossRef]
- Pasan, H.; Snider, E.; Munasinghe, S.; Dissanayake, S.E.; Salke, N.P.; Ahart, M.; Khalvashi-Sutter, N.; Dasenbrock-Gammon, N.; McBride, R.; Smith, G.A. Observation of Conventional near Room Temperature Superconductivity in Carbonaceous Sulfur Hydride. arXiv 2023, arXiv:2302.08622. [Google Scholar]
- Flores-Livas, J.A.; Sanna, A.; Gross, E. High Temperature Superconductivity in Sulfur and Selenium Hydrides at High Pressure. Eur. Phys. J. B 2016, 89, 1–6. [Google Scholar] [CrossRef]
- Zhong, X.; Wang, H.; Zhang, J.; Liu, H.; Zhang, S.; Song, H.-F.; Yang, G.; Zhang, L.; Ma, Y. Tellurium Hydrides at High Pressures: High-Temperature Superconductors. Phys. Rev. Lett. 2016, 116, 057002. [Google Scholar] [CrossRef]
- Drozdov, A.; Eremets, M.; Troyan, I. Superconductivity above 100 K in PH3 at High Pressures. arXiv 2015, arXiv:1508.06224. [Google Scholar]
- Fu, Y.; Du, X.; Zhang, L.; Peng, F.; Zhang, M.; Pickard, C.J.; Needs, R.J.; Singh, D.J.; Zheng, W.; Ma, Y. High-Pressure Phase Stability and Superconductivity of Pnictogen Hydrides and Chemical Trends for Compressed Hydrides. Chem. Mater. 2016, 28, 1746–1755. [Google Scholar] [CrossRef]
- Joubert, J.M.; Crivello, J.C. Stability of Erbium Hydrides Studied by DFT Calculations. Int. J. Hydrogen Energy 2012, 37, 4246–4253. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, Q.; Yang, J.; Wang, L.; Zhang, W.; Yao, G. Predicted High-Temperature Superconductivity in Rare Earth Hydride ErH2 at Moderate Pressure. Chin. Phys. Lett. 2022, 39, 127403. [Google Scholar] [CrossRef]
- Palasyuk, T.; Tkacz, M.; Vajda, P. High Pressure Studies of the Erbium–Hydrogen System. Solid State Commun. 2005, 135, 226–231. [Google Scholar] [CrossRef]
- Hou, P.; Tian, F.; Li, D.; Chu, B.; Zhao, Z.; Liu, B.; Cui, T. High-Pressure Phase Transition of MH(3) (M: Er, Ho). J. Chem. Phys. 2014, 141, 054703. [Google Scholar] [CrossRef] [PubMed]
- Kuzovnikov, M.A.; Eremets, M.I.; Drozdov, A.P.; Tkacz, M. Pressure-Induced Metallization in Erbium Trihydride. Solid State Commun. 2017, 263, 23–26. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal Structure Prediction Via Particle-Swarm Optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Calypso: A Method for Crystal Structure Prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Lu, C.; Chen, C. Indentation-Strain Stiffening in Tungsten Nitrides: Mechanisms and Implications. Phys. Rev. Materials 2020, 4, 043402. [Google Scholar] [CrossRef]
- Lu, C.; Chen, C. High-Pressure Evolution of Crystal Bonding Structures and Properties of FeOOH. J. Phys. Chem. Lett. 2018, 9, 2181–2185. [Google Scholar] [CrossRef]
- Li, X.; Xie, Y.; Sun, Y.; Huang, P.; Liu, H.; Chen, C.; Ma, Y. Chemically Tuning Stability and Superconductivity of P–H Compounds. J. Phys. Chem. Lett. 2020, 11, 935–939. [Google Scholar] [CrossRef]
- Zhong, X.; Sun, Y.; Iitaka, T.; Xu, M.; Liu, H.; Hemley, R.J.; Chen, C.; Ma, Y. Prediction of above-Room-Temperature Superconductivity in Lanthanide/Actinide Extreme Superhydrides. J. Am. Chem. Soc. 2022, 144, 13394–13400. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Scandolo, S.; Giannozzi, P.; Cavazzoni, C.; de Gironcoli, S.; Pasquarello, A.; Baroni, S. First-Principles Codes for Computational Crystallography in the Quantum-Espresso Package. Z. Kristallogr. 2005, 220, 574–579. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Structure of Phase III of Solid Hydrogen. Nat. Phys. 2007, 3, 473–476. [Google Scholar] [CrossRef]
- Hai, Y.-L.; Lu, N.; Tian, H.-L.; Jiang, M.-J.; Yang, W.; Li, W.-J.; Yan, X.-W.; Zhang, C.; Chen, X.-J.; Zhong, G.-H. Cage Structure and near Room-Temperature Superconductivity in TbHN (N = 1–12). J. Phys. Chem. C 2021, 125, 3640–3649. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Allen, P.B.; Dynes, R.C. Transition Temperature of Strong-Coupled Superconductors Reanalyzed. Phys. Rev. B 1975, 12, 905–922. [Google Scholar] [CrossRef]
- Zurek, E.; Bi, T. High-Temperature Superconductivity in Alkaline and Rare Earth Polyhydrides at High Pressure: A Theoretical Perspective. J. Chem. Phys. 2019, 150, 050901. [Google Scholar] [CrossRef]


| Phase | Pressure (GPa) | Lattice Parameters | Coordinates |
|---|---|---|---|
| Imm-ErH6 | 100 | a = 3.16 Å α = 109.47 b = 3.16 Å β = 109.47 c = 3.16 Å γ = 109.47 | H1 0.25000 0.50000 −0.25000 Er1 0.00000 0.00000 0.00000 |
| P-ErH6 | 80 | a = 3.15 Å α = 89.99 b = 3.67 Å β = 100.40 c = 4.71 Å γ = 89.99 | H1 0.82939 0.51335 0.88270 H2 0.78475 0.54530 0.67573 H3 0.36777 0.74998 0.87671 H5 0.72069 0.24999 0.43394 H6 0.82940 0.98659 0.88268 H7 0.78476 0.95469 0.67571 Er1 0.29653 0.24999 0.73683 |
| I4/mmm-ErH4 | 100 | a = 3.31 Å α = 129.59 b = 3.31 Å β = 129.59 c = 3.31 Å γ = 74.05 | H1 1.38370 1.38370 1.00000 H2 0.75000 1.25000 0.50000 Er1 0.00000 0.00000 0.00000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.Z.; Zhang, Z.L.; Chen, Y.M.; Kuang, F.G. Prediction of Superconductivity in Clathrate Er Hydrides under High Pressure. Crystals 2023, 13, 792. https://doi.org/10.3390/cryst13050792
Yan XZ, Zhang ZL, Chen YM, Kuang FG. Prediction of Superconductivity in Clathrate Er Hydrides under High Pressure. Crystals. 2023; 13(5):792. https://doi.org/10.3390/cryst13050792
Chicago/Turabian StyleYan, Xiao Z., Zhao L. Zhang, Yang M. Chen, and Fang G. Kuang. 2023. "Prediction of Superconductivity in Clathrate Er Hydrides under High Pressure" Crystals 13, no. 5: 792. https://doi.org/10.3390/cryst13050792
APA StyleYan, X. Z., Zhang, Z. L., Chen, Y. M., & Kuang, F. G. (2023). Prediction of Superconductivity in Clathrate Er Hydrides under High Pressure. Crystals, 13(5), 792. https://doi.org/10.3390/cryst13050792





