Magnetic Field-Dependent Microstructure Evolution of Solidified Co39.2Ni39.2Al21.6 Eutectic Medium-Entropy Alloy
Abstract
1. Introduction
2. Materials and Methods
2.1. Alloy Preparation
2.2. Solidification under Different Magnetic Field Intensities
2.3. Microstructure Characterization
3. Results
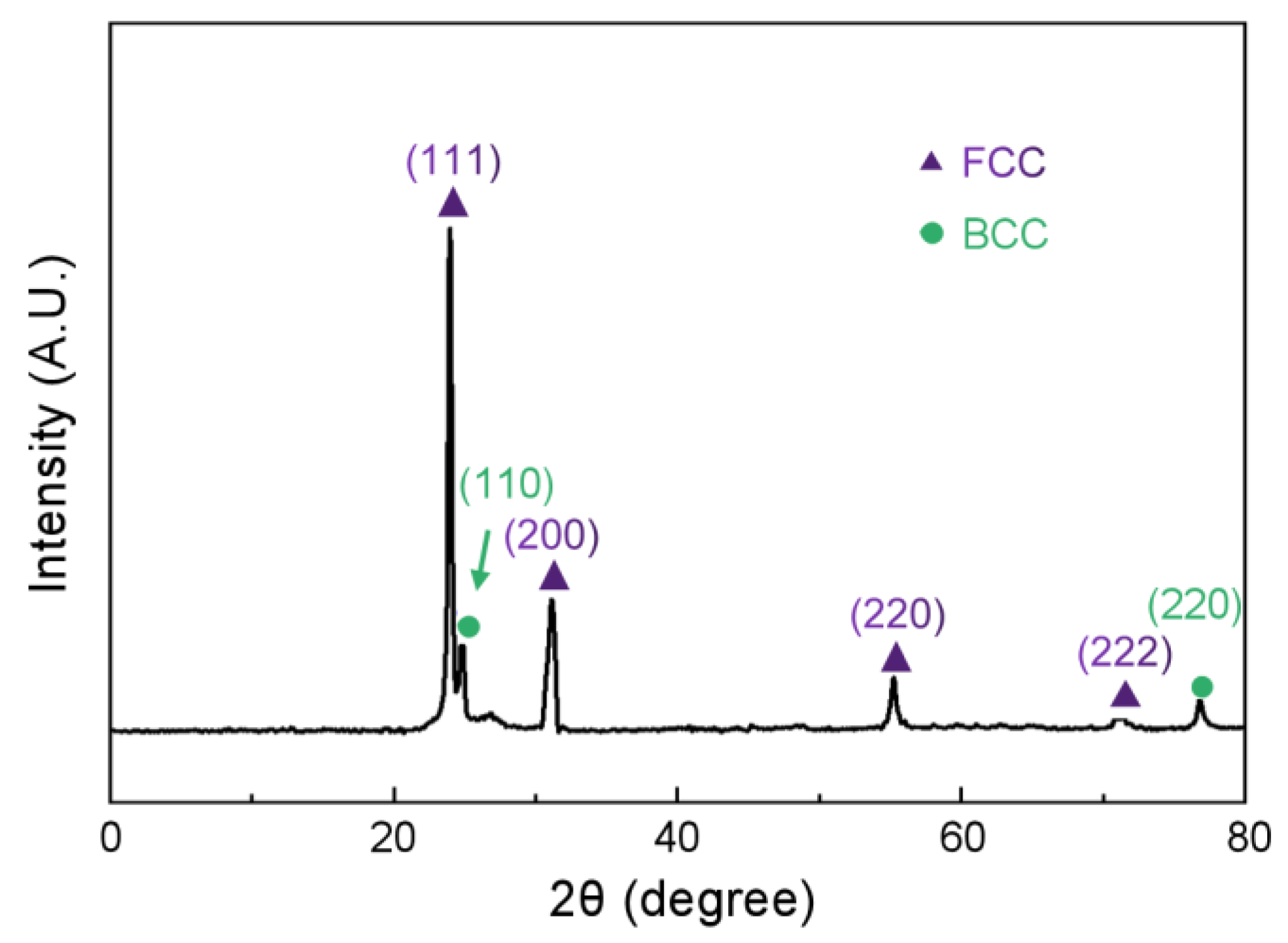
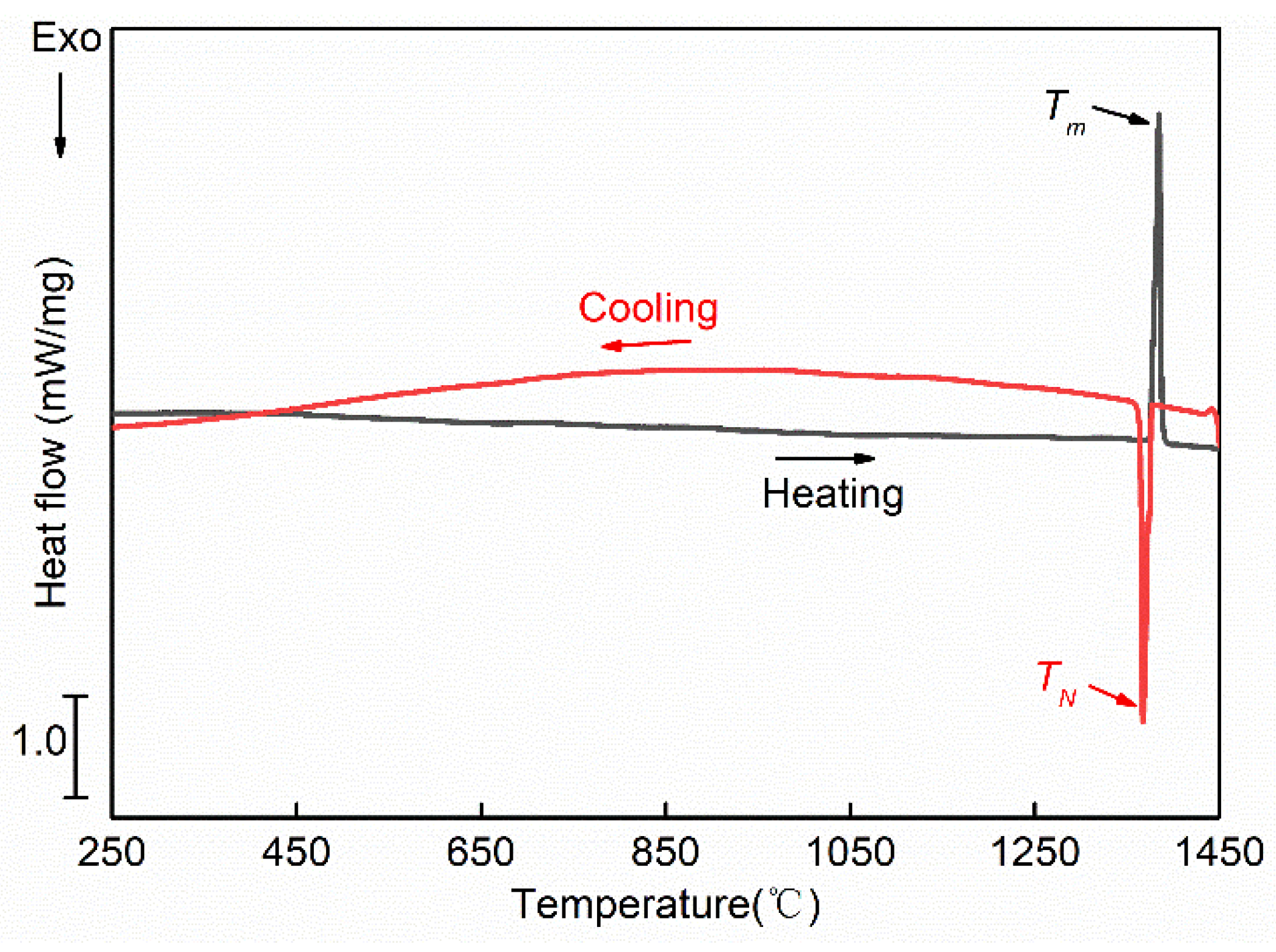
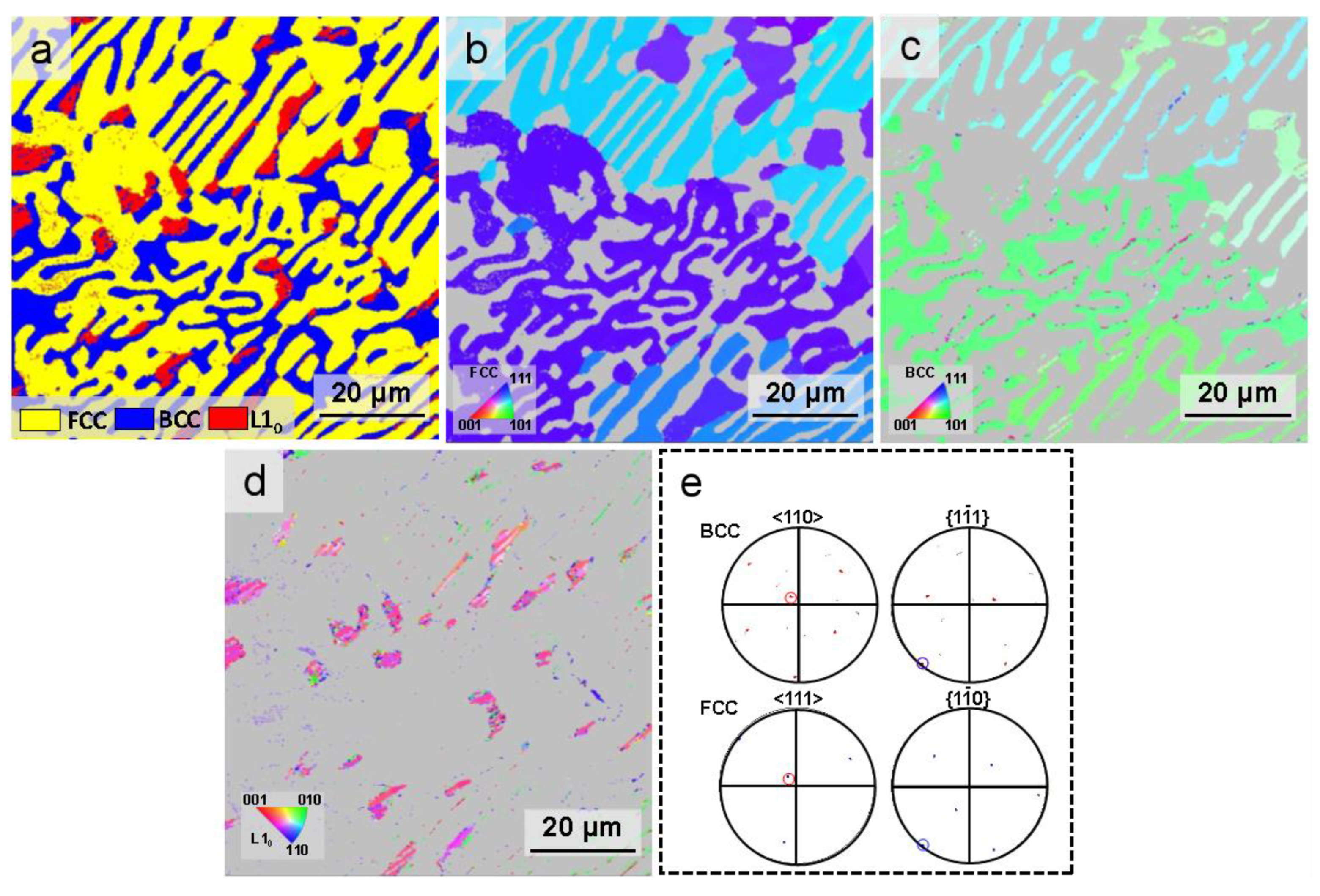
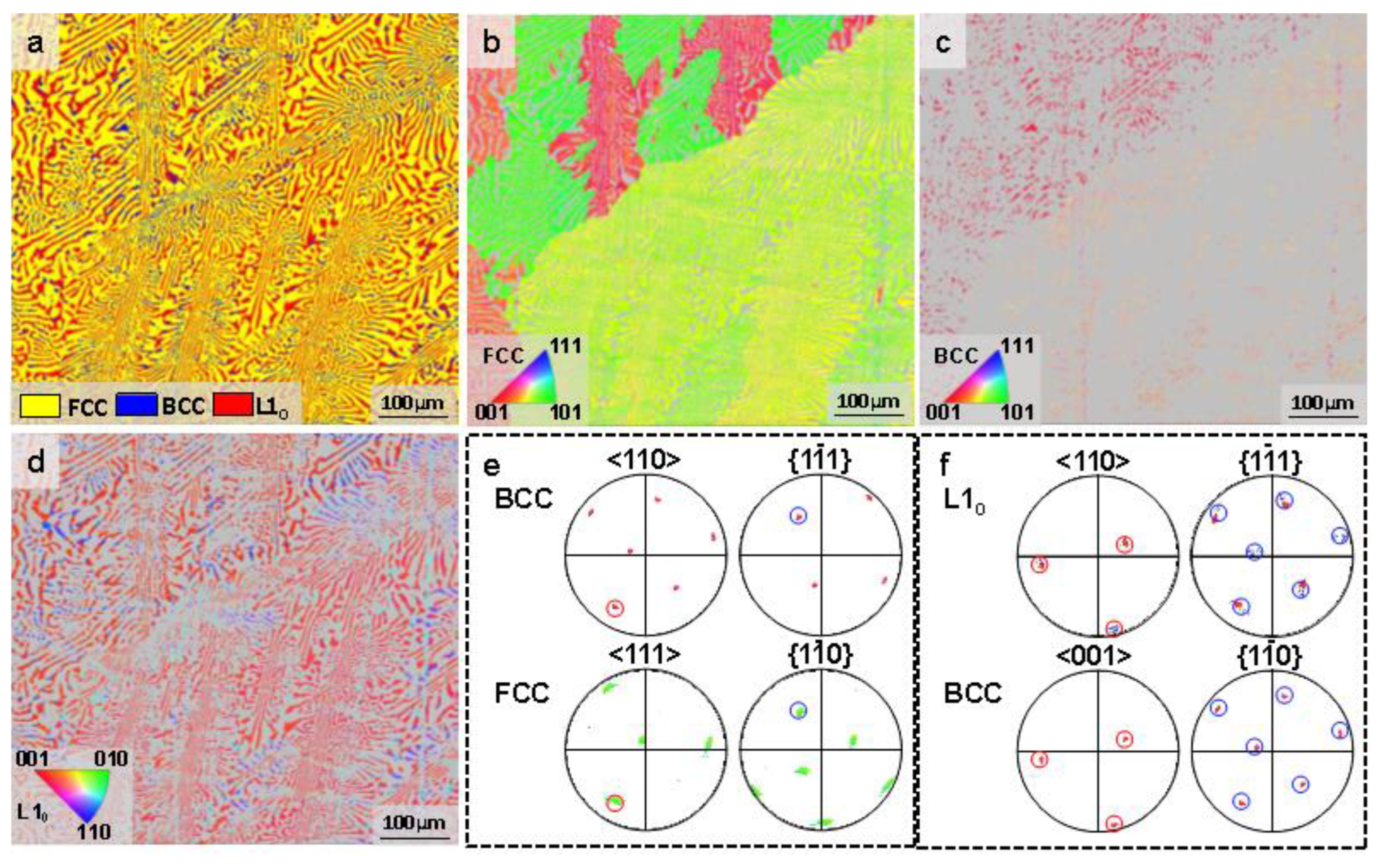
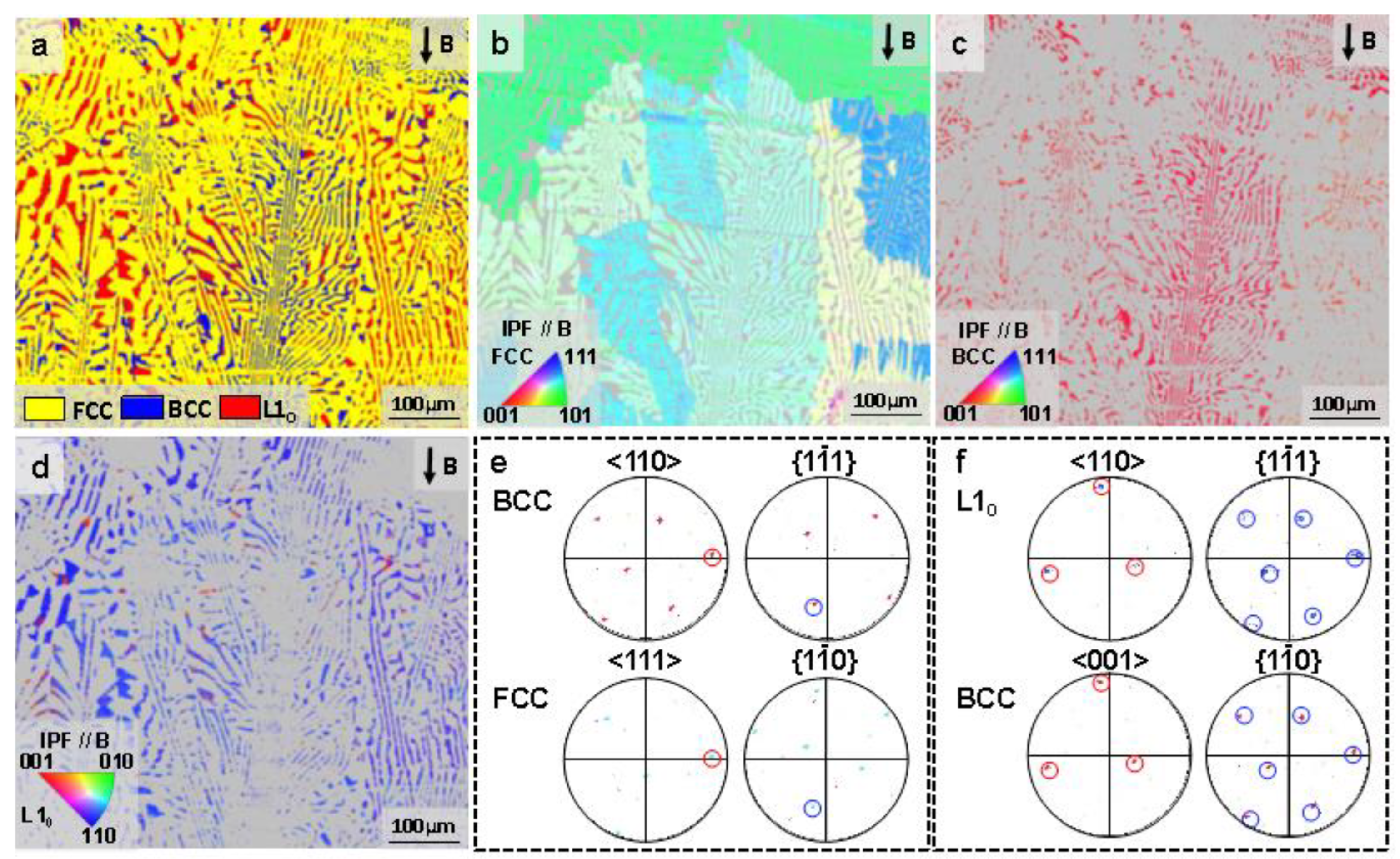
3.1. Original Microstructure and Phase Constituents
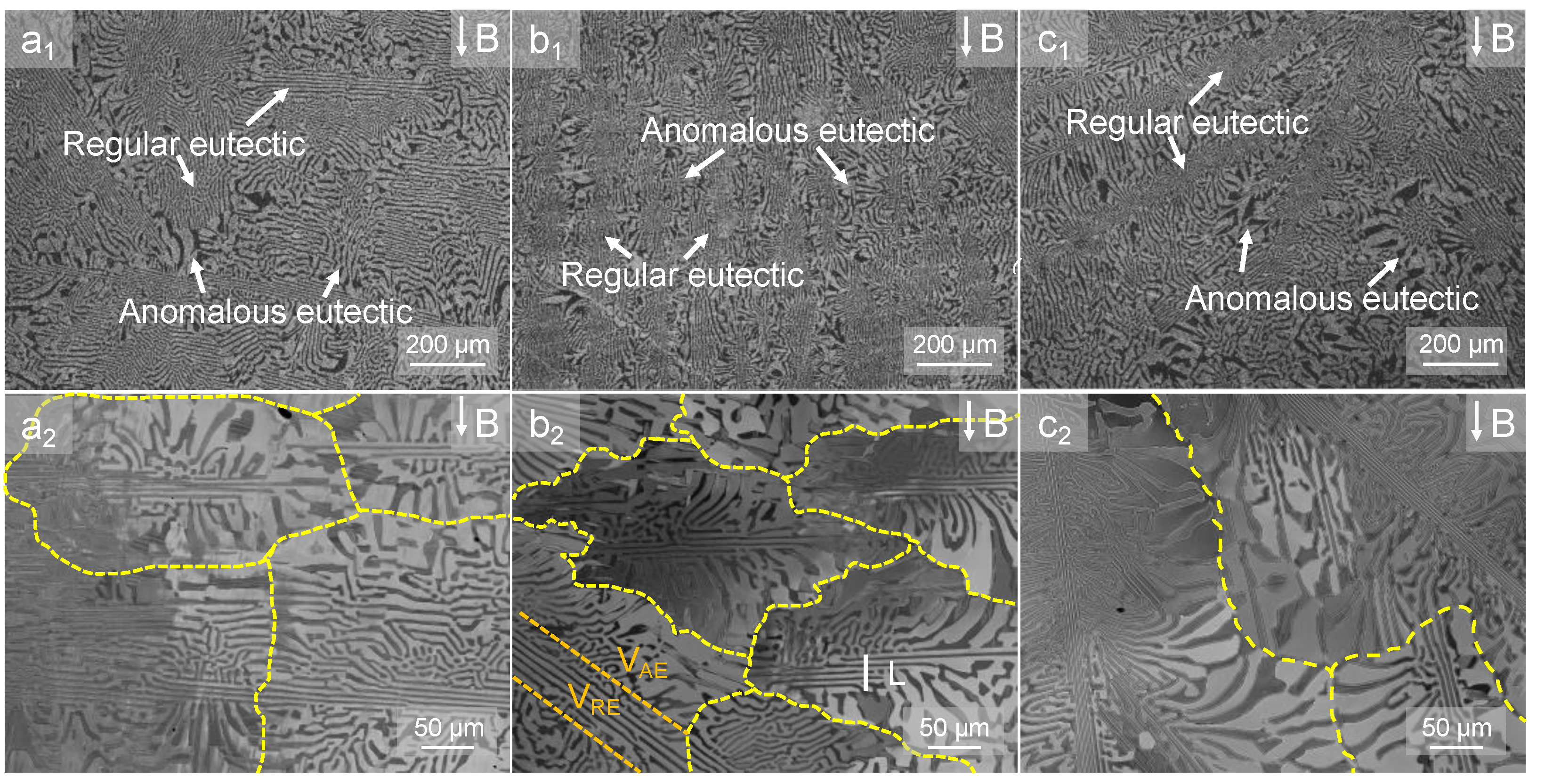
3.2. Solidification Microstructures under Different Magnetic Intensities
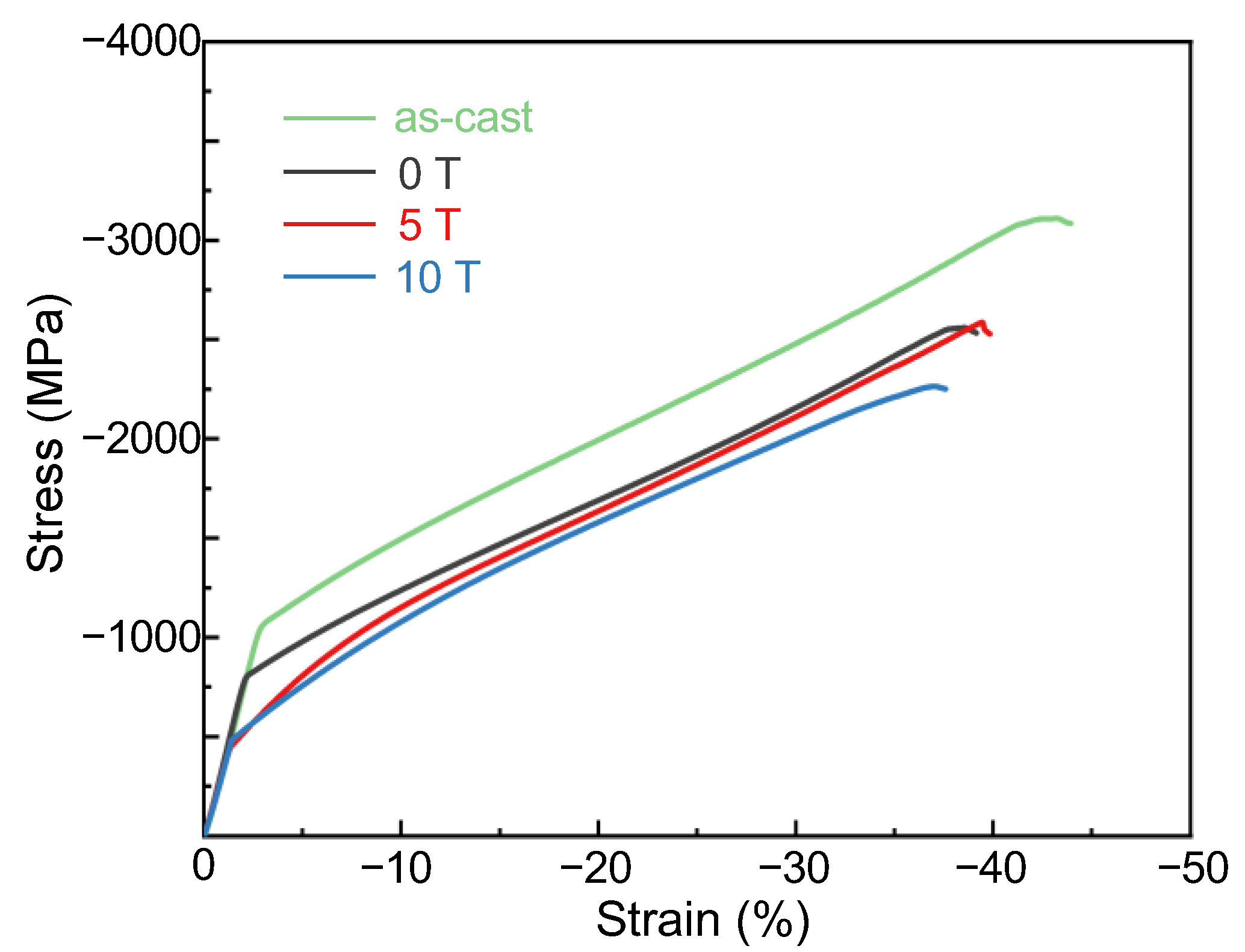
3.3. Mechanical Properties of Samples under Different Magnetic Intensities
4. Discussion
4.1. Influence of a High-Intensity Magnetic Field on Straight Eutectic Spacing
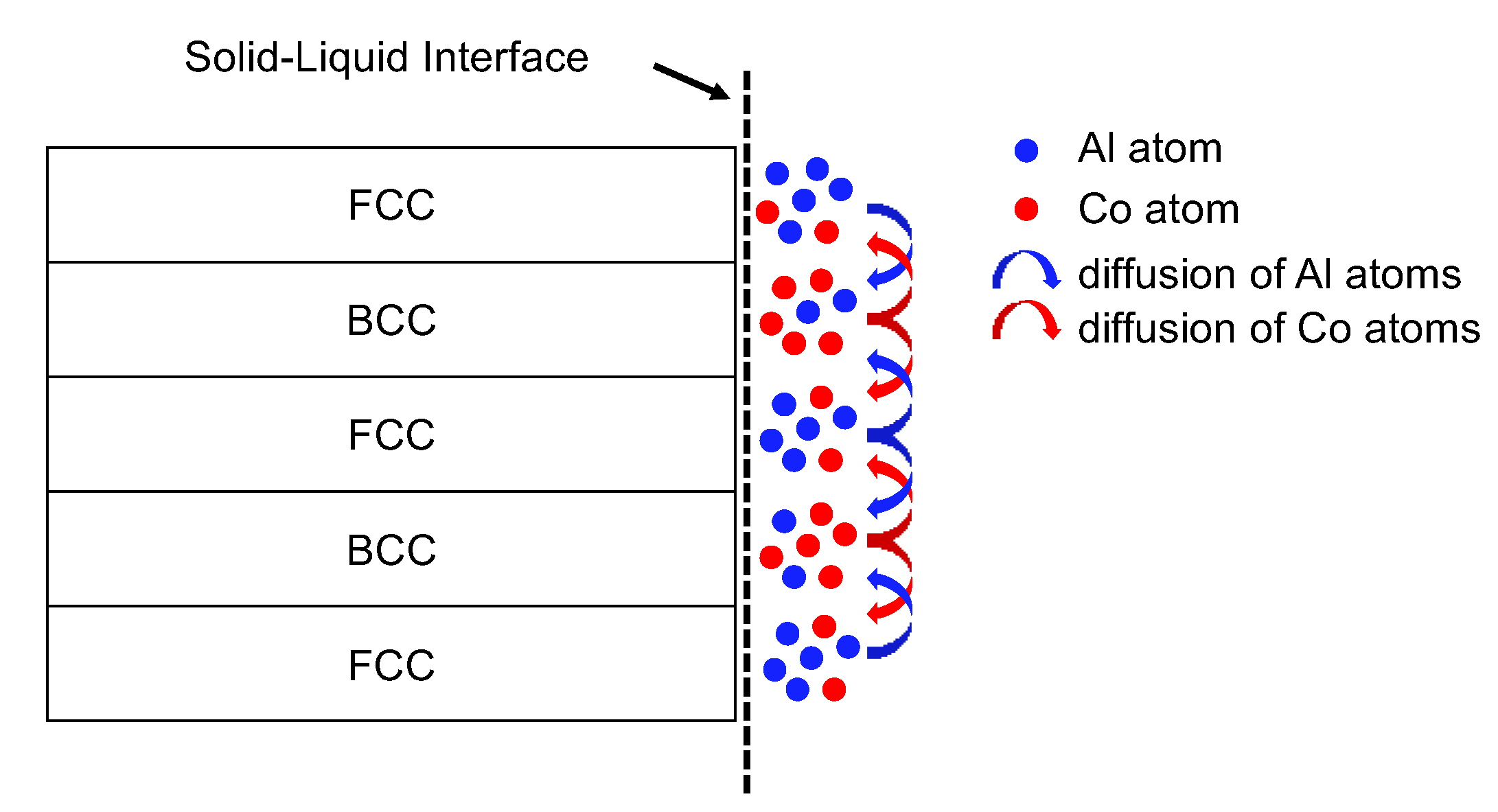
4.2. Formation of Anomalous Eutectics in Herringbone Structures and Their Evolution under a Strong Magnetic Field
5. Conclusions
- (1)
- The original microstructure of the Co39.2Ni39.2Al21.6 EMEA was characterized by FCC/BCC mixed-phase herringbone eutectics consisting of curved wormy anomalous eutectics, and straight lamellar eutectics in the center. The FCC and BCC phases were enriched in Co and Al elements, respectively. A large number of nano-size L10-type martensite layers distributed on the BCC lamellar structure were also present. the orientation relationship between the FCC/BCC lamellar structures and L10/BCC lamellar structures were: <110>BCC//<111>FCC, {1-11}BCC//{1-10}FCC; {100}BCC//{110}M, <001>BCC//<1-10>M.
- (2)
- With increasing magnetic field intensity, the herringbone eutectic structure remained stable, without the formation of the primary phase, and the chemical fluctuation was observed were negligible. Meanwhile, the orientation relationships in the eutectic structures remained unchanged.
- (3)
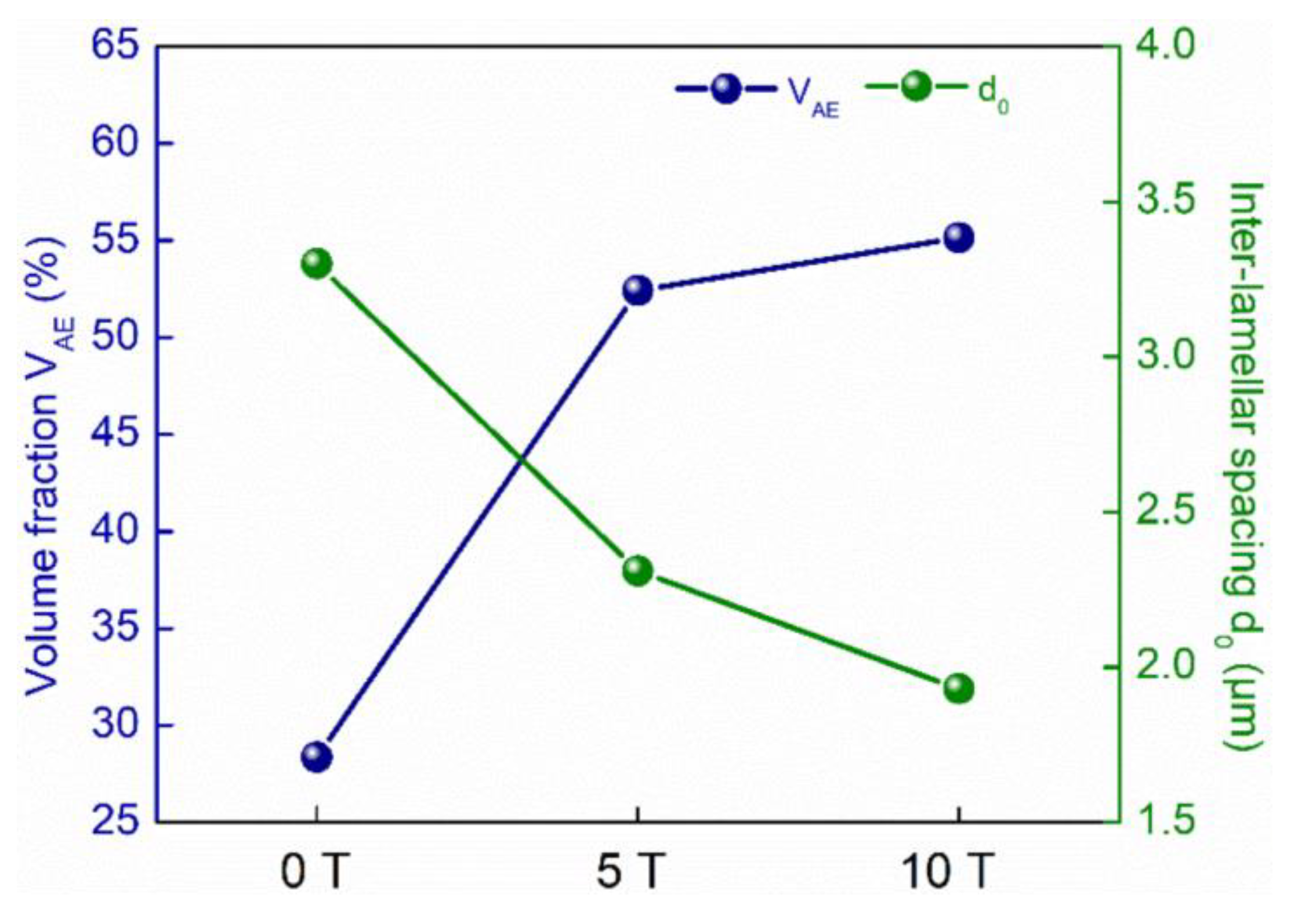
- With increasing magnetic field intensity, the lamellar spacing of the regular lamellar eutectic decreased significantly from 3.3 μm (0 T) to 1.93 μm (10 T); in contrast, the volume fraction of anomalous eutectics increases from 28.35% (0 T) to 55.14% (10 T).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.B.J. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Anwer, Z.; Umer, M.A.; Nisar, F.; Hafeez, M.A.; Yaqoob, K.; Luo, X.; Ahmad, I. Microstructure and Mechanical Properties of Hot Isostatic Pressed Tungsten Heavy Alloy with FeNiCoCrMn High Entropy Alloy Binder. J. Mater. Res. Technal. 2022, 22, 2897–2909. [Google Scholar] [CrossRef]
- Park, C.; Hwang, T.; Kim, G.D.; Nam, H.; Kang, N. Effect of the Initial Grain Size on Laser Beam Weldability for High-Entropy Alloys. Crystals 2023, 13, 65. [Google Scholar] [CrossRef]
- Wang, M.; Ma, Z.L.; Xu, Z.Q.; Cheng, X.W. Designing VxNbMoTa refractory high-entropy alloys with improved properties for high-temperature applications. Scr. Mater. 2021, 191, 131–136. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y. High-entropy alloys in catalyses and supercapacitors: Progress, prospects. Nano Energy 2022, 104, 107958. [Google Scholar] [CrossRef]
- Zhang, Y.; Bu, Z.; Yao, T.; Yang, L.; Li, W.; Li, J. Novel BCC Ti-Al-Nb-Zr medium-entropy alloys with ultrahigh specific strength and ductility. J. Alloys Compd. 2023, 936, 168290. [Google Scholar] [CrossRef]
- Han, K.; Jiang, H.; Huang, T.; Wei, M. Thermoelectric Properties of CoCrFeNiNbx Eutectic High Entropy Alloys. Crystals 2020, 10, 762. [Google Scholar] [CrossRef]
- Lu, Y.; Dong, Y.; Guo, S.; Jiang, L.; Kang, H.; Wang, T.; Wen, B.; Wang, Z.; Jie, J.; Cao, Z.; et al. A Promising New Class of High-Temperature Alloys: Eutectic High-Entropy Alloys. Sci. Rep. 2014, 4, 6200. [Google Scholar] [CrossRef]
- Shi, P.; Li, R.; Li, Y.; Wen, Y.; Zhong, Y.; Ren, W.; Shen, Z.; Zheng, T.; Peng, J.; Liang, X.; et al. Hierarchical crack buffering triples ductility in eutectic herringbone high-entropy alloys. Science 2021, 373, 912–918. [Google Scholar] [CrossRef] [PubMed]
- Nam, S.; Kim, S.J.; Yoon, K.N.; Kim, M.J.; Quevedo-lopez, M.; Huang, J.Y.; Park, E.S.; Choi, H. Design of metastable complex-concentrated alloys through composition tailoring. Mater. Des. 2022, 224, 111391. [Google Scholar] [CrossRef]
- Singh, N.; Shadangi, Y.; Goud, G.S.; Pandey, V.K.; Shivam, V.; Mukhopadhyay, N.K. Fabrication of MgAlSiCrFe Low-Density High-Entropy Alloy by Mechanical Alloying and Spark Plasma Sintering. Trans. Indian Inst. Met. 2021, 74, 2203–2219. [Google Scholar] [CrossRef]
- Rawat, R.; Singh, B.K.; Tiwari, A.; Arun, N.; Pathak, A.P.; Shadangi, Y.; Mukhopadhyay, N.K.; Nelamarri, S.R.; Rao, A.V.; Tripathi, A. Formation of Cu-Ni enriched phases during laser processing of non-equiatomic AlSiCrMnFeNiCu high entropy alloy nanoparticals. J. Alloys Compd. 2022, 927, 166905. [Google Scholar] [CrossRef]
- Ao, X.; Xia, H.; Liu, J.; He, Q.; Lin, S. A numerical study of irregular eutectic in Al-Si alloys under a large undercooling. Comput. Mater. Sci. 2021, 186, 110049. [Google Scholar] [CrossRef]
- Dong, H.; Chen, Y.Z.; Zhang, Z.R.; Shan, G.B.; Zhang, W.X.; Liu, F. Mechanisms of eutectic lamellar destabilization upon rapid solidification of an undercooled Ag-39.9 at.% Cu eutectic alloy. J. Mater. Sci. Technol. 2020, 59, 173–179. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Wang, S.; Zhang, Z.Y.; Tao, Q.; Zhang, P. Microstructure and mechanical properties of undercooled Fe80C5Si10B5 eutectic alloy. J. Alloys Compd. 2018, 747, 846–853. [Google Scholar] [CrossRef]
- Rahul, M.R.; Samal, S.; Phanikumar, G. Metastable microstructures in the solidification of undercooled high entropy alloys. J. Alloys Compd. 2019, 821, 153488. [Google Scholar] [CrossRef]
- Milgrāvis, M.; Krastiņš, I.; Kaldre, I.; Kalvāns, M.; Bojarevičs, A.; Beiners, T. Pulsed and Static Magnetic Field Influence on Metallic Alloys during Solidification. Crystals 2023, 13, 259. [Google Scholar] [CrossRef]
- Li, L.; Ban, C.; Zhang, R.; Zhang, H.; Cai, M.; Zuo, Y.; Zhu, Q.; Wang, X.; Cui, J. Morphological and Crystallographic Characterization of Primary Zinc-Rich Crystals in a Ternary Sn-Zn-Bi Alloy under a High Magnetic Field. Crystals 2017, 7, 204. [Google Scholar] [CrossRef]
- Dong, S.; Liu, T.; Dong, M.; Guo, X.; Yuan, S.; Wang, Q. Enhanced magnetostriction of Tb-Dy-Fe via simultaneous <111>-crystallographic orientation and -morphological alignment induced by directional solidification in high magnetic fields. Appl. Phys. Lett. 2020, 116, 053903. [Google Scholar]
- Li, X.; Gagnoud, A.; Fautrelle, Y.; Ren, Z.; Moreau, R.; Zhang, Y.; Esling, C. Dendrite fragmentation and columnar-to-equiaxed transition during directional solidification at lower growth speed under a strong magnetic field. Acta Mater. 2012, 60, 3321–3332. [Google Scholar] [CrossRef]
- Hu, S.; Dai, Y.; Gagnoud, A.; Fautrelle, Y.; Moreau, R.; Ren, Z.; Deng, K.; Li, C.; Li, X. Effect of a magnetic field on macro segregation of the primary silicon phase in hypereutectic Al-Si alloy during directional solidification. J. Alloys Compd. 2017, 722, 108–115. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, H.; Huang, Y.; Xia, M.; Li, J. Microstructure and magnetic field induced strain of directionally solidified ferromagnetic shape memory CoNiAl alloys. Scr. Mater. 2005, 53, 29–33. [Google Scholar] [CrossRef]
- Dar, R.D.; Yan, H.; Chen, Y. Grain boundary engineering of Co-Ni-Al, Cu-Zn-Al, and Cu-Al-Ni shape memory alloys by intergranular precipitation of a ductile solid solution phase. Scr. Mater. 2016, 115, 113–117. [Google Scholar] [CrossRef]
- Duan, D.; Wu, Y.; Chen, H.; Wang, X.; Liu, X.; Wang, H.; Jiang, S.; Lu, Z. A strategy to design eutectic high-entropy alloys based on binary eutectics. J. Mater. Sci. Technol. 2022, 103, 152–156. [Google Scholar] [CrossRef]
- Wang, J.; He, Y.; Li, J.; Hu, R.; Kou, H.; Beaugnon, E. Experimental platform for solidification and in-situ magnetization measurement of undercooled melt under strong magnetic field. Rev. Sci. Instrum. 2015, 86, 25102. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Ren, Z.; Ren, W.; Deng, K.; Zhong, Y. Solidification structure of eutectic Al-Si alloy under a high magnetic field-aid-electromagnetic vibration. Acta Metall. Sin. 2009, 22, 6. [Google Scholar] [CrossRef]
- Wu, Q.; He, F.; Li, J.; Kim, S.H.; Wang, Z.; Wang, J. Phase-selective recrystallization makes eutectic high-entropy alloys ultra-ductile. Nat. Commun. 2022, 13, 4697. [Google Scholar] [CrossRef] [PubMed]
- Brener, E.; Müller, K.; Temkin, D. Structure formation and the morphology diagram of possible structures in two-dimensional diffusional growth. Phys. Rev. E 1996, 54, 2714. [Google Scholar] [CrossRef]
- Efstathiou, C.; Sehitoglu, H.; Johnson, A.J.; Hamilton, R.F.; Maier, H.J.; Chumlyakov, Y. Large reduction in critical stress in Co-Ni-Al upon repeated transformation. Sci. Mater. 2004, 51, 979–985. [Google Scholar] [CrossRef]
- Maziarz, W. Structure changes of Co–Ni–Al ferromagnetic shape memory alloys after vacuum annealing and hot rolling. J. Alloys Compd. 2008, 448, 223–226. [Google Scholar] [CrossRef]
- Tanaka, Y.; Oikawa, K.; Sutou, Y.; Omori, T.; Kainuma, R.; Ishida, K. Martensitic transition and superelasticity of Co-Ni-Al ferromagnetic shape memory alloys with β + γ two-phase structure. Mater. Sci. Eng. A 2006, 438–440, 1054–1060. [Google Scholar] [CrossRef]
- Cui, J.; Chu, Y.S.; Famodu, O.O.; Furuya, Y.; Hattrick-simpers, J.; James, R.D.; Ludwig, A.; Thienhaus, A.; Wutting, M.; Zhang, Z.; et al. Combinatorial search of thermoelastic shape-memory alloys with extremely small hysteresis width. Nat. Mater. 2006, 5, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Dilibal, S.; Sehitoglu, H.; Hamilton, R.F.; Maier, H.J.; Chumlyakov, Y. On the volume change in Co-Ni-Al during pseudoelasticity. Mater. Sci. Eng. A 2011, 528, 2875–2881. [Google Scholar] [CrossRef]
- Hamilton, R.F.; Sehitoglu, H.; Efstathiou, C.; Maiar, H.J.; Chumlyakov, Y.; Zhang, X.Y. Transformation of Co-Ni-Al single crystals in tension. Sci. Mater. 2005, 53, 131–136. [Google Scholar] [CrossRef]
- Wei, X.X.; Lin, X.; Xu, W.; Huang, Q.S.; Ferry, M.; Li, F.J.; Zhou, Y.H. Remelting-induced anomalous eutectic formation during solidification of deeply undercooled eutectic alloy melts. Acta Mater. 2015, 95, 44–56. [Google Scholar] [CrossRef]
- Yang, L.; Liu, L.J.; Qin, Q.Y.; Li, J.F. Role of Remelting in Grain Refinement of Undercooled Single-Phase Alloys. Metall. Mater. Trans. A 2022, 53, 3100–3109. [Google Scholar] [CrossRef]
- Bayram, Ü.; Maraşlı, N. Influence of Growth Rate on Eutectic Spacing, Microhardness, and Ultimate Tensile Strength in the Directionally Solidified Al-Cu-Ni Eutectic Alloy. Metall. Mater. Trans. B 2008, 49, 3293–3305. [Google Scholar] [CrossRef]
- Yin, y.; Tan, Q.; Wang, T.; Kent, D.; Mo, N.; BermingHam, R.; Li, H.; Zhang, M.X. Eutectic modification of Fe-enriched high-entropy alloys through minor addition of boron. J. Mater. Sci. 2020, 55, 14571–14587. [Google Scholar] [CrossRef]
- Xu, B.; Tong, W.; Kang, T.Y.; Zuo, L.; He, J.C. The Lamellar Eutectic Spacing Changes under the High Magnetic Field during the Diffusion of Liquid Al/Solid Cu Process. Adv. Mat. Res. 2010, 160–162, 603–607. [Google Scholar]
- Wang, P.; Shuai, S.; Huang, C.; Liu, X.; Fu, Y.; Wang, J.; Ren, Z. Revealing the influence of high magnetic field on the solute distribution during directional solidification of Al-Cu alloy. J. Mater. Sci. Technol. 2021, 88, 226–232. [Google Scholar] [CrossRef]
- Kasuga, M.; Takano, T.; Akiyama, S.; Hiroshima, K.; Yano, K.; Kishio, K. Growth of ZnO films by MOCVD in high magnetic field. J. Cryst. Growth 2005, 275, 1545–1550. [Google Scholar] [CrossRef]
- Bu, F.; Zhang, Y.; Liu, H.; Wang, J.; Beaugnon, E.; Li, J.; He, Y. Magnetic field intensity dependent microstructure evolution and recrystallization behavior in a Co–B eutectic alloy. J. Mater. Sci. Technol. 2023, 138, 93–107. [Google Scholar] [CrossRef]
- Hardianto, A.; Mey, G.D.; Malengier, B.; Langenhove, L.V.; Hertleer, C. Textile yarn thermocouples for use in fabrics. J. Eng. Fibers Fabr. 2019, 14, 1–7. [Google Scholar] [CrossRef]
- Kishore, R. Electrical conductivity of metals. Phys. Status Solid 1968, 26, 133–138. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Gagnoud, A.; Ren, Z.; Moreau, R. High Magnetic Field-Induced Formation of Banded Microstructures in Lamellar Eutectic Alloys During Directional Solidification. Metall. Mater. Trans. A 2016, 47, 4038–4052. [Google Scholar] [CrossRef]
- Li, X.; Ren, Z.; Fautrelle, Y. Effect of a high axial magnetic field on the microstructure in a directionally solidified Al–Al2Cu eutectic alloy. Acta Mater. 2006, 54, 5349–5360. [Google Scholar] [CrossRef]
- Dong, H.; Chen, Y.Z.; Wang, K.; Shan, G.B.; Zhang, Z.R.; Zhang, W.X.; Liu, F. Modeling remelting induced destabilization of lamellar eutectic structure in an undercooled Ni-18.7 at.% Sn eutectic alloy. J. Alloys Compd. 2020, 826, 154018. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Gagnoud, A.; Ren, M.; Moreau, R. EBSD Study of the Influence of a High Magnetic Field on the Microstructure and Orientation of the Al-Si Eutectic During Directional Solidification. Metall. Mater. Trans. A 2016, 47, 2952–2963. [Google Scholar] [CrossRef]
- Yu, J.; Du, D.; Ren, Z.; Fautrelle, Y.; Moreau, R.; Li, X. Influence of an Axial Magnetic Field on Microstructures and Alignment in Directionally Solidified Ni-based Superalloy. ISIJ Int. 2017, 57, 337–342. [Google Scholar] [CrossRef]
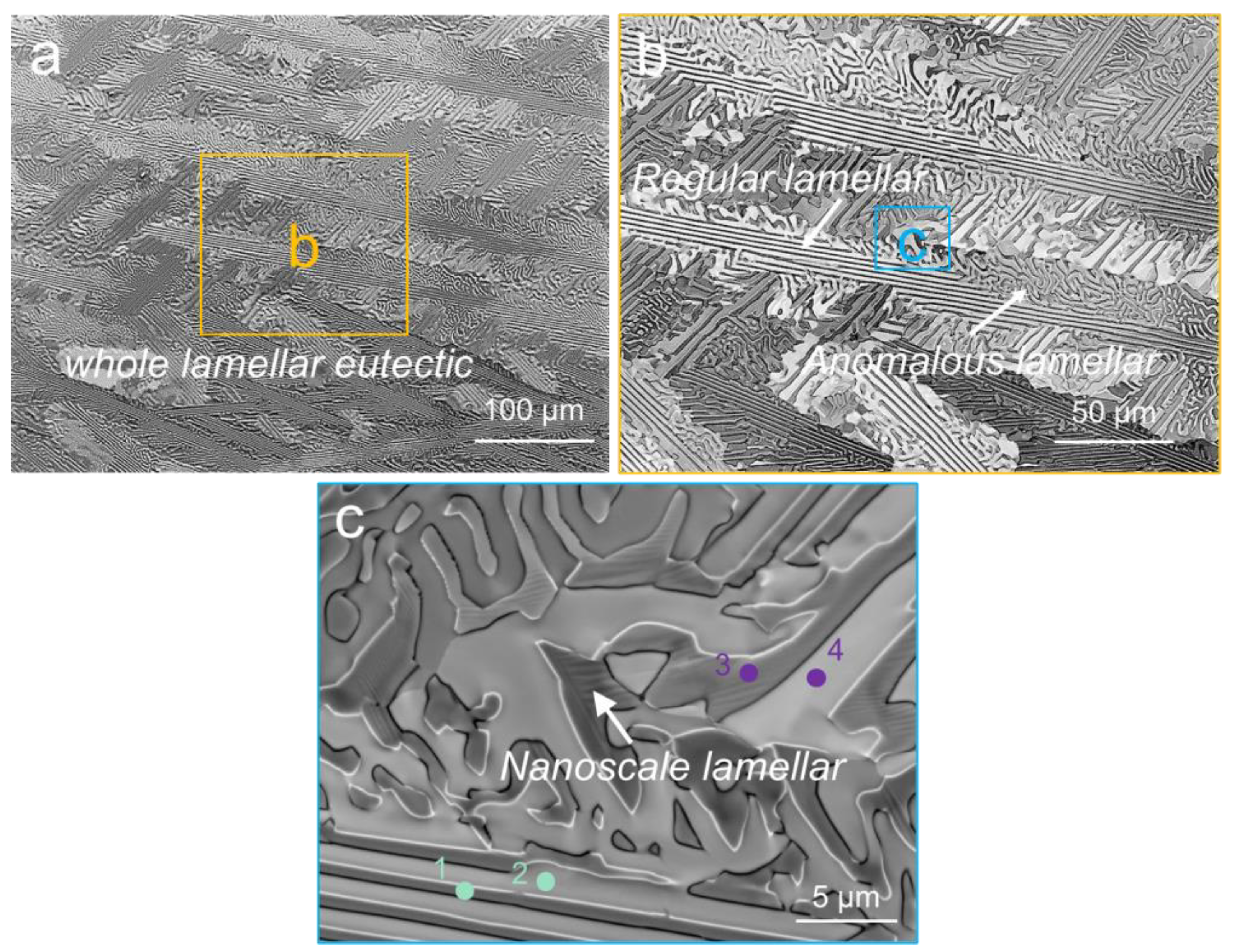


| Region | Co (at %) | Ni (at %) | Al (at %) |
|---|---|---|---|
| Point 1 | 29.03 ± 0.66 | 38.92 ± 0.13 | 32.04 ± 0.58 |
| Point 2 | 40.88 ± 0.16 | 37.26 ± 0.25 | 21.85 ± 0.04 |
| Point 3 | 29.32 ± 0.14 | 38.48 ± 0.22 | 31.89 ± 0.36 |
| Point 4 | 40.27 ± 0.31 | 37.31 ± 0.15 | 21.55 ± 0.07 |
| Sample | Region | Phase | Element | ||
|---|---|---|---|---|---|
| Co (at %) | Ni (at %) | Al (at %) | |||
| 0 T | Regular eutectic | FCC | 46.81 ± 0.62 | 38.65 ± 0.72 | 14.66 ± 0.21 |
| BCC | 28.53 ± 0.21 | 42.37 ± 0.33 | 28.79 ± 0.23 | ||
| Anomalous eutectic | FCC | 46.17 ± 0.75 | 39.15 ± 0.32 | 14.78 ± 0.65 | |
| BCC | 29.12 ± 0.17 | 42.29 ± 0.29 | 28.36 ± 0.09 | ||
| 5 T | Regular eutectic | FCC | 45.85 ± 0.48 | 39.29 ± 0.33 | 15.21 ± 0.54 |
| BCC | 29.21 ± 0.10 | 42.25 ± 0.94 | 28.63 ± 0.31 | ||
| Anomalous eutectic | FCC | 46.28 ± 0.12 | 38.73 ± 0.96 | 15.10 ± 0.35 | |
| BCC | 29.15 ± 0.06 | 42.41 ± 0.18 | 28.59 ± 0.12 | ||
| 10 T | Regular eutectic | FCC | 46.08 ± 0. 31 | 38.91 ± 0.74 | 15.93 ± 0.48 |
| BCC | 28.74 ± 0.36 | 41.86 ± 0.48 | 29.56 ± 0.96 | ||
| Anomalous eutectic | FCC | 45.49 ± 0.84 | 39.03 ± 0.64 | 15.72 ± 0.31 | |
| BCC | 29.79 ± 0.47 | 41.24 ± 0.16 | 21.74 ± 0.22 | ||
| Samples | σ0.2/MPa | ε/% | σf/MPa |
|---|---|---|---|
| as-cast | 1107.69 ± 13.91 | 42.12 ± 1.2 | 3153.85 ± 21.35 |
| 0 T | 815.39 ± 27.62 | 37.27 ± 2.4 | 2552.31 ± 37.96 |
| 5 T | 483.63 ± 21.61 | 39.47 ± 3.1 | 2607.69 ± 37.96 |
| 10 T | 461.32 ± 24.36 | 36.83 ± 4.3 | 2266.23 ± 35.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Bu, F.; Wu, Y.; Xing, C.; Liu, X.; He, Y. Magnetic Field-Dependent Microstructure Evolution of Solidified Co39.2Ni39.2Al21.6 Eutectic Medium-Entropy Alloy. Crystals 2023, 13, 573. https://doi.org/10.3390/cryst13040573
Liu H, Bu F, Wu Y, Xing C, Liu X, He Y. Magnetic Field-Dependent Microstructure Evolution of Solidified Co39.2Ni39.2Al21.6 Eutectic Medium-Entropy Alloy. Crystals. 2023; 13(4):573. https://doi.org/10.3390/cryst13040573
Chicago/Turabian StyleLiu, Haoxiang, Fan Bu, Yuhao Wu, Chenxu Xing, Xudong Liu, and Yixuan He. 2023. "Magnetic Field-Dependent Microstructure Evolution of Solidified Co39.2Ni39.2Al21.6 Eutectic Medium-Entropy Alloy" Crystals 13, no. 4: 573. https://doi.org/10.3390/cryst13040573
APA StyleLiu, H., Bu, F., Wu, Y., Xing, C., Liu, X., & He, Y. (2023). Magnetic Field-Dependent Microstructure Evolution of Solidified Co39.2Ni39.2Al21.6 Eutectic Medium-Entropy Alloy. Crystals, 13(4), 573. https://doi.org/10.3390/cryst13040573






