On Σ-Classes in E8. I. The Neighborhood of E8
Abstract
:1. Introduction
2. Basic Notations
3. The Parallelohedron of the Lattice
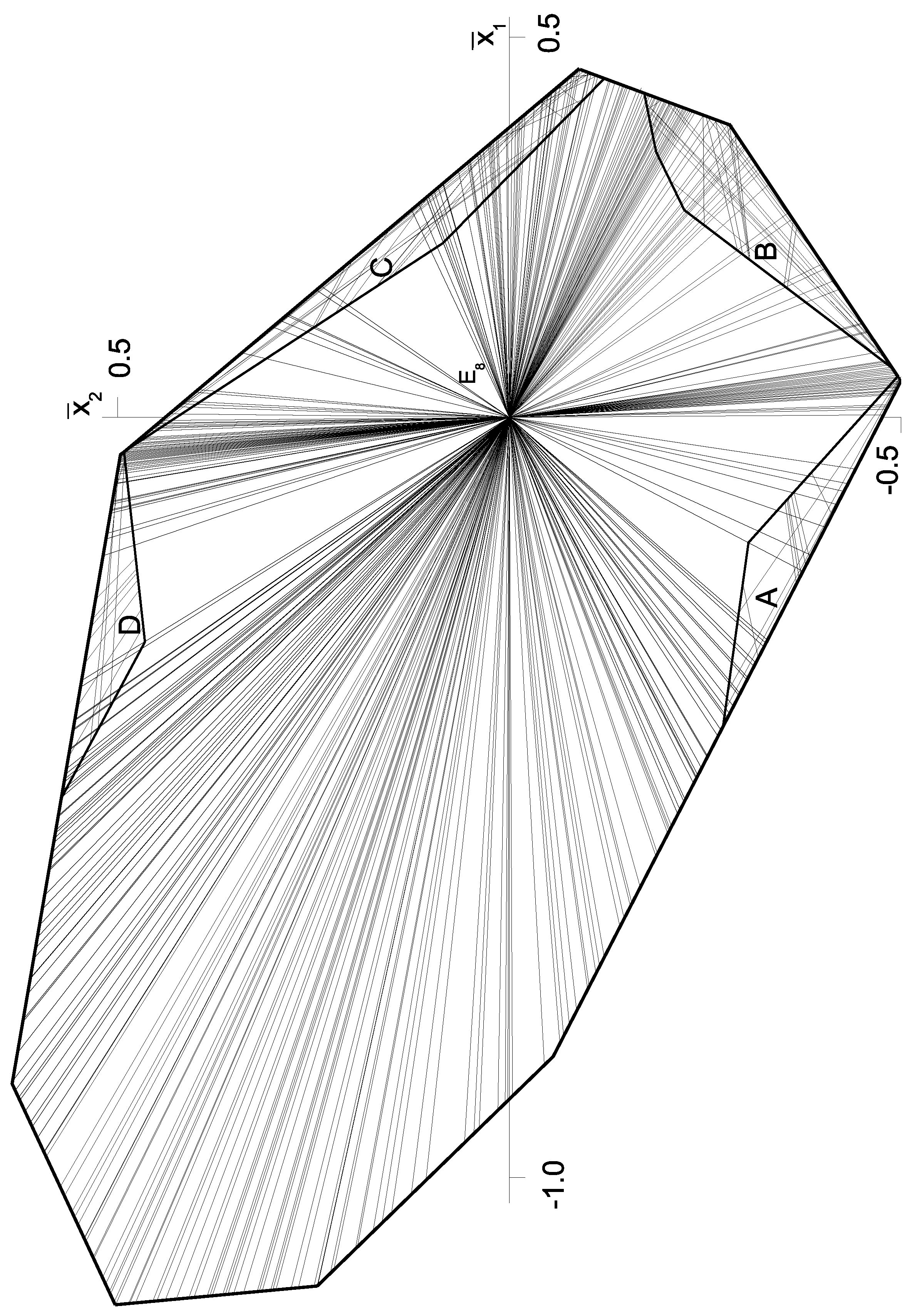
4. The Neighborhood of
5. Results
Supplementary Materials
Funding
Conflicts of Interest
References
- Plesken, W.; Pohst, M. The eight dimensional case and complete description of dimensions less than ten. Math. Comp. 1980, 34, 277–301. [Google Scholar]
- Conway, J.H.; Sloane, J.A. The Cell Structures of Certain Lattices, Miscelanea Matematica; Springer: New York, NY, USA, 1991; pp. 71–107. [Google Scholar]
- Baburin, L.A.; Engel, P. On the enumeration of the combinatorial types of primitive parallelohedra in Ed, 2 ≤ d ≤ 6. Acta Cryst. A 2013, 69, 510–514. [Google Scholar] [CrossRef]
- Engel, P. The contraction types of parallelohedra in E5. Acta Cryst. A 2000, 56, 491–496. [Google Scholar] [CrossRef] [PubMed]
- Engel, P. On Fedorov’s parallelohedra—A review and new results. Cryst. Res. Technol. 2015, 50, 929–943. [Google Scholar] [CrossRef]
- Engel, P. On a special class of parallelohedra in E6. Acta Cryst. A 2019, 75, 574–583. [Google Scholar] [CrossRef] [PubMed]
- Engel, P. On the Σ-classes in E6. Acta Cryst. A 2020, 76, 622–626. [Google Scholar] [CrossRef] [PubMed]
- Engel, P. Mathematical problems in modern crystallography. Comput. Math. Appl. 1988, 16, 425–436. [Google Scholar] [CrossRef]
- Voronoï, G.M. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. recherches sur les paralléloèdres primitifs. J. Reine Angew. Math. 2009, 1908, 198–287, Erratum in J. Reine Angew. Math. 2009, 1909, 67–181. [Google Scholar] [CrossRef]
- Engel, P. On the enumeration of four-dimensional polytopes. Discret. Math. 1991, 91, 9–31. [Google Scholar] [CrossRef] [Green Version]
| No. | Group | Order | Comb. Type | Zones | Belts |
|---|---|---|---|---|---|
| 16.256 | 8(8) | ||||
| 112.272 | 136(0) | ||||
| 48.576 | 24(0) | ||||
| 272.1120 | 56(0) | ||||
| 240.19449 | 8760(0) | ||||
| 264.5304 | 36(0) | ||||
| 24.1296 | 12(12) | ||||
| 348.3588 | 93(0) | ||||
| 60.10404 | 18(18) | ||||
| 72.510 | 9(9) | ||||
| 186.5940 | 174(0) | ||||
| 402.94254 | 1497(0) | ||||
| 510.362880 | 36(36) | ||||
| 40.900 | 10(10) | ||||
| 360.3840 | 180(0) | ||||
| 60.14400 | 20(20) | ||||
| 290.43310 | 1195(0) | ||||
| 390.106200 | 450(0) | ||||
| 180.6510 | 15(15) | ||||
| 1152 | 296.13696 | 580(0) | |||
| 1152 | 200.2992 | 304(0) | |||
| 456.28632 | 264(0) | ||||
| 672 | 398.90384 | 297(0) | |||
| 673 | 426.37638 | 21(21) | |||
| 672 | 308.8028 | 1011(0) | |||
| 24 | 398.127848 | 1036(0) |
| 1 0 0 0 0 0 0 0 | 0 1 0 0 0 0 0 0 | 1 1 0 0 0 0 0 0 | |||
| 0 0 1 0 0 0 0 0 | 1 0 1 0 0 0 0 0 | 0 1 −1 0 0 0 0 0 | |||
| 0 0 0 1 0 0 0 0 | 0 0 1 1 0 0 0 0 | 1 0 1 1 0 0 0 0 | |||
| 0 1 −1 −1 0 0 0 0 | 0 0 0 0 1 0 0 0 | 1 0 0 0 1 0 0 0 | |||
| 0 1 0 0 −1 0 0 0 | 0 0 1 0 −1 0 0 0 | 0 0 1 1 −1 0 0 0 | |||
| 0 0 0 0 0 1 0 0 | 0 1 0 0 0 1 0 0 | 0 1 −1 0 0 1 0 0 | |||
| 0 0 0 1 0 1 0 0 | 0 1 0 1 0 1 0 0 | 0 0 1 1 0 1 0 0 | |||
| 0 0 0 0 1 1 0 0 | 0 1 −1 0 1 1 0 0 | 0 0 0 1 1 1 0 0 | |||
| 1 0 0 0 0 −1 0 0 | 1 0 1 0 0 −1 0 0 | 1 −1 1 0 0 −1 0 0 | |||
| 1 0 0 −1 0 −1 0 0 | 0 0 1 0 −1 −1 0 0 | 1 0 1 0 −1 −1 0 0 | |||
| 0 0 0 0 0 0 1 0 | 1 0 0 0 0 0 1 0 | 0 0 0 1 0 0 1 0 | |||
| 1 0 0 1 0 0 1 0 | 1 0 1 1 0 0 1 0 | 1 −1 1 1 0 0 1 0 | |||
| 1 0 0 0 1 0 1 0 | 1 −1 0 0 1 0 1 0 | 1 0 −1 0 1 0 1 0 | |||
| 1 0 0 1 1 0 1 0 | 1 −1 0 1 1 0 1 0 | 1 −1 1 1 1 0 1 0 | |||
| 0 0 0 1 0 1 1 0 | 0 0 0 1 1 1 1 0 | 1 0 0 1 1 1 1 0 | |||
| 1 0 0 0 0 −1 1 0 | 1 −1 0 0 0 −1 1 0 | 1 −1 1 0 0 −1 1 0 | |||
| 1 −1 1 1 0 −1 1 0 | 1 −1 0 0 1 −1 1 0 | 0 1 0 0 0 0 −1 0 | |||
| 0 0 1 0 0 0 −1 0 | 0 1 0 −1 0 0 −1 0 | 0 1 −1 −1 0 0 −1 0 | |||
| 0 1 0 0 −1 0 −1 0 | 0 0 1 0 −1 0 −1 0 | 0 1 1 0 −1 0 −1 0 | |||
| 0 1 0 −1 −1 0 −1 0 | 0 1 0 0 0 1 −1 0 | 0 0 1 0 −1 −1 −1 0 | |||
| 0 1 0 −1 −1 −1 −1 0 | 0 0 1 −1 −1 −1 −1 0 | 1 −1 0 1 1 0 2 0 | |||
| 0 0 0 0 0 0 0 1 | 1 0 0 0 0 0 0 1 | 1 1 0 0 0 0 0 1 | |||
| 0 1 −1 0 0 0 0 1 | 1 1 −1 0 0 0 0 1 | 0 0 0 1 0 0 0 1 | |||
| 1 0 0 1 0 0 0 1 | 1 1 0 1 0 0 0 1 | 1 0 1 1 0 0 0 1 | |||
| 1 0 0 0 1 0 0 1 | 1 0 −1 0 1 0 0 1 | 1 1 −1 0 1 0 0 1 | |||
| 1 0 0 1 1 0 0 1 | 0 1 −1 0 0 1 0 1 | 0 0 0 1 0 1 0 1 | |||
| 0 1 0 1 0 1 0 1 | 1 1 0 1 0 1 0 1 | 0 1 −1 1 0 1 0 1 | |||
| 0 1 −1 0 1 1 0 1 | 1 1 −1 0 1 1 0 1 | 0 1 −2 0 1 1 0 1 | |||
| 0 0 0 1 1 1 0 1 | 1 0 0 1 1 1 0 1 | 1 1 0 1 1 1 0 1 | |||
| 0 1 −1 1 1 1 0 1 | 1 1 −1 1 1 1 0 1 | 1 0 0 0 0 −1 0 1 | |||
| 0 1 −1 1 1 2 0 1 | 1 0 0 1 0 0 1 1 | 1 0 −1 0 1 0 1 1 | |||
| 1 0 −1 1 1 0 1 1 | 1 0 0 1 1 1 1 1 | 1 0 −1 1 1 1 1 1 | |||
| 1 1 −1 1 1 1 1 1 | 1 0 0 2 1 1 1 1 | 1 0 −1 1 2 1 1 1 | |||
| 0 1 0 0 0 0 −1 1 | 1 1 0 0 0 0 −1 1 | 0 1 −1 0 0 0 −1 1 | |||
| 0 1 −1 −1 0 0 −1 1 | 0 1 0 0 −1 0 −1 1 | 0 1 0 0 0 1 −1 1 | |||
| 0 1 −1 0 0 1 −1 1 | 0 2 −1 0 0 1 −1 1 | 0 1 0 1 0 1 −1 1 | |||
| 0 1 −1 0 1 1 −1 1 | 0 0 1 0 0 0 0 −1 | 0 0 1 0 −1 0 0 −1 | |||
| 0 0 1 0 −1 −1 0 −1 | 0 0 1 −1 −1 −1 0 −1 | 0 0 0 0 0 0 1 −1 | |||
| 1 −1 1 0 0 −1 1 −1 | 0 0 1 −1 −1 −1 −1 −1 | 1 1 −1 1 1 1 0 2 |
| 1 0 0 0 0 0 0 0 | 0 1 0 0 0 0 0 0 | 1 1 0 0 0 0 0 0 | |||
| 0 0 1 0 0 0 0 0 | 1 0 1 0 0 0 0 0 | 0 1 −1 0 0 0 0 0 | |||
| 0 0 0 1 0 0 0 0 | 0 0 1 1 0 0 0 0 | 1 0 1 1 0 0 0 0 | |||
| 0 1 −1 −1 0 0 0 0 | 0 0 0 0 1 0 0 0 | 1 0 0 0 1 0 0 0 | |||
| 0 1 0 0 −1 0 0 0 | 0 0 1 0 −1 0 0 0 | 0 0 1 1 −1 0 0 0 | |||
| 0 0 0 0 0 1 0 0 | 0 1 0 0 0 1 0 0 | 0 1 −1 0 0 1 0 0 | |||
| 0 0 0 1 0 1 0 0 | 0 1 0 1 0 1 0 0 | 0 0 1 1 0 1 0 0 | |||
| 0 0 0 0 1 1 0 0 | 0 1 −1 0 1 1 0 0 | 0 0 0 1 1 1 0 0 | |||
| 1 0 0 0 0 −1 0 0 | 1 0 1 0 0 −1 0 0 | 1 −1 1 0 0 −1 0 0 | |||
| 1 0 0 −1 0 −1 0 0 | 0 0 1 0 −1 −1 0 0 | 1 0 1 0 −1 −1 0 0 | |||
| 0 0 0 0 0 0 1 0 | 1 0 0 0 0 0 1 0 | 0 0 0 1 0 0 1 0 | |||
| 1 0 0 1 0 0 1 0 | 1 0 1 1 0 0 1 0 | 1 −1 1 1 0 0 1 0 | |||
| 1 0 0 0 1 0 1 0 | 1 −1 0 0 1 0 1 0 | 1 0 −1 0 1 0 1 0 | |||
| 1 0 0 1 1 0 1 0 | 1 −1 0 1 1 0 1 0 | 1 −1 1 1 1 0 1 0 | |||
| 2 −1 1 1 1 0 1 0 | 1 −2 1 1 1 0 1 0 | 0 0 0 1 0 1 1 0 | |||
| 0 0 0 1 1 1 1 0 | 1 0 0 1 1 1 1 0 | 1 −1 1 2 1 1 1 0 | |||
| 1 0 0 0 0 −1 1 0 | 1 −1 0 0 0 −1 1 0 | 1 −1 1 0 0 −1 1 0 | |||
| 1 −1 1 1 0 −1 1 0 | 1 −1 2 1 0 −1 1 0 | 1 −1 0 0 1 −1 1 0 | |||
| 2 −1 1 0 1 −1 1 0 | 2 −1 1 1 1 −1 1 0 | 1 −2 1 1 1 −1 1 0 | |||
| 1 −1 1 1 −1 −1 1 0 | 1 −1 2 1 −1 −1 1 0 | 1 −1 1 0 −1 −2 1 0 | |||
| 0 1 0 0 0 0 −1 0 | 0 0 1 0 0 0 −1 0 | 0 1 0 −1 0 0 −1 0 | |||
| 0 1 −1 −1 0 0 −1 0 | 0 1 0 0 −1 0 −1 0 | 0 0 1 0 −1 0 −1 0 | |||
| 0 1 1 0 −1 0 −1 0 | 0 1 0 −1 −1 0 −1 0 | 0 1 0 0 0 1 −1 0 | |||
| 0 0 1 0 −1 −1 −1 0 | 0 1 0 −1 −1 −1 −1 0 | 0 0 1 −1 −1 −1 −1 0 | |||
| 1 −1 1 2 0 0 2 0 | 1 −1 0 1 1 0 2 0 | 1 −2 0 1 1 0 2 0 | |||
| 1 −1 1 1 1 0 2 0 | 2 −1 1 1 1 0 2 0 | 1 −2 1 1 1 0 2 0 | |||
| 1 −2 1 2 1 0 2 0 | 2 −1 0 1 2 0 2 0 | 1 −2 0 1 2 0 2 0 | |||
| 1 0 0 2 1 1 2 0 | 1 −1 0 2 1 1 2 0 | 1 −1 1 2 1 1 2 0 | |||
| 1 −1 0 2 2 1 2 0 | 1 −1 1 1 0 −1 2 0 | 2 −1 1 1 0 −1 2 0 | |||
| 1 −2 1 1 0 −1 2 0 | 1 −1 0 1 1 −1 2 0 | 2 −1 0 1 1 −1 2 0 | |||
| 1 −2 0 1 1 −1 2 0 | 2 −1 1 1 1 −1 2 0 | 1 −2 1 1 1 −1 2 0 | |||
| 2 −2 1 1 1 −1 2 0 | 0 2 0 −1 −1 0 −2 0 | 0 1 0 −2 −1 −1 −2 0 | |||
| 0 0 0 0 0 0 0 1 | 1 0 0 0 0 0 0 1 | 1 1 0 0 0 0 0 1 | |||
| 0 1 −1 0 0 0 0 1 | 1 1 −1 0 0 0 0 1 | 0 0 0 1 0 0 0 1 | |||
| 1 0 0 1 0 0 0 1 | 1 1 0 1 0 0 0 1 | 1 0 1 1 0 0 0 1 | |||
| 1 0 0 0 1 0 0 1 | 1 0 −1 0 1 0 0 1 | 1 1 −1 0 1 0 0 1 | |||
| 1 0 0 1 1 0 0 1 | 0 1 −1 0 0 1 0 1 | 0 0 0 1 0 1 0 1 | |||
| 0 1 0 1 0 1 0 1 | 1 1 0 1 0 1 0 1 | 0 1 −1 1 0 1 0 1 | |||
| 0 1 −1 0 1 1 0 1 | 1 1 −1 0 1 1 0 1 | 0 1 −2 0 1 1 0 1 | |||
| 0 0 0 1 1 1 0 1 | 1 0 0 1 1 1 0 1 | 1 1 0 1 1 1 0 1 | |||
| 0 1 −1 1 1 1 0 1 | 1 1 −1 1 1 1 0 1 | 1 0 0 0 0 −1 0 1 | |||
| 0 1 −1 1 1 2 0 1 | 1 0 0 1 0 0 1 1 | 1 −1 1 2 0 0 1 1 | |||
| 1 0 −1 0 1 0 1 1 | 1 0 0 1 1 0 1 1 | 2 0 0 1 1 0 1 1 | |||
| 1 −1 0 1 1 0 1 1 | 2 −1 0 1 1 0 1 1 | 2 −1 1 1 1 0 1 1 | |||
| 1 0 −1 1 1 0 1 1 | 1 −1 −1 1 1 0 1 1 | 1 −1 1 2 1 0 1 1 | |||
| 2 −1 1 2 1 0 1 1 | 2 −1 0 1 2 0 1 1 | 2 0 −1 1 2 0 1 1 | |||
| 1 −1 −1 1 2 0 1 1 | 1 0 0 1 1 1 1 1 | 1 0 −1 1 1 1 1 1 | |||
| 1 1 −1 1 1 1 1 1 | 1 0 0 2 1 1 1 1 | 2 0 0 2 1 1 1 1 | |||
| 1 −1 0 2 1 1 1 1 | 1 −1 1 2 1 1 1 1 | 1 0 −1 2 1 1 1 1 | |||
| 1 0 −2 0 2 1 1 1 | 2 0 0 1 2 1 1 1 | 1 −1 0 1 2 1 1 1 | |||
| 1 0 −1 1 2 1 1 1 | 2 0 −1 1 2 1 1 1 | 1 −1 −1 1 2 1 1 1 | |||
| 1 0 −2 1 2 1 1 1 | 2 0 0 2 2 1 1 1 | 1 −1 0 2 2 1 1 1 | |||
| 1 0 −1 2 2 1 1 1 | 2 −1 1 1 0 −1 1 1 | 2 −1 0 0 1 −1 1 1 | |||
| 2 0 −1 0 1 −1 1 1 | 2 −1 0 1 1 −1 1 1 | 2 −1 1 1 1 −1 1 1 | |||
| 1 0 −1 1 2 2 1 1 | 1 1 −2 1 2 2 1 1 | 1 0 −1 2 2 2 1 1 | |||
| 0 1 0 0 0 0 −1 1 | 1 1 0 0 0 0 −1 1 | 0 1 −1 0 0 0 −1 1 | |||
| 0 1 −1 −1 0 0 −1 1 | 0 1 0 0 −1 0 −1 1 | 0 1 0 0 0 1 −1 1 | |||
| 0 1 −1 0 0 1 −1 1 | 0 2 −1 0 0 1 −1 1 | 0 1 0 1 0 1 −1 1 | |||
| 0 1 −1 0 1 1 −1 1 | 0 2 −2 −1 1 1 −1 1 | 0 2 −2 0 1 2 −1 1 | |||
| 2 0 0 1 1 0 2 1 | 2 −1 0 1 1 0 2 1 | 2 0 −1 1 1 0 2 1 | |||
| 1 −1 −1 1 1 0 2 1 | 2 0 0 2 1 0 2 1 | 1 −1 0 2 1 0 2 1 | |||
| 2 −1 0 2 1 0 2 1 | 2 −1 1 2 1 0 2 1 | 2 −1 0 1 2 0 2 1 | |||
| 2 0 −1 1 2 0 2 1 | 1 −1 −1 1 2 0 2 1 | 2 −1 −1 1 2 0 2 1 | |||
| 2 −1 0 2 2 0 2 1 | 1 0 0 2 1 1 2 1 | 2 0 0 2 1 1 2 1 | |||
| 1 −1 0 2 1 1 2 1 | 1 0 −1 2 1 1 2 1 | 2 0 −1 1 2 1 2 1 | |||
| 1 −1 −1 1 2 1 2 1 | 2 0 0 2 2 1 2 1 | 1 −1 0 2 2 1 2 1 | |||
| 2 −1 0 2 2 1 2 1 | 1 0 −1 2 2 1 2 1 | 2 0 −1 2 2 1 2 1 | |||
| 1 −1 −1 2 2 1 2 1 | 2 −1 0 1 1 −1 2 1 | 1 0 −1 2 2 2 2 1 | |||
| 0 0 1 0 0 0 0 −1 | 0 0 1 0 −1 0 0 −1 | 0 0 1 0 −1 −1 0 −1 | |||
| 0 0 1 −1 −1 −1 0 −1 | 1 −1 2 −1 −1 −2 0 −1 | 0 0 0 0 0 0 1 −1 | |||
| 1 −1 1 0 0 −1 1 −1 | 1 −1 2 1 −1 −1 1 −1 | 1 −2 2 0 0 −2 1 −1 | |||
| 1 −1 2 0 −1 −2 1 −1 | 1 −2 2 0 −1 −2 1 −1 | 0 0 1 −1 −1 −1 −1 −1 | |||
| 0 0 1 −1 −1 −2 −1 −1 | 0 0 1 −2 −1 −2 −1 −1 | 0 0 2 −1 −2 −2 −1 −1 | |||
| 0 0 1 −2 −2 −2 −1 −1 | 1 −2 1 1 1 0 2 −1 | 1 −2 1 1 0 −1 2 −1 | |||
| 1 −2 2 1 0 −1 2 −1 | 1 −2 1 1 1 −1 2 −1 | 1 1 −1 1 1 1 0 2 | |||
| 1 1 −2 1 2 1 0 2 | 0 1 −2 1 1 2 0 2 | 1 1 −1 1 2 2 0 2 | |||
| 1 1 −2 1 2 2 0 2 | 2 0 0 1 1 0 1 2 | 2 0 −1 1 1 0 1 2 | |||
| 2 0 −1 1 2 0 1 2 | 2 0 0 2 1 1 1 2 | 1 0 −1 2 1 1 1 2 | |||
| 1 0 −1 1 2 1 1 2 | 2 0 −1 1 2 1 1 2 | 2 1 −1 1 2 1 1 2 | |||
| 1 0 −2 1 2 1 1 2 | 2 1 −2 1 2 1 1 2 | 2 0 0 2 2 1 1 2 | |||
| 1 0 −1 2 2 1 1 2 | 2 0 −1 2 2 1 1 2 | 2 1 −1 2 2 1 1 2 | |||
| 1 1 −2 1 2 2 1 2 | 1 0 −1 2 2 2 1 2 | 1 1 −1 2 2 2 1 2 | |||
| 2 1 −1 2 2 2 1 2 | 1 1 −2 2 2 2 1 2 | 0 1 −2 0 1 1 −1 2 | |||
| 1 2 −2 0 1 1 −1 2 | 0 2 −2 0 1 2 −1 2 | 2 0 −1 2 2 1 2 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Engel, P. On Σ-Classes in E8. I. The Neighborhood of E8. Crystals 2023, 13, 246. https://doi.org/10.3390/cryst13020246
Engel P. On Σ-Classes in E8. I. The Neighborhood of E8. Crystals. 2023; 13(2):246. https://doi.org/10.3390/cryst13020246
Chicago/Turabian StyleEngel, Peter. 2023. "On Σ-Classes in E8. I. The Neighborhood of E8" Crystals 13, no. 2: 246. https://doi.org/10.3390/cryst13020246
APA StyleEngel, P. (2023). On Σ-Classes in E8. I. The Neighborhood of E8. Crystals, 13(2), 246. https://doi.org/10.3390/cryst13020246






