A Critical Review of von Mises Criterion for Compatible Deformation of Polycrystalline Materials

Abstract

A von Mises criterion for compatible deformation states that five independent slip systems must operate for polycrystals to deform uniformly and without failure at the grain boundaries, which is supported by the Taylor–Bishop–Hill theory or simply the Taylor model, defining the laws of plastic deformation of polycrystalline aggregates and being one of the key cornerstones of crystal plasticity theory. However, the criterion has fundamental flaws as it is based on an unfounded correlation between phenomenological material flow behaviour in continuum mechanics and crystal structure dependent dislocation slip, and there has been no experimental evidence to show simultaneous operation of five independent slip systems. In this paper, the Von Mises criterion and the Taylor model are revisited and examined critically, and the fundamental issues related to the requirement of independent slip systems for compatible deformation and the selection of the active slip systems are addressed. Detailed analysis is performed of the stress state that eliminates the possibility of the simultaneous operation of five independent slip systems, and of the relative displacement vector due to the dislocation slip which defines the quantity of the strain that can be expressed by a strain tensor, instead of individual strain components. Discussions are made to demonstrate that although three linearly independent slip systems are essentially sufficient for compatible deformation, one slip system, being selected according to Schmidt law, dominates at a time in a characteristic domain as deformation accommodation occurs between grains or characteristic domains rather than at each point.

1. Introduction

von Mises first pointed out in 1928 that five independent slip systems must operate for polycrystals to deform uniformly and without failure at the grain boundaries [1], which is called the von Mises criterion for compatible deformation. In 1938, Taylor published his work on “plastic strain in metals” [2,3], in which he suggested that local deformation within a polycrystalline aggregate is homogeneous when a representative material element is subject to loading consistent with macroscopically uniform deformation. This work is further advanced by Bishop and Hill [4,5] and accordingly called the Taylor–Bishop–Hill theory or simply the Taylor model. The von Mises criterion and Taylor model, in conjunction with the theories of yield, define the laws of plastic deformation of polycrystalline aggregates based on their single crystal behavior by linking the phenomenological material flow to concrete slip in crystals, and are key cornerstones of crystal plasticity theory [6,7,8].

The Taylor model has been widely used to explain and predict strength, ductility and texture evolution during the deformation of polycrystalline materials [9,10,11,12,13]. The greatest successes have occurred in cubic metal crystals with a large number of equivalent slip systems with same deformation resistances [14,15,16,17]. The flow envelope of a crystal can be described as the locus of deviatoric stress components required to generate resolved shear stresses equal to the deformation resistances on a sufficient set of slip systems so as to accommodate arbitrary deformation rates. Cubic metal crystals have high symmetry and the flow envelope is essentially isotropic. In crystals of lower symmetry, the deformation resistances can vary largely among slip systems, which may have different crystallographic features; the stress required to activate slip systems for accommodating an arbitrary deformation rate can become exceedingly high for certain orientations. Thus, the flow envelope can become highly distorted. The corresponding polycrystalline aggregate stress levels obtained from Taylor-type models also become large [14]. It is recognized that, in the case where unbounded deformation resistance is on all but four or fewer linearly independent slip systems, the Taylor estimate of aggregate stress generally becomes unbounded [16]. The Taylor model assures both local and global compatibility but violates local traction equilibrium across grain boundaries. Yet its uniform deformation and equal hardening assumptions seem to be oversimplified. Therefore, it cannot predict grain interactions, local stress equilibrium between the grains, and the influences of morphological textures, including grain shape and orientation. Various adaptations of the Taylor model have been made to account for the effects of differing deformation resistances for different classes of slip systems [18], of self and latent hardening of slip systems [19], of strain rate sensitivity of slip [20], and of finite deformation elastic [19] or viscoplastic flow [21]. Improvements in the prediction of textures and mechanical properties have been made by considering grain interaction, grain morphology and to some extent the local stress equilibrium in such models, as compared to those of the classical full-constraints Taylor model [22,23]. These models can then be embedded as part of today’s state-of-art hierarchical multi-scale models (see e.g., grain interactions, grain morphology, and local stress equilibrium between the grains can be achieved by the Crystal Plasticity Finite Element Method (CPFEM) using a very fine mesh [24] or by the Crystal Plasticity Fast Fourier Transform method [25,26]).

In order to take advantage of the Taylor model in the modern multi-scale simulations, it is important to choose the right criterion for solving problems of ambiguity associated with the simplicity of the Taylor model. One of the longstanding ambiguous problems of the rate-independent full-constraints Taylor model has been the non-unique choice of active slip systems. According to the Taylor model, several solutions can be found for the set of slip systems activated in order to accommodate the plastic deformation rate tensor imposed at each moment to the given crystal, which was pointed out by Bishop and Hill, and Van Houtte [5,27]. All these solutions fulfil the yield condition, i.e., all minimize the internal rate of work as assumed initially by Taylor [2] and fulfil the maximum external work principle which was the approach adopted by Bishop and Hill [4,5]. Another problem is the difficulties in dealing with deformation of hcp metals which have only two independent equivalent easy slip systems at room temperature and the von Mises criterion cannot be fulfilled. There have been studies on solving the uncertainty of slip system selection [6,20,27] and the deformation performance of metals with less than five independent slip systems [28]. However, the problems are still outstanding as fundamental challenges to the theory of crystal plasticity. On the other hand, experimental observations do not fully support the von Mises criterion and the Taylor model in terms of the number of active independent slip systems required for compatible deformation. It has been frequently demonstrated that deformation occurs with less than five active slip systems while maintaining compatibility in both cubic and hcp metals, although the achievable strain depends on individual crystals [29,30,31,32,33]. Cubic metals such as face-centred cubic (fcc) Al, Cu and Ni and body-centred cubic (bcc) Fe have more than five equivalent slip systems and according to the von Mises criterion, five independent slip systems are supposed to be active during their deformation. However, there is no direct experimental evidence to show that five independent slip systems operate simultaneously in the deformation of either single crystals of any orientation or polycrystals in any deformation mode in these metals. There have been efforts to determine active slip systems via direct or indirect observations [29,30,31]. In an extensive study to determine the active slip systems during tensile deformation in pure aluminum and copper, Wither and co-workers [29] were able to directly measure the lattice rotations for a large number of grains in the bulk of the samples using a three-dimensional X-ray diffraction technique. The spread of the individual diffraction peaks was often in the form of weak tails trailing behind the main spot along the rotation direction and the rotation paths in general were smooth with a single path (up to ~6% elongation), indicating a relatively uniform behaviour of each individual grain and single slip domination. They found that grain orientation was the primary parameter controlling the slip systems, leading to grain-orientation dependence of lattice rotations and dislocation structures, and that the highest Schmid factors control the selection of the most active slip system, which is reflected in systematic variations in lattice rotations among grains and dislocation structures within each region.

The problems come from two aspects of matter. Firstly, it is an intrinsic consequence of the theory which links dislocation slip, which relates to the individual or collective atomic response to applied stress and sensitive to crystal structures, to material flow behaviour described in continuum mechanics, which disregards internal structures. The direct link of deformation behaviour described by these two totally different scientific approaches (with totally different assumptions) is intrinsically untenable. Secondly, the selection of active slip systems by minimum energy or maximum work principle works only when each slip system is assigned a fixed amount of shear, which is oversimplified and unrealistic.

This paper aims to clarify a few fundamental issues related to the requirement of independent slip systems for compatible deformation and the selection of the active slip systems. This may help achieve a better understanding of the deformation behaviour from basic constitutional relations to the evolution of microstructure and texture during deformation, and therefore better prediction in modelling and simulation applications. It can be also important for education purposes as the von Mises criterion and Taylor—Bishop—Hill (TBH) theory has been a constant in standard textbooks for physical metallurgy. In this paper, the von Mises criterion and its extended theories including the Taylor model will be revisited critically. This will be followed by a detailed analysis of the stress state that eliminates the possibility of the simultaneous operation of five independent slip systems, and of the relative displacement vector due to dislocation slip which defines the quantity of the strain that can expressed by a strain tensor, instead of individual strain components. Discussions will be made to demonstrate that, although three linearly independent slip systems are essential and sufficient for compatible deformation, one slip system domination at a time in a characteristic domain, selected according to Schmid law, should be the normal reality as deformation is always heterogeneous and strain accommodation occurs between grains or characteristic regions rather than at each individual point.

2. von Mises Criterion Revisit

According to von Mises [1], dislocation slip leads on a macroscopic scale to the translation of one part of a crystal relative to another by a motion corresponding to a simple shear. It is suggested by von Mises that a single simple shear determines the value of one of the independent components of the strain tensor. A general strain tensor has nine components. At equilibrium, the strain tensor is symmetrical and thus there are only six independent components [34]. Since plastic flow usually occurs without a change in volume, which means that the sum of all normal stresses must be zero, the strain tensor generally has five independent components. Therefore, von Mises claims that since the operation of one slip system produces only one independent component of the strain tensor, then five independent slip systems are needed to produce a general, small, homogeneous strain without a change in volume.

Taylor further develops the theory and states that for a volume-preserving arbitrary plastic deformation, five independent slip systems need to be simultaneously active to achieve compatibility among the homogeneously deforming randomly misoriented grains [2,3]. In fcc metals, where 12 equivalent slip systems are present, there is a substantial redundancy of sets of five systems for each grain. According to Taylor, the active five independent slip systems, of all the available sets, are the ones with minimum internal dissipation, i.e., the ones for which

$$\tau {\displaystyle \sum }_i^{5}d{\gamma }_i$$

(1)

is minimum, where γ is the shear strain for a particular slip system and i identifies the active slip systems. Invoking the principle of virtual work (equivalence of the external work increment and the internal dissipation increment),

$$Yd\epsilon =\tau <{\displaystyle \sum }_i^{5}d{\gamma }_i>$$

(2)

must be obeyed, where the brackets indicate an average of the internal dissipation increment over all grains in the aggregate, Y is the uniaxial tensile yield strength, dε the uniaxial tensile strain, and τ the critical resolved shear stress, which is assumed to be constant for all slip systems [2,4]. Thus,

$${\left(\frac{Y}{\tau }\right)}_T={\overline{m}}_T=\frac{\langle {{\displaystyle \sum }}_i^{5}d{\gamma }_i\rangle }{d\epsilon }$$

(3)

gives us the so-called Taylor factor of ${\overline{m}}_T$ = 3.1 for fcc crystal aggregates.

To analyse possible selections of active slip systems for fcc crystals, Taylor wrote down the components of the strain tensor produced by “an arbitrary amount of slip” on a given slip system and all the four in the same set of coordinate axes, forming the five-by-five determinant of the strain tensor component quantities. If this determinant has a value other than zero, then the five chosen slip systems are considered independent of one another, since the determinant will equal zero if any row can be expressed as a linear combination of other rows. Provided then that the value of the determinant is other than zero, one has chosen five slip systems which are independent of one another in the sense that the operation of one of them produces components of the strain tensor which cannot be expressed as linear combinations of the components produced by the operation of the other slip systems. Thus, for fcc metals with 12 slip systems there are ₁₂C₅ = 792 sets of five-slip system combinations and only 384 are independent, as the remaining 408 sets are dependent combinations of slip systems with a net zero strain [2,4].

In their theoretical attempts to deduce the polycrystalline stress-strain curve from that of a single crystal, Bishop and Hill [4,5,35] accept von Mises criterion that five independent slip systems are required for compatible deformation, stressing that any possible strain has five independent components, and therefore in general can only be produced by a multislip over a group of directions containing an independent set of five. Having raised two main criticisms of Taylor approach: (1) it is not proved that a combined stress could always be found to operate any geometrically possible set of shears; and (2) no account is taken of stress-continuity conditions across grain boundaries, Bishop and Hill demonstrated a correlation between a strain tensor and a stress tensor with reference to the cubic axes as a consequence of the virtual work equation,

$${\sigma }_{ij}{\epsilon }_{ij}={\displaystyle \sum }\tau d\gamma$$

(4)

By assuming that the only mechanism of plastic distortion in a single crystal is by slip parallel to preferred planes and directions, they calculated strain tensor components from shears of all possible slip systems and claimed, without verification though, that “we can always find a stress for which the component shear stresses attain the critical values in prescribed senses in a given set of five independent slip-directions”. They argue that the critical value would usually be exceeded in one or more of the other seven directions (with reference to fcc metals), but, for any given strain, “it is always possible to find at least one of the independent sets for which there exists a physically possible stress to operate the constituent shears.”. According to Bishop and Hill, in the selection of the active set of five independent slip systems, there is no need to determine a physically possible combination of shears which are equivalent to the strain. It is necessary merely to calculate the works undertaken in the given strain by stresses not violating the yield condition, and to select from these works the greatest. In their approach, it is only necessary to make the choice from the works done by 56 particular stresses, which correspond to the “vertices” of the polyhedral surface in the stress space representing the yield criterion for the crystal.

Groves and Kelly [36] pointed out later that since five independent slip systems suffice to produce an arbitrary strain without a change in volume, a crystal cannot possess more than five independent slip systems. They also analysed the independent slip systems for bcc metals and crystals with less than five independent slip systems including hcp metals such as Zn and Mg. By applying the von Mises criterion, they concluded that for crystals with less than five independent slip systems general deformation is not possible by slip. The von Mises criterion including the Taylor–Bishop–Hill theory can be summarised as below:

(1)

Five independent slip systems have to operate simultaneously in a grain for compatible deformation and five independent slip systems are sufficient to maintain deformation compatibility.

(2)

For crystals with more than five slip systems, of all possible combinations of slip that can produce the assigned strain, only that combination for which the energy dissipation is the least is active. Alternatively, the maximum work principle can be applied in the selection of active slip systems.

(3)

Crystals with less than five independent slip systems cannot deform while maintaining continuity and constant volume.

The von Mises criterion sets out an essential and sufficient requirement for compatible deformation. As the criterion correlates slip systems to the strain tensor components, the requirement of five independent slip systems should apply to every point of the deforming body. Logically, the von Mises criterion is categorical and suitable for all instances of deformation.

3. von Mises Criterion Criticism

The fact that deformation occurs with less than five slip systems in operation simultaneously while maintaining compatibility in both cubic and hcp metals [29,30,31,32,33] directly conflicts the von Mises criterion and indicates that the criterion as a categorical statement is unsound. Let us examine the essential premise of the von Mises criterion that a dislocation slip determines the value of one of the independent components of the strain sensor. The strain state at a point is a physical quantity independent of any particular coordinate system representation, whereas the strain components represented by a symmetric second-order tensor depend on the selected coordinate-system [37,38]. A strain state can be represented in any coordinate systems with an unlimited number of independent components sets, although the principal strains and strain tensor invariants remain the same. Physically, the dislocation slip leads to relative movement of atoms and a unit slip generates a lattice displacement characterized by its Burgers vector [39], contributing directly to the relative displacement vector in deformation (if a correlation has to be made between slip and deformation described in continuum mechanics) rather than a single component of a strain tensor. The correlation between slip and strain tensor components is unsuitable both physically and dimensionally. This will be described in detail in the following context.

There is also crystallographic unorthodoxy for the simultaneous operation of five slip systems. Take the slip systems of fcc crystals as an example, which are expressed as {h_i k_i l_i} < u_i v_i w_i > (i = 1, 2, 3,…12, with subscript i representing the ith slip system). For a particular grain p in a polycrystalline matrix, the activation of a particular slip system will lead to the lattice rotation about a rotation axis R, which is calculated as

R = [r_i^p s_i^p t_i^p] = [h_i^p k_i^p l_i^p]⊗[u_i^p v_i^p w_i^p]

(5)

The rotation axis R should be always one of the <112> family for fcc metals [40], determined by the dislocation Burgers vector of (a/2)<110>. Since rotation R is not a vector and the final result of a series of rotations depends on the sequence of the rotations. Simultaneous operation of five independent slip systems can only lead to actions of irrational lattice rotations and the destruction of the crystal structure.

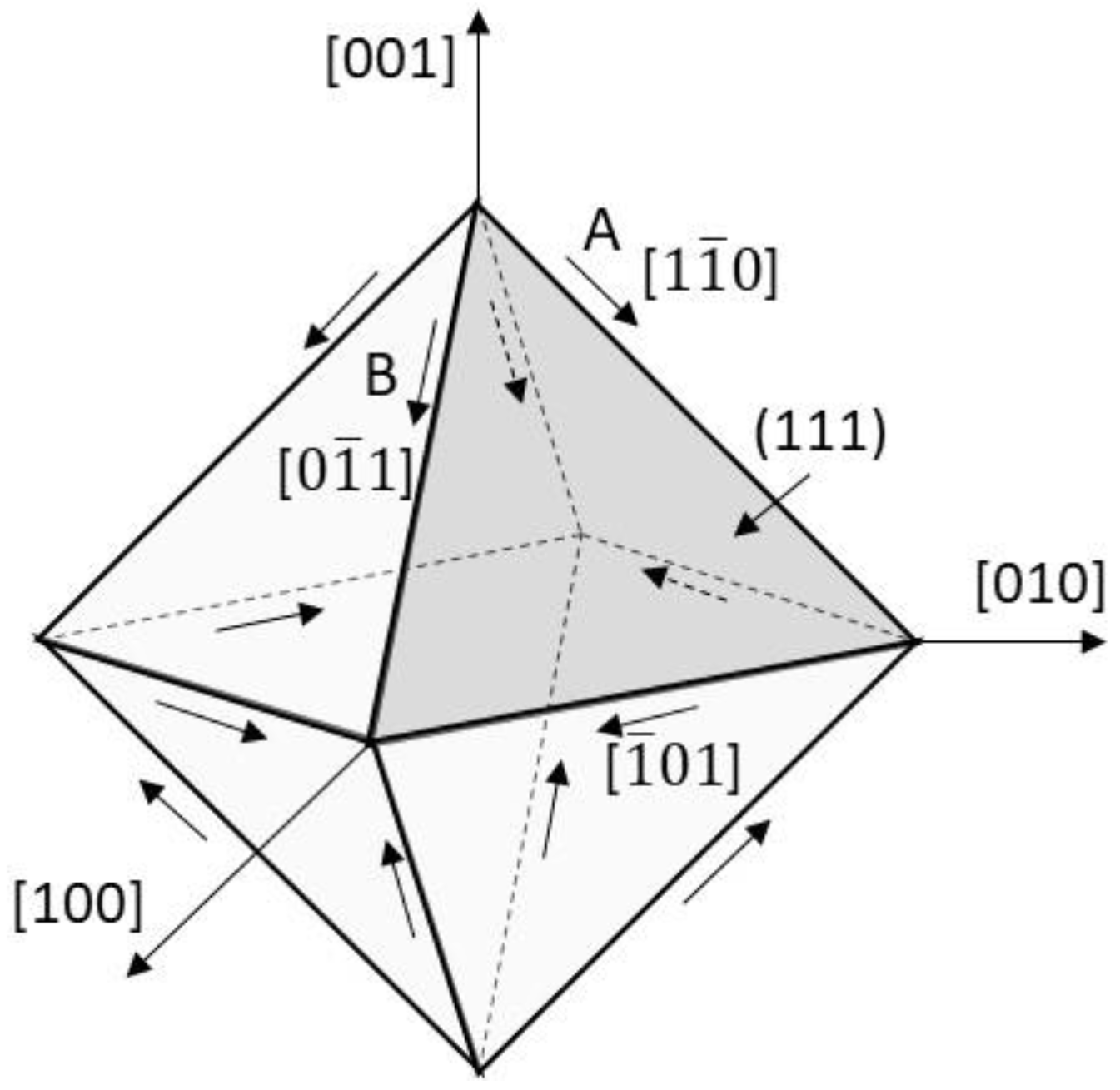
In addition to lattice rotation disorder, the simultaneous operation of more than one slip systems will result in an irrational atomic path during slip and a temporary breakdown of the periodic order of the crystal. Figure 1 shows the octahedron formed by (111) planes and <110> directions, displaying all the 12 slip systems in fcc metals. If two slip systems on the same slip plane, for example, slip system A and B on (111) plane, slip simultaneously (known as coplanar slip), the path of atoms involved must follow a route determined by the sum of the two Burgers vectors, i.e.,

$$\mathrm{A}+\mathrm{B}=\langle 1\overline{1}0\rangle +\langle 0\overline{1}1\rangle =\langle 1\overline{2}1\rangle$$

(6)

The resultant path is along the <1$\overline{2}$1> direction. This cannot happen as the atomic translation during the dislocation slip must follow a <110> direction with the highest density of atoms. If these atoms are also involved in the operation of more slip systems on the other slip planes, their path will be out of any of the (111) slip planes, following an irrational lattice direction.

Hosford [40] discussed the rotation reference system for the Taylor model in comparison to the theoretical model (Equation (5)). In the Taylor model, a loading axis is selected as the reference line for rotation and the slip plane normal in consideration always rotates away from the loading axis. Thus, the rotation axis is normal to both loading axis and slip plane normal. In contrast, Equation (5) is applied without using the sample reference direction and the rotation axis must be normal to both slip direction and slip plane normal. Calculations performed by Chen et al. [41] showed that the rotation paths are related to irrational lattice directions for the Taylor model.

Although it is repeatedly claimed that one slip system can produce only one independent strain tensor component in the core literature of the von Mises criterion [1,2,3,4,5,36], their analysis of linear independency of slip systems is always performed by assigning “an arbitrary amount of slip” from a given slip system to all strain components with the help of geometrical projection. The strain tensor components are then obtained by adding the contributions from a set of selected five slip systems. In their calculations, only unit slip from each slip system is considered, instead of “an arbitrary amount of slip”. Yet, the strain tensor components are obtained by directly adding the “shear” from all possible slip systems, which is simply inappropriate as two order operations are required to transfer the “shear” to strain tensor components, i.e., (1) dividing the slip distance or “shear” by the reference length to obtain strain and (2) project the strain to corresponding axis directions in the selected coordinate system.

In terms of the selection of the active slip systems, the minimum internal dissipation [2] or minimum energy consumption principle [5] has an issue of uncertainty or uniqueness, i.e., there are more than one set of slip systems that meet the requirement [4]. Yet, the assumptions that only the simple shear takes place during deformation (ignores lattice rotation) and one slip system can only contribute a unit slip are over simplified. In determining the energy dissipation or consumption, one should not only consider all possible combinations of slip systems (5 out of 12 in the case of fcc lattice) but also the possible combinations of shear values from each slip system. The number of latter combinations is infinite and thus the application of the principle is practically unfeasible. The maximum work principle is also practically unfeasible as it counts the work done by the stresses along the “vertices” of the polyhedral surface in the stress space representing the yield criterion for the crystal, which are known for a specifically oriented single crystal but unknown to individual grains in a polycrystalline aggregate. In fact, as will be discussed later, the concept of stress “vertices” is inappropriate apart from describing stress invariants.

Above all, if the logic used in the argument for von Mises criterion is right, that five independent slip systems are required for compatible deformation because of the existence of five independent strain tensor components, six independent slip systems would have to be required to perform deformation with a volume change (material continuity will not be maintained) as there are six independent strain components under this condition. This is obviously untrue.

4. Stress State Elimination of Simultaneous Five Slip System in Operation

In continuum mechanics, the stress state at a given point is described by a second order stress tensor σ. The stress tensor is comprised of nine components that fully define the stress state at a point inside a material in the deformed state. The tensor relates a unit-length direction vector n to the stress vector T⁽ⁿ⁾ across an imaginary surface perpendicular to n:

$$T^{\left(n\right)}=\mathit{n}·\sigma \mathrm{or} {\mathrm{T}}_j^{\left(n\right)}={\sigma }_{ij}{n}_i$$

(7)

where i and j are iterated over x, y, and z and ${\sigma }_{ij}$ is called Cauchy stress tensor [37,38]. It is assumed that the element is at an equilibrium state so that ${\sigma }_{ij}={\sigma }_{ji}$ and therefore, there are totally six independent stress components.

The stress tensor components ${\sigma }_{ij}$ depend on the orientation of the coordinate system at the point under consideration. However, the stress tensor as a physical quantity is independent of the coordinate system selected to represent it. Each tensor is associated with a set of invariants which are also independent of the coordinate system. With a given stress tensor determined with respect to a coordinate system (x, y, z), it may be necessary to calculate the components of the stress tensor at the same point with respect to a rotated coordinate system (x′, y′, z′), i.e., the stresses acting on a plane with a different orientation passing through that point of interest—forming an angle with the coordinate system (x, y, z). This allows the maximum normal stress and maximum shear stress to be determined, as well as the orientation of the planes where they act upon, and can be achieved by performing a tensor transformation under a rotation of the coordinate system.

The Cauchy stress tensor ${\sigma }_{ij}$ is a contravariant second order tensor, which is a statement of how it transforms under a change of the coordinate system. From system (x, y, z) to system (x′, y′, z′), the components σ_ij in the initial system are transformed into the components σ_ij′ in the new system according to the tensor transformation rule [38]:

$${\sigma }_{ij}^{\prime }=a_{im}{a}_{jn}{\sigma }_{mn} \mathrm{or} {\sigma }^{\prime }=A\sigma A^T$$

(8)

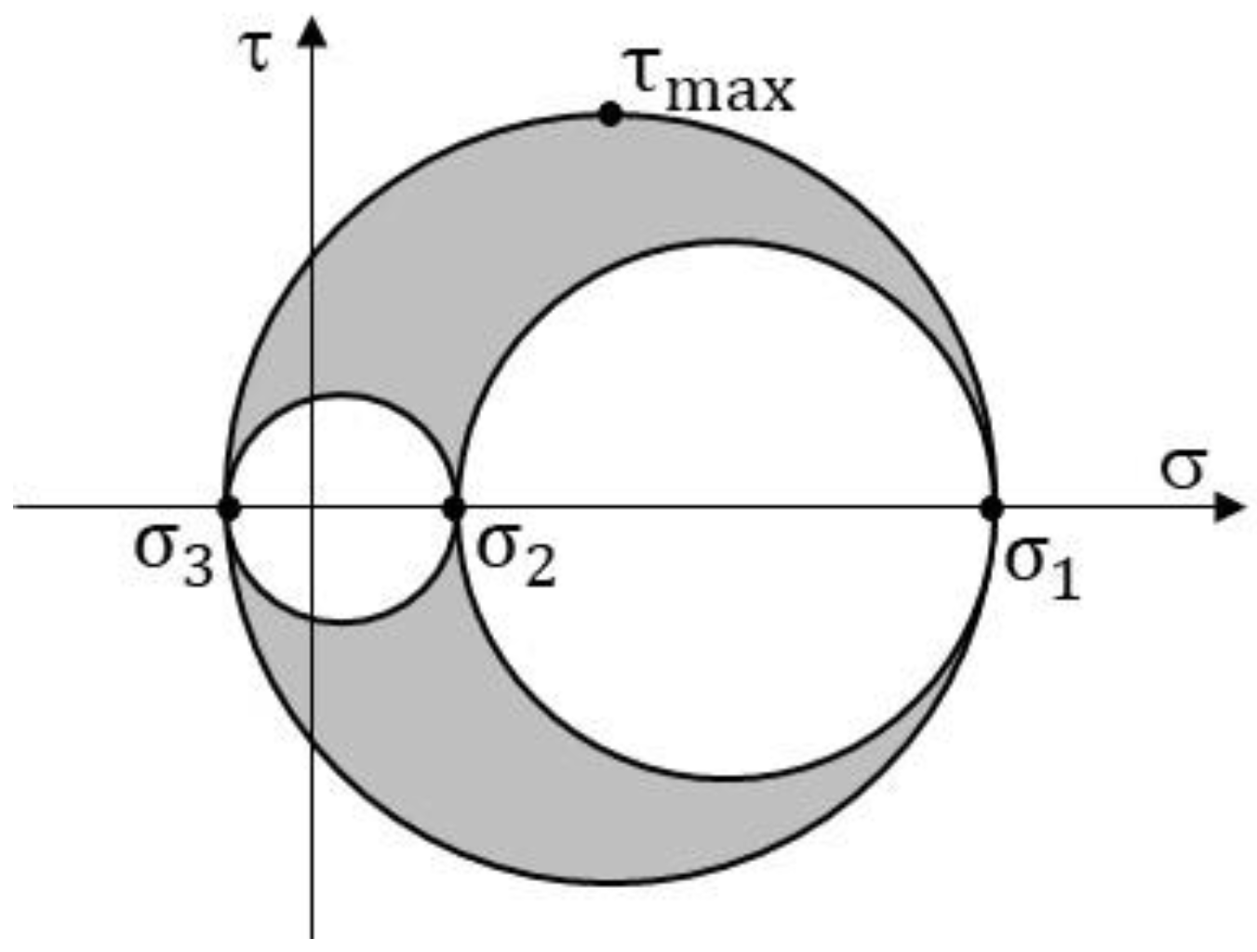
where A is a rotation matrix with components a_ij. Both σ_ij and ${\sigma }_{ij}^{\prime }$ represent the same stress state in different coordinate systems. At a given point there is only one stress state at a time. Each component of ${\sigma }_{\mathit{ij}}^{\prime }$ is a continuous and smooth function of the rotation matrix and there are no stress vertices at any point in any direction. A graphical representation of this transformation law is the Mohr’s circle for stress as shown in Figure 2, in which the shaded regions represent all admissible points in the stress space. It can be seen from the figure that the maximum shear stress (τ_max) occurs only on two orthogonal planes, perpendicular to the plane defined by the maximum and minimum principal stresses. In the case where a slip system is aligned with the maximum shear stress, it is likely that only this one slip system can obtain the resolved shear stress required for operation, since the slip planes between different slip systems are not orthogonal in most crystals. In general, it is not necessary for a slip system to be aligned with the maximum shear stress to act. However, for fcc metals, there is only one situation in which the resolved shear stresses are equal on more than two slip systems. This is the case of axial symmetrical uniaxial tension or compression in which the crystal or grain in consideration is oriented such that two of the vertices of the (111) plane octahedron (see Figure 1), i.e., a <001> direction, are in line with the tension or compression direction. Therefore, all the octahedral stress planes as shown in Figure 3 are effectively coincided with the corresponding triangle planes of the (111) plane octahedron. Here, there are eight slip systems that undergo the same resolved shear stress. Although this resolved stress is a fraction less than the maximum shear stress, these eight slip systems will operate simultaneously because the resolved shear stress on the other available slip systems (the quadrant plane slip systems in Figure 1) is zero. Unfortunately, this simultaneous operation of multiple slip systems cannot happen in reality because the value of the probability density function for the coincidence of a <001> direction and the loading axis is zero. For hcp and bcc crystals, such an alignment does not exist.

In conclusion, there is no such a stress state that can produce an equal resolved shear stress on five independent slip systems and their simultaneous operation is not possible. Bishop and Hill mistakenly use the vertices of the yield surface, instead of actual stress state, in their analysis of stress states required to activate multiple slip, leading to a false conclusion that there are 56 vertices for a stress state [4].

5. Strain Tensor and Slip

The strain state in continuum mechanics is an assignment of deformation intensity of any point. Strain describes deformation in terms of relative displacement of particles in the body, excluding rigid-body motions. A solid is deformed under an applied force, giving rise to a change of volume and shape. A configuration change of a continuous body can be described by a displacement field as a vector field of all displacement vectors for all particles in the body, which relate the deformed configuration with the undeformed configuration. In the approximation of infinitesimal strain, the position of each point of a solid is described by the vector X, which has the components $X_i$ (i = 1, 2, 3) in a Cartesian coordinate system. All points of a solid are in general shifted under strain. If the position of a given point was X before strain and $x$ with components $x_i \left(i=1, 2, 3\right)$ after strain, the displacement of the point is characterized by the displacement vector defined as

$$u=x-X$$

(9)

The coordinates $x_i$ of a shifted point are functions of the coordinates $X_i$ of the same point before strain and the displacement vector u is a function of$x_i$. This function completely determines the deformed state of a solid. The quantity of strain, however, is determined by the relative displacement vector du,

$$\mathrm{d}u=\mathrm{d}x-\mathrm{d}X$$

(10)

For an infinitesimal element dX, it is possible to use a Taylor series expansion around a particular point, neglecting higher-order terms, to approximate the components of the relative displacement vector for the neighbouring point as

$$u\left(X+\mathrm{d}X\right)=u\left(X\right)+\mathrm{d}u\approx u\left(X\right)+{\nabla }_{X}u·\mathrm{d}X$$

(11)

Deformation can be measured by the difference between the squares of the differential line element dX in the undeformed state and dx, in the deformed configuration:

$$\mathrm{d}{x}^2-\mathrm{d}{X}^2=\mathrm{d}x·\mathrm{d}x-\mathrm{d}X·\mathrm{d}X\mathrm{or}{\left(\mathrm{dx}\right)}^2-{\left(\mathrm{dX}\right)}^2={\mathrm{dx}}_{\mathrm{i}}{\mathrm{dx}}_{\mathrm{i}}-{\mathrm{dX}}_{\mathrm{j}}{\mathrm{dX}}_{\mathrm{j}}$$

(12)

Substituting the expression for dx_i through du_i the following expression for ${\left(\mathrm{d}\mathrm{x}\right)}^2$ is obtained:

$${\left(\mathrm{dx}\right)}^2={\left(\mathrm{dX}\right)}^2+2{\mathsf{\epsilon }}_{\mathrm{ij}}{\mathrm{dx}}_{\mathrm{i}}{\mathrm{dx}}_{\mathrm{j}}$$

(13)

where a second rank tensor has been introduced:

$${\mathsf{\epsilon }}_{\mathrm{ij}}=\frac{1}{2}\left(\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+\frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{i}}}-\frac{\partial {\mathrm{u}}_{\mathrm{l}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\frac{\partial {\mathrm{u}}_{\mathrm{l}}}{{\mathrm{x}}_{\mathrm{j}}}\right)$$

(14)

The second rank tensor ${\mathsf{\epsilon }}_{\mathrm{ij}}$ is generally called the strain tensor. From the definition (14), one can see it is a symmetric tensor:

$${\mathsf{\epsilon }}_{\mathrm{ij}}={\mathsf{\epsilon }}_{\mathrm{ji}},\hspace{1em}\hspace{1em}\forall \mathrm{i},\mathrm{j}=1,2,3$$

(15)

Any symmetric tensor can be reduced to the principle axes. This implies that the coordinate system can be selected at each given point in such a way that only diagonal elements ${\mathsf{\epsilon }}_{11,}{\mathsf{\epsilon }}_{22}{\mathrm{and}\mathsf{\epsilon }}_{33}$ will be non-zero and all non-diagonal elements vanish. If the strain tensor at a given point is reduced to its principle axes, the element of the length (Equation (13)) in the elementary volume built around this point takes the form:

$${\left(\mathrm{dx}\right)}^2=\left(1+2{\mathsf{\epsilon }}_{11}\right){({\mathrm{dX}}_1)}^2+\left(1+2{\mathsf{\epsilon }}_{22}\right){({\mathrm{dX}}_2)}^2+\left(1+2{\mathsf{\epsilon }}_{33}\right){({\mathrm{dX}}_3)}^2$$

(16)

This expression has three independent terms. This means that the deformation at any given elementary volume is comprised as a set of three independent components along three relatively orthogonal directions—the principal axes of the tensor. Each of these components represents a simple stretching or compressing along the corresponding direction: the length dX_i along the i-th principle axis turns into the length ${\mathrm{dx}}_{\mathrm{i}}$:

$${\mathrm{dx}}_{\mathrm{i}}=\sqrt{1+2{\mathsf{\epsilon }}_{\mathrm{ii}}{\mathrm{dX}}_{\mathrm{i}}}$$

(17)

The relative elongation along the i-th axis is thus given as:

$$\frac{{\mathrm{dx}}_{\mathrm{i}}-{\mathrm{dX}}_{\mathrm{i}}}{{\mathrm{dX}}_{\mathrm{i}}}=\sqrt{1+2{\mathsf{\epsilon }}_{\mathrm{ii}}}-1$$

(18)

At small strains, the displacements ${\mathrm{u}}_{\mathrm{i}}$ and their derivatives are small. Thus, in the general expression (14) the last term is negligible and can be omitted and the components ${\mathsf{\epsilon }}_{\mathrm{ij}}$ of the strain tensor are determined by the following expression:

$${\mathsf{\epsilon }}_{\mathrm{ij}}=\frac{1}{2}\left(\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+\frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\right)$$

(19)

In this case the relative elongations are thus equal to:

$$\sqrt{1+2{\mathsf{\epsilon }}_{\mathrm{ii}}}-1\approx {\mathsf{\epsilon }}_{\mathrm{ii}}$$

(20)

and given by the eigen values of the strain tensor. Here we can draw three key points:

(1)

The displacement vector determines the strain state;

(2)

The relative displacement vector determines the quantity of strain;

(3)

The second rank strain tensor is a representation of the strain quantity of a particular measure of deformation in a particular coordinate system.

Dislocation slip generates a relative movement of lattice defined by its Burgers vector, b, resulting in a relative displacement vector. In a way similar to the approach adopted by Groves and Kelly [36], the simple shear deformation due to dislocation slip can be expressed by a strain tensor with more than one non-zero strain components. Figure 4 shows a plane on which slip occurs. A general point P is moved to position P′ by the slip. The vectors from the origin to P and P′ are r and r′ respectively. In addition, is the unit vector n normal to the plane, and b perpendicular to the plane from O. The length of the perpendicular from O to the plane is simply r·n. Unit vector n has components of n₁, n₂, n₃, and r has components of x₁, x₂, x₃. For a strain γ(r⋅n) due to dislocation slip, the relative displacement vector that represents the slip is then given by,

$$r^{\prime }-r=\mathrm{g}\left(r·n\right)b$$

(21)

where b is a unit vector in the direction of slip and has components of b₁, b₂ and b₃. The displacement vector u can be written as

$$u=u_0+\mathrm{d}u=u_0+\mathsf{\gamma }\left(r·n\right)b$$

(22)

If the strain angle γ is small, the components of the strain tensor ${\mathsf{\epsilon }}_{\mathrm{ij}}$ can be obtained according to Equation (19) as below

$${\mathsf{\epsilon }}_{\mathrm{ij}}=\frac{1}{2}\left(\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}+\frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{i}}}\right)=\frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}=\frac{1}{2}\left(\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}\mathsf{\gamma }\left(r·n\right){\mathrm{b}}_{\mathrm{i}}+\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}}\mathrm{L}\left(r·n\right){\mathrm{b}}_{\mathrm{j}}\right)$$

(23)

Hence, for example,

$$\begin{gathered} {\mathsf{\epsilon }}_{12}=\frac{1}{2}\left(\frac{\partial {\mathrm{u}}_1}{\partial {\mathrm{x}}_2}+\frac{\partial {\mathrm{u}}_2}{\partial {\mathrm{x}}_1}\right)=\frac{1}{2}\frac{\partial }{\partial {\mathrm{x}}_2}\mathsf{\gamma }\left(r·n\right){\mathrm{b}}_1+\frac{1}{2}\frac{\partial }{\partial {\mathrm{x}}_1}\mathsf{\gamma }\left(r·n\right){\mathrm{b}}_2 \\ =\frac{1}{2}{\mathsf{\gamma }\mathrm{b}}_1\frac{\partial }{\partial {\mathrm{x}}_2}\left({\mathrm{x}}_1{\mathrm{n}}_1+{\mathrm{x}}_2{\mathrm{n}}_2+{\mathrm{x}}_3{\mathrm{n}}_3\right)+\frac{1}{2}{\mathsf{\gamma }\mathrm{b}}_2\frac{\partial }{\partial {\mathrm{x}}_1}\left({\mathrm{x}}_1{\mathrm{n}}_1+{\mathrm{x}}_2{\mathrm{n}}_2+{\mathrm{x}}_3{\mathrm{n}}_3\right) \\ =\frac{1}{2}\mathsf{\gamma }\left({\mathrm{n}}_2{\mathrm{b}}_1+{\mathrm{n}}_1{\mathrm{b}}_2\right) \end{gathered}$$

(24)

We can then write the strain tensor like this,

$${\mathsf{\epsilon }}_{\mathrm{ij}}=\mathsf{\gamma }\left[\begin{array}{c}{\mathrm{n}}_1{\mathrm{b}}_1 \frac{1}{2}({\mathrm{n}}_2{\mathrm{b}}_1+{\mathrm{n}}_1{\mathrm{b}}_2) \frac{1}{2}({\mathrm{n}}_3{\mathrm{b}}_1+{\mathrm{n}}_1{\mathrm{b}}_3)\\ \frac{1}{2}({\mathrm{n}}_1{\mathrm{b}}_2+{\mathrm{n}}_2{\mathrm{b}}_1) {\mathrm{n}}_2{\mathrm{b}}_2 \frac{1}{2}({\mathrm{n}}_3{\mathrm{b}}_2+{\mathrm{n}}_2{\mathrm{b}}_3)\\ \frac{1}{2}({\mathrm{n}}_1{\mathrm{b}}_3+{\mathrm{n}}_3{\mathrm{b}}_1) \frac{1}{2}({\mathrm{n}}_2{\mathrm{b}}_3+{\mathrm{n}}_3{\mathrm{b}}_2) {\mathrm{n}}_3{\mathrm{b}}_3\end{array}\right]$$

(25)

For multiple slip in general, an individual strain tensor component is the sum of contributions from all active slip systems.

$${\mathsf{\epsilon }}_{\mathrm{ij}}={\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{q}}}{\mathsf{\gamma }}^{\mathrm{k}}\left({\mathrm{n}}_{\mathrm{i}}^{\mathrm{k}}{\mathrm{b}}_{\mathrm{j}}^{\mathrm{k}}+{\mathrm{n}}_{\mathrm{j}}^{\mathrm{k}}{\mathrm{b}}_{\mathrm{i}}^{\mathrm{k}}\right)/2$$

(26)

where b = (b₁, b₂, b₃) and n = (n₁, n₂, n₃) are the unit vectors representing the slip direction and slip plane normal in the sample coordinate system, and q is the number of active slip systems.

For a more accurate description of the strain tensor components due to the dislocation slip, a parameter describing the rotation should be included. The most important point to demonstrate here, however, is that for a single dislocation slip, n_i and b_i are non-zero by definition in general (except one situation where the chosen coordinate system is coincident with n and b) and the strain tensor has at least three non-zero components of ε_ii. It is clear that the quantity of strain due to dislocation slip is described by a strain tensor rather than a strain tensor component, and that the number of independent strain tensor components is irrelevant to the number of slip systems in operation.

6. Independent Slip Systems Required for Compatible Deformation and Their Selection

As a matter of fact, every single slip system can physically operate without requiring the involvement of other slip systems and the amount of slip on any particular system is independent of other systems. In this sense, all individual slip systems are independent. This independency is important as it implies that a strain can result from any arbitrary combination of slip from the slip systems involved. In terms of performing compatible deformation, the linear independency of slip systems should be defined in their Burgers vector space. According to the theory of linear algebra, any three non-zero vectors are linearly dependent if and only if they are coplanar. In other words, a set of three non-coplanar vectors are linearly independent. In a three-dimensional space as it is in the plastic deformation of crystalline material, there are only three linearly independent vectors. Any four or more slip systems, in terms of their contribution to plastic deformation, are linearly dependent and it is impossible to have five linearly independent slip systems running simultaneously in a three-dimensional space.

It can be simply demonstrated that three linearly independent slip systems (Burgers vectors b₁, b₂ and b₃ satisfy conditions for independency as for general vectors in a three-dimensional space) are essential for compatible deformation because strain accommodation always involves three-dimensional material flow and also sufficient as they can produce any arbitrary amount of relative displacement vector du,

$$\mathrm{d}u={\mathbf{c}}_1{b}_1+{\mathbf{c}}_2{b}_2+{\mathbf{c}}_3{b}_3$$

(27)

where c₁, c₂ and c₃ are constants. The strain state and quantity here are fully defined by the relative displacement vectors. For crystals with only two linearly independent slip systems, such as hcp metals Zn, Mg and alpha-Ti, an extra freedom of deformation is needed. This will be briefly discussed in the following paragraphs. For crystals with more than three equal and independent slip systems, a set of three non-coplanar slip systems will be selected by the system. The selection of three active slip systems, although reduced in numbers, is still an unsolved matter. Fundamental principles of the minimum internal dissipation of maximum work may have to be considered, which is beyond the scope of this review.

It should be noted that the above analysis is not a mathematical verification. It is rather an argument based on mathematical theorems. This is because slip systems are determined by the crystal structure of the material and the collective behaviour of slip systems is not only determined by the stress state but also the microstructure. According to linear algebra, parallel vectors are linearly dependent and equivalent in treatment. However, parallel dislocations may act differently. This is because real material has a structure rather than continuum and strictly speaking, the linear algebra theory is not applicable when the internal structures of material are considered. At the microscopic scale, the structure has its maximum impact and there are occasions where the ductility of material is less sensitive to the amount of slip systems available. For example, fcc metal iridium is brittle and many bcc metals are difficult to deform at low temperature, although they have plenty of independent slip systems, whereas some minerals are deformable when there is only one slip system that can be readily activated [42,43].

As discussed earlier, the selection of active slip systems by minimum internal dissipation and minimum energy or maximum principle is not feasible due to their lack of uniqueness in selection, the inability to consider all combinations of stress and strain from all potentially active slip systems, and the inappropriate adoption of stress “vertices”, which are meaningful only when a stress invariant is considered in the case of the stress octahedron as shown in Figure 2. Both the crystallographic restrictions to multiple slip, in order for individual atoms to follow a low energy path defined by the Burgers vector and for the crystal to maintain its periodicity during deformation and the unavailability of a stress state that provides an equal resolved shear stress to multiple slip systems, suggest that only one slip system can be activated at a time in a grain or a particular volume.

The activation of slip systems is a function of their orientation relative to the imposed macroscopic stress state and therefore, Schmid’s law has to be applied, which defines explicitly the condition as to when a slip system can be activated. Since both the crystallographic periodicity and the nature of stress state as discussed above suggest that only one slip system operates at a time, it is feasible to apply Schmid’s law. Now, strain accommodation with the involvement of three independent slip systems must be considered occurring among grains or characteristic domains, instead of at each point of the deforming body. It has been long recognised that plastic deformation in polycrystals is heterogeneous and governed by the interplay between intra-granular slip and grain boundary-mediated plasticity [6,44,45]. During deformation, grains are subdivided into domains characterized by different orientations [46,47,48]. This grain splitting is described with specific terminology as deformation bands and transition bands, etc [49]. Geometrical necessary dislocations are often generated to accommodate strain gradient over a range of scales [50,51,52]. Within each characteristic domain, the orientation is substantially the same and it has to be one slip system in operation at one time in the domain during deformation. However, the dominant slip system can change due to unequal hardening among slip systems. In an in situ study of tensile deformation of an Al—Mg—Si aluminum alloy by P. Chen et al. [41], the lattice rotation behaviour obtained from the EBSD data showed that at a moment there is one dominant slip in a grain and it was always the grain with the greatest Schmid factor that was active. In this in situ study, rotation path change was observed in grains in which there is a slip system which has a Schmid factor close to the greatest value, whereas grains with an outstanding Schmid factor tended to undergo a single rotation path. In an extensive study to determine the active slip systems during tensile deformation in pure aluminum and copper, Wither and co-workers were able to directly measure the lattice rotations for a large number of grains in the bulk of the samples using a three-dimensional X-ray diffraction technique [29,30,31]. The spread of individual diffraction peaks was often in the form of weak tails trailing behind the main spot along the rotation direction and the rotation paths in general were smooth with a single path (up to ~6% elongation), indicating a relatively uniform behaviour of each individual grain and single slip domination. More than one slip system involvement would result in multiple rotation paths and complicated diffraction peaks. They found that grain orientation was the primary parameter controlling the slip systems, leading to grain-orientation dependence of lattice rotations and dislocation structures, and that the highest Schmid factors controlled the selection of the most active slip system, which was reflected in systematic variations in lattice rotations among grains and dislocation structures within each region. In other circumstances where the orientation becomes unstable, such as a cube-textured grain during plane strain compression, constant changes of the active slip system can take place and the orientation spread within the grain is scattered without a clear rotation path [46,53]. It is interesting to notice that Mg alloys can exhibit respectable ductility in the range of 15–25% at room temperature without involving non-basal slip, despite only having two independent basal slip systems. An investigation on the deformation accommodation in an AZ31 Mg alloy showed that deformation was significantly heterogeneous from inside grain-to-grain boundaries and basal slip is responsible for both uniform deformation inside grain and highly strained grain boundary areas [32]. This suggests that the third dimension strain accommodation can be provided by adjacent grains or domains of different orientations, and by other mechanisms such as the twinning and lattice rotation, which may have added an extra dimension to slip, in addition to grain boundary shear, sliding and rotation.

7. Summary Remarks

The von Mises criterion for compatible deformation of polycrystalline materials and the extended Taylor–Bishop–Hill theory represent a pioneering scientific approach in attempting to connect material response in the form of plastic deformation to external stress in continuum mechanics to the atomic mechanism–dislocation slip responsible for the deformation under the applied stress. Effectively, they define the laws of plastic deformation of polycrystalline aggregates, in conjunction with the theories of yield and are key cornerstones of the crystal plasticity theory. However, there are intrinsic flaws in these theories, which are inevitable because the scientific foundation of the connection does not exist; dislocation slip describes the crystal structure and the microstructure-related atomic behaviour under stress, whereas the plastic deformation theory in continuum mechanics disregards internal structures. These flaws must be taken into account in the applications of the von Mises criterion and Taylor—Bishop—Hill theory for predicting deformation behaviour and texture development, etc. Firstly, the correlation between the slip and strain tensor components is invalid both physically and dimensionally. A strain state at a point is a physical quantity that is independent of any particular coordinate system representation, but strain components represented by a symmetric second-order tensor depend on the selected coordinate system. There are an unlimited number of independent components sets. Dislocation slip leads to a relative movement of atoms and contributes to the relative displacement vector in deformation rather than a single component of a strain tensor. Secondly, the selection of active slip systems by the minimum internal dissipation or the minimum energy consumption principle is practically unfeasible due to its non-uniqueness in the determination of the actual slip systems in operation and oversimplification in the calculation of possible combinations of stress and strain. Thirdly, although the von Mises criterion and the Taylor—Bishop—Hill theory have conceptual significance in understanding the relationship between macroscopic plastic deformation and microstructural behaviour of material, the requirement set out for compatible deformation is neither sufficient nor essential as the availability of active slip systems does not guarantee ductility. In contrast to the requirement for five independent slip systems for compatible deformation by the von Mises criterion, an argument is made in this review that three independent slip systems are essential for compatible deformation because strain accommodation always involves three-dimensional material flow, and they are also sufficient as they can produce any arbitrary amount of relative displacement vector. Certainly, this argument is made in the realm of continuum mechanics. Crystal structure and microstructure determine the plastic deformation behaviour in polycrystalline materials. The analysis of crystallographic restrictions for multi-slip and of the nature of stress state, i.e., at a given point there is only one stress state at a time and each stress component is a continuous and smooth function of the rotation matrix and there are no stress vertices at any point, suggests that there can only be one slip system in operation at one time in a volume of a certain orientation, which can be a grain or a characteristic domain. Schmid’s law determines which slip system is activated, which is supported by extensive investigations. Strain accommodation has to occur among grains or characteristic domains to maintain the compatibility of the material in deformation.