Using First-Principles Calculations to Investigate the Interfacial Properties of Ni(100)/Ni3Al(100) Eutectic Structures
Abstract
1. Introduction
2. Computational Method
3. Results and Discussion
3.1. Bulk Properties of Ni and Ni3Al
3.2. Surface Convergence
3.3. Surface Stability of Ni3Al Surfaces
4. Interfacial Properties
4.1. Atomic Structures of the Ni/Ni3Al Eutectic Interface
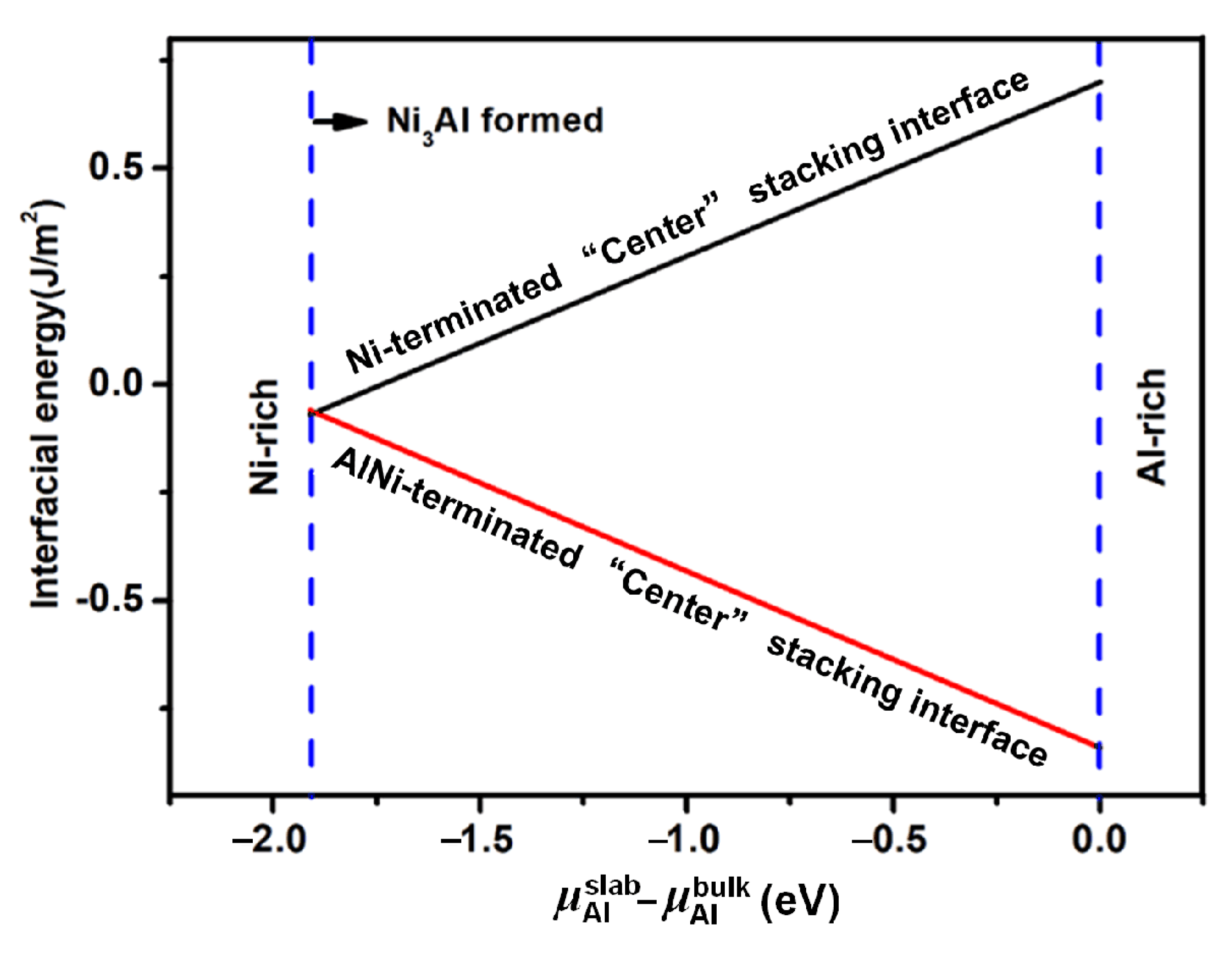
4.2. Interfacial Stability
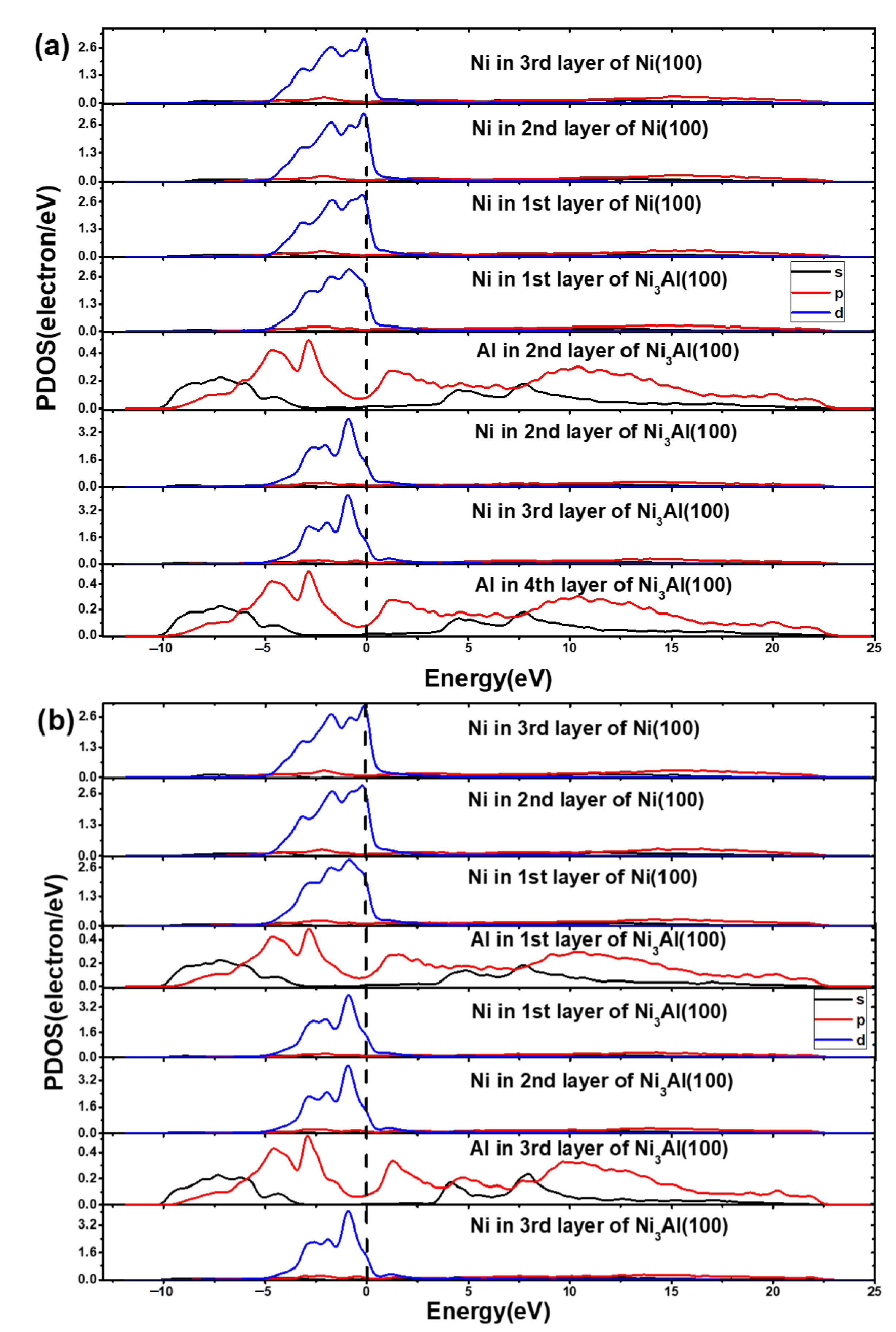
4.3. Electronic Structure
5. Conclusions
- A nine-layered Ni(100) slab and a nine-layered Ni3Al(100) slab with AlNi termination and Ni termination were utilized to establish six different interface models of Ni(100)/Ni3Al(100) eutectic structures, namely, Ni-terminated and AlNi-terminated “Top” site stacking interface, Ni-terminated and AlNi-terminated “Bridge” site stacking interface, and Ni-terminated and AlNi-terminated “Center” site stacking interface configurations.
- The AlNi-terminated “Center” site stacking interface model of the Ni(100)/Ni3Al(100) eutectic structure was determined to be the most stable interfacial configuration from a comprehensive analysis of the adhesion work, interfacial energy and electronic structures.
- The PDOS and charge density difference indicated the combined bonding characteristics of covalent and metallic bonds at the interface of the AlNi-terminated and “Center” site stacking interface of the Ni(100)/Ni3Al(100) eutectic structure, which had a higher stability than the Ni-terminated and “Center” site stacking interfacial model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, H.S.; Xiong, H.P.; Long, W.M.; Chen, B.; Shen, Y.X.; Pang, S.J. Microstructures and mechanical properties of Ti3Al/Ni-based superalloy joints brazed with AuNi filler metal. J. Mater. Sci. Technol. 2019, 35, 2070–2078. [Google Scholar] [CrossRef]
- Wang, H.F.; Su, H.J.; Zhang, J.; Zhang, Y.B.; Yue, Q.Z.; Liu, L.; Huang, T.W.; Yang, W.C.; Fu, H.Z. Investigation on solidification path of Ni-based single crystal superalloys with different Ru contents. Mater. Charact. 2017, 130, 211–218. [Google Scholar] [CrossRef]
- Cheng, G.P.; He, Y.Z. Two phase matrix of Ni3Al and γ-Ni coatings prepared by laser cladding. Appl. Mech. Mater. 2011, 66–68, 2005–2009. [Google Scholar] [CrossRef]
- Wilson, B.C.; Cutler, E.R.; Fuchs, G.E. Effect of solidification parameters on the microstructures and properties of CMSX-10. Mater. Sci. Eng. A 2008, 479, 356–364. [Google Scholar] [CrossRef]
- Wang, F.; Ma, D.; Zhang, J.; Lin, L.; Bogner, S.; Polaczek, A.B. Effect of local cooling rates on the microstructures of single crystal CMSX-6 superalloy: A comparative assessment of the Bridgman and the downward directional solidification processes. J. Alloys Compd. 2014, 616, 102–109. [Google Scholar] [CrossRef]
- Wang, F.; Ma, D.; Zhang, J.; Bogner, S.; Polaczek, A.B. Solidification behavior of a Ni-based single crystal CMSX-4 superalloy solidified by downward directional solidification process. Mater. Charact. 2015, 101, 20–25. [Google Scholar] [CrossRef]
- Liu, G.; Liu, L.; Ai, C.; Ge, B.M.; Zhang, J.; Fu, H.Z. Influence of withdrawal rate on the microstructure of Ni-base single-crystal superalloys containing Re and Ru. J. Alloys Compd. 2011, 509, 5866–5872. [Google Scholar] [CrossRef]
- Qin, S.Y.; Hao, J.Q.; Yan, L.G.; Zhang, X.F. Ultrafast solution treatment to improve the comprehensive mechanical properties of superalloy by pulsed electric current. Scripta Mater. 2021, 199, 113879. [Google Scholar] [CrossRef]
- Sheffler, K.D.; Barkalow, R.H.; Yuen, A.; Leverant, G.R. The anisotropy of deformation and fracture in a directionally solidified Ni/Ni3Al-Ni3Cb lamellar eutectic alloy. Metall. Trans. A 1977, 8, 83–89. [Google Scholar] [CrossRef]
- Wang, F.; Ma, D.; Polaczek, A.B. Preferred growth orientation and microsegregation behaviors of eutectic in nickel-based single-crystal superalloy. Sci. Technol. Adv. Mater. 2015, 16, 025004. [Google Scholar] [CrossRef]
- Chen, D.; Ma, X.L.; Wang, Y.M. First-principles study of the interfacial structures of Au/MgO(001). Phys. Rev. B 2007, 75, 125409. [Google Scholar] [CrossRef]
- Yang, Q.G.; Lu, C.; Han, Y.; Chen, X.H.; Yang, J.; Huang, J.H.; Chen, S.H.; Ye, Z. Influence of Cu/W interfacial structure on the resistance against harmful helium atoms: A mechanism analysis. J. Alloys Compd. 2022, 903, 163817. [Google Scholar] [CrossRef]
- Peng, P.; Zhou, D.W.; Liu, J.S.; Yang, R.; Hu, Z.Q. First-principles study of the properties of Ni/Ni3Al interface doped with B or P. Mater. Sci. Eng. A 2006, 416, 169–175. [Google Scholar] [CrossRef]
- Gong, X.F.; Yang, G.X.; Fu, Y.H.; Xie, Y.Q.; Zhuang, J.; Ning, X.J. First-principles study of Ni/Ni3Al interface strengthening by alloying elements. Compt. Mater. Sci. 2009, 47, 320–325. [Google Scholar] [CrossRef]
- Wu, Y.X.; Zhang, W.L.; Guo, J.; Hou, J.S.; Li, X.Y.; Huang, R.Z.; Ma, X.F.; Zhang, Q.F. The first-principles study on the occupation behavior and the ductility mechanism of Zr in Ni-Ni3Al system with lattice misfit. J. Mater. Sci. Technol. 2014, 30, 517–522. [Google Scholar] [CrossRef]
- Wen, Q.H.; Wang, M.X.; Kong, L.T.; Zhu, H. Effects of alloying elements on the Ni/Ni3Al interface strength and vacancy diffusion behavior. J. Appl. Phys. 2020, 128, 175307. [Google Scholar] [CrossRef]
- Ahmed, F.A.; Xue, H.T.; Tang, F.L.; An, J.P.; Luo, Y.Q.; Lu, X.F.; Ren, J.Q. Segregation of alloying elements and their effects on the thermodynamic stability and fracture strength of γ-Ni/γ’-Ni3Al interface. J. Mater. Sci. 2020, 55, 12513–12524. [Google Scholar] [CrossRef]
- Yang, T.X.; Wei, M.Z.; Ding, Z.Y.; Han, X.J.; Li, J.G. Ab initio calculations on the Mg/TiN heterogeneous nucleation interface. J. Phys. Chem. Solids 2020, 143, 109479. [Google Scholar] [CrossRef]
- Yang, T.X.; Chen, X.H.; Li, W.; Han, X.J.; Liu, P. First-principles calculations to investigate the interfacial energy and electronic properties of Mg/AlN interface. J. Phys. Chem. Solids 2022, 167, 110705. [Google Scholar] [CrossRef]
- Woodward, C.; Walle, A.; Asta, M.; Trinkle, D.R. First-principles study of interfacial boundaries in Ni-Ni3Al. Acta Mater. 2014, 75, 60–70. [Google Scholar] [CrossRef]
- Wang, C.; Wang, C.Y. Ni/Ni3Al interface: A density functional theory study. Appl. Surf. Sci. 2009, 255, 3669–3675. [Google Scholar] [CrossRef]
- Kayser, F.X.; Stassis, C. The elastic constants of Ni3Al at 0 and 23.5 °C. Phys. Status Solidi A 1981, 64, 335–342. [Google Scholar] [CrossRef]
- Wu, Q.; Li, S.S. Alloying element additions to Ni3Al: Site preferences and effects on elastic properties from first-principles calculations. Compt. Mater. Sci. 2012, 53, 436–443. [Google Scholar] [CrossRef]
- Fiorentini, V.; Methfessel, M. Extracting convergent surface energies from slab calculations. J. Phys. Condens. Matter 1999, 8, 6525. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, J.T.; Zhang, X.X.; Yang, P.; Ren, J.Q.; Lu, X.F. Effect of alloying elements on the interface of fcc-Fe/Ni3Al by first principle calculations. Comp. Mater. Sci. 2022, 214, 111673. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Zhou, Y. First-principles study of Al/Al3Ti heterogeneous nucleation interface. Appl. Surf. Sci. 2014, 307, 593–600. [Google Scholar] [CrossRef]
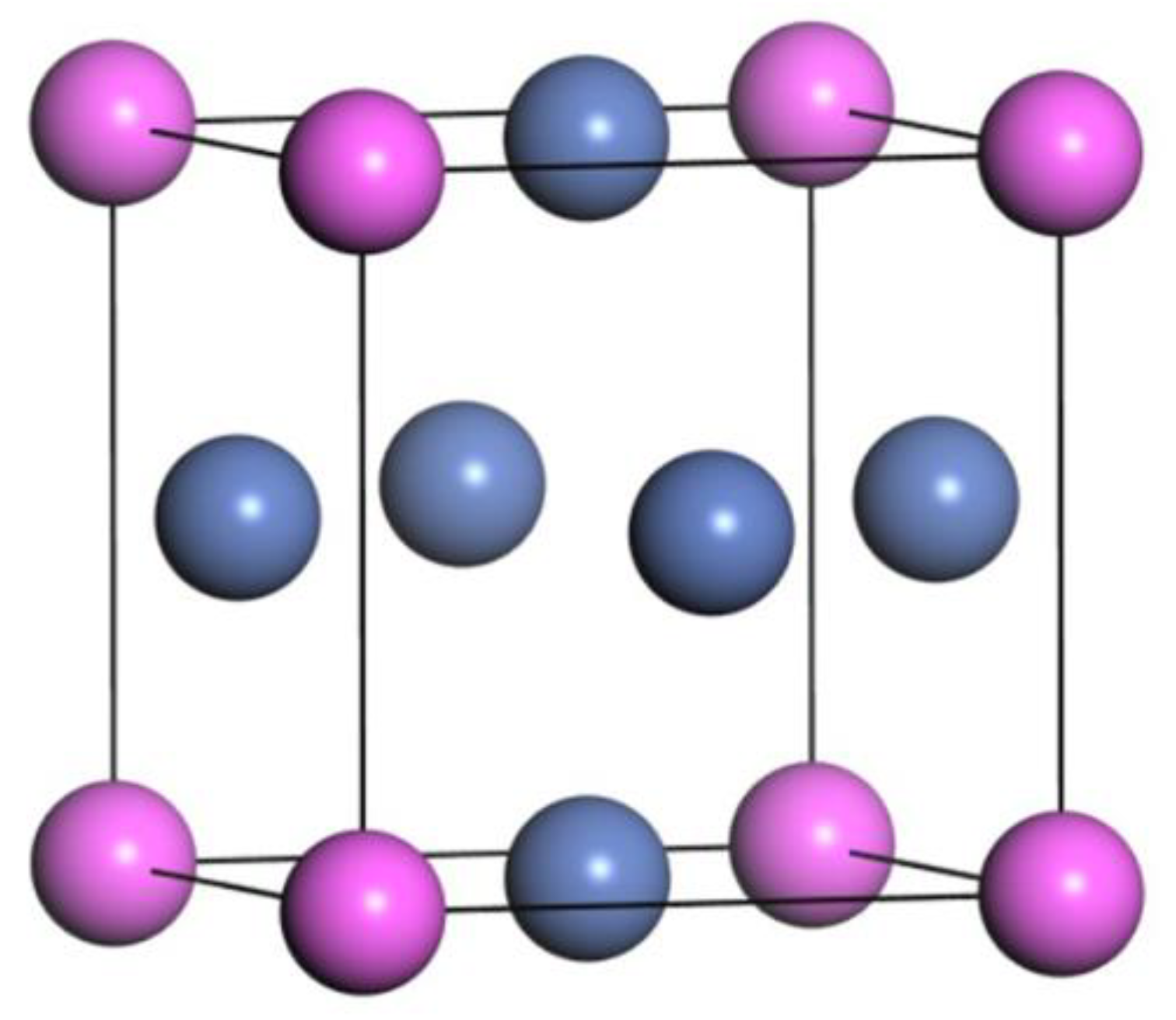



| a(Å) | C11(GPa) | C12(GPa) | C44(GPa) | B(GPa) | ||
|---|---|---|---|---|---|---|
| Ni | PBE | 3.529 | 283.78 | 178.75 | 110.95 | 203.76 |
| Exp. [20] | 3.524 | 248.1 | 154.9 | 124.2 | 186 | |
| Cal. [21] | 3.526 | 303.4 | 205.7 | 136.3 | 196.8 | |
| Ni3Al | PBE | 3.577 | 240.14 | 153.89 | 124.59 | 182.64 |
| Exp. [22] | 3.567 | 224.5 | 148.6 | 124.4 | 173.9 | |
| DFT [23] | 3.58 | 243.8 | 148.7 | 123.4 | 182.4 [21] |
| Atomic Layer (n) | Surface Energy (J/m2) | |
|---|---|---|
| Ni (100) | 3 | 2.24 |
| 5 | 2.22 | |
| 7 | 2.21 | |
| 9 | 2.20 | |
| 11 | 2.19 |
| Termination | Interlayer | Slab Thickness | ||||
|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 9 | 11 | ||
| Ni termination | Δ12 | −3.93% | −4.14% | −4.25% | −4.32% | −4.24% |
| Δ23 | 0.02% | −0.04% | −0.56% | −0.55% | ||
| Δ34 | 0.05% | −0.39% | −0.45% | |||
| Δ45 | −0.64% | −0.75% | ||||
| Δ56 | −0.003% | |||||
| AlNi termination | Δ12 | −3.22% | −3.02% | −3.08% | −3.02% | −3.02% |
| Δ23 | −0.21% | −0.44% | −0.39% | −0.39% | ||
| Δ34 | −0.36% | −0.31% | −0.26% | |||
| Δ45 | 0.03% | 0.02% | ||||
| Δ56 | 0.04% | |||||
| Termination | Stacking | Fully Relaxed | |
|---|---|---|---|
| d0(Å) | Wad(J/m2) | ||
| Ni termination | Top | 2.30 | 2.36 |
| Bridge | 2.05 | 3.19 | |
| Center | 1.73 | 4.34 | |
| AlNi termination | Top | 2.33 | 2.26 |
| Bridge | 2.1 | 3.03 | |
| Center | 1.78 | 4.15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Long, W.; Jiu, Y.; Yang, T.; Zhong, S.; Yang, J.; Fu, W.; Qiao, J. Using First-Principles Calculations to Investigate the Interfacial Properties of Ni(100)/Ni3Al(100) Eutectic Structures. Crystals 2023, 13, 199. https://doi.org/10.3390/cryst13020199
Ding Z, Long W, Jiu Y, Yang T, Zhong S, Yang J, Fu W, Qiao J. Using First-Principles Calculations to Investigate the Interfacial Properties of Ni(100)/Ni3Al(100) Eutectic Structures. Crystals. 2023; 13(2):199. https://doi.org/10.3390/cryst13020199
Chicago/Turabian StyleDing, Zongye, Weimin Long, Yongtao Jiu, Tianxing Yang, Sujuan Zhong, Jingwei Yang, Weijie Fu, and Jian Qiao. 2023. "Using First-Principles Calculations to Investigate the Interfacial Properties of Ni(100)/Ni3Al(100) Eutectic Structures" Crystals 13, no. 2: 199. https://doi.org/10.3390/cryst13020199
APA StyleDing, Z., Long, W., Jiu, Y., Yang, T., Zhong, S., Yang, J., Fu, W., & Qiao, J. (2023). Using First-Principles Calculations to Investigate the Interfacial Properties of Ni(100)/Ni3Al(100) Eutectic Structures. Crystals, 13(2), 199. https://doi.org/10.3390/cryst13020199






