Dynamic Analysis of Multilayered Piezoelectric Quasicrystal Three-Dimensional Sector Plates with Imperfect Interfaces
Abstract
:1. Introduction
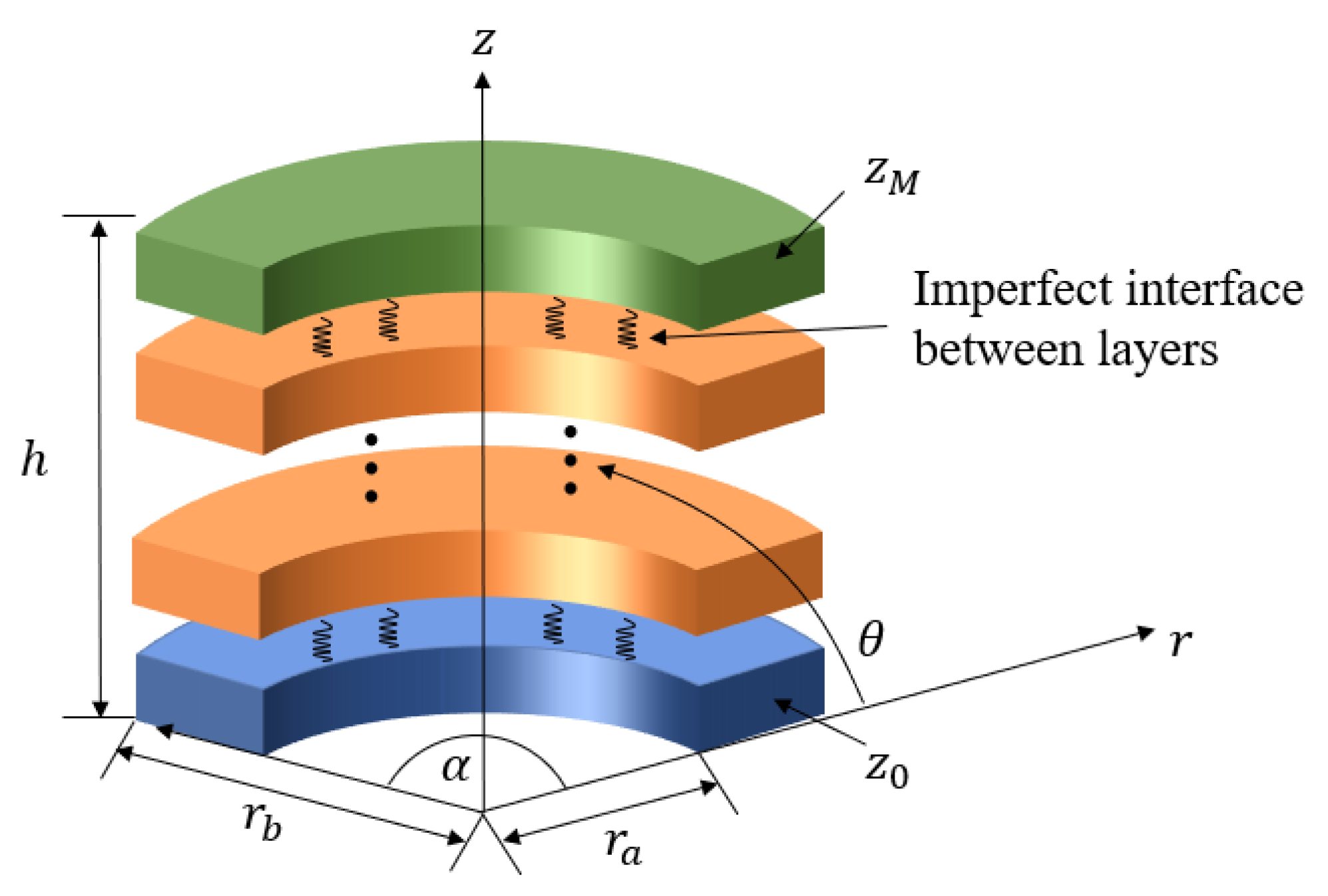
2. Problem Description
2.1. Basic Equations
2.2. State Equations of a Homogeneous QC Sector Plate Layer
3. General Solutions for a 2D QC Sector Plate
4. Analysis of Imperfect Conductive Interfaces
5. Numerical Examples
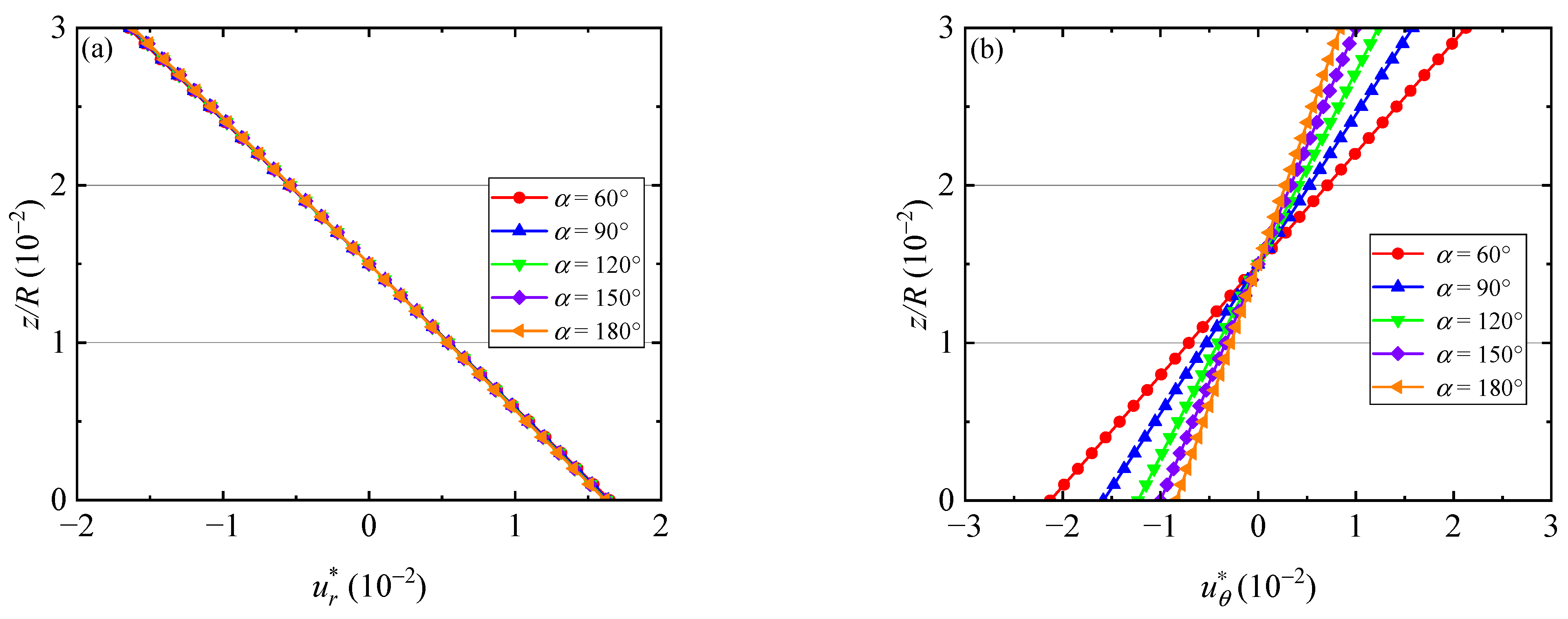
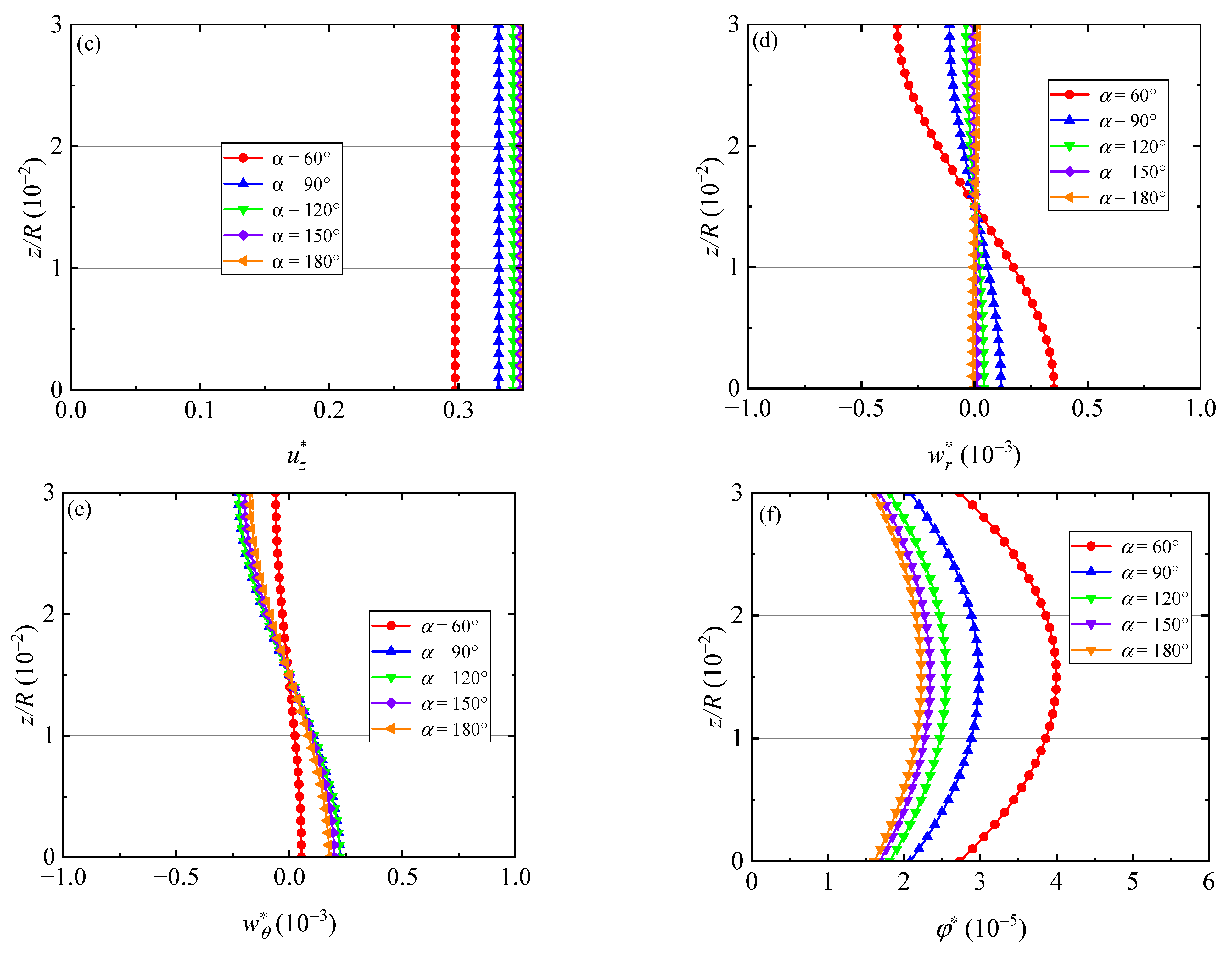
5.1. Effect of Different Angle Spans
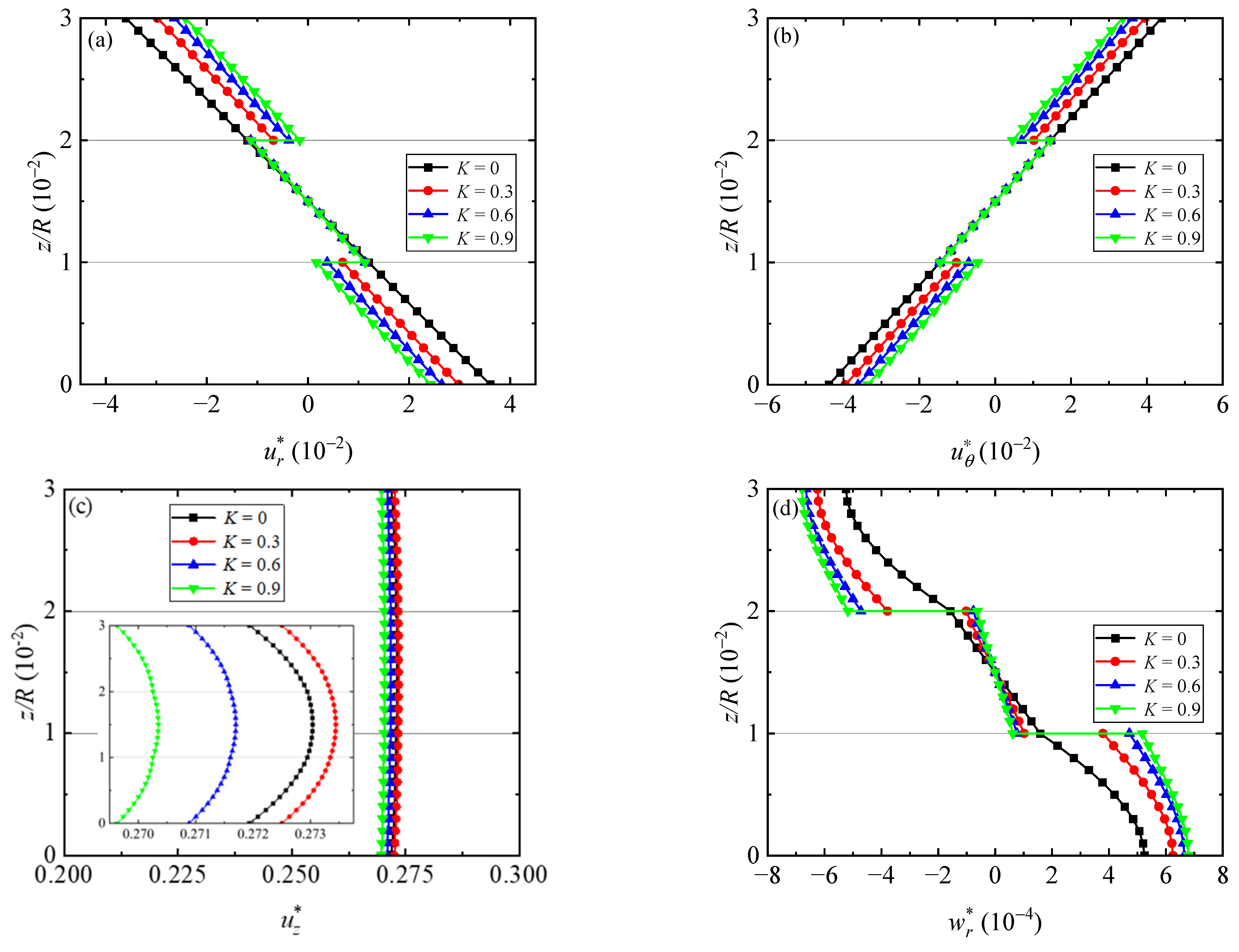
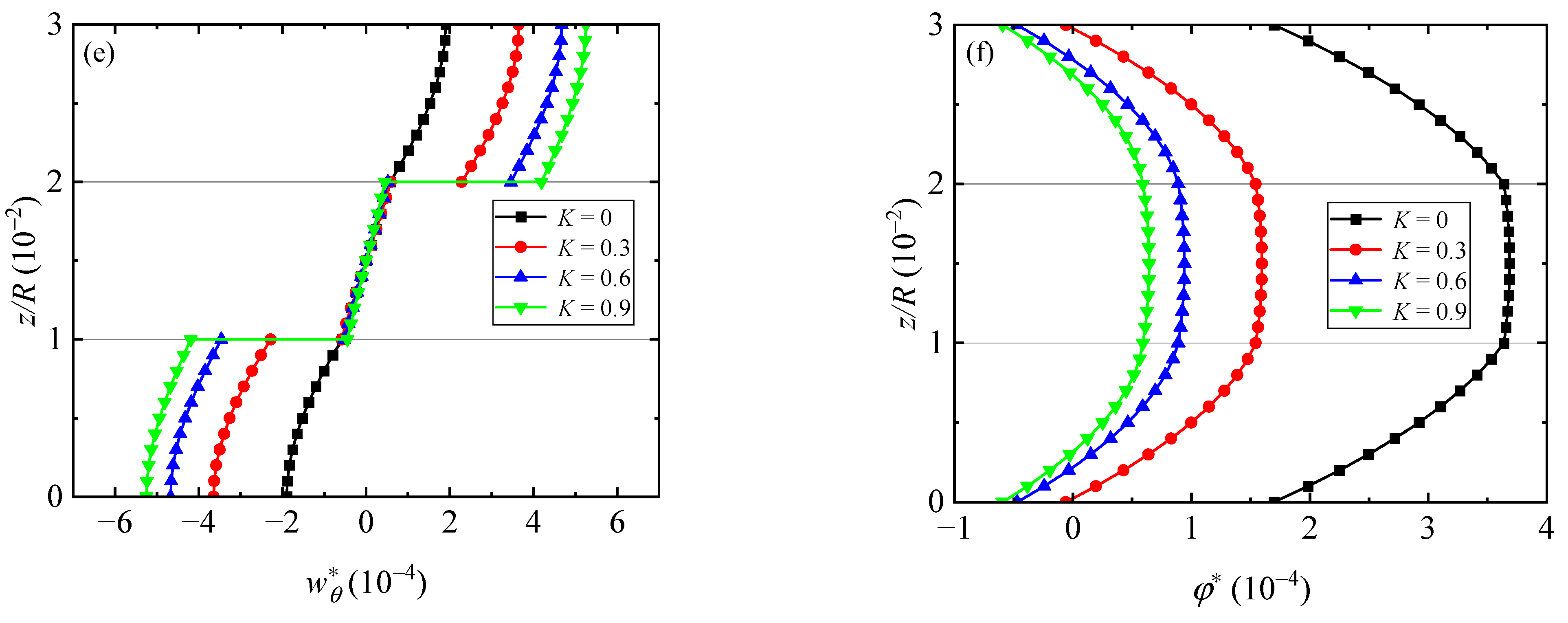
5.2. Effect of Different Interface Compliances
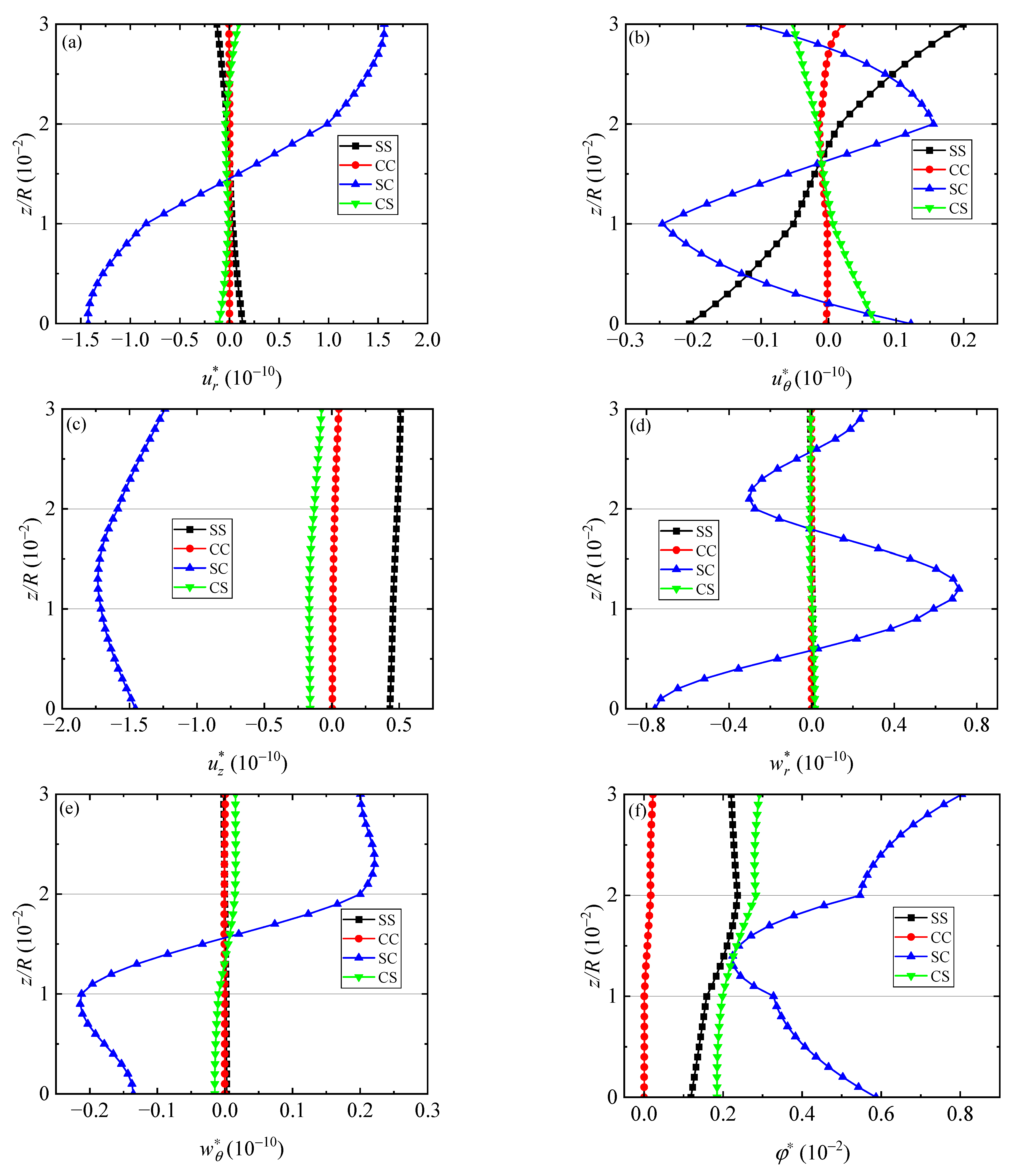
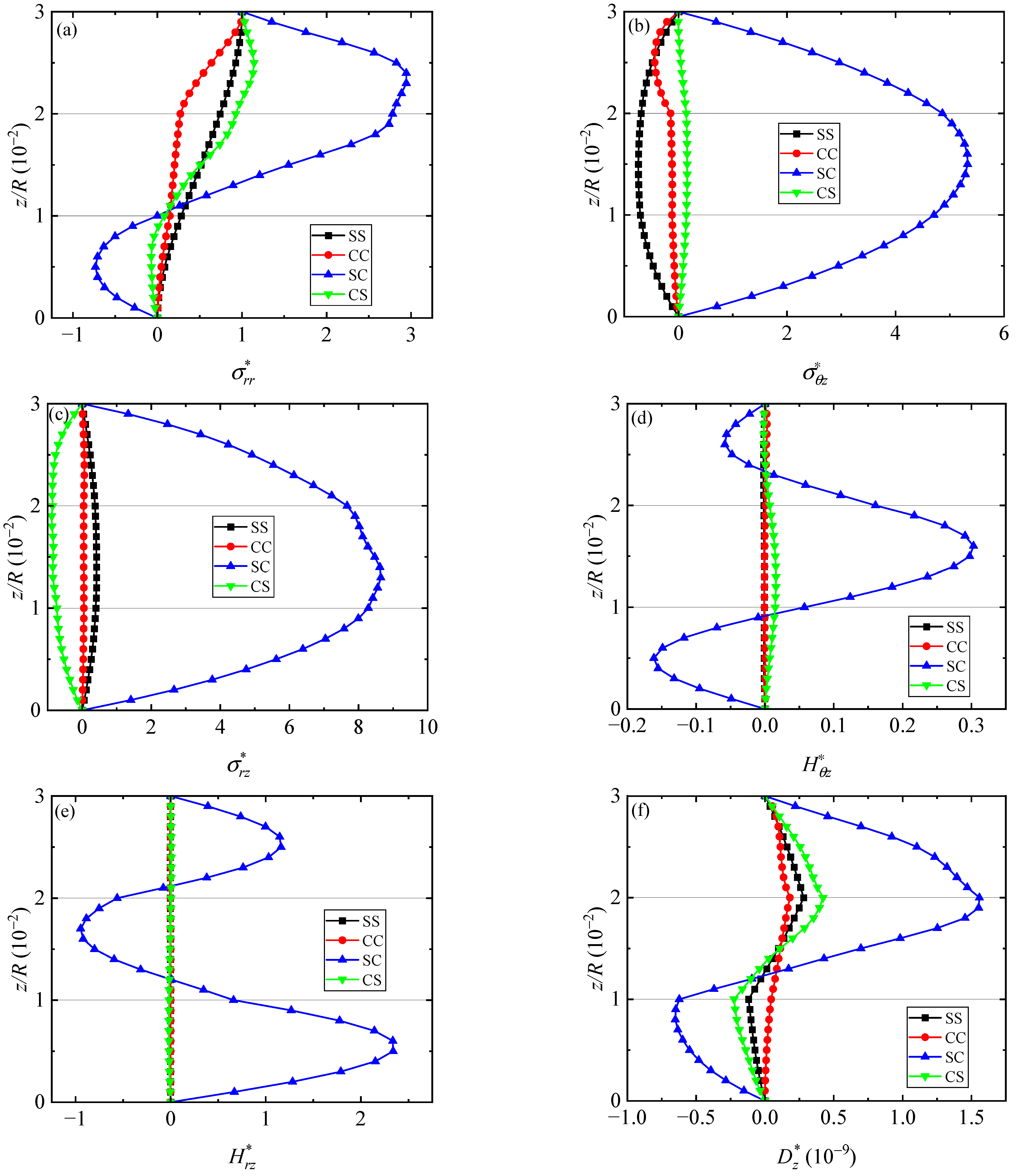
5.3. Effect of Different Boundary Conditions
6. Summary
- The variation of the sector angle α changes the stiffness of laminated QC sector plates, and consequently, it results in different modes for different α;
- An increase in interface compliance will reduce the stiffness and strength of the laminated QC sector plate, and the displacements in the r- and θ-directions (in addition to ) are discontinuous from one layer to the other due to the interface imperfection;
- Out of all the boundary conditions, the impacts of simply supported and clamped boundary conditions on field variables are notably distinct. The mixed case where one side is simply supported and the other is clamped has the most significant effect on the amplitude variation of field variables along the thickness direction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Fan, T.Y.; Guo, Y.C. Mathematical methods for a class of mixed boundary-value problems of planar pentagonal quasicrystal and some solutions. Sci. China Ser. A-Math. 1997, 40, 990–1003. [Google Scholar] [CrossRef]
- Fan, T.Y. Mathematical theory and methods of mechanics of quasicrystalline materials. Engineering 2013, 5, 407–448. [Google Scholar] [CrossRef]
- Bohra, M.; Pavan, T.M.; Fournee, V.; Mandal, R.K. Growth, structure and thermal stability of quasicrystalline Al-Pd-Mn-Ga thin films. Appl. Surf. Sci. 2020, 505, 4. [Google Scholar] [CrossRef]
- Shi, N.C.; Min, L.Q.; Shen, B.M. The configuration of quasi-crystal unit-cell and deduction of quasi-lattice. Sci. China Ser. B-Chem. 1992, 35, 735–744. [Google Scholar]
- Dubois, J.M. Properties- and applications of quasicrystals and complex metallic alloys. Chem. Soc. Rev. 2012, 41, 6760–6777. [Google Scholar] [CrossRef]
- Fujiwara, T.; Ishii, Y. Introduction to quasicrystals. In Quasicrystals; Fujiwara, T., Ishii, Y., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2008; pp. 1–9. [Google Scholar]
- Bak, P. Phenomenological theory of icosahedral incommensurate (quasiperiodic) order in Mn-Al alloys. Phys. Rev. Lett. 1985, 54, 1517–1519. [Google Scholar] [CrossRef]
- Lubensky, T.C.; Ramaswamy, S.; Toner, J. Dislocation motion in quasicrystals and implication for macroscopic properties. Phys. Rev. B 1986, 33, 7715–7719. [Google Scholar] [CrossRef] [PubMed]
- Lubensky, T.; Ramaswamy, S.; Toner, J. Hydrodynamics of icosahedral quasicrystals. Phys. Rev. B 1985, 32, 7444. [Google Scholar] [CrossRef]
- Bak, P. Symmetry, stability, and elastic properties of icosahedral incommensurate crystals. Phys. Rev. B 1985, 32, 5764. [Google Scholar] [CrossRef]
- Ding, D.H.; Yang, W.G.; Hu, C.Z.; Wang, R. Generalized elasticity theory of quasicrystals. Phys. Rev. B 1993, 48, 7003–7010. [Google Scholar] [CrossRef] [PubMed]
- Agiasofitou, E.; Lazar, M. On the equations of motion of dislocations in quasicrystals. Mech. Res. Commun. 2014, 57, 27–33. [Google Scholar] [CrossRef]
- Fan, T.; Wang, X.; Li, W.; Zhu, A.Y. Elasto-hydrodynamics of quasicrystals. Philos. Mag. 2009, 89, 501–512. [Google Scholar] [CrossRef]
- Rochal, S.; Lorman, V. Anisotropy of acoustic-phonon properties of an icosahedral quasicrystal at high temperature due to phonon-phason coupling. Phys. Rev. B 2000, 62, 874. [Google Scholar] [CrossRef]
- Rochal, S.; Lorman, V. Minimal model of the phonon-phason dynamics in icosahedral quasicrystals and its application to the problem of internal friction in the i-AlPdMn alloy. Phys. Rev. B 2002, 66, 144204. [Google Scholar] [CrossRef]
- Agiasofitou, E.; Lazar, M. The elastodynamic model of wave-telegraph type for quasicrystals. Int. J. Solids Struct. 2014, 51, 923–929. [Google Scholar] [CrossRef]
- Ferreira, T.; De Oliveira, I.L.; Zepon, G.; Bolfarini, C. Rotational outward solidification casting: An innovative single-step process to produce a functionally graded aluminum reinforced with quasicrystal approximant phases. Mater. Des. 2020, 189, 10. [Google Scholar] [CrossRef]
- Li, L.H.; Yun, G.H. Elastic fields around a nanosized elliptic hole in decagonal quasicrystals. Chin. Phys. B 2014, 23, 5. [Google Scholar] [CrossRef]
- Pan, E.; Heyliger, P.R. Free vibrations of simply supported and multilayered magneto-electro-elastic plates. J. Sound Vib. 2002, 252, 429–442. [Google Scholar] [CrossRef]
- Yang, L.Z.; Gao, Y.; Pan, E.; Waksmanski, N. An exact solution for a multilayered two-dimensional decagonal quasicrystal plate. Int. J. Solids Struct. 2014, 51, 1737–1749. [Google Scholar] [CrossRef]
- Guo, J.H.; Liu, G.T. Analytic solutions to problem of elliptic hole with two straight cracks in one-dimensional hexagonal quasicrystals. Appl. Math. Mech. -Engl. Ed. 2008, 29, 485–493. [Google Scholar] [CrossRef]
- Guo, J.H.; Zhang, M.; Chen, W.Q.; Zhang, X. Free and forced vibration of layered one-dimensional quasicrystal nanoplates with modified couple-stress effect. Sci. China (Phys. Mech. Astron.) 2020, 63, 124–125. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, J.H.; Xing, Y.M. Bending deformation of multilayered one-dimensional hexagonal piezoelectric quasicrystal nanoplates with nonlocal effect. Int. J. Solids Struct. 2018, 132, 278–302. [Google Scholar] [CrossRef]
- Huang, Y.Z.; Li, Y.; Zhang, L.L.; Zhang, H.; Gao, Y. Dynamic analysis of a multilayered piezoelectric two-dimensional quasicrystal cylindrical shell filled with compressible fluid using the state-space approach. Acta Mech. 2020, 231, 2351–2368. [Google Scholar] [CrossRef]
- Li, X.F. Elastohydrodynamic problems in quasicrystal elasticity theory and wave propagation. Philos. Mag. 2013, 93, 1500–1519. [Google Scholar] [CrossRef]
- Pan, E.; Han, F. Exact solution for functionally graded and layered magneto-electro-elastic plates. Int. J. Eng. Sci. 2005, 43, 321–339. [Google Scholar] [CrossRef]
- Guo, J.H.; Chen, J.Y.; Pan, E. A three-dimensional size-dependent layered model for simply-supported and functionally graded magnetoelectroelastic plates. Acta Mech. Solida Sin. 2018, 31, 652–671. [Google Scholar] [CrossRef]
- Lu, C.F.; Lim, C.W.; Chen, W.Q. Exact solutions for free vibrations of functionally graded thick plates on elastic foundations. Mech. Adv. Mater. Struct. 2009, 16, 576–584. [Google Scholar] [CrossRef]
- Ying, J.; Lu, C.F.; Lim, C.W. 3D thermoelasticity solutions for functionally graded thick plates. J. Zhejiang Univ.-Sci. A 2009, 10, 327–336. [Google Scholar] [CrossRef]
- Striz, A.G.; Wang, X.; Bert, C.W. Harmonic differential quadrature method and applications to analysis of structural components. Acta Mech. 1995, 111, 85–94. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lv, C.F.; Bian, Z.G. Free vibration analysis of generally laminated beams via state-space-based differential quadrature. Compos. Struct. 2004, 63, 417–425. [Google Scholar] [CrossRef]
- Lü, C.F.; Chen, W.Q.; Shao, J.W. Semi-analytical three-dimensional elasticity solutions for generally laminated composite plates. Eur. J. Mech.- A/Solids 2008, 27, 899–917. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Chen, W.Q.; Lü, C.F. Semi-analytical solution for orthotropic piezoelectric laminates in cylindrical bending with interfacial imperfections. Compos. Struct. 2010, 92, 1009–1018. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature: A powerful new technique for analysis of composite structures. Compos. Struct. 1997, 39, 179–189. [Google Scholar] [CrossRef]
- Wang, X.; Bert, C.W.; Striz, A.G. Differential quadrature analysis of deflection, buckling, and free-vibration of beams and rectangular plates. Comput. Struct. 1993, 48, 473–479. [Google Scholar] [CrossRef]
- Alibeigloo, A.; Kani, A.M. 3D free vibration analysis of laminated cylindrical shell integrated piezoelectric layers using the differential quadrature method. Appl. Math. Model. 2010, 34, 4123–4137. [Google Scholar] [CrossRef]
- Jang, S.K.; Bert, C.W. Free-vibration of stepped beams—Exact and numerical-solutions. J. Sound Vib. 1989, 130, 342–346. [Google Scholar] [CrossRef]
- Feng, X.; Fan, X.Y.; Li, Y.; Zhang, H.; Zhang, L.; Gao, Y. Static response and free vibration analysis for cubic quasicrystal laminates with imperfect interfaces. Eur. J. Mech.-A/Solids 2021, 90, 104365. [Google Scholar] [CrossRef]
- Botta, F.; Cerri, G. Wave propagation in Reissner-Mindlin piezoelectric coupled cylinder with non-constant electric field through the thickness. Int. J. Solids Struct. 2007, 44, 6201–6219. [Google Scholar] [CrossRef]
- Huang, B.; Kim, H.S. Free-edge interlaminar stress analysis of piezo-bonded composite laminates under symmetric electric excitation. Int. J. Solids Struct. 2014, 51, 1246–1252. [Google Scholar] [CrossRef]
- Khalid, S.; Lee, J.; Kim, H.S. Series solution-based approach for the interlaminar stress analysis of smart composites under thermo-electro-mechanical loading. Mathematics 2022, 10, 15. [Google Scholar] [CrossRef]
- Li, X.Y.; Li, P.D.; Wu, T.H.; Shi, M.X.; Zhu, Z. Three-dimensional fundamental solutions for one-dimensional hexagonal quasicrystal with piezoelectric effect. Phys. Lett. A 2014, 378, 826–834. [Google Scholar] [CrossRef]
- Chen, T.Y. Thermal conduction of a circular inclusion with variable interface parameter. Int. J. Solids Struct. 2001, 38, 3081–3097. [Google Scholar] [CrossRef]
- Fan, H.; Sze, K.Y. A micro-mechanics model for imperfect interface in dielectric materials. Mech. Mater. 2001, 33, 363–370. [Google Scholar] [CrossRef]
- Wang, X.; Pan, E. A moving screw dislocation interacting with an imperfect piezoelectric bimaterial interface. Phys. Status Solidi B-Basic Solid State Phys. 2007, 244, 1940–1956. [Google Scholar] [CrossRef]
- Fan, H.; Wang, G.F. Screw dislocation interacting with imperfect interface. Mech. Mater. 2003, 35, 943–953. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, Z. Three-dimensional solution of smart laminated anisotropic circular cylindrical shells with imperfect bonding. Int. J. Solids Struct. 2003, 40, 5901–5921. [Google Scholar] [CrossRef]
- Benveniste, Y. A general interface model for a three-dimensional curved thin anisotropic interphase between two anisotropic media. J. Mech. Phys. Solids 2006, 54, 708–734. [Google Scholar] [CrossRef]
- Wang, X.; Pan, E.; Roy, A.K. New phenomena concerning a screw dislocation interacting with two imperfect interfaces. J. Mech. Phys. Solids 2007, 55, 2717–2734. [Google Scholar] [CrossRef]
- Kattis, M.A.; Mavroyannis, G. Feeble interfaces in bimaterials. Acta Mech. 2006, 185, 11–29. [Google Scholar] [CrossRef]
- Wang, X.; Pan, E. Exact solutions for simply supported and multilayered piezothermoelastic plates with imperfect interfaces. Open Mech. J. 2007, 1, 1–10. [Google Scholar] [CrossRef]
- Chen, W.Q.; Cai, J.B.; Ye, G.R.; Wang, Y.F. Exact three-dimensional solutions of laminated orthotropic piezoelectric rectangular plates featuring interlaminar bonding imperfections modeled by a general spring layer. Int. J. Solids Struct. 2004, 41, 5247–5263. [Google Scholar] [CrossRef]
- Hwu, C. Anisotropic Elastic Plates; Springer: New York, NY, USA, 2010; pp. 1–673. [Google Scholar]
- Liu, C.; Feng, X.; Li, Y.; Zhang, L.; Gao, Y. Static solution of two-dimensional decagonal piezoelectric quasicrystal laminates with mixed boundary conditions. Mech. Adv. Mater. Struct. 2022, 1–17. [Google Scholar] [CrossRef]

| C11 | C12 | C13 | C33 | C44 | K1 | K2 | K4 | R1 | |
| QC1 | 234.33 | 57.41 | 66.63 | 232.22 | 70.19 | 122 | 24 | 12 | 8.846 |
| QC2 | 166 | 77 | 78 | 162 | 43 | 122 | 24 | 12 | 8.846 |
| e15 | e31 | e33 | ξ11 | ξ22 | ξ33 | d112 | ρ | ||
| QC1 | 5.8 | −2.2 | 9.3 | 22.4 | 22.4 | 25.2 | 0 | 4186 | |
| QC2 | 11.6 | −4.4 | 18.6 | 11.2 | 11.2 | 12.6 | 0 | 5800 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 | Mode 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 60° | 0.25155 | 0.55443 | 1.02786 | 1.67456 | 2.45837 | 2.48360 | 3.06823 | 3.47521 | 3.78644 |
| 90° | 0.16669 | 0.46087 | 0.93422 | 1.58251 | 1.69499 | 2.12678 | 2.39382 | 3.00043 | 3.08747 |
| 120° | 0.13666 | 0.42830 | 0.90155 | 1.34053 | 1.55034 | 1.65306 | 2.36242 | 2.52675 | 2.78594 |
| 150° | 0.12279 | 0.41327 | 0.88645 | 1.15013 | 1.37255 | 1.53545 | 2.26953 | 2.34788 | 2.63863 |
| 180° | 0.11528 | 0.40512 | 0.87826 | 1.03778 | 1.19043 | 1.52736 | 2.11632 | 2.33999 | 2.55534 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 | Mode 9 | |
|---|---|---|---|---|---|---|---|---|---|
| K* = 0 | 0.83093 | 1.62415 | 2.70589 | 4.06200 | 5.48448 | 5.66161 | 5.67968 | 6.74528 | 7.11564 |
| K* = 0.3 | 0.74856 | 1.36473 | 2.12847 | 3.01609 | 4.00536 | 5.17402 | 5.46680 | 5.66087 | 6.30747 |
| K* = 0.6 | 0.69391 | 1.22516 | 1.87138 | 2.62394 | 3.47311 | 4.50307 | 5.44953 | 5.52350 | 5.64239 |
| K* = 0.9 | 0.65336 | 1.13344 | 1.71800 | 2.40713 | 3.19707 | 4.17784 | 5.16437 | 5.43269 | 5.62441 |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 | Mode 9 | |
|---|---|---|---|---|---|---|---|---|---|
| K* = 0 | 0.83093 | 1.62415 | 2.70589 | 4.06200 | 5.48448 | 5.66161 | 5.67968 | 6.74528 | 7.11564 |
| K* = 0.3 | 0.74782 | 1.36231 | 2.12296 | 3.00605 | 3.98948 | 5.15054 | 5.46678 | 5.66055 | 6.27623 |
| K* = 0.6 | 0.69318 | 1.22307 | 1.86704 | 2.61649 | 3.46174 | 4.48616 | 5.44951 | 5.50065 | 5.64205 |
| K* = 0.9 | 0.65270 | 1.13167 | 1.71449 | 2.40124 | 3.18810 | 4.16407 | 5.14512 | 5.43267 | 5.62406 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Feng, X.; Zhang, L.; Pan, E.; Gao, Y. Dynamic Analysis of Multilayered Piezoelectric Quasicrystal Three-Dimensional Sector Plates with Imperfect Interfaces. Crystals 2023, 13, 1412. https://doi.org/10.3390/cryst13101412
Wang Y, Feng X, Zhang L, Pan E, Gao Y. Dynamic Analysis of Multilayered Piezoelectric Quasicrystal Three-Dimensional Sector Plates with Imperfect Interfaces. Crystals. 2023; 13(10):1412. https://doi.org/10.3390/cryst13101412
Chicago/Turabian StyleWang, Yuxuan, Xin Feng, Liangliang Zhang, Ernian Pan, and Yang Gao. 2023. "Dynamic Analysis of Multilayered Piezoelectric Quasicrystal Three-Dimensional Sector Plates with Imperfect Interfaces" Crystals 13, no. 10: 1412. https://doi.org/10.3390/cryst13101412
APA StyleWang, Y., Feng, X., Zhang, L., Pan, E., & Gao, Y. (2023). Dynamic Analysis of Multilayered Piezoelectric Quasicrystal Three-Dimensional Sector Plates with Imperfect Interfaces. Crystals, 13(10), 1412. https://doi.org/10.3390/cryst13101412







